Structural Performance of Columns with Glass Fiber-Reinforced Polymer Bars Under Axial Compression
Highlights
- The study experimentally, numerically and analytically investigates GFRP-reinforced concrete columns under axial compression, comparing them with steel-RC columns.
- Load capacity of GFRP-RC columns achieved 85–90% of the load carrying capacity of the steel-reinforced column, with the contribution of GFRP bars of 10–12% of total axial load capacity.
- Reducing stirrup spacing from 75 mm to 50 mm increased load capacity by 15% and ductility by 12%, improving structural behavior.
- Numerical models (ABAQUS) matched experimental results within 7–10% and analytical predictions within 10–15%, confirming the reliability of modified design equations.
- The proposed design factor (1.15) investigated based on tested specimens enhances predictive accuracy in the Indian context, supporting safer adoption of GFRP-RC columns.
- GFRP reinforcement is a viable alternative to conventional steel in corrosive or marine environments, extending service life.
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Study
2.1.1. Material Properties
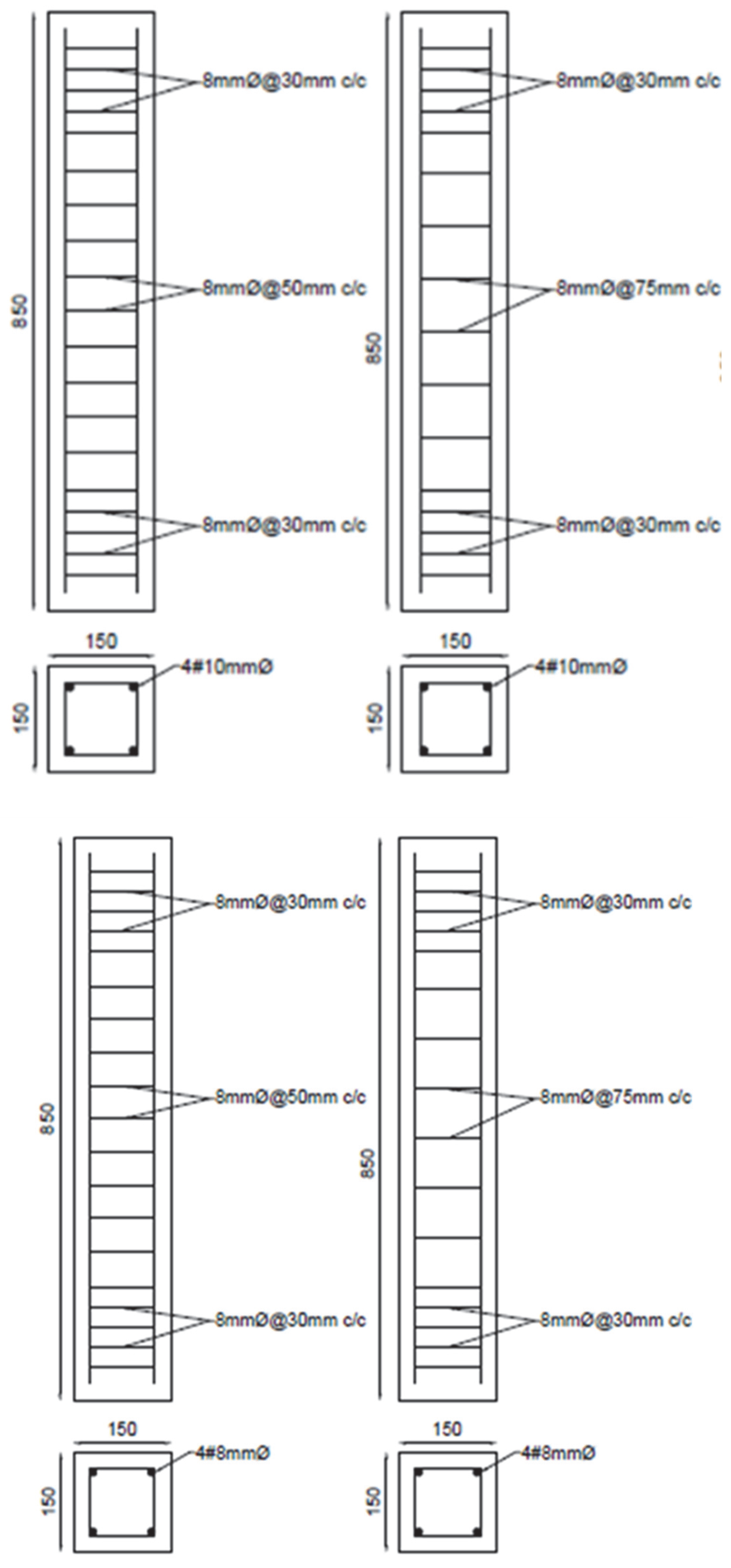
2.1.2. Test Specimens
2.1.3. Casting the Test Specimens
2.1.4. Test Setup
2.2. Software Modeling
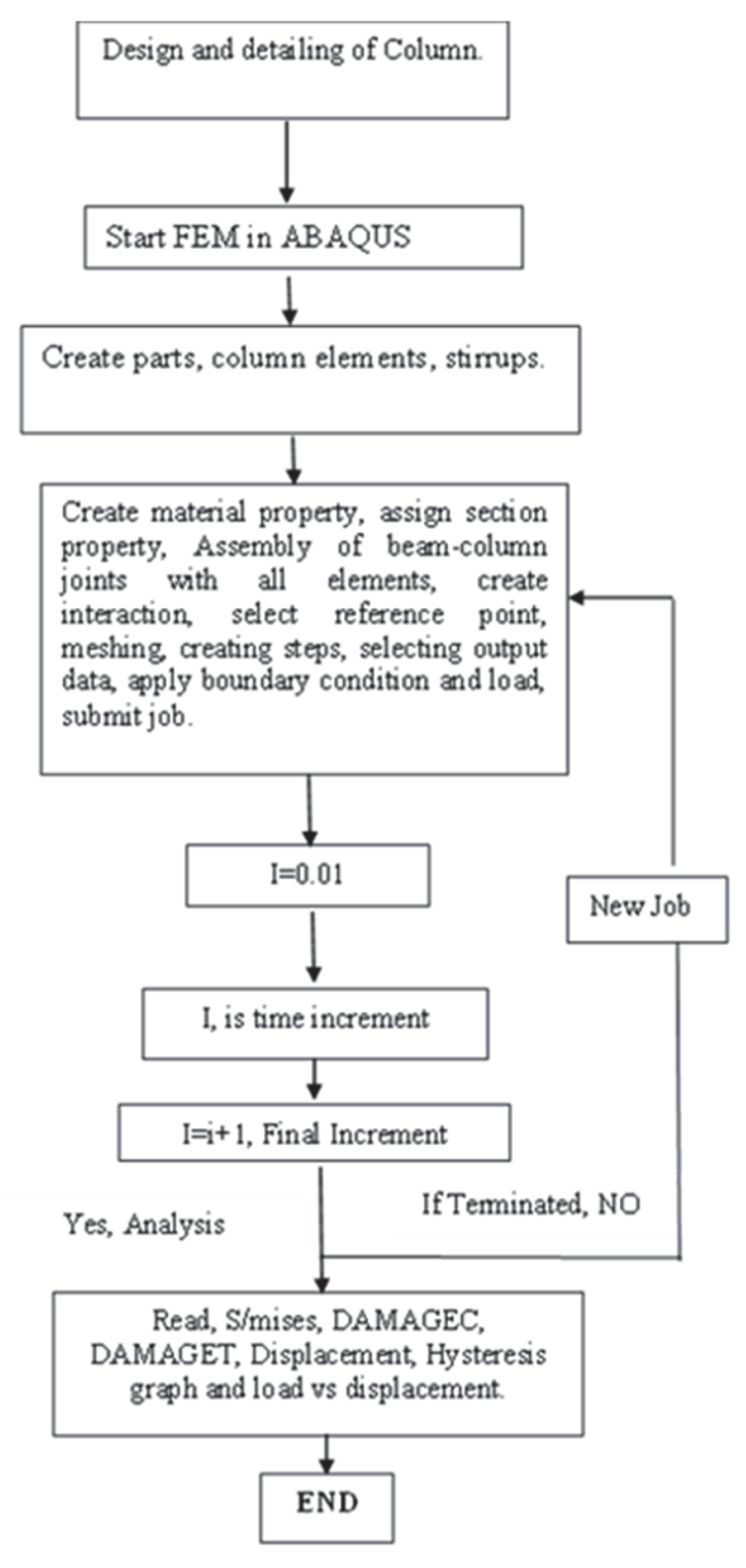
2.2.1. Analysis Process Flow
2.2.2. Assignment of Material Properties
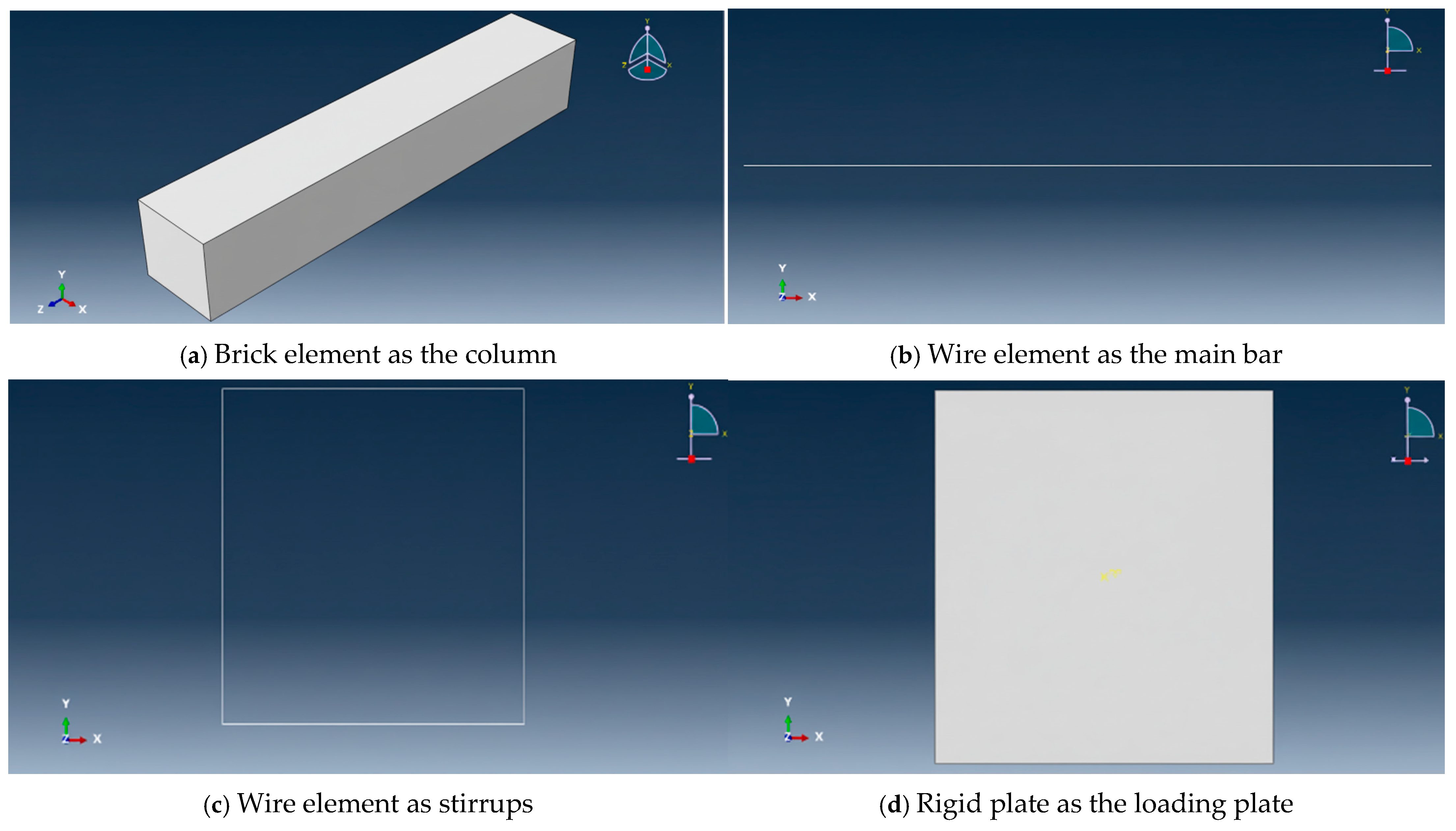
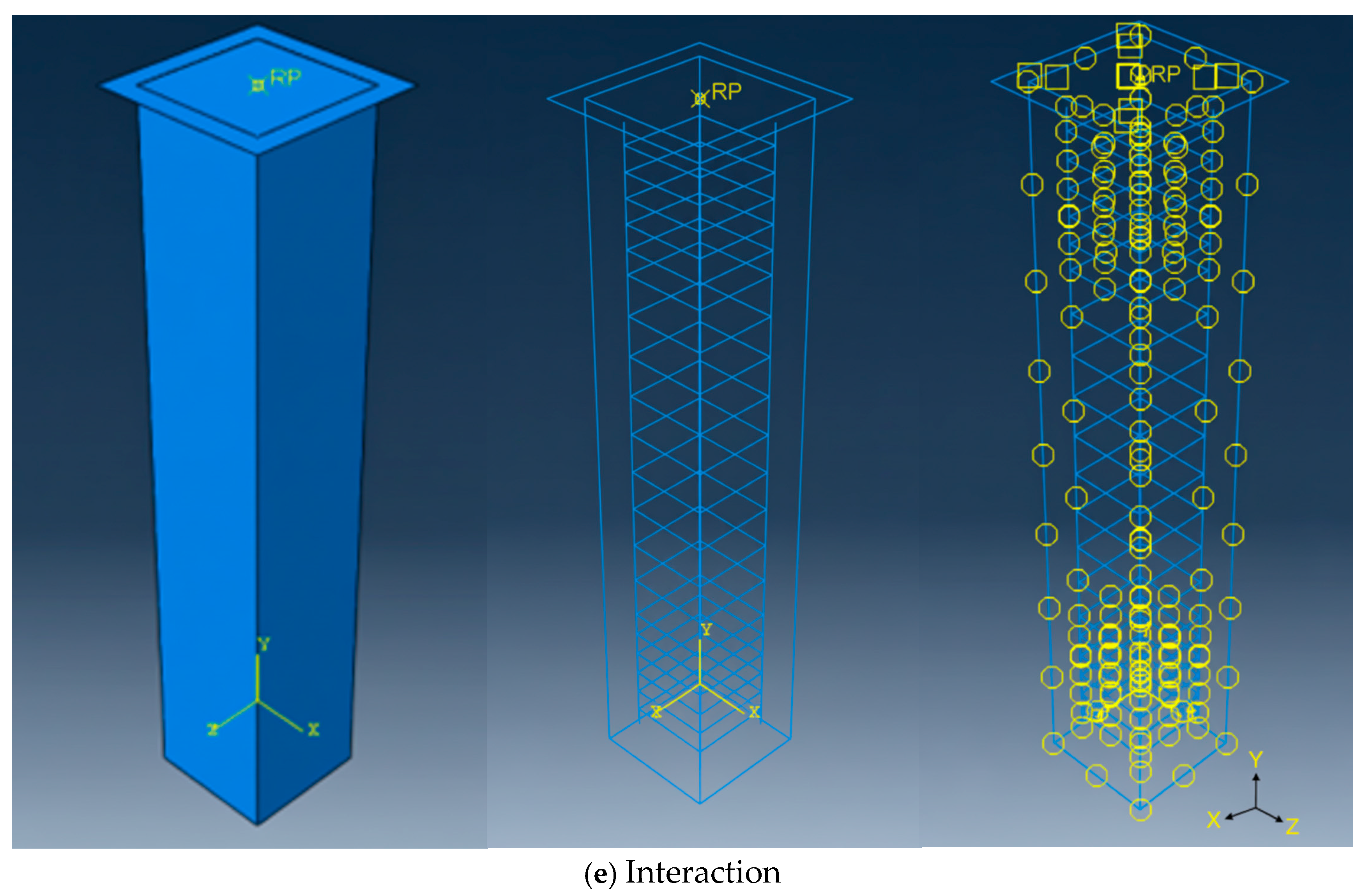
2.2.3. Modeling and Assembly of the Parts
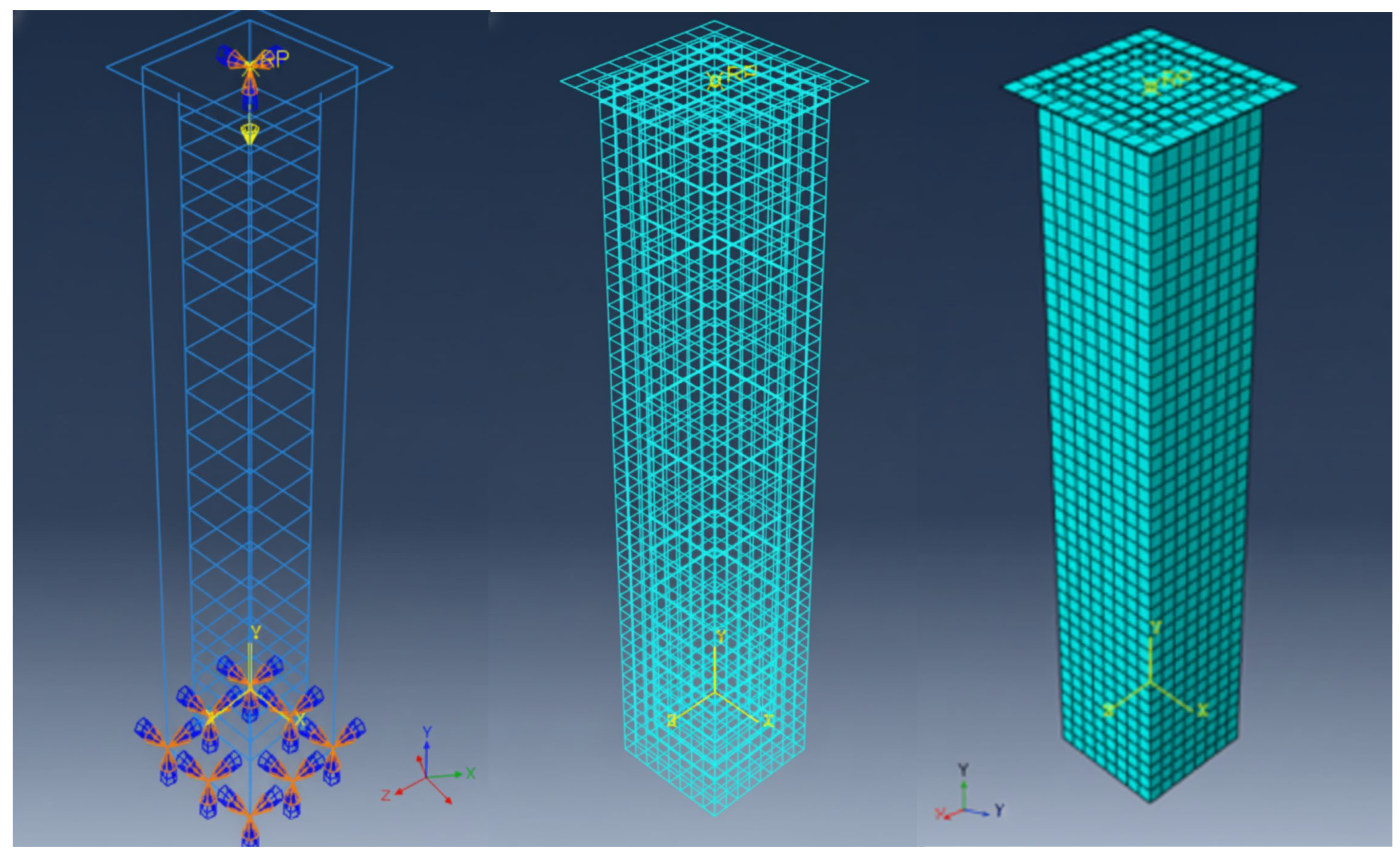
2.2.4. Boundary Conditions, Loading and Meshing
2.2.5. Numerical Output
2.3. Analytical Method
2.3.1. Prediction of the Ultimate Load
2.3.2. Ductility Index
- Displacement ductility index (μ∆).
- Curvature ductility index (μφ).
- Energy-based ductility index.
3. Results and Discussion
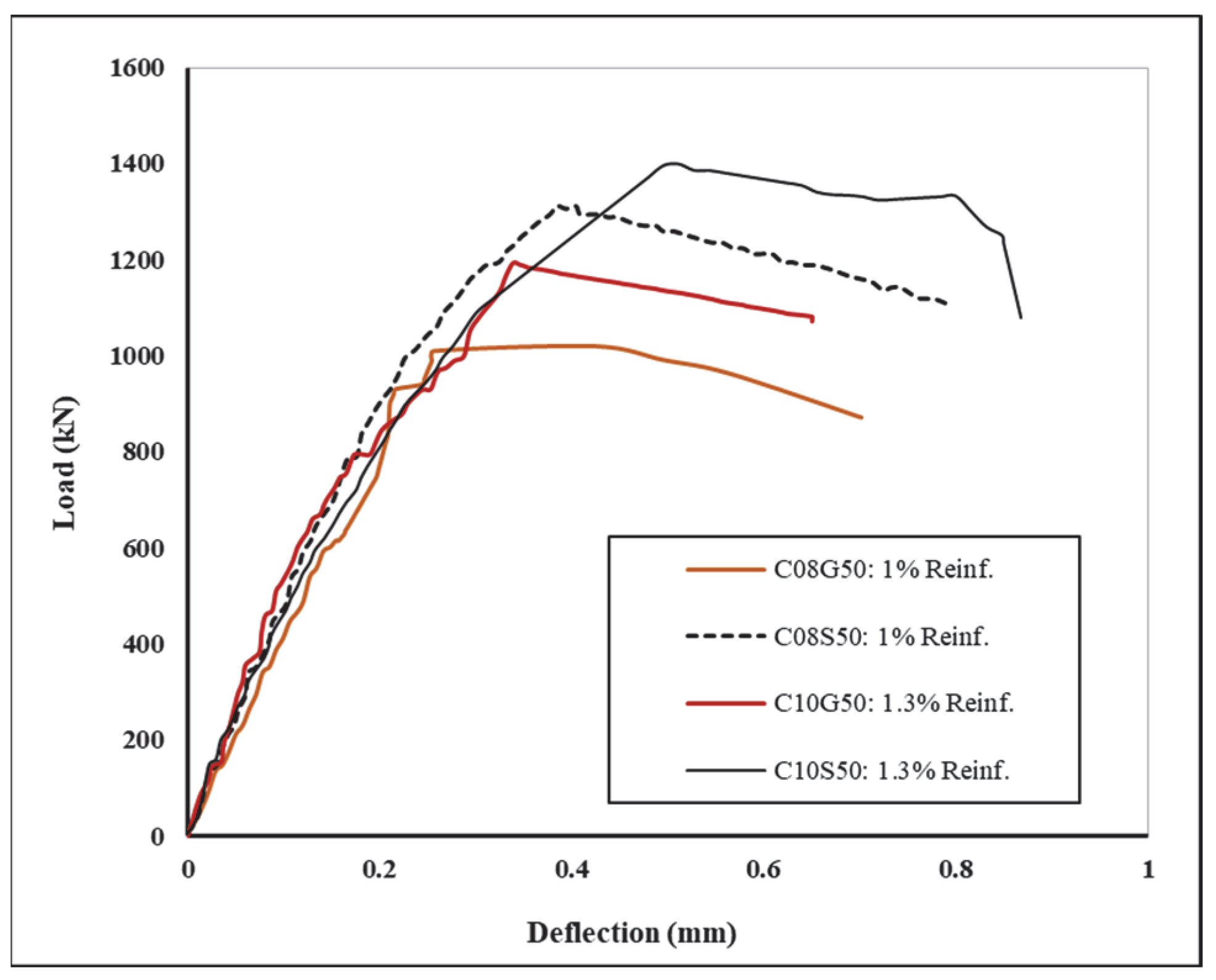
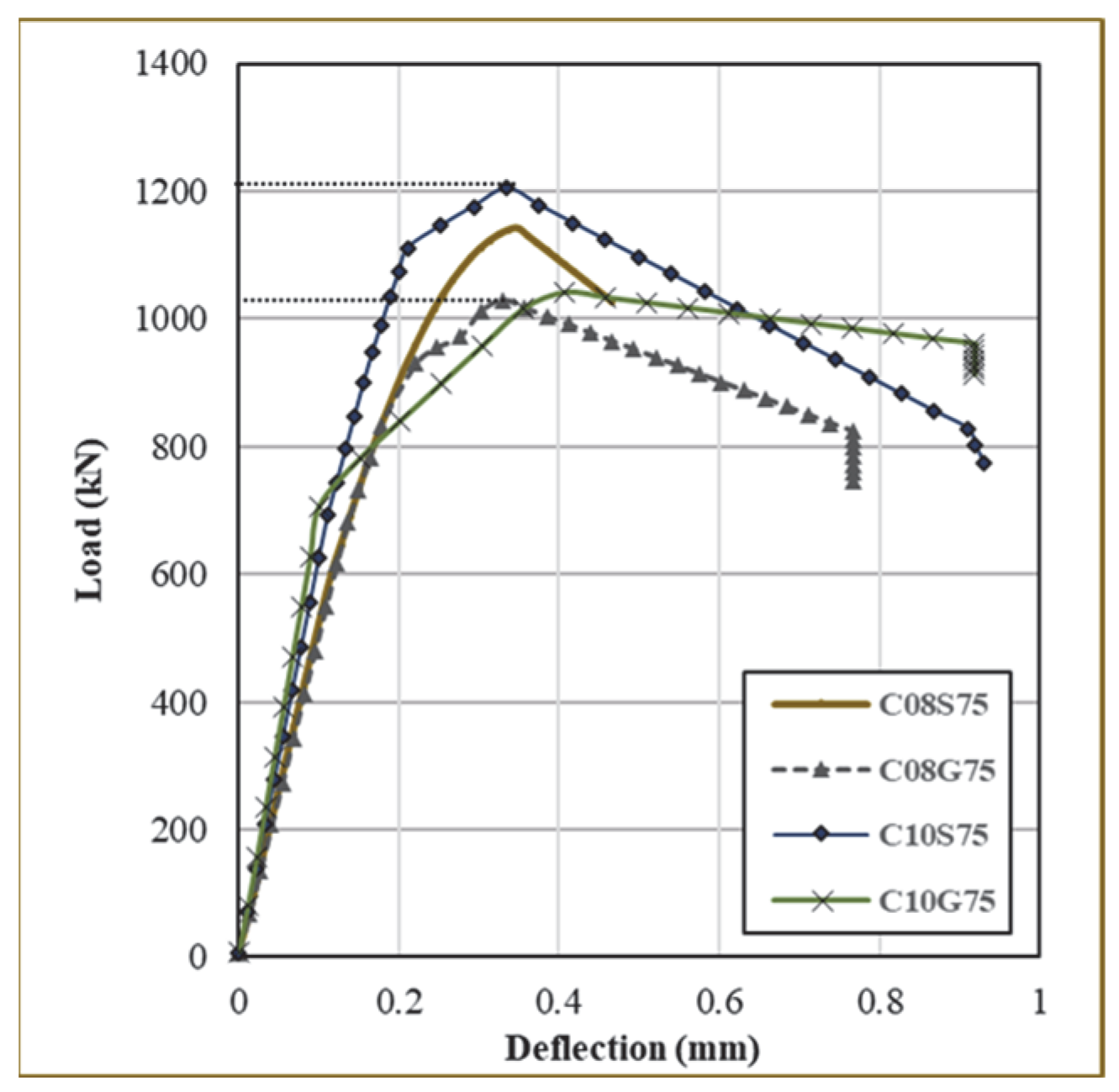
3.1. Experimental Study: Load-Deflection Performance and Failure Pattern
- (a)
- Specimens with a spacing of 50 mm (6db) and a reinforcement ratio of 1%
- (b)
- Specimens with a spacing of 50 mm (5db) and a reinforcement ratio of 1.3%
- (c)
- Specimens with a spacing of 75 mm (9db) and a reinforcement ratio of 1%
- (d)
- Specimens with a spacing of 75 mm (7db) and a reinforcement ratio of 1.3%
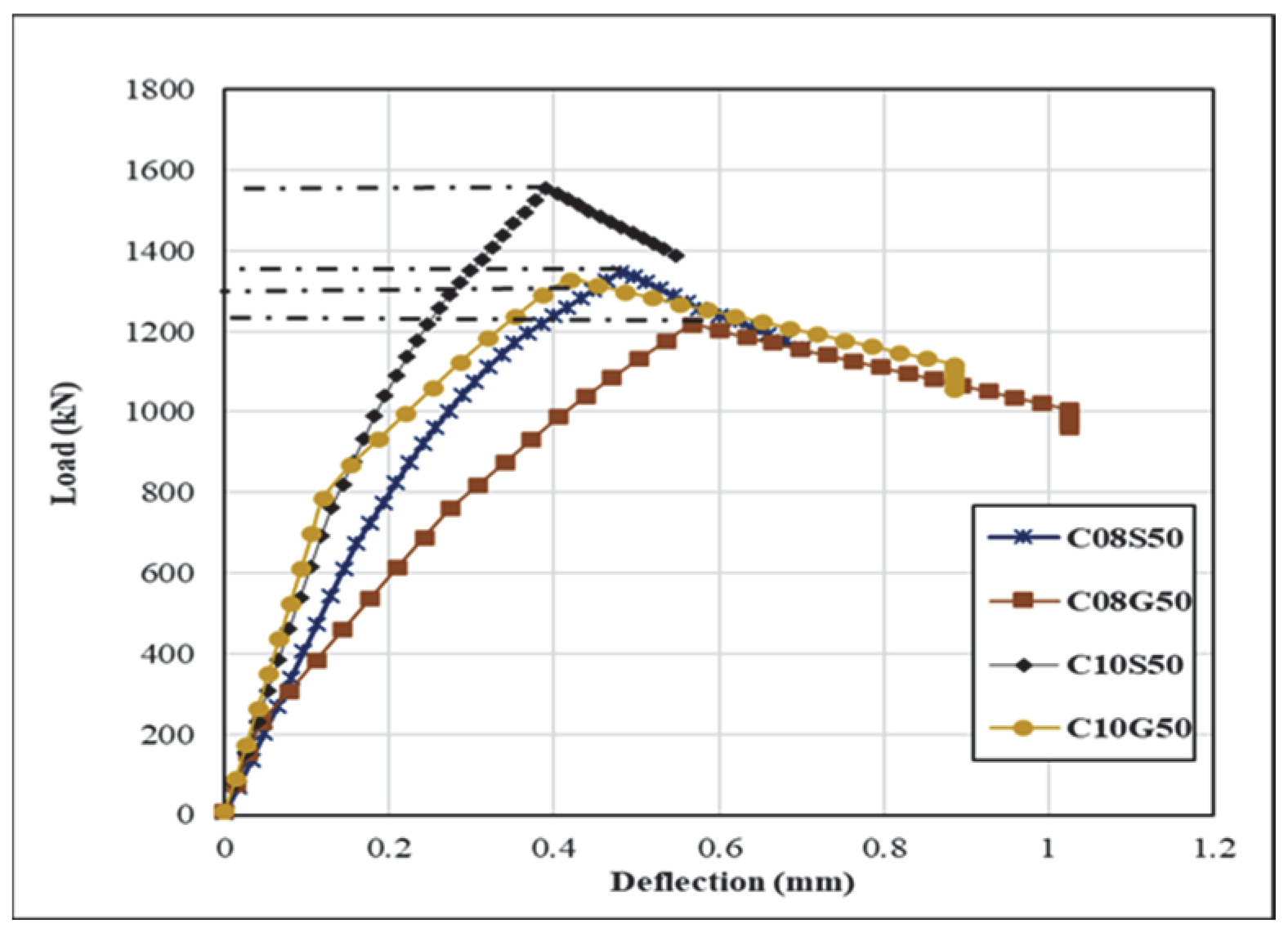
3.2. Numerical Results
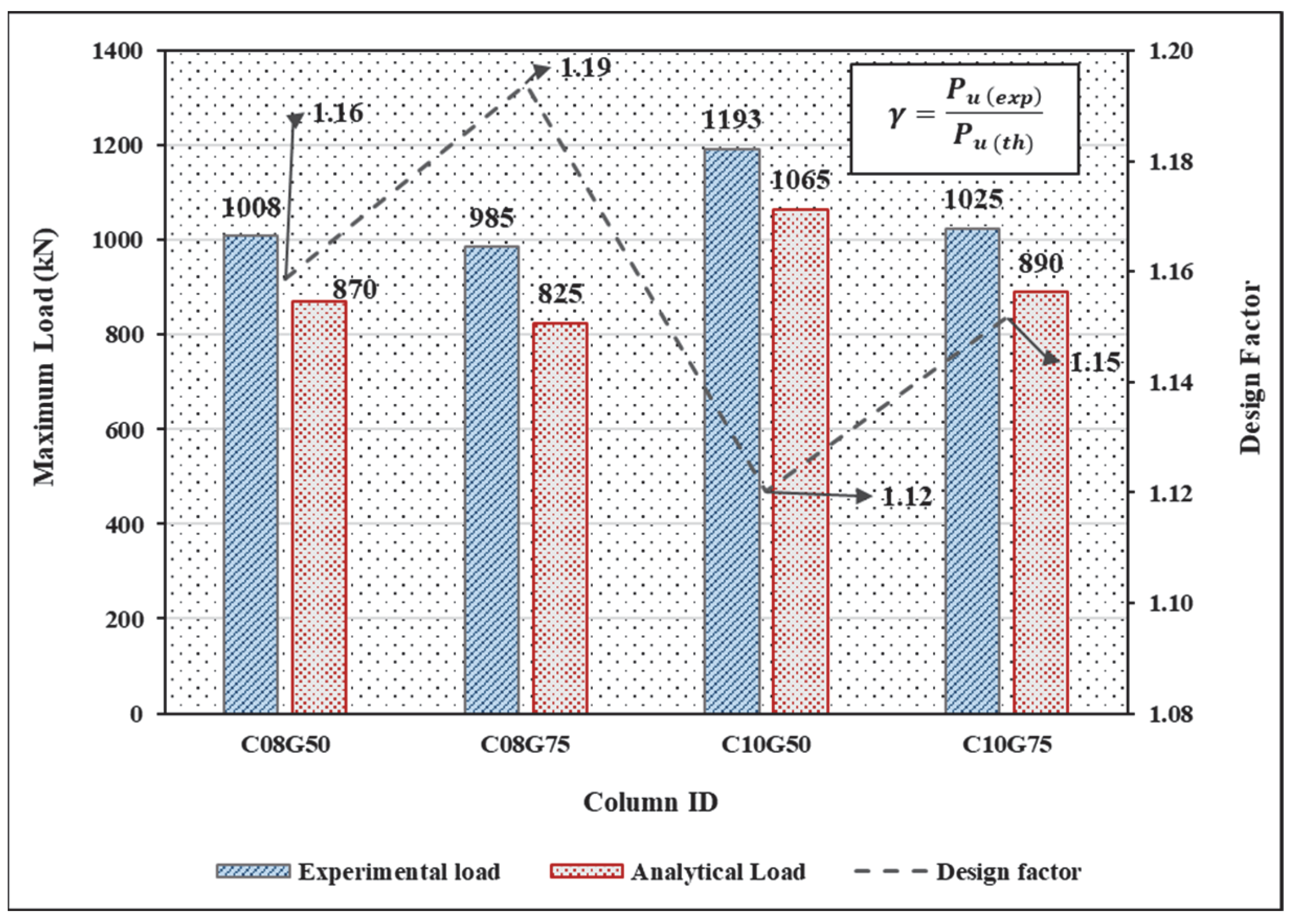
3.3. Analytical Results
Validation of the Design Factor with Data from the Literature
4. Conclusions
- Experimental results
- Software analysis
- Analytical studies
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, V.C.; Wang, S. Flexural Behaviors of Glass Fiber-Reinforced Polymer (GFRP) Reinforced Engineered Cementitious Composite Beams. ACI Mater. J. 2002, 99, 11–21. [Google Scholar] [CrossRef]
- Gu, X.; Dai, Y.; Jiang, J. Flexural Behavior Investigation of Steel-GFRP Hybrid-Reinforced Concrete Beams Based on Experimental and Numerical Methods. Eng. Struct. 2020, 206, 110117. [Google Scholar] [CrossRef]
- Elansary, A.; Farag, A.; Abdeen, M.; Zawam, M.; El-Shabrawy, M. Estimation of Corrosion-Free Reinforcement as Replacement to Steel Rebars for Concrete Walls. J. Inst. Eng. Ser. A 2022, 103, 1073–1087. [Google Scholar] [CrossRef]
- Castela, A.S.; Silva, M.A.G.; Duarte, R.G. Influence of GFRP Confinement of Reinforced Concrete Columns on the Corrosion of Reinforcing Steel in a Salt Water Environment. J. Mater. Civ. Eng. 2014, 27, 04014107. [Google Scholar] [CrossRef]
- Kinjawadekar, T.A.; Patil, S.; Nayak, G.; Kumar, S. Investigation on Glass Fiber-Reinforced Polymer Bars in Concrete Beams. Adv. Polym. Technol. 2025, 2025, 6680051. [Google Scholar] [CrossRef]
- Duan, D.; Ouyang, L.; Gao, W.; Xu, Q.; Liu, W.; Yang, J. Fire Performance of FRP-RC Flexural Members. Polymers 2022, 14, 346. [Google Scholar] [CrossRef]
- Gouda, O.; Asadian, A.; Galal, K. Flexural and Serviceability Behavior of Concrete Beams Reinforced with Ribbed GFRP Bars. J. Compos. Constr. 2022, 26, 04022064. [Google Scholar] [CrossRef]
- Hasan, H.A.; Sheikh, M.N.; Hadi, M.N.S. Performance Evaluation of High Strength Concrete and Steel Fibre High Strength Concrete Columns Reinforced with GFRP Bars and Helices. Constr. Build. Mater. 2017, 134, 297–310. [Google Scholar] [CrossRef]
- Kinjawadekar, T.A.; Patil, S.; Nayak, G.; Kinjawadekar, A.; Kulal, S.A. Experimental Study on Mechanical Properties of Hybrid Fiber-Reinforced Concrete. J. Archit. Eng. 2024, 30, 06024001. [Google Scholar] [CrossRef]
- Hadhood, A.; Mohamed, H.M.; Ghrib, F.; Benmokrane, B. Efficiency of Glass-Fiber Reinforced-Polymer (GFRP) Discrete Hoops and Bars in Concrete Columns under Combined Axial and Flexural Loads. Compos. B Eng. 2017, 114, 223–236. [Google Scholar] [CrossRef]
- Pandey, A.K.P.K.; Dada, M.; Patton, M.L.; Adak, D. A Comparative Review on the Structural Behaviour of GFRP Rebars with Conventional Steel Rebars in Reinforced Concrete Columns. Innov. Infrastruct. Solut. 2024, 9, 373. [Google Scholar] [CrossRef]
- Elkafrawy, M.; Gowrishankar, P.; Aswad, N.G.; Alashkar, A.; Khalil, A.; AlHamaydeh, M.; Hawileh, R. GFRP-Reinforced Concrete Columns: State-of-the-Art, Behavior, and Research Needs. Buildings 2024, 14, 3131. [Google Scholar] [CrossRef]
- Syed, A.U.; Goldack, A. Slenderness Limit for GFRP Reinforced Concrete Columns Based on Axial Force Ratio. Eng. Struct. 2024, 298, 117026. [Google Scholar] [CrossRef]
- Abadel, A.; Alenzi, S.; Almusallam, T.; Abbas, H.; Al-Salloum, Y. Shear Behavior of Self-Consolidating Concrete Deep Beams Reinforced with Hybrid of Steel and GFRP Bars. Ain Shams Eng. J. 2023, 18, e01872. [Google Scholar] [CrossRef]
- Yoo, S.W.; Choo, J.F. Behavior of CFRP-Reinforced Concrete Columns at Elevated Temperatures. Constr. Build. Mater. 2022, 358, 129425. [Google Scholar] [CrossRef]
- Arczewska, P.; Polak, M.A.; Penlidis, A. Relation between Tensile Strength and Modulus of Rupture for GFRP Reinforcing Bars. J. Mater. Civ. Eng. 2019, 31, 04018362. [Google Scholar] [CrossRef]
- Hossain, K.M.A.; Ametrano, D.; Lachemi, M. Bond Strength of GFRP Bars in Ultra-High Strength Concrete Using RILEM Beam Tests. J. Build. Eng. 2017, 10, 69–79. [Google Scholar] [CrossRef]
- Tu, J.; Gao, K.; He, L.; Li, X. Experimental Study on the Axial Compression Performance of GFRP-Reinforced Concrete Square Columns. Adv. Struct. Eng. 2019, 22, 1554–1565. [Google Scholar] [CrossRef]
- Ali, M.A.; El-Salakawy, E. Seismic Performance of GFRP-Reinforced Concrete Rectangular Columns. J. Compos. Constr. 2016, 20, 04015074. [Google Scholar] [CrossRef]
- Youssef, J.; Hadi, M.N.S. Axial Load-Bending Moment Diagrams of GFRP Reinforced Columns and GFRP Encased Square Columns. Constr. Build. Mater. 2017, 135, 550–564. [Google Scholar] [CrossRef]
- Zadeh, H.J.; Nanni, A. Design of RC Columns Using Glass FRP Reinforcement. J. Compos. Constr. 2013, 17, 294–304. [Google Scholar] [CrossRef]
- El-Gamal, S.; AlShareedah, O. Behavior of Axially Loaded Low Strength Concrete Columns Reinforced with GFRP Bars and Spirals. Eng. Struct. 2020, 216, 110732. [Google Scholar] [CrossRef]
- Raza, A.; El Ouni, M.H.; uz Zaman Khan, Q.; Berradia, M. Structural Assessment of Eccentrically Loaded GFRP Reinforced Circular Concrete Columns: Experiments and Finite Element Analysis. Compos. Struct. 2021, 275, 114528. [Google Scholar] [CrossRef]
- Pantelides, C.P.; Asce, M.; Gibbons, M.E.; Reaveley, L.D. Axial Load Behavior of Concrete Columns Confined with GFRP Spirals. J. Compos. Constr. 2013, 6, 305–313. [Google Scholar] [CrossRef]
- Bank, L.C.; Campbell, T.I.; Dolan, C.W. Guide for the Design and Construction of Concrete Reinforced with FRP Bars Reported by ACI Committee 440. Concrete 2003, 322, 1–42. [Google Scholar] [CrossRef]
- Abdallah, A.E.M.; El-Salakawy, E. Confinement Properties of GFRP-Reinforced Concrete Circular Columns under Simulated Seismic Loading. J. Compos. Constr. 2021, 25, 04020088. [Google Scholar] [CrossRef]
- Luca, A.D.; Asce, M.; Nardone, F.; Matta, F.; Asce, A.M.; Nanni, A.; Asce, F.; Lignola, G.P.; Prota, A. Structural Evaluation of Full-Scale FRP-Confined Reinforced Concrete Columns. J. Compos. Constr. 2011, 15, 112–123. [Google Scholar] [CrossRef]
- Raza, A.; Ali, B.; Asad Nawaz, M.; Ahmed, I. Structural Performance of FRP-RC Compression Members Wrapped with FRP Composites. Structures 2020, 27, 1693–1709. [Google Scholar] [CrossRef]
- Tobbi, H.; Farghaly, A.S.; Benmokrane, B. Behavior of Concentrically Loaded Fiber-Reinforced Polymer Reinforced Concrete Columns with Varying Reinforcement Types and Ratios. ACI Struct. J. 2014, 111, 375–385. [Google Scholar] [CrossRef]
- Karimipour, A.; Mohebbi Najm Abad, J.; Fasihihour, N. Predicting the Load-Carrying Capacity of GFRP-Reinforced Concrete Columns Using ANN and Evolutionary Strategy. Compos. Struct. 2021, 275. [Google Scholar] [CrossRef]
- Sümer, Y.; Öztemel, M. Investigation of the Effect of GFRP Reinforcement Bars on the Flexural Strength of Reinforced Concrete Beams Using the Finite Element Method. Fibers 2025, 13, 125. [Google Scholar] [CrossRef]
- IS 456:2000; Plain and Reinforced Concrete. Bureau of Indian Standard: New Delhi, India, 2000.
- IS 10262:2019; Concrete Mix Proportioning—Guidelines. Bureau of Indian Standard: New Delhi, India, 2019.
- Ahmad, H.; Elnemr, A.; Ali, N.; Hussain, Q.; Chaiyasarn, K.; Joyklad, P. Finite Element Analysis of Glass Fiber-Reinforced Polymer-(Gfrp) Reinforced Continuous Concrete Beams. Polymers 2021, 13, 4468. [Google Scholar] [CrossRef]
- Afifi, M.Z.; Mohamed, M.H.; Benmokrane, B. Axial Capacity of Circular Concrete Columns Reinforced with GFRP Bars and Spirals. J. Compos. Constr. 2013, 18, 04013017. [Google Scholar] [CrossRef]
- Mohamed, H.M.; Afifi, M.Z.; Benmokrane, B. Performance Evaluation of Concrete Columns Reinforced Longitudinally with FRP Bars and Confined with FRP Hoops and Spirals under Axial Load. J. Bridge Eng. 2014, 19, 04014020. [Google Scholar] [CrossRef]
- Al-Salloum, H.A.; Elsanadedy, H.; Abbas, H.; Almusallam, T.; Abadel, A.; Al-Salloum, Y. Investigating the Performance of Basalt FRP-reinforced Concrete Columns: Experimental and Analytical Insights. Arch. Civ. Mech. Eng. Publ. Model 2024, 24, 216. [Google Scholar]
- Cao, Q.; Ju, H.; Wu, Z.; Ma, Z.J. Experimental Study on Seismic Performance of GFRP and Highly Ductile Stainless Steel Hybrid Reinforced Concrete Columns. Eng. Struct. 2025, 322, 119130. [Google Scholar] [CrossRef]
- Mohammed, S.A.; Said, A.M.I. Analysis of Concrete Beams Reinforced by GFRP Bars with Varying Parameters. J. Mech. Behav. Mater. 2022, 31, 767–774. [Google Scholar] [CrossRef]
- Karim, H.; Sheikh, M.N.; Hadi, M.N.S. Axial Load-Axial Deformation Behaviour of Circular Concrete Columns Reinforced with GFRP Bars and Helices. Constr. Build. Mater. 2016, 112, 1147–1157. [Google Scholar] [CrossRef]
- Khan, Q.S.; Sheikh, M.N.; Hadi, M.N.S. Axial-Flexural Interactions of GFRP-CFFT Columns with and without Reinforcing GFRP Bars. J. Compos. Constr. 2017, 21, 04016109. [Google Scholar] [CrossRef]

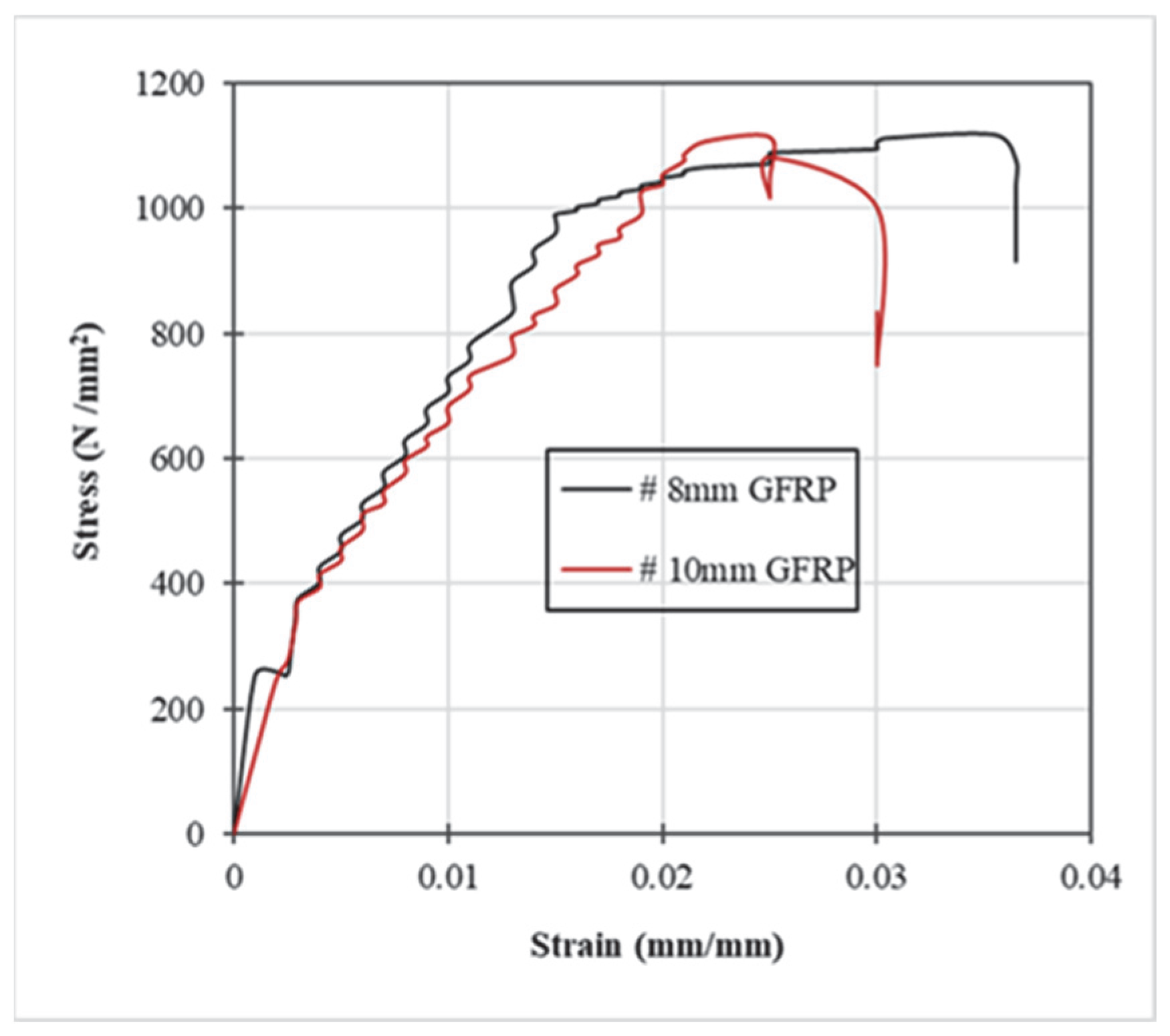








| Grade | Cement (kg) | Coarse Aggregate (kg) | Fine Aggregate (kg) | W/C Ratio | Water (Liter) | Mix Proportion |
|---|---|---|---|---|---|---|
| M30 | 450.00 | 500.00 | 892.00 | 0.42 | 189.00 | 1:1.25:2.23 |
| Grade | W/C Ratio | Compression Strength (MPa) | Split Tension Strength (MPa) | Flexural Strength (MPa) |
|---|---|---|---|---|
| M30 | 0.42 | 41.15 | 3.85 | 6.58 |
| Type of Reinforcement | Strength in Tension MPa | Elastic Modulus GPa | Relative Extension % |
|---|---|---|---|
| GFRP | 1100 | 51.5 | 2.04 |
| Steel | 540 | 210 | 12 |
| Specimen | Number of Specimens | Type of Main Reinforcement | Main Reinforcement: Diameter of Bar (mm) | Transverse Steel Reinforcement (mm) | Spacing (mm) |
|---|---|---|---|---|---|
| C10-S50 | 2 | Steel | 10 | 8 mm | 50 mm |
| C10-S75 | 2 | 8 mm | 75 mm | ||
| C08-S50 | 2 | 08 | 8 mm | 50 mm | |
| C08-S75 | 2 | 8 mm | 75 mm | ||
| C10-G50 | 2 | GFRP | 10 | 8 mm | 50 mm |
| C10-G75 | 2 | 8 mm | 70 mm | ||
| C08-G50 | 2 | 08 | 8 mm | 50 mm | |
| C08-G75 | 2 | 8 mm | 75 mm |
| Properties | Value |
|---|---|
| Concrete | |
| Density | 2.5 × 10−5 N/mm3 |
| Poisson’s ration | 0.2 |
| Young’s modulus | 27,386.13 N/mm2 |
| Cover | 25 mm |
| Steel | |
| Density | 7.85 × 10−5 N/mm3 |
| Poisson’s ratio | 0.3 |
| Elastic modulus | 210,000 N/mm2 |
| GFRP | |
| Density | 2.0 × 10−5 N/mm3 |
| Poisson’s ratio | 0.3 |
| Elastic modulus | 50 N/mm2 |
| Parameters | Ψ | Ε | Fb0/fc0 | K | Μ |
|---|---|---|---|---|---|
| Values | 310 | 0.1 | 1.16 | 0.667 | 0.0001 |
| Grade of Concrete | Spacing of Stirrups | Column ID | Experimental Analysis | Numerical Analysis | ||||
|---|---|---|---|---|---|---|---|---|
| Load- Bearing Capacity (kN) | Deflection at Maximum Load (mm) | Ductility Index µ | Load-Bearing Capacity (kN) | Deflection at Maximum Load (mm) | Ductility Index µ | |||
| M30 | 50 | C08S50 | 1295 | 0.40 | 0.70 | 1346 | 0.45 | 0.73 |
| C08G50 | 1008 | 0.35 | 0.71 | 1216 | 0.56 | 0.75 | ||
| C10S50 | 1398 | 0.50 | 0.74 | 1555 | 0.42 | 0.70 | ||
| C10G50 | 1193 | 0.35 | 0.80 | 1327 | 0.42 | 0.70 | ||
| 75 | C08S75 | 1130 | 0.32 | 0.60 | 1142 | 0.35 | 0.65 | |
| C08G75 | 985 | 0.65 | 0.69 | 1030 | 0.33 | 0.60 | ||
| C10S75 | 1230 | 0.30 | 0.64 | 1205 | 0.32 | 0.62 | ||
| C10G75 | 1025 | 0.30 | 0.70 | 1040 | 0.41 | 0.64 | ||
| Dataset | Steel-Reinforced Member vs. GFRP-Reinforced Member p Value (Significance α = 0.05) | ||
|---|---|---|---|
| Load-Bearing Capacity (kN) | Deflection at Maximum Load (mm) | Ductility Index µ | |
| Experimental | 0.12 | 0.32 | 0.31 |
| Numerical | 0.16 | 0.51 | 0.68 |
| Specimen ID | Strain at Maximum Load |
|---|---|
| C08G50 | 0.0030 |
| C10G50 | 0.0037 |
| C08G75 | 0.0035 |
| C10G75 | 0.0039 |
| 0.0035 |
| Reference | Type of Column | Type of Load | (kN) | Longitudinal Reinforcement Ratio | Modified (kN) (Equation (6)) | (kN) | |
|---|---|---|---|---|---|---|---|
| [29] | Short | Concentric | 1050 | 1–2% | 1207.50 | 1150 | 4.72 |
| [39] | 1300 | 1–2% | 1495.00 | 1400 | 6.35 | ||
| [34] | 1250 | 1–2.5% | 1437.5 | 1350 | 6.08 | ||
| [40] | 1750 | 1.5–3.5% | 2012.5 | 1800 | 10.53 | ||
| [36] | 928 | 0.8–1.1% | 1067.2 | 943.20 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinjawadekar, T.A.; Patil, S.; Nayak, G. Structural Performance of Columns with Glass Fiber-Reinforced Polymer Bars Under Axial Compression. Fibers 2025, 13, 156. https://doi.org/10.3390/fib13110156
Kinjawadekar TA, Patil S, Nayak G. Structural Performance of Columns with Glass Fiber-Reinforced Polymer Bars Under Axial Compression. Fibers. 2025; 13(11):156. https://doi.org/10.3390/fib13110156
Chicago/Turabian StyleKinjawadekar, Trupti Amit, Shantharam Patil, and Gopinatha Nayak. 2025. "Structural Performance of Columns with Glass Fiber-Reinforced Polymer Bars Under Axial Compression" Fibers 13, no. 11: 156. https://doi.org/10.3390/fib13110156
APA StyleKinjawadekar, T. A., Patil, S., & Nayak, G. (2025). Structural Performance of Columns with Glass Fiber-Reinforced Polymer Bars Under Axial Compression. Fibers, 13(11), 156. https://doi.org/10.3390/fib13110156








