Numerical Simulation of Engineering Cementitious Composite Beams Strengthened with Fiber-Reinforced Polymer and Steel Bars

Abstract

In this paper, the flexural performance of the Engineering Cementitious Composite (ECC)-concrete composite beam hybrid reinforced by steel and Fiber Reinforced Polymer (FRP) bars is assessed using nonlinear finite element analysis. The concrete damage plasticity model is used to model the nonlinear behavior of ECC and concrete materials. A perfect bond is assumed at the interface surface between the ECC and concrete. The validity of the numerical model is established through comparison with a previously published experimental study (overall error of about 5.4%). Consequently, the developed model is utilized to consider the effect of hybrid (FRP/steel) tensile reinforcement ratio, thickness of the ECC layer, type of FRP bars, and compressive strength of concrete on the flexure performance. It was evident from the results that the ratio of hybrid (FRP/steel) tensile reinforcement should be carefully chosen to achieve an adequate balance between ductility and carrying load capacity. Additionally, the thickness of the ECC layer plays a crucial role in controlling the hybrid reinforcement’s tensile ratio to prevent rapid failure following the yielding of steel rebars within the ECC layer. Furthermore, the type of FRP bars used in the hybrid reinforcement has influenced the flexural behavior of the composite beam. Conversely, increasing the compressive strength of the concrete has minimal impact on enhancing the mechanical characteristics of the beams, even when considering a change in the type of FRP bars.

1. Introduction

The use of Fiber-Reinforced Polymer (FRP) is on the rise in reinforced concrete (RC) structures. To reduce rust and corrosion problems, the use of FRP bars as an alternative to steel bars is a prime area of research. Compared to steel, FRP bars possess higher tensile strength, a lower weight, higher moisture resistance, higher corrosion resistance, a lower elastic modulus, and lower ductility [1,2,3,4]. The disadvantage of using FRP bars as a prime reinforcement in concrete structures is due to their low ductility, which leads to brittle failure in concrete structures. To overcome the brittle failure of concrete structures reinforced with FRP, some researchers proposed the use of both FRP and steel bars as reinforcement. As a result, enhanced ductility, durability, and corrosion resistance were observed [5,6,7,8,9]. Another alternative to enhance ductility and lower crack width is the use of engineering cementitious composite (ECC) in the tension zone around the reinforcement [10]. ECC properties such as high resistance to erosion, freezing-thawing, and sulfate environments enhance its desirability for use in the construction industry [11,12,13]. Other applications for ECC include repairing bridge decks and aging infrastructure [14,15,16] and retrofitting walls that exhibit seismic loads [17]. Ref. [18] conducted an experimental program to study the flexural performance of concrete beams reinforced by a hybrid system consisting of steel and basalt FRP bars (BFRP). The BFRP showed the same bond strength with concrete as steel bars. In terms of deflection, crack width, and flexural capacity, the hybrid steel and BFRP beams are higher than the RC beams with steel only. The authors also concluded that for structures with high requirements for flexural capacity and low requirements for deflection, hybrid RC beams can be used. Ref. [19] studied the effects of layered ECC-concrete beams on flexural performance. The authors found that the increase in both flexural strength and ductility is proportional to the increase in the ECC thickness in the tension zone. Ref. [20] experimentally and theoretically investigated the effect of using BFRP on the flexural properties of ECC beams and ECC/concrete composite beams. The experimental results showed that using an ECC matrix reinforced by BFRP instead of steel bars improved deformation capacity, strength, and energy dissipation and showed effective resistance to shear failure compared to traditional concrete beams. Refs. [21,22] studied the behavior of concrete/ECC hybrid composite beams reinforced with steel and FRP bars in terms of ductility, energy dissipation, ultimate strength, and stiffness. It was concluded that there is an improvement in the ultimate moment, yield moment, and stiffness of hybrid composite beams when compared to RC beams with the same reinforcement ratio. Also, the energy dissipation of the ECC beam is higher than that of the traditional RC beam and concrete/ECC beam. As the previous studies show, strengthening and repairing the flexural members using a composite of ECC and concrete material reinforced by a combination of steel and FRP bars is a relatively functional mechanism to enhance the flexural behavior of concrete structures. However, since the utilization of this technique is relatively new, there are limited numerical studies on this technique. Therefore, due to the high cost of the ECC and fiber materials for conducting studies, more research is needed to better understand the member’s performance and confirm its effectiveness. The use of non-linear finite element analysis is needed to simulate the behavior of composite hybrid reinforced structural members. The objectives of this research are to develop a non-linear finite element model of ECC-concrete composite beams reinforced with a hybrid FRP and steel bars system that was experimentally studied by [22] for verification purposes and extend the model to study the effect of concrete compressive strength, beam height, steel reinforcement ratio, FRP reinforcement ratio, and type of FRP bars on the composite hybrid beams ductility and load capacity.

2. Materials and Methods

Ref. [22] tested 32-hybrid reinforced composite ECC beams under four-point loading. The beam specimens were divided into eight sequences according to the reinforcement ratio of BFRP and steel bars. Each sequence has four specimens with different ECC layer thicknesses. The strain in the composite beam was measured by placing strain gauges along its height, while its deflection at various points was determined using a displacement transducer at the load point, mid-span point, and support point, as shown in Figure 1 (a more detailed schematic can be found in [22]). The results of [22] are used to verify the nonlinear finite element model developed in this study.

2.1. Material Properties

2.1.1. Concrete

In this study, the compressive behavior of concrete is modeled according to Carreira and Chu [23], and the tension behavior is modeled according to Aslani and Jowkarmeimandi [24], as those models were the most suitable for the data used in the verification section (Section 2.3). The cubic compressive (${\mathrm{f}}_{\mathrm{c}}^{’}$) strength is equal to 30 MPa, Poisson’s ratio (ν) is equal to 0.2, and the ultimate strain (ε_u) is equal to 0.003. The cylinder’s compressive strength is established by multiplying the cube’s compressive strength by 0.8 [25]. The damage in concrete is modeled using the concrete damage plasticity model (CDPM) introduced by [26]. The concrete plastic damage parameters are shown in

Table 1. Concrete plastic damage parameters, [26].

Parameter	Value
Flow potential eccentricity (ϵ)	0.1
Dilation angle (ψ)	30
Compressive meridian at in initial yield (k)	2/3
Viscosity (μ)	0.0005
Initial biaxial compressive yield stress to initial uniaxial compressive yield stress (fb0/fc0)	1.16

.

2.1.2. ECC Material

Ref. [22] tested three prismatic specimens of size 40×40×160 mm to obtain the compressive stress–strain curves of ECC. The compressive stress of ECC recorded was 31.4 MPa, and its corresponding strain was 0.0036. To use the CDPM in [27], the compressive strength must be obtained through testing cylinder specimens; thus, [28] is used to obtain the cylinder compressive strength (27 MPa). As for the tension properties, the tensile strength at first cracking was recorded at 2 MPa with a corresponding strain of 0.00023, and the ultimate tensile strength was recorded at 2.4 MPa with a corresponding strain of 0.025. The tensile stress–strain behavior is modeled as an elastic-strain hardening material.

2.1.3. Steel Reinforcement and Steel Plates

The steel properties used in [22], such as the yield stress (f_y) and ultimate stress (f_u), are summarized in

Table 2. Tensile properties of top and bottom steel bars [22].

Bars Type	Diameter (mm)	Elastic Modulus (GPa)	fy (MPa)	fu (MPa)	Ultimate Strain
Top steel bar	10	198	403	495	0.051
Bottom steel bar	12	199	408	503	0.0675
Stirrups	8	198	406	485	0.075

. The Poisson ratio is equal to 0.3. The reinforcement steel is modeled as an elastic-strain hardening material (bi-linear). The steel plates (used to distribute the loads in the experiment) are defined as an elastic material with a modulus of elasticity of 200 GPa and a Poisson’s ratio of 0.3.

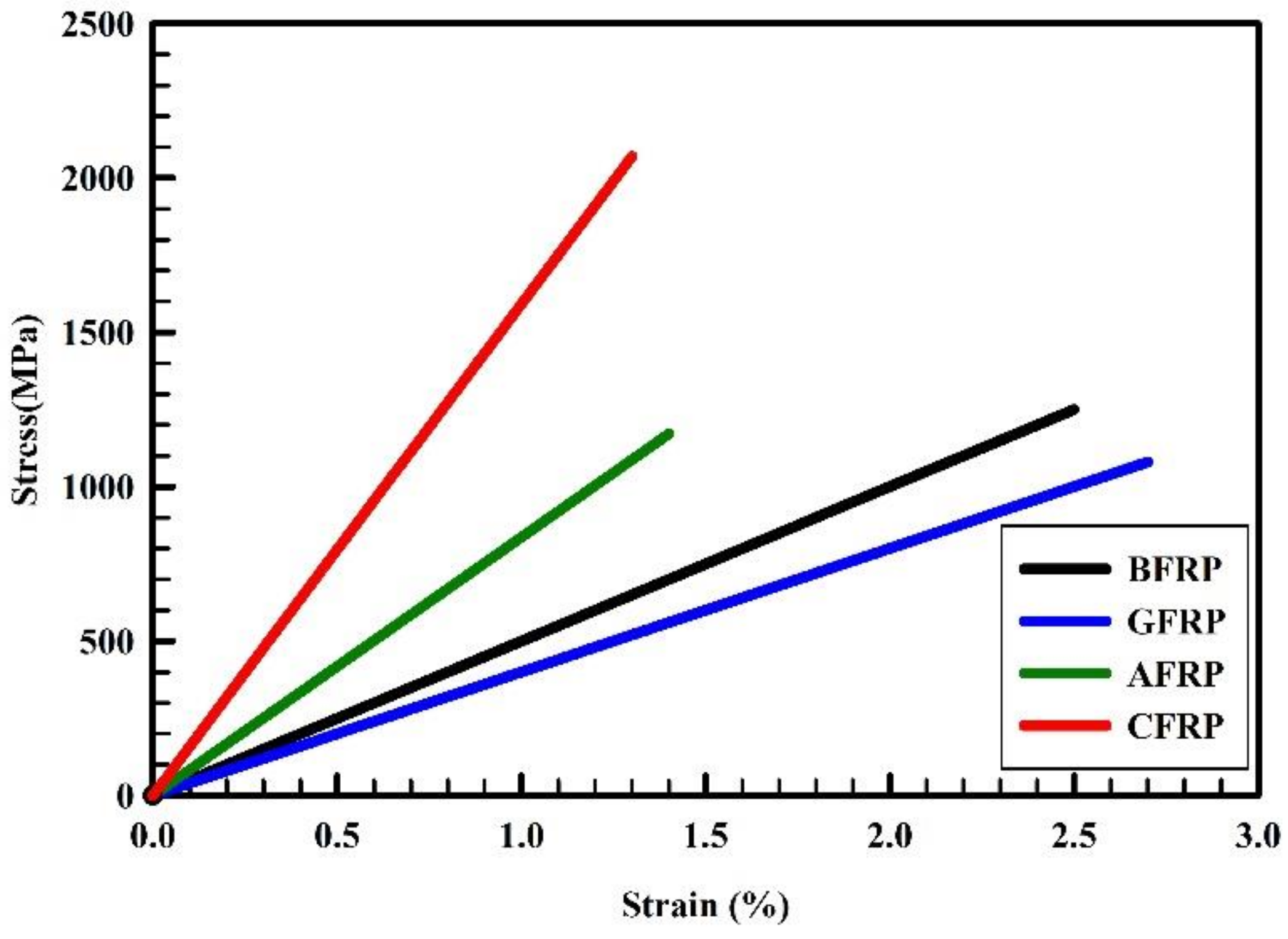
2.1.4. FRP Reinforcement

In this study, four FRP types are used: Aramid FRP (AFRP), Glass FRP (GFRP), Carbon FRP (CFRP), and Basalt FRP (BFRP). BFRP is used for verification of the proposed model. Per [22], BFRP is a linear elastic material with an ultimate tensile strength of 1250 MPa and a modulus of elasticity of 50 GPa. The stress–strain curve of all types of FRP bars is shown in Figure 2.

Table 3. Properties of FRP reinforcement [22,29,30].

Bars Type	Ultimate Tensile Stress (MPa)	Elastic Modulus (GPa)
CFRP	2070	156
AFRP	1172	83
BFRP	1250	50
GFRP	1080	40

shows the properties of the FRP reinforcement.

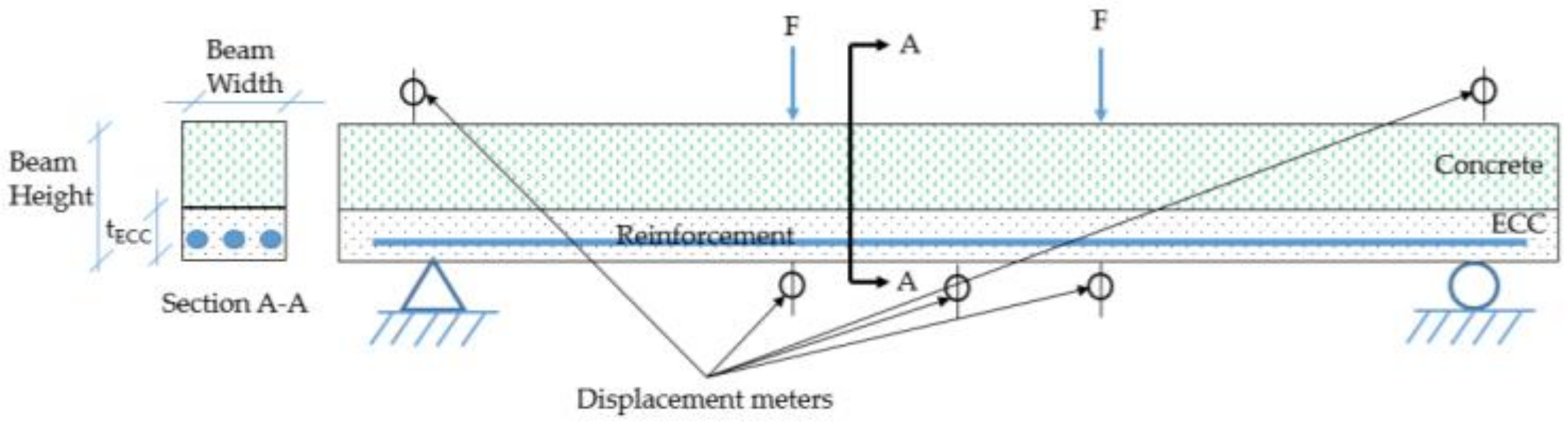
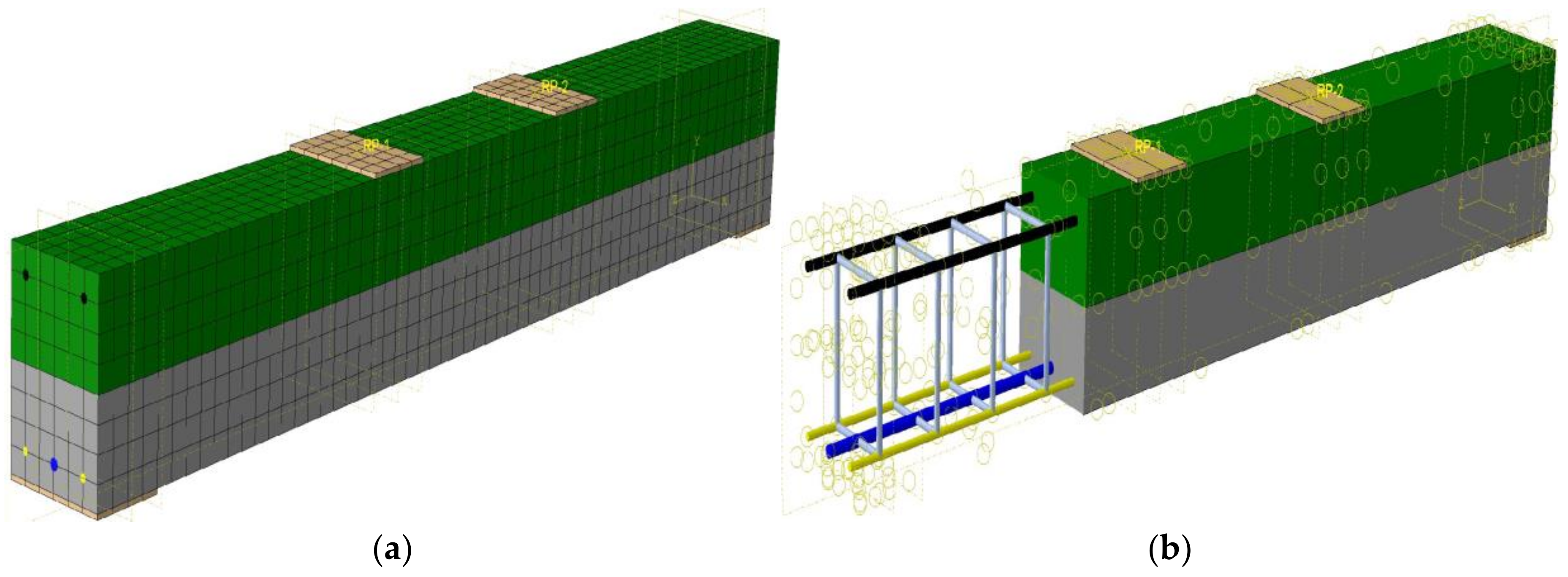
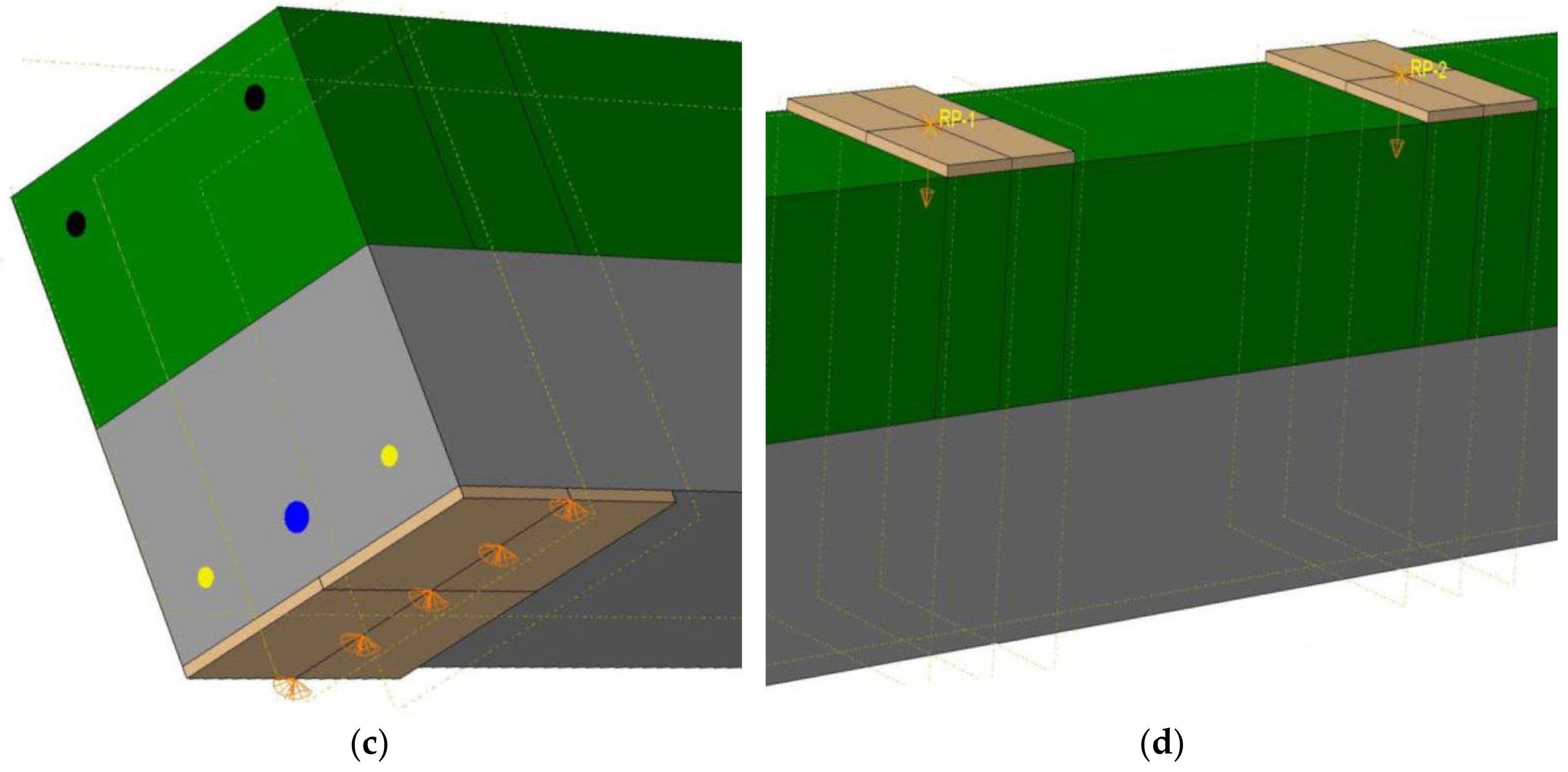
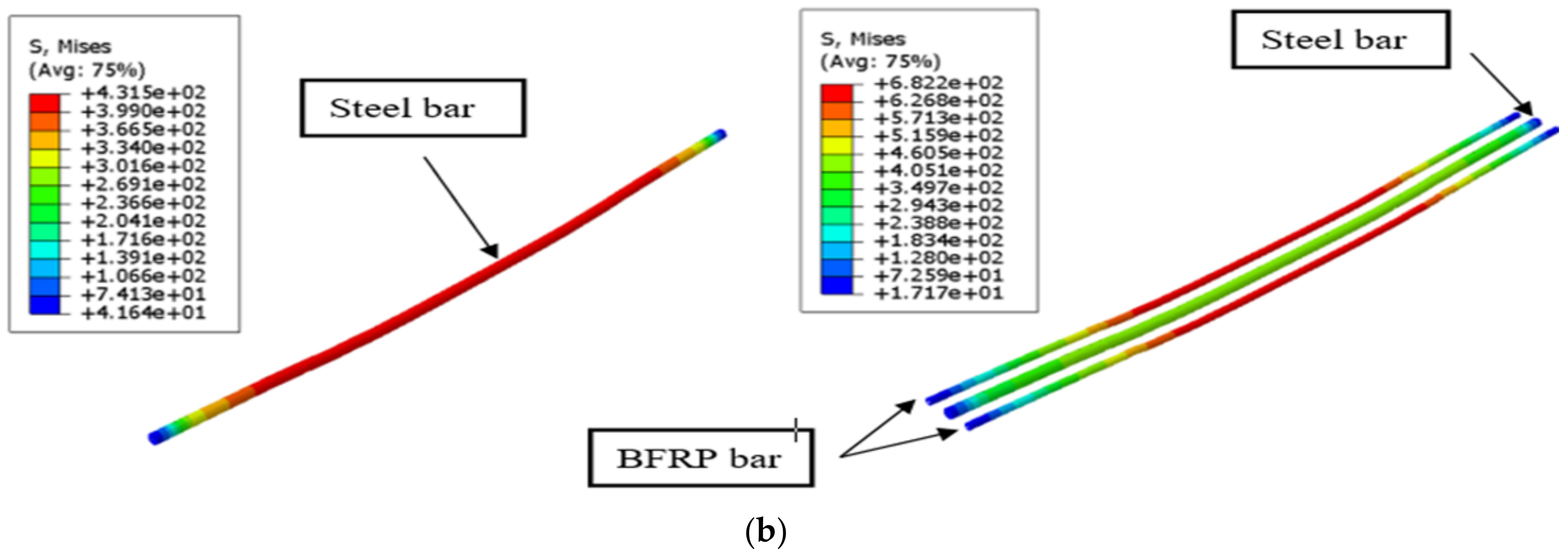
2.2. Nonlinear Finite Element Model (NLFEM)

In this paper, the finite element software ABAQUS/Standard ver. 6.9 [27] is used. The convergence and mesh sensitivity analysis carried out in the verification step (Section 2.3) yielded a medium-mesh size of 25 mm. The experimental study [22] showed no delamination or separation between the ECC layer and concrete; thus, the interface surface between the ECC layer and concrete is assumed to be perfectly bonded. The surface between the support/load steel plates and the beam is tied together to eliminate any relative motion between them, this is achieved by using the tie constraint described in [27]. A perfect bond is assumed between the reinforcement (steel bars, stirrups, FRP bars) and either concrete or ECC. This was characterized using the embedded region constraint in [27]. Both the ECC and concrete are assumed to be the host region and the reinforcement, regardless of its type, as the embedded region. The displacement control method is utilized to apply the load to the simply supported beam. The simply supported boundary conditions are applied along the support’s plates. Details of the finite element model are shown in Figure 3.

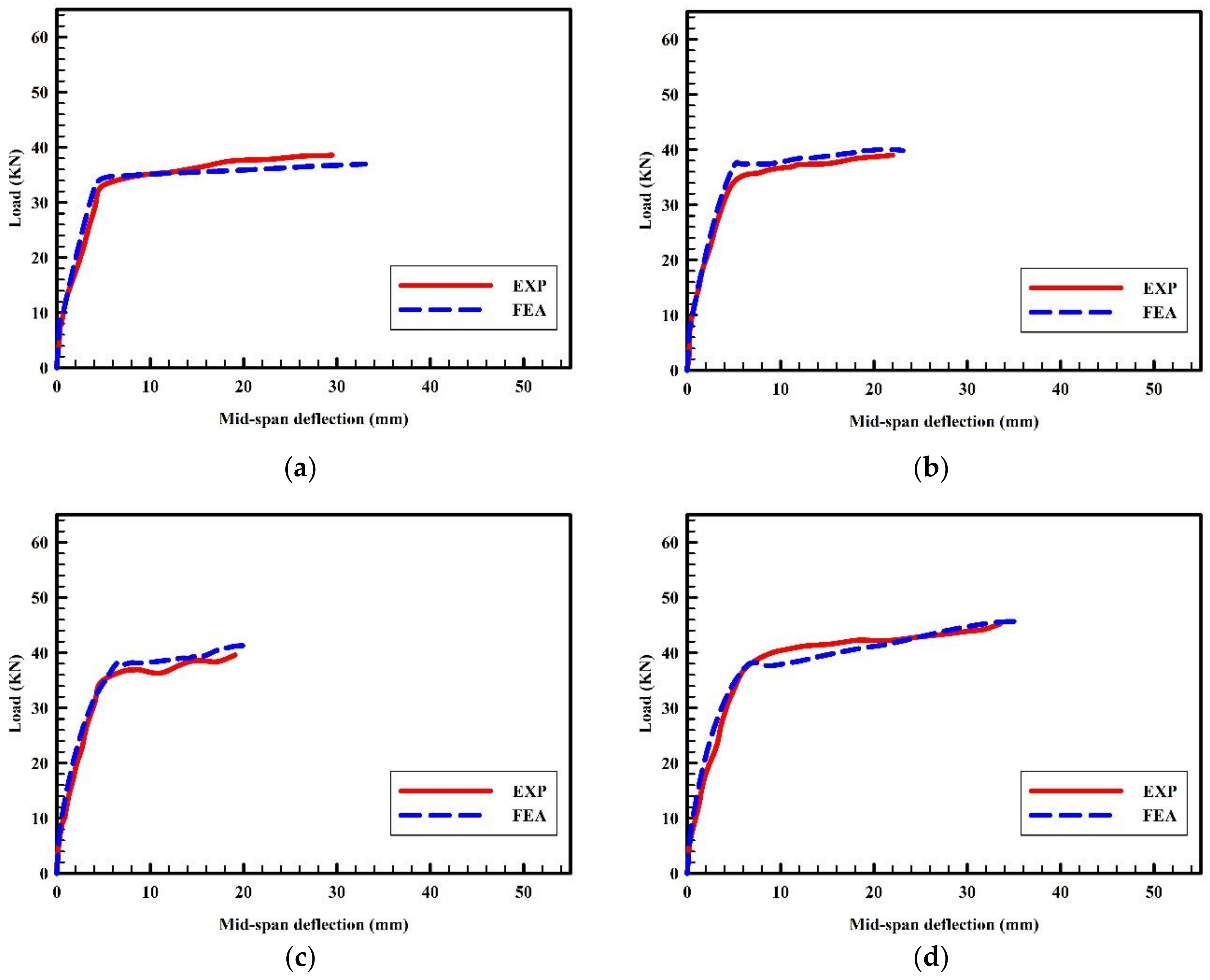
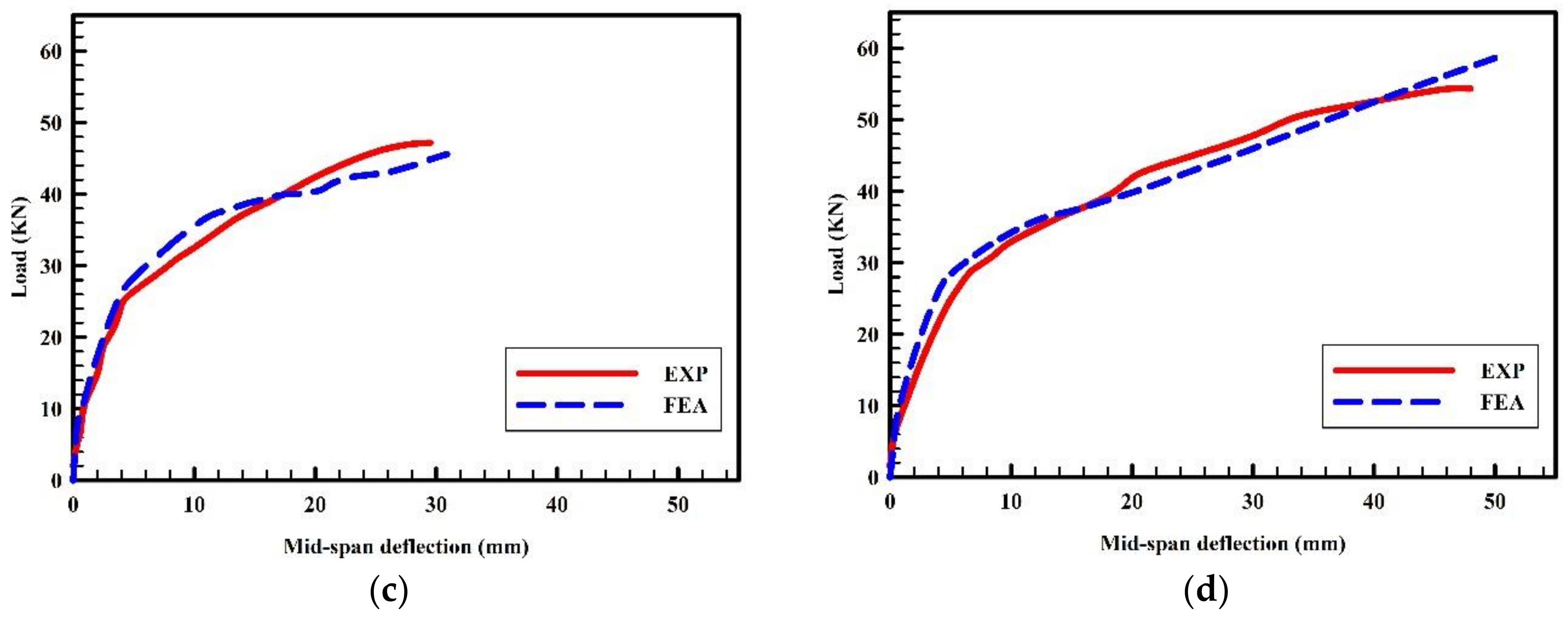
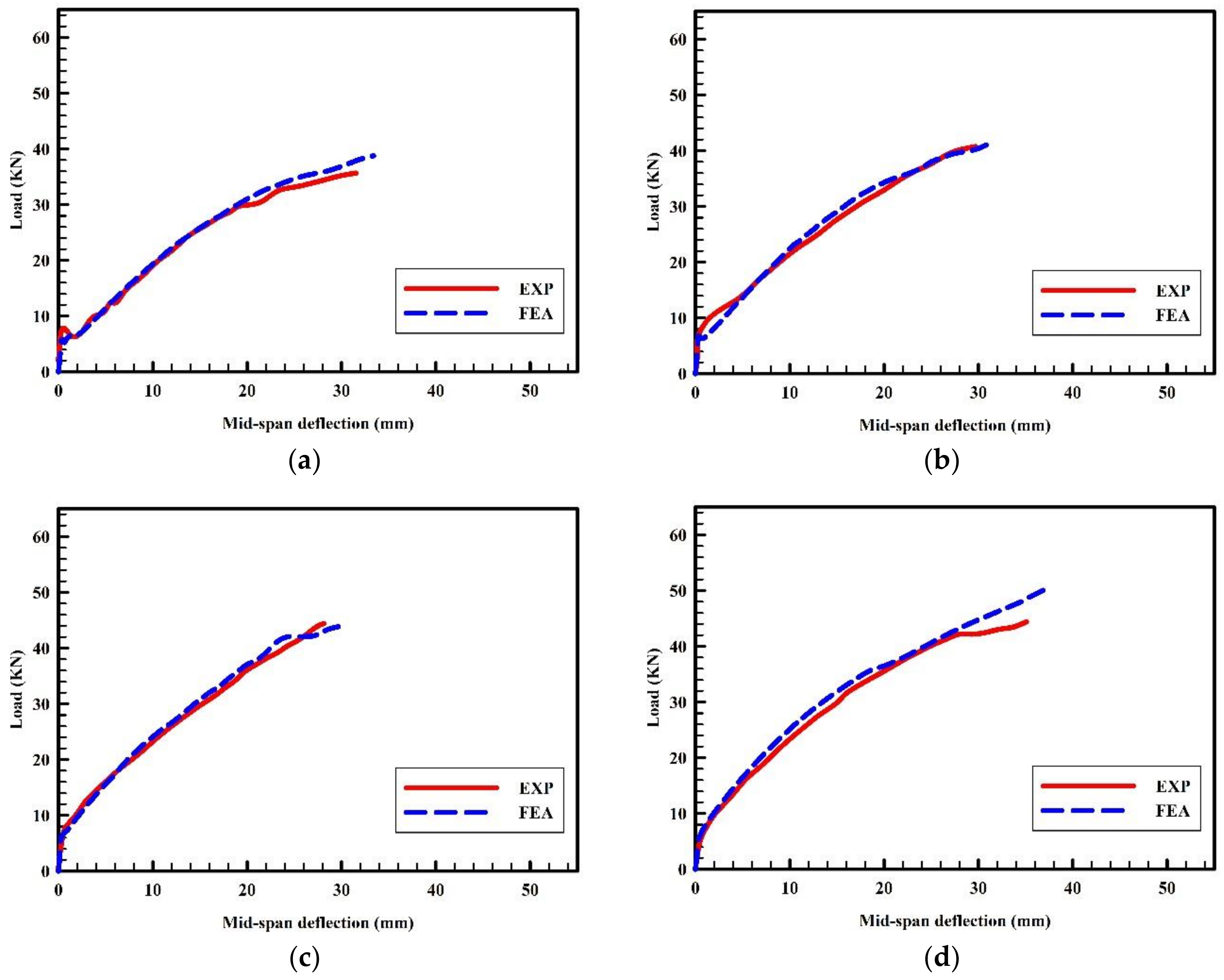
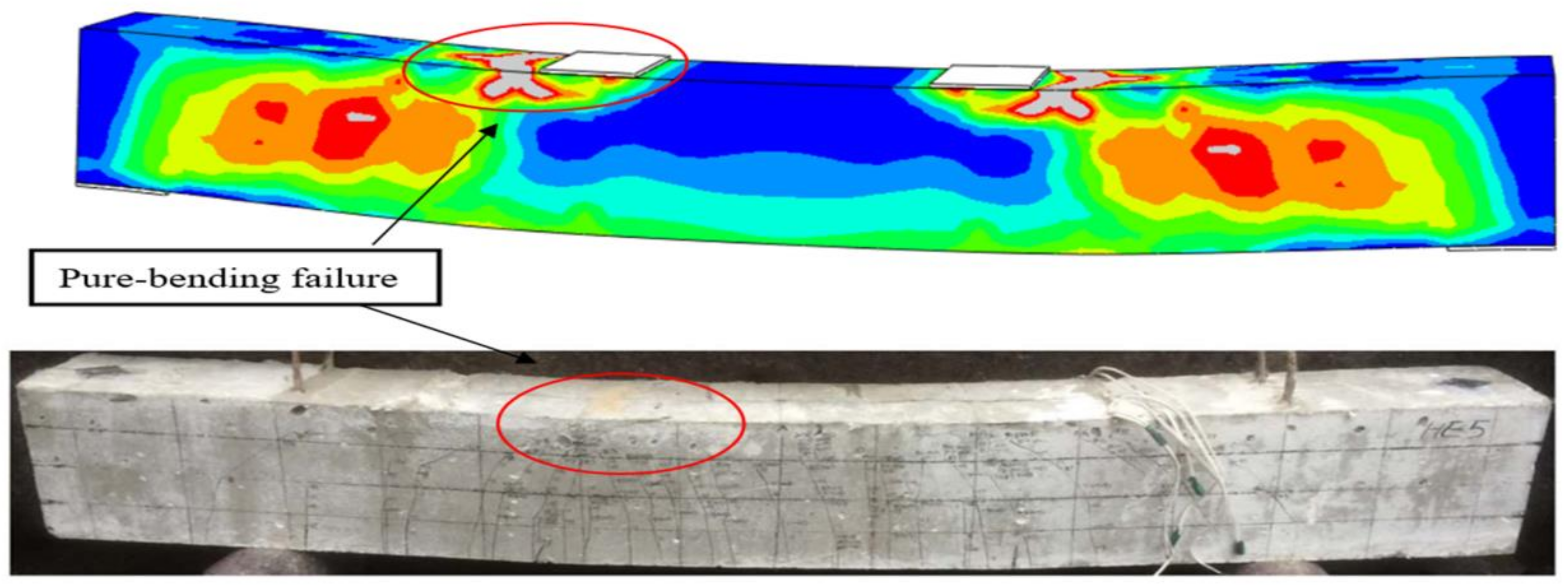
2.3. Model Verification

The model is verified by comparing the following load-deflection curves: ultimate deflection, ultimate load, crack pattern, and failure mode, between the experiment and NLFEM. Three groups of beams are modeled; each group has four tested beams from the published work of [22]. The first group is composed of steel-reinforced beams, the second is composed of hybrid-reinforced beams, and the third is composed of FRP-reinforced beams. All groups have the same geometry (150 mm × 200 mm × 1500 mm) with the same top steel reinforcement (two steel bars- size 10 mm diameter) and the same shear reinforcement (8 mm stirrup at 100 mm spacing).

Table 4. Tested beam reinforcement details and ECC height [22].

Group	Beam Notation	As (Steel)	Afrp (BFRP)	ECC Layer Thickness (mm)
I	B1	2ϕ12 (226.2 mm2)	_	0
	B2	2ϕ12 (226.2 mm2)	_	50
	B3	2ϕ12 (226.2 mm2)	_	100
	B4	2ϕ12 (226.2 mm2)	_	200
II	B5	1 ϕ12 (113.1 mm2)	2ϕ8 (100.53 mm2)	0
	B6	1 ϕ12 (113.1 mm2)	2ϕ8 (100.53 mm2)	50
	B7	1 ϕ12 (113.1 mm2)	2ϕ8 (100.53 mm2)	100
	B8	1 ϕ12 (113.1 mm2)	2ϕ8 (100.53 mm2)	200
III	B9	_	3ϕ8 (150.80 mm2)	0
	B10	_	3ϕ8 (150.80 mm2)	50
	B11	_	3ϕ8 (150.80 mm2)	100
	B12	_	3ϕ8 (150.80 mm2)	200

Note: A_s: is the cross-sectional area of steel reinforcement and A_frp: is the cross-sectional area of the BFRP fiber reinforcement.

shows the reinforcement detail and thickness of the ECC layer. Note that zero ECC thickness indicates a fully concrete beam, while 200 mm ECC thickness indicates a fully ECC beam.

Figure 4, Figure 5 and Figure 6 show the load-deflection curves between the experiment (EXP) and the finite element analysis (FEA). Based on the loading deflection curves, suitable agreement is observed between the experimental data and the NLFEM response. Both Group I (steel reinforcement only) and II (hybrid reinforcement) exhibit ductile failure, while Group III (BFRP reinforcement only) exhibits brittle failure, which is in agreement with the literature.

The ultimate load and corresponding deflection from the experimental and NLFEM are listed in

Table 5. Validation results for ultimate load and deflection.

Group	Beam Notation	Ultimate Deflection (mm)			Ultimate Load (kN)
		Experiment [22]	NLFEA	%Error	Experiment [22]	NLFEA	%Error
I	B1	29.5	32.05	8.64	38.6	36.98	4.2
	B2	22.0	23.09	4.95	39	39.83	2.13
	B3	19.1	19.99	4.66	39.6	41.28	4.24
	B4	33.3	35.15	5.56	45	45.68	1.51
II	B5	31.1	33.29	7.04	42.4	42.61	0.5
	B6	41.5	41.47	0.07	53.6	54.79	2.22
	B7	29.5	30.89	4.51	47.2	45.59	3.41
	B8	47.9	50.14	4.68	54.2	58.73	8.36
III	B9	31.5	33.41	6.06	35.6	38.79	8.96
	B10	29.7	31.36	5.59	40.8	41.39	1.45
	B11	28.1	29.67	5.59	44.6	43.88	1.61
	B12	35.0	36.92	5.49	45	49.0	8.89
	Overall			5.25			3.96

. The error percentage between the experimental and NLFEM responses is within acceptable levels, overall error is 5.25% and 3.96% for the ultimate deflection and the ultimate load, respectively, which is less than the usual acceptable error (10%).

Figure 7, Figure 8, Figure 9 and Figure 10 show the comparison between the experimental failure modes in [22] and the NLFEM for group II (composite hybrid reinforced beams). It is shown that the dominant failure is ductile for all beams. For all beams, the steel reinforcement yielded, while the axial stress in BFRP reinforcement ranged from 46% to 66% of its ultimate tensile strength (the axial stress for reinforcement is only shown in Figure 7b). It is observed that increasing the ECC layer decreased the formation of diagonal shear cracks, conforming to the findings in [31,32,33,34]. In all the beams, the cracks extended to the compression zone. Based on the validation study, the NLFEM developed was used to conduct the parametric study in the next section.

3. Results and Discussion

3.1. Parametric Study Parameters

The parameters used in this study to investigate the mechanical characteristics of ECC beams hybrid reinforced with FRP and steel bars are longitudinal tensile steel reinforcement ratio (ρ_s), longitudinal tensile FRP reinforcement ratio (ρ_frp), ECC layer thickness (t_ECC), FRP bar type, beam height, and compressive strength of concrete, as listed in

Table 6. Summary of the investigated parameters.

Model	fʹc (MPa)	Beam Height (mm)	ρs(%)	FRP Type	ρfrp (%)	tECC (mm)
M1	24	200	0.43	BFRP	0.38	100
M2	24	200	0.43	CFRP	0.38	100
M3	24	200	0.43	AFRP	0.38	100
M4	24	200	0.43	GFRP	0.38	100
M5	30	200	0.43	BFRP	0.38	100
M6	30	200	0.43	CFRP	0.38	100
M7	30	200	0.43	AFRP	0.38	100
M8	30	200	0.43	GFRP	0.38	100
M9	40	200	0.43	BFRP	0.38	100
M10	40	200	0.43	CFRP	0.38	100
M11	40	200	0.43	AFRP	0.38	100
M12	40	200	0.43	GFRP	0.38	100
M13	24	250	0.43	BFRP	0.38	100
M14	24	300	0.43	BFRP	0.38	100
M15	24	200	0.19	BFRP	0.38	50
M16	24	200	0.19	BFRP	0.86	50
M17	24	200	0.19	BFRP	1.53	50
M18	24	200	0.43	BFRP	0.38	50
M19	24	200	0.43	BFRP	0.86	50
M20	24	200	0.43	BFRP	1.53	50
M21	24	200	0.77	BFRP	0.38	50
M22	24	200	0.77	BFRP	0.86	50
M23	24	200	0.77	BFRP	1.53	50
M24	24	200	1.22	BFRP	0.38	50
M25	24	200	1.22	BFRP	0.86	50
M26	24	200	1.22	BFRP	1.53	50
M27	24	200	0.19	BFRP	0.38	100
M28	24	200	0.19	BFRP	0.86	100
M29	24	200	0.19	BFRP	1.53	100
M30	24	200	0.43	BFRP	0.86	100
M31	24	200	0.43	BFRP	1.53	100
M32	24	200	0.77	BFRP	0.38	100
M33	24	200	0.77	BFPR	0.86	100
M34	24	200	0.77	BFPR	1.53	100
M35	24	200	1.22	BFPR	0.38	100
M36	24	200	1.22	BFPR	0.86	100
M37	24	200	1.22	BFPR	1.53	100

. The mechanical characteristics evaluated in this study are the ultimate load (P_u), the ultimate deflection (Δ_U), the ductility index (μ, defined as the ratio between ultimate deflection and yield deflection), the energy absorption (area under the load-deflection curve), and the stiffness (slope of the second linear portion). The deflection load response for all developed models is composed of three stages: the first is from the initial to the point where the first crack appeared, known as the pre-cracking or un-cracked stage. The second one is from the cracking point to the point at which the steel rebars are yielding, known as the yield point. Finally, the third stage is from the yield point to the last point, representing the failure point.

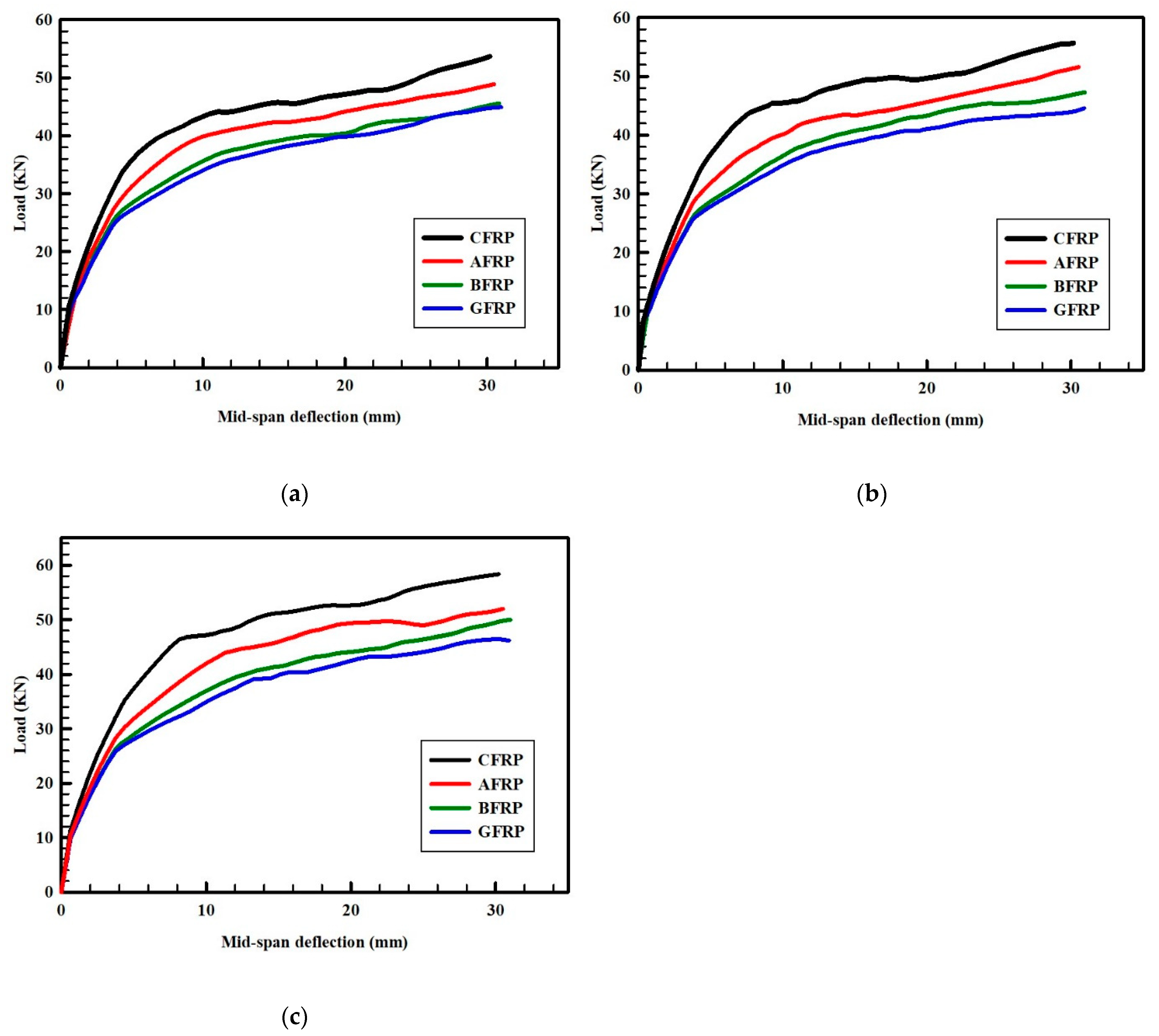
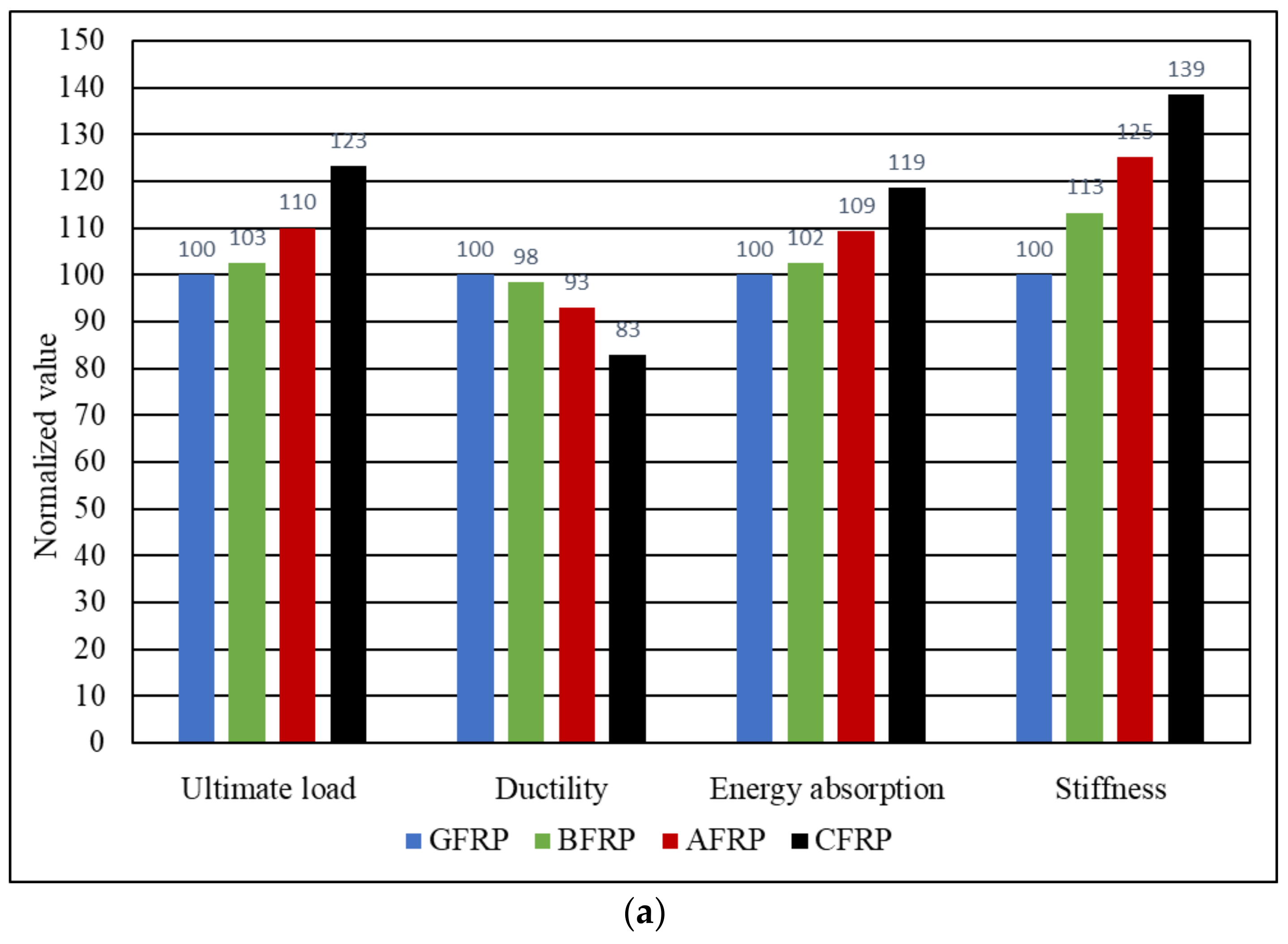
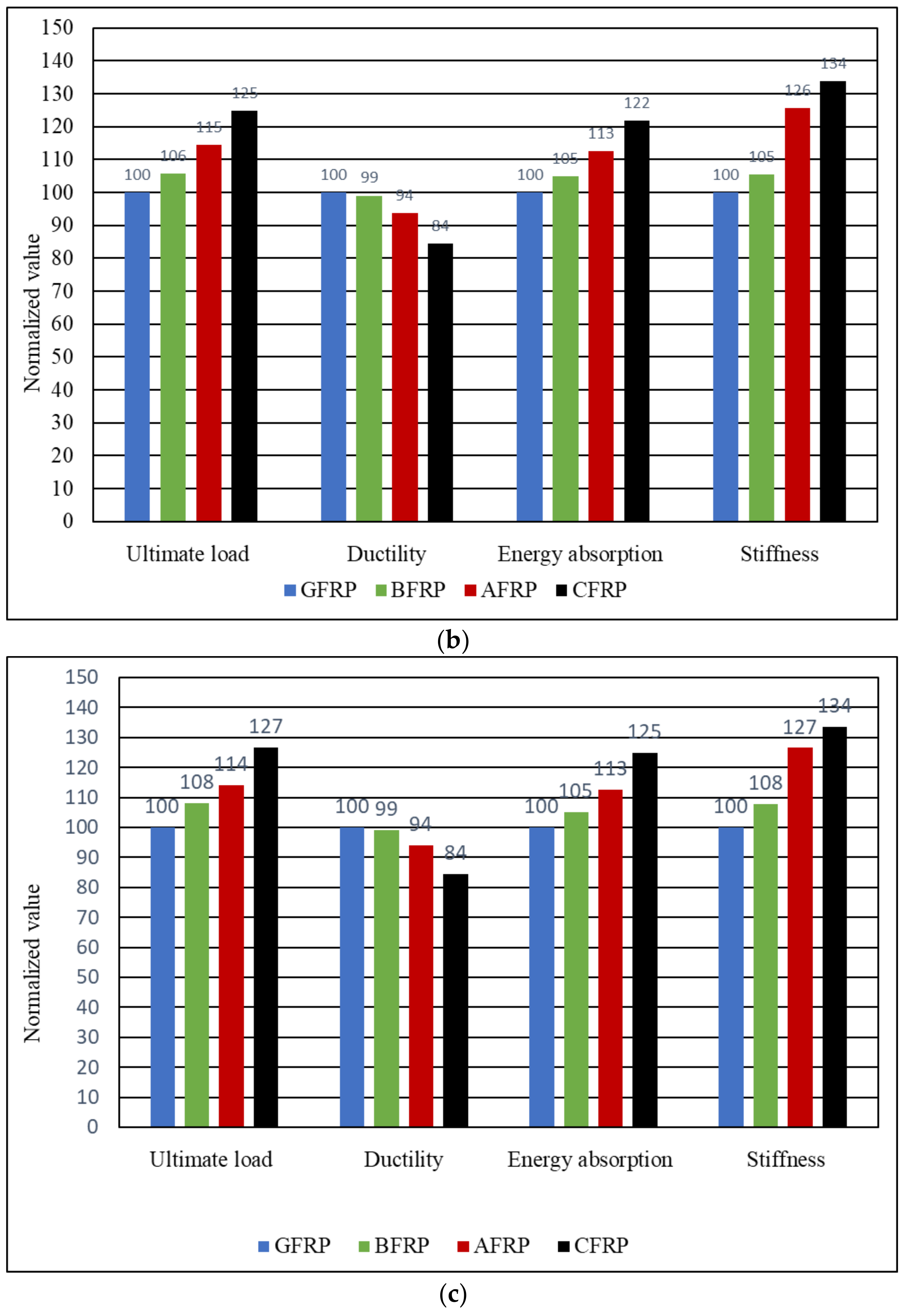
3.2. Effect of FRP Type and Concrete Compressive Strength

In studying the effect of the FRP type and compressive strength of concrete the following parameters are kept constant: beam height (200 mm), t_ECC (100 mm), ρ_s (0.0043), and ρ_FRP (0.0038). As shown in Figure 11, regardless of the concrete compressive strength and FRP type, the initial slope (pre-cracking stage) is approximately the same. As expected, the highest load-carrying capacity is for the CFRP reinforcement and 40 MPa compressive strength of concrete, followed by AFRP, BFRP, and GFRP. Due to the higher tensile strength of CFRP reinforcement when compared to other FRP reinforcements (Figure 2).

In Figure 12, the ultimate load, ductility index, energy absorption, and stiffness were normalized to the GFRP values shown for the different concrete compressive strengths (24 MPa, 30 MPa, and 40 MPa). It is evident that the same trend holds irrespective of concrete compressive strength, and the influence of the FRP type is more pronounced at lower concrete compressive strengths than expected. Regarding the ductility index, there is no discernable difference between GFRP and BFRP. Despite BFRP being stiffer and possessing a higher tensile strength than GFRP, GFRP fails at a higher strain value than BFRP, as shown in Figure 2.

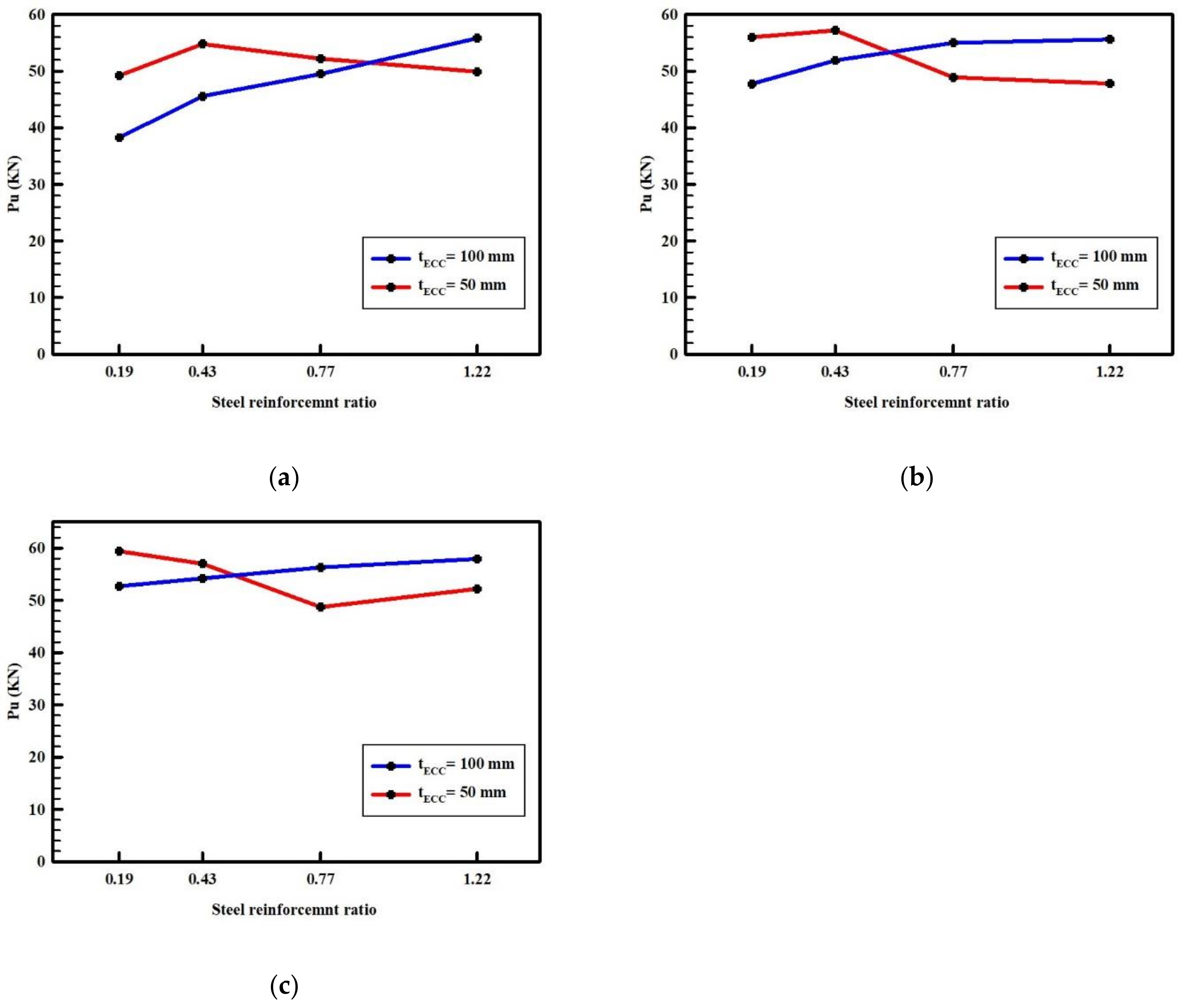
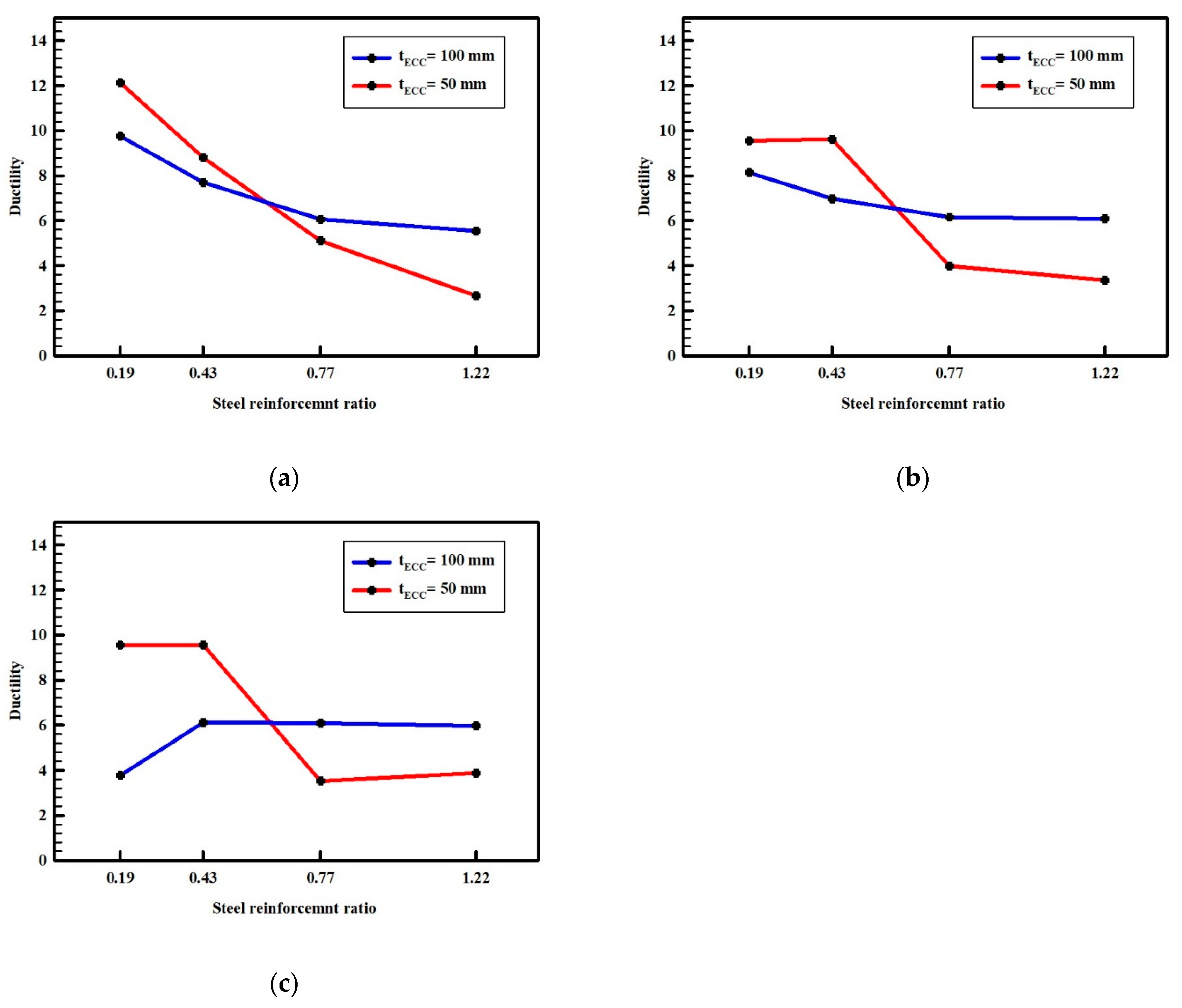
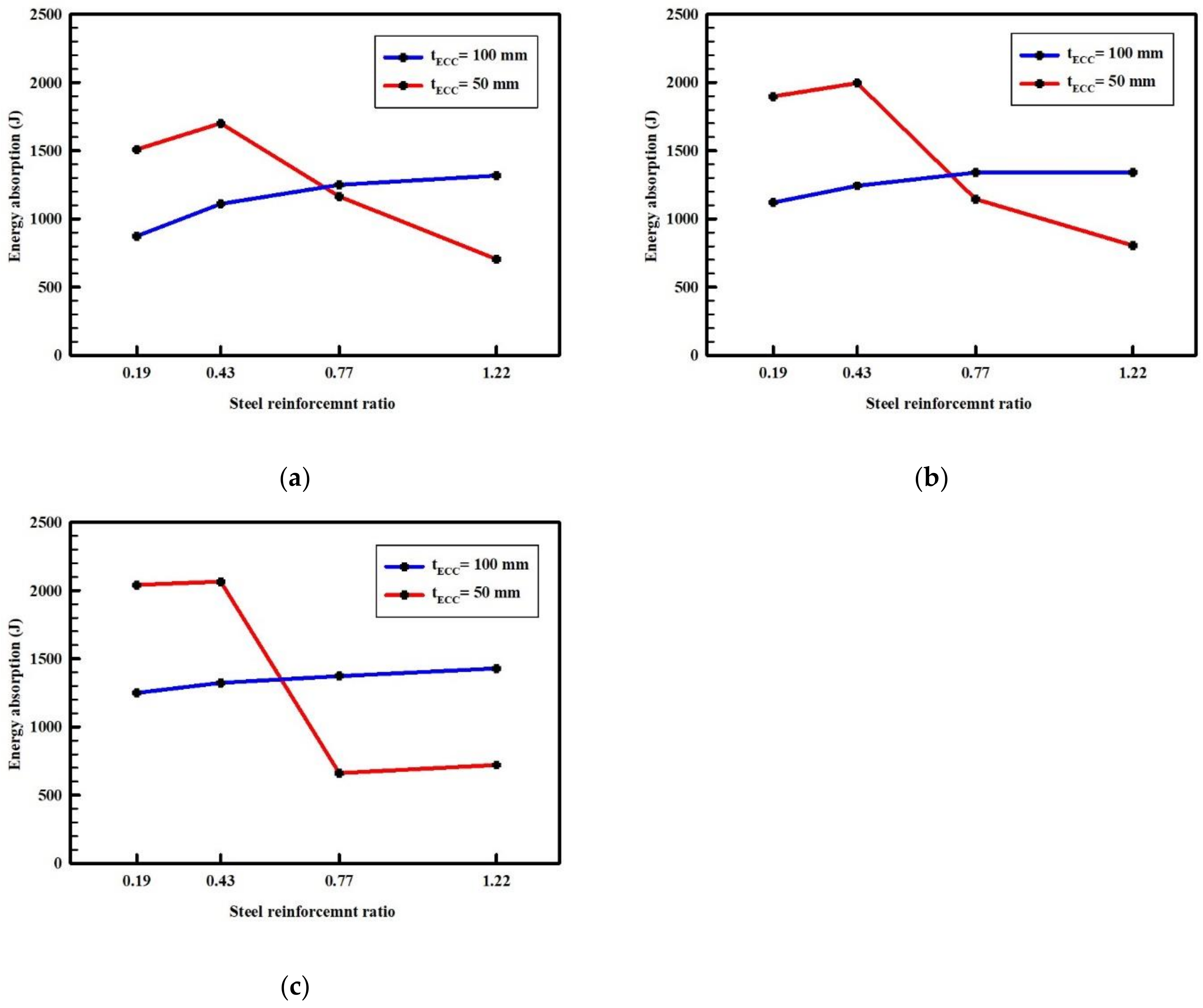
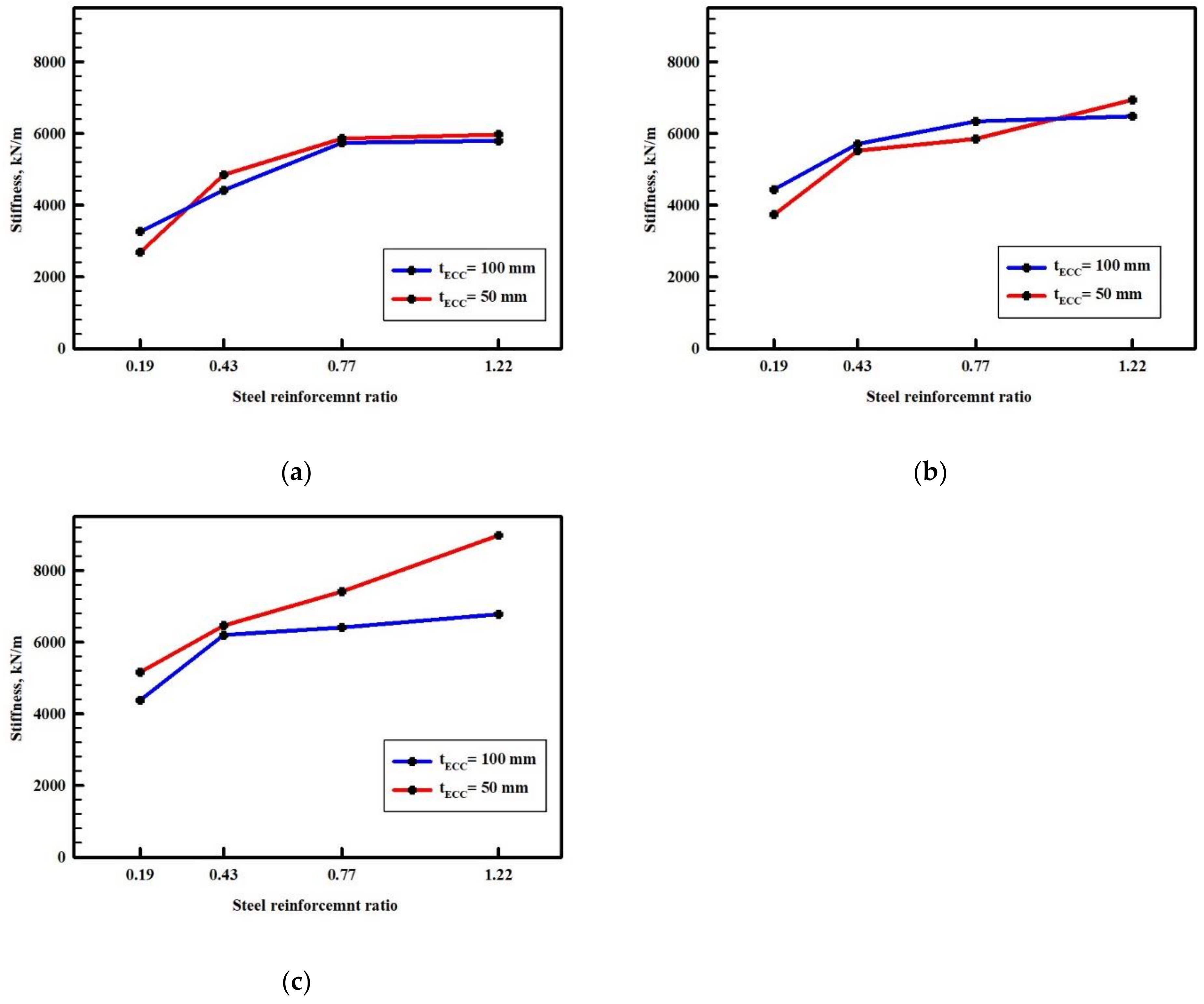
3.3. Effect of Hybrid Tensile Reinforcement Ratio and t_ECC

In this section, the behavior of the composite hybrid reinforced beam is numerically modeled to discuss the effectiveness of the thickness of the ECC layer against various steel and BFRP reinforcement ratios on the ultimate load, ductility index, energy absorption, and stiffness. The steel reinforcement ratios used are 0.19%, 0.43%, 0.77%, and 1.22%, while the BFRP reinforcement ratios used are 0.38%, 0.86%, and 1.53% (Table 4 shows actual bar sizes). Both the concrete compressive strength and beam height are kept constant at 24 MPa and 200 mm, respectively. The ECC thicknesses used are 50 mm and 100 mm, placed in the tension zone.

As shown in Figure 13, using a higher cross-sectional area of steel reinforcement reduced the ultimate load to 95.3% and 91.1% by using 0.77% and 1.2% steel reinforcement ratios and a 0.38% BFRP ratio, respectively. However, as shown in Figure 14, a significant decrease in the ductility factor of the composite hybrid beams as the steel reinforcement ratio increases, reaching less than 3, which does not meet the service requirement, is observed.

Moreover, the early failure of the beams reinforced by steel reinforcement ratios of 0.77% and 1.2% led to a high decrease in the energy absorption of the beams, as shown in Figure 15. However, the beam reinforced with a steel reinforcement ratio of 0.19% and a BFRP ratio of 0.38% recorded a drop in the ultimate load and energy absorption and an improvement in ductility of about 89.9%, 88.7%, and 137.73%, respectively, compared with the beam reinforced with a 0.43% steel ratio.

In the case of the 50 mm ECC layer, it can be observed from Figure 16 that increasing the steel ratio is advantageous for improving the stiffness of the beams. However, an early failure occurred rapidly after the yielding of steel rebars at lower ultimate displacement, leading to insufficient ductility (less than 3) in the composite hybrid beams. This behavior, explained by the high stress concentration from the increasing steel ratio in the ECC layer, led to crushing in the ECC layer between the support and the loading point.

Generally, the 0.43% steel reinforcement ratio obtains a higher load-carrying capacity and sufficient ductility for the composite hybrid beam when the ECC layer is 50 mm in the tension zone. For the case of using a 100 mm ECC layer, providing a higher tensile steel reinforcement ratio significantly enhanced the ultimate load capacity, even with the BFRP ratio used, due to the increasing tensile resistance. For instance, when the BFRP reinforcement ratio was 0.38% and the composite hybrid beams were reinforced by 1.2% and 0.77% steel reinforcement ratio, the ultimate load increased by 122.4% and 108.6%, respectively, compared with the composite beam reinforced by 0.43% steel reinforcement ratio. In contrast to the reinforced composite hybrid beam with a 0.19% steel ratio, which caused a reduction in the ultimate load by about 83.9%.

The increase in the tensile steel reinforcement ratio results in increases in the yielding load and its corresponding deflection. In contrast, a slight decrease was shown in the ultimate deflection. This is because the compressive failure mode of all the beams means a fixed value of the concrete maximum compression strain, so a lower strain from the steel reinforcement can show enough tensile resistance to balance the concrete compression strain, and then the ultimate deflection is reduced. This behavior led to a decreasing ductility factor of the beam with an increasing reinforcement ratio. The beam reinforced by 1.2% and 0.77% steel ratio and 0.38% BFRP reduced the ductility factor by 72% and 78.7%, respectively, while the ductility improved by 126.6% by reducing the reinforcement ratio to 0.19%. Compared with the reference beam, the consumption of more steel reinforcement ratio improved the energy absorption and the flexural stiffness by about 118.63% and 131.2% at a steel reinforcement ratio of 1.2%, 112.5%, and 130%, respectively, using a steel reinforcement ratio of 0.77%. In comparison, the beam reinforced with a 0.19% steel reinforcement ratio showed drops in toughness and flexural stiffness, reaching up to 78.67% and 73.8%, respectively.

Generally, with the BFRP reinforcement ratio held constant, a correlation between the thickness of the ECC layer and the effective steel reinforcement ratio can be observed, leading to an appropriate load-carrying capacity and sufficient ductility of the composite hybrid beams. In composite beams with a 50 mm ECC layer in the tension zone, the 0.43% steel reinforcement ratio performs better in terms of load-carrying capacity and ductility. However, using 0.77% and 1.22% steel reinforcement ratios exhibits higher load-carrying capacity, while a 0.19% steel reinforcement ratio provides higher ductility performance in the case of composite beams with a 100 mm thickness of ECC material. Moreover, it can be noted from Figure 13 that in both cases of using 50 mm and 100 mm ECC layers with a constant steel reinforcement ratio, there was a correlation between the BFRP reinforcement ratio and the ultimate load of the beam. As evident, the peak load capacity, beam toughness, and stiffness for each specimen tend to be enhanced by utilizing a higher ratio of BFRP. On the other hand, the brittle, elastic nature of the BFRP bar material led to a reduction in the ductility of the beam. Therefore, a sufficient fiber reinforcement ratio must be chosen to meet the suitable ductility of the composite hybrid beam.

4. Conclusions

In this study, the flexural behavior of ECC-concrete beams reinforced by a hybrid combination of steel and FRP bars is numerically investigated based on a non-linear finite element method. Twelve models of beams reinforced with different configurations of steel and FRP bars and various matrix types were simulated, based on a previous experimental study, to ensure the accuracy of the numerical model in predicting the beams’ flexural behavior. Subsequently, thirty-seven models were developed to investigate the effectiveness of steel reinforcement ratio, BFRP reinforcement ratio, FRP bar type, concrete compressive strength, and beam depth on the composite hybrid beam’s flexural behavior. The general findings of this research are highlighted below:

• The numerical simulation models accurately predict the load-deflection response with an error of less than 10% of the ultimate load, ultimate deflection, and stiffness. This provides researchers with a valuable tool for studying the behavior of ECC-concrete hybrid reinforced beams, particularly considering the higher costs associated with ECC material and FRP bars.
• In hybrid composite beams (using 50 mm ECC), when the BFRP reinforcement ratio is kept constant, utilizing a higher steel reinforcement ratio results in a reduction in ultimate load capacity, toughness, and ultimate deflection, along with insufficient ductility (less than 3), leading to early failure immediately after yielding of steel rebars due to high stress concentration in the ECC layer.
• In hybrid composite beams (using 100 mm ECC), when the BFRP reinforcement ratio is kept constant, using a higher steel reinforcement ratio leads to improvements in ultimate load, toughness, and flexural stiffness, but reduces beam ductility and shows a slight decrease in maximum deflection.
• With the remaining steel reinforcement ratio constant in the hybrid reinforcement system, an increase in the ratio of BFRP enhances ultimate load capacity, toughness, and flexural stiffness, but causes a decline in maximum deflection and ductility.
• The BFRP/steel tensile reinforcement ratio should be carefully designed to achieve the required strength, acceptable ductile performance, and improved load-carrying capacity of the composite beam.
• Strengthening composite hybrid beams with CFRP bars instead of BFRP results in better mechanical behavior in terms of ultimate load, toughness, flexural stiffness, and plastic stiffness, albeit with a reduction in ductility index. Conversely, replacing BFRP with GFRP bars exhibits a higher enhancement in ductility performance but a reduction in other mechanical properties. Additionally, the use of AFRP bars provides moderate mechanical behavior, performing better than BFRP but still inferior to CFRP bars.
• Using a higher grade of concrete strength in composite hybrid beams contributes minimally to improving mechanical behavior, with no noticeable effect on enhancement or reduction when using different types of FRP bars.
• In composite hybrid reinforced beams, using a 100 mm ECC layer in the tension zone significantly impacts the load-deflection response and greatly improves mechanical performance with increasing effective beam depth.