Post-Cracking Behaviour of Fibre-Reinforced Shotcrete: A Numerical Comparison between Beams and Panels
Abstract
:1. Introduction
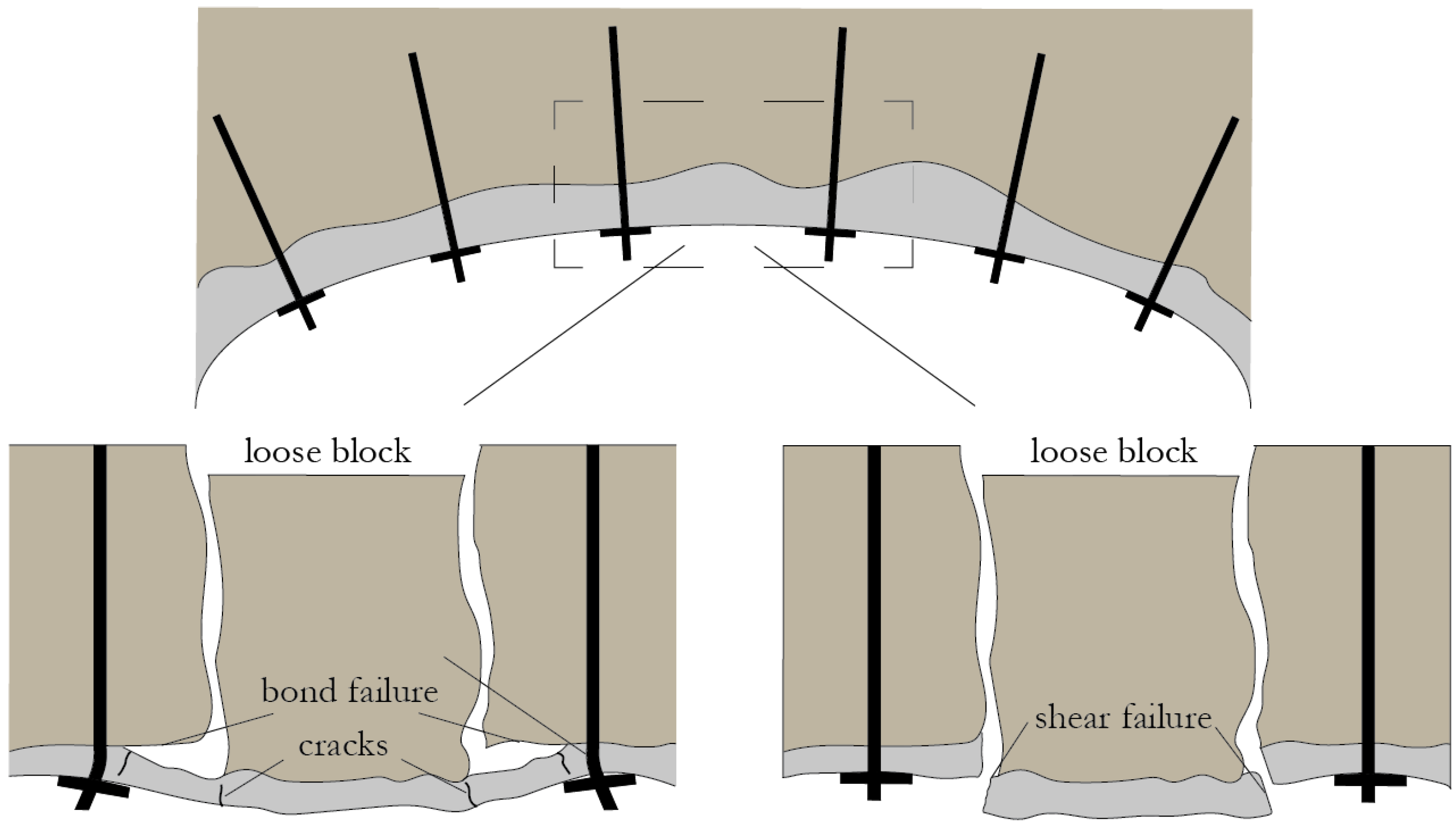
1.1. Structural Testing of Shotcrete
1.2. Aim of This Paper
2. Numerical Model for Fibre-Reinforced Shotcrete
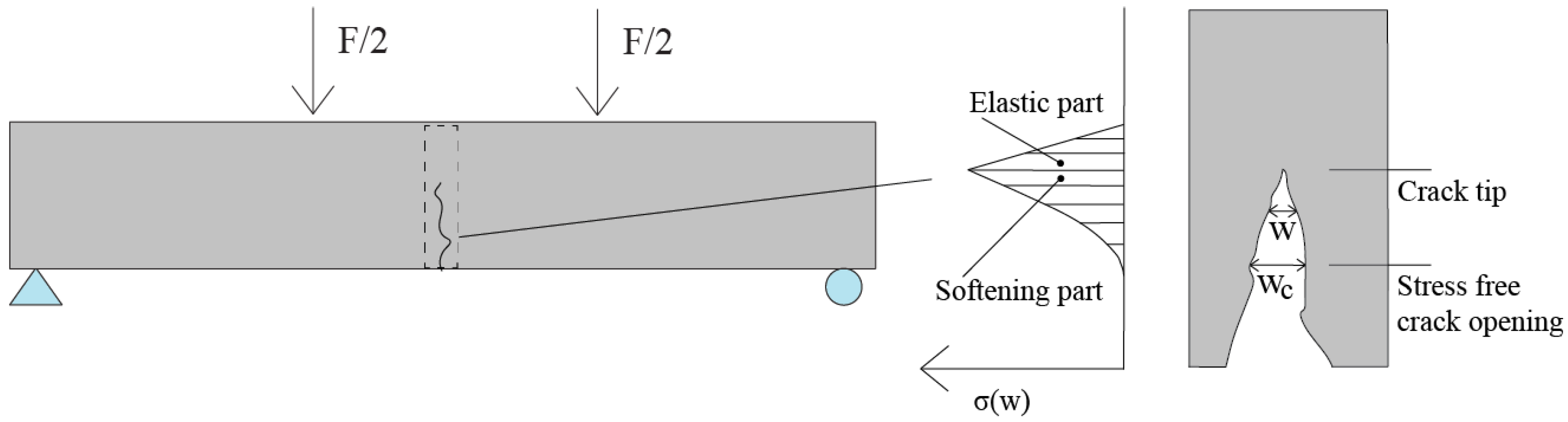
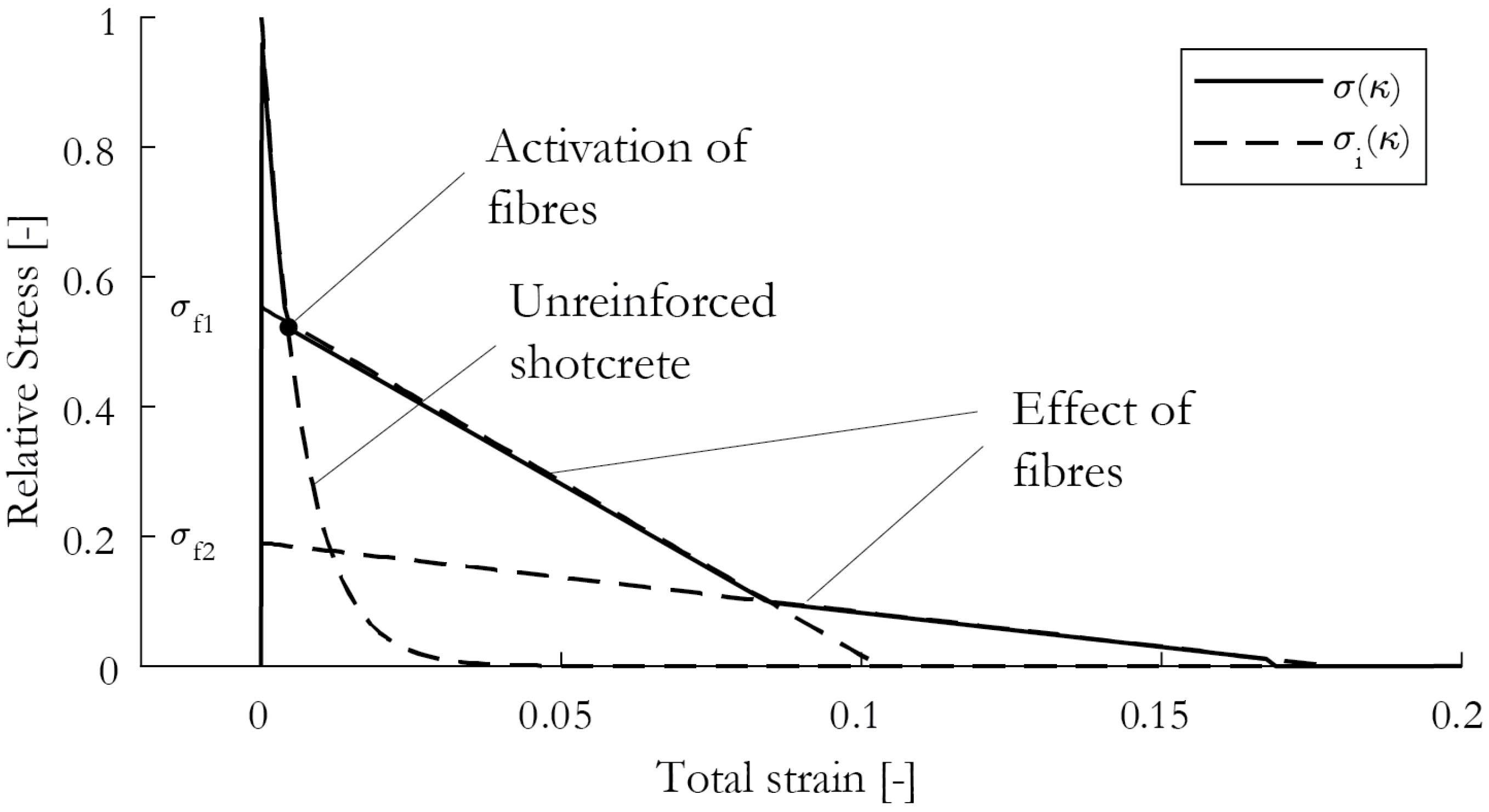
2.1. Damage Model for Shotcrete
2.2. Simulation of Beams
2.3. Simulation of Panels
3. Comparison between Beams and Panels
- Define Material Model A based on fitting of numerical simulations to experimental results for tests on beams (see Table 1);
- Define Material Model B based on fitting of numerical simulations to experimental results for tests on panels (see Table 2);
- Use Material Model A to simulate the structural response of a panel;
- Compare results between experiments on a panel and simulations with Material Model A;
- Use Material Model B to simulate the structural response of a beam;
- Compare results between experiments on a beam and simulations with Material Model B.
4. Results and Discussion
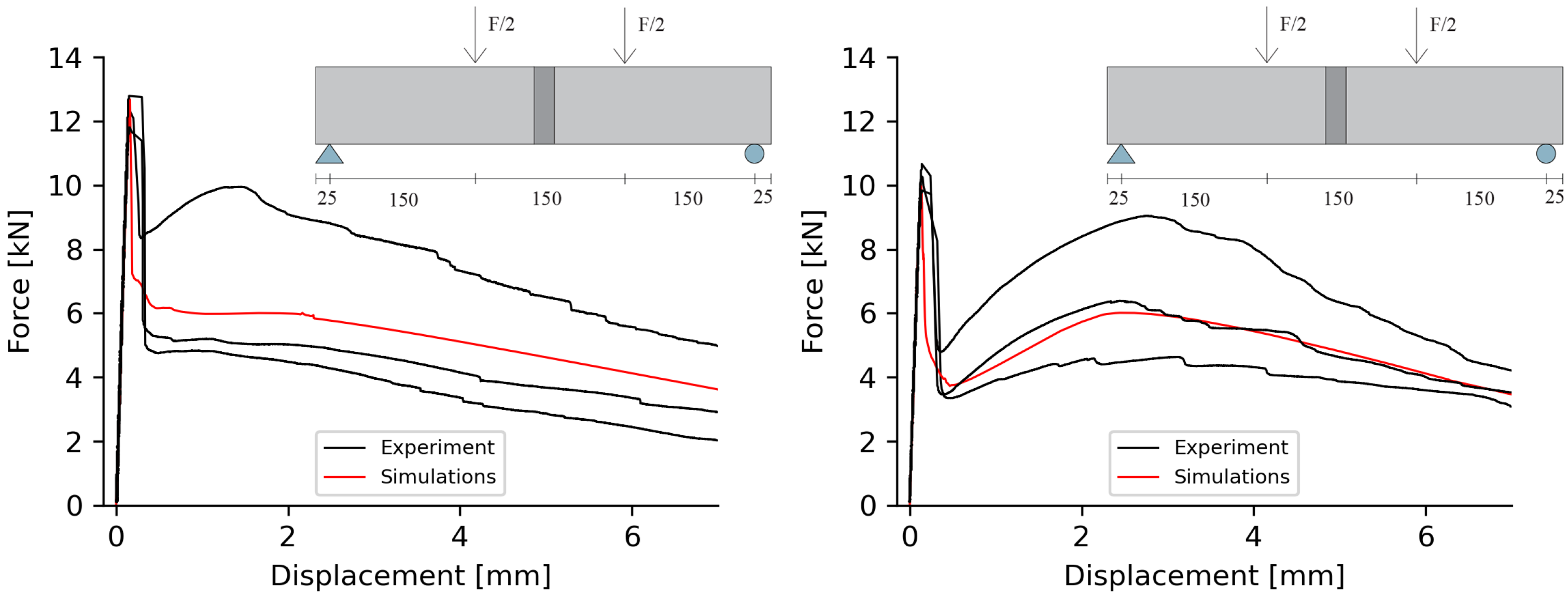
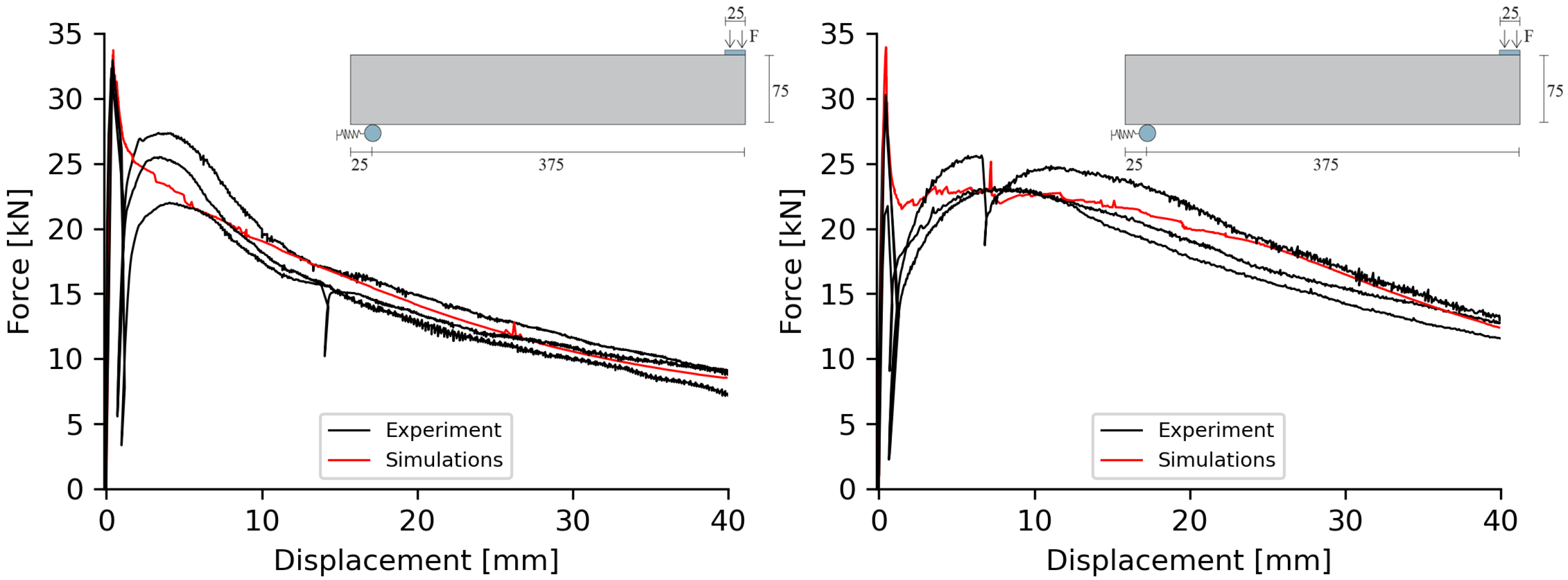
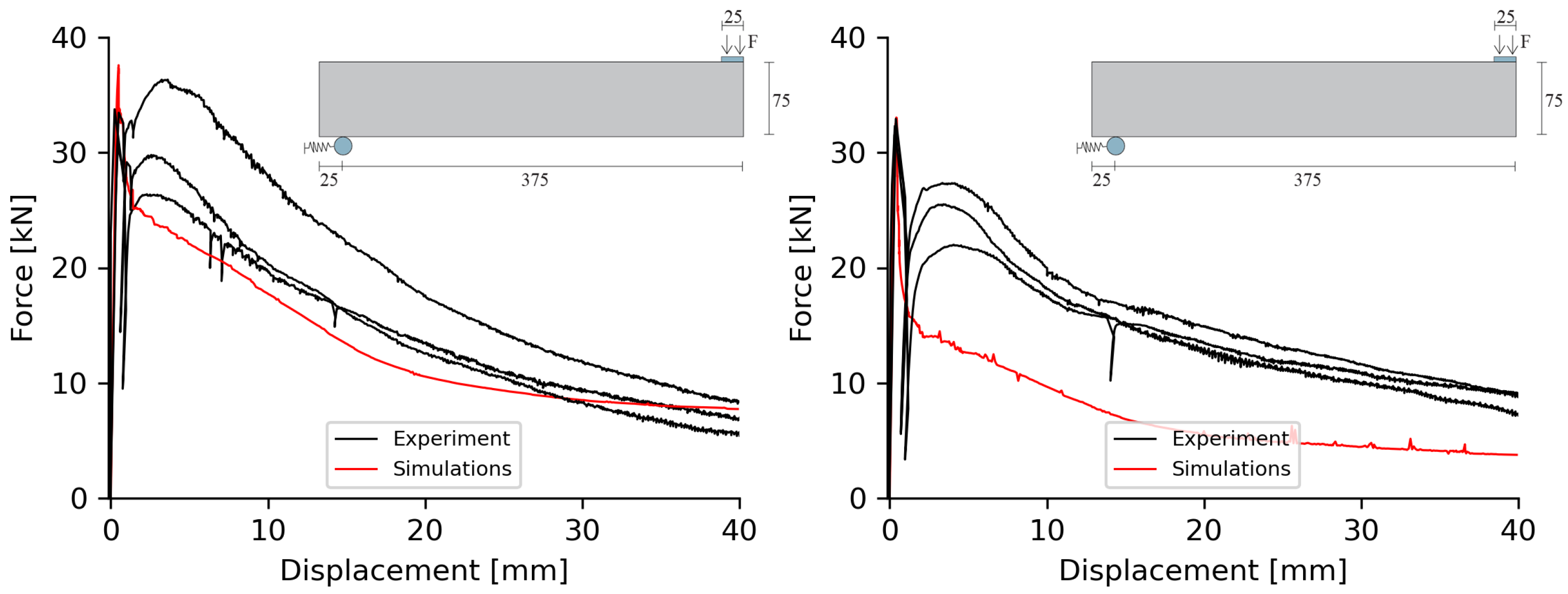
4.1. Simulation of Panels
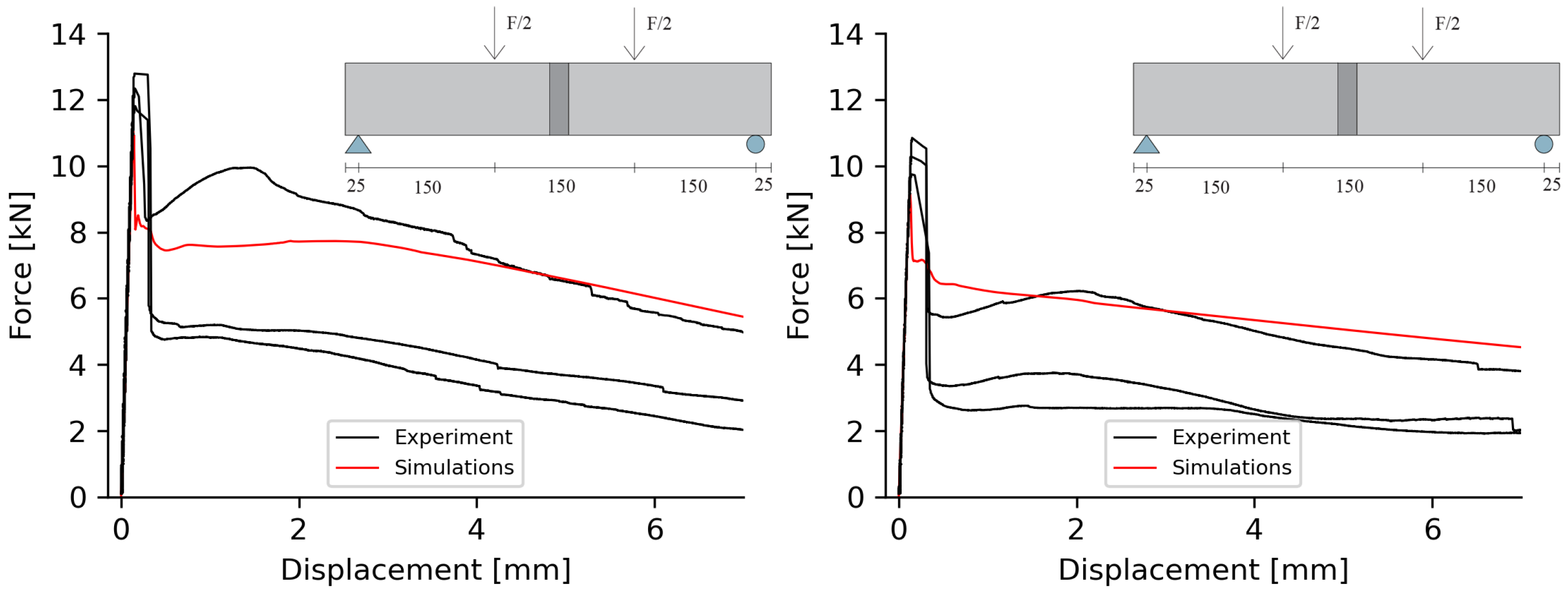
4.2. Simulation of Beams
4.3. Interpretation of Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RMR | Rock Mass Rating |
| FRS | Fibre-Reinforced Shotcrete |
| CDM | Continuum Damage Model |
References
- Barton, N.; Lien, R.; Lunde, J. Engineering classification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Bieniawski, Z. Engineering classification of jointed rock masses. Civ. Eng. S. Afr. 1973, 15, 335–343. [Google Scholar] [CrossRef]
- Barrett, S.; McCreath, D. Shortcrete support design in blocky ground: Towards a deterministic approach. Tunn. Undergr. Space Technol. 1995, 10, 79–89. [Google Scholar] [CrossRef]
- Sjölander, A.; Ansell, A.; Nordström, E. On the design of permanent shotcrete rock support. Fibers 2023, 11, 20. [Google Scholar] [CrossRef]
- ASTM. ASTM C1550-20; Standard Test Method for Flexural Toughness of Fiber Reinforced Concrete (Using Centrally Loaded Round Panel). Technical Report. ASTM International: Pennsylvania, PA, USA, 2020. [Google Scholar]
- CEN. EN 14488-5; Testing Sprayed Concrete—Part 5: Determination of Energy Absorption Capacity of Fibre Reinforced Slab Specimens. Technical Report. European Committee for Standardisation: Brussels, Belgium, 2006. [Google Scholar]
- Bjontegaard, O. Energy Absorption Capacity for Fibre Reinforced Sprayed Concrete. Effect of Friction in Round and Square Panel Tests with Continuous Support (Series 4); Technical Report; Statens Vegvesen: Oslo, Norway, 2009. [Google Scholar]
- CEN. EN 14488-3; Testing Sprayed Concrete—Part 3: Flexural Strengths (First Peak, Ultimate and Residual) of Fibre Reinforced Beam Specimens. Technical Report. European Committee for Standardisation: Brussels, Belgium, 2006. [Google Scholar]
- Rengarajan, M. Laboratory Testing of Shotcrete with Fibres of Steel, Basalt or Synthetic Materials. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2020. [Google Scholar]
- Brodd, E.; Östlund, L. Environmental and Technical Evaluation of Cement Reduction and Test Methods for Fibre Reinforced Shotcrete in Tunnels. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2022. [Google Scholar]
- Sjölander, A.; Ansell, A. Probabilistic modelling of fibre reinforced shotcrete. In Proceedings of the WTC 2019 ITA-AITES World Tunnel Congress, Naples, Italy, 3–9 May 2019. [Google Scholar]
- Conforti, A.; Minelli, F.; Plizzari, G.A.; Tiberti, G. Comparing test methods for the mechanical characterization of fiber reinforced concrete. Struct. Concr. 2018, 19, 656–669. [Google Scholar] [CrossRef]
- Bernard, E.S. Correlations in the behaviour of fibre reinforced shotcrete beam and panel specimens. Mater. Struct. 2002, 35, 156–164. [Google Scholar] [CrossRef]
- Bernard, E.S. Development of a 1200 mm Diameter Round Panel Test for Post-crack Assessment of Fiber Reinforced Concrete. ASTM Int. Adv. Civ. Eng. Mater. 2013, 2, 457–471. [Google Scholar] [CrossRef]
- Buratti, N.; Incerti, A.; Tilocca, A.; Mazzotti, C.; Paparella, M.; Draconte, M. Energy absorption tests on fibre-reinforced-shotcrete round and square panels. In Proceedings of the Tunnels and Underground Cities: Engineering and Innovation Meet Archaeology, Architecture and Art, Naples, Italy, 3–9 May 2019; pp. 1842–1851. [Google Scholar]
- Parmentier, B.; De Grove, E.; Vandewalle, L.; Van Rickstal, F.; Walraven, J.; Stoelhorst, D. Dispersion of the mechanical properties of FRC investigated by different bending tests. In Proceedings of the Fib Symposium “Tailor Made Concrete Structures”, Amsterdam, The Netherlands, 19–21 May 2008; pp. 507–512. [Google Scholar]
- CEN. EN 14487-1; Sprayed Concrete—Part 1: Definitions, Specifications and Conformity. Technical Report. European Committee for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- Comsol. Comsol Multiphysics Ver. 5.4 Documentation; Comsol: Stockholm, Sweden, 2019. [Google Scholar]
- Oliver, J.; Cervera, M.; Oller, S.; Lubliner, J. Isotropic damage models and smeared crack analysis of concrete. In Proceedings of the 2nd International Conference on Computer Adided Analysis and Design of Concrete Strucutres, Zell Am See, Austria, 4–6 April 1990; pp. 945–957. [Google Scholar]
- Gasch, T. Multiphysical Analysis Methods to Predict the Ageing and Durability of Concrete. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2019. [Google Scholar]
- Sjölander, A.; Hellgren, R.; Ansell, A. Modelling aspects to predict failure of a bolt-anchored and fibre reinforced shotcrete lining. In Proceedings of the 8th International Symposium on Sprayed Concrete, Trondheim, Norway, 11–14 June 2018. [Google Scholar]
- Sjölander, A.; Hellgren, R.; Malm, R.; Ansell, A. Verification of failure mechanisms and design philosophy for a bolt-anchored and fibre-reinforced shotcrete lining. Eng. Fail. Anal. 2020, 116, 104741. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Sjölander, A.; Ansell, A.; Nordström, E. Data from structural testing of sprayed and cast shotcrete reinforced with fibres of steel, basalt and synthetic material. Mendeley Data 2022, V1. [Google Scholar] [CrossRef]
- EFNARC. EFNARC Three Point Bending Test on Square Panel with Notch; Technical Report; EFNARC: Flums, Switzerland, 2011. [Google Scholar]
- Meng, W.; Yao, Y.; Mobasher, B.; Khayat, K.H. Effects of loading rate and notch-to-depth ratio of notched beams on flexural performance of ultra-high-performance concrete. Cem. Concr. Compos. 2017, 83, 349–359. [Google Scholar] [CrossRef]
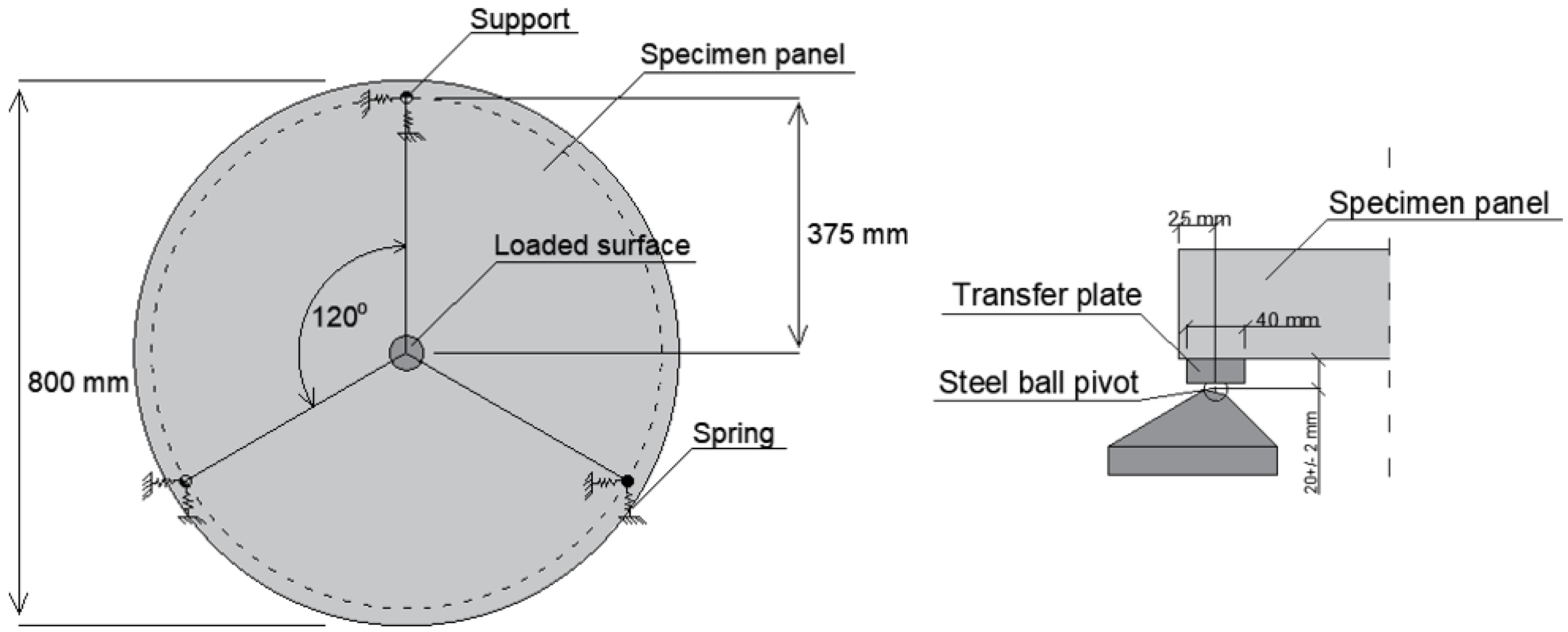
| Fibre | Dosage | |||||||
|---|---|---|---|---|---|---|---|---|
| [MPa] | [N/m] | [mm] | [mm] | [mm] | [-] | [-] | ||
| Steel 3D | 30 kg/m | 4.5 | 125 | 0.045 | 1.65 | 7 | 0.18 | 0.01 |
| Steel 3D | 40 kg/m | 4.9 | 125 | 0.042 | 1.5 | 7 | 0.2 | 0.01 |
| Steel 4D | 20 kg/m | 4 | 125 | 0.07 | 1.2 | 6 | 0.15 | 0.01 |
| Steel 4D | 30 kg/m | 4.3 | 125 | 0.052 | 1 | 7 | 0.29 | 0.01 |
| Synthetic | 9 kg/m | 4.4 | 125 | 0.088 | 2.1 | 10 | 0.17 | 0.01 |
| Basalt | 16 kg/m | 3.6 | 125 | 0.08 | 1.6 | 6 | 0.32 | 0.01 |
| Fibre | Dosage | |||||||
|---|---|---|---|---|---|---|---|---|
| [MPa] | [N/m] | [mm] | [mm] | [mm] | [-] | [-] | ||
| Steel 3D | 30 kg/m | 4.1 | 125 | 0.041 | 5 | 8 | 0.14 | 0.0001 |
| Steel 3D | 40 kg/m | 4.5 | 125 | 0.036 | 1.8 | 8 | 0.29 | 0.0002 |
| Steel 4D | 20 kg/m | 3.8 | 125 | 0.042 | 5 | 13 | 0.16 | 0.009 |
| Steel 4D | 30 kg/m | 4.1 | 125 | 0.035 | 2 | 16 | 0.27 | 0.01 |
| Synthetic | 9 kg/m | 4.1 | 125 | 0.053 | 1.7 | 17 | 0.31 | 0.0008 |
| Basalt | 16 kg/m | 3.6 | 125 | 0.04 | 1.7 | 4 | 0.46 | 0.002 |
| Fiber | Dosage | Exp. 1 | Exp. 2 | Exp. 3 | Mean | Sim. | Sim./Exp. |
|---|---|---|---|---|---|---|---|
| [J] | [J] | [J] | [J] | [J] | [-] | ||
| Steel 3D | 30 kg/m | 472 | 516 | 564 | 517 | 452 | 87% |
| Steel 3D | 40 kg/m | 597 | 792 | 592 | 660 | 534 | 81% |
| Steel 4D | 20 kg/m | 583 | 577 | 653 | 604 | 295 | 49% |
| Steel 4D | 30 kg/m | - | 835 | 927 | 881 | 535 | 61% |
| Synthetic | 9 kg/m | 703 | 806 | 736 | 748 | 393 | 53% |
| Basalt | 16 kg/m | 511 | 644 | 379 | 512 | 421 | 82% |
| Fiber | Dosage | Exp. 1 | Exp. 2 | Exp. 3 | Mean | / | ||
|---|---|---|---|---|---|---|---|---|
| [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [MPa] | [-] | ||
| Steel 3D | 30 kg/m | 5 | 2.8 | 2.8 | 3.5 | 3.1 | 3.4 | 110% |
| Steel 3D | 40 kg/m | 3.2 | 2.9 | 5.7 | 3.9 | 3.2 | 3.8 | 119% |
| Steel 4D | 20 kg/m | 1.7 | 2.4 | 4 | 2.7 | 1.9 | 2.6 | 137% |
| Steel 4D | 30 kg/m | 4.9 | 4.4 | 3.4 | 4.2 | 3.8 | 4.3 | 113% |
| Synthetic | 9 kg/m | 2.1 | 2.6 | 2.8 | 2.5 | 2.3 | 2.5 | 109% |
| Basalt | 16 kg/m | 5.2 | 3.7 | 2.8 | 3.9 | 3.1 | 3.7 | 119% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Östlund, L.; Sjölander, A.; Brodd, E. Post-Cracking Behaviour of Fibre-Reinforced Shotcrete: A Numerical Comparison between Beams and Panels. Fibers 2023, 11, 59. https://doi.org/10.3390/fib11070059
Östlund L, Sjölander A, Brodd E. Post-Cracking Behaviour of Fibre-Reinforced Shotcrete: A Numerical Comparison between Beams and Panels. Fibers. 2023; 11(7):59. https://doi.org/10.3390/fib11070059
Chicago/Turabian StyleÖstlund, Lina, Andreas Sjölander, and Elin Brodd. 2023. "Post-Cracking Behaviour of Fibre-Reinforced Shotcrete: A Numerical Comparison between Beams and Panels" Fibers 11, no. 7: 59. https://doi.org/10.3390/fib11070059
APA StyleÖstlund, L., Sjölander, A., & Brodd, E. (2023). Post-Cracking Behaviour of Fibre-Reinforced Shotcrete: A Numerical Comparison between Beams and Panels. Fibers, 11(7), 59. https://doi.org/10.3390/fib11070059







