Asymptotic Modeling of Optical Fibres: Annular Capillaries and Microstructured Optical Fibres
Abstract
1. Introduction
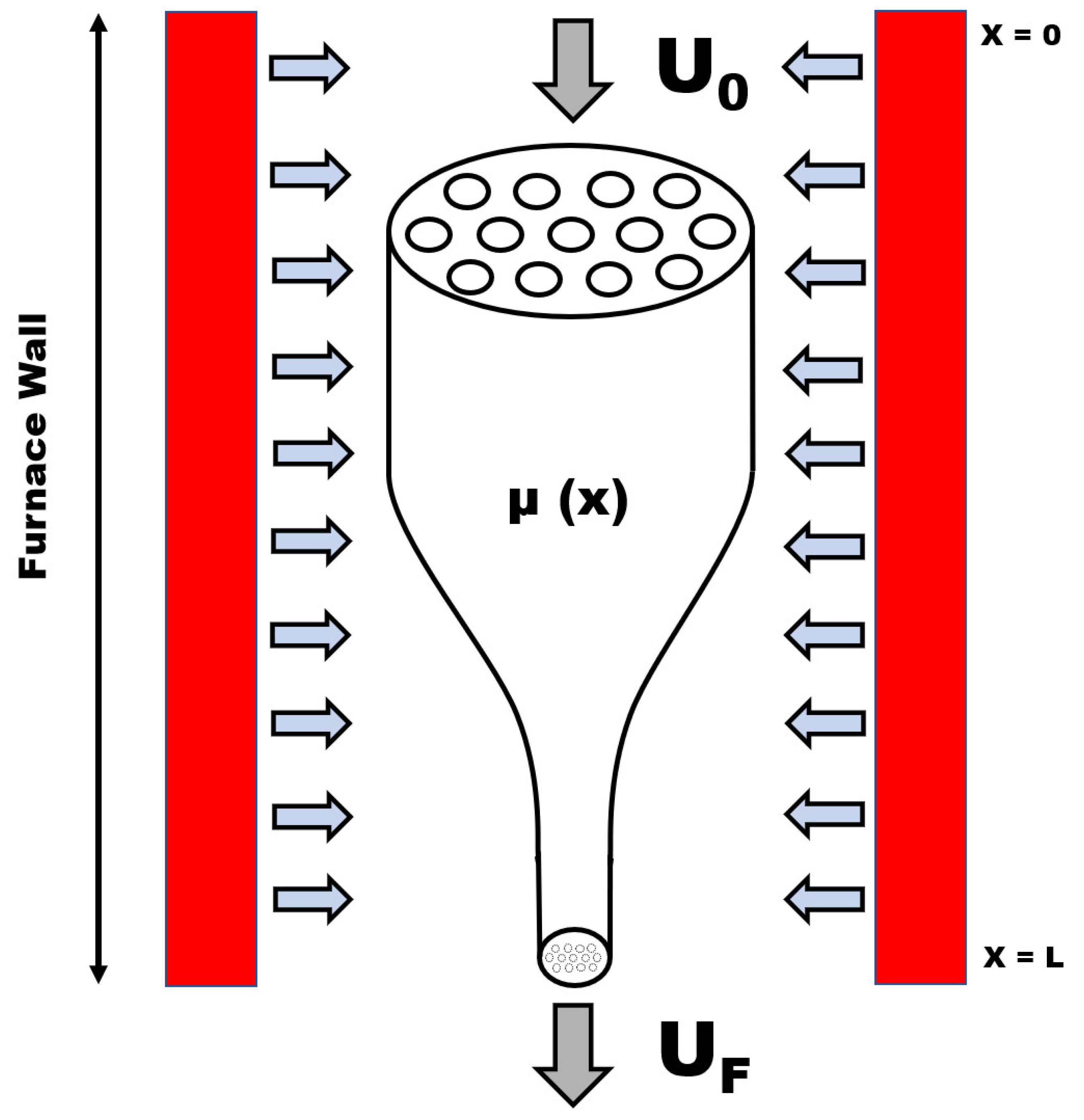
2. Model Description
2.1. Three-Dimensional Model
2.2. Non-Dimensionalization
2.3. Final Asymptotic Equations
2.3.1. Leading-Order Model for the Transverse Flow
2.3.2. The Case of a Circular Tube
2.3.3. The Cross-Plane Problem and the Complex Variable Formulation
2.3.4. The Generalised Elliptical Pore Model (GEPM)
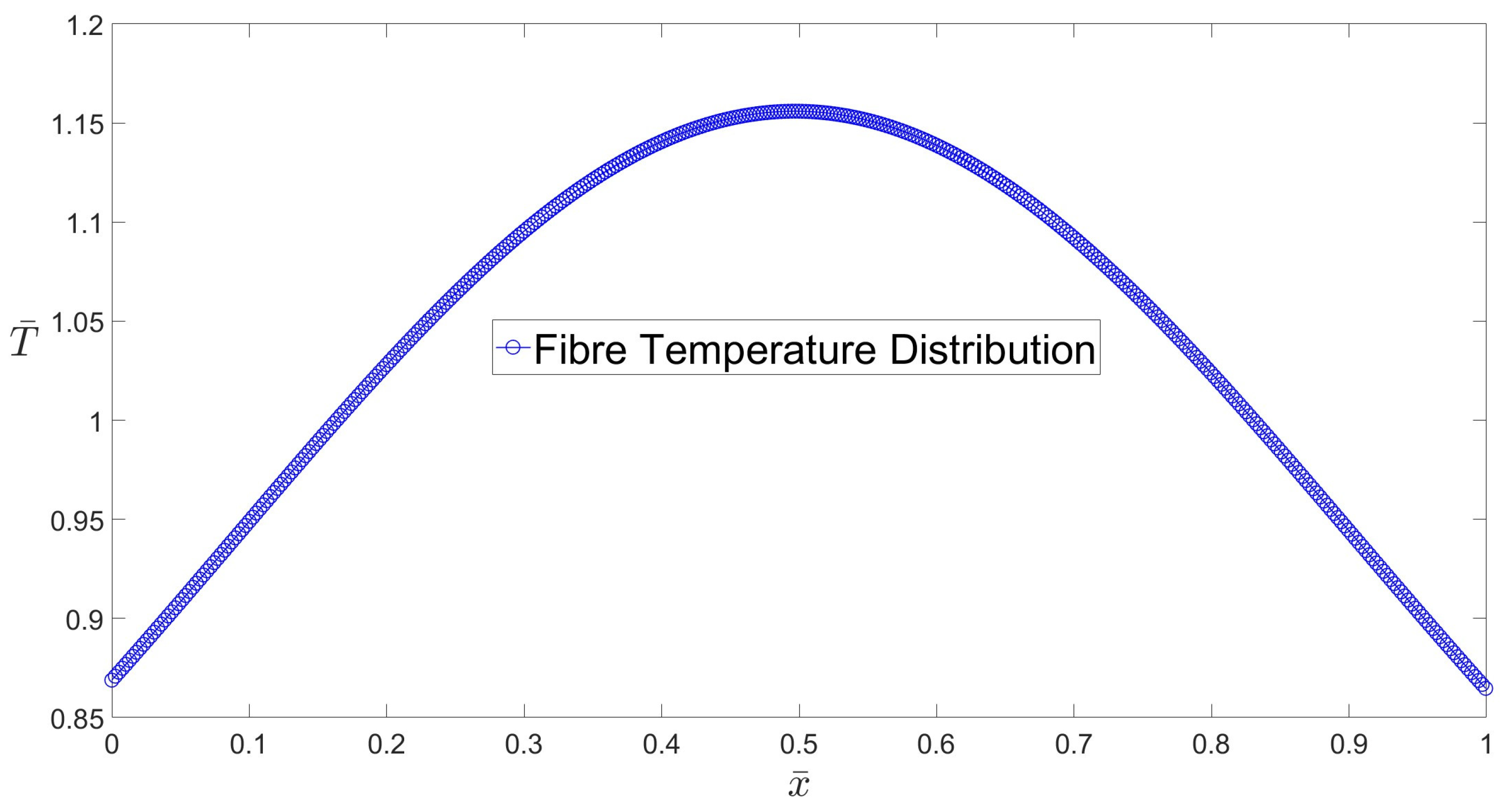
2.3.5. Fibre Temperature Profile and Glass Viscosity
3. Results
3.1. Solution Methodology
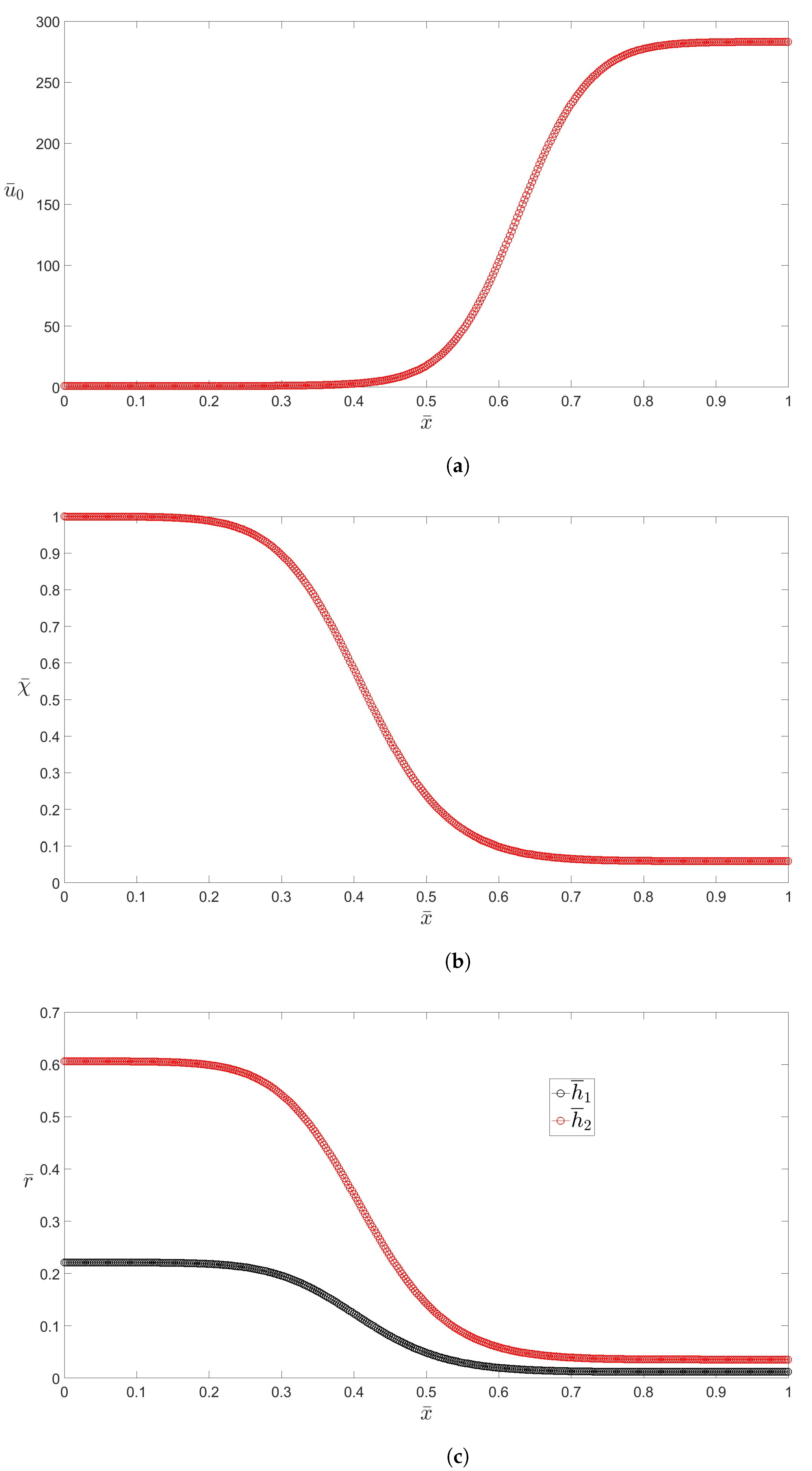
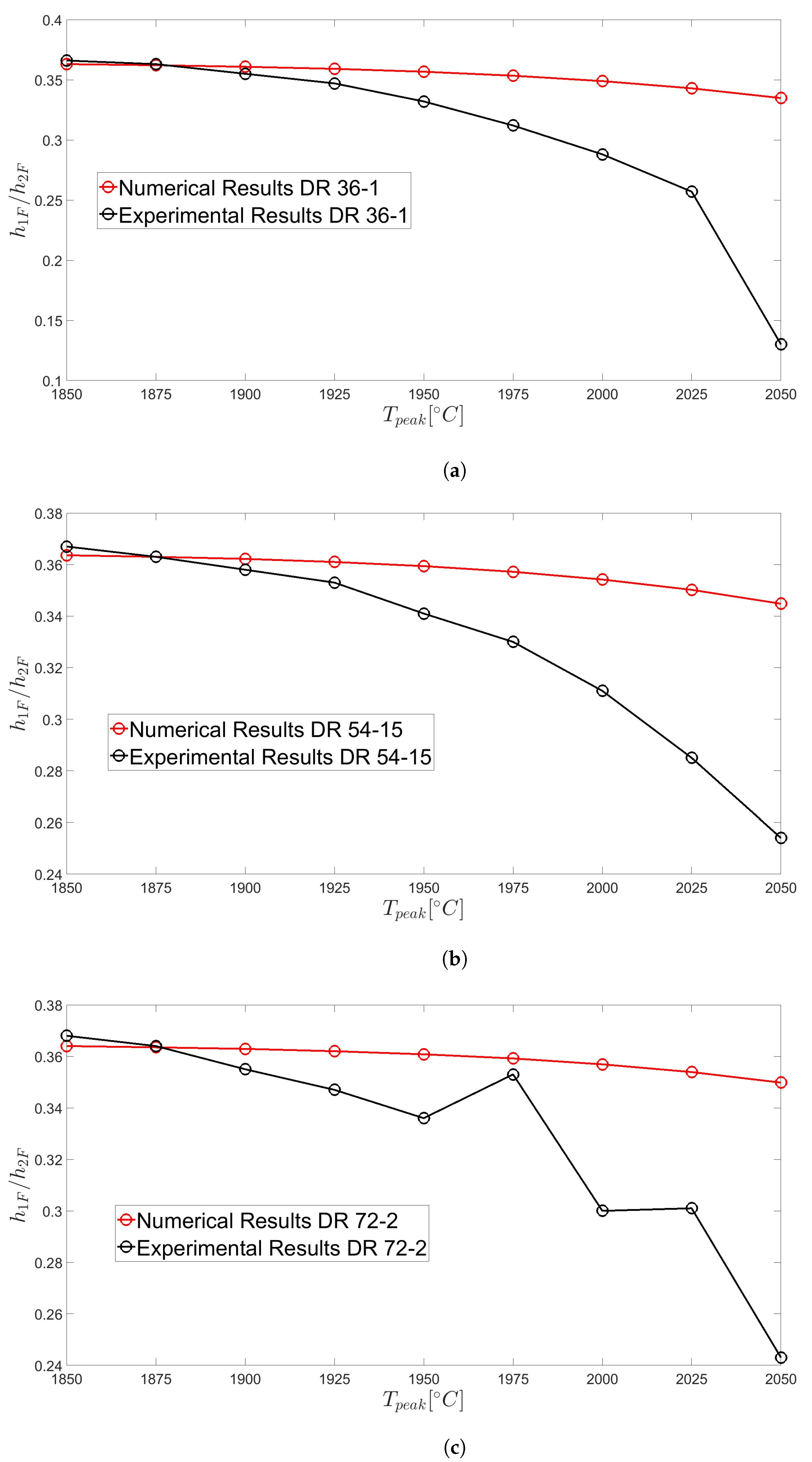
3.2. Annular Capillaries: Slow Drawing Ratios (SDRs)
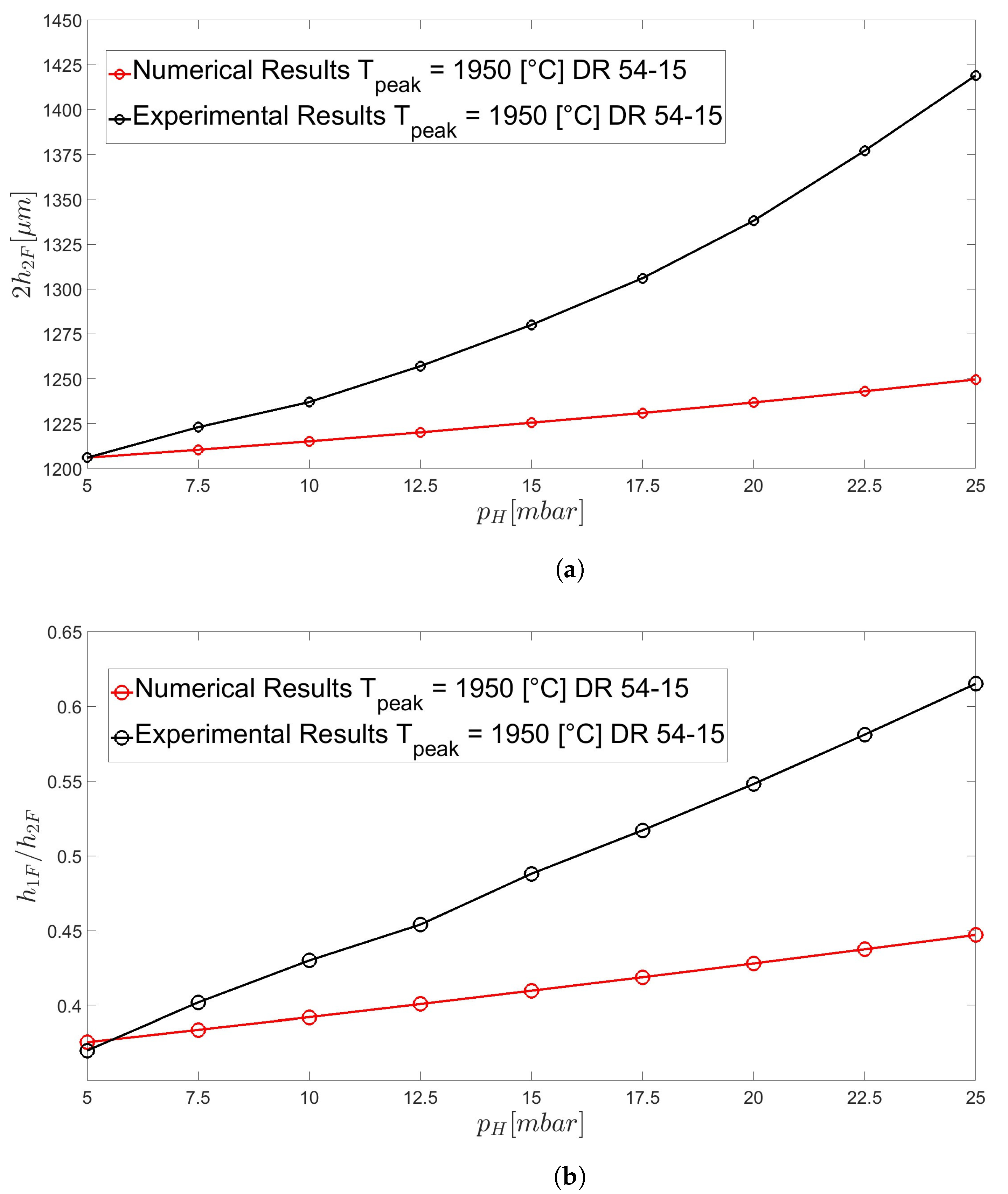
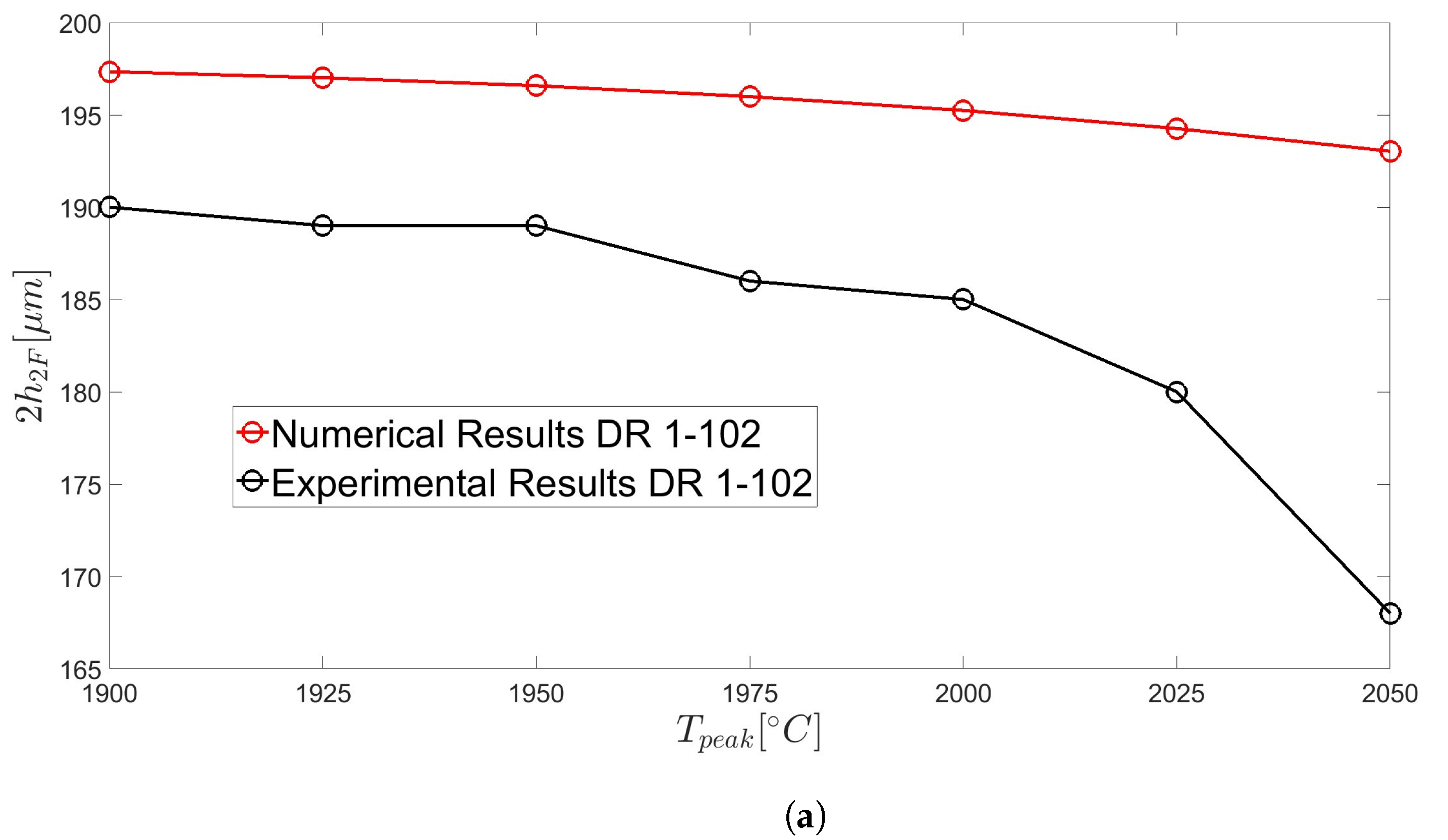
3.3. Annular Capillaries: High Drawing Ratios (HDRs)
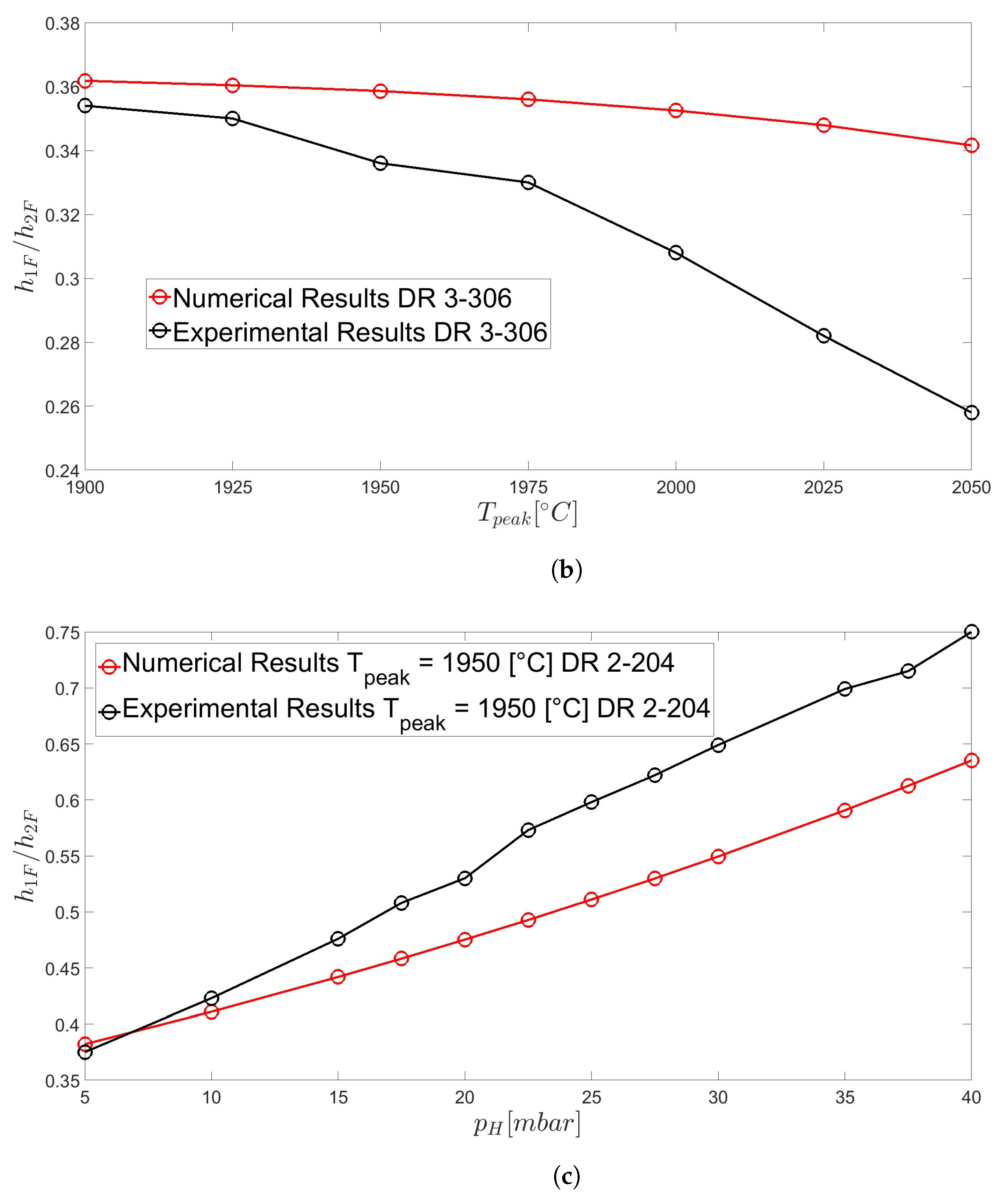
3.4. Holey Fibres (HFs)
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MOFs | Microstructured optical fibres |
| SCFs | Suspended-core fibres |
| HCFs | Hollow-core fibres |
| TIR | Total internal reflection |
| FEM | Finite element method |
| GEPM | Generalized elliptical pore model |
| DR | Drawing ratio |
| SDRs | Slow drawing ratios |
| HDRs | High drawing ratios |
| HFs | Holey fibres |
| SEM | Scanning electron microscope |
| CFD | Computational fluid dynamics |
| ILU | Incomplete lower–upper |
| PBG | Photonic band gap |
References
- Russell, P.S. Photonic-Crystal Fibers. J. Light. Technol. 2006, 24, 4729–4749. [Google Scholar] [CrossRef]
- Knight, J.C. Photonic crystal fibres. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef] [PubMed]
- Buczynski, R. Photonic Crystal Fibers. Acta Phys. Pol. A 2004, 106, 141–167. [Google Scholar] [CrossRef]
- Monro, T.M.; Ebendorff-Heidepriem, H. Progress in Microstructured Oprical Fibers. Annu. Rev. Mater. Res. 2006, 36, 467–495. [Google Scholar] [CrossRef]
- Wadsworth, W.; Percival, R.; Bouwmans, G.; Knight, J.; Russell, P. High power air-clad photonic crystal fibre laser. Opt. Express 2003, 11, 48–53. [Google Scholar] [CrossRef] [PubMed]
- Humbert, G.; Knight, J.; Bouwmans, G.; Russell, P.; Williams, D.; Roberts, P.; Mangan, B. Hollow core photonic crystal fibers for beam delivery. Opt. Express 2004, 12, 1477–1484. [Google Scholar] [CrossRef] [PubMed]
- Di Teodoro, F.; Brooks, C.D. 1.1 MW peak-power, 7 W average-power, high-spectral-brightness, diffraction-limited pulses from a photonic crystal fiber amplifier. Opt. Lett. 2005, 30, 2694–2696. [Google Scholar] [CrossRef]
- Dainese, P.; St., Russell, P.J.; Joly, N.; Knight, J.C.; Wiederhecker, G.S.; Fragnito, H.L.; Laude, V.; Khelif, A. Stimulated Brillouin scattering from multi-GHz-guided acoustic phonons in nanostructured photonic crystal fibres. Nat. Phys. 2006, 2, 388–392. [Google Scholar] [CrossRef]
- Chernikov, S.V.; Zhu, Y.; Taylor, J.R.; Gapontsev, V.P. Supercontinuum self-Q-switched ytterbium fiber laser. Opt. Lett. 1997, 22, 298–300. [Google Scholar] [CrossRef]
- Nyachionjeka, K.; Tarus, H.; Langat, K. Design of a photonic crystal fiber for optical communications application. Sci. Afr. 2020, 9, e00511. [Google Scholar] [CrossRef]
- Benabid, F.; Knight, J.C.; Antonopoulos, G.; Russell, P.S.J. Stimulated Raman scattering in hydrogen-filled hollow-core photonic crystal fiber. Science 2002, 298, 399–402. [Google Scholar] [CrossRef] [PubMed]
- Monro, T.M.; Belardi, W.; Furusawa, K.; Baggett, J.C.; Broderick, N.G.R.; Richardson, D.J. Sensing with microstructured optical fibres. Meas. Sci. Technol. 2001, 12, 854–858. [Google Scholar] [CrossRef]
- Marques, C.A.F.; Pospori, A.; Demirci, G.; Çetinkaya, O.; Gawdzik, B.; Antunes, P.; Bang, O.; Mergo, P.; André, P.; Webb, D.J. Fast Bragg Grating Inscription in PMMA Polymer Optical Fibres: Impact of Thermal Pre-Treatment of Preforms. Sensors 2017, 17, 891. [Google Scholar] [CrossRef] [PubMed]
- Monro, T.M.; Warren-Smith, S.; Schartner, E.P.; François, A.; Heng, S.; Ebendorff-Heidepriem, H.; Afshar, S. Sensing with suspended-core optical fibers. Opt. Fiber Technol. 2010, 16, 343–356. [Google Scholar] [CrossRef]
- Pinto, A.M.R.; Frazão, O.; Santos, J.L.; Lopez-Amo, M.; Kobelke, J.; Schuster, K. Interrogation of a Suspended-Core Fabry–Perot Temperature Sensor Through a Dual Wavelength Raman Fiber Laser. J. Light. Technol. 2010, 28, 3149–3155. [Google Scholar] [CrossRef]
- Fu, L.; Thomas, B.K.; Dong, L. Efficient supercontinuum generations in silica suspended core fibers. Opt. Express 2008, 16, 19629–19642. [Google Scholar] [CrossRef] [PubMed]
- Savelii, I.; Jules, J.C.; Gadret, G.; Kibler, B.; Fatome, J.; El-Amraoui, M.; Manikandan, N.; Zheng, X.; Désévédavy, F.; Dudley, J.M.; et al. Suspended core tellurite glass optical fibers for infrared supercontinuum generation. Opt. Mater. 2011, 33, 1661–1666. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Wang, Z. Application of Hollow-Core Photonic Crystal Fibers in Gas Raman Lasers Operating at 1.7 μm. Crystals 2021, 11, 121. [Google Scholar] [CrossRef]
- Jin, W.; Xuan, H.F.; Ho, H.L. Sensing with hollow-core photonic bandgap fibers. Meas. Sci. Technol. 2010, 21, 094014. [Google Scholar] [CrossRef]
- Poletti, F.; Petrovich, M.N.; Richardson, D.J. Hollow-core photonic bandgap fibers: Technology and applications. Nanophotonics 2013, 2, 315–340. [Google Scholar] [CrossRef]
- Matovich, M.A.; Pearson, J.R.A. Spinning a Molten Threadline. Steady-State Isothermal Viscous Flows. Ind. Eng. Chem. Fundam. 1969, 8, 512–520. [Google Scholar] [CrossRef]
- Paek, U.C.; Runk, R.B. Physical behavior of the neck–down region during furnace drawing of silica fibers. J. Appl. Phys. 1978, 49, 4417–4422. [Google Scholar] [CrossRef]
- Glicksman, L.R. The Dynamics of a Heated Free Jet of Variable Viscosity Liquid at Low Reynolds Numbers. J. Basic Eng. 1968, 90, 343–354. [Google Scholar] [CrossRef]
- Myers, M.R. A model for unsteady analysis of preform drawing. AIChE J. 1989, 35, 592–602. [Google Scholar] [CrossRef]
- Yarin, A.L.; Gospodinov, P.; Roussinov, V.I. Stability loss and sensitivity in hollow fiber drawing. Phys. Fluids 1994, 6, 1454–1463. [Google Scholar] [CrossRef]
- Fitt, A.D.; Furusawa, K.; Monro, T.M.; Please, C.P.; Richardson, D.J. The mathematical modelling of capillary drawing for holey fibre manufacture. J. Eng. Math. 2002, 43, 201–227. [Google Scholar] [CrossRef]
- Luzi, G.; Epple, P.; Scharrer, M.; Fujimoto, K.; Rauh, C.; Delgado, A. Influence of Surface Tension and Inner Pressure on the Process of Fibre Drawing. J. Light. Technol. 2010, 28, 1882–1888. [Google Scholar] [CrossRef]
- Luzi, G.; Epple, P.; Scharrer, M.; Fujimoto, K.; Rauh, C.; Delgado, A. Asymptotic Analysis of Flow Processes at Drawing of Single Optical Microfibres. Int. J. Chem. React. Eng. 2011, 9, 1–28. [Google Scholar] [CrossRef]
- Voyce, C.J.; Fitt, A.D.; Monro, T.M. The mathematical modelling of rotating capillary tubes for holey-fibre manufacture. J. Eng. Math. 2008, 60, 69–87. [Google Scholar] [CrossRef]
- Voyce, C.J.; Fitt, A.D.; Monro, T.M. Mathematical Modeling as an Accurate Predictive Tool in Capillary and Microstructured Fiber Manufacture: The Effects of Preform Rotation. J. Light. Technol. 2008, 26, 791–798. [Google Scholar] [CrossRef]
- Taroni, M.; Breward, C.J.W.; Cummings, L.J.; Griffiths, I.M. Asymptotic solutions of glass temperature profiles during steady optical fibre drawing. J. Eng. Math. 2013, 80, 1–20. [Google Scholar] [CrossRef]
- Luzi, G.; Lee, S.; Gatternig, B.; Delgado, A. An Asymptotic Energy Equation for Modelling Thermo Fluid Dynamics in the Optical Fibre Drawing Process. Energies 2022, 15, 7922. [Google Scholar] [CrossRef]
- Dewynne, J.N.; Ockendon, J.R.; Wilmott, P. A systematic derivation of the leading-order equations for extensional flows in slender geometries. J. Fluid Mech. 1992, 244, 323. [Google Scholar] [CrossRef]
- Dewynne, J.N.; Howell, P.D.; Wilmott, P. Slender Viscous Fibres With Inertia And Gravity. Q. J. Mech. Appl. Math. 1994, 47, 541–555. [Google Scholar] [CrossRef]
- Griffiths, I.M.; Howell, P.D. The surface-tension-driven evolution of a two-dimensional annular viscous tube. J. Fluid Mech. 2007, 593, 181–208. [Google Scholar] [CrossRef]
- Griffiths, I.M.; Howell, P.D. Mathematical modelling of non-axisymmetric capillary tube drawing. J. Fluid Mech. 2008, 605, 181–206. [Google Scholar] [CrossRef]
- Cummings, L.J.; Howell, P.D. On the evolution of non-axisymmetric viscous fibres with surface tension, inertia and gravity. J. Fluid Mech. 1999, 389, 361–389. [Google Scholar] [CrossRef]
- Stokes, Y.M.; Buchak, P.; Crowdy, D.G.; Ebendorff-Heidepriem, H. Drawing of micro-structured fibres: Circular and non-circular tubes. J. Fluid Mech. 2014, 755, 176–203. [Google Scholar] [CrossRef][Green Version]
- Chen, M.J.; Stokes, Y.M.; Buchak, P.; Crowdy, D.G.; Ebendorff-Heidepriem, H. Microstructured optical fibre drawing with active channel pressurisation. J. Fluid Mech. 2015, 783, 137–165. [Google Scholar] [CrossRef]
- Stokes, Y.M.; Wylie, J.J.; Chen, M.J. Coupled fluid and energy flow in fabrication of microstructured optical fibres. J. Fluid Mech. 2019, 874, 548–572. [Google Scholar] [CrossRef]
- Buchak, P.; Crowdy, D.G.; Stokes, Y.M.; Ebendorff-Heidepriem, H. Elliptical pore regularisation of the inverse problem for microstructured optical fibre fabrication. J. Fluid Mech. 2015, 778, 5–38. [Google Scholar] [CrossRef][Green Version]
- Crowdy, D.G. Compressible bubbles in Stokes flow. J. Fluid Mech. 2003, 476, 345–356. [Google Scholar] [CrossRef]
- Buchak, P.; Crowdy, D.G. Surface-tension-driven Stokes flow: A numerical method based on conformal geometry. J. Comput. Phys. 2016, 317, 347–361. [Google Scholar] [CrossRef]
- Xue, S.C.; Tanner, R.I.; Barton, G.W.; Lwin, R.; Large, M.; Poladian, L. Fabrication of microstructured optical fibers-part I: Problem formulation and numerical modeling of transient draw process. J. Light. Technol. 2005, 23, 2245–2254. [Google Scholar] [CrossRef]
- Xue, S.C.; Large, M.; Barton, G.W.; Tanner, R.I.; Poladian, L.; Lwin, R. Role of material properties and drawing conditions in the fabrication of microstructured optical fibers. J. Light. Technol. 2006, 24, 853–860. [Google Scholar] [CrossRef]
- Xue, S.C.; Tanner, R.I.; Barton, G.W.; Lwin, R.; Large, M.; Poladian, L. Fabrication of microstructured optical fibers-part II: Numerical modeling of steady-state draw process. J. Light. Technol. 2005, 23, 2255–2266. [Google Scholar] [CrossRef]
- Luzi, G.; Epple, P.; Scharrer, M.; Fujimoto, K.; Rauh, C.; Delgado, A. Numerical Solution and Experimental Validation of the Drawing Process of Six-Hole Optical Fibers Including the Effects of Inner Pressure and Surface Tension. J. Light. Technol. 2012, 30, 1306–1311. [Google Scholar] [CrossRef]
- Chen, M.J.; Stokes, Y.M.; Buchak, P.; Crowdy, D.G.; Ebendorff-Heidepriem, H. Asymptotic Modelling of a Six-Hole MOF. J. Light. Technol. 2016, 34, 5651–5656. [Google Scholar] [CrossRef]
- Chen, M.J.; Stokes, Y.M.; Buchak, P.; Crowdy, D.G.; Foo, H.T.; Dowler, A.; Ebendorff-Heidepriem, H. Drawing tubular fibres: Experiments versus mathematical modelling. Opt. Mater. Express 2016, 6, 166. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Langlois, W.E.; Deville, M.O. Slow Viscous Flow; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Frosz, M.H.; Ahmed, G.; Lapshina, N.; Keding, R.; Babic, F.; Joly, N.Y.; St., Russell, P.J. Reducing losses in solid-core photonic crystal fibers using chlorine dehydration. Opt. Mater. Express 2016, 6, 2975. [Google Scholar] [CrossRef]
- Barnes, H.A.; Hutton, J.F.; Walters, K. Polyflow User’s Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Stepien, R.; Cimek, J.; Pysz, D.; Kujawa, I.; Klimczak, M.; Buczynski, R. Soft glasses for photonic crystal fibers and microstructured optical components. Opt. Eng. 2014, 53, 071815. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value | Units |
|---|---|---|---|
| Hot zone length | L | 0.12 | m |
| Density | 2200 | kg m | |
| Surface tension | 0.25 | N m | |
| Initial external radius | 1 × 10 | m | |
| Initial internal radius | 3.65 × 10 | m | |
| Drawing ratio | DR 36-1 | ||
| Feed speed | 6 × 10 | m s | |
| Draw speed | 1.67 × 10 | m s | |
| Drawing ratio | DR 54-15 | ||
| Feed speed | 9 × 10 | m s | |
| Draw speed | 2.5 × 10 | m s | |
| Drawing ratio | DR 72-2 | ||
| Feed speed | 1.2 × 10 | m s | |
| Draw speed | 3.33 × 10 | m s | |
| Drawing ratio | DR 1-102 | ||
| Feed speed | 1.67 × 10 | m s | |
| Draw speed | 1.7 × 10 | m s | |
| Drawing ratio | DR 2-204 | ||
| Feed speed | 3.33 × 10 | m s | |
| Draw speed | 3.4 × 10 | m s | |
| Drawing ratio | DR 3-306 | ||
| Feed speed | 5.00 × 10 | m s | |
| Draw speed | 5.1 × 10 | m s | |
| Drawing ratio | DR 20-187 | ||
| Feed speed | 3.33 × 10 | m s | |
| Draw speed | 3.12 × 10 | m s | |
| Drawing ratio | DR 10-42 | ||
| Feed speed | 1.67 × 10 | m s | |
| Draw speed | 7.0 × 10 | m s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luzi, G.; Klapper, V.; Delgado, A. Asymptotic Modeling of Optical Fibres: Annular Capillaries and Microstructured Optical Fibres. Fibers 2023, 11, 104. https://doi.org/10.3390/fib11120104
Luzi G, Klapper V, Delgado A. Asymptotic Modeling of Optical Fibres: Annular Capillaries and Microstructured Optical Fibres. Fibers. 2023; 11(12):104. https://doi.org/10.3390/fib11120104
Chicago/Turabian StyleLuzi, Giovanni, Vinzenz Klapper, and Antonio Delgado. 2023. "Asymptotic Modeling of Optical Fibres: Annular Capillaries and Microstructured Optical Fibres" Fibers 11, no. 12: 104. https://doi.org/10.3390/fib11120104
APA StyleLuzi, G., Klapper, V., & Delgado, A. (2023). Asymptotic Modeling of Optical Fibres: Annular Capillaries and Microstructured Optical Fibres. Fibers, 11(12), 104. https://doi.org/10.3390/fib11120104







