Factors of Weave Estimation and the Effect of Weave Structure on Fabric Properties: A Review
Abstract
1. Introduction
2. Weave Factors
3. Weave Structure and Properties of Woven Fabric
3.1. Physical and Mechanical Properties
3.1.1. Physical and Mechanical Properties of Woven Fabric
3.1.2. Role of Weaves in Fabric Engineering
3.1.3. Fabric Structural Factor and Tensile Properties of Fabric
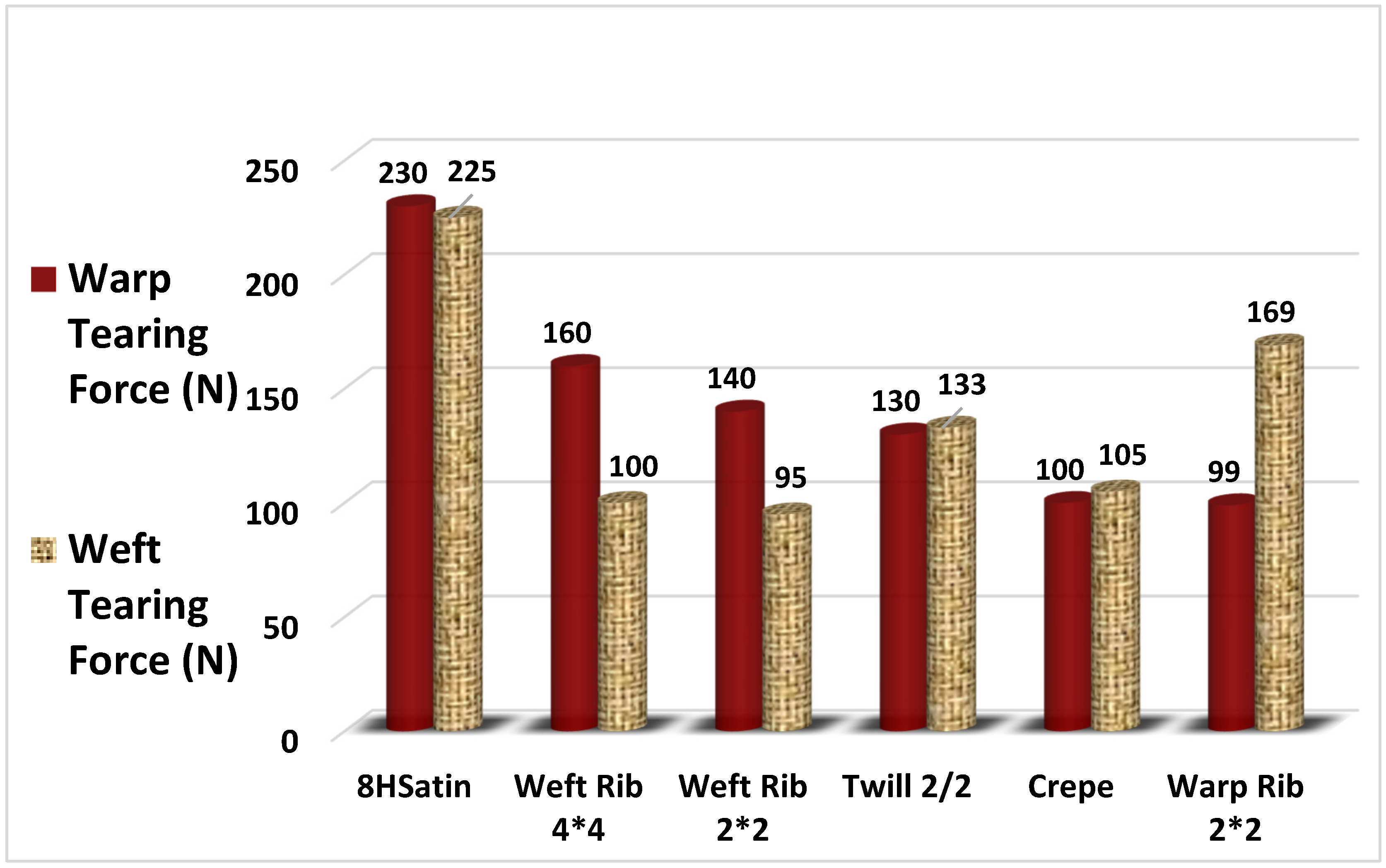
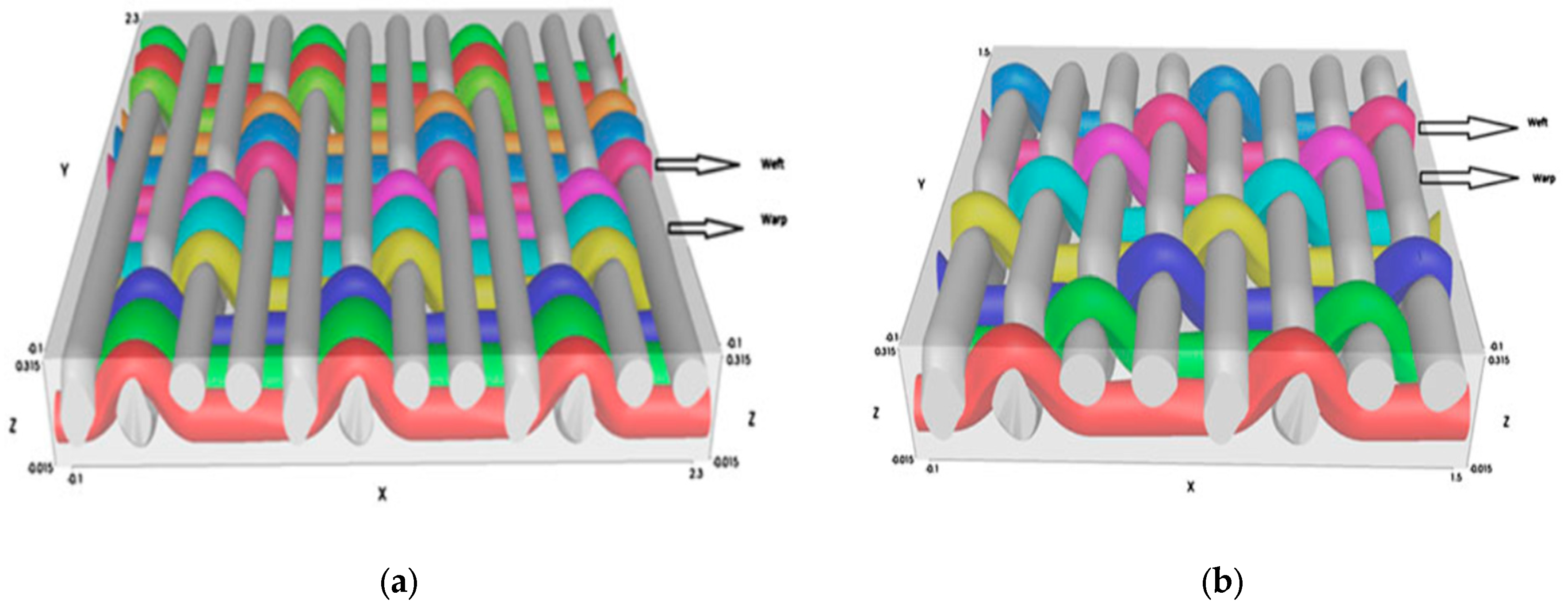
3.1.4. Weave Parameters and Tear Strength
3.1.5. Weave Structural Parameters and Fabric Friction Properties
3.1.6. Shear Properties and Fabric Structural Factor
3.1.7. Weave Factor and Slippage of Yarns in Fabrics
3.2. Comfort Related Properties
3.2.1. Weave Structure and Thermal Properties
3.2.2. Weave Structure and Air Permeability
3.2.3. Weave Structure and Comfort Properties
3.2.4. Weave Structure and Moisture Transport and Microbial Barrier Properties
3.2.5. Weave Structure and Water-Vapor Transport and Liquid Moisture Transport
3.2.6. Weave Structure and Compressional Properties
3.2.7. Weave Structure and Fabric Elasticity
3.2.8. Weave Structure and Fabric Roughness
3.2.9. Weave Parameters and Drapability of Fabric
3.3. Special Application Properties
3.3.1. Weave Structure and Ballistic Effects
3.3.2. Weave Structure on Woven Pressure Sensor and on Acoustic Properties
4. Conclusions and Recommendation
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brierley, S. Cloth Settings Reconsidered. Text. Manuf. 1952, 79, 349–351. [Google Scholar]
- Galceran, V. Seccion Segunda: Relation Entre La Densidad y el Ligamento Sin Variar el Numero del Hilo. Technol. Tejido Terasa 1961, 232–247. (In Spanish) [Google Scholar]
- Peirce, F.T. 5—The Geometry of Cloth Structure. J. Text. Inst. Trans. 1937, 28, T45–T96. [Google Scholar] [CrossRef]
- Milašius, V. An Integrated Structure Factor for Woven Fabrics Part I: Estimation of the Weave. J. Text. Inst. 2000, 91, 268–276. [Google Scholar] [CrossRef]
- Milašius, V. An Integrated Structure Factor for Woven Fabrics Part II: The Fabric-Firmness Factor. J. Text. Inst. 2000, 91, 277–284. [Google Scholar] [CrossRef]
- Milašius, V.; Milašius, R.; Kumpikaite, E.O.A. Influence of Fabric Structure on Some Technological and End-Use Properties. Fibres Text. East. Eur. 2003, 11, 48–51. [Google Scholar]
- Banerjee, P.K. Principles of Fabric Formation; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Behera, B.K.; Hari, P.K. Woven Textile Structure: Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Horrocks, A.R.; Anand, S.C. Handbook of Technical Textiles; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Hu, J. Structure and Mechanics of Woven Fabrics; Woodhead Publishing Limited, Elsevier: Cambridge, MA, USA, 2004. [Google Scholar]
- Azeem, M.; Ahmad, Z.; Wiener, J.; Fraz, A.; Siddique, H.F.; Havalka, A. Influence of Weave Design and Yarn Types on Mechanical and Surface Properties of Woven Fabric. Fibres Text. East. Eur. 2018, 26, 42–45. [Google Scholar]
- Morino, H.; Matsudaira, M. Predicting Mechanical Properties and Hand Values from the Parameters of Weave Structures. Text. Res. J. 2005, 67, 252–257. [Google Scholar] [CrossRef]
- Kumpikaitė, E.; Milašius, V. Influence of Fabric Structure on Its Weavability. Mater. Sci. 2003, 9, 395–400. [Google Scholar]
- Kumpikaitė, E.; Milašius, V. Analysis of Interrelation between Fabric Structure Factors and Beat-up Parameters. Mater. Sci. 2003, 9, 228–232. [Google Scholar]
- Kumpikaitė, E. Analysis of Dependencies of Woven Fabric’s Breaking Force and Elongation at Break on Its Structure Parameters. Fibres Text. East. Eur. 2007, 15, 35–38. [Google Scholar]
- Kumpikaitė, E. Influence of Fabric Structure on the Character of Fabric Breakage. Fibres Text. East. Eur. 2008, 16, 44–46. [Google Scholar]
- Adomaitienė, A.; Kumpikaitė, E. Effect of Raw Material on Changes in the Weft Setting of Fabric. Fibres Text. East. Eur. 2009, 17, 49–51. [Google Scholar]
- Sankaran, V.; Subramaniam, V. Effect of Weave Structures on the Low Stress Mechanical Properties of Woven Cotton Fabrics. Fibres Text. East. Eur. 2012, 20, 56–59. [Google Scholar]
- Ashenhurst, T.R. A Treatise on Textile Calculations and the Structure of Fabrics; Broadbent: Huddersficld, UK, 1884. [Google Scholar]
- Algirdas Milašius, V.M. New Representation of the Fabric Weave Factor. Fibres Text. East. Eur. 2008, 16, 48–51. [Google Scholar]
- Milašius, V.; Milašius, A.; Milašius, R. Comparison of Integrating Structure Factors of Woven Fabric. Mater. Sci. 2001, 7, 48–53. [Google Scholar]
- Algirdas Milašius, V.M. New Employment of Integrating Structure Factor for Investigation of Fabric Forming. Fibres Text. East. Eur. 2005, 13, 44–46. [Google Scholar]
- Schwartz, P. Structure and Mechanics of Textile Fibre Assemblies; Woodhead Publishing: Sawston, UK, 2019. [Google Scholar]
- Kumar, B.; Hu, J. Woven Fabric Structures and Properties. In Engineering of High-Performance Textiles; Elsevier: Amsterdam, The Netherlands, 2017; pp. 133–151. [Google Scholar]
- Hearle, J.W.S.; Thwaites, J.J.; Amirbayat, J. Mechanics of Flexible Fiber Assemblies; NATO Advanced Study Institute Series; Sijthoff & Noordhoff: Alpen aan den Rijn, The Netherlands, 1980; p. 38. [Google Scholar]
- Hearle, J.W.; Grosberg, P.; Backer, S. Structural Mechanics of Fibers, Yarns, and Fabrics; Wiley-Interscience: Hoboken, NJ, USA, 1969; Volume 1. [Google Scholar]
- Goswani, B. Shear Behavior of Cotton-Polyester-Blend Fabrics. J. Appl. Pol. Sci. Appl. Pol. Sym. 1978, 33, 245–259. [Google Scholar]
- Wang, F.; Xu, G.; Xu, B. Predicting the Shearing Rigidity of Woven Fabrics. Text. Res. J. 2005, 75, 30–34. [Google Scholar] [CrossRef]
- Alam, M.S.; Majumdar, A.; Ghosh, A. Development and Experimental Validation of a Mathematical Model of Shear Rigidity of Woven Fabric Structures. J. Text. Inst. 2021, 113, 824–832. [Google Scholar] [CrossRef]
- Anandjiwala, R.D.; Gonsalves, J.W. Nonlinear Buckling of Woven Fabrics Part I: Elastic and Nonelastic Cases. Text. Res. J. 2006, 76, 160–168. [Google Scholar] [CrossRef]
- El Messiry, M.; El-Tarfawy, S. Mechanical Properties and Buckling Analysis of Woven Fabric. Text. Res. J. 2019, 89, 2900–2918. [Google Scholar] [CrossRef]
- El-Messiry, M.; El-Tarfawy, S. Effect of Fabric Properties on Yarn Pulling Force for Stab Resistance Body Armour. In Proceedings of the Sixth World Conference on 3D Fabrics and their Applications, North Carolina State University (NCSU), Raleigh, NC, USA, 26–28 May 2015. [Google Scholar]
- Taylor, H.M. 9—Tensile and Tearing Strength of Cotton Cloths. J. Text. Inst. Trans. 1959, 50, T161–T188. [Google Scholar] [CrossRef]
- Ping, G.; Greenwood, K. 8—The Scope Eor Eabric Engineering by Means of the Weave. J. Text. Inst. 1986, 77, 88–103. [Google Scholar] [CrossRef]
- Banerjee, P.K.; Mishra, S.; Ramkumar, T. Effect of Sett and Construction on Uniaxial Tensile Properties of Woven Fabrics. J. Eng. Fibers Fabr. 2010, 5, 8–21. [Google Scholar] [CrossRef]
- Nikolić, M.; Mihailović, T.; Simović, L. Real Value of Weave Binding Coefficient as a Factor of Woven Fabric Strength. Fibres Text. East. Eur. 2000, 8, 74–78. [Google Scholar]
- Witkowska, B.; Frydrych, I. A Comparative Analysis of Tear Strength Methods. Fibres Text. East. Eur. 2004, 12, 42–47. [Google Scholar]
- Kumpikaitė, E.; Sviderskytė, A. The Influence of Woven Fabric Structure on the Woven Fabric Strength. Mater. Sci. 2006, 12, 162–166. [Google Scholar]
- Hakan, Ö.; Engin, M. The effects of fabric structural parameters on the breaking, bursting and impact strengths of diced woven fabrics. Tekst. Konfeksiyon 2013, 23, 113–123. [Google Scholar]
- Jahan, I. Effect of Fabric Structure on the Mechanical Properties of Woven Fabrics. Adv. Res. Text Eng. 2017, 2, 1018. [Google Scholar] [CrossRef]
- Ferdous, N.; Rahman, S.; bin Kabir, R.; Ahmed, A.E. A Comparative Study on Tensile Strength of Different Weave Structures. Intl. J. Sci. Res. Eng. Tech. 2014, 3, 1307–1313. [Google Scholar]
- Helena, G.; Emil, Č.; Krste, D. Influence of Weave and Weft Characteristics on Tensile Properties of Fabrics. Fibres Text. East. Eur. 2008, 16, 45–51. [Google Scholar]
- Brierley, S. Theory and Practice of Cloth Setting. Text. Manuf. 1931, 58, 47–49. [Google Scholar]
- Milašius, R.; Legaudienė, B.; Laureckienė, G. Influence of Weave Parameters on Woven Fabric Tear Strength. Fibres Text. East. Eur. 2018, 26, 48–51. [Google Scholar] [CrossRef]
- Thanikai Vimal, J.; Prakash, C.; Jebastin Rajwin, A. Effect of Weave Parameters on the Tear Strength of Woven Fabrics. J. Nat. Fibers 2020, 17, 1239–1248. [Google Scholar] [CrossRef]
- Morino, H.; Matsudaira, M. Objective Evaluation of Seam Pucker Using Artificial Intelligence, Part II: Method of Evaluating Seam Pucker. Korean Inst. Ind. Tech. 1984, 67, 252–257. [Google Scholar]
- Wang, P.; Ma, Q.; Sun, B.; Hu, H.; Gu, B. Finite Element Modeling of Woven Fabric Tearing Damage. Text. Res. J. 2011, 81, 1273–1286. [Google Scholar] [CrossRef]
- Eltahan, E. Structural Parameters Affecting Tear Strength of the Fabrics Tents. Alex. Eng. J. 2018, 57, 97–105. [Google Scholar] [CrossRef]
- Eryuruk, S.H.; Kalaoğlu, F. The Effect of Weave Construction on Tear Strength of Woven Fabrics. AUTEX Res. J. 2015, 15, 207–214. [Google Scholar] [CrossRef]
- Jeguirim, S.E.G.; Dhouib, A.B.; Sahnoun, M.; Cheickrouhou, M.; Schacher, L.; Adolphe, D. Sensory and Instrumental Techniques Evaluating the Effect of Structure Parameters on the Tactile Properties of Knitted Fabrics. J. Texture Stud. 2010, 41, 714–735. [Google Scholar] [CrossRef]
- Sülar, V.; Öner, E.; Okur, A. Roughness and Frictional Properties of Cotton and Polyester Woven Fabrics. Indian J. Fibre Text. Res. 2013, 38, 349–356. [Google Scholar]
- Gerhardt, L.C.; Mattle, N.; Schrade, G.U.; Spencer, N.D.; Derler, S. Study of Skin-Fabric Interactions of Relevance to Decubitus: Friction and Contact-Pressure Measurements. Skin. Res. Technol. 2008, 14, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.; Xing, M.M.Q.; Pan, N.; Maibach, H.I. Textiles and Human Skin, Microclimate, Cutaneous Reactions: An Overview. Cutan. Ocul. Toxicol. 2006, 25, 23–39. [Google Scholar] [CrossRef] [PubMed]
- Becerir, B.; Akgun, M.; Alpay, H.R. Effect of Some Yarn Properties on Surface Roughness and Friction Behavior of Woven Structures. Text. Res. J. 2016, 86, 975–989. [Google Scholar] [CrossRef]
- Das, A.; Kothari, V.K.; Vandana, N. A Study on Frictional Characteristics of Woven Fabrics. AUTEX Res. J. 2005, 5, 133–140. [Google Scholar]
- Beyene, K.A.; Gebeyaw, S. The Effects of Yarn and Fabric Structural Parameters on Surface Friction of Plain-Woven Fabrics. Res. J. Text. Appar. 2021, 19, 1–12. [Google Scholar] [CrossRef]
- Wilson, D. A Study of Fabric-on-Fabric Dynamic Friction. J. Text. Inst. Trans. 1964, 55, T163–T164. [Google Scholar] [CrossRef]
- Carr, W.W.; Posey, J.E.; Tincher, W.C. Frictional Characteristics of Apparel Fabrics. Text. Res. J. 1988, 58, 129–136. [Google Scholar] [CrossRef]
- Zurek, W.; Jankowiak, D. Surface Frictional Resistance of Fabrics Woven from Filament Yarns. Text. Res. J. 1985, 55, 113–121. [Google Scholar] [CrossRef]
- Kothari, V.K.; Ganga, M.K. Assessment of Frictional Properties of Some Woven Fabrics. Indian J. Fibre Text. Res. 1994, 19, 151–155. [Google Scholar]
- Das, A.; Kothari, K.; Nagaraju, V. Frictional Characteristics of Woven Suiting and Shirting Fabrics. Indian J. Fibre Text. Res. 2007, 32, 337–343. [Google Scholar]
- Jeddi, A.A.A.; Shams, S.; Nosraty, H.; Sarsharzadeh, A. Relations between Fabric Structure and Friction: Part I: Woven Fabrics. J. Text. Inst. 2003, 94, 223–234. [Google Scholar] [CrossRef]
- Bertaux, E.; Lewandowski, M.; Derler, S. Relationship between Friction and Tactile Properties for Woven and Knitted Fabrics. Text. Res. J. 2007, 77, 387–396. [Google Scholar] [CrossRef]
- Grosberg, P.; Park, B.J. The Mechanical Properties of Woven Fabrics Part V: The Initial Modulus and the Frictional Restraint in Shearing of Plain Weave Fabrics. Text. Res. J. 1996, 36, 420–431. [Google Scholar] [CrossRef]
- Kawabata, S.; Niwa, M.; Kawai, H. 5—The Finite-Deformation Theory of Plain-Weave Fabrics. Part III: The Shear-Deformation Theory. J. Text. Inst. 1973, 64, 62–85. [Google Scholar] [CrossRef]
- Treloar, L.R.G. 42—The Effect of Test-Piece Dimensions on the Behaviour of Fabrics in Shear. J. Text. Inst. Trans. 1965, 56, T533–T550. [Google Scholar] [CrossRef]
- Subramaniam, V.; Sivakumar, M.; Srinivasan, V.; Sasikala, M. Determining Factors That Affect Fabric Shear Behavior with the Twist Method. Text. Res. J. 1990, 60, 368–370. [Google Scholar] [CrossRef]
- Üren, N.; Okur, A. Kumaşlarin Kayma Deformasyonu ve Ölçüm Yöntemleri. Tekst. Muhendis 2014, 21, 51–65. [Google Scholar] [CrossRef][Green Version]
- Shanbeh, M.; Safar Johari, M.; Zarrebini, M.; Barburski, M.; Komisarczyk, A. Analysis of Shear Characteristics of Woven Fabrics and Their Interaction with Fabric Integrated Structural Factors. J. Eng. Fibers Fabr. 2019, 14, 1–13. [Google Scholar] [CrossRef]
- Malčiauskienė, E.; Milašius, A.; Laureckienė, G.; Milašius, R. Influence of Weave into Slippage of Yarns in Woven Fabric. Mater. Sci. 2011, 17, 47–51. [Google Scholar] [CrossRef]
- Shimazaki, K.; Lloyd, D.W. Opening Behavior of Lockstitch Seams in Woven Fabrics under Cyclic Loading Conditions. Text. Res. J. 1990, 60, 654–662. [Google Scholar] [CrossRef]
- Galuszynski, S. 31—Some Aspects of the Mechanism of Seam Slippage in Woven Fabrics. J. Text. Inst. 1985, 76, 425–433. [Google Scholar] [CrossRef]
- Gurarda, A. Investigation of the Seam Performance of PET/Nylon-Elastane Woven Fabrics. Text. Res. J. 2008, 78, 21–27. [Google Scholar] [CrossRef]
- Lopes Miguel, R.A.; Lucas, J.M.; de Lurdes Carvalho, M.; Manich, A.M. Fabric Design Considering the Optimisation of Seam Slippage. Int. J. Cloth. Sci. Technol. 2005, 17, 225–231. [Google Scholar] [CrossRef]
- Yildirim, K. Predicting Seam Opening Behavior of Woven Seat Fabrics. Text. Res. J. 2010, 80, 472–480. [Google Scholar] [CrossRef]
- Malčiauskienė, E.; Milašius, A.; Milašius, R. Weave Factor for Seam Slippage Prediction of Unbalance Fabrics. Fibres Text. East. Eur. 2011, 19, 101–104. [Google Scholar]
- Fanger, P.O. Thermal Comfort; Danish Technical Press: Copenhagen, Denmark, 1970. [Google Scholar]
- Parsons, K.C. Ergonomics Assessment of Environments in Buildings. In Proceedings of the CIBS Technical Conference, 1985. [Google Scholar]
- Małgorzata, M. Investigation of the Thermal Insulation Properties of Multilayer Textiles. Fibres Text. East. Eur. 2006, 14, 98–102. [Google Scholar]
- Matusiak, M. Thermal Comfort Index as a Method of Assessing the Thermal Comfort of Textile Materials. Fibres Text. East. Eur. 2010, 18, 45–50. [Google Scholar]
- Hes, L. Marketing Aspects of Clothing Comfort Evaluation. In Proceedings of the International Textile and Apparel Symposium, Izmir, Turkey, 2004. [Google Scholar]
- Hes, L.; Dolezal, I. A New Computer-Controlled Skin Model for Fast Determination of Water Vapour and Thermal Resistance of Fabrics. In Proceedings of the 7th Asian Textile Conference, New Delhi, India, 1–3 December 2003. [Google Scholar]
- Hes, L.; De, M.; Jo, A.; Djulay, V.V. Effect of Mutual Bonding of Textile Layers on Thermal Insulation and Thermal Contact Properties of Fabric Assemblies. Text. Res. J. 1996, 66, 245–250. [Google Scholar] [CrossRef]
- Karahan, H.A.; Özdogğan, E.; Demir, A.; Koçum, I.C.; Öktem, T.; Ayhan, H. Effects of Atmospheric Pressure Plasma Treatments on Some Physical Properties of Wool Fibers. Text. Res. J. 2009, 79, 1260–1265. [Google Scholar] [CrossRef]
- Majumdar, A. Modelling of Thermal Conductivity of Knitted Fabrics Made of Cotton-Bamboo Yarns Using Artificial Neural Network. J. Text. Inst. 2011, 102, 752–762. [Google Scholar] [CrossRef]
- Venkatesh, J.; Gowda, K.N.N. Effect of Plasma Treatment on the Moisture Management Properties of Regenerated Bamboo Fabric. Int. J. Sci. Res. Pub. 2013, 3, 1–8. [Google Scholar]
- Kan, C.W.; Yuen, C.W.M. Plasma Technology in Wool. Text. Prog. 2007, 39, 121–187. [Google Scholar] [CrossRef]
- Kan, C.W. KES-Analysis of a Temperature Plasma Treated Wool Fabric. Fibres Text. East. Eur. 2008, 16, 99–102. [Google Scholar]
- Das, A.; Kothari, V.K.; Balaji, M. Studies on Cotton-Acrylic Bulked Yarns and Fabrics. Part II: Fabric Characteristics. J. Text. Inst. 2007, 98, 363–376. [Google Scholar] [CrossRef]
- Chidambaram, P.; Govind, R.; Chandramouli Venkataraman, K. The Effect of Loop Length and Yarn Linear Density on the Thermal Properties of Bamboo Knitted Fabric. Autex Res. J. 2011, 11, 102–105. [Google Scholar]
- Prakash, C.; Thanikai Vimal, J.; Jebastin Rajwin, A.; Paranthaman, R. Effect of Weave Parameters on Thermal Properties of Woven Fabrics. J. Nat. Fibers 2021, 18, 1375–1383. [Google Scholar] [CrossRef]
- Zhu, G.; Militky, J.; Wang, Y.; Sundarlal, B.V.; Kremenakova, D. Study on the Wicking Property of Cotton Fabric. Fibres Text. East. Eur. 2015, 23, 137–140. [Google Scholar]
- Matusiak, M.; Sikorski, K. Influence of the Structure of Woven Fabrics on Their Thermal Insulation Properties. Fibres Text. East. Eur. 2011, 19, 46–53. [Google Scholar]
- Asayesh, A.; Talaei, M.; Maroufi, M. The Effect of Weave Pattern on the Thermal Properties of Woven Fabrics. Int. J. Cloth. Sci. Technol. 2018, 30, 525–535. [Google Scholar] [CrossRef]
- Rimvydas, M.; Žaneta, R. Investigation of Correlation of Fabric Inequality in Width with Fabric Shrinkage. Fibres Text. East. Eur. 2003, 11, 42–45. [Google Scholar]
- Zupin, Ž.; Hladnik, A.; Dimitrovski, K. Prediction of One-Layer Woven Fabrics Air Permeability Using Porosity Parameters. Text. Res. J. 2012, 82, 117–128. [Google Scholar] [CrossRef]
- Milašius, R.; Milašius, V. Investigation of Unevenness of Some Fabric Cross-Section Parameters. Fibres Text. East. Eur. 2002, 10, 47–49. [Google Scholar]
- Fatahi, I.; Yazdi, A.A. Predicting Air Permeability Property Values from the Parameters of Weave Structure. Fibres Text. East. Eur. 2012, 20, 78–81. [Google Scholar]
- Tung, K.; Hwang, K. Fluid Flow through Basic Weaves of Monofilament Filter Cloth. Text. Res. J. 1996, 66, 311–323. [Google Scholar]
- Milašius, R.; Milašius, V.; Kumpikaitė, E.; Olšauskienė, A. Development of Employment of Fabric Firmness Factor ϕ. In Proceedings of the Transactions of Conference “ArchTex-2002”, Lodz, Poland, 2003; pp. 31–39. [Google Scholar]
- Hoerner, S.F. Aerodynamic Properties of Screens and Fabrics. Text. Res. J. 1952, 22, 274–280. [Google Scholar] [CrossRef]
- Gooijer, H.; Warmoeskerken, M.M.C.G.; Groot Wassink, J. Flow Resistance of Textile Materials Part I: Monofilament Fabrics. Text. Res. J. 2003, 73, 437–443. [Google Scholar] [CrossRef]
- Havrdová, M. Air Permeability and a Structure of Woven Fabrics. Vlákna A Text. 2003, 10, 86–90. [Google Scholar]
- Havlová, M. Model of Vertical Porosity Occurring in Woven Fabrics and Its Effect on Air Permeability. Fibres Text. East. Eur. 2014, 22, 58–63. [Google Scholar]
- Havlová, M. Air Permeability and Constructional Parameters of Woven Fabrics. Fibres Text. East. Eur. 2013, 21, 84–89. [Google Scholar]
- Umair, M.; Hussain, T.; Shaker, K.; Nawab, Y.; Maqsood, M.; Jabbar, M. Effect of Woven Fabric Structure on the Air Permeability and Moisture Management Properties. J. Text. Inst. 2016, 107, 596–605. [Google Scholar] [CrossRef]
- Robertson, A.F. Air Porosity of Open-Weave Fabrics* Part I: Metallic Meshes. Text. Res. J. 1950, 20, 838–844. [Google Scholar] [CrossRef]
- Havlova, M. Influence of Vertical Porosity on Woven Fabric Air Permeability. In Proceedings of the 7th International Conference TEXSCI, Liberec, Czech Republic, 6–8 September 2010; pp. 6–8. [Google Scholar]
- Szosland, J. Identification of Structure of Inter Thread Channels in Models of Woven Fabrics. Fibres Text. East. Eur. 1999, 7, 41–45. [Google Scholar]
- Backer, S. The Relationship between the Structural Geometry of a Textile Fabric and Its Physical Properties, I: Literature Review. Text. Res. J. 1948, 18, 650–658. [Google Scholar] [CrossRef]
- Backer, S. The Relationship between the Structural Geometry of a Textile Fabric and Its Physical Properties Part IV: Interstice Geometry and Air Permeability. Text. Res. J. 1951, 21, 703–714. [Google Scholar] [CrossRef]
- Saidenov, G.B. Methods of Calculating the Air Permeability of Fabrics as a Functions of Their Structure. Candidate Dissertation, Moscow Textile Institute, Moscow, Russia, 1965. [Google Scholar]
- Olšauskienė, A.; Milašius, R. Influence of Fabric Structure on Air Permeability. In Proceedings of the International Conference The Textiles: Research in Design and Technology, Kaunas, Lithuania, 21–22 September 2000; pp. 201–206. [Google Scholar]
- Ogulata, R.T. Air Permeability of Woven Fabrics. J. Text. Appar. Technol. Manag. 2006, 5, 1–10. [Google Scholar]
- Fatahi, I.; Yazdi, A.A. Assessment of the Relationship between Air Permeability of Woven Fabrics and Its Mechanical Properties. Fibres Text. East. Eur. 2010, 18, 68–71. [Google Scholar]
- Galuszynski, S. Fabric Tightness: A Coefficient to Indicate Fabric Structure. J. Text. Inst. 1981, 72, 44–49. [Google Scholar] [CrossRef]
- Olšauskienė, A.; Milašius, R. Dependence of Air Permeability on Various Integrated Fabric Firmness Factors. Mater. Sci. 2003, 9, 401–404. [Google Scholar]
- Baruah, S.; Kalita, B.B.; Jose, S.; Borah, M.P.; Kalita, S. Impact of Weave on Physico-Comfort Properties of Eri/Modal Union Fabric. J. Nat. Fibers 2021, 1–9. [Google Scholar] [CrossRef]
- Clulow, E.E. The Assessment of Comfort. J. Text. Inst. 1987, 78, 322–323. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P.; Wang, F. Fabric-Skin Friction Property Measurement System. Int. J. Cloth. Sci. Technol. 2010, 22, 285–296. [Google Scholar] [CrossRef]
- Süle, G. Investigation of Bending and Drape Properties of Woven Fabrics and the Effects of Fabric Constructional Parameters and Warp Tension on These Properties. Text. Res. J. 2012, 82, 810–819. [Google Scholar] [CrossRef]
- Goyal, R.; Prahbu, C.N. Moisture Management: A Key to Comfort. Colour 2008, 55, 132–133. [Google Scholar]
- Li, Y. The Science of Clothing Comfort. Text. Prog. 2001, 31, 1–135. [Google Scholar] [CrossRef]
- Tahvildar, A.; Ezazshahabi, N.; Mousazadegan, F. Appearance and Comfort Properties Considering Yarn-Spinning System and Weave Structure in Worsted Woven Fabrics. J. Eng. Fibers Fabr. 2019, 14, 1–8. [Google Scholar] [CrossRef]
- Akgün, M.; Kamaci, H.A. Effect of Fabric Structural Parameters on Various Comfort Properties of Automobile Seat Cover Fabrics. Eur. Mech. Sci. 2021, 5, 105–108. [Google Scholar] [CrossRef]
- Nazir, M.U.; Shaker, K.; Nawab, Y.; Fazal, M.Z.; Khan, M.I.; Umair, M. Investigating the Effect of Material and Weave Design on Comfort Properties of Bilayer-Woven Fabrics. J. Text. Inst. 2017, 108, 1319–1326. [Google Scholar] [CrossRef]
- Lei, M.; Li, Y.; Liu, Y.; Ma, Y.; Cheng, L.; Hu, Y. Effect of Weaving Structures on the Water Wicking-Evaporating Behavior of Woven Fabrics. Polymers 2020, 12, 422. [Google Scholar] [CrossRef]
- Rogina-Car, B.; Kovačević, S.; Schwarz, I.; Dimitrovski, K. Microbial Barrier Properties of Cotton Fabric-Influence of Weave Architecture. Polymers 2020, 12, 1570. [Google Scholar] [CrossRef]
- Laing, R.M.; Sleivert, G.G. Clothing, Textiles, and Human Performance. Text. Prog. 2002, 32, 1–122. [Google Scholar]
- Hang, X.D.; Sun, W.; Ye, C. Finite Volume Solution of Heat and Moisture Transfer through Three-Dimensional Textile Materials. Comput. Fluids 2012, 57, 25–39. [Google Scholar] [CrossRef]
- Hauke, G.; Moreau, R. An Introduction to Fluid Mechanics and Transport Phenomena; Springer: Amsterdam, The Netherlands, 2008; Volume 86. [Google Scholar]
- Fourt, L.; Harris, M. Diffusion of Water Vapor Through Textiles. Text. Res. J. 1947, 17, 256–263. [Google Scholar] [CrossRef]
- Song, Y.N.; Ma, R.J.; Xu, L.; Huang, H.D.; Yan, D.X.; Xu, J.Z.; Zhong, G.J.; Lei, J.; Li, Z.M. Wearable Polyethylene/Polyamide Composite Fabric for Passive Human Body Cooling. ACS Appl. Mater. Interfaces 2018, 10, 41637–41644. [Google Scholar] [CrossRef]
- Atasağun, H.G.; Okur, A.; Psikuta, A.; Rossi, R.M.; Annaheim, S. The Effect of Garment Combinations on Thermal Comfort of Office Clothing. Text. Res. J. 2019, 89, 4425–4437. [Google Scholar]
- Qian, J.; Li, Y.; Xiang, Z.; Cai, H.; Zhang, P. Effect of Weave Structure and Yarn Fineness on the Coolness and Thermal-Wet Comfort Properties of Woven Fabric. Text. Res. J. 2022, 004051752210958. [Google Scholar] [CrossRef]
- Van Wyk, C.M. 20—Note on the Compressibility of Wool. J. Text. Inst. Trans. 1946, 37, T285–T292. [Google Scholar] [CrossRef]
- De Jong, S.; Snaith, J.W.; Michie, N.A. A Mechanical Model for the Lateral Compression of Woven Fabrics. Text. Res. J. 1986, 56, 759–767. [Google Scholar] [CrossRef]
- Ajayi, J.O.; Elder, H.M. Fabric Friction, Handle, and Compression. J. Text. Inst. 1997, 88, 232–241. [Google Scholar] [CrossRef]
- Ukponmwan, J.O. Compressibility Analysis of Dry Abraded Woven Fabrics. Text. Res. J. 1994, 64, 756–760. [Google Scholar] [CrossRef]
- Ukponmwan, J.O. Compressibility Analysis of Wet Abraded Woven Fabrics. J. Test. Eval. 1993, 21, 312–321. [Google Scholar]
- Asayesh, A.; Mirgoli, F.; Gholamhosseini, A. An Investigation into the Effect of Fabric Structure on the Compressional Properties of Woven Fabrics. J. Text. Inst. 2018, 109, 32–38. [Google Scholar]
- Sajn Gorjanc, D.; Bizjak, M.; Gorjanc, D.S. The Influence of Constructional Parameters on Deformability of Elastic Cotton Fabrics. J. Eng. Fibers Fabr. 2014, 9, 38–46. [Google Scholar]
- Akgun, M. Assessment of the Surface Roughness of Cotton Fabrics through Different Yarn and Fabric Structural Properties. Fibers Polym. 2014, 15, 405–413. [Google Scholar]
- Akgun, M. The Effect of Fabric Balance and Fabric Cover on Surface Roughness of Polyester Fabrics. Fibers Polym. 2013, 14, 1372–1377. [Google Scholar]
- Mooneghi, S.A.; Mohammad, S.; Varkiyani, H.; Saharkhiz, S. Study on Fabric Surface Roughness and Its Influence on Worsted Fabric Abrasion Resistance. J. Eng. Fibers Fabr. 2015, 10, 79–86. [Google Scholar]
- Pensé-Lhéritier, A.M.; Guilabert, C.; Bueno, M.A.; Sahnoun, M.; Renner, M. Sensory Evaluation of the Touch of a Great Number of Fabrics. Food Qual. Pref. 2006, 17, 482–488. [Google Scholar]
- Ezazshahabi, N.; Tehran, M.A.; Latifi, M.; Madanipour, K. Surface Roughness Assessment of Woven Fabrics Using Fringe Projection Moiré Techniques. Fibres Text. East. Eur. 2015, 23, 76–84. [Google Scholar]
- Beyene, K.A.; Kumelachew, D.M. An Investigation of the Effects of Weave Types on Surface Roughness of Woven Fabric. Text. Res. J. 2021, 92, 2276–2284. [Google Scholar]
- Peirce, F.T. 26—The “Handle” of Cloth as a Measurable Quantity. J. Text. Inst. Trans. 1930, 21, T377–T416. [Google Scholar]
- Cusick, G.E. 21—The Measurement of Fabric Drape. J. Text. Inst. 1968, 59, 253–260. [Google Scholar]
- Chu, C.C.; Cummings, C.L.; Teixeira, N.A. Mechanics of Elastic Performance of Textile Materials Part V: A Study of the Factors Affecting the Drape of Fabrics—The Development of a Drape Meter. Text. Res. J. 1950, 20, 539–548. [Google Scholar]
- Chauncey, C.C.; Milton, M.P.; Walter, J. Hamburger Investigation of the Factors Affecting the Drapeability of Fabrics. Text. Res. J. 1960, 30, 66–67. [Google Scholar]
- Cusick, G.E. 46—The Dependence of Fabric Drape on Bending and Shear Stiffness. J. Text. Inst. Trans. 1965, 56, T596–T606. [Google Scholar]
- Cusick, G.E. 30—The Resistance of Fabrics to Shearing Forces. J. Text. Inst. Trans. 1961, 52, T395–T406. [Google Scholar]
- Matsudaira, M.; Yang, M.; Kinari, T.; Shintaku, S. Polyester “Shingosen” Fabrics Characterized by Dynamic Drape Coefficientwith Swinging Motion. Text. Res. J. 2002, 72, 410–416. [Google Scholar]
- Matsudaira, M.; Yang, M. Some Features of the Static and Dynamic Drape Behaviour of Polyester-Fibre Shingosen Fabrics. J. Text. Inst. 2000, 91, 600–615. [Google Scholar]
- Amirbayat, J.; Hearle, J.W.S. The Anatomy of Buckling of Textile Fabrics: Drape and Conformability. J. Text. Inst. 1989, 80, 51–70. [Google Scholar]
- Ucar, N.; Kalaoglu, F.; Bahtiyar, D.; Bilac, O.E. Investigating the Drape Behavior of Seamed Knit Fabricswith Image Analysis. Text. Res. J. 2004, 74, 166–171. [Google Scholar]
- Hearle, J.W.S.; Amirbayat, J. Analysis of Drape by Means of Dimensionless Groups. Text. Res. J. 1986, 56, 727–733. [Google Scholar]
- Hu, J.; Chan, Y.-F. Effect of Fabric Mechanical Properties on Drape. Text. Res. J. 1998, 68, 57–64. [Google Scholar] [CrossRef]
- Wu, Z.; Au, C.K.; Yuen, M. Mechanical Properties of Fabric Materials for Draping Simulation. Int. J. Cloth. Sci. Tech. 2003, 15, 56–68. [Google Scholar] [CrossRef]
- Shyr, T.W.; Wang, P.N.; Cheng, K.B. A Comparison of the Key Parameters Affecting the Dynamic and Static Drape Coefficients of Natural-Fibre Woven Fabrics by a Newly Devised Dynamic Drape Automatic Measuring System. Fibres Text. East. Eur. 2007, 15, 81–86. [Google Scholar]
- Dinparast Tohidi, S.; Asghar Asgharian Jeddi, A.; Tohidi, S.D.; A Jeddi, A.A.; Nosrati, H. Analyzing of the Woven Fabric Geometry on the Bending Rigidity Properties. Intl. J. Text. Sci. 2013, 2013, 73–80. [Google Scholar]
- Matusiak, M. Influence of the Structural Parameters of Woven Fabrics on Their Drapeability. Fibres Text. East. Eur. 2017, 25, 56–64. [Google Scholar] [CrossRef]
- David, N.V.; Gao, X.L.; Zheng, J.Q. Ballistic Resistant Body Armor: Contemporary and Prospective Materials and Related Protection Mechanisms. Appl. Mech. Rev. 2009, 62, 1–20. [Google Scholar]
- Naik, D.; Sankaran, S.; Mobasher, B.; Rajan, S.D.; Pereira, J.M. Development of Reliable Modeling Methodologies for Fan Blade out Containment Analysis—Part I: Experimental Studies. Int. J. Impact Eng. 2009, 36, 1–11. [Google Scholar] [CrossRef]
- Christiansen, E.L.; Crews, J.L.; Williamsen, J.E.; Robinson, J.H.; Nolen, A.M. Enhanced Meteroid and Orbital Debris Shielding. Int. J. Impact Eng. 1995, 17, 217–228. [Google Scholar] [CrossRef]
- Lane, R.A. High Performance Fibers for Personnel and Vehicular Protection Systems. AMPTIAC Q. 2005, 9, 3–9. [Google Scholar]
- Jacobs, M.J.N.; van Dingenen, J.L.J. Ballistic Protection Mechanisms in Personal Armour. J. Mater. Sci. 2001, 36, 3137–3142. [Google Scholar] [CrossRef]
- Prewo, K.M. Aramid Fiber Reinforcements, Reference Book for Composites Technology; Lee, S.M., Ed.; Technomic Publications Co.: Lancaster, PA, USA, 1989; Volume 1. [Google Scholar]
- Prevorsek, D.C. Ultrahigh Modulus/Strength Polyethylene Fibers and Composites. Reference Book for Composites Technology, 1; Lee, S.M., Ed.; Technomic Publications Co.: Lancaster, PA, USA, 1989; Volume 1. [Google Scholar]
- Figucia, F. The Effect of Kevlar Fabric Construction on Ballistic Resistance; U.S. Army Natick Research, Development, and Engineering Center: Natick, MA, USA, 1975. [Google Scholar]
- Cunniff, P.M. An Analysis of the System Effects in Woven Fabrics under Ballistic Impact. Text. Res. J. 1992, 62, 495–509. [Google Scholar]
- Cheeseman, B.A.; Bogetti, T.A. Ballistic Impact into Fabric and Compliant Composite Laminates. Compos. Struct. 2003, 61, 161–173. [Google Scholar]
- Roylance, D.; Wilde, A.; Tocci, G. Ballistic Impact of Textile Structures. Text. Res. J. 1973, 43, 34–41. [Google Scholar]
- Figucia, F. Energy Absorption of Kevlar Fabrics under Ballistic Impact; U.S. Army Natick Research, Development, and Engineering Center: Natick, MA, USA, 1980; pp. 29–41. [Google Scholar]
- Chu, C.-K.; Chen, Y.-L. Ballistic-Proof Effects of Various Woven Constructions. Fibres Text. East. Eur. 2010, 18, 63–67. [Google Scholar]
- Lee, Y.S.; Wetzel, E.D.; Wagner, N.J. The Ballistic Impact Characteristics of Kevlar R Woven Fabrics Impregnated with a Colloidal Shear Thickening Fluid. J. Mater. Sci. 2003, 38, 2825–2833. [Google Scholar]
- Shimek, M.E.; Fahrenthold, E.P. Effects of Weave Type on the Ballistic Performance of Fabrics. AIAA J. 2012, 50, 2558–2565. [Google Scholar]
- Yang, C.; Tran, P.; Ngo, T.; Mendis, P.; Humphries, W. Effect of Textile Architecture on Energy Absorption of Woven Fabrics Subjected to Ballistic Impact. In Applied Mechanics and Materials; Trans Tech Publications: Bach, Switzerland, 2014; Volume 553, pp. 757–762. [Google Scholar]
- Nawab, Y.; Hamdani, S.T.A.; Shaker, K. Structural Textile Design: Interlacing and Interlooping; CRC Press: Boca Raton, FL, USA, 2017; p. 298. [Google Scholar]
- Shaker, K.; Umair, M.; Hamdani, S.T.A.; Nawab, Y. Effect of Fabric Structure on the Performance of 3D Woven Pressure Sensor. Fibers Polym. 2021, 22, 847–853. [Google Scholar]
- EU Commission. Directive 2002/49/EC of the European Parliament and of the Council of 25 June 2002 Relating to the Assessment and Management of Environmental Noise. In Declaration by the Commission in the Conciliation Committee on the Directive Relating to the Assessment and Management of Environmental Noise; EU Commission: Brussels, Belgium, 2002. [Google Scholar]
- Tang, X.; Yan, X. Acoustic Energy Absorption Properties of Fibrous Materials: A Review. Compos. Part A 2017, 101, 360–380. [Google Scholar]
- Tiuc, A.E.; Vermeşan, H.; Gabor, T.; Vasile, O. Improved Sound Absorption Properties of Polyurethane Foam Mixed with Textile Waste. Energy Procedia 2016, 85, 559–565. [Google Scholar]
- Barburski, M.; Blaszczak, J.R.; Pawliczak, Z. Influence of Designs of Weaves on Acoustic Attenuation of Fabrics. J. Ind. Text. 2019, 49, 33–45. [Google Scholar]
- Li, H.; Zhang, N.; Fan, X.; Gong, J.; Zhang, J.; Zhao, X. Investigation of Effective Factors of Woven Structure Fabrics for Acoustic Absorption. Appl. Acous. 2020, 161, 1–8. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Begum, M.S.; Milašius, R. Factors of Weave Estimation and the Effect of Weave Structure on Fabric Properties: A Review. Fibers 2022, 10, 74. https://doi.org/10.3390/fib10090074
Begum MS, Milašius R. Factors of Weave Estimation and the Effect of Weave Structure on Fabric Properties: A Review. Fibers. 2022; 10(9):74. https://doi.org/10.3390/fib10090074
Chicago/Turabian StyleBegum, Most. Setara, and Rimvydas Milašius. 2022. "Factors of Weave Estimation and the Effect of Weave Structure on Fabric Properties: A Review" Fibers 10, no. 9: 74. https://doi.org/10.3390/fib10090074
APA StyleBegum, M. S., & Milašius, R. (2022). Factors of Weave Estimation and the Effect of Weave Structure on Fabric Properties: A Review. Fibers, 10(9), 74. https://doi.org/10.3390/fib10090074






