Shear and Flexural Behavior of Flat Slabs Casted with Polyolefin Fiber-Reinforced Concrete
Abstract
:1. Introduction
2. Characterization of Experimental Program
2.1. Concrete Mixture
2.2. Steel Reinforcement
2.3. Polyolefin Fibers
3. Preparing of Specimens
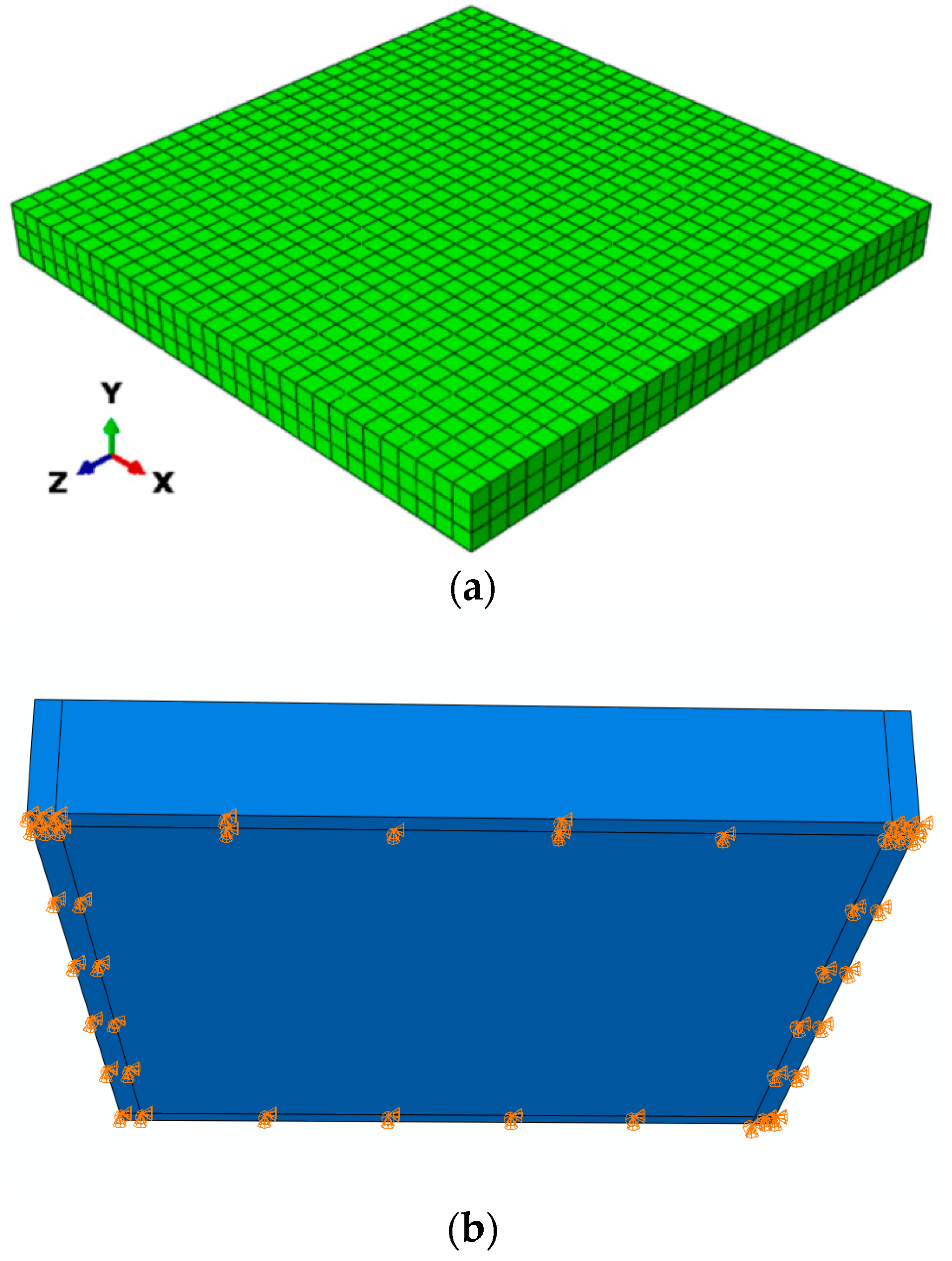
3.1. Non-Linear Analysis
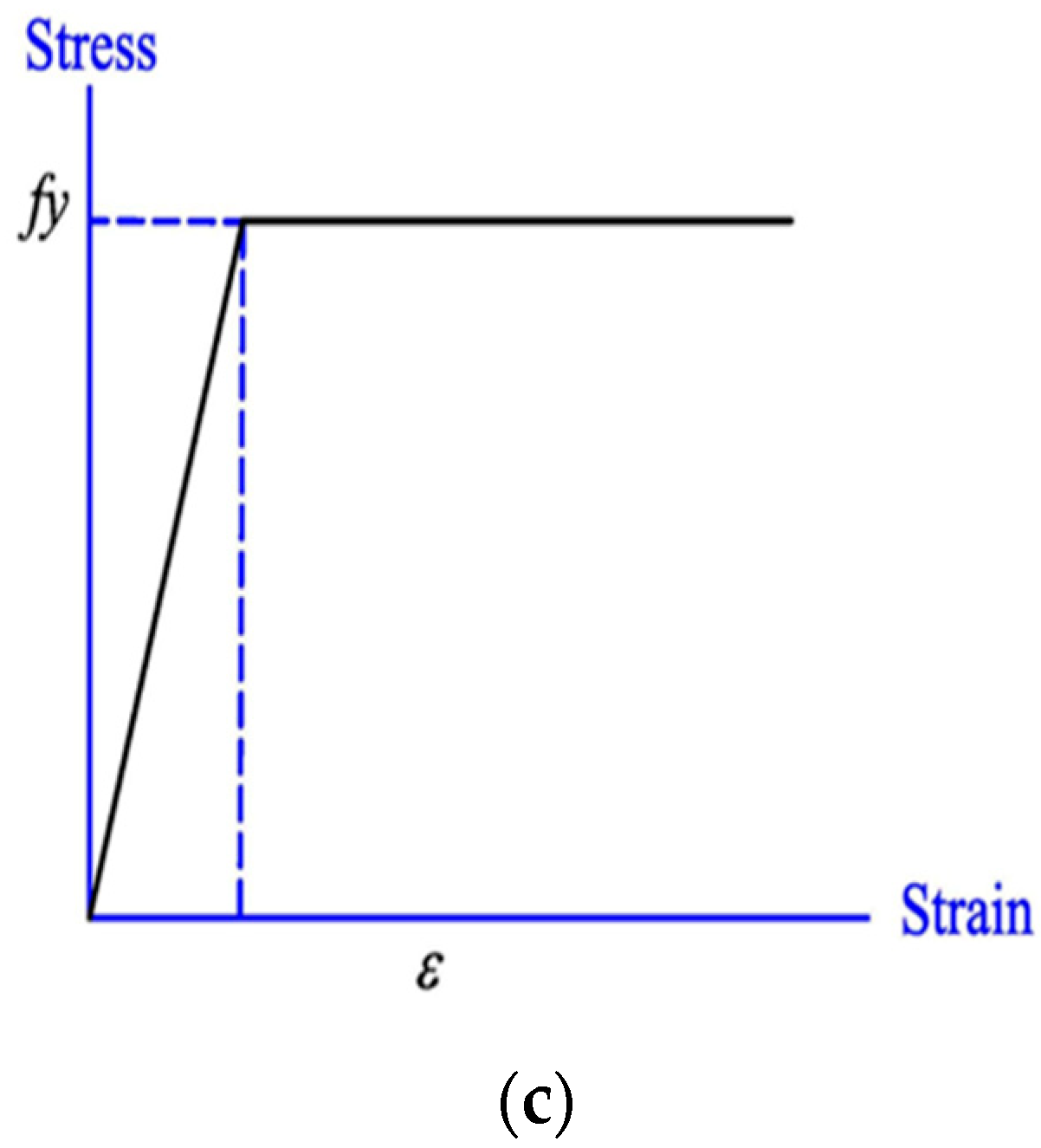
3.2. Constitutive Material Stress—Strain Curve
3.2.1. Concrete
3.2.2. Steel
4. Result Discussion
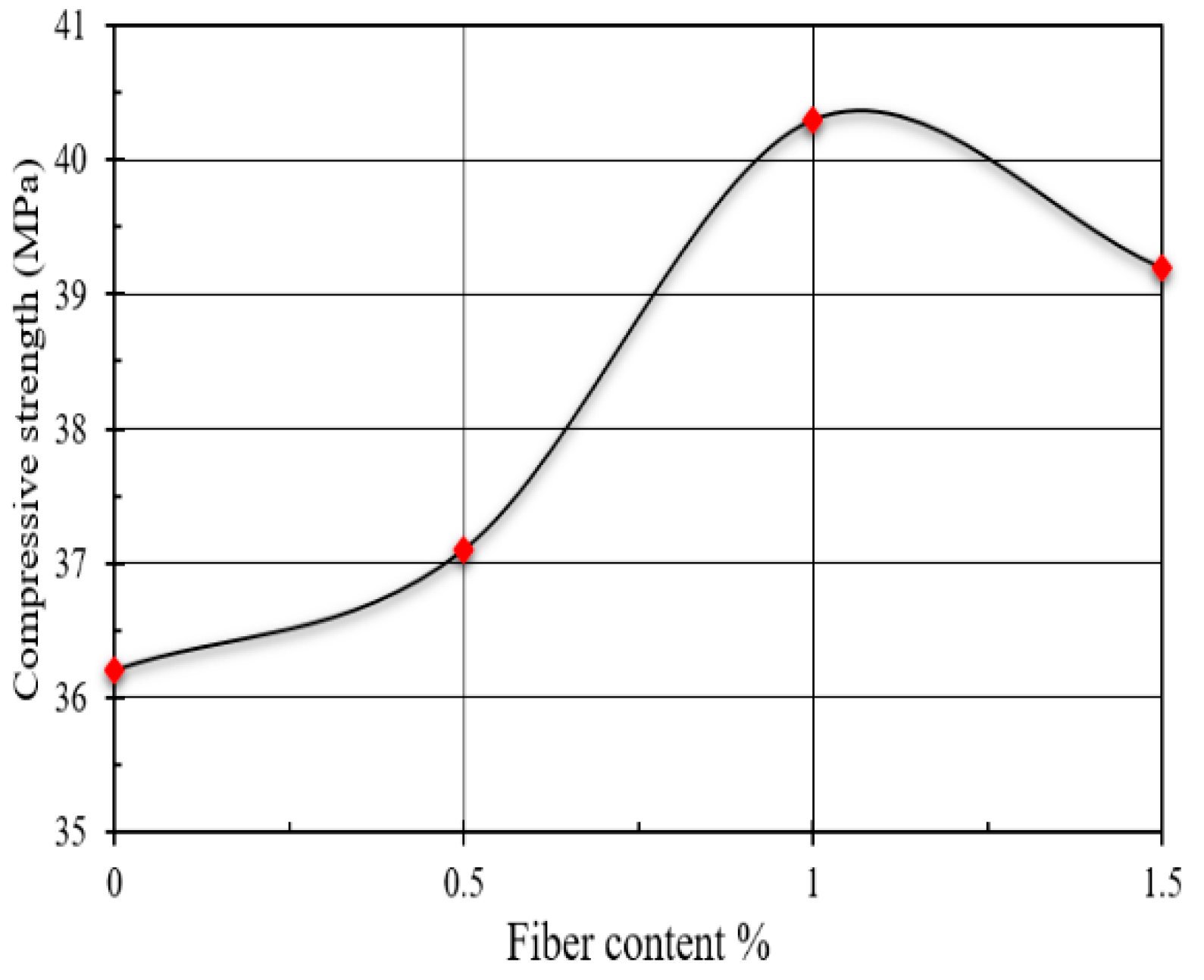
4.1. Concrete Specifications
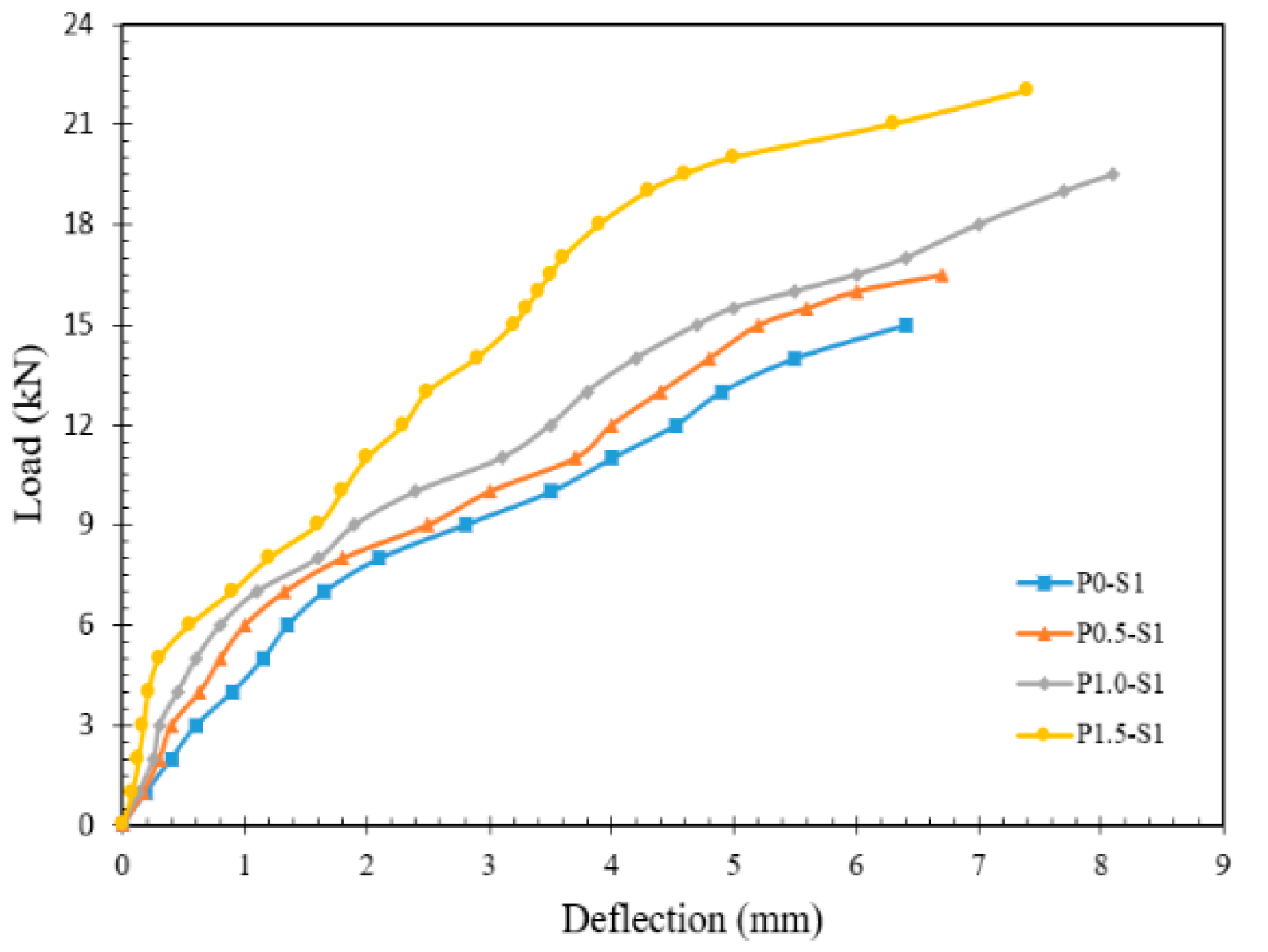
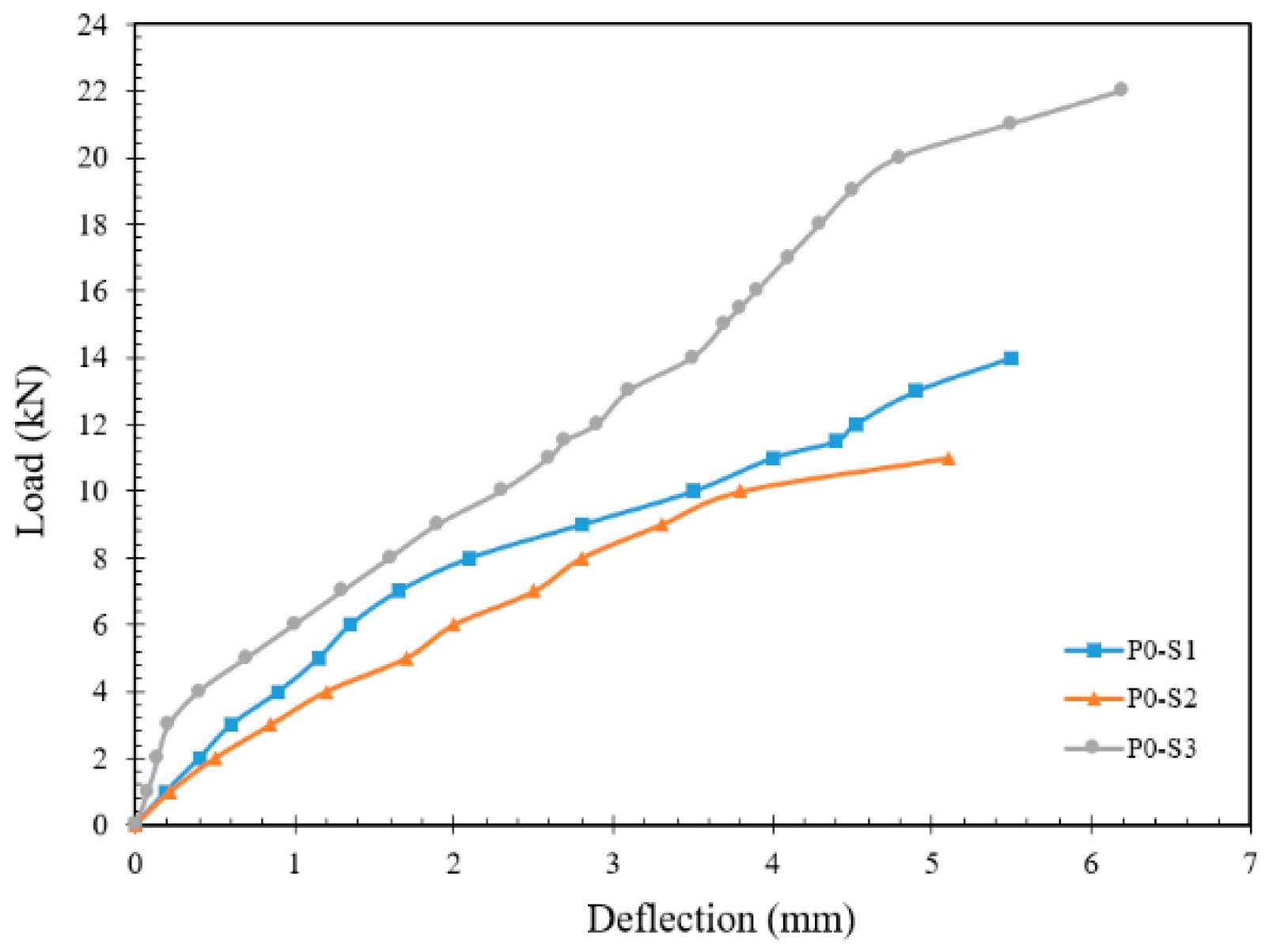
4.2. Load–Deflection Curves
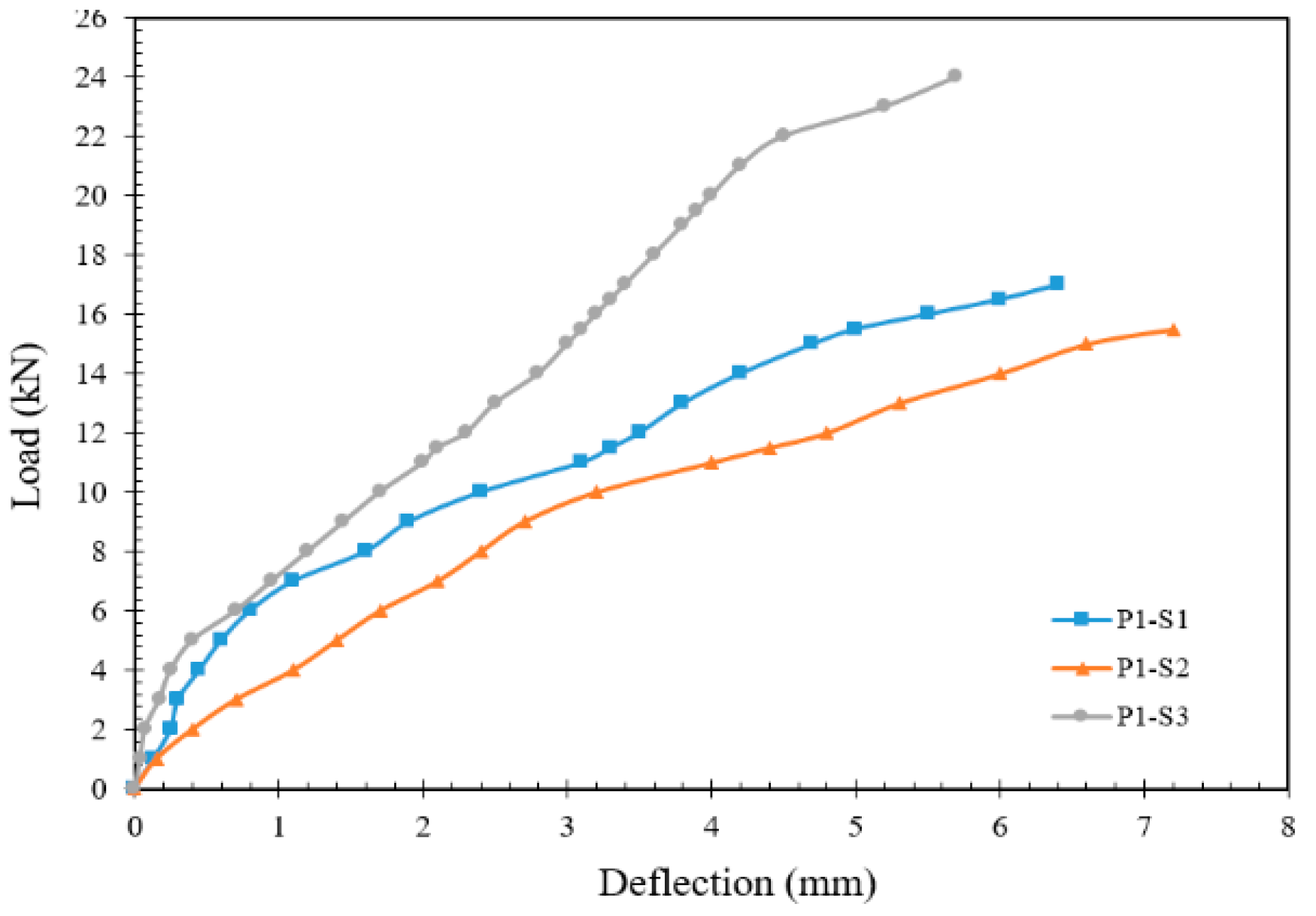
4.2.1. Experimental Tested Slabs
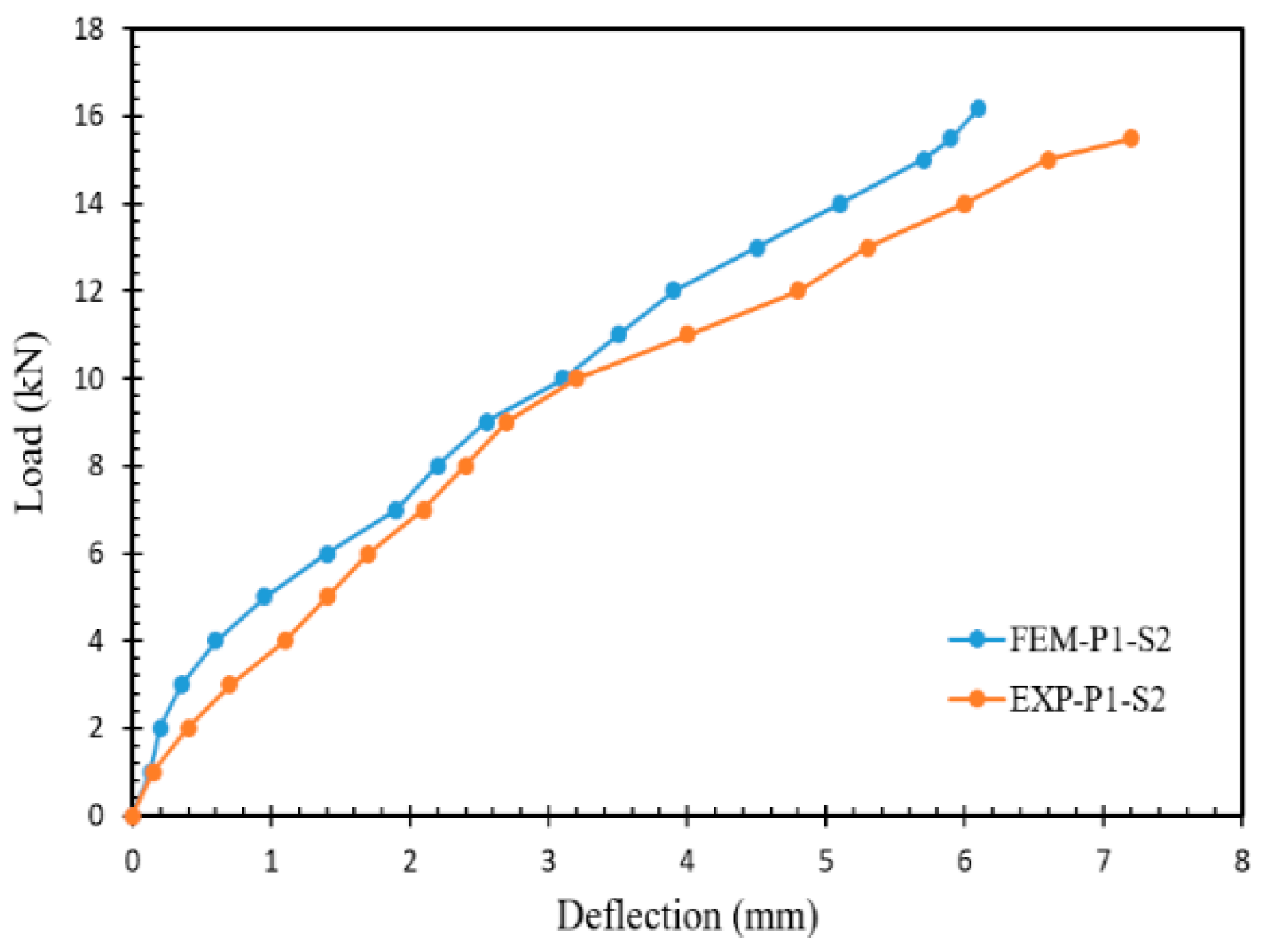
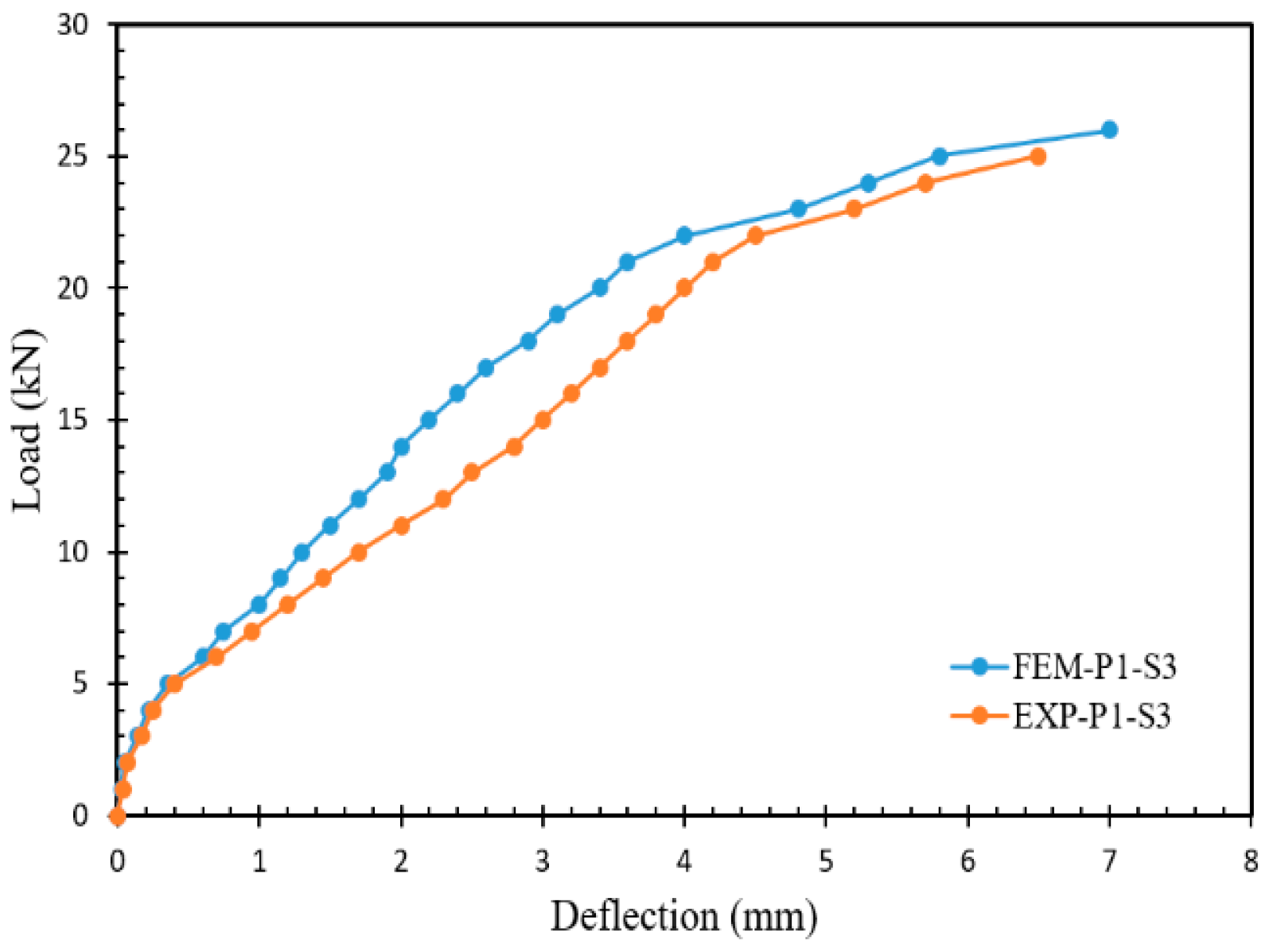
4.2.2. Comparison with the Numerical Outcomes
5. Conclusions
- The presence of polyolefin fiber improved the strength behavior of the slab. As the polyolefin fiber content increased, the observed deflection values decreased. For example, at a load of 12 kN, the deflection values varied from 4.52 mm to 4 mm, 3.5 mm, and 2.3 mm, when fiber content changed from zero to 1.5%;
- Deflection values increased for specimens with a hole in the slab set 2, as compared with slab sets 1 and 3;
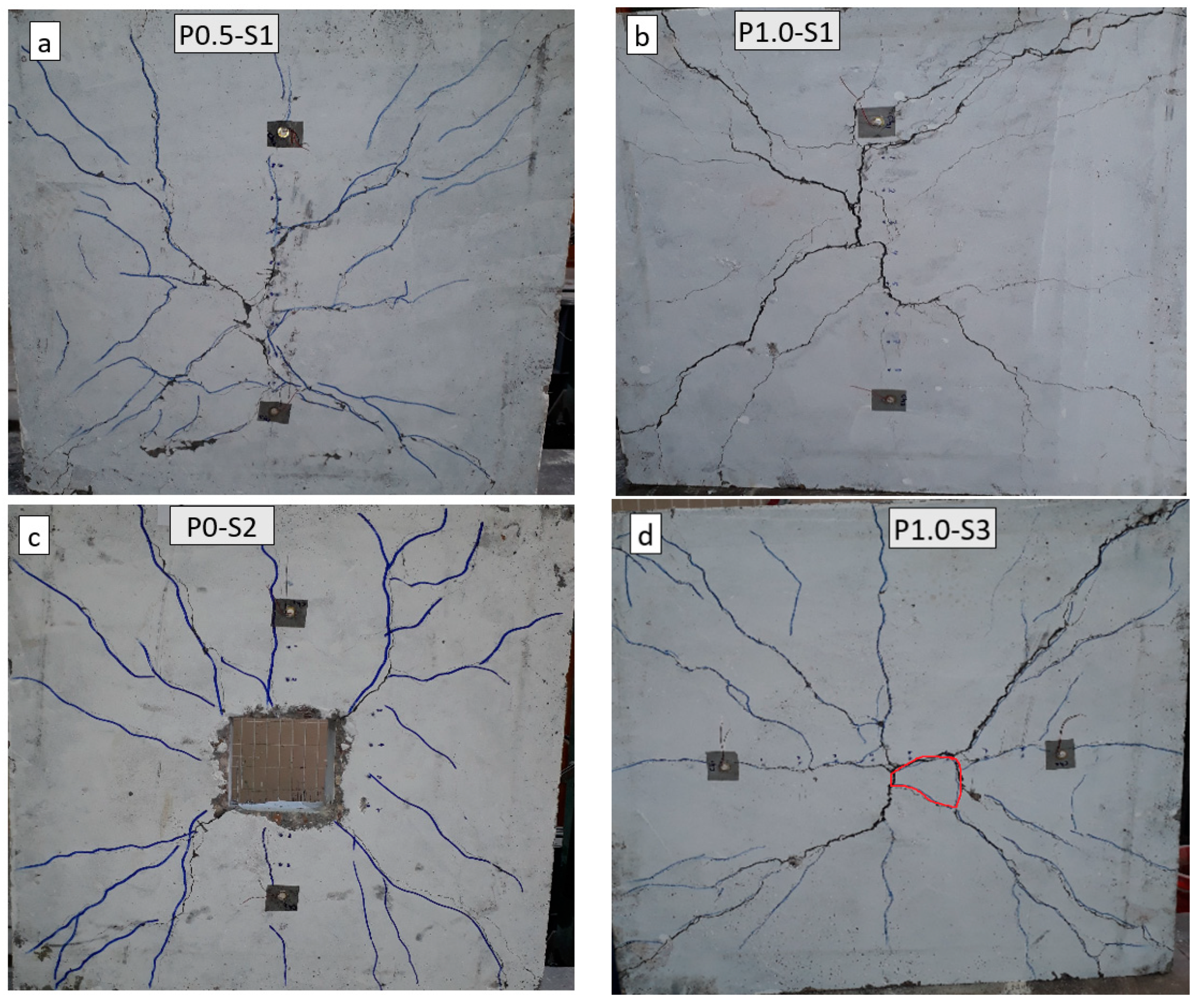
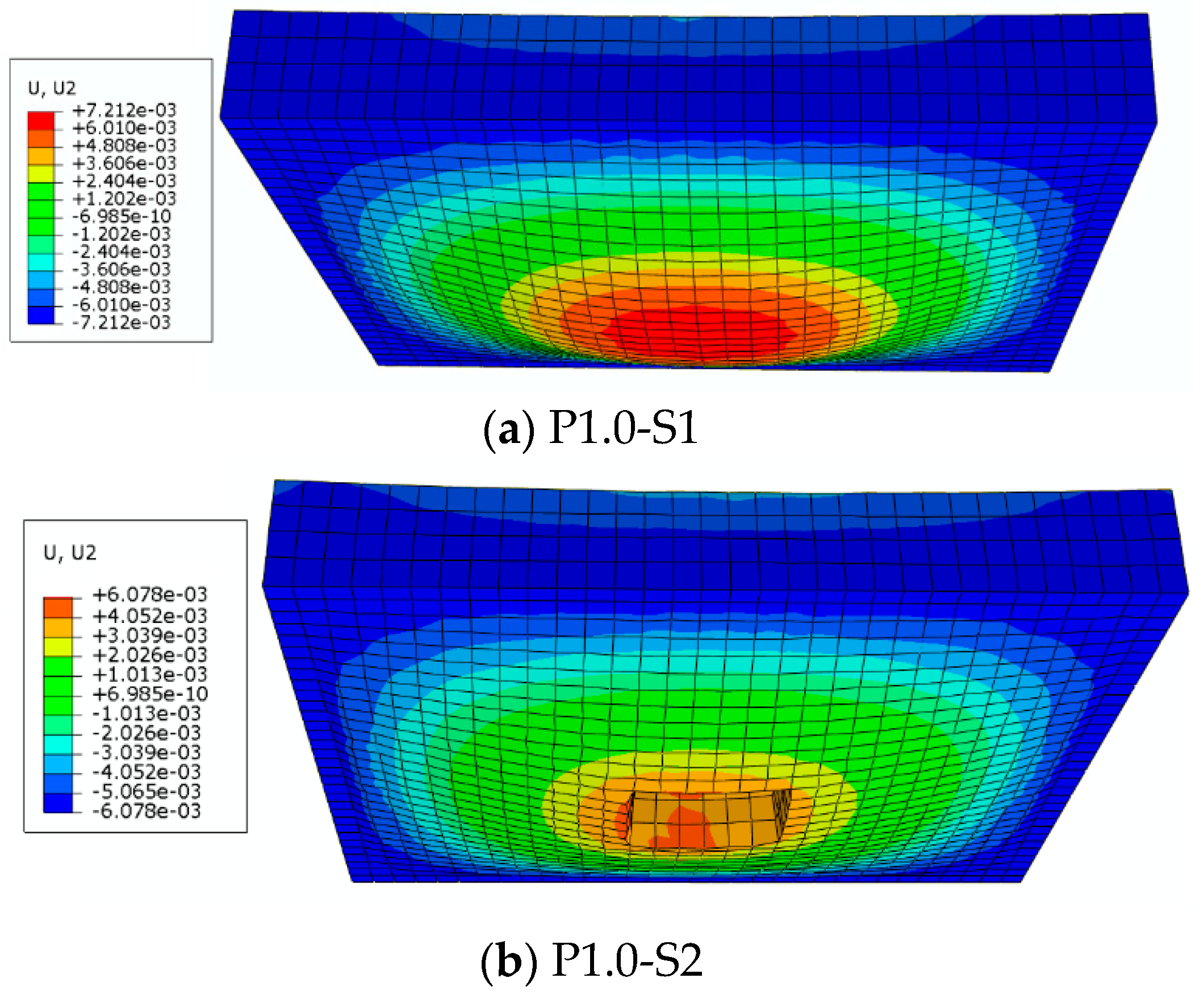
- Two types of failure were observed, flexural for samples (P0-S1 to P1.0-S2) and shear failure for specimens (P0-S3 and P1.0-S3). In the meantime, punching occurred for all slab sets;
- The average deflection value for slab set 1 was 3.58 mm, which was close to the deflection values for 1% polyolefin fiber with an error of 2.29%;
- The computed maximum load and deflection ratios between the experimental and numerical values varied from 0.91 to 0.98 and 1.01 to 1.28, respectively. Excellent consent was found for maximum load, especially in specimens P0-S3 (0.98) and P1.0-S3 (0.97). The same was true for maximum deflection with samples P0-S1 (1.01) and P1.5-S1 (1.06).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alberti, M.; Enfedaque, A.; Gálvez, J.; Agrawal, V. Reliability of polyolefin fibre reinforced concrete beyond laboratory sizes and construction procedures. Compos. Struct. 2016, 140, 506–524. [Google Scholar] [CrossRef]
- Al-Rousan, R.Z. Failure Analysis of Polypropylene Fiber Reinforced Concrete Two-Way Slabs Subjected to Static and Impact Load Induced by Free Falling Mass. Lat. Am. J. Solids Struct. 2018, 15, 05. [Google Scholar] [CrossRef] [Green Version]
- Ramadevi, K.; Babu, D.L.V. Behaviour of hybrid fiber reinforced concrete slabs in frames under static loading. Ecol. Environ. Conserv. 2012, 18, 975–979. [Google Scholar]
- Alberti, M.G.; Enfedaque, A.; Galvez, J. Improving the Reinforcement of Polyolefin Fiber Reinforced Concrete for Infrastructure Applications. Fibers 2015, 3, 504–522. [Google Scholar] [CrossRef] [Green Version]
- Bompa, D.V.; Oneţ, T. Punching shear strength of RC flat slabs at interior connections to columns. Mag. Concr. Res. 2016, 68, 24–42. [Google Scholar] [CrossRef] [Green Version]
- Bartolac, M.; Damjanović, D.; Duvnjak, I. Punching strength of flat slabs with and without shear rein-forcement. Građevinar 2015, 67, 771–786. [Google Scholar]
- Brunesi, E.; Nascimbene, R. Numerical web-shear strength assessment of precast prestressed hollow core slab units. Eng. Struct. 2015, 102, 13–30. [Google Scholar] [CrossRef]
- Sadowska-Buraczewska, B.; Szafraniec, M.; Barnat-Hunek, D.; Łagód, G. Flexural Behavior of Composite Concrete Slabs Made with Steel and Polypropylene Fibers Reinforced Concrete in the Compression Zone. Materials 2020, 13, 3616. [Google Scholar] [CrossRef]
- Marcalikova, Z.; Bilek, V.; Sucharda, O.; Cajka, R. Analysis of Fiber-Reinforced Concrete Slabs under Centric and Eccentric Load. Materials 2021, 14, 7152. [Google Scholar] [CrossRef]
- Helal, R.A.; Al-Baghdadi, H.M.; Al-Salim, N.H.A. Using Mortar Infiltrated Fiber Concrete as Repairing Materials for Flat Slabs. Civ. Eng. J. 2020, 6, 1956–1973. [Google Scholar] [CrossRef]
- Abdulhameed, A.A.; Al-Zuhairi, A.H.; Al Zaidee, S.R.; Hanoon, A.N.; Al Zand, A.W.; Hason, M.M.; Abdulhameed, H.A. The Behavior of Hybrid Fiber-Reinforced Concrete Elements: A New Stress-Strain Model Using an Evolutionary Approach. Appl. Sci. 2022, 12, 2245. [Google Scholar] [CrossRef]
- Kytinou, V.K.; Chalioris, C.E.; Karayannis, C.G. Analysis of Residual Flexural Stiffness of Steel Fiber-Reinforced Concrete Beams with Steel Reinforcement. Materials 2020, 13, 2698. [Google Scholar] [CrossRef] [PubMed]
- Zainal, S.M.I.S.; Hejazi, F.; Aziz, F.N.A.A.; Jaafar, M.S. Constitutive Modeling of New Synthetic Hybrid Fibers Reinforced Concrete from Experimental Testing in Uniaxial Compression and Tension. Crystals 2020, 10, 885. [Google Scholar] [CrossRef]
- ASTM C349; Standard Test Method for Compressive Strength of Hydraulic-Cement Mortars (Using Portions of Priss Broken in Flexure). ASTM International: West Conshohocken, PA, USA, 2018; pp. 1–4. [CrossRef]
- ASTM C204; Standard Test Methods for Fineness of Hydraulic Cement by Air—Permeability. ASTM International: West Conshohocken, PA, USA, 2019; pp. 1–11. [CrossRef]
- ASTM C191; Standard Test Methods for Time of Setting of Hydraulic Cement by Vicat Needle. ASTM International: West Conshohocken, PA, USA, 2021; pp. 1–8. [CrossRef]
- Iraqi Specifications No. (45), 1984 for Aggregates of Natural Resources Used for Concrete and Construction. Available online: http://www.sciepub.com/reference/124724 (accessed on 1 March 2022).
- ASTM C33/86; Standard Specification for Concrete Aggregates. ASTM International: West Conshohocken, PA, USA, 1986.
- ASTM C494; Standard Specification for Chemical Admixtures for Concrete. ASTM International: West Conshohocken, PA, USA, 2019; pp. 1–15. [CrossRef]
- ASTM A615/615M-05a; Standard Specification for Deformed and Plain Carbon Structural Bars for Concrete Reinforcement. Annual Book of ASTM Standards: 2005. ASTM: West Conshohocken, PA, USA, 2005; Volume 01.
- Alshaikh, I.M.; Abu Bakar, B.; Alwesabi, E.A.; Zeyad, A.M.; Magbool, H.M. Finite element analysis and experimental validation of progressive collapse of reinforced rubberized concrete frame. Structures 2021, 33, 2361–2373. [Google Scholar] [CrossRef]
- Agrahari, S.; Ramancharla, P.K. Understanding The Behavior of Flat Slab by Linear and Nonlinear Finite Element Analysis. In Proceedings of the New Technologies for Urban Safety of Mega Cities in Asia, Conference: USMCA17, Sendai, Japan, 26–28 November 2017. [Google Scholar]
- Georgewill, V.A.; Ngekpe, B.E.; Akobo, I.Z.S.; Jaja, G.W.T. Punching Shear Failure of Reinforced Concrete Flat Slab System—A Review. Eur. J. Adv. Eng. Technol. 2019, 6, 10–16. [Google Scholar]
- BS EN 12390-3:2009; Testing Hardened Concrete. Compressive Strength of Test Specimens. British Standards Institution: London, UK, 2009.
- ASTM C496/C496M; Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens. ASTM International: West Conshohocken, PA, USA, 2017; pp. 1–5. [CrossRef]
- ASTM C78/C78M; Standard Test Method for Flexural Strength of Concrete (Using Simple Beam with Third-Point Loading). ASTM International: West Conshohocken, PA, USA, 2018; pp. 1–5. [CrossRef]
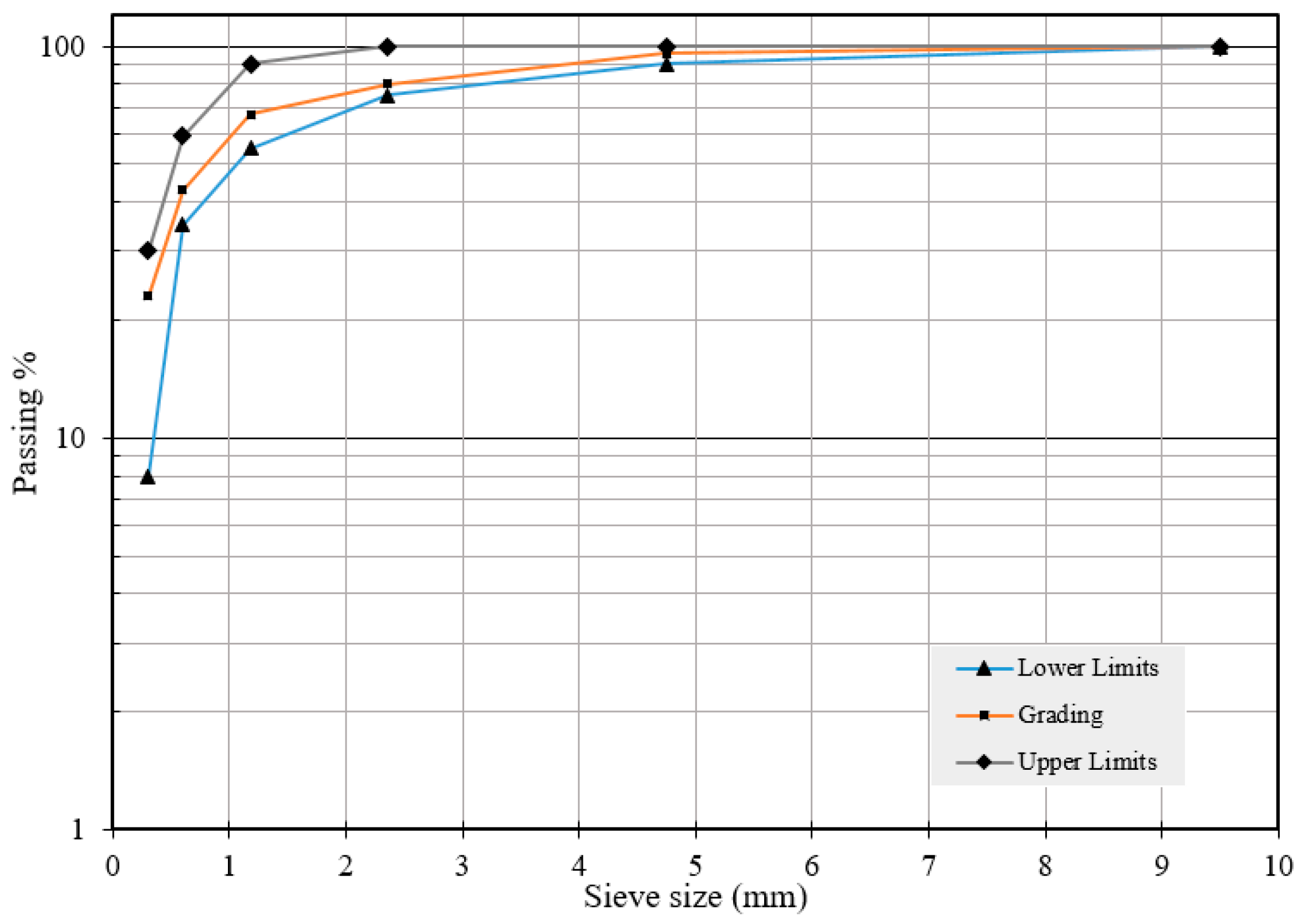
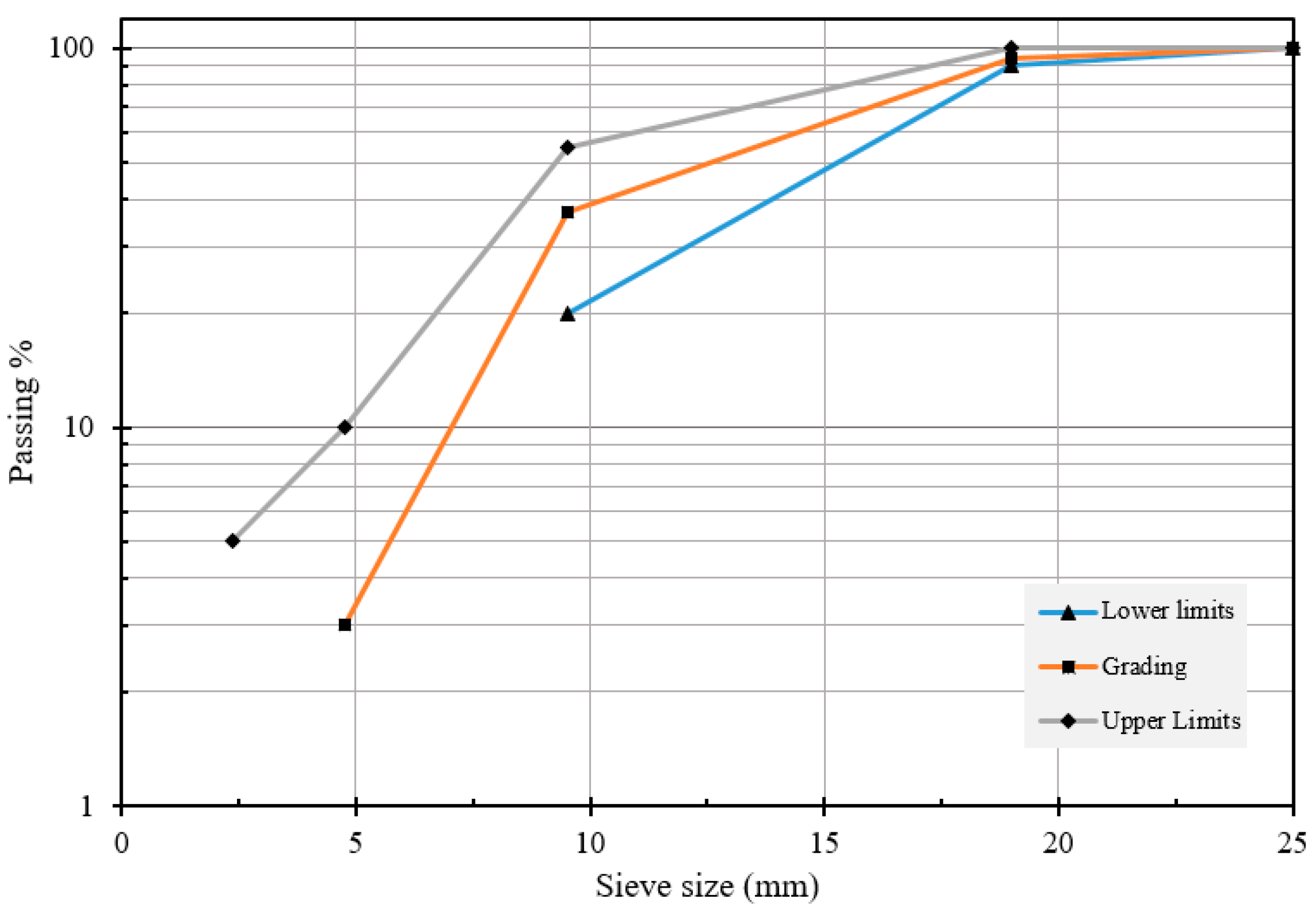

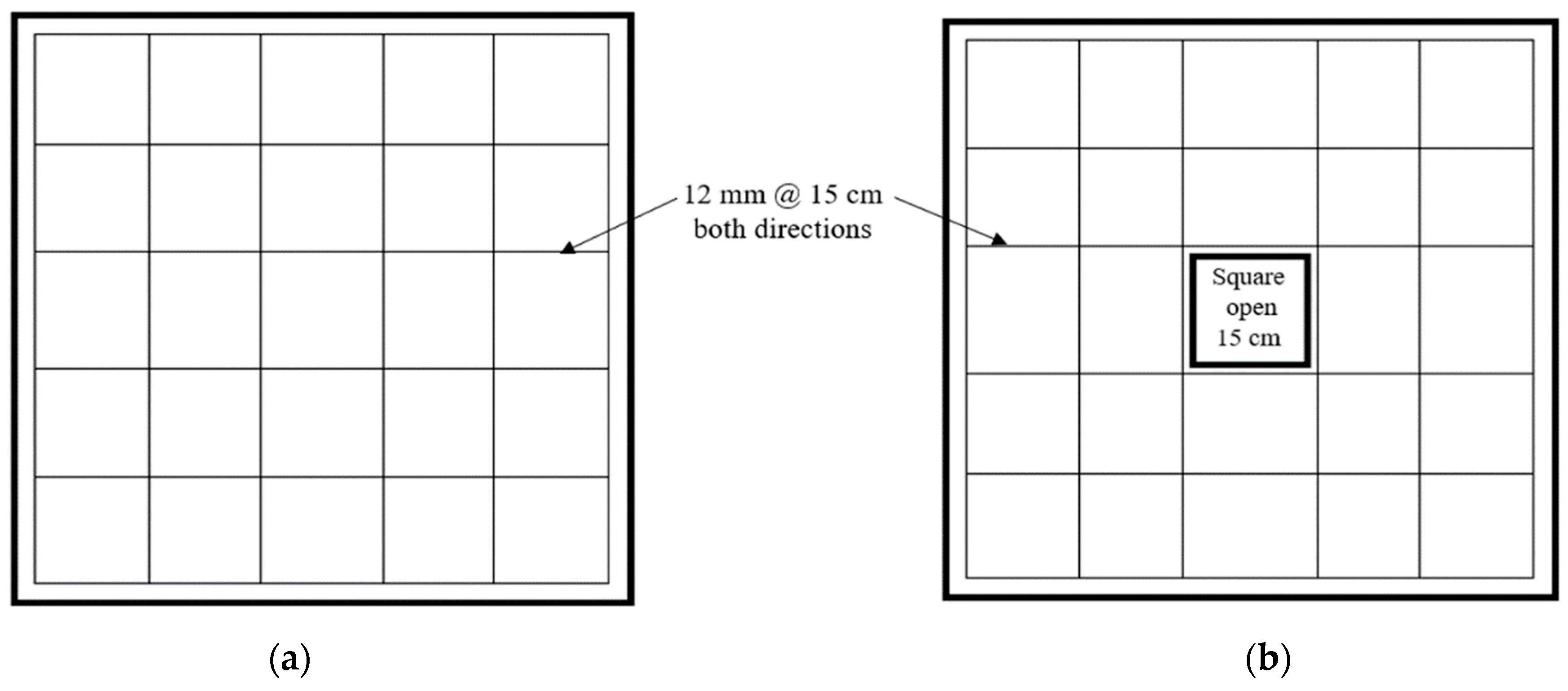
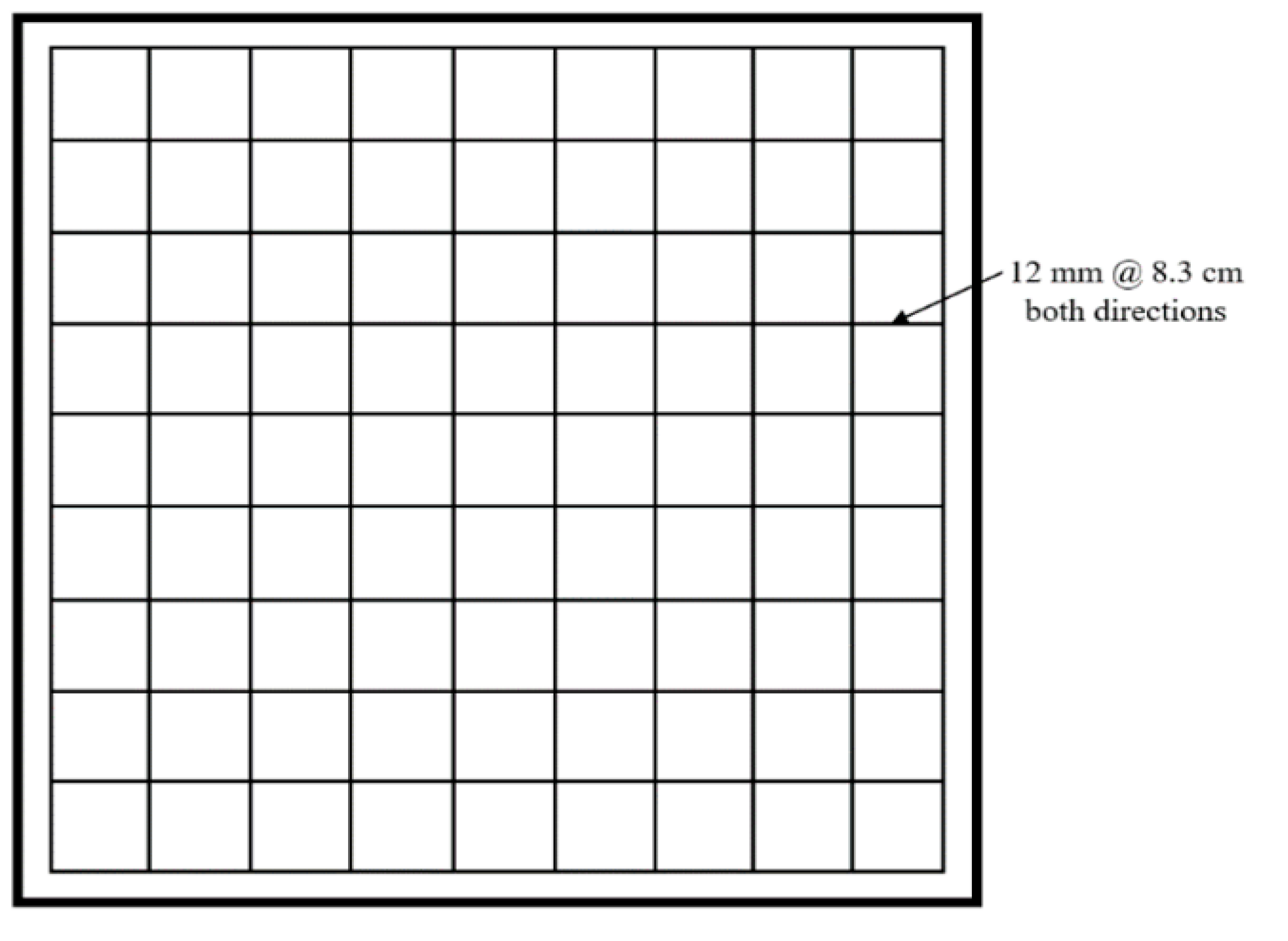






| Characteristics | ASTM Standards | Examination Method | Outcome |
|---|---|---|---|
| Compressive Strength | C349 [14] | After 3 days (MPa) | 18.5 |
| After 7 days (MPa) | 27.1 | ||
| Fineness | C204 [15] | Mesh 170% | 5.8 |
| Permeability of Blain air (m2/kg) | 311 | ||
| Setting Time | C191 [16] | Initial (Min.) | 141 |
| Final (Min.) | 257 |
| Cement Main Structure | Cement Chemical Composition | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C3S | C3A | C2S | C4AF | SiO2 | Fe2O3 | MgO | K2O | Insoluble Residue | Na2O | LOI | CaO | Al2O3 | SO3 |
| 50.1 | 6.31 | 24.1 | 10.2 | 20.4 | 3.4 | 1.45 | 0.56 | 0.52 | 0.33 | 1.2 | 61.9 | 5.1 | 1.88 |
| Nominal Diameter mm | Actual Diameter mm | Yield Stress MPa | Ultimate Stress MPa |
|---|---|---|---|
| 12 | 11.86 | 430 | 465 |
| Length mm | Valent Diameter mm | Density kg/L | Elastic Modulus GPa | Tensile Strength MPa |
|---|---|---|---|---|
| 60 | 0.84 | 0.91 | 7.5 | 465 |
| Material | Poisson’s Ratio | Density kg/m3 | Young Modulus MPa |
|---|---|---|---|
| Concrete | 0.20 | 2400 | 25.789 |
| Steel bar | 0.30 | 7800 | 209 |
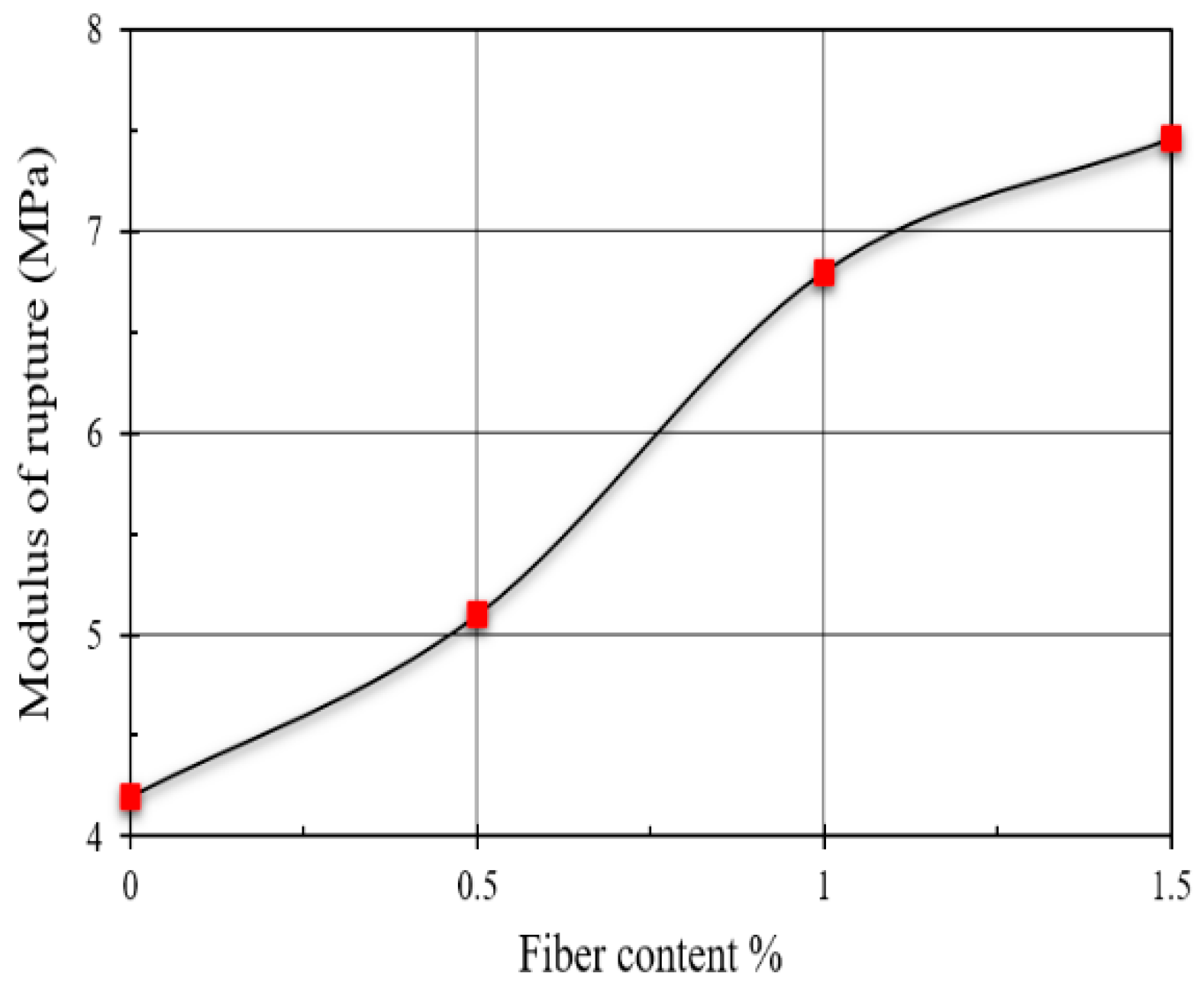
| Symbols | Fiber Content (%) | Compression Cube Test (MPa) | Splitting Tensile Strength (MPa) | Modulus of Rupture (MPa) |
|---|---|---|---|---|
| P0 | 0.0 | 36.2 | 2.32 | 4.20 |
| P0.5 | 0.5 | 37.1 | 2.64 | 5.10 |
| P1.0 | 1.0 | 40.3 | 3.12 | 6.80 |
| P1.5 | 1.5 | 39.2 | 3.61 | 7.46 |
| Slab Item | Maximum Load (kN) | Maximum Deflection (mm) | Failure Mode | ||||
|---|---|---|---|---|---|---|---|
| Experimental | Numerical | Experimental | Numerical | ||||
| P0-S1 | 15.5 | 17.0 | 0.91 | 7.1 | 7 | 1.01 | Flexural |
| P0.5-S1 | 16.5 | 18.0 | 0.92 | 7.7 | 6 | 1.28 | Flexural |
| P1.0-S1 | 19.5 | 21.0 | 0.93 | 8.1 | 7.2 | 1.13 | Flexural |
| P1.5-S1 | 22.0 | 23.2 | 0.95 | 7.4 | 7 | 1.06 | Flexural |
| P0-S2 | 11.5 | 12.0 | 0.96 | 6.3 | 5.4 | 1.17 | Flexural |
| P1.0-S2 | 15.5 | 16.1 | 0.96 | 6.8 | 6.1 | 1.11 | Flexural |
| P0-S3 | 23.0 | 23.5 | 0.98 | 6.1 | 5.4 | 1.13 | Shear |
| P1.0-S3 | 26.0 | 26.7 | 0.97 | 8.7 | 7 | 1.24 | Shear |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.M.; Hussain, H.K.; Ojaimi, M.F. Shear and Flexural Behavior of Flat Slabs Casted with Polyolefin Fiber-Reinforced Concrete. Fibers 2022, 10, 34. https://doi.org/10.3390/fib10040034
Abbas AM, Hussain HK, Ojaimi MF. Shear and Flexural Behavior of Flat Slabs Casted with Polyolefin Fiber-Reinforced Concrete. Fibers. 2022; 10(4):34. https://doi.org/10.3390/fib10040034
Chicago/Turabian StyleAbbas, Abdulnasser M., Haleem K. Hussain, and Mohammed Farhan Ojaimi. 2022. "Shear and Flexural Behavior of Flat Slabs Casted with Polyolefin Fiber-Reinforced Concrete" Fibers 10, no. 4: 34. https://doi.org/10.3390/fib10040034
APA StyleAbbas, A. M., Hussain, H. K., & Ojaimi, M. F. (2022). Shear and Flexural Behavior of Flat Slabs Casted with Polyolefin Fiber-Reinforced Concrete. Fibers, 10(4), 34. https://doi.org/10.3390/fib10040034






