Influence of MHD on Thermal Behavior of Darcy-Forchheimer Nanofluid Thin Film Flow over a Nonlinear Stretching Disc
Abstract
1. Introduction
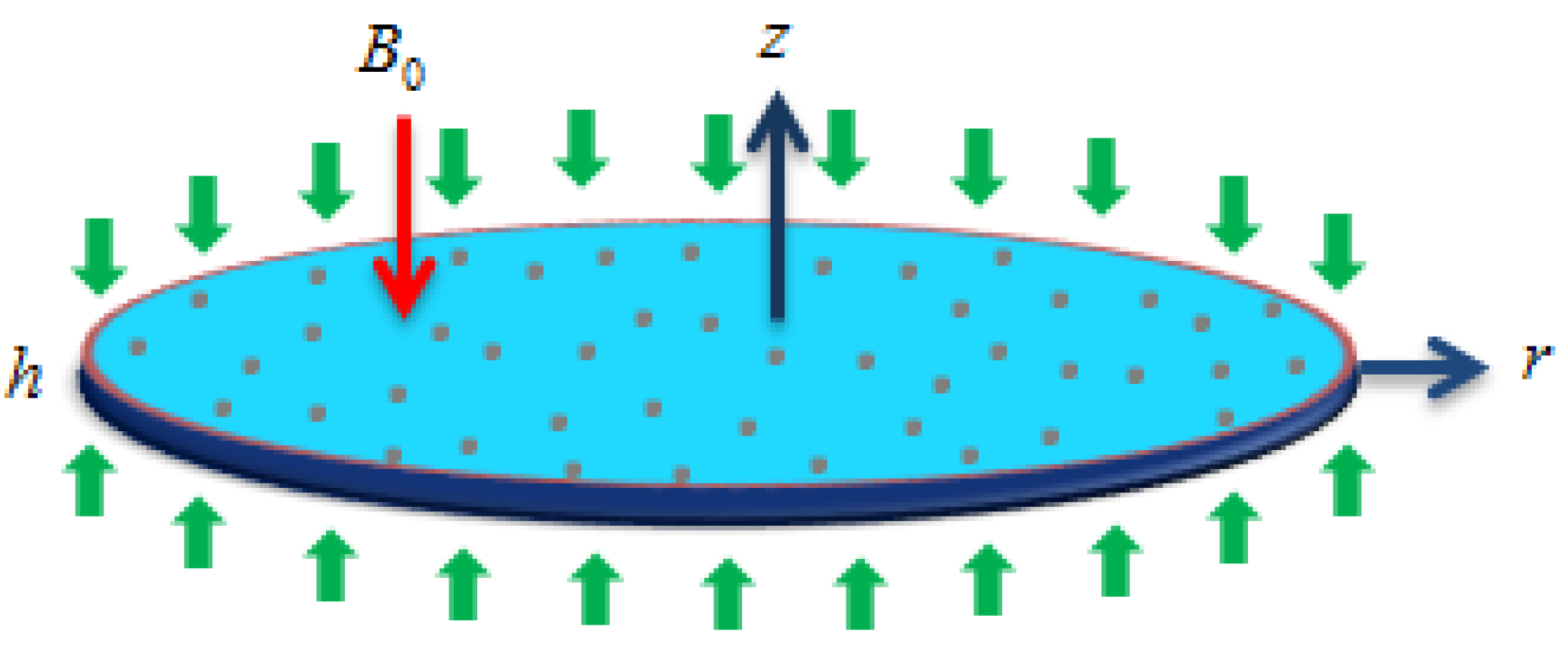
2. Problem Formulation
3. HAM Solution
4. Results and Discussion
5. Conclusions
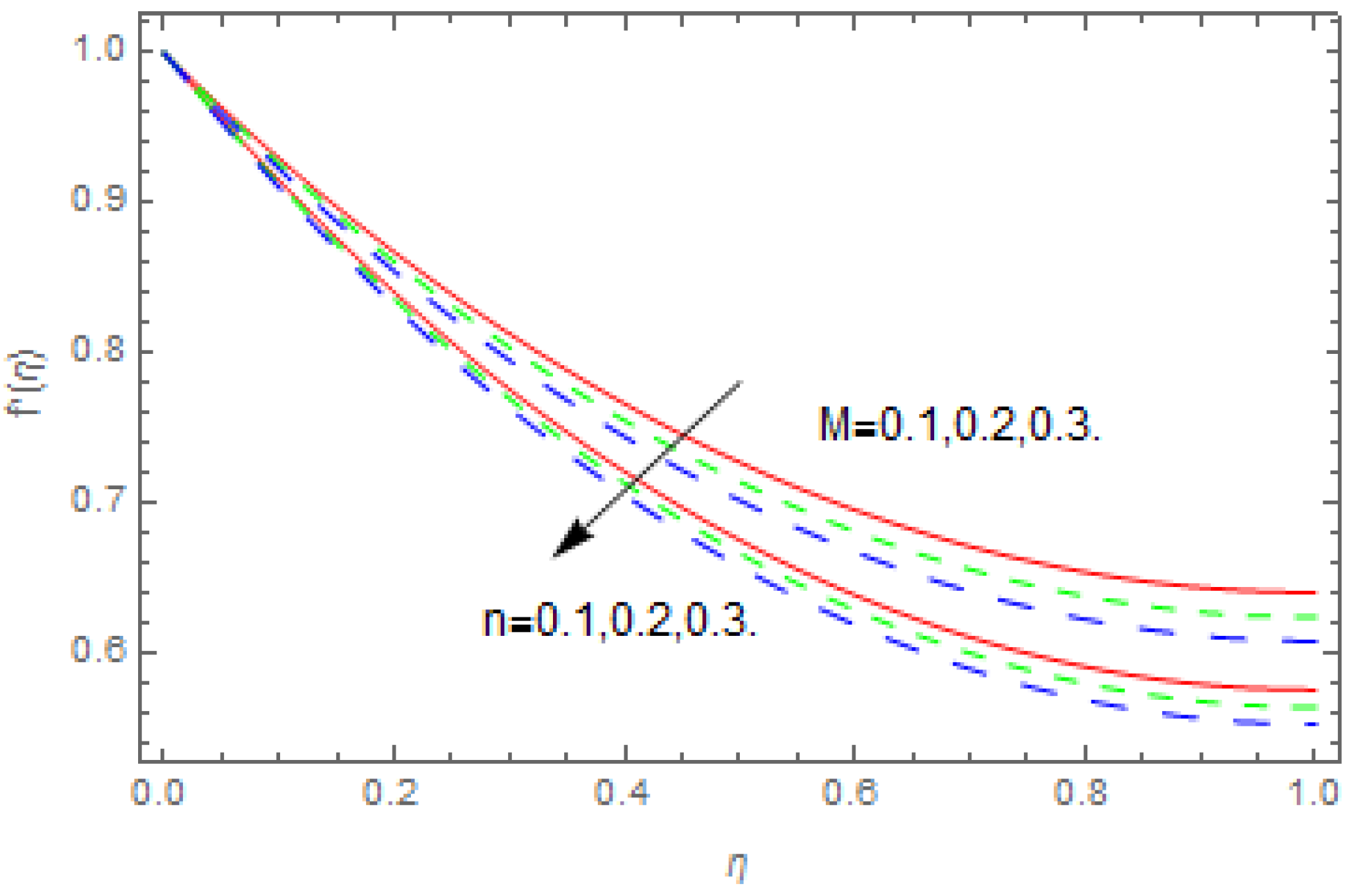
- Increasing the magnetic field parameter, positive integer, porosity parameter, coefficient of inertia, and fluid layer thickness reduces the velocity profile.
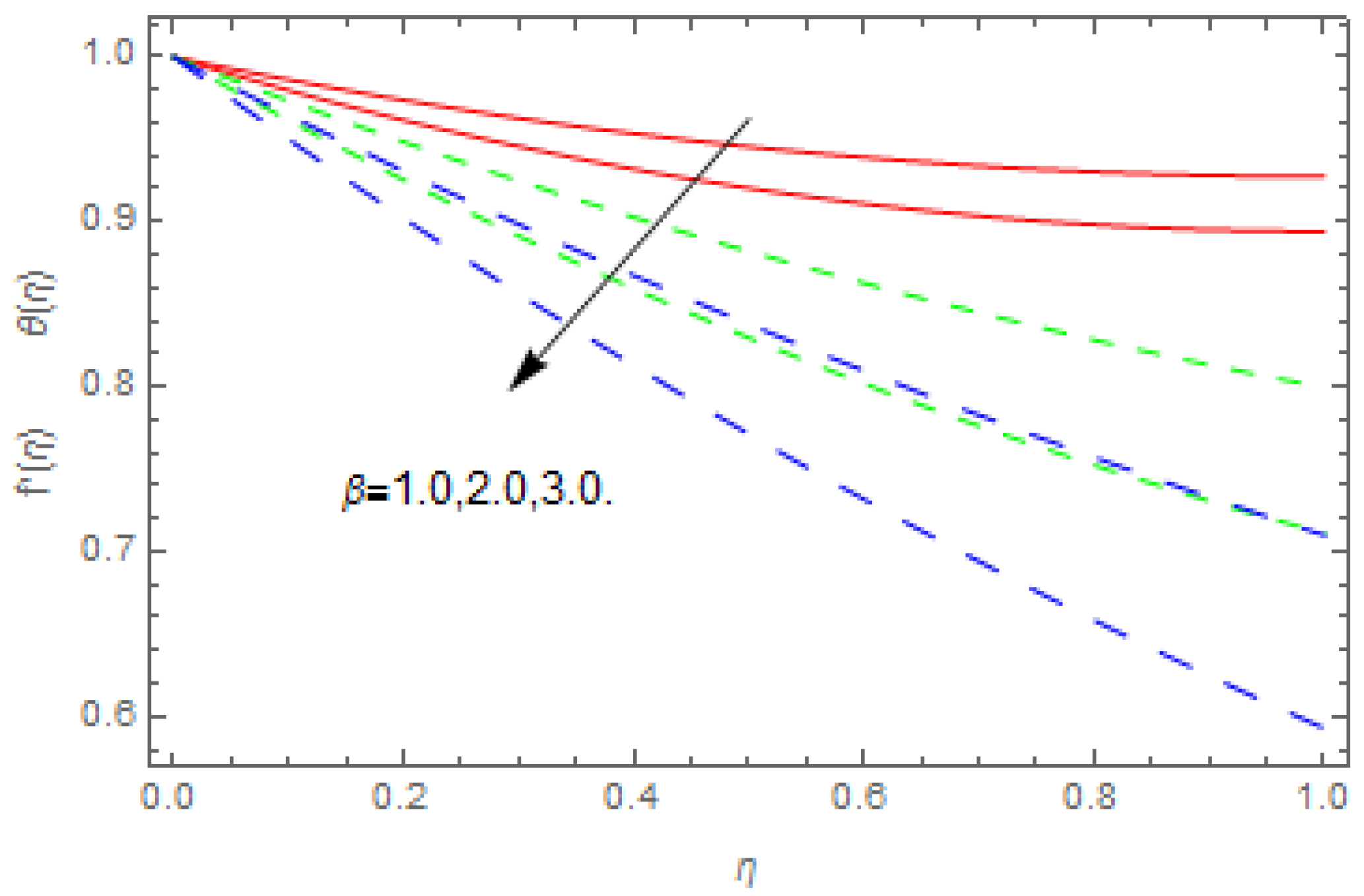
- Increasing the Prandtl number and fluid layer thickness reduces the temperature profile.
- Increasing the heat source/sink, thermal radiation, and Eckert number increases the temperature profile.
- Increasing the fluid layer thickness, magnetic field parameter, porosity parameter, coefficient of inertia, and positive integer increases the skin friction coefficient.
- Increasing the heat source/sink, thermal radiation, Eckert number, and positive integer increases the local Nusselt number.
- Increasing the Eckert number reduces the local Nusselt number.
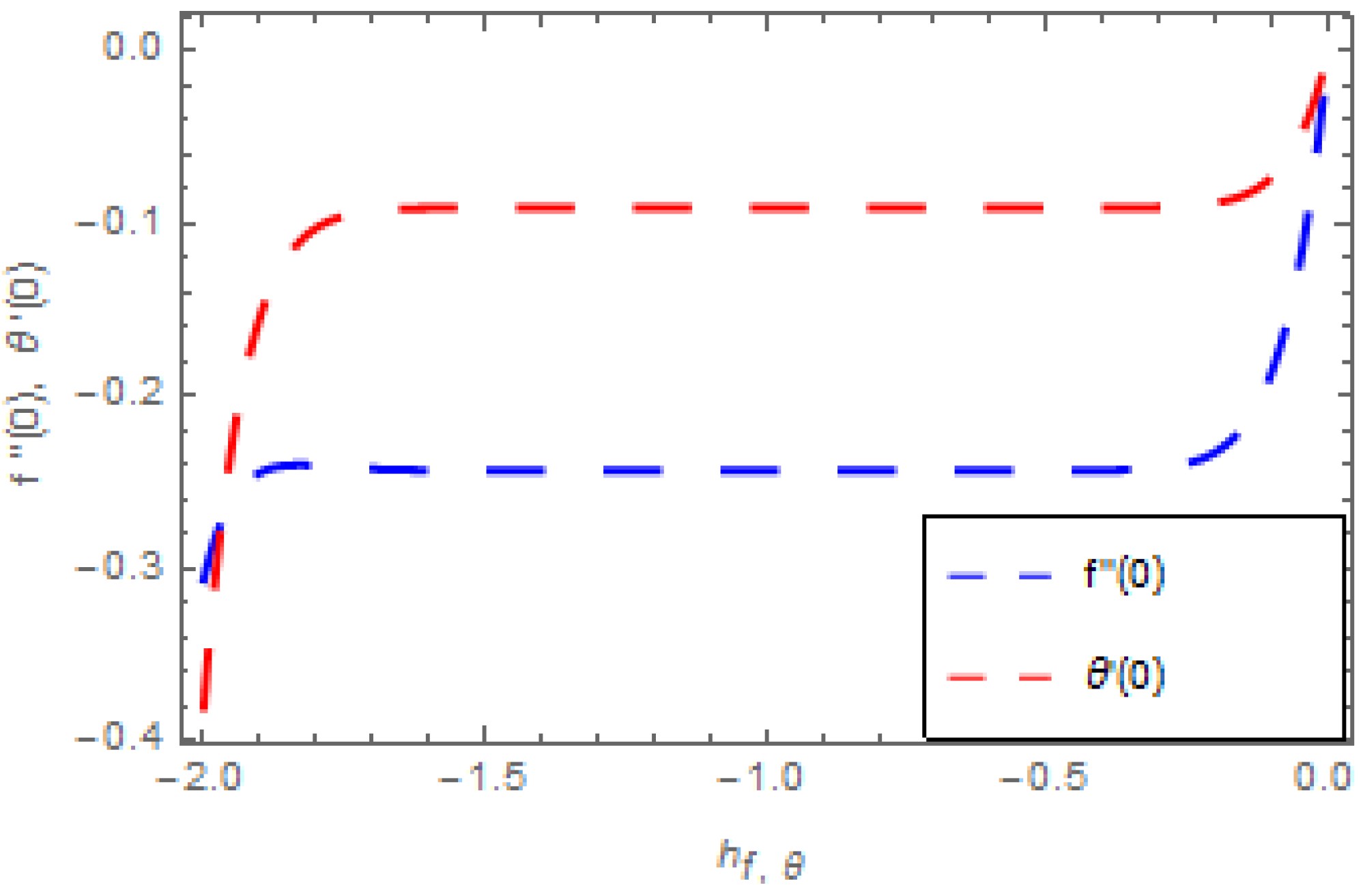
- An agreement between the HAM and numerical techniques is observed here.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a | Stretching parameter |
| B0 | Magnetic field (N m A−1) |
| cP | Specific heat (J kg−1 K−1) |
| k | Thermal conductivity (W m−1 K−1) |
| n | Positive integer |
| Q0 | Heat flux (W m−2) |
| qr | Radioactive heat flux (J) |
| u, v | Velocity components (m s−1) |
| ρ | Dynamic viscosity (MPa) |
| σ | Electrical conductivity (S m−1) |
| Assisting parameter | |
| Cf | Skin friction coefficient |
| Pr | Prandtl number |
| κ | Porosity parameter |
| β | Fluid layer thickness parameter |
| Ec | Eckert number |
| F | Permeability (m2) |
| h | Thin layer thickness |
| k* | Stefan Boltzmann constant |
| T | Fluid temperature (K) |
| Tref | Reference temperature |
| Uw | Stretching velocity (m s−1) |
| η | Similarity variable |
| v | Kinematic viscosity (m2 s−1) |
| σ* | Absorption coefficient |
| M | Magnetic field parameter |
| Nu | Nusselt number |
| R | Thermal Redation parameter |
| Heat source/sink parameter | |
| Fr | Coefficient of inertia parameter |
References
- Choi, S.U.S.; Estman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–106. [Google Scholar]
- Wang, X.Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Eastman, J.A.; Phillpot, S.R.; Choi, S.U.S.; Keblinski, P. Thermal transport in nanofluids. Annu. Rev. Mater. Res. 2004, 34, 219–246. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Murshed, S.M.S.; Leong, K.C.; Yang, C. Enhanced thermal conductivity of TiO2—Water based nanofluids. Int. J. Therm. Sci. 2005, 44, 367–373. [Google Scholar] [CrossRef]
- Maïga, S.E.B.; Nguyen, C.T.; Galanis, N.; Roy, G. Heat transfer behaviours of nanofluids in a uniformly heated tube. Superlattices Microstruct. 2004, 35, 543–557. [Google Scholar]
- Bianco, V.; Chiacchio, F.; Manca, O.; Nardini, S. Numerical investigation of nanofluids forced convection in circular tubes. Appl. Therm. Eng. 2009, 29, 3632–3642. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Kasaeian, A.; Azarian, R.D.; Mahian, O.; Kolsi, O.; Chamkha, A.J.; Wongwises, S.; Pop, I. Nanofluid flow and heat transfer in porous media: A review of the latest developments. Int. J. Heat Mass Transf. 2017, 107, 778–791. [Google Scholar] [CrossRef]
- Ramzan, M.; Chung, J.D.; Ullah, N. Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int. J. Mech. Sci. 2017, 130, 31–40. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S.A. Magnetohydrodynamic nanofluid convective flow in a porous enclosure by means of LBM. Int. J. Heat Mass Transf. 2017, 113, 796–805. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Mixed convection flow of thermally stratified MHD nanofluid over an exponentially stretching surface with viscous dissipation effect. J. Taiwan Inst. Chem. Eng. 2017, 71, 307–314. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Idress, M.; Khan, W.; Islam, S.; Gul, T. Impact of thermal radiation and heat source/sink on Eyring–Powell Fluid Flow over an unsteady oscillatory porous stretching surface. Math. Comput. Appl. 2018, 23, 20. [Google Scholar] [CrossRef]
- Alharbi, S.O.; Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S.; Khan, I. Entropy generation in MHD Eyring–Powell fluid flow over an Unsteady oscillatory porous stretching surface under the impact of thermal radiation and heat source/sink. Appl. Sci. 2018, 8, 2588. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer flow of radiative carbon nanotubes with microstructure and inertial characteristics in the rotating frame. Stud. Therm. Eng. 2018, 12, 823–832. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Dawar, A.; Bonyah, E.; Ullah, H.; Khan, A. Darcy-Forchheimer flow of MHD CNTs nanofluid radiative thermal behaviour and convective non uniform heat source/sink in the rotating frame with microstructure and inertial characteristics. AIP Adv. 2018, 8, 125024. [Google Scholar] [CrossRef]
- Khan, A.S.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-Dimensional nanofluid flow with heat and mass transfer analysis over a linear stretching surface with convective boundary conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S. Unsteady squeezing flow of magnetohydrodynamic carbon nanotube nanofluid in rotating channels with entropy generation and viscous dissipation. Adv. Mech. Eng. 2019, 11, 1–18. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical investigation of nanofluid free convection under the influence of electric field in a porous enclosure. J. Mol. Liq. 2018, 249, 1212–1221. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liq. 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Khan, W.; Islam, S.; Idrees, M. An optimal analysis for Darcy-Forchheimer 3-D Williamson nanofluid flow over a stretching surface with convective conditions. Adv. Mech. Eng. 2019, 11, 1–15. [Google Scholar] [CrossRef]
- Ramzan, M.; Sheikholeslami, M.; Saeed, M.; Chung, J.D. On the convective heat and zero nanoparticle mass flux conditions in the flow of 3D MHD Couple Stress nanofluid over an exponentially stretched surface. Sci. Rep. 2019, 9, 562. [Google Scholar] [CrossRef] [PubMed]
- Sajid, M.; Hayat, T.; Asghar, S. Non-similar solution for the axisymmetric flow of a third-grade fluid over a radially stretching sheet. Acta Mech. 2007, 189, 193–205. [Google Scholar] [CrossRef]
- Attia, H.A.; Ewis, K.M.; Abdeen, M.A.M. Stagnation point flow through a porous medium towards a radially stretching sheet in the presence of uniform suction or injection and heat generation. J. Fluids Eng. 2012, 134, 081202. [Google Scholar] [CrossRef]
- But, A.S.; Ali, A. Effects of Magnetic Field on entropy generation in flow and heat transfer due to a radially stretching surface. Phys. Lett. 2013, 30, 024701. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R. Effect of magnetic dipole on viscous ferro-fluid past a stretching surface with thermal radiation. J. Mol. Liq. 2016, 215, 215–549. [Google Scholar] [CrossRef]
- Ellahi, R.; Mubeshir Bhatti, M.; Khalique, C.M. Three-dimensional flow analysis of Carreau fluid model induced by peristaltic wave in the presence of magnetic field. J. Mol. Liq. 2017, 241, 1059–1068. [Google Scholar] [CrossRef]
- Ellahi, R. Special Issue on recent developments of nanofluids. Appl. Sci. 2018, 8, 192. [Google Scholar] [CrossRef]
- Ellahi, R.; Fetecau, C.; Sheikholeslami, M. Recent advances in the application of differential equations in mechanical engineering problems. Math. Probl. Eng. 2018, 2018, 1584930. [Google Scholar] [CrossRef]
- Abu-Nada, E. Application of nanofluids for heat transfer enhancement of separated flows encountered in a backward facing step. Int. J. Heat Fluid Flow 2008, 29, 242–249. [Google Scholar] [CrossRef]
- Hayat, T.; Sajjad, R.; Muhammad, T.; Alsaedi, A.; Ellahi, R. On MHD nonlinear stretching flow of Powell—Eyring nanomaterial. Results Phys. 2017, 7, 535–543. [Google Scholar] [CrossRef]
- Hsiao, K.-L. Stagnation electrical MHD nanofluid mixed convection with slip boundary on a stretching sheet. Appl. Therm. Eng. 2016, 98, 850–886. [Google Scholar] [CrossRef]
- Abu-Nada, E. The present research investigates second law analysis of laminar flow over a backward facing step (BFS). Entropy generation due to separation, reattachment, recirculation and heat transfer is studied numerically. Entropy 2005, 7, 234–252. [Google Scholar] [CrossRef]
- Hsiao, K.-L. Combined electrical MHD heat transfer thermal extrusion system using Maxwell fluid with radiative and viscous dissipation effects. Appl. Therm. Eng. 2017, 112, 1281–1288. [Google Scholar] [CrossRef]
- Pour, M.; Nassab, S. Numerical investigation of forced laminar convection flow of nanofluids over a backward facing step under bleeding condition. J. Mech. 2012, 28, N7–N12. [Google Scholar] [CrossRef]
- Tian, X.-Y.; Li, B.W.; Hu, Z.-M. Convective stagnation point flow of a MHD non-Newtonian nanofluid towards a stretching plate. Int. J. Heat Mass Transf. 2018, 127, 768–780. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Alzahrani, E.; Kumam, P.; Khan, A.J.; Islam, S. Hall Effect on couple stress 3D nanofluid flow over an exponentially stretched surface with Cattaneo Christov heat flux model. IEEE Access 2019, 7, 64844–64855. [Google Scholar] [CrossRef]
- Ellahi, R.; Alamri, S.Z.; Basit, A.; Majeed, A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J. Taibah Univ. Sci. 2018, 12, 476–482. [Google Scholar] [CrossRef]
- Khan, A.S.; Nie, Y.; Shah, Z. Impact of thermal radiation on magnetohydrodynamic unsteady thin film flow of Sisko fluid over a stretching surface. Processes 2019, 7, 369. [Google Scholar] [CrossRef]
- Ullah, A.; Alzahrani, E.O.; Shah, Z.; Ayaz, M.; Islam, S. Nanofluids thin film flow of Reiner-Philippoff fluid over an unstable stretching surface with brownian motion and thermophoresis effects. Coatings 2019, 9, 21. [Google Scholar] [CrossRef]
- Alsagri, A.S.; Nasir, S.; Gul, T.; Islam, S.; Nisar, K.S.; Shah, Z.; Khan, I. MHD thin film flow and thermal analysis of blood with CNTs nanofluid. Coatings 2019, 9, 175. [Google Scholar] [CrossRef]
- Saeed, A.; Shah, Z.; Islam, S.; Jawad, M.; Ullah, A.; Gul, T.; Kumam, P. Three-dimensional casson nanofluid thin film flow over an inclined rotating disk with the impact of heat generation/consumption and thermal radiation. Coatings 2019, 9, 248. [Google Scholar] [CrossRef]



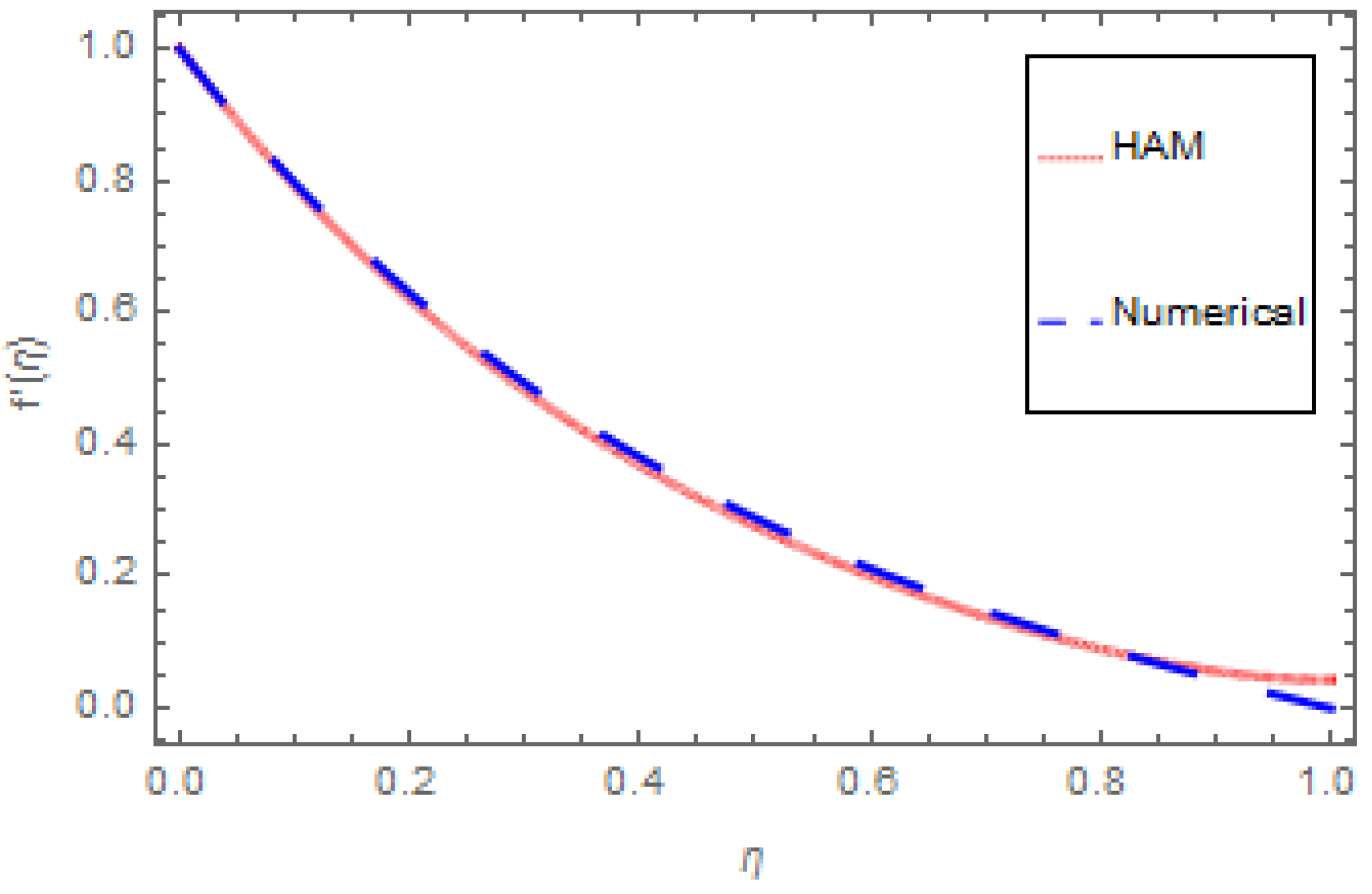
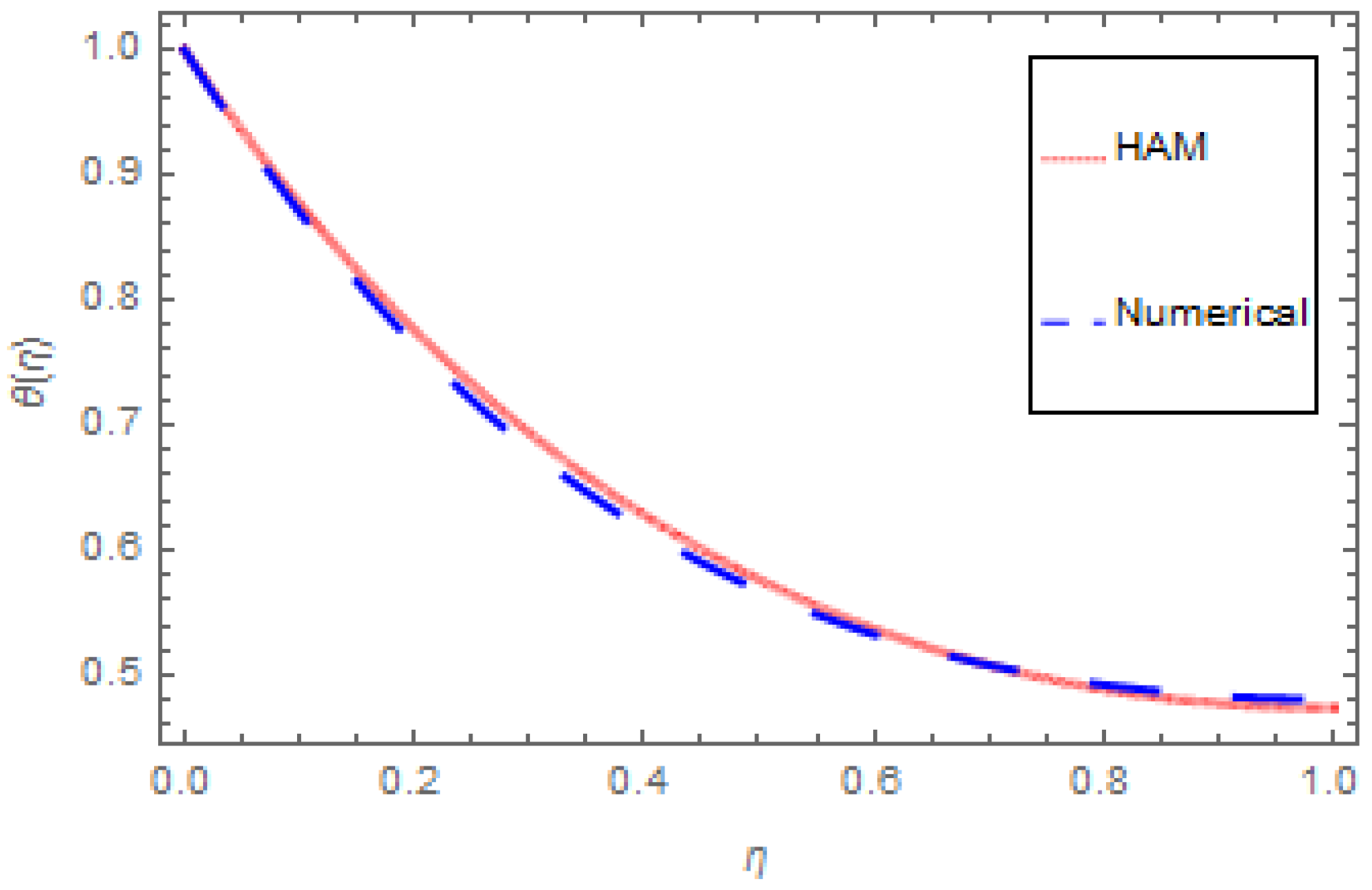
| β | M | κ | Fr | n | Cf |
|---|---|---|---|---|---|
| 0.2 | 0.6 | 0.1 | 0.1 | 2.0 | 0.534624 |
| 0.3 | 0.761014 | ||||
| 0.4 | 0.950758 | ||||
| 0.7 | 0.553042 | ||||
| 0.8 | 0.571415 | ||||
| 0.9 | 0.589744 | ||||
| 0.2 | 0.552042 | ||||
| 0.3 | 0.571415 | ||||
| 0.4 | 0.589744 | ||||
| 0.2 | 0.607370 | ||||
| 0.4 | 0.642203 | ||||
| 0.6 | 0.676780 | ||||
| 3.0 | 0.847565 | ||||
| 4.0 | 1.012080 |
| R | |||||
|---|---|---|---|---|---|
| 0.5 | 1.0 | 0.1 | 0.1 | 2.0 | 2.394070 |
| 0.6 | 2.553680 | ||||
| 0.7 | 2.713280 | ||||
| 1.1 | 2.955850 | ||||
| 1.2 | 3.194332 | ||||
| 1.3 | 3.428861 | ||||
| 0.3 | 2.763659 | ||||
| 0.5 | 2.813816 | ||||
| 0.7 | 2.863768 | ||||
| 0.2 | 2.827741 | ||||
| 0.3 | 2.811727 | ||||
| 0.6 | 2.785875 | ||||
| 3.0 | 4.552986 | ||||
| 4.0 | 6.435682 |
| η | HAM | Numerical |
|---|---|---|
| 0.0 | 1.000000 | 0.000000 |
| 0.1 | 0.961455 | 0.961589 |
| 0.2 | 0.945490 | 0.945568 |
| 0.3 | 0.931736 | 0.931656 |
| 0.4 | 0.920188 | 0.920156 |
| 0.5 | 0. 910827 | 0.910817 |
| 0.6 | 0.903656 | 0.903699 |
| 0.7 | 0.899547 | 0.899635 |
| 0.8 | 0.890117 | 0.890124 |
| 0.8 | 0.889466 | 0.883445 |
| 1.0 | 0.887864 | 0.887895 |
| η | HAM | Numerical |
|---|---|---|
| 0.0 | 1.000000 | 1.000000 |
| 0.1 | 0.993277 | 0.993900 |
| 0.2 | 0.986997 | 0.965800 |
| 0.3 | 0.981248 | 0.988250 |
| 0.4 | 0.976111 | 0.983133 |
| 0.5 | 0.971651 | 0.978612 |
| 0.6 | 0.967931 | 0.974732 |
| 0.7 | 0.964988 | 0.971530 |
| 0.8 | 0.962865 | 0.969025 |
| 0.9 | 0.961583 | 0.967233 |
| 1.0 | 0.961154 | 0.966158 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dawar, A.; Shah, Z.; Kumam, P.; Khan, W.; Islam, S. Influence of MHD on Thermal Behavior of Darcy-Forchheimer Nanofluid Thin Film Flow over a Nonlinear Stretching Disc. Coatings 2019, 9, 446. https://doi.org/10.3390/coatings9070446
Dawar A, Shah Z, Kumam P, Khan W, Islam S. Influence of MHD on Thermal Behavior of Darcy-Forchheimer Nanofluid Thin Film Flow over a Nonlinear Stretching Disc. Coatings. 2019; 9(7):446. https://doi.org/10.3390/coatings9070446
Chicago/Turabian StyleDawar, Abdullah, Zahir Shah, Poom Kumam, Waris Khan, and Saeed Islam. 2019. "Influence of MHD on Thermal Behavior of Darcy-Forchheimer Nanofluid Thin Film Flow over a Nonlinear Stretching Disc" Coatings 9, no. 7: 446. https://doi.org/10.3390/coatings9070446
APA StyleDawar, A., Shah, Z., Kumam, P., Khan, W., & Islam, S. (2019). Influence of MHD on Thermal Behavior of Darcy-Forchheimer Nanofluid Thin Film Flow over a Nonlinear Stretching Disc. Coatings, 9(7), 446. https://doi.org/10.3390/coatings9070446







