Long-Term Hydrolytic Degradation of the Sizing-Rich Composite Interphase
Abstract
:1. Introduction
1.1. Sizing and its Composition
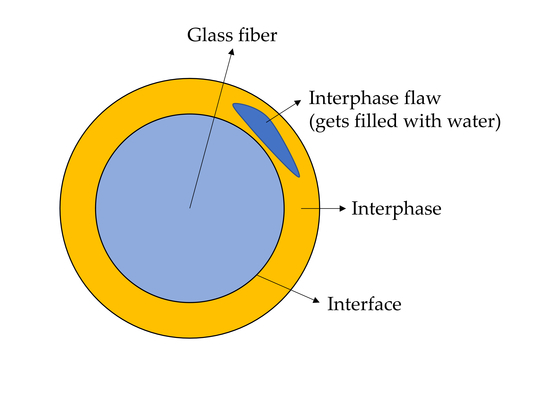
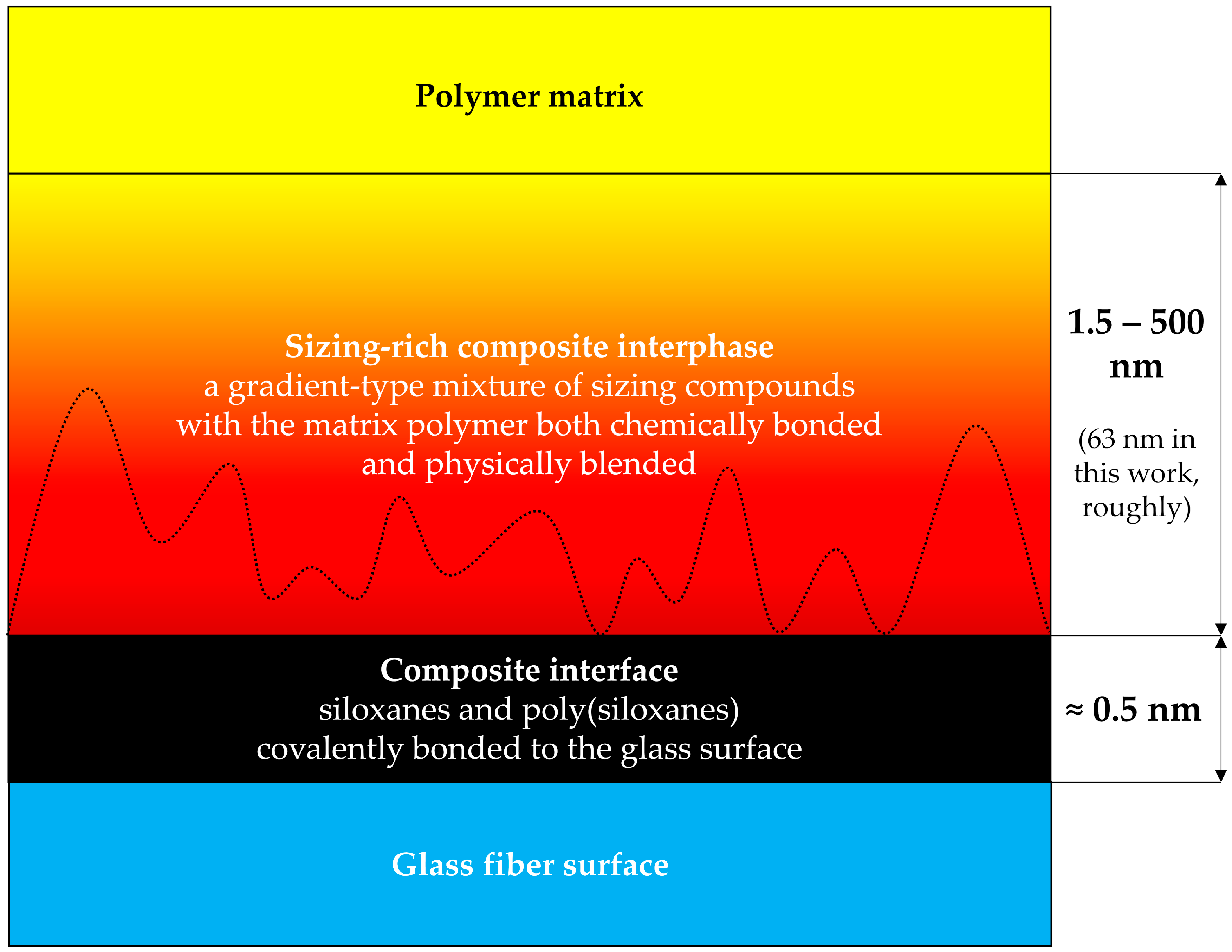
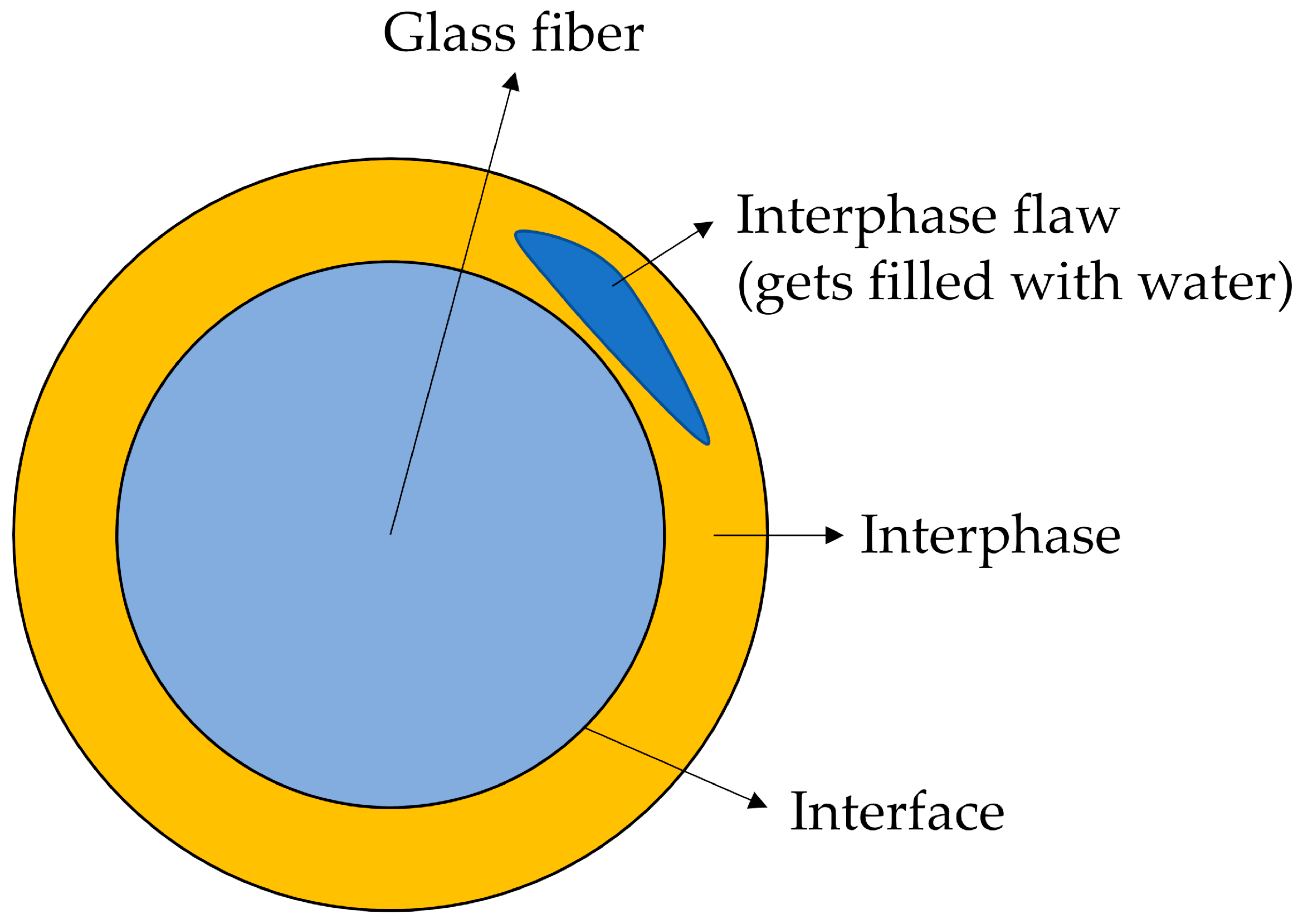
1.2. The Structure of the Sizing-Rich Composite Interphase
1.3. The Aim of This Work
2. Materials and Methods
2.1. Materials
2.2. Experimental Methods
2.2.1. Loss on Ignition
2.2.2. Constituent Volume and Mass Fractions of the Composite
2.2.3. Conditioning of Composite Plates
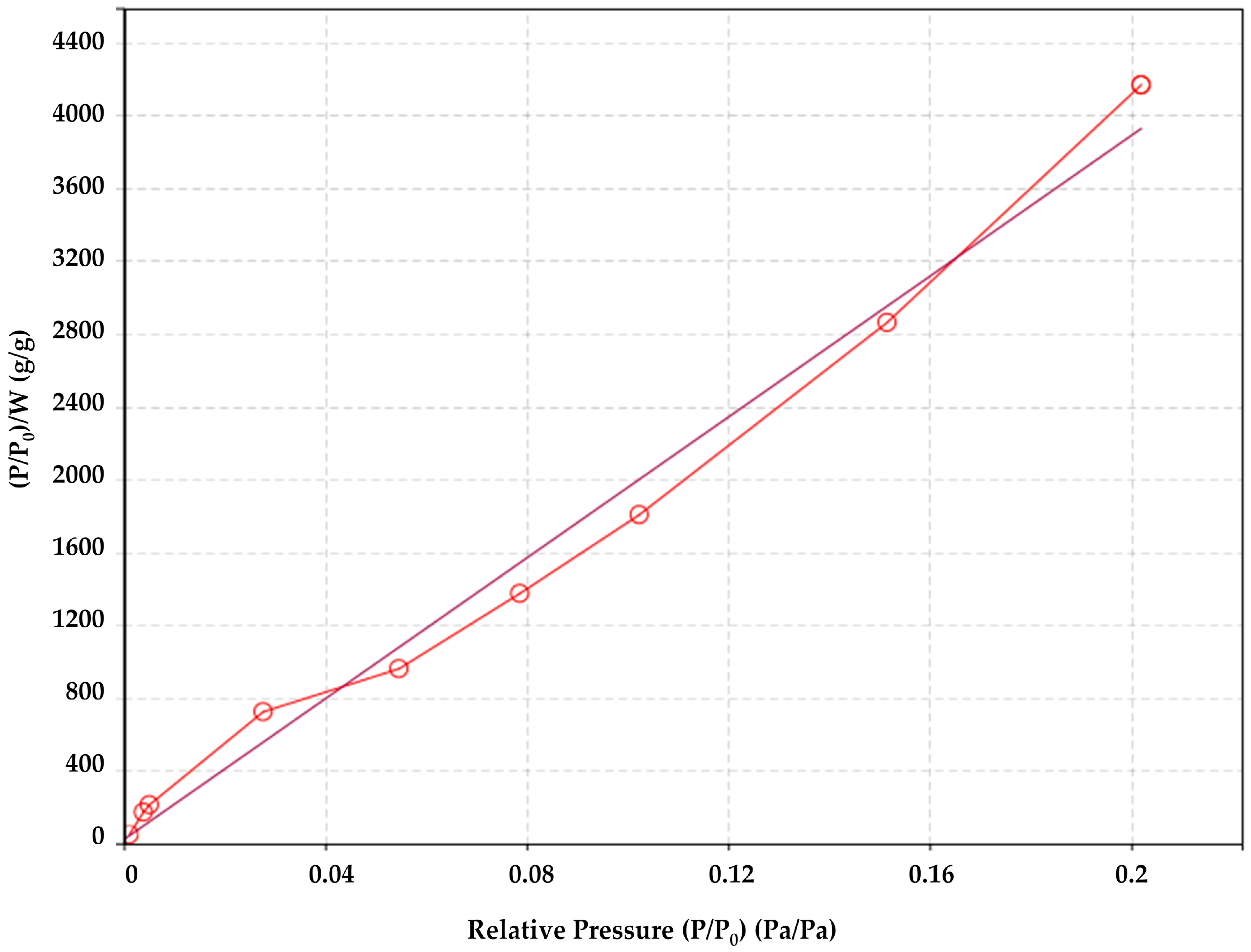
2.2.4. Specific Surface Area of the Fibers Obtained by N2 Sorption/Desorption and Brunauer–Emmett–Teller (BET) Theory
3. Analytical Model
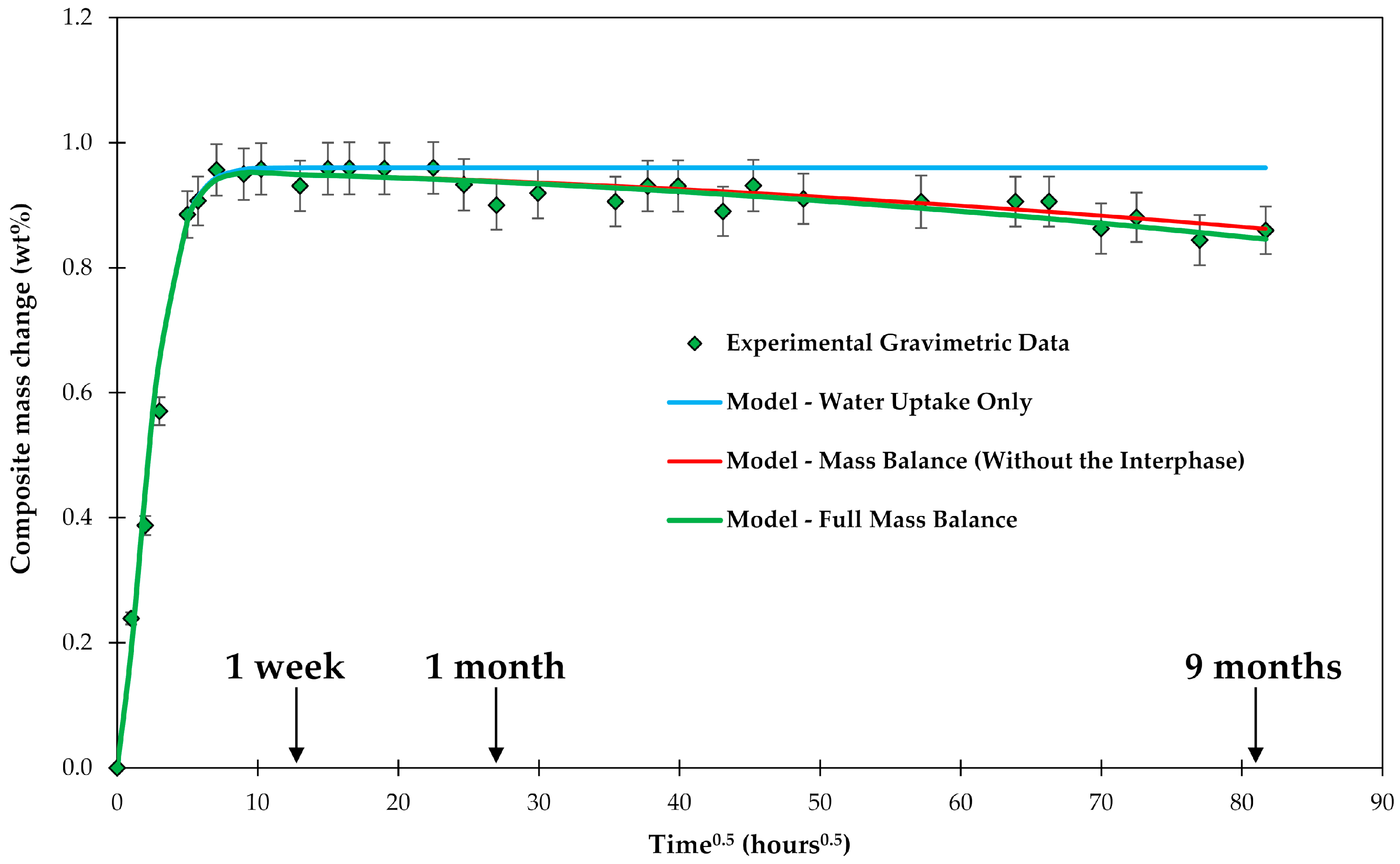
3.1. Mass Balance
3.2. Water Uptake
3.3. Oxidation of the Epoxy Matrix
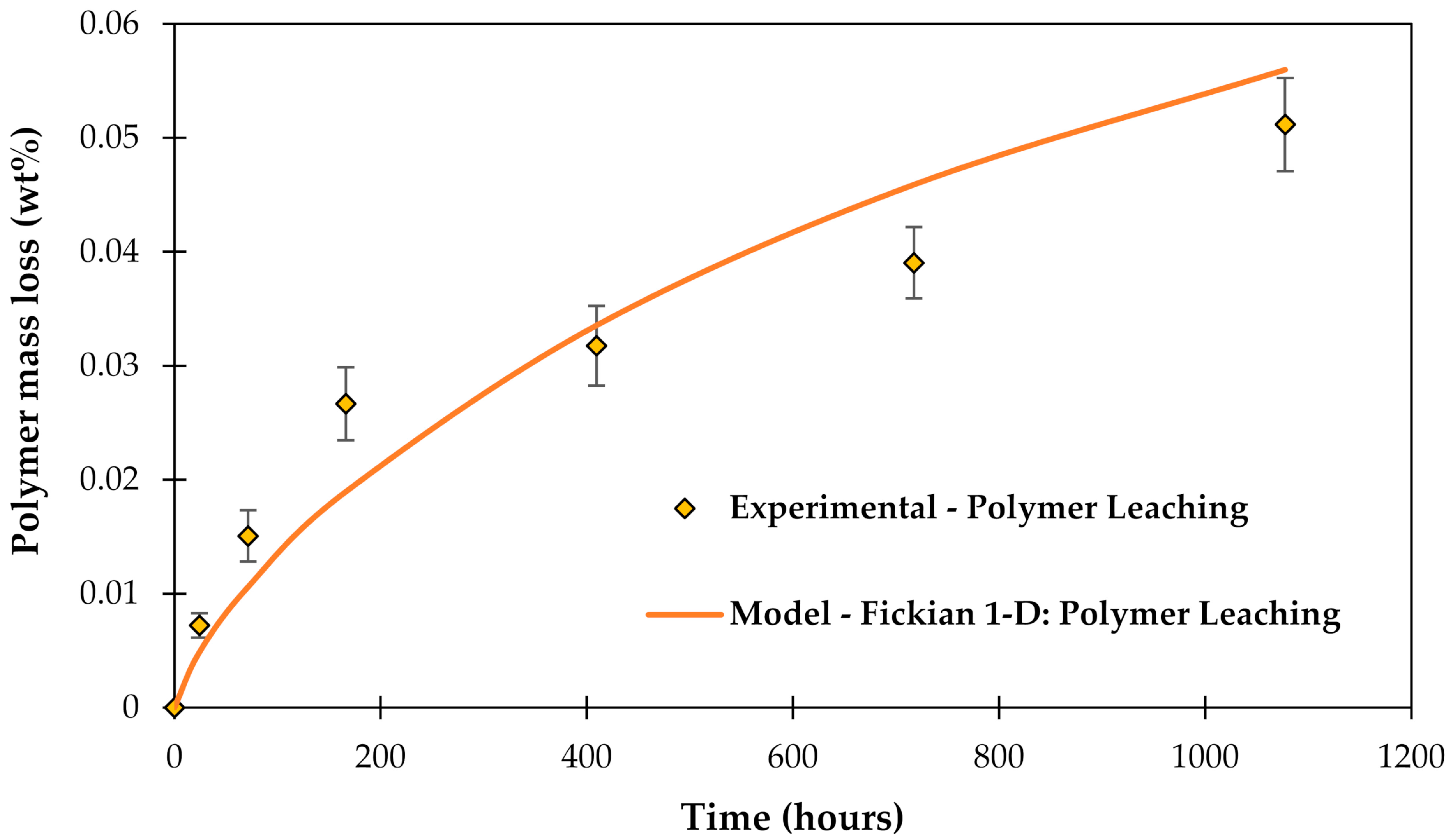
3.4. Leaching of Molecules out of the Epoxy Matrix
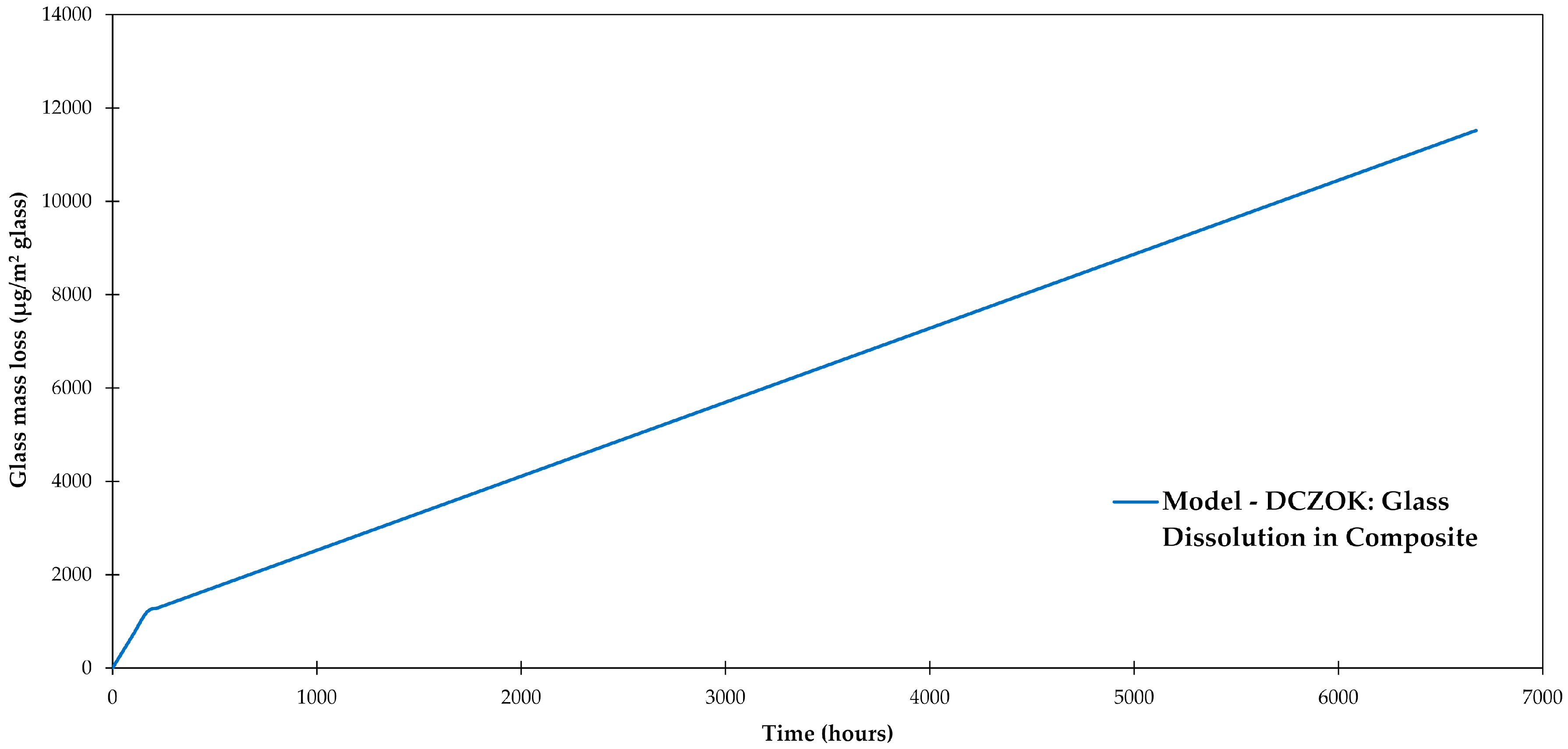
3.5. Glass Dissolution
3.6. Interphase Dissolution
4. Results and Discussion
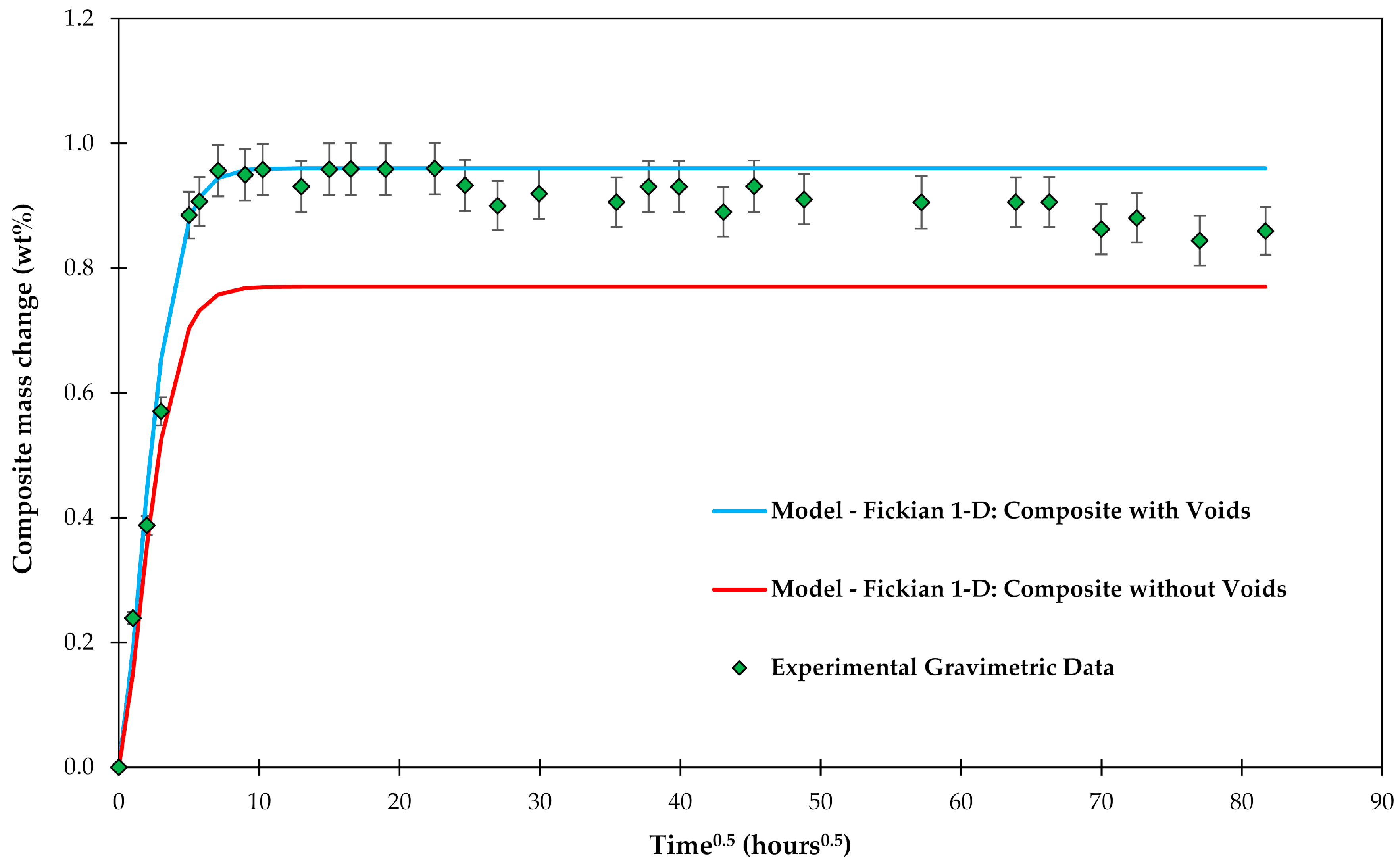
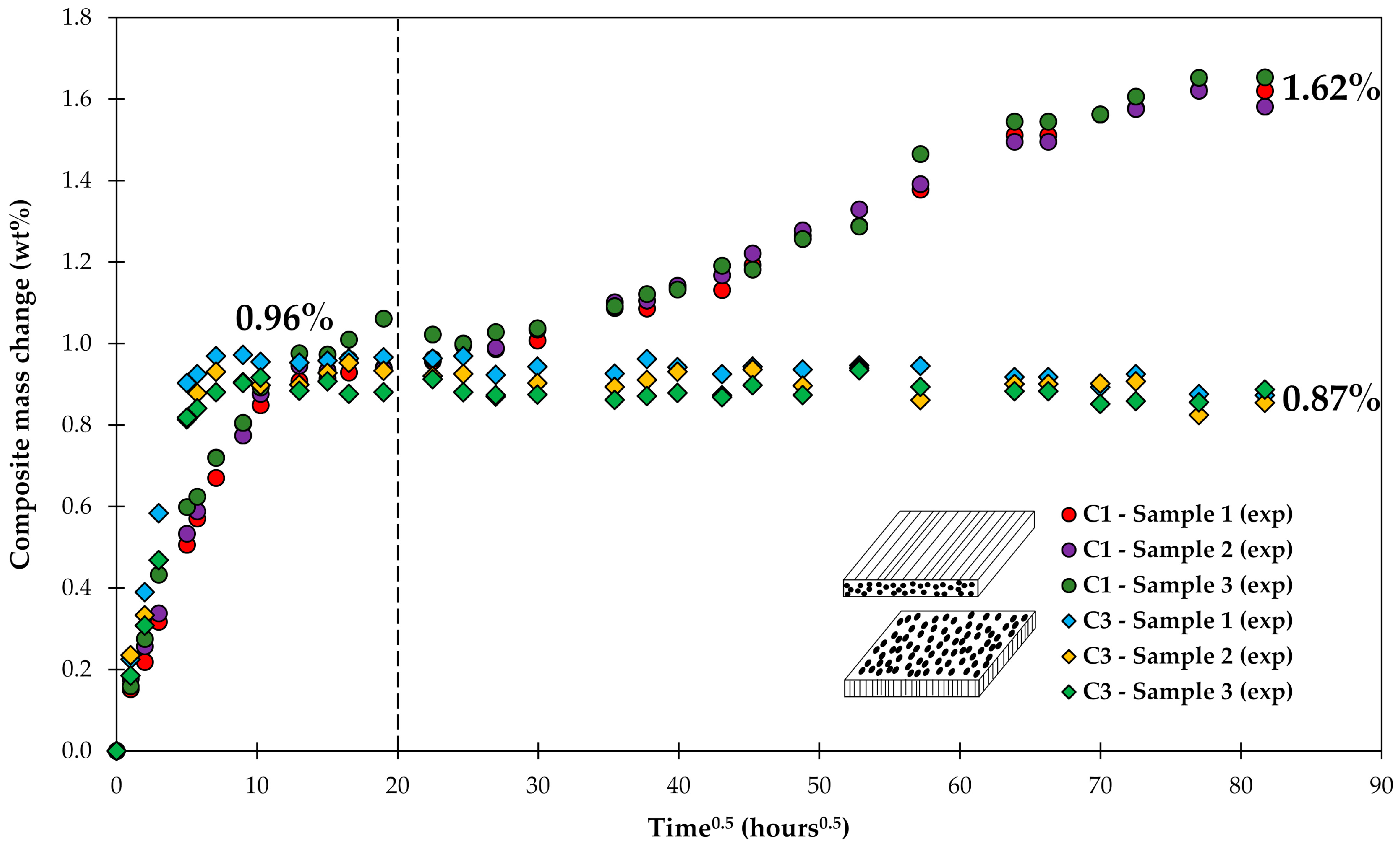
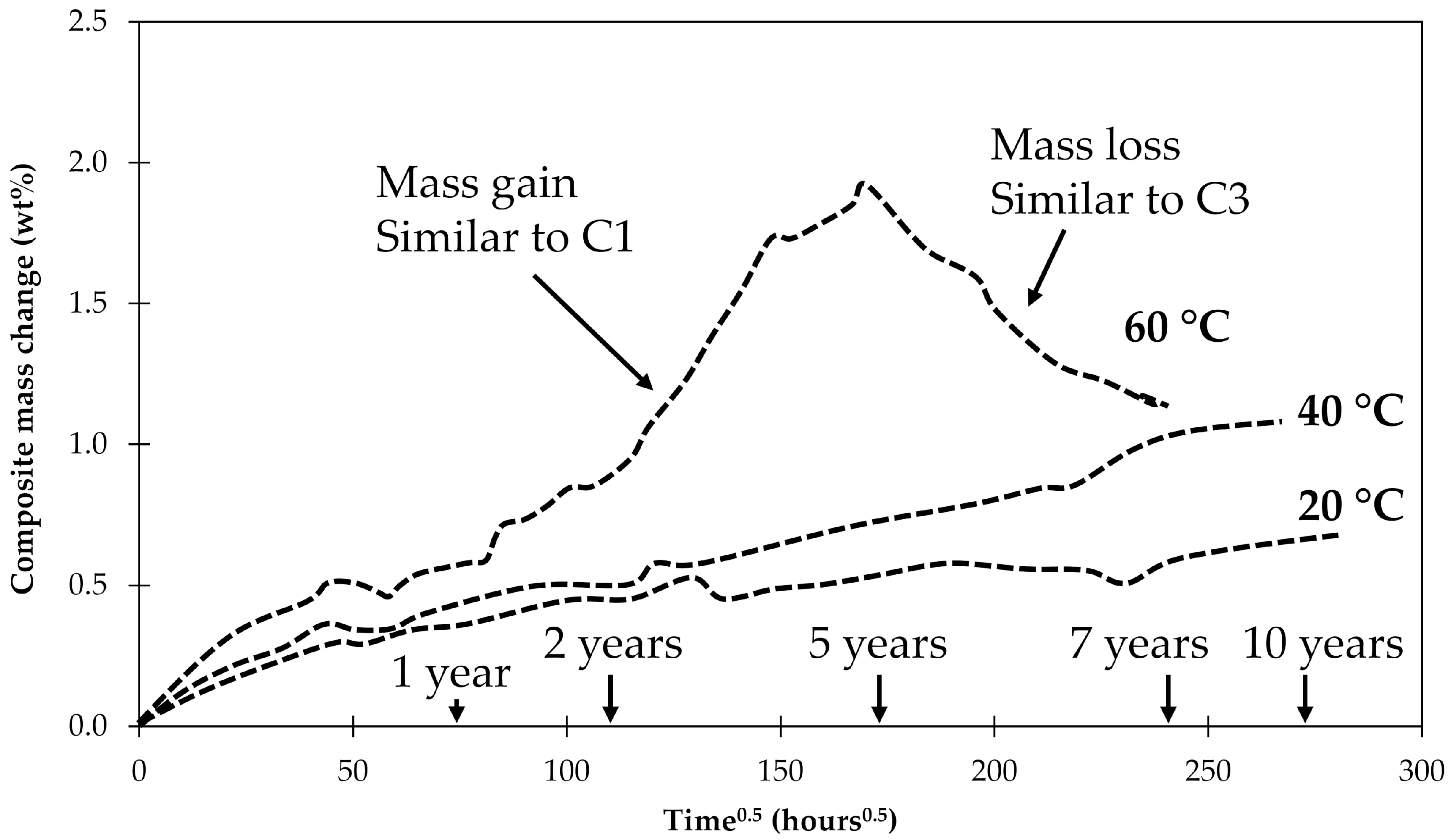
4.1. Samples with Short Fibers C3
4.2. Samples with Long Fibers C1
4.3. General Aspects
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ρf | Density of the glass fibers (g/m3) |
| ρm | Density of the matrix polymer (g/m3) |
| ρi | Density of the sizing-rich composite interphase (g/m3) |
| ρwater | Density of the water (g/m3) |
| h | Thickness of a material plate (m) |
| νf | Volume fraction of the fibers (m3/m3) |
| νm | Volume fraction of the matrix polymer (m3/m3) |
| νi | Volume fraction of the composite interphase (m3/m3) |
| νv | Volume fraction of the voids (m3/m3) |
| M(t) | Time-dependent water content of the composite (wt %) |
| M∞ | Saturation water content of the composite (wt %) |
| Mm(t) | Time-dependent water content of the matrix polymer (wt %) |
| Saturation water content of the matrix polymer (wt %) | |
| Saturation water content of the voids (wt %) | |
| D | Through-thickness water diffusivity of the material (mm2/h) |
| Mleaching(t) | Time-dependent content of leached compounds from the polymer (wt %) |
| Initial leachable compound content in the polymer (wt %) | |
| Dleaching | Through-thickness leachable compound diffusivity of the material (mm2/h) |
| r(t) | Time-dependent fiber radius (m) |
| r0 | Initial fiber radius (m) |
| Fiber radius when the steady-state dissolution is reached (m) | |
| K0 | Glass dissolution rate constant (g/(m2·s)) |
| Apparent glass dissolution rate constant (g/(m2·s)) | |
| Apparent glass dissolution rate constant (non-steady-state; Phase I) (g/(m2·s)) | |
| Apparent glass dissolution rate constant (steady-state; Phase II) (g/(m2·s)) | |
| tst | Time when long-term steady-state is reached (s) |
| n | Number of fibers (–) |
| l | Length of fibers and the interphase (m) |
| S(t) | Time-dependent glass fiber surface area (m2) |
| S0 | Initial glass fiber surface area (m2) |
| t | Time (s) |
| m; mdissolved | Glass mass loss due to dissolution (g) |
| Dissolved glass mass when the steady-state is reached (g) | |
| ξsizing | Protective effect of sizing against glass dissolution (–) |
| norder | Order of the water availability term (–) |
| Si(t) | Time-dependent surface area of the composite interphase (m2) |
| Si0 | Initial surface area of the composite interphase (m2) |
| Specific surface area of the composite interphase (m2) | |
| Zero-order rate constant of the composite interphase dissolution (g/(m2·s)) | |
| mi(t) | Time-dependent mass of the composite interphase (g) |
| mi0 | Initial mass of the composite interphase (g) |
| GF | Glass fiber |
| GFRP | Glass fiber-reinforced polymer; same as glass fiber-reinforced composite |
| DCZOK | Dissolving cylinder zero-order kinetic (model) |
| DGEBA | Bisphenol A diglycidyl ether |
| HDDGE | 1,6-Hexanediol diglycidyl ether |
| POPA | Poly(oxypropylene)diamine |
| IPDA | Isophorondiamine |
| R-glass | “Reinforcement” glass |
| FRP | Fiber-reinforced polymer, same as fiber-reinforced composite |
| HR-ICP-MS | High-resolution inductively coupled plasma mass spectrometry\ |
| VARTM | Vacuum-assisted resin transfer molding |
| BET | Brunauer–Emmett–Teller theory |
| LOI | Loss on ignition |
| γ-APS APTES | γ-aminopropyltriethoxysilane |
| PPO | Poly(propylene oxide) |
| PEO | Poly(ethylene oxide) |
| PDMS | Polydimethylsiloxane |
References
- Berg, J.; Jones, F.R. The role of sizing resins, coupling agents and their blends on the formation of the interphase in glass fiber composites. Compos. Part A 1998, 29, 1261–1272. [Google Scholar] [CrossRef]
- Feih, S.; Wei, J.; Kingshott, P.; Sørensen, B.F. The influence of fiber sizing on the strength and fracture toughness of glass fiber composites. Compos. Part A 2005, 36, 245–255. [Google Scholar] [CrossRef]
- Dai, Z.; Shi, F.; Zhang, B.; Li, M.; Zhang, Z. Effect of sizing on carbon fiber surface properties and fibers/epoxy interfacial adhesion. Appl. Surf. Sci. 2011, 257, 6980–6985. [Google Scholar] [CrossRef]
- Yuan, X.; Zhu, B.; Cai, X.; Liu, J.; Qiao, K.; Yu, J. Optimization of interfacial properties of carbon fiber/epoxy composites via a modified polyacrylate emulsion sizing. Appl. Surf. Sci. 2017, 401, 414–423. [Google Scholar] [CrossRef]
- DiBenedetto, A.T. Tailoring of interfaces in glass fiber reinforced polymer composites: A review. Mater. Sci. Eng. A 2001, 302, 74–82. [Google Scholar] [CrossRef]
- Plonka, R.; Mäder, E.; Gao, S.L.; Bellmann, C.; Dutschk, V.; Zhandarov, S. Adhesion of epoxy/glass fiber composites influenced by aging effects on sizings. Compos. Part A 2004, 35, 1207–1216. [Google Scholar] [CrossRef]
- Grabovac, I.; Whittaker, D. Application of bonded composites in the repair of ships structures—A 15-year service experience. Compos. Part A 2009, 40, 1381–1398. [Google Scholar] [CrossRef]
- McGeorge, D.; Echtermeyer, A.T.; Leong, K.H.; Melve, B.; Robinson, M.; Fischer, K.P. Repair of floating offshore units using bonded fibre composite materials. Compos. Part A 2009, 40, 1364–1380. [Google Scholar] [CrossRef]
- Gustafson, C.-G.; Echtermeyer, A. Long-term properties of carbon fibre composite tethers. Int. J. Fatigue 2006, 28, 1353–1362. [Google Scholar] [CrossRef]
- Salama, M.M.; Stjern, G.; Storhaug, T.; Spencer, B.; Echtermeyer, A. The first offshore field installation for a composite riser joint. OTC-14018-MS. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2002. [Google Scholar] [CrossRef]
- Echtermeyer, A.T.; Gagani, A.I.; Krauklis, A.E.; Mazan, T. Multiscale modelling of environmental degradation—First steps. In Durability of Composites in a Marine Environment 2. Solid Mechanics and Its Applications; Davies, P., Rajapakse, Y.D.S., Eds.; Springer: Cham, Switzerland, 2018; Volume 245, pp. 135–149. ISBN 978-3-319-65145-3. [Google Scholar]
- Thomason, J.L. Glass Fiber Sizings: A Review of the Scientific Literature; James L Thomason: Middletown, DE, USA, 2012; ISBN 978-0-9573814-1-4. [Google Scholar]
- Weitsman, Y. Coupled damage and moisture-transport in fiber-reinforced, polymeric composites. Int. J. Solids Struct. 1987, 23, 1003–1025. [Google Scholar] [CrossRef]
- Weitsman, Y.J.; Elahi, M. Effects of fluids on the deformation, strength and durability of polymeric composites—An overview. Mech. Time-Depend. Mater. 2000, 4, 107–126. [Google Scholar] [CrossRef]
- Roy, S. Moisture-induced degradation. In Long-Term Durability of Polymeric Matrix Composites; Pochiraju, V.K., Tandon, P.G., Schoppner, A.G., Eds.; Springer: Boston, MA, USA, 2012; pp. 181–236. ISBN 978-1-4419-9307-6. [Google Scholar]
- Peters, L. Influence of glass fibre sizing and storage conditions on composite properties. In Durability of Composites in a Marine Environment 2. Solid Mechanics and Its Applications; Davies, P., Rajapakse, Y.D.S., Eds.; Springer: Cham, Switzerland, 2018; Volume 245, pp. 19–31. ISBN 978-3-319-65145-3. [Google Scholar]
- Culler, S.R.; Ishida, H.; Koenig, J.L. Hydrothermal Stability of γ-Aminopropyltriethoxysilane Coupling Agent on Ground Silicon Powder and E-Glass Fibers; Technical Report; Department of Macromolecular Science: Cleveland, OH, USA, 1983. [Google Scholar]
- Wang, D.; Jones, F.R.; Denison, P. TOF SIMS and XPS study of the interaction of hydrolysed γ-aminopropyltriethoxysilane with E-glass surfaces. J. Adhes. Sci. Technol. 1992, 6, 79–98. [Google Scholar] [CrossRef]
- Wang, D.; Jones, F.R.; Denison, P. Surface analytical study of the interaction between γ-amino propyl triethoxysilane and E-glass surface. Part I Time-of-flight secondary ion mass spectrometry. J. Mater. Sci. 1992, 27, 36–48. [Google Scholar] [CrossRef]
- Wang, D.; Jones, F.R. Surface analytical study of the interaction between γ-amino propyl triethoxysilane and E-glass surface. Part II X-ray photoelectron spectroscopy. J. Mater. Sci. 1993, 28, 2481–2488. [Google Scholar] [CrossRef]
- Wang, M.; Xu, X.; Ji, J.; Yang, Y.; Shen, J.; Ye, M. The hygrothermal aging process and mechanism of the novolac epoxy resin. Compos. Part B 2016, 107, 1–8. [Google Scholar] [CrossRef]
- Halpin, J.C. Effects of Environmental Factors on Composite Materials; Technical Report AFML-TR-67–423; Air Force Materials Laboratory: Dayton, OH, USA, 1969. [Google Scholar]
- ASTM D4963/D4963M-2011 Standard Test Method for Ignition Loss of Glass Strands and Fabrics; ASTM: West Conshohocken, PA, USA, 2011.
- Loewenstein, K.L. Glass Science and Technology (Book 6), The Manufacturing Technology of Continuous Glass Fibres; Elsevier: Amsterdam, The Netherlands, 1993; ISBN 978-0444893468. [Google Scholar]
- Thomason, J.L.; Adzima, L.J. Sizing up the interphase: An insider’s guide to the science of sizing. Compos. Part A 2001, 32, 313–321. [Google Scholar] [CrossRef]
- Plueddemann, E.P. Silane Coupling Agents, 2nd ed.; Plenum Press: New York, NY, USA, 1991; ISBN 978-0-306-43473-0. [Google Scholar]
- Emadipour, H.; Chiang, P.; Koenig, J.L. Interfacial strength studies of fibre-reinforced composites. Res. Mech. 1982, 5, 165–176. [Google Scholar]
- Krauklis, A.E.; Echtermeyer, A.T. Dissolving cylinder zero-order kinetic model for predicting hygrothermal aging of glass fibre bundles and fibre-reinforced composites. In Proceedings of the 4th International Glass Fibre Symposium, Aachen, Germany, 29–31 October 2018; pp. 66–72, ISBN 978-3-95886-249-4. [Google Scholar]
- Joliff, Y.; Belec, L.; Chailan, J.-F. Impact of the interphases on the durability of a composite in humid environment—A short review. In Proceedings of the 20th International Conference on Composite Structures ICCS20, Paris, France, 4–7 September 2017. [Google Scholar]
- Zhuang, R.-C.; Burghardt, T.; Mäder, E. Study on interfacial adhesion strength of single glass fiber/polypropylene model composites by altering the nature of the surface of sized glass fibers. Compos. Sci. Technol. 2010, 70, 1523–1529. [Google Scholar] [CrossRef]
- Wolff, V.; Perwuelz, A.; El Achari, A.; Caze, C.; Carlier, E. Determination of surface heterogeneity by contact angle measurements on glass fibres coated with different sizings. J. Mater. Sci. 1999, 34, 3821–3829. [Google Scholar] [CrossRef]
- Ishida, H.; Koenig, J.L. An investigation of the coupling agent/matrix interface of fiberglass reinforced plastics by fourier transform infrared spectroscopy. Polym. Phys. B 1979, 17, 615–626. [Google Scholar] [CrossRef]
- Watson, H.; Mikkola, P.J.; Matisons, J.G.; Rosenholm, J.B. Deposition characteristics of ureido silane ethanol solutions onto E-glass fibres. Colloids Surf. A 2000, 161, 183–192. [Google Scholar] [CrossRef]
- Feresenbet, E.; Raghavan, D.; Holmes, G.A. Influence of silane coupling agent composition on the surface characterization of fiber and on fiber-matrix interfacial shear strength. J. Adhes. 2003, 79, 643–665. [Google Scholar] [CrossRef]
- Fagerholm, H.M.; Lindsjö, C.; Rosenholm, J.B.; Rökman, K. Physical characterization of E-glass fibres treated with alkylphenylpoly(oxyethylene)alcohol. Colloids Surf. 1992, 69, 79–86. [Google Scholar] [CrossRef]
- Thomason, J.L.; Dwight, D.W. The use of XPS for characterization of glass fibre coatings. Compos. Part A 1999, 30, 1401–1413. [Google Scholar] [CrossRef]
- Turrión, S.G.; Olmos, D.; González-Benito, J. Complementary characterization by fluorescence and AFM of polyaminosiloxane glass fibers coatings. Polym. Test. 2005, 24, 301–308. [Google Scholar] [CrossRef]
- Mai, K.; Mäder, E.; Mühle, M. Interphase characterization in composites with new non-destructive methods. Compos. Part A 1998, 29, 1111–1119. [Google Scholar] [CrossRef]
- Thomason, J.L.; Dwight, D.W. XPS analysis of the coverage and composition of coatings on glass fibers. J. Adhes. Sci. Technol. 2000, 14, 745–764. [Google Scholar] [CrossRef]
- Wang, D.; Jones, F.R. TOF SIMS and XPS study of the interaction of silanized E-glass with epoxy resin. J. Mater. Sci. 1993, 28, 1396–1408. [Google Scholar] [CrossRef]
- Chiang, C.H.; Ishida, H.; Koenig, J.L. The structure of aminopropyltriethoxysilane on glass surfaces. J. Colloid Interface Sci. 1980, 74, 396–404. [Google Scholar] [CrossRef]
- Rocha, I.B.C.M.; Raijmaekers, S.; Nijssen, R.P.L.; van der Meer, F.P.; Sluys, L.J. Hygrothermal ageing behaviour of a glass/epoxy composite used in wind turbine blades. J. Compos. Struct. 2017, 174, 110–122. [Google Scholar] [CrossRef]
- Kim, J.K.; Sham, M.L.; Wu, J. Nanoscale characterization of interphase in silane treated glass fibre composites. Compos. Part A 2001, 32, 607–618. [Google Scholar] [CrossRef]
- ASTM D5229/D5229M-14 Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2014.
- Perreux, D.; Choqueuse, D.; Davies, P. Anomalies in moisture absorption of glass fibre reinforced epoxy tubes. Compos. Part A 2002, 33, 147–154. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Echtermeyer, A.T. Mechanism of yellowing: carbonyl formation during hygrothermal aging in a common amine epoxy. Polymers 2018, 10, 1017. [Google Scholar] [CrossRef] [PubMed]
- Krauklis, A.E.; Echtermeyer, A.T. Long-term dissolution of glass fibers in water described by dissolving cylinder zero-order kinetic model: Mass loss and radius reduction. Open Chem. 2018, 16, 1189–1199. [Google Scholar] [CrossRef]
- 3B Fibreglass Technical Data Sheet; HiPer-Tex W2020 Rovings: Belgium, Brussel, 2012.
- Gagani, A.I.; Fan, Y.; Muliana, A.H.; Echtermeyer, A.T. Micromechanical modeling of anisotropic water diffusion in glass fiber epoxy reinforced composites. J. Compos. Mater. 2017, 52, 2321–2335. [Google Scholar] [CrossRef]
- Zinck, P.; Gerard, J.F. On the hybrid character of glass fibres surface networks. J. Mater. Sci. 2005, 40, 2759–2760. [Google Scholar] [CrossRef]
- ASTM D3171/D3171-15 Standard Test Methods for Constituent Content of Composite Materials; ASTM International: West Conshohocken, PA, USA, 2015.
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- International Standard ISO 9277:2010(E) Determination of the Specific Surface Area of Solids by Gas Adsorption—BET Method; ISO: Berlin, Germany, 2010.
- Popineau, S.; Rondeau-Mouro, C.; Sulpice-Gaillet, C.; Shanahan, M.E.R. Free/bound water absorption in an epoxy adhesive. Polymer 2005, 46, 10733–10740. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Hygrothermal aging of amine epoxy: reversible static and fatigue properties. Open Eng. 2018, 8, 447–454. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Near-Infrared Spectroscopic Method For Monitoring Water Content In Epoxy Resins And Fiber-Reinforced Composites. Materials 2018, 11, 586. [Google Scholar] [CrossRef]
- Thomason, J.L. The interface region in glass-fibre-reinforced epoxy resin composites: 2. Water absorption, voids and the interface. Composites 1995, 26, 477–485. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975; ISBN 978-0-19-853411-6. [Google Scholar]
- Maggana, C.; Pissis, P. Water sorption and diffusion studies in an epoxy resin system. J. Polym. Sci. Part B 1999, 37, 1165–1182. [Google Scholar] [CrossRef]
- Toscano, A.; Pitarresi, G.; Scafidi, M.; Di Filippo, M.; Spadaro, G.; Alessi, S. Water diffusion and swelling stresses in highly crosslinked epoxy matrices. Polym. Degrad. Stab. 2016, 133, 255–263. [Google Scholar] [CrossRef]
- Bruchet, A.; Elyasmino, N.; Decottignies, V.; Noyon, N. Leaching of bisphenol A and F from new and old epoxy coatings: Laboratory and field studies. Water Sci. Technol. 2014, 14, 383–389. [Google Scholar] [CrossRef]
- Schutte, C.L. Environmental durability of glass-fiber composites. Mater. Sci. Eng. R Rep. 1994, 13, 265–323. [Google Scholar] [CrossRef]
- Krauklis, A.E.; Gagani, A.I.; Vegere, K.; Kalnina, I.; Klavins, M.; Echtermeyer, A.T. Dissolution kinetics of R-glass fibres: Influence of water acidity, temperature and stress corrosion. Fibers 2019, 7, 22. [Google Scholar] [CrossRef]
- Khawam, A.; Flanagan, D.R. Solid-state kinetic models: basics and mathematical fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef] [PubMed]
- Gagani, A.I.; Mialon, E.P.V.; Echtermeyer, A.T. Immersed interlaminar fatigue of glass fiber epoxy composites using the I-beam method. Int. J. Fatigue 2019, 119, 302–310. [Google Scholar] [CrossRef]
- Rocha, I.B.C.M.; van der Meer, F.P.; Raijmaekers, S.; Lahuerta, F.; Nijssen, R.P.L.; Mikkelsen, L.P.; Sluys, L.J. A combined experimental/numerical investigation on hygrothermal aging of fiber-reinforced composites. Eur. J. Mech. Sol. 2019, 73, 407–419. [Google Scholar] [CrossRef]
- Bonniau, P.; Bunsell, A.R. Water absorption by glass fibre reinforced epoxy resin. In Composite Structures; Marshall, I.H., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp. 92–105. ISBN 978-94-009-8122-5. [Google Scholar]
- Gagani, A.I.; Krauklis, A.E.; Sæter, E.; Vedvik, N.P.; Echtermeyer, A.T. A novel method for testing and determining ILSS for marine and offshore composites. Comp. Struct. 2019, 220, 431–440. [Google Scholar] [CrossRef]



| Process | Sign | Reference |
|---|---|---|
| Water uptake of the polymer matrix | + | [49] |
| Water uptake by the composite interphase | + | [56] |
| Water uptake by the voids | + | [12,49,57] |
| Thermo-oxidation of the polymer matrix | + | [46] |
| Leaching from polymer matrix | − | [46] |
| Glass fiber dissolution | − | [28,47] |
| Sizing-rich interphase dissolution | − | This work |
| Specimen | D (mm2/h) |
|---|---|
| Epoxy | 0.0068 |
| C1 | 0.0051 |
| C3 | 0.0210 |
| Phase | (g/(m2·h)) |
|---|---|
| Phase I | 6.91 × 10−6 |
| Phase II | 1.54 × 10−6 |
| Scenario | (g/h) | Sizing Coverage (%) | (nm) | (m2) | (g/(m2·h)) | Time to Total Dissolution (years) |
|---|---|---|---|---|---|---|
| Scenario 1 | 1.80 × 10−7 | 100 | 65 | 4.43 × 10−5 | 4.06 × 10−3 | 22.7 |
| Scenario 2 | 1.80 × 10−7 | 100 | 65 | 1.01 | 1.78 × 10−7 | 30.5 |
| Scenario 3 | 1.80 × 10−7 | 90, after [39] | 72 | 0.91 | 1.98 × 10−7 | 30.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Long-Term Hydrolytic Degradation of the Sizing-Rich Composite Interphase. Coatings 2019, 9, 263. https://doi.org/10.3390/coatings9040263
Krauklis AE, Gagani AI, Echtermeyer AT. Long-Term Hydrolytic Degradation of the Sizing-Rich Composite Interphase. Coatings. 2019; 9(4):263. https://doi.org/10.3390/coatings9040263
Chicago/Turabian StyleKrauklis, Andrey E., Abedin I. Gagani, and Andreas T. Echtermeyer. 2019. "Long-Term Hydrolytic Degradation of the Sizing-Rich Composite Interphase" Coatings 9, no. 4: 263. https://doi.org/10.3390/coatings9040263
APA StyleKrauklis, A. E., Gagani, A. I., & Echtermeyer, A. T. (2019). Long-Term Hydrolytic Degradation of the Sizing-Rich Composite Interphase. Coatings, 9(4), 263. https://doi.org/10.3390/coatings9040263