Abstract
In this research, the three-dimensional nanofluid thin-film flow of Casson fluid over an inclined steady rotating plane is examined. A thermal radiated nanofluid thin film flow is considered with suction/injection effects. With the help of similarity variables, the partial differential equations (PDEs) are converted into a system of ordinary differential equations (ODEs). The obtained ODEs are solved by the homotopy analysis method (HAM) with the association of MATHEMATICA software. The boundary-layer over an inclined steady rotating plane is plotted and explored in detail for the velocity, temperature, and concentration profiles. Also, the surface rate of heat transfer and shear stress are described in detail. The impact of numerous embedded parameters, such as the Schmidt number, Brownian motion parameter, thermophoretic parameter, and Casson parameter (Sc, Nb, Nt, γ), etc., were examined on the velocity, temperature, and concentration profiles, respectively. The essential terms of the Nusselt number and Sherwood number were also examined numerically and physically for the temperature and concentration profiles. It was observed that the radiation source improves the energy transport to enhance the flow motion. The smaller values of the Prandtl number, Pr, augmented the thermal boundary-layer and decreased the flow field. The increasing values of the rotation parameter decreased the thermal boundary layer thickness. These outputs are examined physically and numerically and are also discussed.
1. Introduction
Energy is a requirement of production for every industry and is used in every engineering field. Important sources of energy are gas turbines, exchange membrane, and fuel cells [1], hydraulic-fracturing [2,3], etc. Suspensions of nanoparticles in fluids show a vital enrichment of their possessions at modest nanoparticle concentrations. Numerous researchers have worked on nanofluids and studied their role in heat transfer analysis, like nuclear reactors and other transportations. Nanofluids are smart fluids, where heat transfer can be decreased or increased in the base fluids. This research work focuses on investigating the vast range of uses that involve nanofluids, emphasizing their enriched heat transfer possessions, which are governable, and the defining features that these nanofluids preserve that make them suitable for such uses. Moreover, nanofluids are a new kind of energy transference fluid that are the suspension of base fluids and nanoparticles. For cooling requirements, usual heat transfer liquids cannot be used, due to their lesser thermal conductivity. By implanting nanoparticles into normal fluids, their thermal enactment can be enriched considerably. Choi [4] is widely accepted as the first publication that introduces the concept of nanofluids. He clarifies nano liquids as a liquid containing smaller scale particles known as nanoparticles about 1 to 100 nm in measure.
Bhatti et al. [5] explored the simultaneous impacts of the varying magnetic field of Jeffrey nanofluid. They examined the impact of physical parameters over the flow field. Xiao et al. [3] examined the relative permeability of nanofibers with the capillary pressure effect using the Fractal-Monte Carlo technique. They observed the impact of the embedding parameters with applications. Ellahi et al. [6] investigated the MHD non-Newtonian nanofluid with a temperature dependent viscosity flow through a pipe. The microchannel heat sink flow exploration cooled by a Cu water nanofluid by applying the least square method and the porous media approach was observed by Hatami et al. [7]. Hatami et al. [8] explored nanofluid laminar flow between rotating disks with heat transfer. Srinivas Acharya et al. [9] investigated nanofluid mixed convection flow with ion slip and Hall effects between two concentric cylinders. Khan et al. [10] investigated boundary-layer nanofluid flow through a stretching surface. Khanafer et al. [11] described two-dimensional Buoyancy driven flow with enhanced heat transfer enclosure utilizing nanofluids. Mahanthesh et al. [12] investigated unsteady MHD three-dimensional Eyring-Powell nanofluid flow with thermal radiation through a stretching sheet. Rashidi et al. [13] explored nanofluid with entropy generation and MHD flow on a steady porous rotating disk. Rashidi et al. [14] investigated 3-D film condensation on a steady inclined rotating disk.
Gul et al. [15] studied the heat and mass transfer analysis of a liquid film over an inclined plane. They compared integer and non-integer order results under the influence of embedded parameters. Saleh et al. [16] studied carbon-nanotubes suspended nanofluid flow with convective conditions using the Laplace transform. Sheikholeslami et al. [17] examined nanofluid flow in a semi-annulus enclosure with heat transfer and MHD effects. Sheikholeslami et al. [18] investigated flow in a semi-porous channel of MHD nanofluid with an analytical investigation. Later, these investigators [19] deliberated unsteady nanofluid flow through a stretching surface. Hayat et al. [20] explored the boundary layer flow of Maxwell nanofluid. Malik et al. [21] explored MHD flow through a stretching Erying-Powell nanofluid. Nadeem et al. [22] examined the flow of Maxwell liquid with nanoparticles through a vertical stretching surface. Raju et al. [23] examined flow with free convective heat transfer through a cone of MHD nano liquid. Rokni et al. [24] explored flow with the heat transfer of nanofluids through plates. Nadeem et al. [25] investigated flow on a stretching sheet of nano non-Newtonian liquid. Shehzad et al. [26] investigated the convective boundary conditions of Jaffrey nanoliquid flow with an MHD effect. Sheiholeslami et al. [27] explored flow with a magnetic field and heat transfer of nano liquid. Mahmoodi et al. [28] examined flow for cooling applications of nanonfluid with heat transfer. Recently, Shah et al. [29,30,31,32] investigated a rotating system in the effects of hall current and thermal radiations of nanofluid flow. Further theoretical investigations were examined by Sheikholeslami using different phenomena for nanofluids, with present usages and possessions with applications of numerous methods, can be found in [33,34,35,36,37]. Pour and Nassab [38] examined the convectional flow of nanofluids using the numerical technique. The influence of the physical parameters was observed in their study.
The exploration of thin film has achieved substantial presentation due to its frequent usages in the field of technology, industry, and engineering in a short interval of time. The investigation of thin liquid flow is necessary, due to its practical uses, such as cable and fibber undercoat. Several well-known uses of thin film are the fluidization of devices, elastic sheet drawing, and constant formation. Regarding their uses, it is vital that scientists develop research on the stretching sheet of liquid films. Sandeep et al. [39] studied non-Newtonian nanoliquids’ thin films’ fluid flow with heat transfer. Wang [40] detected an unsteady flow of thin film fluid through a stretching sheet. Usha et al. [41] investigated unsteadily finite thin liquid past a stretching sheet. Liu et al. [42] investigated thin film flow with heat transfer on a stretching surface. Aziz et al. [43] perceived the flow on a stretching sheet of a thin fluid film for the production of heat inside. Tawade et al. [44] examined fluid flow with thermal radiation and heat transmission of a thin film. Fluid film flow on a stretching sheet with heat transfer was investigated by Andersson et al. [45]. Also, investigators [46,47,48,49,50,51] examined the flow of liquid film on a stretching surface for further dissimilar cases. Hatami et al. [52] examined 3-D nanofluid flow on a steady rotating disk. A similar related study about nanofluid can be seen in [52,53,54,55,56]. Jawad et al. [57] examined Darcy-Forchheimer nanofluid thin film flow with Joule dissipation and Navier’s partial slip of the MHD effect. Jawad et al. [58] studied 3-D single-wall carbon nanotubes rotating flow with the impact of nonlinear thermal radiation and viscous dissipation in the presence of aqueous suspensions. Other related work can be seen in [59,60,61,62,63].
In view of the above important discussion, the aim of the current study is to investigate liquid film flow over an inclined plane. The momentum, thermal, and concentration boundary-layers under the influence of physical constraints for heat and mass transfer analysis will be examined physically and numerically.
2. Problem Formulation
Consider a steady three-dimensional Casson nanofluid thin-film flow over a rotating disk. The rotation of the disk is due to the angular velocity (Ω) in its own plane as displayed in Figure 1. An angle, β, is made by the inclined disk with the horizontal axis. Also, h denotes the film thickness of the nanofluid, and W represents the spraying velocity. The radius of the disk is very large as compared to the liquid film thickness and hence the termination influence is unnoticed. is gravitational acceleration, T0 is the temperature at the film surface, while Tw represents the surface temperature of the disk. Likewise, C0 and Ch are the concentration on the film and on the disk surfaces, respectively. Pressure is a function of the z-axis only and the ambient pressure (P0) at the sheet of the film is kept constant. The equations of continuity, momentum, concentration, and energy for a steady state are shown in Equations (1) to (6) [8,9,10]:
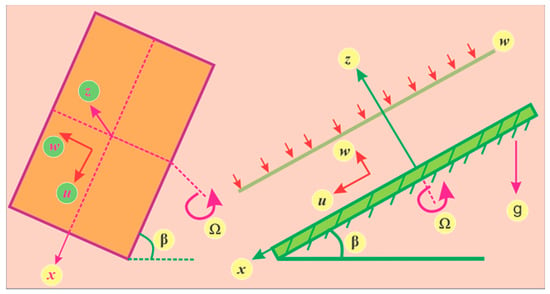
Figure 1.
Geometry of the problem.
In the above equations, u, v, and w represent the velocity components in the x, y, and z axis, respectively.
The boundary conditions are as follows:
Consider the similarity transformations of the form:
The transformations introduced in Equation (8) are implemented in Equations (2) to (7). Equation (1) is proved identically and Equations (2) to (6) are obtained in the forms:
If θ(η) and ϕ(η) are a function of z only, Equations (5) and (6) take the forms:
Physical parameters and other dimensionless numbers of interest are defined as:
Here, Pr is the Prandtl number, Sc is the Schmidt number, Nb is the Brownian motion parameter, and Nt is the thermophoretic parameter.
Where the normalized thickness constant is presented as:
The condensation velocity is defined as:
The pressure can be attained by the integration of Equation (4).
For the exact solution, let Pr = 0 and using θ(δ) = 1, the exact solution is:
An asymptotic limit for small, δ, is defined in Equation (17). The reduction of θ’(0) for rising δ is not monotonic. So, Nu is defined as:
The Sherwood number is defined as:
3. Solution by Homotopy Analysis Method
The optimal approach is used for the solution process. Equations (9) to (14) with boundary conditions (15) are solved by HAM. Mathematica software is used for this aim. The basic derivation of the model equation through HAM is given in detail below.
Linear operators are denoted as and is represented as
The modelled Equations (9) to (14) with boundary conditions (15) are solved analytically as well as numerically. The comparison between the analytical and numerical solution is shown graphically as well as numerically in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 for the velocities, temperature, and concentration profiles. From these tables, an excellent agreement between the HAM and numerical (ND-Solve Techniques) methods is obtained.

Table 1.
Comparison of HAM and numerical solution for f(η).

Table 2.
Comparison of HAM and numerical solution for k(η).

Table 3.
Comparison of HAM and numerical solution for g(η).

Table 4.
Comparison of HAM and numerical solution for s(η).

Table 5.
Comparison of HAM and numerical solution for θ(η).

Table 6.
Comparison of HAM and numerical solution for ϕ(η).
4. Results and Discussion
The three-dimensional flow of the liquid film through a steady rotating inclined surface with mass and heat transmission was examined. The influence of the embedded parameters, magnetic field, M, Casson parameter, γ, Schmidt number, Sc, Brownian motion parameter, Nb, and thermophoretic parameter, Nt, was investigated for the axial velocity, f(η), radial velocity, k(η), drainage flow, g(η), and induced flow, s(η), temperature field, θ(η), and concentration profile, ϕ(η), respectively. Figure 2, Figure 3, Figure 4 and Figure 5 display the influence of the Casson fluid parameter, γ, on f(η), k(η), g(η), and s(η). Rising γ generates resistance in the flow path and decreases the flow motion of nanoparticles. It is observed that an increase of the Casson fluid parameter, γ, leads to a decrease of f(η), k(η), g(η), and s(η). The opposite trend is found in case of the z-direction, that is the enormous value of γ decreases the f(η), k(η), g(η), and s(η). The influence of Pr on θ(η) is displayed in Figure 6. It is interesting to note that θ(η) decreases with large values of Pr and increases with smaller values. In fact, the thermal diffusivity of nanofluids has greater values by reducing Pr, and this effect is inconsistent for larger Pr. Hence, the greater values of Pr drop the thermal boundary layer. The influence of the radiation parameter, R, on θ(η) is presented in Figure 7. It is observed that if R increases, then the boundary layer area θ(η) is augmented. The effect of Nb on θ(η) is displayed in Figure 8. The converse influence was created for ϕ(η) and θ(η), which means augmented Nb decreases the concentration profile, ϕ(η). The concentration boundary layer thickness decreased due to the rising values of Nb and as a result, the concentration field, ϕ(η), declined. The features of the thermophoretic parameter, Nt, on the concentration profile, ϕ(η), are presented in Figure 9. The enhancement of Nt increases ϕ(η). Thus, Nt depends on the temperature gradient of the nanofluids. The kinetic energy of the nanofluids rises with the increasing value of Nt, and as a result, ϕ(η) increases. Figure 10 identifies the influence of Sc. The dimensionless number, Sc, is stated as the ratio of momentum and mass diffusivity. It is obvious that the amassed Sc reduces the ϕ(η) and as a result, the boundary layer thickness is decreased.
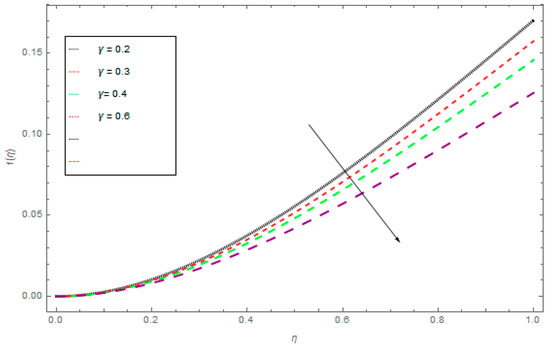
Figure 2.
The influence of γ on f(η) when Ω = 1, ρ = 1, σ = 0.5, k = 1, M = 1.
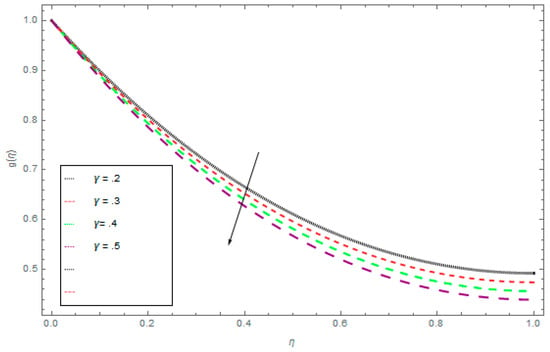
Figure 3.
The influence of γ on g(η) when Ω = 1, ρ = 1, σ = 0.5, k = 1, M = 1.
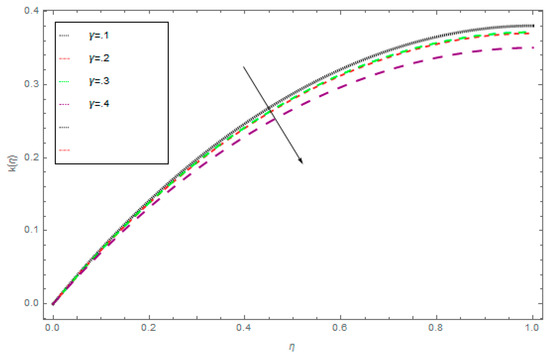
Figure 4.
The influence of γ on k(η) when Ω = 1, ρ = 1, σ = 0.5, k = 1, M = 1.
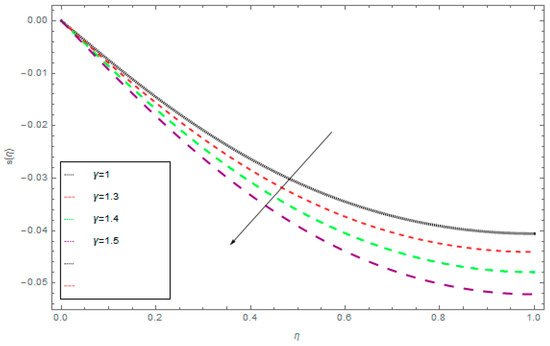
Figure 5.
The influence of γ on s(η) when Ω = 1, ρ = 1, σ = 0.5, k = 1, M = 1.
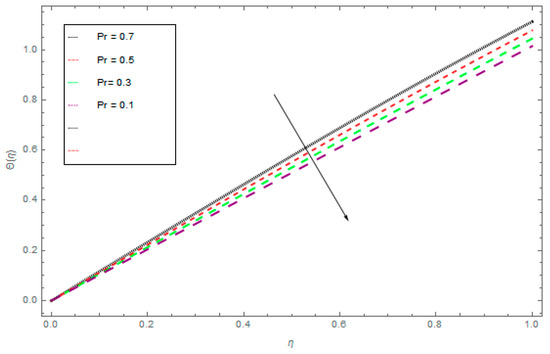
Figure 6.
The influence of Pr on θ(η) when Ω = 1, ρ = 1, σ = 0.5, k = 1, M = 1.
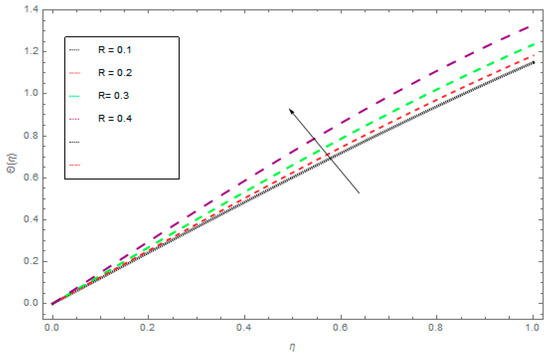
Figure 7.
The influence of R on θ(η) when Ω = 1, ρ = 1, σ = 0.5, k = 1, M = 1.
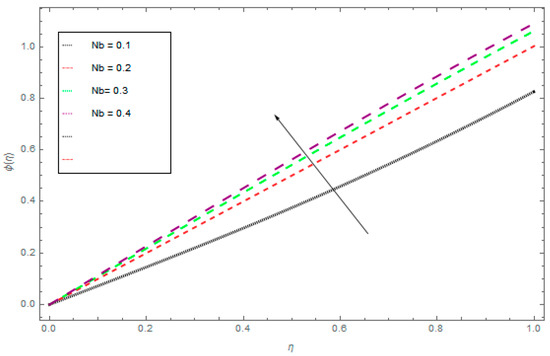
Figure 8.
The effect of Nb on ϕ(η) when Nt = 0.6, Sc = 0.6, S = 0.7.
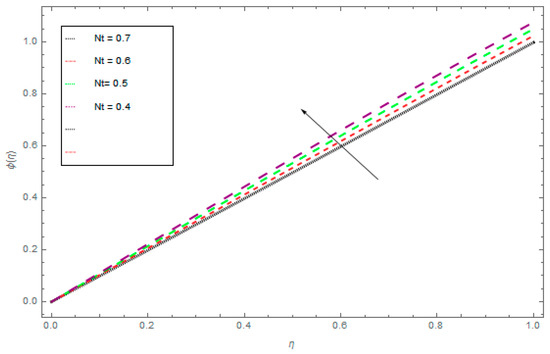
Figure 9.
The influence of Nt on ϕ(η) when Nb = 0.6, Sc = 0.7, S = 0.7.
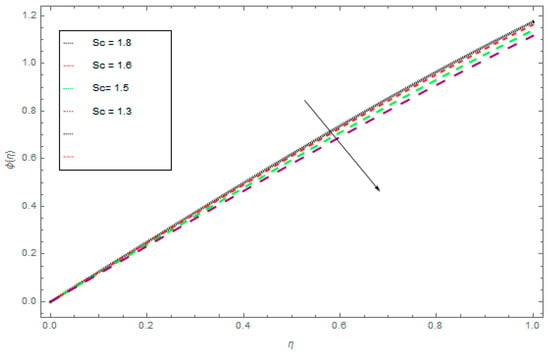
Figure 10.
The influence of the Schmidt number (Sc) on ϕ(η) when Nb = 0.6, Nt = 0.5.
Figure 11 and Figure 12 demonstrate the effects of Pr and R. It can be seen that rising values of Pr and R increase Nu. In fact, the coaling phenomenon is enhanced with increased values of these parameters. Figure 13 identifies that Nu reduces for the amassed values of k.
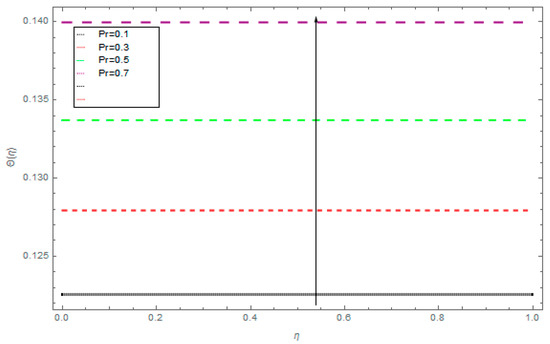
Figure 11.
The impact of the Prandtl number (Pr) on the Nusselt number.
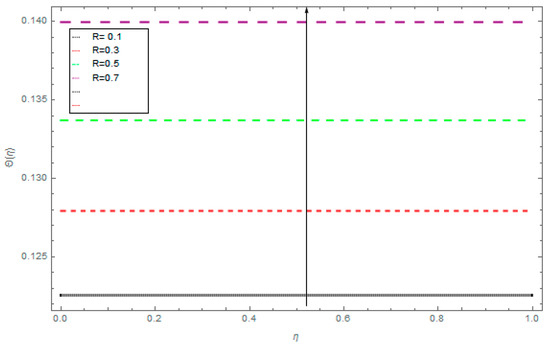
Figure 12.
The influence of radiation parameter (R) on the Nusselt number.
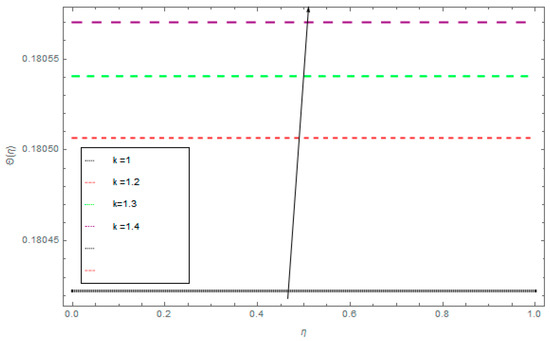
Figure 13.
The influence of k on the Nusselt number.
5. Conclusions
In this article, the three-dimensional thin-film Casson fluid flow over an inclined steady rotating plane was examined. The thin film flow was thermally radiated and the suction/injection effect was also considered. By the similarity variables, the PDEs were converted into ODES. The obtained ODEs were solved by the HAM with association of the MATHEMATICA program. The main features of the study are highlighted as:
- Smaller values of the Prandtl number enhance the thermal boundary layer.
- An increasing value of the magnetic field stops the fluid motion.
- Larger amounts of the thermal radiation parameter and thermophoretic parameter enhances the thermal boundary layer.
- The Casson fluid parameter produces a resistance force and its increasing value decreases the fluid motion.
Author Contributions
A.S., Z.S. and S.I. modeled the problem and wrote the manuscript. P.K. and T.Z. thoroughly checked the mathematical modeling and English corrections. A.S., M.J. and A.U. solved the problem using Mathematica software, S.I., T.G. and P.K. contributed to the results and discussions. All authors finalized the manuscript after its internal evaluation.
Funding
This research was funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT.
Acknowledgments
This project was supported by the Theoretical and Computational Science (TaCS) Center under Computational and Applied Science for Smart Innovation Research Cluster (CLASSIC), Faculty of Science, KMUTT.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Nb | Brownian motion parameter |
| T | Cauchy stress tensor |
| C | Concentration of the fluid |
| h | Film thickness |
| M | Magnetic parameter |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Nt | Thermoporetic parameter |
| R | Radiation parameter |
| x, y, z | Rectangular coordinates |
| Re | Reynold number |
| Sh | Sherwood number |
| Cf | Skin friction coefficient |
| W | Spraying velocity |
| T∞ | Temperature of the fluid at large distance |
| f | Transformed dependent variable |
| u | Velocity component in x-direction |
| v | Velocity component in y-direction |
| μ | Coefficient of viscosity |
| γ | Casson fluid parameter |
| ρ | Density of the fluid |
| p | Fluid pressure |
| I | Identity tensor chord |
| v | Kinematic viscosity |
| Ω | Rotation parameter |
| τ | Shearing stress |
| ψ | Stream function |
| β | Thickness of the fluid |
| η | Transformed independent variable |
| ∞ | Condition at infinity |
References
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double-layer effects in proton exchange membrane full cells. Int. J. Hydrogen Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Long, G.; Liu, S.; Xu, G.; Wong, S.W.; Chen, H.; Xiao, B.A. Perforation-erosion model for hydraulic-fracturing applications. SPE. Prod. Oper. 2018, 33, 770–783. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Chen, H.; Cai, H.; Deng, L.A. Novel fractal model for relative permeability of gas diffusion layer in proton exchange membrane fuel cell with capillary pressure effect. Fractals 2019, 27, 1950012. [Google Scholar] [CrossRef]
- Choi, S.; Eastman, J. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Bhatti, M.M.; Zeeshan, A.; Ellah, R. Simultaneous effects of coagulation and variable magnetic field on peristaltically induced motion of Jeffrey nanofluid containing gyrotactic microorganism. Microvasc. Res. 2017, 110, 32–42. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Hatami, M.; Ganji, D.D. Thermal and flow analysis of microchannel heat sink (MCHS) cooled by Cu water nanofluid using porous media approach and least square method. Energy Convers. Manag. 2014, 78, 347–358. [Google Scholar] [CrossRef]
- Hatami, M.; Sheikholeslami, M.; Ganji, D.D. Laminar flow and heat transfer of nanofluid between contracting and rotating disks by least square method. Powder Technol. 2014, 253, 769–779. [Google Scholar] [CrossRef]
- Srinivasacharya, D.; Shafeeurrahman, M. Hall and ion slip effects on mixed convection flow of nanofluid between two concentric cylinders. J. Assoc. Arab Univ. Basic Appl. Sci. 2017, 24, 223–231. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K.; Lightstone, M.; Buoyancydriven. Heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int. J. Heat Mass Transf. 2003, 46, 3639–3653. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Gorla, R.S.R. Unsteady three-dimensional MHD flow of a nano Eyring-Powell fluid past a convectively heated stretching sheet in the presence of thermal radiation, viscous dissipation and Joule heating. J. Assoc. Arab Univ. Basic Appl. Sci. 2017, 23, 75–84. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Dinarvand, S. Purely analytic approximate solutions for steady three-dimensional problem of condensation film on inclined rotating disk by homotopy analysis method. Nonlinear Anal. Real World Appl. 2009, 10, 2346–2356. [Google Scholar] [CrossRef]
- Gul, T.; Khan, M.A.; Khan, A.; Shuaib, M. Fractional-order three-dimensional thin-film nanofluid flow on an inclined rotating disk. Eur. Phys. J. Plus 2018, 133, 500–5011. [Google Scholar] [CrossRef]
- Saleh, H.; Alali, E.; Ebaid, A. Medical applications for the flow of carbon-nanotubes suspended nanofluids in the presence of convective condition using Laplace transform. J. Assoc. Arab Univ. Basic Appl. Sci. 2017, 24, 206–212. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gorji-Bandpy, M.; Ganji, D.D. Numerical investigation of MHD effects on Al2O3-water nanofluid flow and heat transfer in a semi-annulus enclosure using LBM. Energy 2013, 60, 501–510. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Analytical investigation of MHD nanofluid flow in a semi-porous channel. Powder Technol. 2013, 246, 327–336. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Entropy 2015, 6, 542–552. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaed, A. Three-dimensional boundary layer flow of Maxwell nanofluid. Appl. Math. Mech. Engl. Ed. 2015, 36, 747–762. [Google Scholar] [CrossRef]
- Malik, M.Y.; Khan, I.; Hussain, A.; Salahuddin, T. Mixed convection flow of MHD Erying-Powell nanofluid over a stretching sheet. A numerical study. AIP Adv. 2015, 5, 117–118. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Khan, Z.H. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. Eng. 2014, 45, 121–126. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N.; Malvandi, A. Free convective heat and mass transfer of MHD non-Newtonian nanofluids over a cone in the presence of non-uniform heat source/sink. J. Mol. Liq. 2016, 221, 101–115. [Google Scholar] [CrossRef]
- Rokni, H.B.; Alsaad, D.M.; Valipour, P. Electro hydrodynamic nanofluid flow and heat transfer between two plates. J. Mol. Liq. 2016, 216, 583–589. [Google Scholar] [CrossRef]
- Nadeem, S.; Rizwan, U.H.; Khan, Z.H. Numerical solution of non-Newtonian nanofluid flow over a stretching sheet. J. Appl. Nano Sci. 2014, 5, 625–631. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Hayat, A.; Alsaedi, A. MHD flow of Jeffrey nanofluid with convective boundary conditions. Braz. Soc. Mech. Sci. Eng. 2014, 3, 873–883. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, H.M.; Ganji, D.D. Nanofluid flow and heat transfer in a rotating system in the presence of a magnetic field. J. Mol. Liq. 2014, 190, 112–120. [Google Scholar] [CrossRef]
- Mahmoodi, M.; Kandelousi, S.H. Kerosene−alumina nanofluid flow and heat transfer for cooling application. J. Cent. South Univ. 2016, 23, 983–990. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative heat and mass transfer analysis of micropolar nanofluid flow of casson fluid between two rotating parallel plates with effects of hall current. ASME J. Heat Transf. 2019, 141, 022401. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. Three dimensional third grade nanofluid flow in a rotating system between parallel plates with Brownian motion and thermophoresis effects. Results Phys. 2018, 10, 36–45. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018, 9, 1201–1214. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Khan, A.M.; Ali, I.; Islam, S. Effects of hall current on steady three dimensional non Newtonian nanofluid in a rotating frame with Brownian motion and thermophoresis effects. J. Eng. Technol. 2017, 6, 280–296. [Google Scholar]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liq. 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Tassaddiq, A.; Shafee, A.; Khan, I. Application of electric field transfer in an enclosure including double for augmentation of ferrofluid heat moving walls. IEEE Access 2019, 7, 21048–21056. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafi, A.; khan, I.; Itili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Fe3O4-Ethylene glycol nanofluid forced convection inside a porous enclosure in existence of Coulomb force. J. Mol. Liq. 2018, 249, 429–437. [Google Scholar] [CrossRef]
- Pour, M.; Nassab, S. Numerical investigation of forced laminar convection flow of nanofluids over a backward facing step under bleeding condition. J. Mech. 2012, 28, N7–N12. [Google Scholar] [CrossRef]
- Nasir, S.; Islam, S.; Gul, T.; Shah, Z.; Khan, M.A.; Khan, W.; Khan, A.Z.; Khan, S. Three-dimensional rotating flow of MHD single wall carbon nanotubes over a stretching sheet in presence of thermal radiation. Appl. Nano Sci. 2018, 8, 1361–1378. [Google Scholar] [CrossRef]
- Sandeep, N.; Malvandi, A. Enhanced heat transfer in liquid thin film flow of non-Newtonian nanofluids embedded with graphene nanoparticles. Adv. Powder Technol. 2016, 27, 2448–2456. [Google Scholar] [CrossRef]
- Wang, C.Y. Liquid film on an unsteady stretching surface. Q. Appl. Math. 1990, 84, 601–610. [Google Scholar] [CrossRef]
- Usha, R.; Sridharan, R. On the motion of a liquid film on an unsteady stretching surface. ASME Fluids Eng. 1993, 150, 43–48. [Google Scholar] [CrossRef]
- Liu, I.C.; Andersson, I.H. Heat transfer in a liquid film on an unsteady stretching sheet. Int. J. Therm. Sci. 2008, 47, 766–772. [Google Scholar] [CrossRef]
- Aziz, R.C.; Hashim, I.; Alomari, A.K. Thin film flow and heat transfer on an unsteady stretching sheet with internal heating. Meccanica 2011, 46, 349–357. [Google Scholar] [CrossRef]
- Tawade, L.; Abel, M.; Metri, P.G.; Koti, A. Thin film flow and heat transfer over an unsteady stretching sheet with thermal radiation internal heating in presence of external magnetic field. Int. J. Adv. Appl. Math. Mech. 2016, 3, 29–40. [Google Scholar]
- Anderssona, H.I.; Aarseth, J.B.; Dandapatb, B.S. Heat transfer in a liquid film on an unsteady stretching. Int. J. Heat Mass Transf. 2000, 43, 69–74. [Google Scholar] [CrossRef]
- Gul, T.; Haleem, I.; Ullah, I.; Khan, M.A.; Bonyah, E.; Khan, I.; Shuaib, M. The study of the entropy generation in a thin film flow with variable fluid properties past over a stretching sheet. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Gul, T. Scattering of a thin layer over a nonlinear radially extending surface with Magneto hydrodynamic and thermal dissipation. Surf. Rev. Lett. 2019, 26, 1850123. [Google Scholar] [CrossRef]
- Alsagri, A.S.; Nasir, S.; Gul, T.; Islam, S.; Nisar, K.S.; Shah, K.S.; Khan, I. MHD thin film flow and thermal analysis of blood with CNTs nanofluid. Coatings 2019, 9, 175. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq, M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef]
- Ullah, A.; Alzahrani, E.O.; Shah, Z.; Ayaz, M.; Islam, S. Nanofluids thin film flow of reiner-philippoff fluid over an unstable stretching surface with brownian motion and thermophoresis effects. Coatings 2019, 9, 21. [Google Scholar] [CrossRef]
- Khan, A.S.; Nie, Y.; Shah, Z. Impact of thermal radiation and heat source/sink on MHD time-dependent thin-film flow of Oldroyed-B, Maxwell, and Jeffry Fluids over a stretching surface. Processes 2019, 7, 191. [Google Scholar] [CrossRef]
- Chen, C.H. Heat transfer in a power-law liquid film over a unsteady stretching sheet. J. Heat Mass Transf. 2003, 39, 791–796. [Google Scholar] [CrossRef]
- Chen, C.H. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J. Non-Newton. Fluid Mech. 2006, 135, 128–135. [Google Scholar] [CrossRef]
- Wang, C.; Pop, L. Analysis of the flow of a power-law liquid film on an unsteady stretching surface by means of homotopy analysis method. J. Non-Newton. Fluid Mech. 2006, 138, 161–172. [Google Scholar] [CrossRef]
- Mahmoud, M.A.A. On flow and heat transfer in a thin liquid film over an unsteady stretching sheet with variable fluid properties and radiation. Open Sci. J. Math. Appl. 2015, 3, 14–18. [Google Scholar]
- Hatami, M.; Jing, D.; Majeed, A.Y. Three-dimensional analysis of condensation nanofluid film on an inclined rotating disk by efficient analytical methods. Arab. J. Basic Appl. Sci. 2018, 25, 28–37. [Google Scholar] [CrossRef][Green Version]
- Jawad, M.; Shah, Z.; Islam, S.; Bonyah, E.; Khan, Z.A. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018, 11, 115014. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Majdoubi, J.; Tlili, I.; Khan, W.; Khan, I. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry 2019, 11, 207. [Google Scholar] [CrossRef]
- Nasir, S.; Shah, Z.; Islam, S.; Khan, W.; Bonyah, E.; Ayaz, M.; Khan, A. Three dimensional Darcy-Forchheimer radiated flow of single and multiwall carbon nanotubes over a rotating stretchable disk with convective heat generation and absorption. AIP Adv. 2019, 9, 035031. [Google Scholar] [CrossRef]
- Feroz, N.; Shah, Z.; Islam, S.; Alzahrani, E.O.; Khan, W. Entropy generation of carbon nanotubes flow in a rotating channel with hall and ion-slip effect using effective thermal conductivity model. Entropy 2019, 21, 52. [Google Scholar] [CrossRef]
- Alharbi, S.O.; Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S.; Khan, I. Entropy generation in MHD eyring–powell fluid flow over an unsteady oscillatory porous stretching surface under the impact of thermal radiation and heat source/sink. Appl. Sci. 2018, 8, 2588. [Google Scholar] [CrossRef]
- Nasir, S.; Shah, Z.; Islam, S.; Khan, W.; Khan, S.N. Radiative flow of magneto hydrodynamics single-walled carbon nanotube over a convectively heated stretchable rotating disk with velocity slip effect. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Khan, A.S.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-dimensional nanofluid flow with heat and mass transfer analysis over a linear stretching surface with convective boundary conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).