Abstract
This article investigates the unsteady flow and heat transfer analyses of a viscous-based nanofluid over a moving surface emerging from a moving slot. This new form of boundary layer flow resembles with the boundary layer flow over a stretching/shrinking surface depending on the motion of the moving slot. The governing partial differential equations are transformed to correct similar form using the Blasius–Rayleigh–Stokes variable. The transformed equations are solved numerically. Existence of dual solutions is observed for a certain range of moving slot parameter. The range of dual solution is strongly influenced by Brownian and thermophoretic diffusion of nanoparticles.
1. Introduction
The mechanism of drag and heat loss reduction [1] has been the focus of intensive analysis due to its application in the prevention of loss of mechanical energy. Drag and heat loss reduction may create energy savings, processing time reduction, enhancement in thermal rating, and make equipment more durable. Several well-known methods have been proposed by researchers to reduce the drag and heat loss in physical systems out of them utilization of stretching/shrinking surfaces [2] and enhancing the thermal conductivity of the involved fluid are famous [3].
Nanofluids, an achievement of researchers and scientists of the developing world of nanotechnology, exploit the thermal conductivity of solids to enhance the thermal conductivity of a fluid by adding nano-sized solid particles. Materials commonly used for nanoparticles include oxides such as alumina, silica, titania and copper oxide, and metals such as copper and gold. Carbon nanotubes and diamond nanoparticles have also been used to realize nanofluids. Nanoparticles vary from 1 to 100 nm in diameter. Thermal conductivity can be increased up to two times by adding small amount of nanoparticles. Popular base fluids include water and organic fluids such as ethanol and ethylene glycol. The volumetric fraction of the nanoparticles is usually below 5%.
A wide range of nanofluids exist in nature, like blood, which is a complex biological compound, made up of different nanoparticles that perform various functions at molecular level. A number of natural processes occurring in atmosphere and biosphere have wide variety of composition of different fluids and nanoparticles. Manufacturing and industrial waste materials are also composed of nanoscale particles and fluids. Various self-assembly processes for nanostructures generate from the addition of nanoparticles in base fluid. Considering the wide-ranging uses of nanofluid in industry and science, and the model of nanofluid presented by Buongiorno [4], many experimentalists and researchers have showed great interest in the study of nanofluids in the last few years [5,6,7,8,9,10,11,12].
Keeping the fact in view that the unsteady flows are more generalized, and the applications of nanofluids and stretching surfaces in drag and heat loss reduction, this article analyzes the unsteady flow of nanofluid over a moving surface. The study of flow over a linearly stretching sheet was initiated by Crane [13]. He derived the analytical solution of two-dimensional momentum equations. This notable work of Crane [13] has been studied by many researchers in many directions. Some recent works on the topic of stretching/shrinking surfaces are References [14,15,16,17,18] and the references given therein.
In 1997, Todd [19] introduced a new family of unsteady boundary layer flow over a moving surface emerging from a moving slot. He proposed a new set of transformations containing the Blasius–Rayleigh–Stoke variable to write the governing unsteady partial differential equations in similar form. Fang et al. [20] conducted the heat-transfer analysis for this boundary layer flow. In this article, we carry out the numerical analysis of unsteady flow of nanofluid past a movable surface emerging from a moving slot by converting the governing coupled unsteady partial differential equations into similar form using the transformation involving the Blasius–Rayleigh–Stoke variable. The results are presented graphically and the effects of nanoparticles on skin friction, Nusselt number and Sherwood number are discussed in detail. Dual solutions are observed for a specific range of moving slot parameter and are found to be altered due to the presence of nanoparticles. Furthermore, the numerical data is used to write the correlation expressions for certain important flow quantities by performing linear regression. Correlation expressions enable the readers to obtain the values of numerical results for different values of involved parameters from analytical expressions.
2. Mathematical Formulation
Consider the unsteady two-dimensional flow and heat transfer of an incompressible viscous-based nanofluid over a heated moving semi-infinite plate. The surface is emerging out along the x-axis from a moving slot (see Figure 1 for geometry of the problem). At time , the fluid is at rest. The governing boundary layer [21] equations are given as:
where and are the velocity components in and directions. is the fluid temperature, is the nanoparticles volume fraction, is the kinematic viscosity, is the thermal diffusivity of the fluid, is the ratio of heat capacities of the nanoparticles and base fluid , and are the Brownian and thermophoretic diffusion coefficients respectively. For water nanofluids at room temperature with nanoparticles of 1–100 nm diameters, the Brownian diffusion coefficient ranges from 4 × 10−10 to 4 × 10−12 m2/s. For alumina/water and copper/water is 3.1 and 3.4 MJ/m3 respectively. The thermophoretic diffusion is equal to 6 × 10−5 for aluminum/water nanofluid and 6 × 10−6 for copper/water nanofluid.
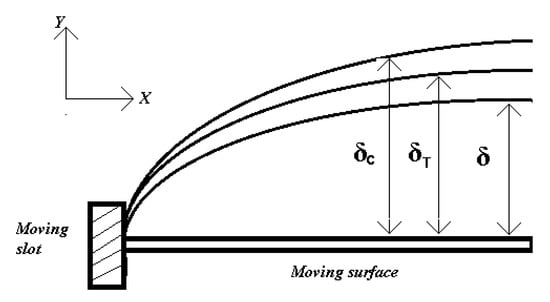
Figure 1.
Systematic diagram of the problem. δ, δc, δT represent the thicknesses of momentum, thermal and nanoparticles concentration boundary layers respectively.
The corresponding boundary conditions are:
Since the unsteady flow is a generalized case of steady flow, Todd [19] generalized the Blasius and Rayleigh–Stokes variables to get similar equations for the boundary layer flow of viscous fluid over a moving surface, termed as the Blasius–Rayleigh–Stokes variable:
This variable depicts that the slot at Y = 0 is moving with a constant speed . To obtain similarity solutions for the system of Equations (1)–(5), we introduce the following similarity variables
in the governing equations to get the following ordinary differential equations:
subject to boundary conditions:
where prime represents the differentiation with respect to variable . Pr is Prandtl number, is thermophoresis diffusion parameter, is Brownian diffusion parameter and is Lewis number given by the following expressions:
The range of the parameters of interest, namely thermophoresis diffusion parameter and Brownian diffusion parameter is given as: and .
3. Results and Discussions
In this special case of unsteady flow, the slot is moving with constant speed . For , the surface velocity is zero as in the case of Sakiadis flow [22]. For , the slot is moving with the constant speed in the opposite direction of stretching surface and the situation is termed as leading-edge accretion. For , the direction of slot motion is same as stretching sheet and the situation is termed as leading-edge ablation. As , the speed of slot approaches infinity in opposite direction to the stretching surface, which correspond to the Rayleigh starting-plate problem. The analytical solution for this case has been obtained using the perturbation method (see Appendix A). Since the exact analytical solution of the system (8)–(11) is not available for general α, we adopt the numerical method for the solution. In Table 1, the comparison of numerical results of skin friction with results of Fang [20] is tabulated. In Table 2, the comparison of the analytical result for is given with the numerical solution. Table 1 and Table 2 establish the reliability of our results.

Table 1.
Comparison of Fang [20] and Present study for values of different moving slot parameters.

Table 2.
Comparison of analytical and numerical solutions for Nusselt and Sherwood number for .
The numerical solution domain of , for the skin friction and Nusselt number mentioned by Fang [20] also hold for Sherwood number. In this study, we focus on the effects of nanoparticles on the heat transfer and behavior of nanoparticles concentration for the surface accretion and ablation.
Figure 2 demonstrates numerical solutions of velocity profile for various values of slot moving constant ranging between . In Figure 3 the dual solution for the velocity profile is plotted for . The thickness of boundary layer is much greater for lower solution branch as compared to upper solution branch.
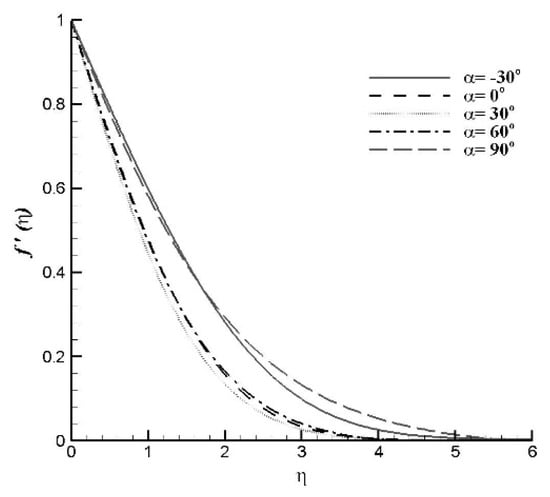
Figure 2.
Velocity profiles for varying slot moving parameter .
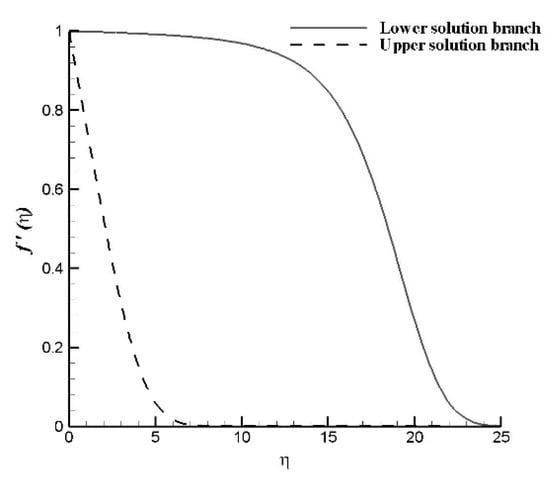
Figure 3.
Profiles of velocity for different branches at
Figure 4 represents the dual solution for a fixed value of moving slot parameter , with two distinct values of Prandtl number. For the above-mentioned values of parameters, both solutions show maximum temperature gradient which can be viewed in the region away from the wall. The change of heat transfer at the wall is less for lower solution as compared to the upper solution. The thermal layer thickness is greater for lower solution as compare to upper solution branch.
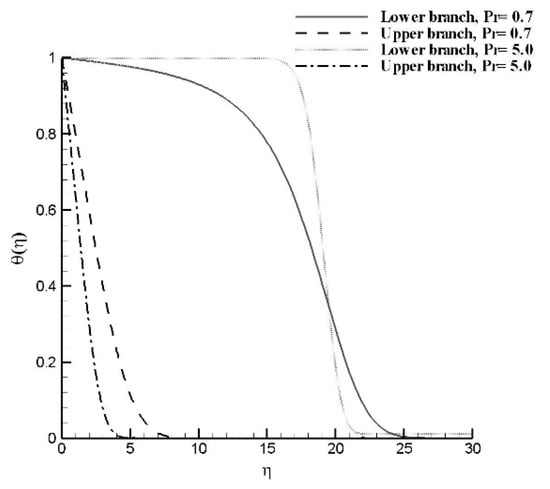
Figure 4.
Temperature and its flux profiles for several branches at for varying with and .
Figure 5 and Figure 6 illustrate the numerical solution domain of reduced Nusselt number as a function of for different values of Brownian and thermophoretic diffusion parameters, and respectively. For Nusselt number, the correlation expression in the form of and has also been written by applying the linear regression on the set of 2401 numerical values. The values of coefficients and constant of the correlation expression in the form
for and is given in Table 3 with maximum percentage error for different Prandtl number and moving slot parameter.
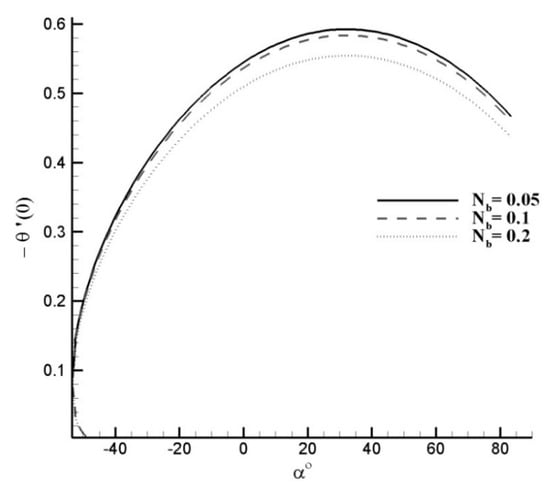
Figure 5.
Effects of slot moving parameter α on reduced Nusselt number for varying Nb with Pr = Le = 1.0 and Nt = 0.1.
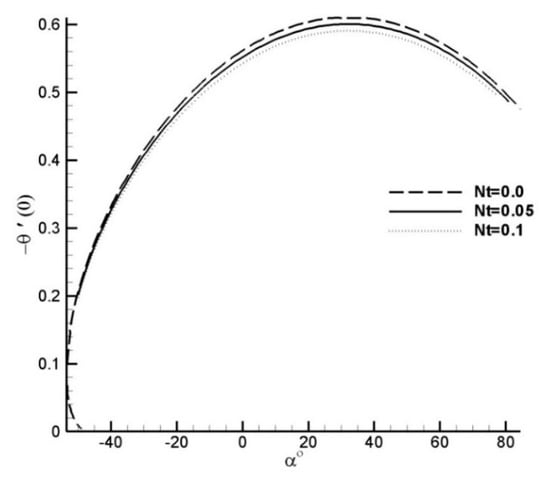
Figure 6.
Effects of slot moving parameter α on reduced Nusselt number for varying Nt with Pr = Le = 1.0 and Nb = 0.1.

Table 3.
Correlation expression for reduced Nusselt number and maximum percentage error defined for varying Prandtl number and moving slot parameter considering values of Brownian and thermophoresis diffusion parameters in the interval (0.01, 0.5).
It is observed that the Nusselt number decreases with an increase in parameters and , since higher temperatures correspond to higher Brownian and thermophoretic diffusion which resultantly reduces the surface heat flux. The same observation can be made from the correlation expressions since the coefficients of and are negative for all value of Pr and α. Furthermore, it is seen that dual solutions exist for a certain interval of slot moving parameter and that interval can be viewed in Figure 5 and Figure 6. The important observation is that the range of reduces dramatically with an increase of and the duality of solution vanishes for . For this reason, the correlation expression for is derived for . The variation of has no effect on the duality of the solution.
For a fixed value of moving slot parameter , Figure 7 and Figure 8 show the dual solution for the variation of and . The thickness of concentration boundary layer is greater for the smaller solution branch. As the value of increases, the concentration boundary layers become thinner for upper as well as for lower solution domains. The concentration thickness of boundary layer is less for the lower solution branch. As the value of increases, the concentration boundary layers become thicker for upper and lower solution domains. In Figure 9, Figure 10 and Figure 11, the effects of Lewis number, thermophoretic diffusion and Brownian diffusion on the nanoparticles concentration flux at the surface are plotted. The Sherwood number is plotted against the moving slot parameter α. Dual solution for Sherwood number is observed in the interval (−53°, −49.5°). Figure depicts that Sherwood number is growing function of α in the interval (−49.5°, 30°), and decreasing function in the interval (30°, αU). As Le increases, i.e., the dominancy of viscous diffusion increases over the Brownian diffusion, the mass flux at the surface increases. Similar effects of Brownian diffusion and opposite effects of thermophoretic diffusion on Sherwood number are observed. In dual solution range, the effects of thermophoretic and Brownian diffusions on Sherwood number are found negligible.
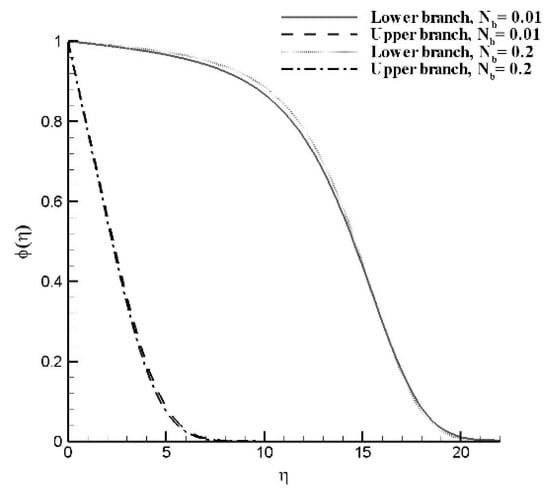
Figure 7.
Dual solutions of nanoparticles concentration profile for and varying , with , .
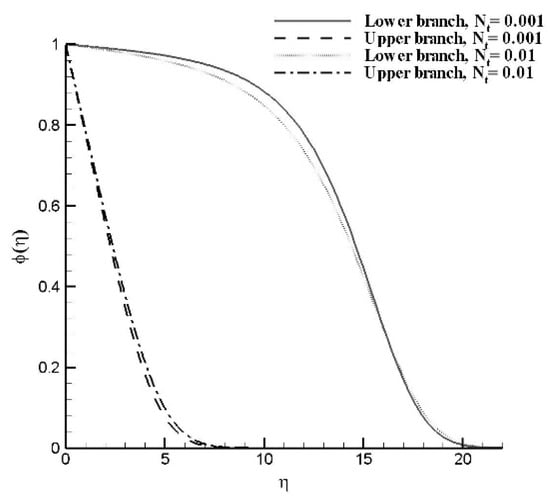
Figure 8.
Dual solutions of nanoparticles concentration profile for and varying , with , .
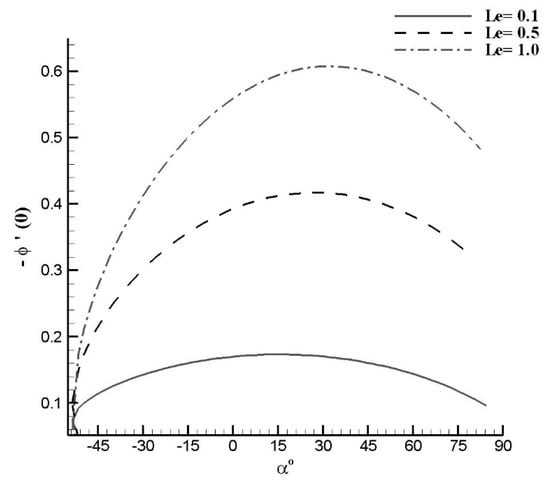
Figure 9.
Effects of slot moving parameter α on reduced Sherwood number for varying Le with Pr = 1.0, Nb = 0.05, Nt = 0.001.
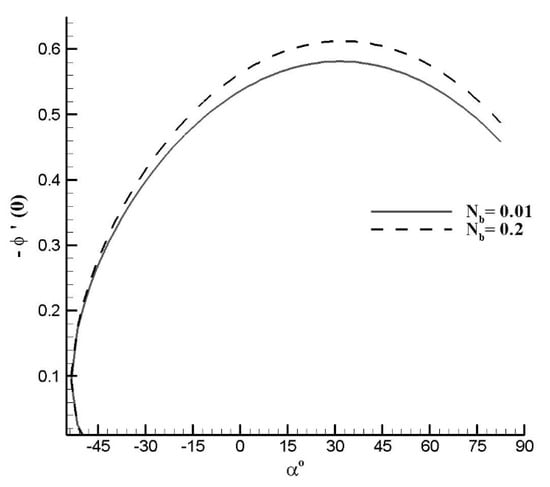
Figure 10.
Effects of slot moving parameter α on reduced Sherwood number for varying Nb with Pr = Le = 1.0, Nt = 0.001.
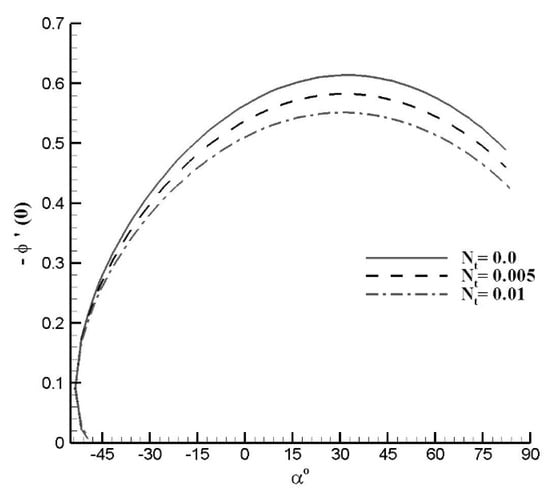
Figure 11.
Effects of slot moving parameter α on reduced Sherwood number for varying Nt with Pr = Le = 1.0, Nb = 0.05.
4. Conclusions
In this work, the unsteady flow and heat transfer of a viscous-based nanofluid over a moving surface emerging from a moving slot has been considered. The effects of involved parameters on the temperature and concentration profiles are illustrated graphically. Furthermore, the variation of reduced Nusselt and Sherwood numbers with the involved parameters; namely Lewis number, Brownian motion parameter and thermophoretic diffusion parameter; are presented graphically.
The obtained results are concluded as follows:
- With the increase in the value of Brownian diffusion parameter , the temperature enhances while the nanoparticles volume fraction decreases.
- By increasing the thermophoretic diffusion parameter , both temperature and nanoparticles concentration are increased.
- Concentration of nanoparticles reduces with the enhancement of Lewis number .
- Dual solutions exist for both thermal and concentration boundary layers. The mass flux rate attains the maximum value of slot moving parameter , as the Lewis number is increased.
- Heat flux at the surface reduces with the increase of and in the upper solution branch. The reduced Sherwood number is enhanced when is increased, whereas it reduces with increasing .
Author Contributions
Conceptualization and Supervision, A.A.; Methodology, S.M.; Writing—Original Draft Preparation, D.L., S.M. and A.A.; Writing—Review and Editing, U.F. and A.A.; Funding Acquisition, D.L. and U.F.
Funding
This research was funded by China Postdoctoral Science foundation (No. 189607).
Acknowledgments
Adeel Ahmad would like to acknowledge the support by the CIIT Research Grant Program of COMSATS University Islamabad, Pakistan (No. 16-68/CRGP/CIIT/ISB/17/71141).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclatures
| U | Velocity component in X direction |
| V | Velocity component in Y direction |
| Uw | Plate velocity |
| ψ | Stream function |
| T | Temperature |
| T∞ | Ambient temperature |
| TW | Wall temperature |
| C | Nanoparticles concentration |
| C∞ | Ambient nanoparticles concentration |
| CW | Wall nanoparticles concentration |
| η | Similarity variable |
| α | Moving slot parameter |
| DB | Brownian diffusion coefficient |
| DT | Thermophoretic diffusion coefficient |
| Le | Lewis number |
| Nb | Brownian diffusion parameter |
| Nt | Thermophoretic diffusion parameter |
| Pr | Prandtl number |
| φ | Nondimensional nanoparticles concentration |
| θ | Nondimensional temperature |
| ν | Kinematic viscosity |
| σ | Thermal diffusivity |
| ε | Ratio of heat capacities of the nanoparticles |
| Heat capacity of fluid | |
| Heat capacity of nanoparticles |
Appendix A
For , the governing equations reduce to
We derive the analytical expressions for the skin friction, Nusselt number and Sherwood number subject to the boundary conditions in Equation (A1). The exact solution of Equation (A1) is:
It is noted that the magnitude of thermophoretic and Brownian diffusion parameters for nanoparticles is very small [1,9], therefore we consider and of . We expand and in small parameter and write
By substituting the expressions in Equation (A5) in Equations (A2) and (A3), the leading order boundary value problem is given by
where and are constants of O(1) such that and . The solution of above boundary value problem can be written as
The first order system can be written as
with the boundary conditions
For the above boundary value problem, the exact solution is given by
where erf is the error function and erfi is the imaginary error function.
References
- Singh, R.P. “Drag Reduction”. In Encyclopedia of Polymer Science and Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Zhao, H.; Wu, J.Z.; Luo, J.S. Turbulent drag reduction by traveling wave of flexible wall. Fluid Dyn. Res. 2004, 34, 175–198. [Google Scholar] [CrossRef]
- Gyr, A.; Bewersdorff, H.W. Drag Reduction of Turbulent Flow by Additives; Academic Publishers: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Das, K. Nanofluid flow over a shrinking sheet with surface slip. Microfluid. Nanofluid. 2014, 16, 391–401. [Google Scholar] [CrossRef]
- Bashirnezhad, K.; Bazri, S.; Safaei, M.R. Viscosity of nanofluids: A review of recent experimental studies. Int. Commun. Heat Mass Transf. 2016, 73, 114–123. [Google Scholar] [CrossRef]
- Ahmad, A. Flow of ReinerPhilippoff based nano-fluid past a stretching sheet. J. Mol. Liquids 2016, 219, 643–646. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Groşanc, T.; Pop, I. Steady-state free convection in right-angle porous trapezoidal cavity filled by a nanofluid: Buongiorno’s mathematical model. Eur. J. Mech. B/Fluids 2015, 53, 241–250. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I. Free convection in a porous horizontal cylindrical annulus with a nanofluid using Buongiorno’s model. Comput. Fluids 2015, 118, 182–190. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Cimpean, D.S.; Pop, I. Free convection in a partially heated wavy porous cavity filled with a nanofluid under the effects of Brownian diffusion and thermophoresis. Appl. Therm. Eng. 2017, 113, 413–418. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Wakif, A.; Hussanan, A. Second law analysis of dissipative nanofluid flow over a curved surface in the presence of Lorentz force: Utilization of the Chebyshev–Gauss–Lobatto spectral method. Nanomaterials 2019, 9, 195. [Google Scholar] [CrossRef] [PubMed]
- Crane, L.J. Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Magyari, E.; Keller, B. Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface. J. Phys. D Appl. Phys. 1999, 32, 577. [Google Scholar] [CrossRef]
- Liao, S. A new branch of solutions of boundary-layer flows over an impermeable stretched plate. Int. J. Heat Mass Transf. 2005, 48, 2529–2539. [Google Scholar] [CrossRef]
- Fang, T. Flow over a stretchable disk. Phys. Fluids 2007, 19, 128105. [Google Scholar] [CrossRef]
- Ramesh, G.K.; Gireesha, B.J.; Bagewadi, C.S. Heat transfer in MHD dusty boundary layer flow over an inclined stretching sheet with non-uniform heat source/sink. Adv. Math. Phys. 2012, 2012, 657805. [Google Scholar] [CrossRef]
- Imran, S.M.; Asghar, S.; Mushtaq, M. Mixed Convection Flow over an Unsteady Stretching Surface in a Porous Medium with Heat Source. Math. Probl. Eng. 2012, 2012, 485418. [Google Scholar] [CrossRef]
- Todd, L. A family of laminar boundary layers along a semi-infinite flat plate. Fluid Dyn. Res. 1997, 19, 235–249. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J.; Yao, S. A new family of unsteady boundary layers over a stretching surface. Appl. Math. Comput. 2010, 217, 3747–3755. [Google Scholar] [CrossRef]
- Pritchard, P.J.; Mitchell, J.W. Fox and McDonald’s Introduction to Fluid Mechanics, 9th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Sakiadis, B.C. Boundary layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).