Passive Vibration Reduction Analysis of the Mistuned Blisk Deposited Hard Coating Using Modified Reduced-Order Model
Abstract
1. Introduction
2. Theoretical Investigation of the HCM Blisk
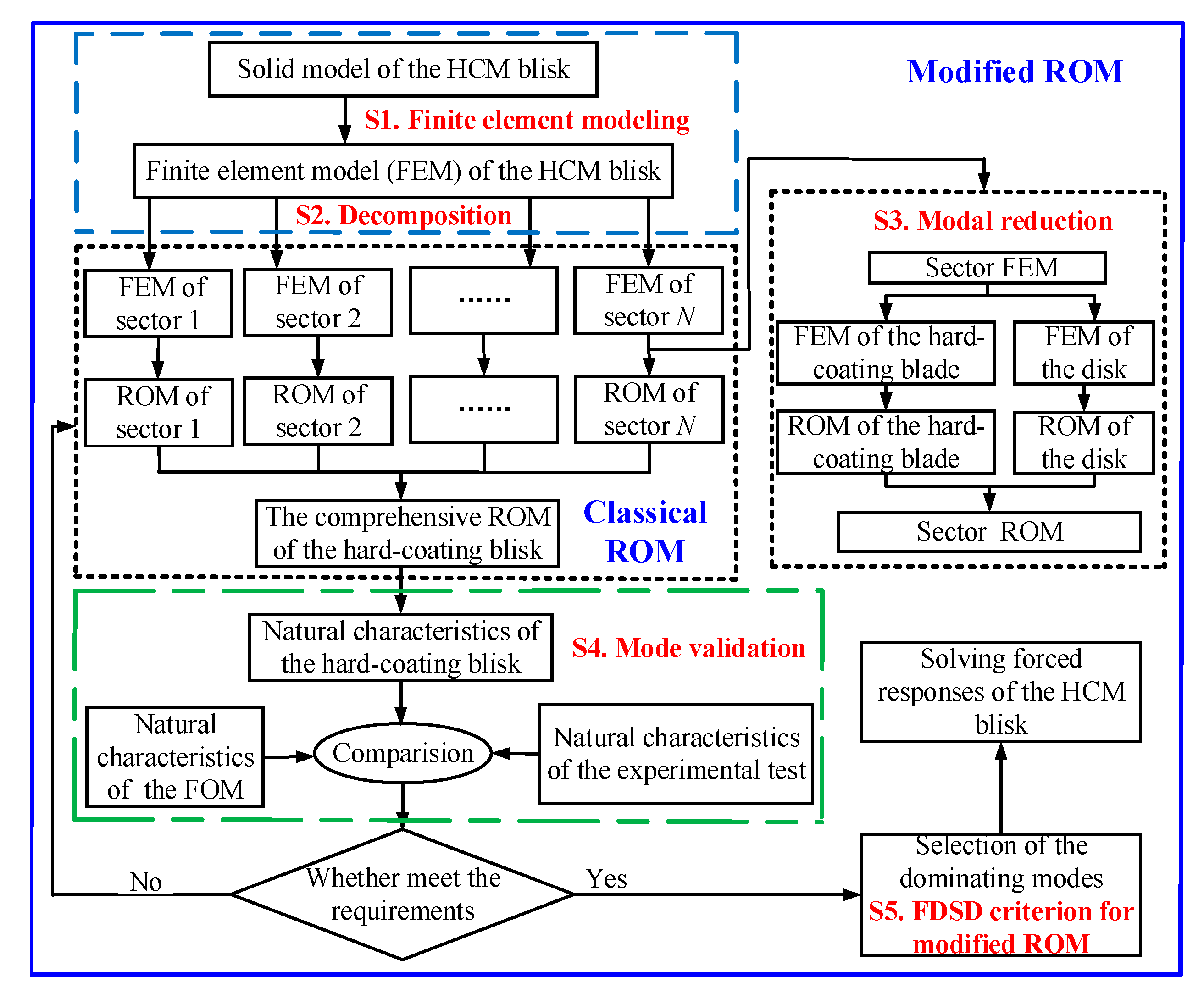
2.1. The Classical ROM of the HCM Blisk
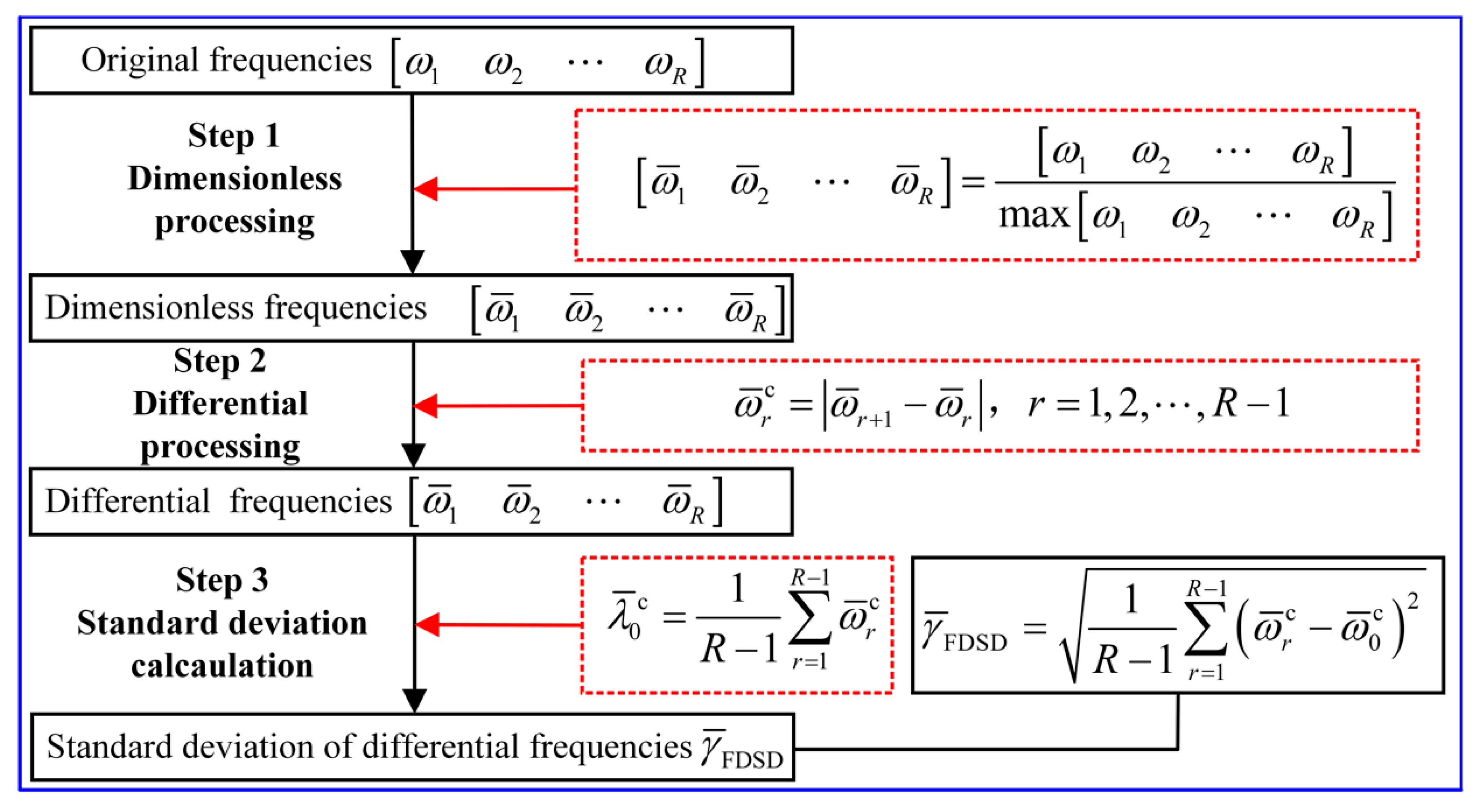
2.2. The Modified ROM of the HCM Blisk
3. Benchmark
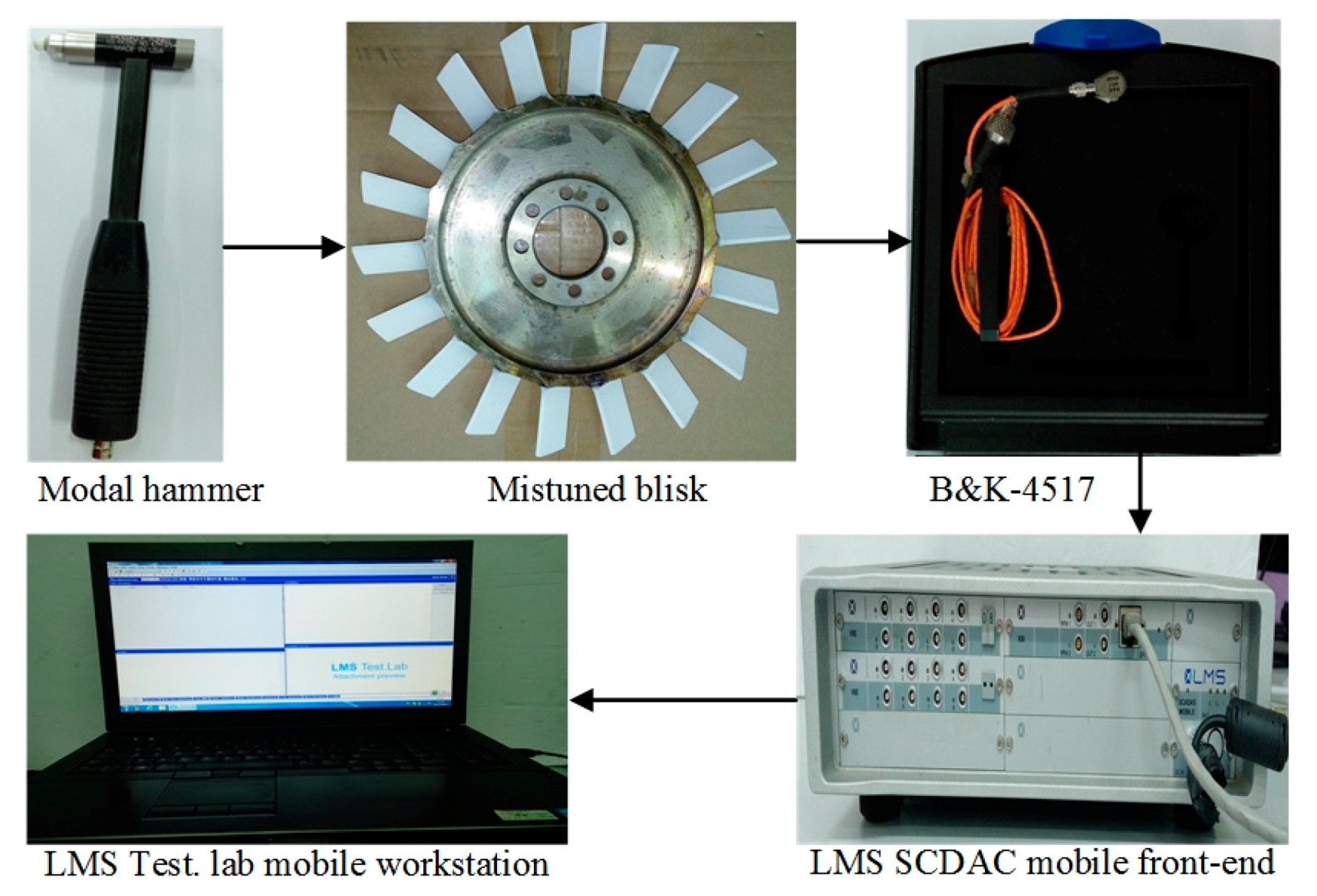
3.1. Research Systems
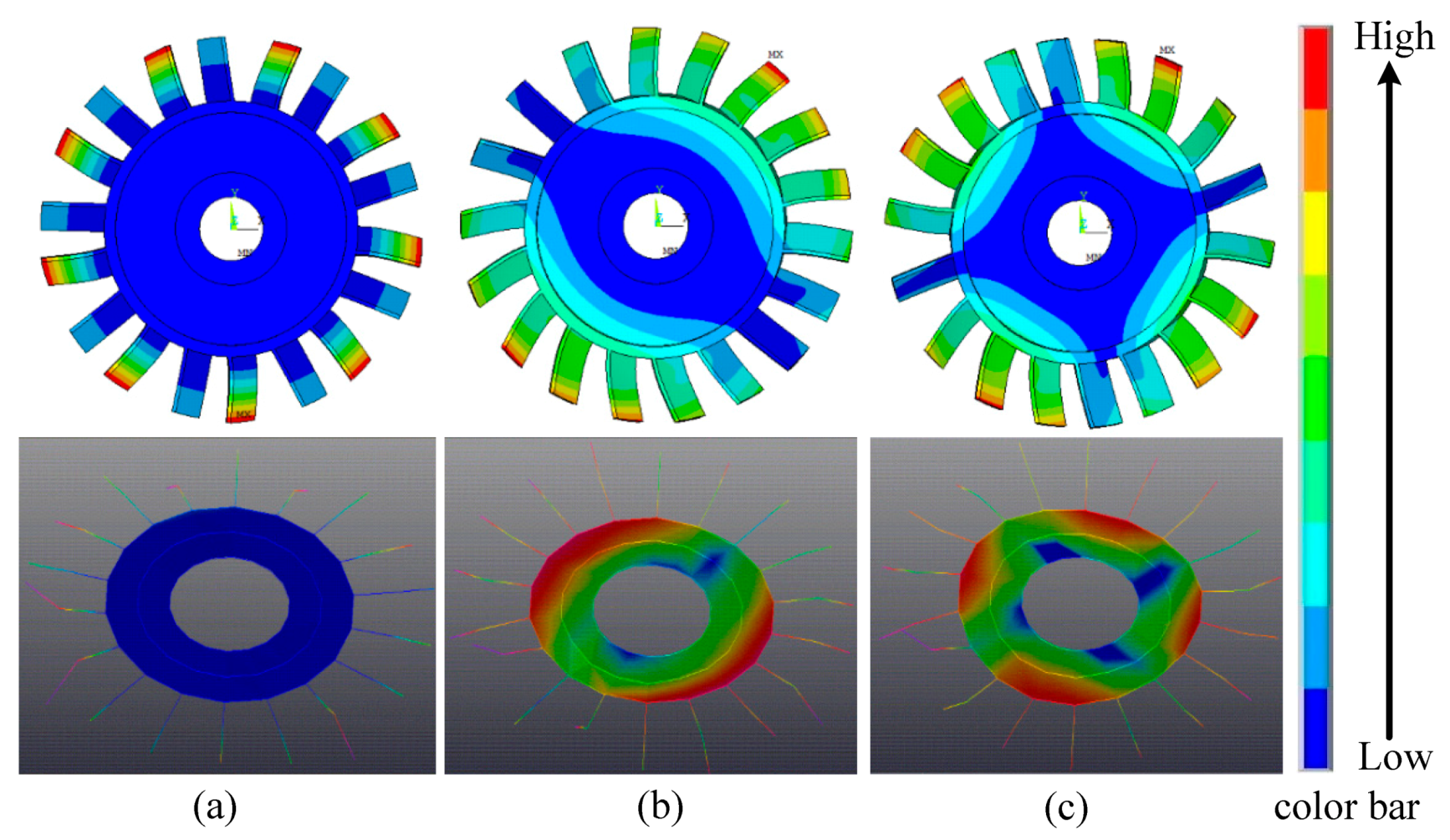
3.2. Mode Validation
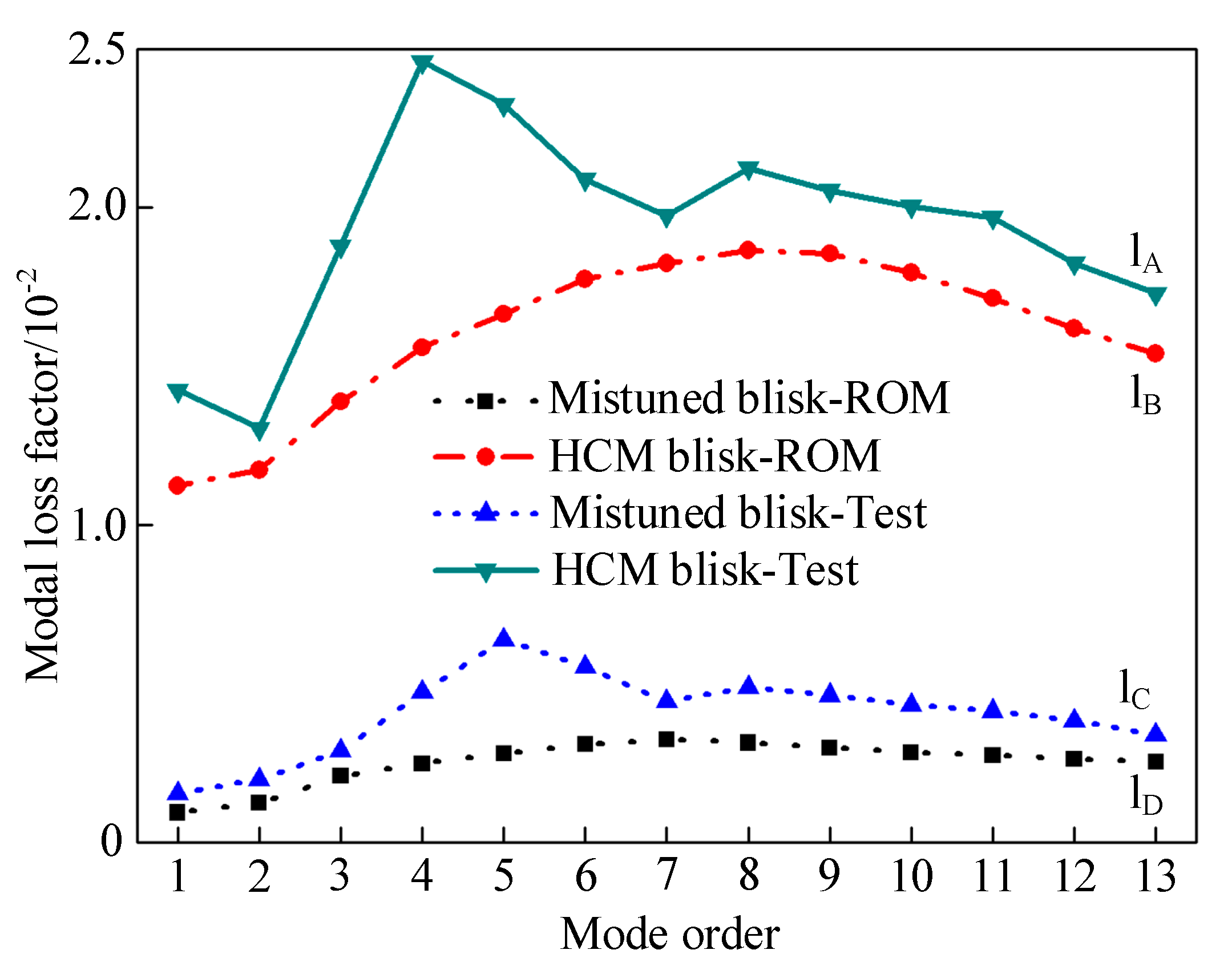
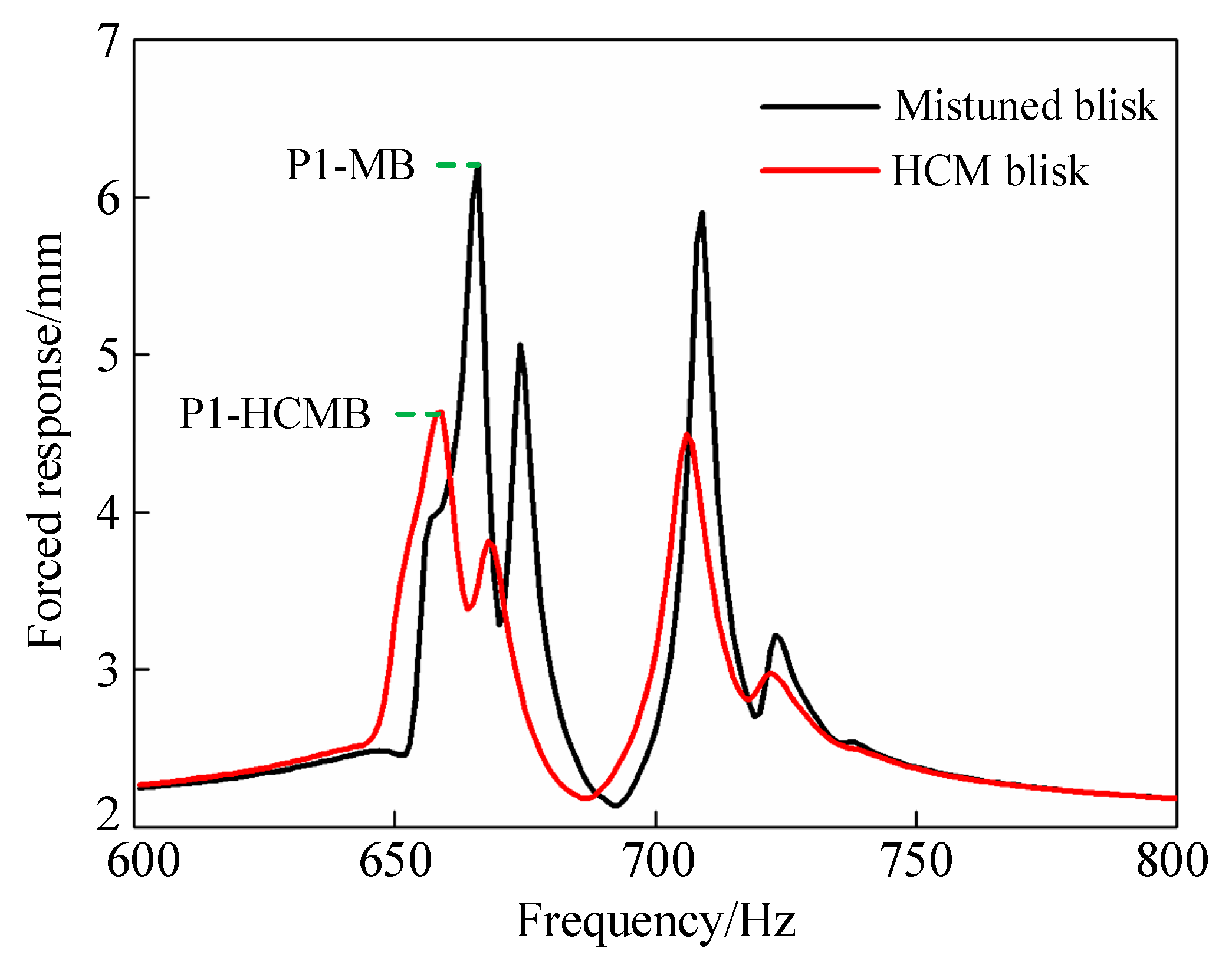
3.3. The Influence of Hard Coating
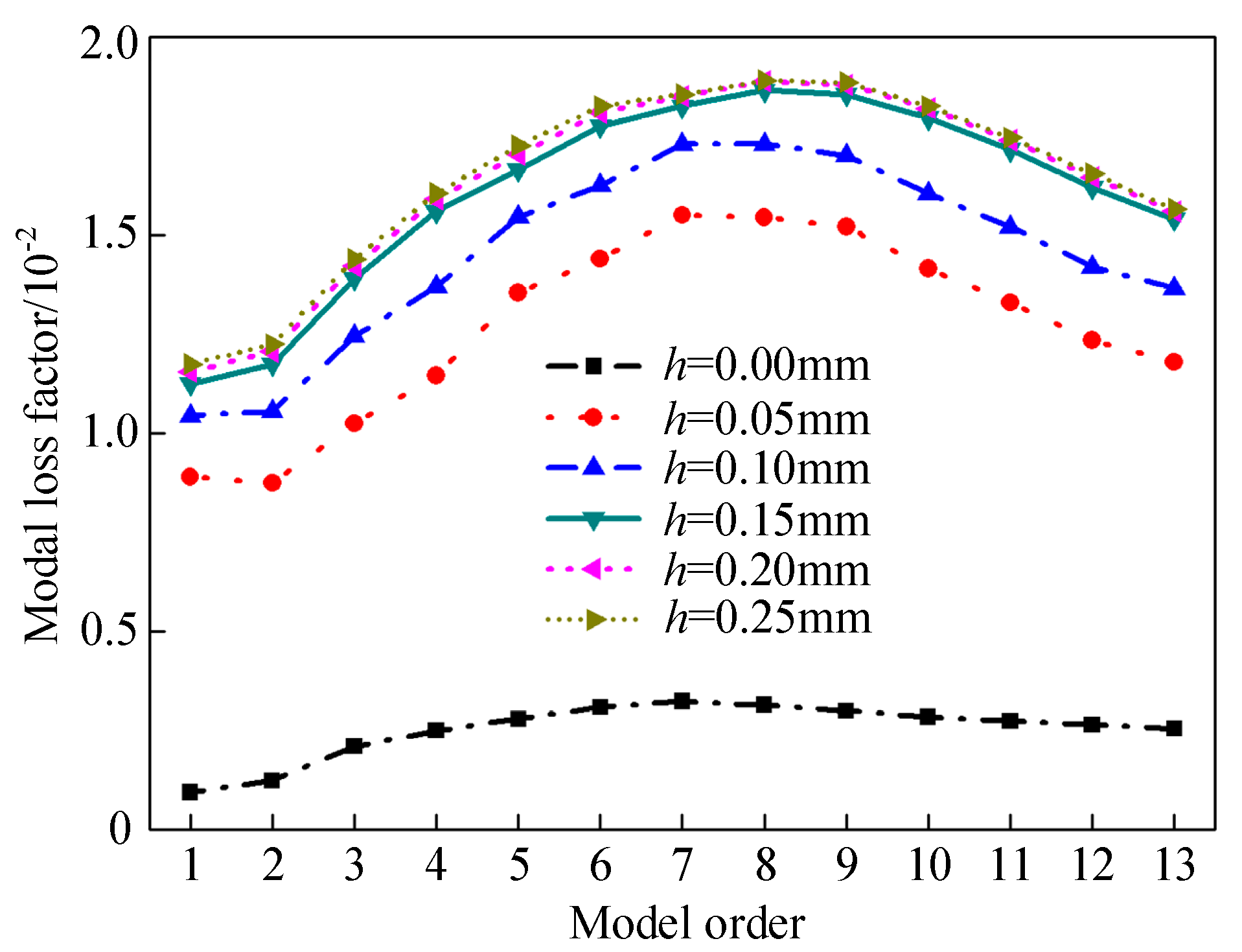
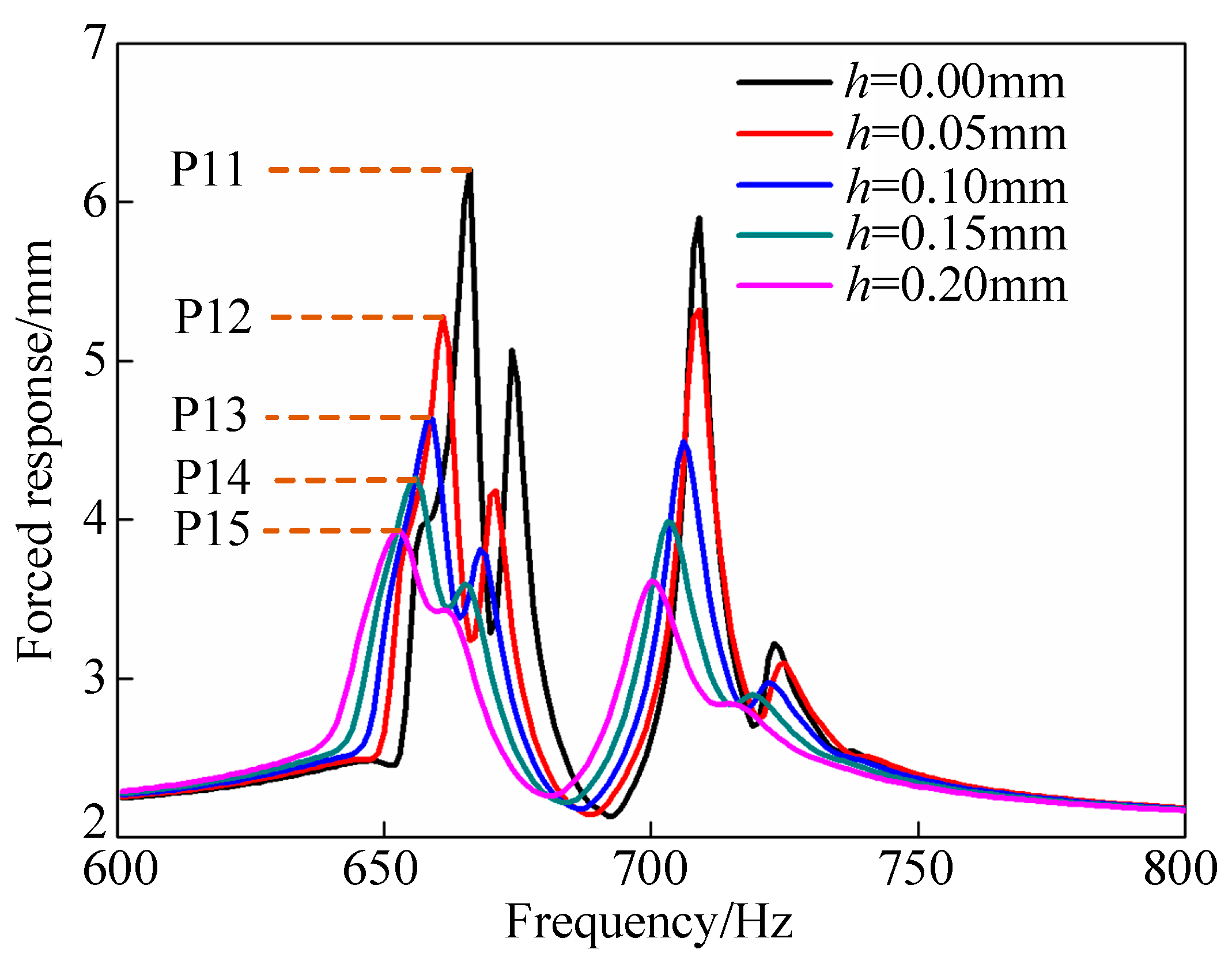
3.4. The Influence of Coating Thickness
4. Conclusions
Supplementary Materials
Supplementary File 1Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bußmann, M.; Bayer, E. Market-oriented blisk manufacturing: A challenge for production engineering. In Proceedings of the First European Air and Space Conference (CEAS), Berlin, Germany, 10–13 September 2007. [Google Scholar]
- Younossi, O.; Arena, M.V.; Moore, R.M.; Lorell, M.A.; Mason, J.; Graser, J.C. Military Jet Engine Acquisition: Technology Basics and Cost-Estimating Approach Ology; RAND Corporation: Santa Monica, CA, USA, 2002. [Google Scholar]
- Duan, Y.; Zang, C.; Petrov, E.P. Forced response analysis of high-mode vibrations for mistuned bladed disks with effective reduced-order models. J. Eng. Gas Turbines Power 2016, 138, 112502. [Google Scholar] [CrossRef]
- Sinha, A. Reduced-order model of a bladed rotor with geometric mistuning. J. Turbomach. 2009, 131, 031007. [Google Scholar] [CrossRef]
- Klauke, T.; Kuhhorn, A.; Beirow, B.; Golze, M. Numerical Investigations of localized vibrations of mistuned blade integrated disks (blisks). J. Turbomach. 2009, 131, 031002. [Google Scholar] [CrossRef]
- Castanier, M.P.; Pierre, C. Modeling and analysis of mistuned bladed disk vibration: Current status and emerging directions. J. Propuls. Power 2006, 22, 384–396. [Google Scholar] [CrossRef]
- Zhao, P.F.; Zhang, Q.; Wu, J.; Zhang, D. Experimental study of dynamic characteristics of dry friction damping of turbine blade steel. Adv. Mater. Res. 2013, 690, 1979–1982. [Google Scholar] [CrossRef]
- Li, G.; Zhang, Q.; Zhao, W.; Zhou, Q.; Xie, Y. Dynamic Response Analysis of Blades with Damping Structures of Shroud and Snubber. In Proceedings of the First International Conference on Information Sciences, Machinery, Materials and Energy, Chongqing, China, 11–13 April 2015; Atlantis Press: Paris, France, 2015. [Google Scholar]
- He, B.; Ouyang, H.; Ren, X.; He, S. Dynamic response of a simplified turbine blade model with under-platform dry friction dampers considering normal load variation. Appl. Sci. 2017, 7, 228. [Google Scholar] [CrossRef]
- Pesaresi, L.; Salles, L.; Jones, A.; Green, J.S.; Schwingshackl, C.W. Modelling the nonlinear behavior of an under-platform damper test rig for turbine applications. Mech. Syst. Signal Process. 2017, 85, 662–679. [Google Scholar] [CrossRef]
- Laxalde, D.; Thouverez, F.; Sinou, J.J. Forced response analysis of blisks with friction ring dampers. J. Vib. Acoust. 2010, 132, 011013. [Google Scholar] [CrossRef]
- Baek, S.; Epureanu, B.I. Reduced-order modeling of bladed disks with friction ring dampers. J. Vib. Acoust. 2017, 139, 061011. [Google Scholar] [CrossRef]
- Ren, Z.; Atalla, N.; Ghinet, S. Optimization Based identification of the dynamic properties of linearly viscoelastic materials using vibrating beam technique. J. Vib. Acoust. 2011, 133, 041012. [Google Scholar] [CrossRef]
- Han, B.; Zhang, M.; Qi, C.; Cui, N.; Wang, Y. Characterization and friction-reduction performances of composite coating produced by laser cladding and ion sulfurizing. Mater. Lett. 2015, 150, 35–38. [Google Scholar] [CrossRef]
- Wei, S.; Pei, X.; Shi, B.; Shao, T.; Li, T.; Li, Y.; Xie, Y. Wear resistance and anti-friction of expansion cone with hard coating. Pet. Explor. Dev. 2016, 43, 326–331. [Google Scholar]
- Morita, T.; Inoue, K.; Ding, X.; Usui, Y.; Ikenaga, M. Effect of hybrid surface treatment composed of nitriding and DLC coating on friction-wear properties and fatigue strength of alloy steel. Mater. Sci. Eng. A 2016, 661, 105–114. [Google Scholar] [CrossRef]
- Stathopoulos, V.; Sadykov, V.; Pavlova, S.; Bespalko, Y.; Fedorova, Y.; Bobrova, L.; Salanov, A.; Ishchenko, A.; Stoyanovsky, V.; Larina, T.; et al. Design of functionally graded multilayer thermal barrier coatings for gas turbine application. Surf. Coat. Technol. 2016, 295, 20–28. [Google Scholar] [CrossRef]
- Gong, X.; Chen, R.; Wang, Q.; Wang, Y.; Zhang, N.; Zhang, Z.; Fu, H. Cyclic oxidation behavior and oxide scale adhesion of Al/NiCrAlY coating on pure titanium alloy. J. Alloy. Compd. 2017, 729, 679–687. [Google Scholar] [CrossRef]
- Zheng, H.; Li, B.; Tan, Y.; Li, G.; Shu, X.; Peng, P. Derivative effect of laser cladding on interface stability of YSZ@Ni coating on GH4169 alloy: An experimental and theoretical study. Appl. Surf. Sci. 2018, 427, 1105–1113. [Google Scholar] [CrossRef]
- Gao, Y.; Syed, J.A.; Lu, H.; Meng, X. Anti-corrosive performance of electropolymerized phosphomolybdic acid doped PANI coating on 304SS. Appl. Surf. Sci. 2016, 360, 389–397. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, Z.; Gong, Y.; Nie, G. Microstructures and corrosion resistance of Fe-based amorphous/nanocrystalline coating fabricated by laser cladding. J. Alloy. Compd. 2017, 728, 1116–1123. [Google Scholar] [CrossRef]
- Bakhsheshi-Rad, H.; Hamzah, E.; Ismail, A.; Daroonparvar, M.; Yajid, M.; Medraj, M. Preparation and characterization of NiCrAlY/nano-YSZ/PCL composite coatings obtained by combination of atmospheric plasma spraying and dip coating on Mg-Ca alloy. J. Alloy. Compd. 2016, 658, 440–452. [Google Scholar] [CrossRef]
- Torvik, P.J.; Langley, B. Material Properties of Hard Coatings Developed for High Damping. In Proceedings of the 51st AIAA/SAE/A Sub-Structure Joint Propulsion Conference, Orlando, FL, USA, 27–29 July 2015. [Google Scholar]
- Sun, W.; Han, Q.; Qi, F. Optimal design of damping capacities for hard coating thin plate. Adv. Vib. Eng. 2013, 12, 179–192. [Google Scholar]
- Yang, Z.X.; Han, Q.K.; Jin, Z.H.; Qu, T. Solution of natural characteristics of a hard-coating plate based on Lindstedt—Poincaré perturbation method and its valedictions by FEM and measurement. Nonlinear Dyn. 2015, 81, 1207–1218. [Google Scholar] [CrossRef]
- Sun, W.; Liu, Y.; Du, G. Analytical modeling of hard-coating cantilever composite plate considering the material nonlinearity of hard coating. Math. Probl. Eng. 2015, 2015, 1–14. [Google Scholar] [CrossRef]
- Yang, Z.X.; Han, Q.K.; Chen, Y.G.; Jin, Z.H. Nonlinear harmonic response characteristics and experimental investigation of cantilever hard-coating plate. Nonlinear Dyn. 2017, 236, 500–538. [Google Scholar] [CrossRef]
- Sun, W.; Liu, R. Damping optimization of hard-coating thin plate by the modified modal strain energy method. Coatings 2017, 7, 32. [Google Scholar] [CrossRef]
- Sun, W.; Liu, Y. Vibration analysis of hard-coated composite beam considering the strain dependent characteristic of coating material. Acta Mech. Sin. 2016, 32, 731–742. [Google Scholar] [CrossRef]
- Sun, W.; Wang, Z.; Zhu, M.; Du, G. Identifying the mechanical parameters of hard coating with strain dependent characteristic by an inverse method. Shock Vib. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Li, H.; Sun, W.; Zhu, M.; Xue, P. Experimental Study on the influence on vibration characteristics of thin cylindrical shell with hard coating under cantilever boundary condition. Shock Vib. 2017, 2017, 1–23. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, W.; Yang, J. A new finite element formulation for nonlinear vibration analysis of the hard-coating cylindrical shell. Coatings 2017, 7, 70. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, M.; Wang, Z. Free vibration analysis of a hard-coating cantilever cylindrical shell with elastic constraints. Aerosp. Sci. Technol. 2017, 63, 232–244. [Google Scholar] [CrossRef]
- Yen, H.Y. New Analysis and Design Procedures for Ensuring Gas Turbine Blades and Adhesive Bonded Joints Structural Integrity and Durability. Ph.D. Thesis, Aeronautical and Astronautical Engineering. The Ohio State University, Columbus, OH, USA, 2000. [Google Scholar]
- Sun, J.; Kari, L. Coating methods to increase material damping of compressor blades: Measurements and Modeling. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; pp. 1157–1165. [Google Scholar]
- Filippi, S.; Torvik, P.J. A methodology for predicting the response of blades with nonlinear coatings. J. Eng. Gas Turbines Power 2011, 133, 042503. [Google Scholar] [CrossRef]
- Zhou, B.; Thouverez, F.; Lenoir, D. An adaptive control strategy based on passive piezoelectric shunt techniques applied to mistuned bladed disks. J. Comput. Appl. Math. 2013, 246, 289–300. [Google Scholar] [CrossRef]
- Yuan, J.; Allegri, G.; Scarpa, F.; Rajasekaran, R.; Patsias, S. Probabilistic dynamics of mistuned bladed disc systems using subset simulation. J. Sound Vib. 2015, 350, 185–198. [Google Scholar] [CrossRef]
- Yuan, J.; Allegri, G.; Scarpa, F.; Patsias, S.; Rajasekaran, R. A novel hybrid Neumann expansion method for stochastic analysis of mistuned bladed discs. Mech. Syst. Signal Process. 2016, 72, 241–253. [Google Scholar] [CrossRef]
- Yuan, J.; Scarpa, F.; Allegri, G.; Titurus, B.; Patsias, S.; Rajasekaran, R. Efficient computational techniques for mistuning analysis of bladed discs: A review. Mech. Syst. Signal Process. 2017, 87, 71–90. [Google Scholar] [CrossRef]
- Bisegna, P.; Caruso, G. A Continuous model for the dynamical analysis of mistuned bladed rotors. Int. J. Rotating Mach. 2012, 2012, 1–10. [Google Scholar] [CrossRef][Green Version]
- Najafi, A.; Ghazavi, M.-R.; Jafari, A.-A. Stability and hamiltonian hopf bifurcation for a nonlinear symmetric bladed rotor. Nonlinear Dyn. 2014, 78, 1049–1064. [Google Scholar] [CrossRef]
- Rivas-Guerra, A.J.; Mignolet, M.P. Local/Global effects of mistuning on the forced response of bladed disks. J. Eng. Gas Turbines Power 2004, 126, 131–141. [Google Scholar] [CrossRef]
- Hurty, W.C. Dynamic analysis of structural systems using component modes. AIAA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- Craig, R.R.; Bampton, M.C.C.; Craig, J.R.R. Coupling of substructures for dynamic analyses. AIAA J. 1968, 6, 1313–1319. [Google Scholar] [CrossRef]
- Craig, R.R. Structural Dynamics: An Introduction to Computer Methods; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1994. [Google Scholar]
- Irretier, H. Spectral analysis of mistuned bladed disk assemblies by component mode synthesis. Vib. Bl. Disk Assem. 1983, 115–125. [Google Scholar]
- Craig, R.R.; Chang, C.-J. Free-interface methods of substructure coupling for dynamic analysis. AIAA J. 1976, 14, 1633–1635. [Google Scholar] [CrossRef]
- Craig, R.R.; Chang, C.J. Substructure Coupling for Dynamic Analysis and Testing; NASA: Washington, DC, USA, 1977.
- Bladh, R.; Castanier, M.P.; Pierre, C. Component-mode-based reduced order modeling techniques for mistuned bladed disks-part I: Theoretical models. J. Eng. Gas Turbines Power 2001, 123, 89–99. [Google Scholar] [CrossRef]
- Bladh, R.; Castanier, M.P.; Pierre, C. Component-mode-based reduced order modeling techniques for mistuned bladed disks-part II: Application. J. Eng. Gas Turbines Power 2001, 123, 100–108. [Google Scholar] [CrossRef]
- Yang, M.-T.; Griffin, J.H. A reduced order model of mistuning using a subset of nominal system modes. J. Eng. Gas Turbines Power 1999, 123, 893–900. [Google Scholar] [CrossRef]
- Hohl, A.; Wallaschek, J. A method to reduce the energy localization in mistuned bladed disks by application-specific blade pattern arrangement. J. Eng. Gas Turbines Power 2016, 138, 092502. [Google Scholar] [CrossRef]
- Yang, M.-T.; Griffin, J.H. A normalized modal eigenvalue approach for resolving modal interaction. J. Eng. Gas Turbines Power 1997, 119, 647–650. [Google Scholar] [CrossRef]
- Beirow, B.; Giersch, T.; Kühhorn, A.; Nipkau, J. Optimization-aided forced response analysis of a mistuned compressor blisk. J. Eng. Gas Turbines Power 2015, 137, 012504. [Google Scholar] [CrossRef]
- Petrov, E.P.; Sanliturk, K.Y.; Ewins, D.J. A new method for dynamic analysis of mistuned bladed disks based on the exact relationship between tuned and mistuned systems. J. Eng. Gas Turbines Power 2002, 124, 586–597. [Google Scholar] [CrossRef]
- Feiner, D.M.; Griffin, J.H. A fundamental model of mistuning for a single family of modes. J. Turbomach. 2002, 124, 597–605. [Google Scholar] [CrossRef]
- Chan, Y.J.; Ewins, D.J. Prediction of vibration response levels of mistuned integral bladed disks (blisks): Robustness studies. J. Turbomach. 2012, 134, 044501. [Google Scholar] [CrossRef]
- Kaneko, Y.; Nakanishi, R.; Mori, K.; Ohyama, H. Study on Vibration characteristics of mistuned bladed disk (vibration response analysis by reduced model fmm). Trans. Jpn. Soc. Mech. Eng. Ser. C 2013, 7, 328–342. [Google Scholar] [CrossRef][Green Version]
- Yang, M.-T.; Griffin, J.H. A Reduced order approach for the vibration of mistuned bladed disk assemblies. J. Eng. Gas Turbines Power 1997, 119, 161–167. [Google Scholar] [CrossRef]
- Lim, S.-H.; Bladh, R.; Castanier, M.P.; Pierre, C. Compact, generalized component mode mistuning representation for modeling bladed disk vibration. AIAA J. 2007, 45, 2285–2298. [Google Scholar] [CrossRef]
- McGee, O.G.; Fang, C.; El-Aini, Y. A reduced-order meshless energy model for the vibrations of mistuned bladed disks—Part I: Theoretical basis. J. Turbomach. 2013, 135, 061001. [Google Scholar] [CrossRef]
- Fang, C.; McGee, O.G.; El Aini, Y. A reduced-order meshless energy model for the vibrations of mistuned bladed disks—Part II: Finite element benchmark comparisons. J. Turbomach. 2013, 135, 061002. [Google Scholar] [CrossRef]
- Zheng, H.; Tan, X.; Cai, C. Damping analysis of beams covered with multiple PCLD patches. Int. J. Mech. Sci. 2006, 48, 1371–1383. [Google Scholar] [CrossRef]
- Curà, F.; Mura, A.; Scarpa, F. Modal strain energy based methods for the analysis of complex patterned free layer damped plates. J. Vib. Control 2012, 18, 1291–1302. [Google Scholar] [CrossRef]
- Yoon, Y.C.; Kim, K.H.; Lee, S.H. Dynamic particle difference method for the analysis of proportionally damped system and cracked concrete beam. Int. J. Fract. 2017, 203, 237–262. [Google Scholar] [CrossRef]
- Lázaro, M.; Pérez-Aparicio, J.L.; Epstein, M. Computation of eigenvalues in proportionally damped viscoelastic structures based on the fixed-point iteration. Appl. Math. Comput. 2012, 219, 3511–3529. [Google Scholar] [CrossRef][Green Version]
- Ma, F.; Morzfeld, M. A General methodology for decoupling damped linear systems. Procedia Eng. 2011, 14, 2498–2502. [Google Scholar] [CrossRef]
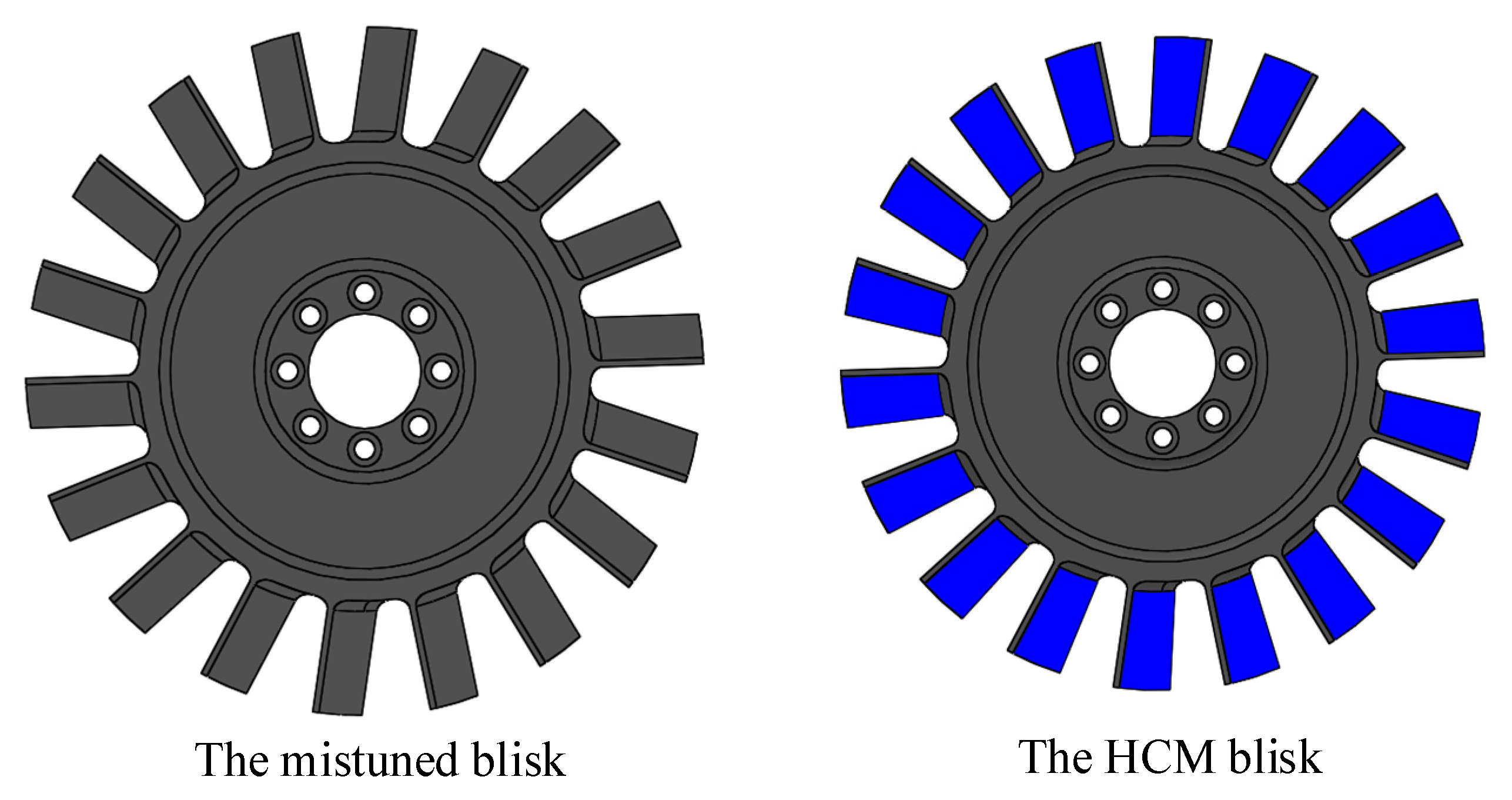
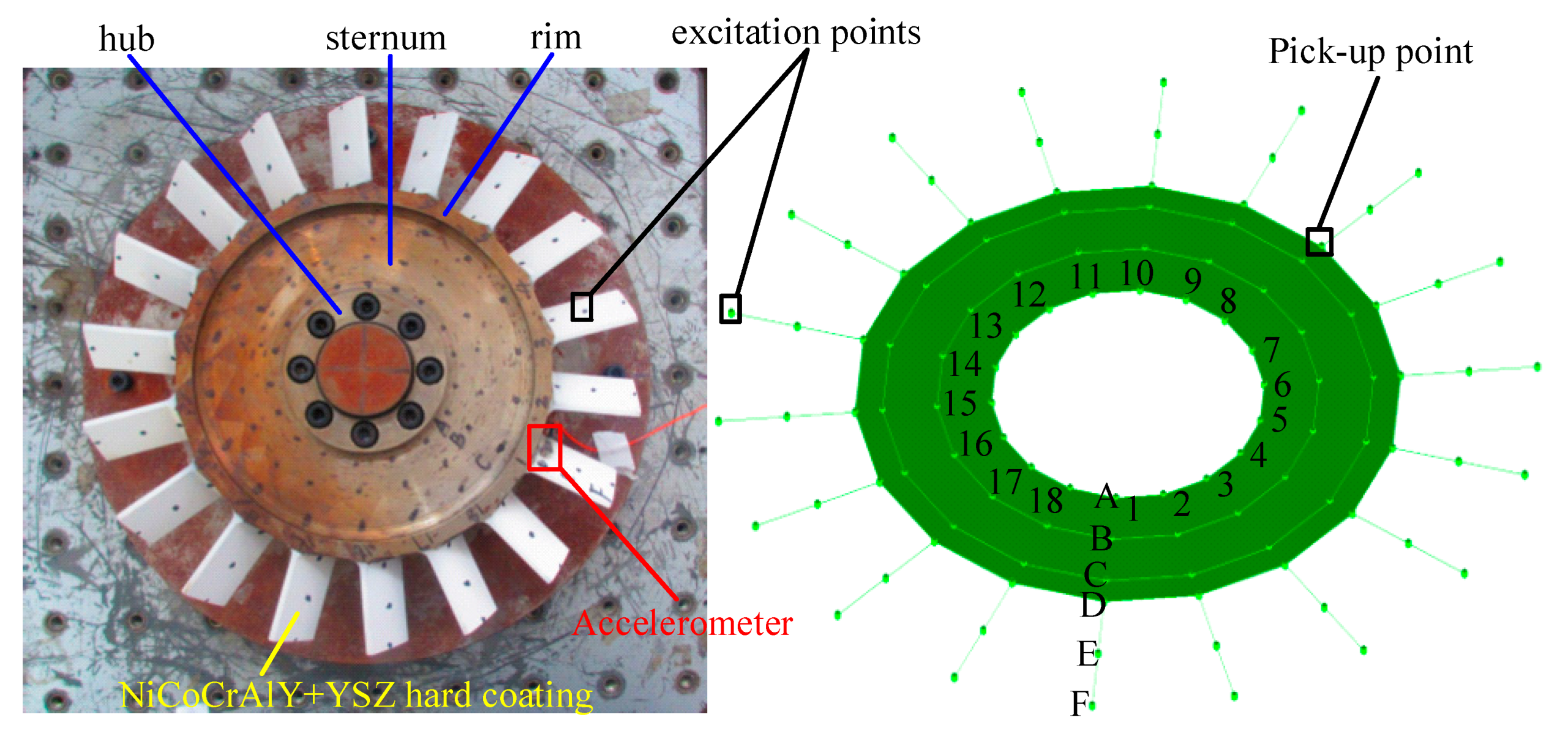
| Disk | Hard-Coating Blades | ||
|---|---|---|---|
| Inner radius of hub | 50 mm | Height of blade | 50 mm |
| Outer radius of hub | 80 mm | Width of blade | 25 mm |
| Thickness of hub | 19 mm | Thickness of blade | 3 mm |
| Inner radius of rim | 182 mm | Number of blade | 18 |
| Outer radius of rim | 200 mm | --- | --- |
| Thickness of rim | 20 mm | Single coating thickness | 0.1 mm |
| Thickness of sternum | 7 mm | Coating area | 100%, both sides |
| Catalog | Mistuned Blisk | Hard Coating |
|---|---|---|
| Material type | Q235-A (F) steel | NiCoCrAlY + YSZ |
| Young’s modulus (GPa) | 208 | 54.5 |
| Mass density (kg/m3) | 7860 | 5600 |
| Loss factor | 0.0006 | 0.0212 |
| Poisson’s ratio | 0.30 | 0.30 |
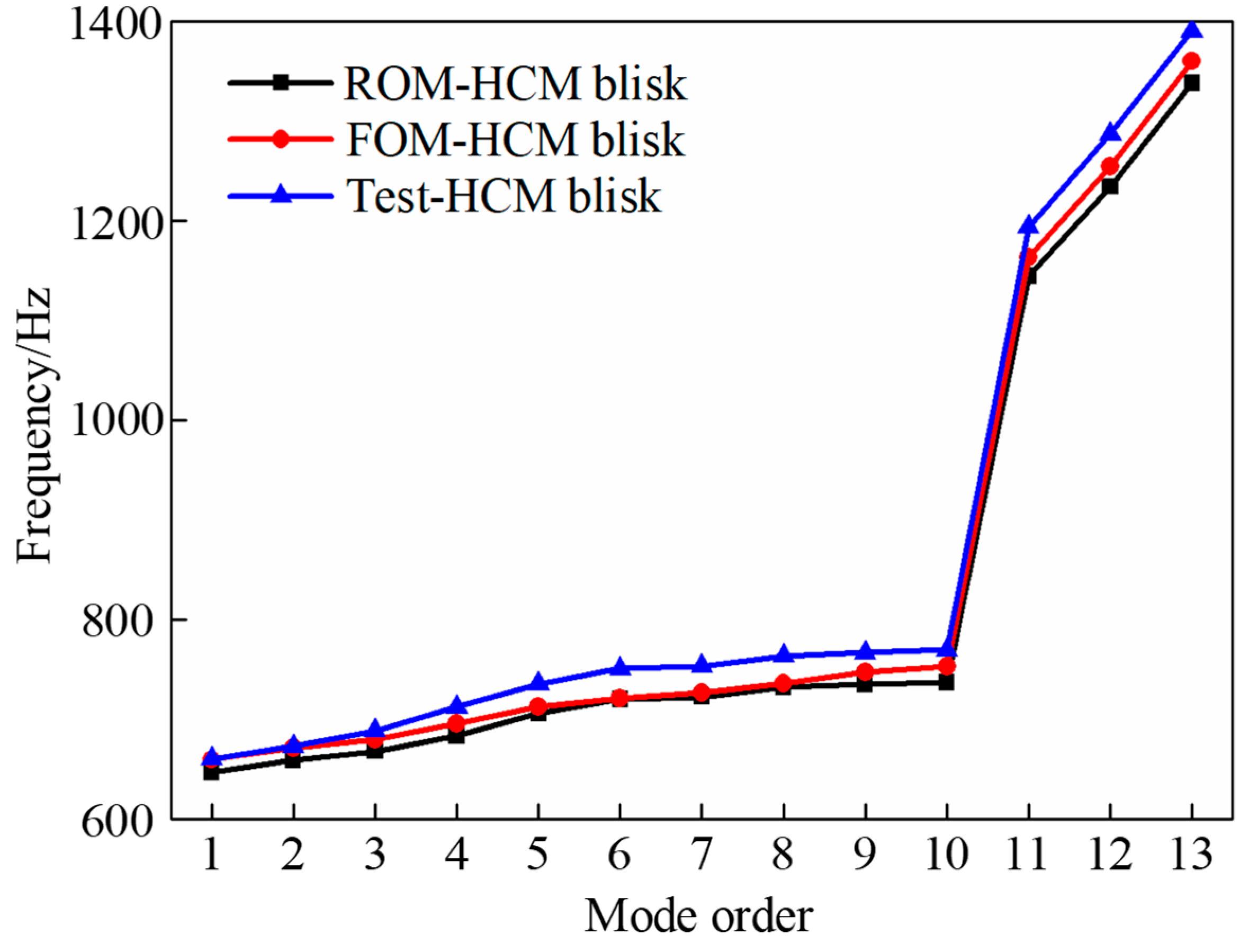
| Mode Order | Modified ROM | Test | ||||
|---|---|---|---|---|---|---|
| Mistuned Blisk/Hz | HCM Blisk/Hz | Change Rate/% | Mistuned Blisk/Hz | HCM Blisk/Hz | Change Rate/% | |
| 1 | 655.99 | 647.39 | −1.33 | 693.07 | 660.59 | −4.92 |
| 2 | 668.38 | 659.49 | −1.35 | 705.80 | 673.18 | −4.85 |
| 3 | 676.34 | 668.15 | −1.23 | 716.54 | 689.09 | −3.98 |
| 4 | 690.33 | 683.85 | −0.95 | 732.30 | 712.57 | −2.77 |
| 5 | 714.70 | 706.01 | −1.23 | 759.01 | 735.87 | −3.14 |
| 6 | 728.95 | 720.51 | −1.17 | 775.04 | 751.22 | −3.17 |
| 7 | 731.27 | 722.67 | −1.19 | 778.49 | 753.72 | −3.29 |
| 8 | 741.11 | 732.28 | −1.21 | 789.87 | 763.98 | −3.39 |
| 9 | 743.69 | 735.07 | −1.17 | 793.59 | 767.14 | −3.45 |
| 10 | 745.74 | 737.37 | −1.14 | 796.76 | 769.79 | −3.50 |
| 11 | 1162.90 | 1144.60 | −1.60 | 1237.86 | 1193.76 | −3.69 |
| 12 | 1265.40 | 1234.10 | −2.54 | 1347.00 | 1287.14 | −4.65 |
| 13 | 1373.20 | 1337.70 | −2.65 | 1458.73 | 1390.19 | −4.93 |
| Mode Order | Coating Thickness (mm)/Natural Frequencies (Hz) | Maximum Change Rate/% | |||||
|---|---|---|---|---|---|---|---|
| h = 0.0 | h = 0.05 | h = 0.10 | h = 0.15 | h = 0.20 | h = 0.25 | ||
| 1 | 655.99 | 649.78 | 647.39 | 644.66 | 641.65 | 638.40 | −2.76 |
| 2 | 668.38 | 661.76 | 659.49 | 656.83 | 653.85 | 650.60 | −2.73 |
| 3 | 676.34 | 670.41 | 668.15 | 665.49 | 662.49 | 659.20 | −2.60 |
| 4 | 690.33 | 685.79 | 683.85 | 681.43 | 678.60 | 675.44 | −2.20 |
| 5 | 714.70 | 708.52 | 706.00 | 703.09 | 699.85 | 696.33 | −2.64 |
| 6 | 728.95 | 723.06 | 720.51 | 717.55 | 714.24 | 710.65 | −2.58 |
| 7 | 731.27 | 725.28 | 722.67 | 719.66 | 716.31 | 712.68 | −2.61 |
| 8 | 741.11 | 734.97 | 732.28 | 729.18 | 725.75 | 722.03 | −2.64 |
| 9 | 743.69 | 737.75 | 735.07 | 731.97 | 728.54 | 724.82 | −2.60 |
| 10 | 745.74 | 740.03 | 737.37 | 734.29 | 730.86 | 727.14 | −2.56 |
| 11 | 1162.90 | 1147.40 | 1144.60 | 1141.70 | 1138.60 | 1137.40 | −2.24 |
| 12 | 1265.40 | 1237.30 | 1234.10 | 1230.80 | 1227.40 | 1223.90 | −3.39 |
| 13 | 1373.20 | 1341.70 | 1337.70 | 1333.70 | 1329.50 | 1325.30 | −3.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, F.; Li, B.; Liu, X. Passive Vibration Reduction Analysis of the Mistuned Blisk Deposited Hard Coating Using Modified Reduced-Order Model. Coatings 2019, 9, 812. https://doi.org/10.3390/coatings9120812
Gao F, Li B, Liu X. Passive Vibration Reduction Analysis of the Mistuned Blisk Deposited Hard Coating Using Modified Reduced-Order Model. Coatings. 2019; 9(12):812. https://doi.org/10.3390/coatings9120812
Chicago/Turabian StyleGao, Feng, Bingqiang Li, and Xiuting Liu. 2019. "Passive Vibration Reduction Analysis of the Mistuned Blisk Deposited Hard Coating Using Modified Reduced-Order Model" Coatings 9, no. 12: 812. https://doi.org/10.3390/coatings9120812
APA StyleGao, F., Li, B., & Liu, X. (2019). Passive Vibration Reduction Analysis of the Mistuned Blisk Deposited Hard Coating Using Modified Reduced-Order Model. Coatings, 9(12), 812. https://doi.org/10.3390/coatings9120812





