Analysis of a Thin Layer Formation of Third-Grade Fluid
Abstract
1. Introduction
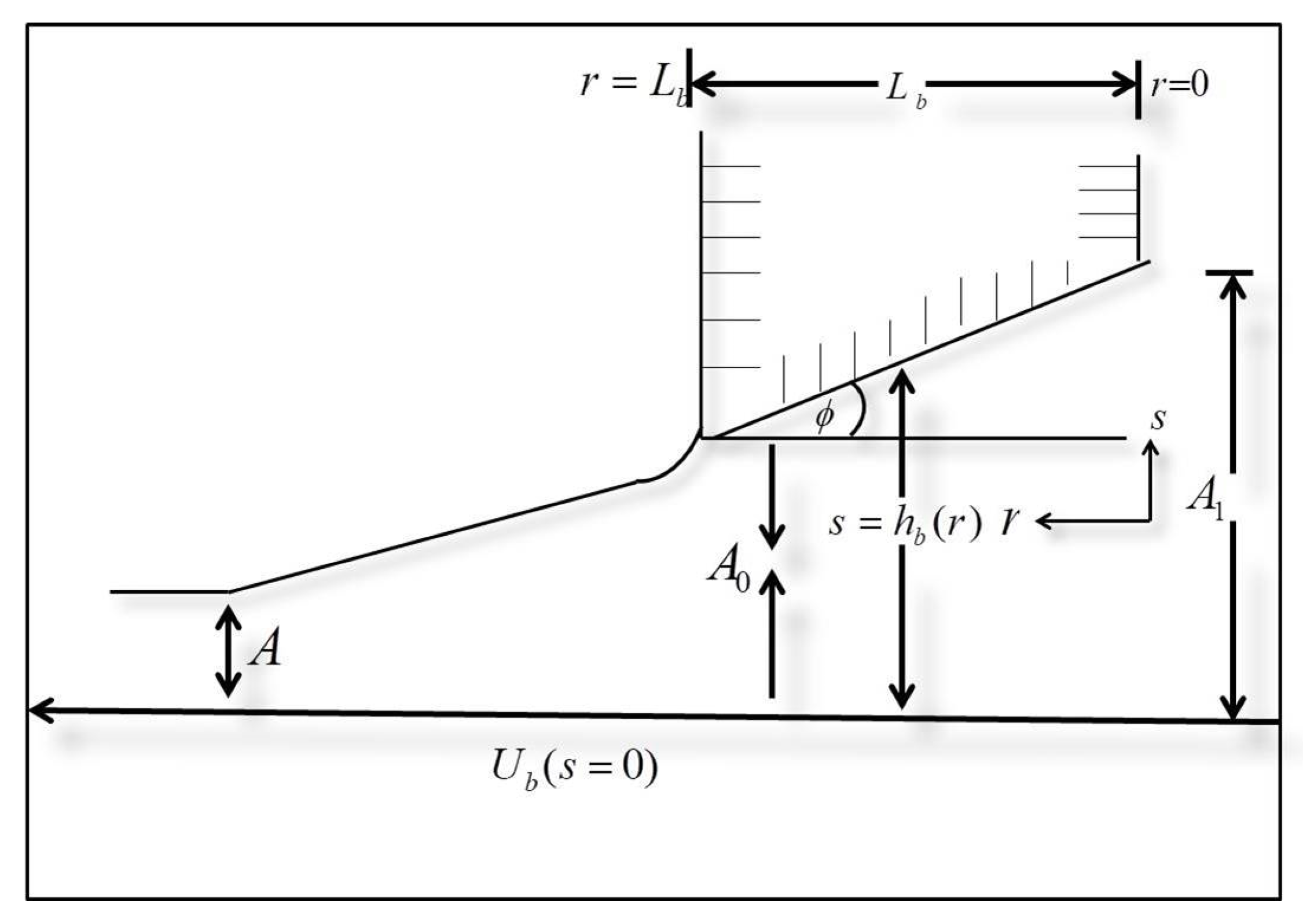
2. Materials and Methods
3. OHAM Formulation
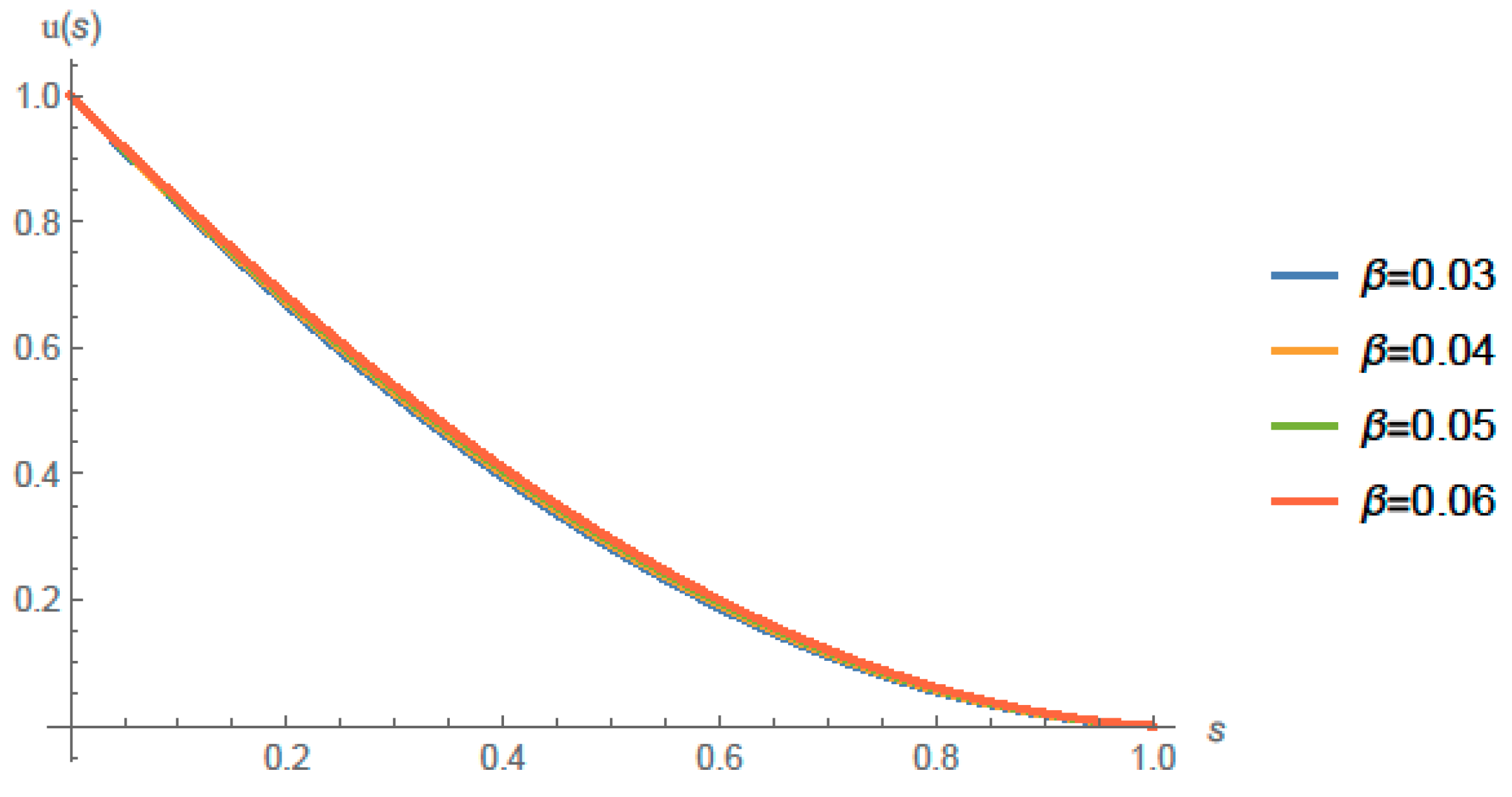
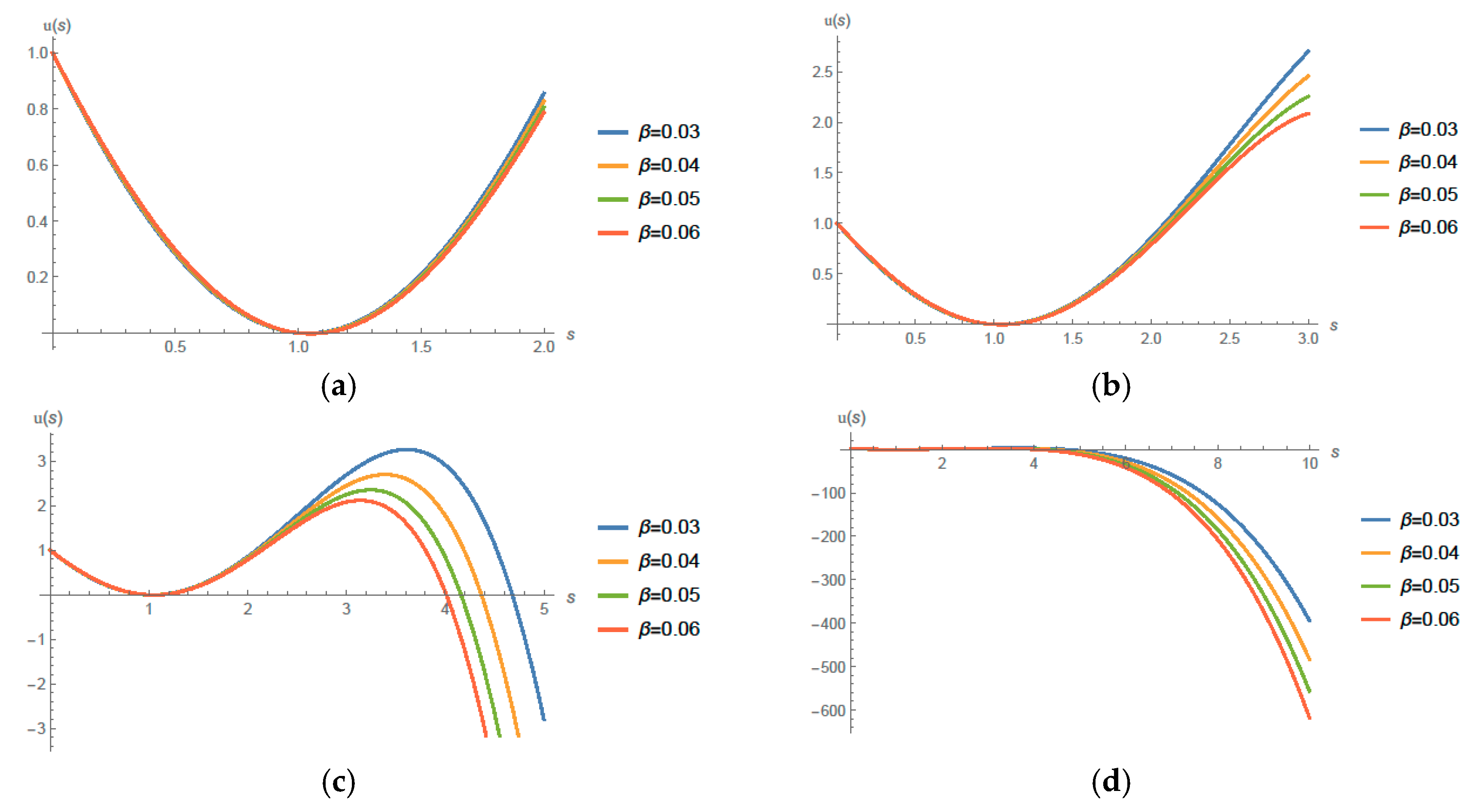
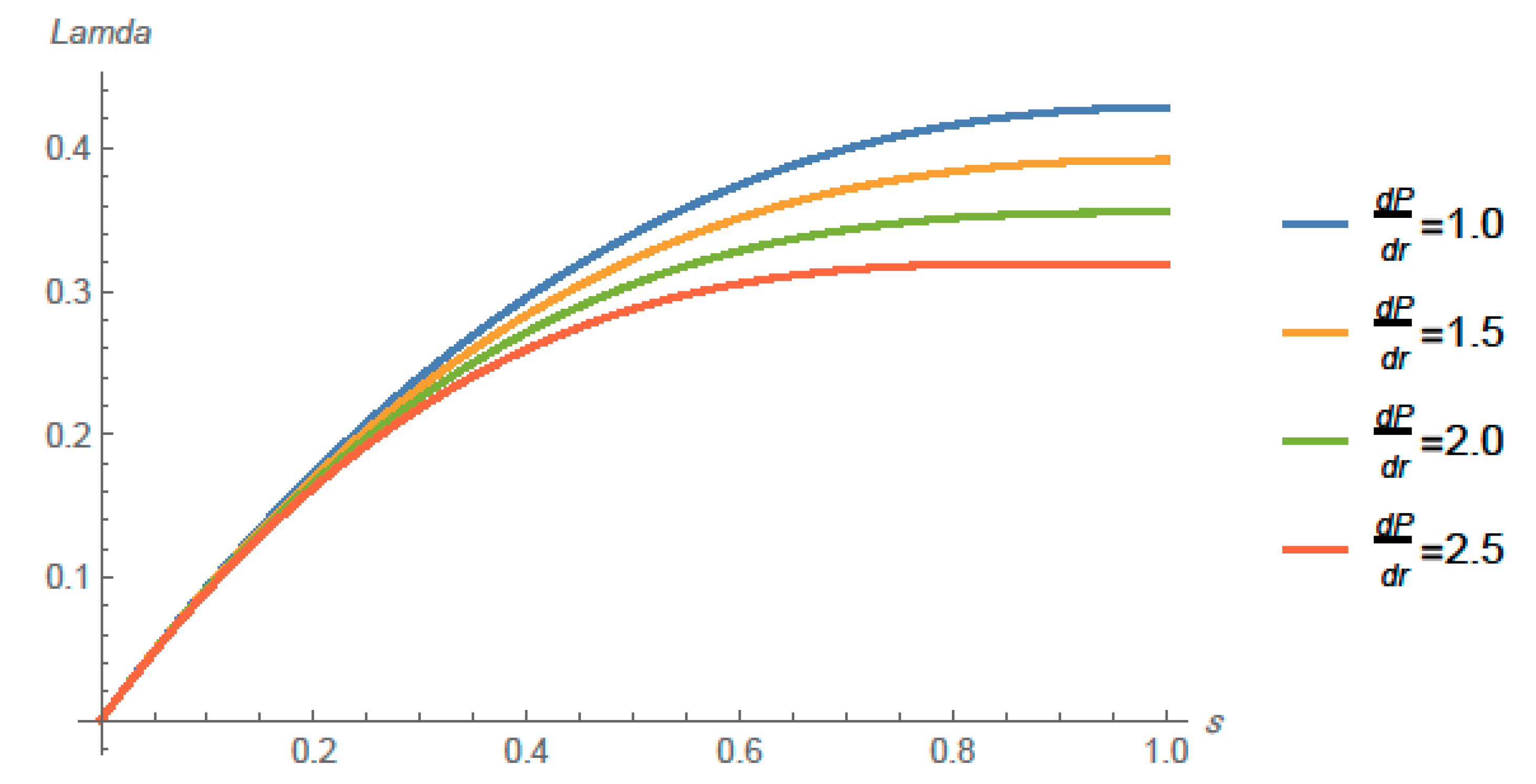
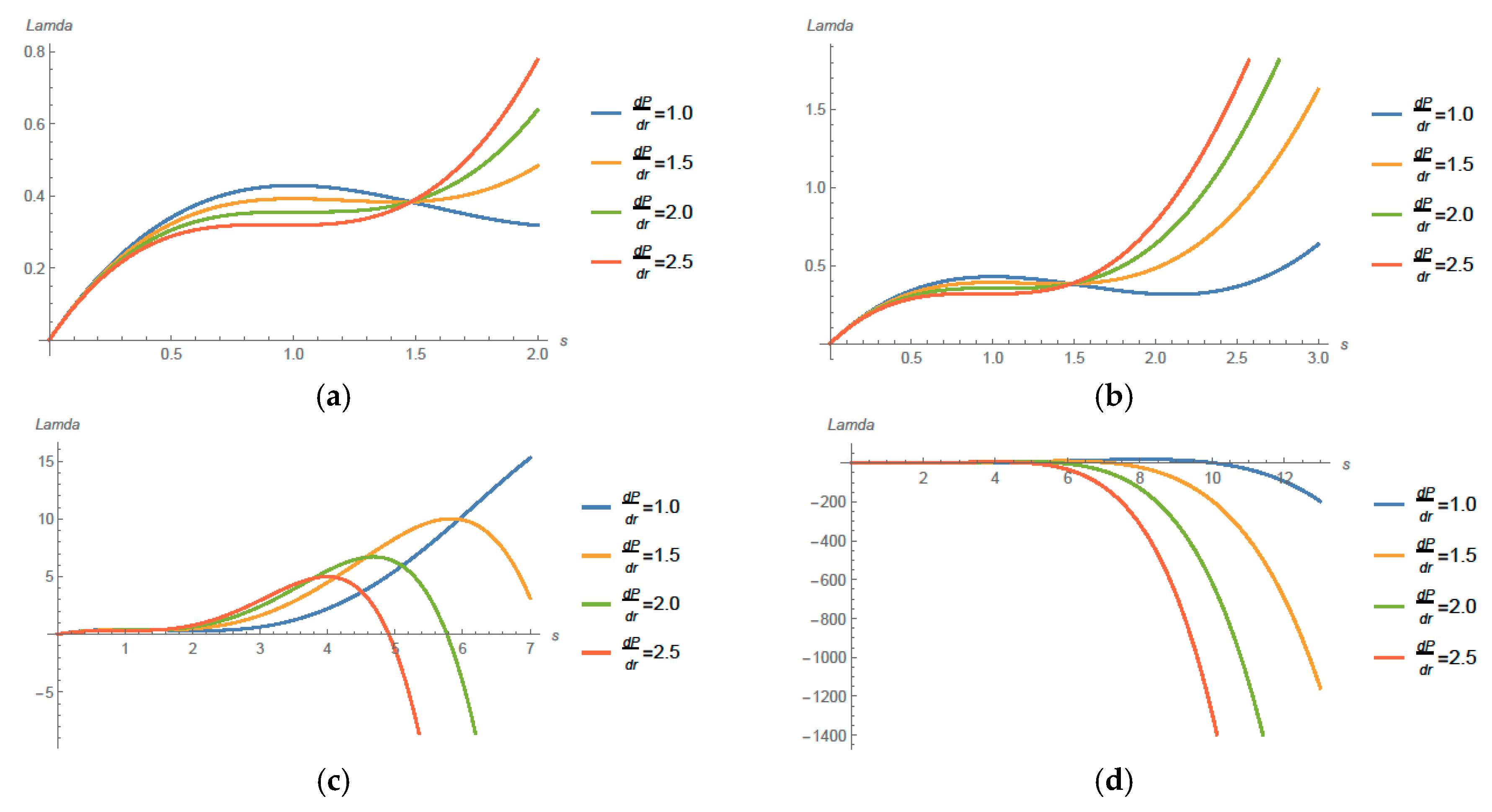
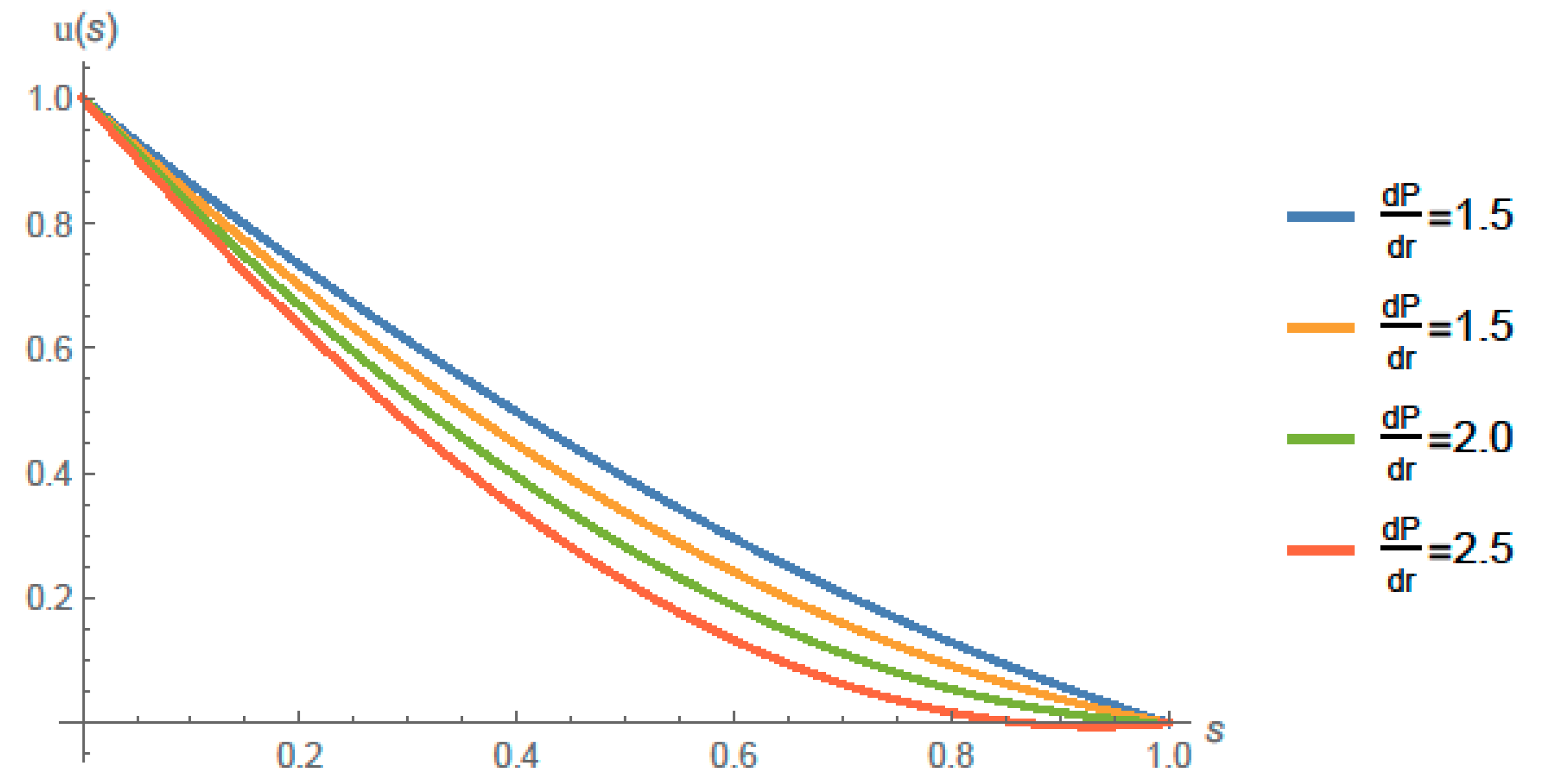
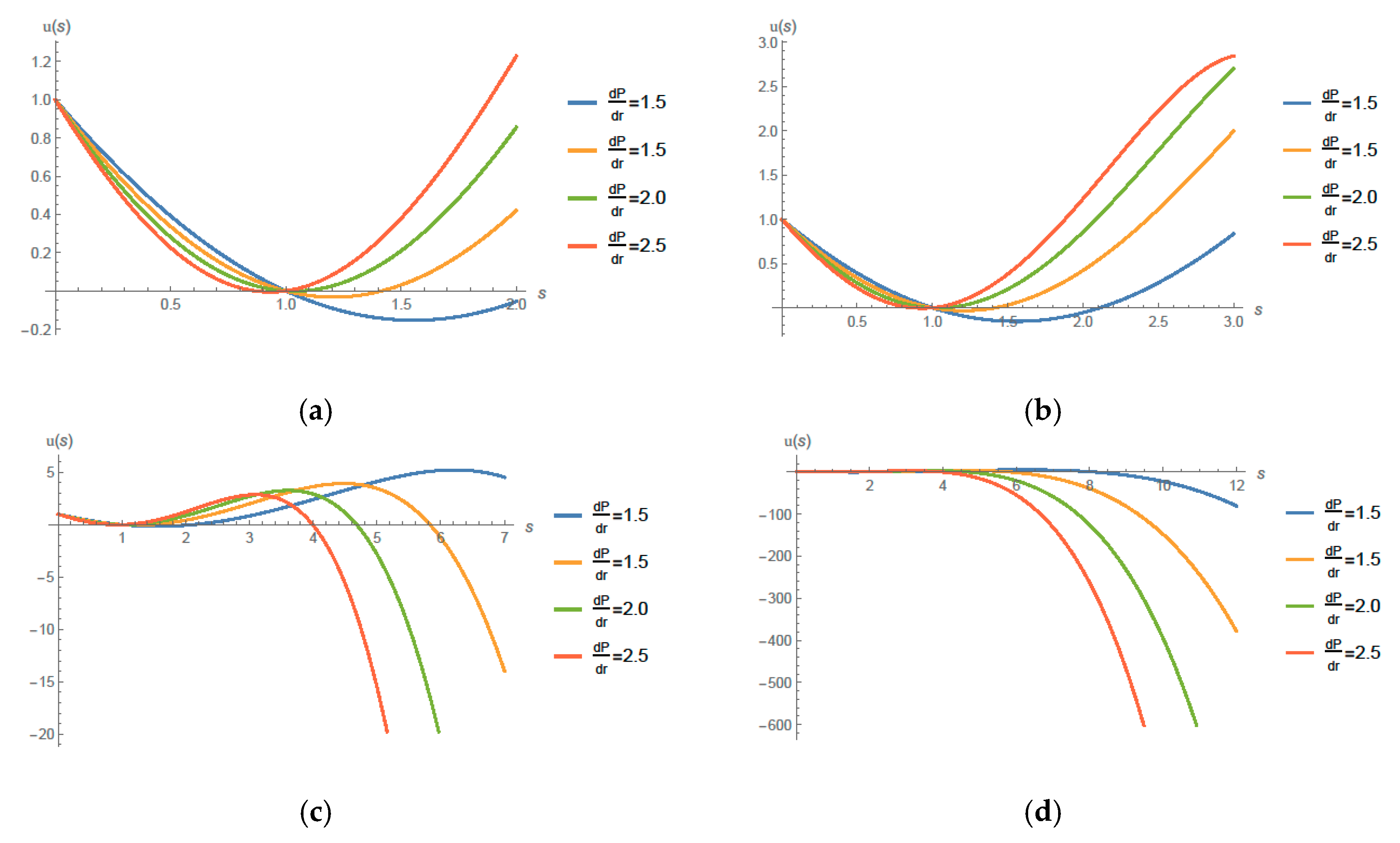
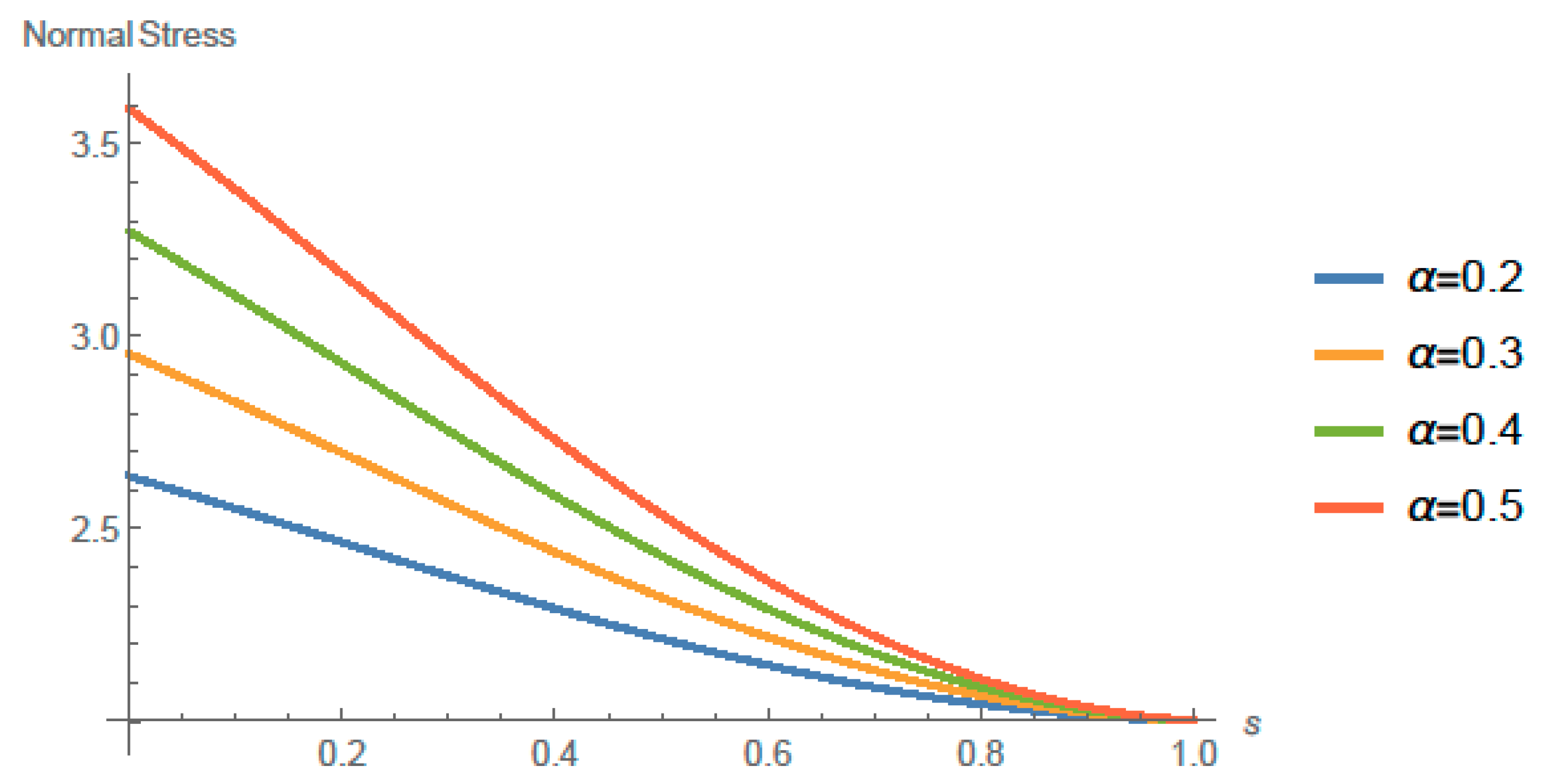
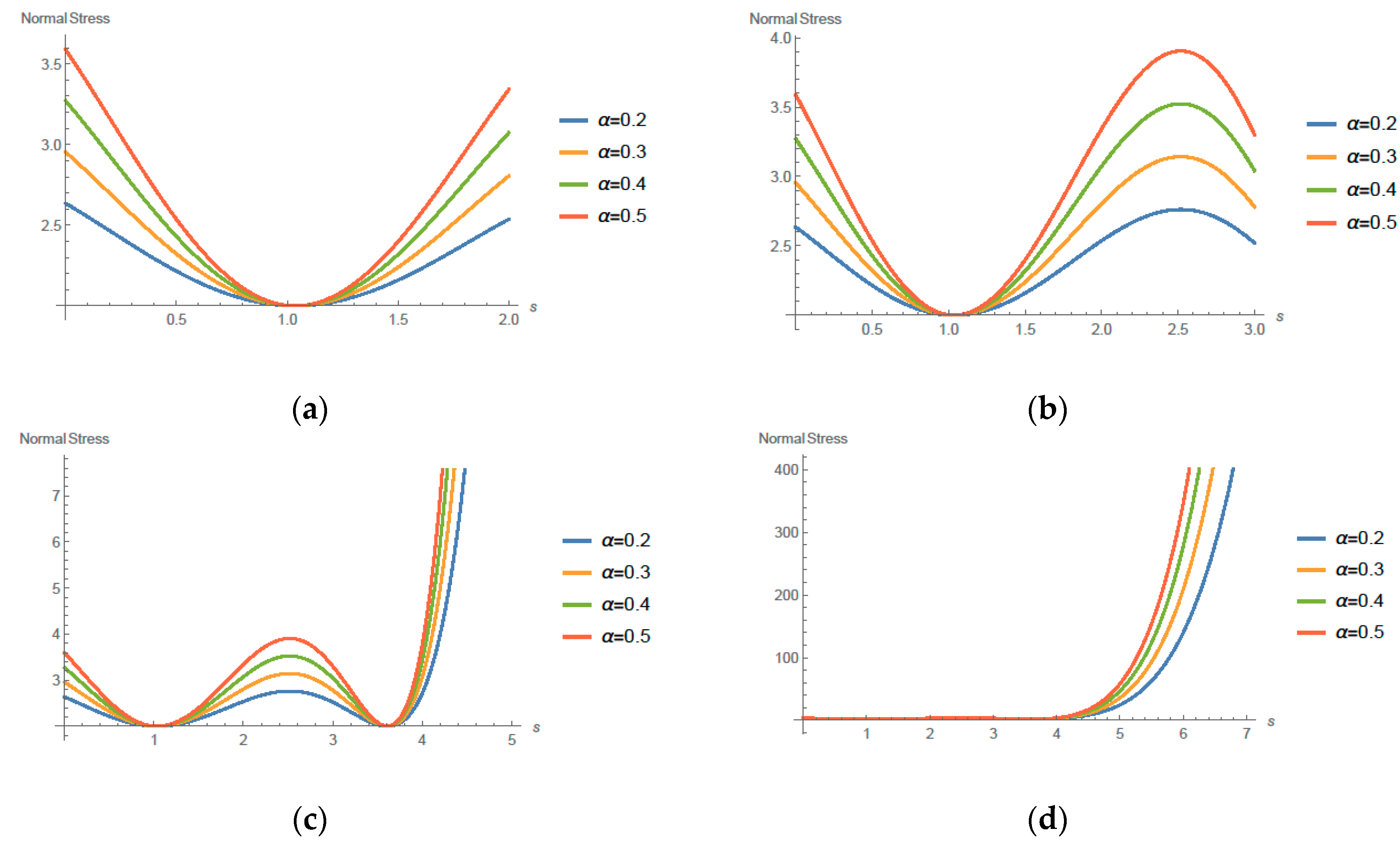
4. Solution and Main Results
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bhatti, S.; Zahid, M.; Rana, M.A.; Siddiqui, A.M.; Abdul Wahab, H. Numerical analysis of blade coating of a third-order fluid. J. Plast. Film Sheet. 2019, 35, 157–180. [Google Scholar] [CrossRef]
- Kandasamy, R.; Muhammad, R. Thermal radiation energy on squeezed MHD flow of Cu, Al2O3 and CNTs-nanofluid over a sensor surface. Alex. Eng. J. 2016, 55, 2405–2421. [Google Scholar]
- Tripathi, J.J.; Kedar, G.D.; Deshmukh, K.C. Generalized thermoelastic diffusion in a thick circular plate including heat source. Alex. Eng. J. 2016, 55, 2241–2249. [Google Scholar] [CrossRef]
- Javed, T.; Ahmad, H.; Ghaffari, A. Influence of radiation on vertical wavy surface with constant heat flux: Using Keller box scheme. Alex. Eng. J. 2016, 55, 2221–2228. [Google Scholar] [CrossRef]
- Banik, S.; Mallik, S.H.; Kanoria, M. Thermoelastic interaction with energy dissipation in an infinite solid with distributed periodicallyvarying heat sources. Int. J. Pure Appl. Math. 2007, 34, 231. [Google Scholar]
- Singh, B. Wave propagation in a generalized thermoelastic material with voids. Appl. Math. Comput. 2007, 189, 698–709. [Google Scholar] [CrossRef]
- Mallik, S.H.; Kanoria, M. Generalized thermoelastic functionally graded solid with a periodically varying heat source. Int. J. Solids Struct. 2007, 44, 7633–7645. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, S.; Alsaedi, A.; Ahmad, B. Numerical study for Soret and Dufour effects on mixed convective peristalsis of Oldroyd 8-constants fluid. Int. J. Therm. Sci. 2017, 112, 68–81. [Google Scholar] [CrossRef]
- Ailawalia, P.; Kumar, S.; Pathania, D.S. Internal heat source in thermoelastic microelongated solid under green lindsay theory. J. Theor. Appl. Mech. 2016, 46, 65–82. [Google Scholar] [CrossRef]
- Mallik, S.H.; Kanoria, M. A two dimensional problem for a transversely isotropic generalized thermoelastic thick plate with spatially varying heat source. Eur. J. Mech.-A/Solids 2008, 27, 607–621. [Google Scholar] [CrossRef]
- Das, P.; Kar, A.; Kanoria, M. Analysis of magneto-thermoelastic response in a transversely isotropic hollow cylinder under thermal shock with three-phase-lag effect. J. Therm. Stresses 2013, 36, 239–258. [Google Scholar] [CrossRef]
- Tripathi, J.; Warbhe, S.; Deshmukh, K.C.; Verma, J. Fractional order generalized thermoelastic response in a half space due to a periodically varying heat source. Multidiscip. Model. Mater. Struct. 2018, 14, 2–15. [Google Scholar] [CrossRef]
- Sur, A.; Kanoria, M. Analysis of thermoelastic response in a functionally graded infinite space subjected to a Mode-I crack. Int. J. Adv. Appl. Math. Mech. 2015, 3, 33–44. [Google Scholar]
- Abbas, I.A.; Marin, M. Analytical solution of thermoelastic interaction in a half-space by pulsed laser heating. Phys. E Low-Dimens. Syst. Nanostructures 2017, 87, 254–260. [Google Scholar] [CrossRef]
- Carapau, F.; Correia, P.; Grilo, L.M. Specific shear-dependent viscoelastic third-grade fluid model. AIP Conf. Proc. 2016, 1790, 140008. [Google Scholar]
- Middleman, S. Fundamentals of Polymer Processing; McGraw-Hill: New York, NY, USA, 1977. [Google Scholar]
- Ruschak, K.J. Coating flows. Annu. Rev. Fluid Mech. 1985, 17, 65–89. [Google Scholar] [CrossRef]
- Blake, T.D.; Ruschak, K.J.; Kistler, S.F.; Schweizer, P.M. Liquid Film Coating; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Gaskell, P.H.; Savage, M.D.; Summers, J.L. The Mechanics of Thin Film Coatings. In Proceedings of the First European Coating Symposium, Leeds University, Leeds, UK, 19–22 September 1995; p. 424. [Google Scholar]
- Bourgin, P. Fluid Mechanics of Coating Processes. In Proceedings of the Euromech 367, 2nd European Coating Symposium (ECS’97), Universite Louis Pasteur, Strasbourg, France, 22–25 July 1997; p. 504. [Google Scholar]
- Sajid, M.; Ali, N.; Javed, M.A. An exact solution for the calendering analysis of a third-order fluid. J. Plast. Film Sheet. 2017, 33, 124–141. [Google Scholar] [CrossRef]
- Herisanu, N.; Marinca, V. Accurate analytical solutions to oscillators with discontinuities and fractional-power restoring force by means of the optimal homotopy asymptotic method. Comput. Math. Appl. 2010, 60, 1607–1615. [Google Scholar] [CrossRef]
- Marinca, V.; Herisanu, N. Determination of periodic solutions for the motion of a particle on a rotating parabola by means of the optimal homotopy asymptotic method. J. Sound Vib. 2010, 329, 1450–1459. [Google Scholar] [CrossRef]
- Iqbal, S.; Idrees, M.; Siddiqui, A.M.; Ansari, A.R. Some solutions of the linear and nonlinear Klein-Gordon equations using the optimal homotopy asymptotic method. Appl. Math. Comput. 2010, 216, 2898–2909. [Google Scholar] [CrossRef]
- Iqbal, S.; Javed, A. Application of optimal homotopy asymptotic method for the analytic solution of singular Lane-Emden type equation. Appl. Math. Comput. 2011, 217, 7753–7761. [Google Scholar] [CrossRef]
- Iqbal, S.; Ansari, A.R.; Siddiqui, A.M.; Javed, A. Use of optimal homotopy asymptotic method and Galerkin-s finite element formulation in the study of heat transfer flow of a third grade fluid between parallel plates. J. Heat Transf. 2011, 133, 091702. [Google Scholar] [CrossRef]
- Javed, A.; Memon, N.A.; Iqbal, S. Optimal homotopy asymptotic method for solving sixth-order boundary value problems. QUEST Res. J. 2010, 9, 6–10. [Google Scholar]
- Hashmi, M.S.; Khan, N.; Iqbal, S. Numerical solutions of weakly singular Volterra integral equations using the optimal homotopy asymptotic method. Comput. Math. Appl. 2012, 64, 1567–1574. [Google Scholar] [CrossRef][Green Version]
- Hashmi, M.S.; Khan, N.; Iqbal, S. Optimal homotopy asymptotic method for solving nonlinear Fredholm integral equations of second kind. Appl. Math. Comput. 2012, 218, 10982–10989. [Google Scholar] [CrossRef]
- Younas, H.M.; Mustahsan, M.; Manzoor, T.; Salamat, N.; Iqbal, S. Dynamical study of fokker-planck equations by using optimal homotopy asymptotic method. Mathematics 2019, 7, 264. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Kaloni, P.N. Plane steady flows of a third grade fluid. Int. J. Eng. Sci. 1987, 25, 171–188. [Google Scholar] [CrossRef]
- Zahid, M.; Haroon, T.; Rana, M.A.; Siddiqui, A.M. Roll coating analysis of a third grade fluid. J. Plast. Film Sheet. 2017, 33, 72–91. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Zahid, M.; Rana, M.A.; Haroon, T. Calendering analysis of a third-order fluid. J. Plast. Film Sheet. 2014, 30, 345–368. [Google Scholar] [CrossRef]
- Sullivan, T.M.; Middleman, S. Film thickness in blade coating of viscous and viscoelastic liquids. J. Non-Newton. Fluid Mech. 1986, 21, 13–38. [Google Scholar] [CrossRef]
- Greener, Y.; Middleman, S. Blade-coating of a viscoelastic fluid. Polym. Eng. Sci. 1974, 14, 791–796. [Google Scholar] [CrossRef]
- Ross, A.B.; Wilson, S.K.; Duffy, B.R. Blade coating of a power-law fluid. Phys. Fluids 1999, 11, 958–970. [Google Scholar] [CrossRef]
- Hwang, S.S. Non-Newtonian liquid blade coating process. J. Fluids Eng. 1982, 104, 469–474. [Google Scholar] [CrossRef]
- Dien, I.K.; Elrod, H.G. A generalized steady-state Reynolds equation for non-Newtonian fluids, with application to journal bearings. J. Lubr. Technol. 1983, 105, 385–390. [Google Scholar] [CrossRef]
- Tichy, J.A. Non-Newtonian lubrication with the convected Maxwell model. J. Tribol. 1996, 118, 344–348. [Google Scholar] [CrossRef]
- Hsu, T.C.; Malone, M.; Laurence, R.L.; Middleman, S. Separating forces in blade coating of viscous and viscoelastic liquids. J. Non-Newton. Fluid Mech. 1985, 18, 273–294. [Google Scholar] [CrossRef]
- Fosdick, R.L.; Rajagopal, K.R. Thermodynamics and stability of fluids of third grade. Proc. R. Soc. Lond. A 1980, 369, 351–377. [Google Scholar] [CrossRef]
- Atif, H.M.; Ali, N.; Javed, M.A.; Abbas, F. Theoretical analysis of roll-over-web coating of a micropolar fluid under lubrication approximation theory. J. Plast. Film Sheet. 2018, 34. [Google Scholar] [CrossRef]
- Ali, N.; Atif, H.M.; Javed, M.A.; Sajid, M. A theoretical analysis of roll-over-web coating of couple stress fluid. J. Plast. Film Sheet. 2018, 34, 43–59. [Google Scholar] [CrossRef]
| β and C1 | |
|---|---|
| β | C1 |
| 0.03 | −0.6027727875127079 |
| 0.04 | −0.5367678225757836 |
| 0.05 | 0.4849617709110862 |
| 0.06 | −0.44305755184121864 |
| For Fixed β = 0.03 | |
|---|---|
| Pr | C1 |
| 1 | −0.7389837541589072 |
| 1.5 | −0.6670404279185341 |
| 2 | −0.6027727875127079 |
| 2.5 | −0.5456887819699325 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manzoor, T.; Nazar, K.; Zafar, M.; Iqbal, S.; Ali, M.; Kim, W.Y.; Saleem, M.; Manzoor, S. Analysis of a Thin Layer Formation of Third-Grade Fluid. Coatings 2019, 9, 741. https://doi.org/10.3390/coatings9110741
Manzoor T, Nazar K, Zafar M, Iqbal S, Ali M, Kim WY, Saleem M, Manzoor S. Analysis of a Thin Layer Formation of Third-Grade Fluid. Coatings. 2019; 9(11):741. https://doi.org/10.3390/coatings9110741
Chicago/Turabian StyleManzoor, Tareq, Kashif Nazar, Muhammad Zafar, Shaukat Iqbal, Muddassir Ali, Woo Young Kim, Mahmood Saleem, and Sanaullah Manzoor. 2019. "Analysis of a Thin Layer Formation of Third-Grade Fluid" Coatings 9, no. 11: 741. https://doi.org/10.3390/coatings9110741
APA StyleManzoor, T., Nazar, K., Zafar, M., Iqbal, S., Ali, M., Kim, W. Y., Saleem, M., & Manzoor, S. (2019). Analysis of a Thin Layer Formation of Third-Grade Fluid. Coatings, 9(11), 741. https://doi.org/10.3390/coatings9110741





