Coupling the Microscopic Healing Behaviour of Coatings to the Thermoreversible Diels-Alder Network Formation
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Instruments
2.2.1. Dynamic Rheology
2.2.2. Dynamic Mechanical Analysis
2.2.3. Atomic Force Microscopy
3. Results
3.1. Dynamic Reversibility of Diels-Alder Cycloadducts
3.1.1. Thermomechanical Behaviour
3.2. Dynamically Reversible Polymer Network Coatings
3.2.1. Thermally Reversible Thermoset Coatings
3.2.2. Thermally Reversible Elastomeric Coatings
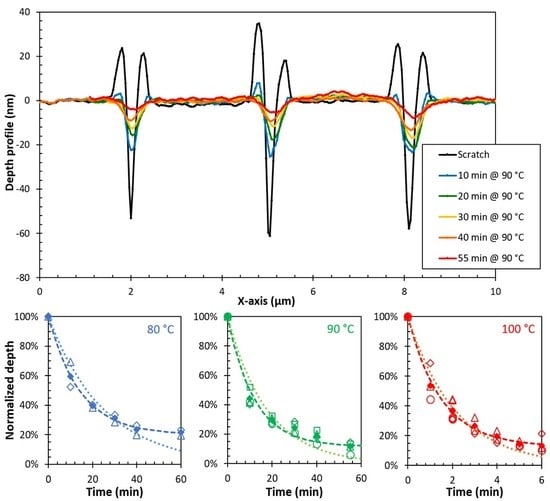
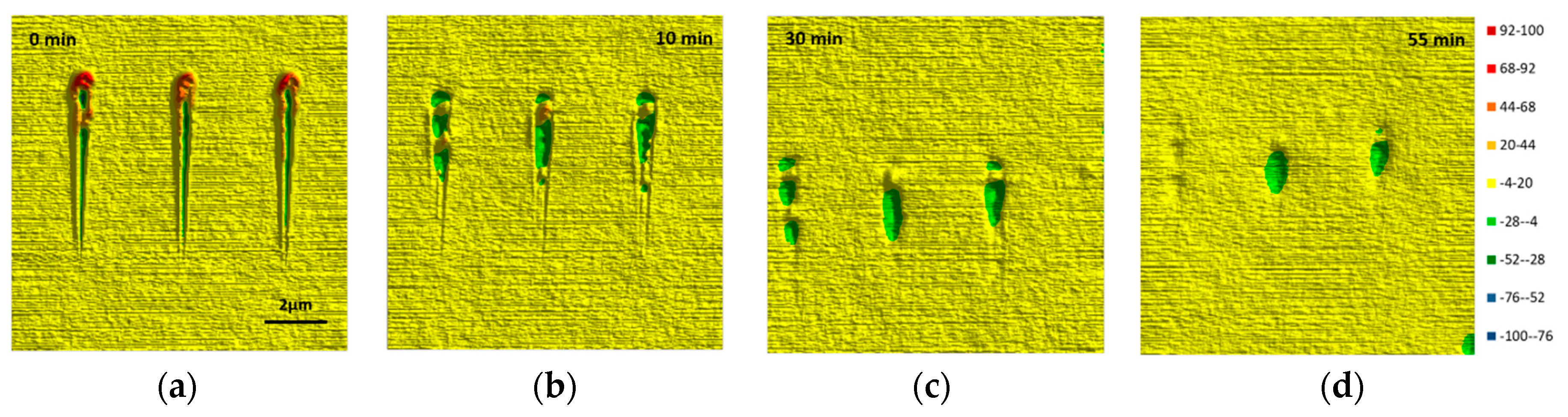
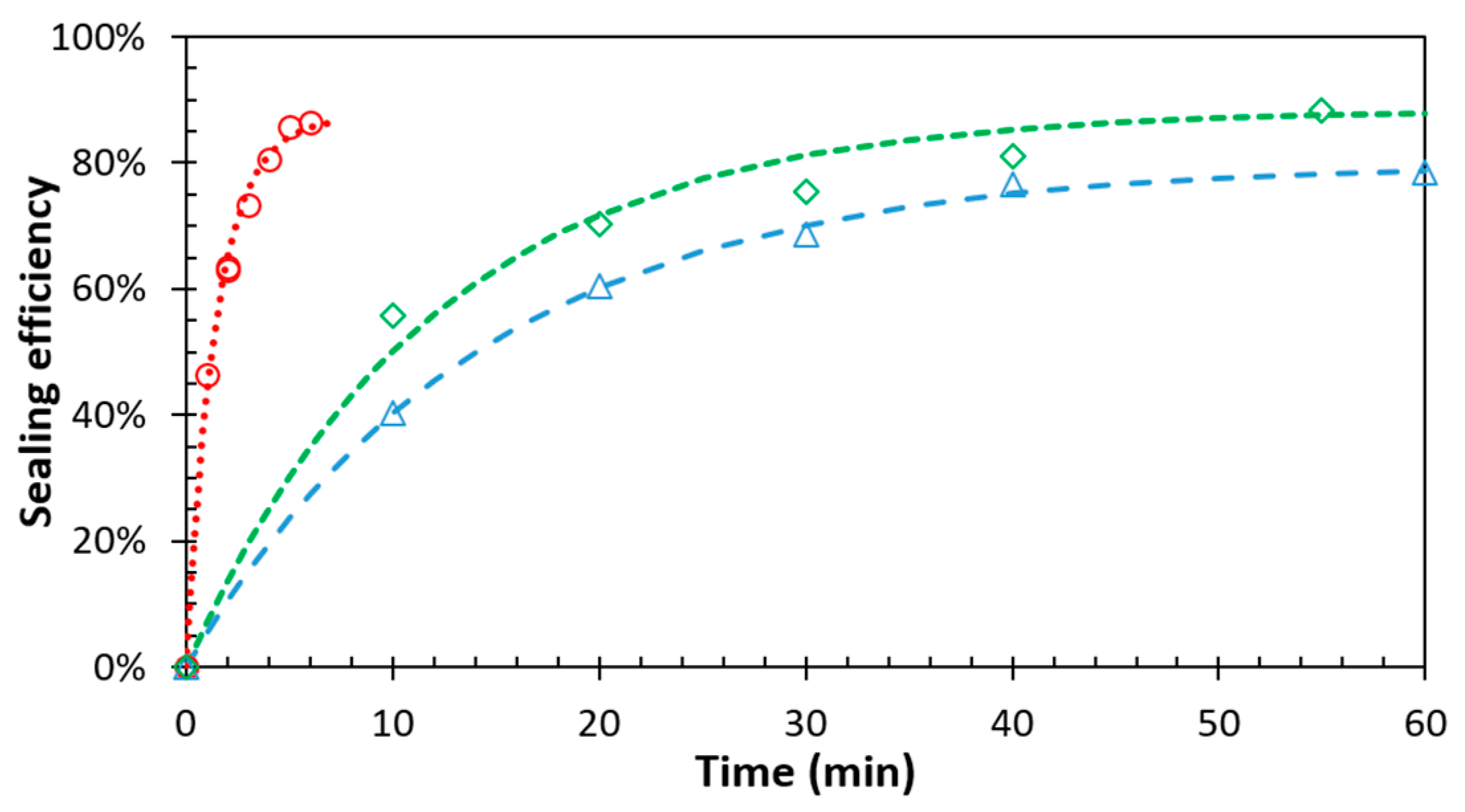
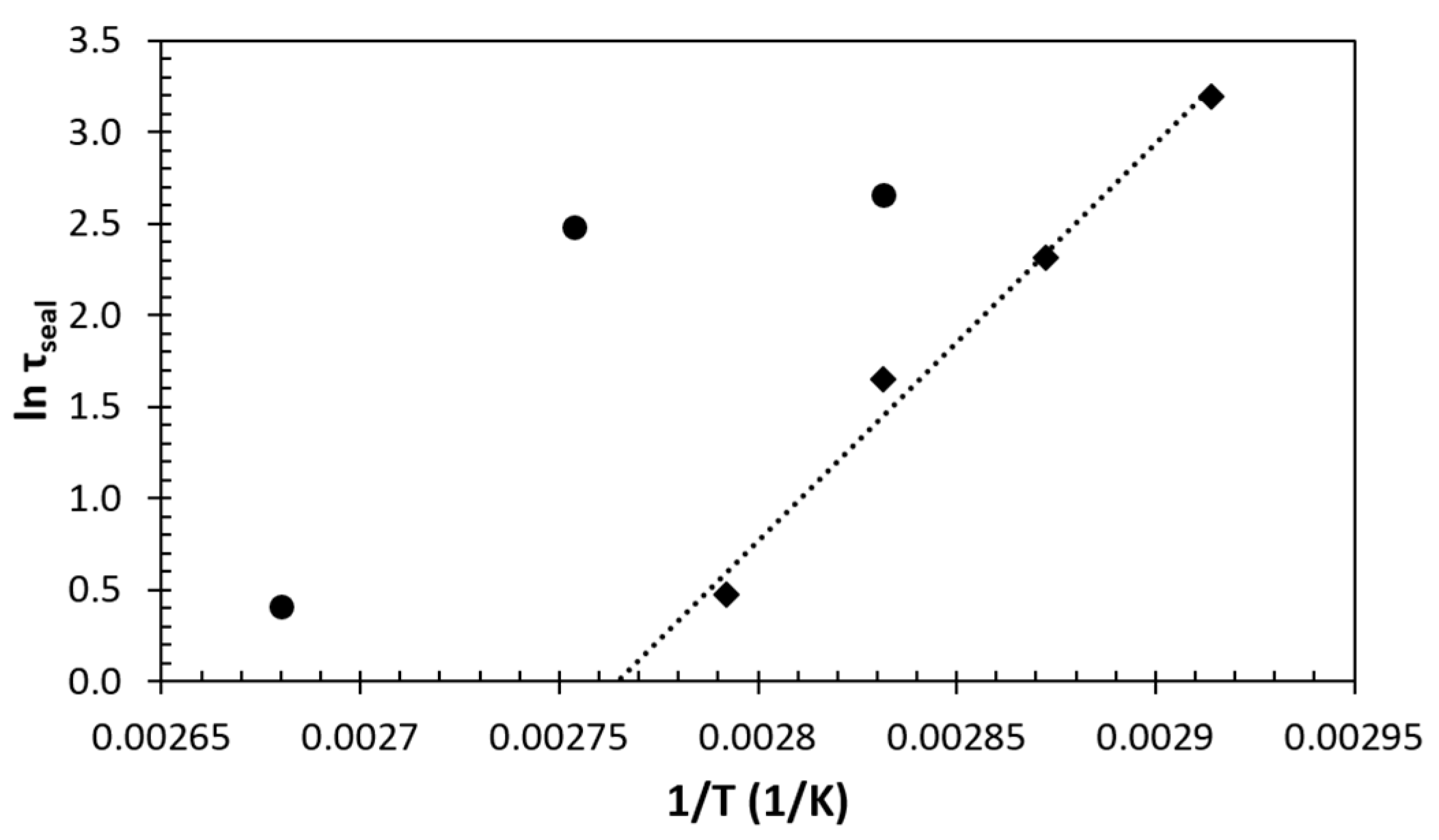
3.3. Temperature Dependence of the Sealing Mechanism
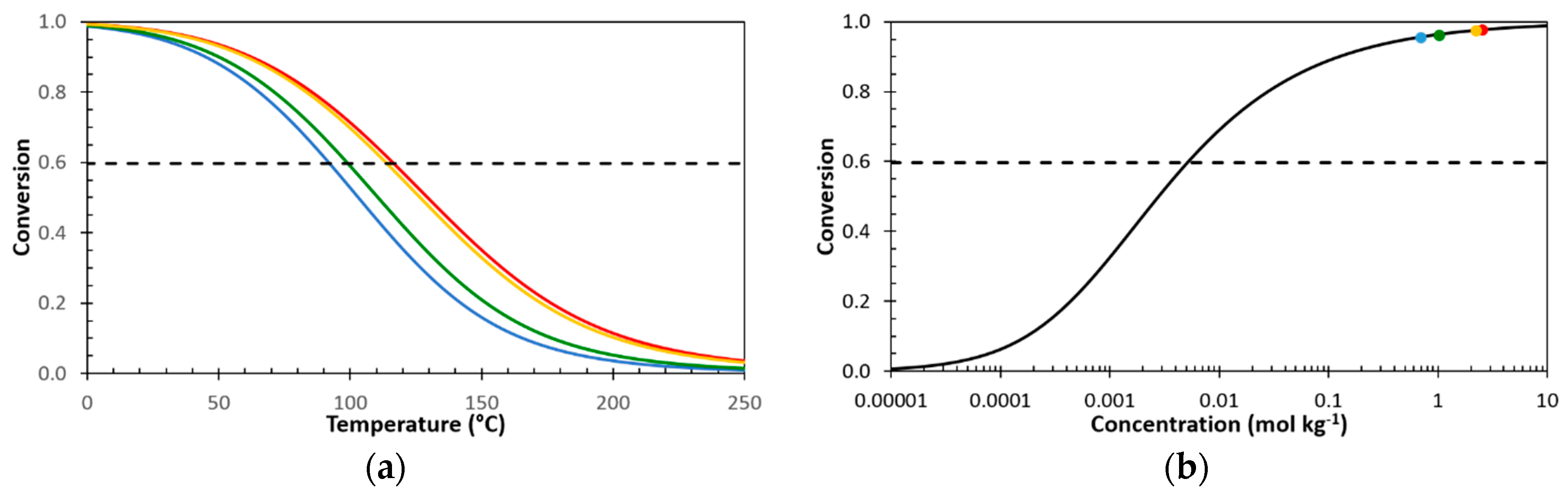
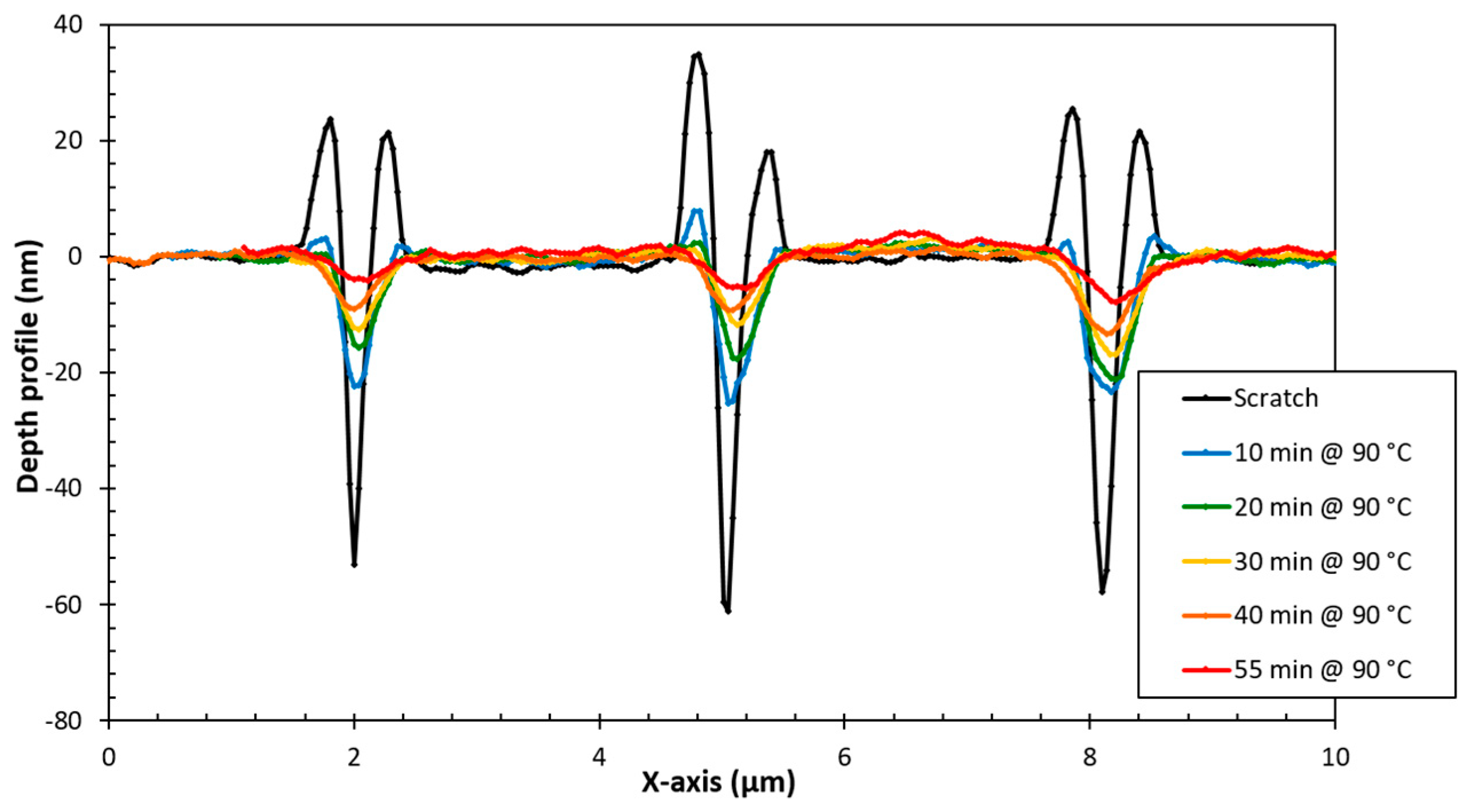
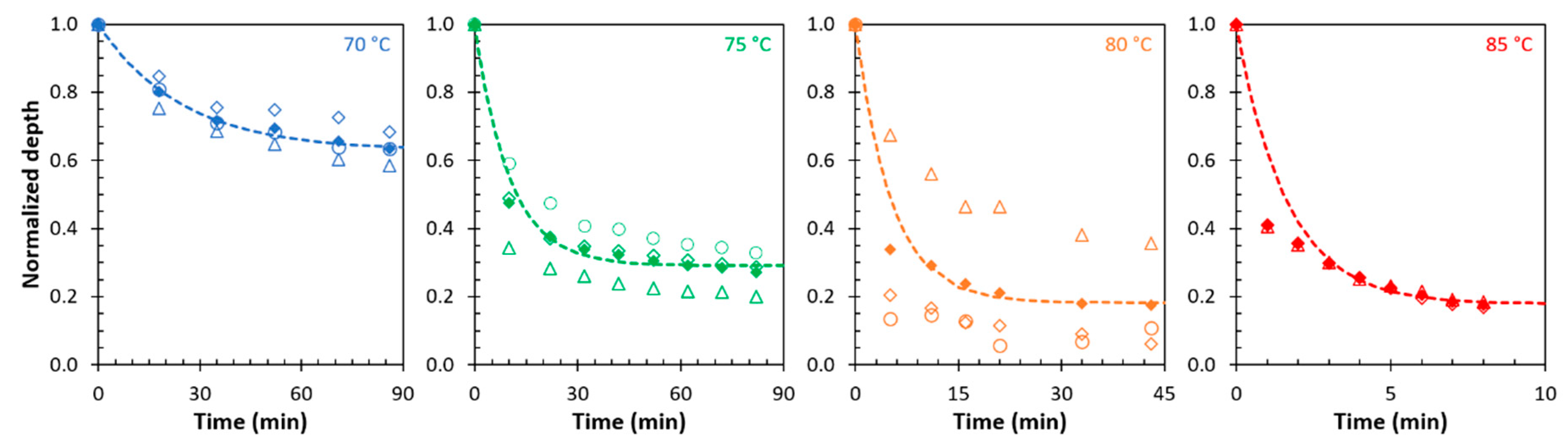
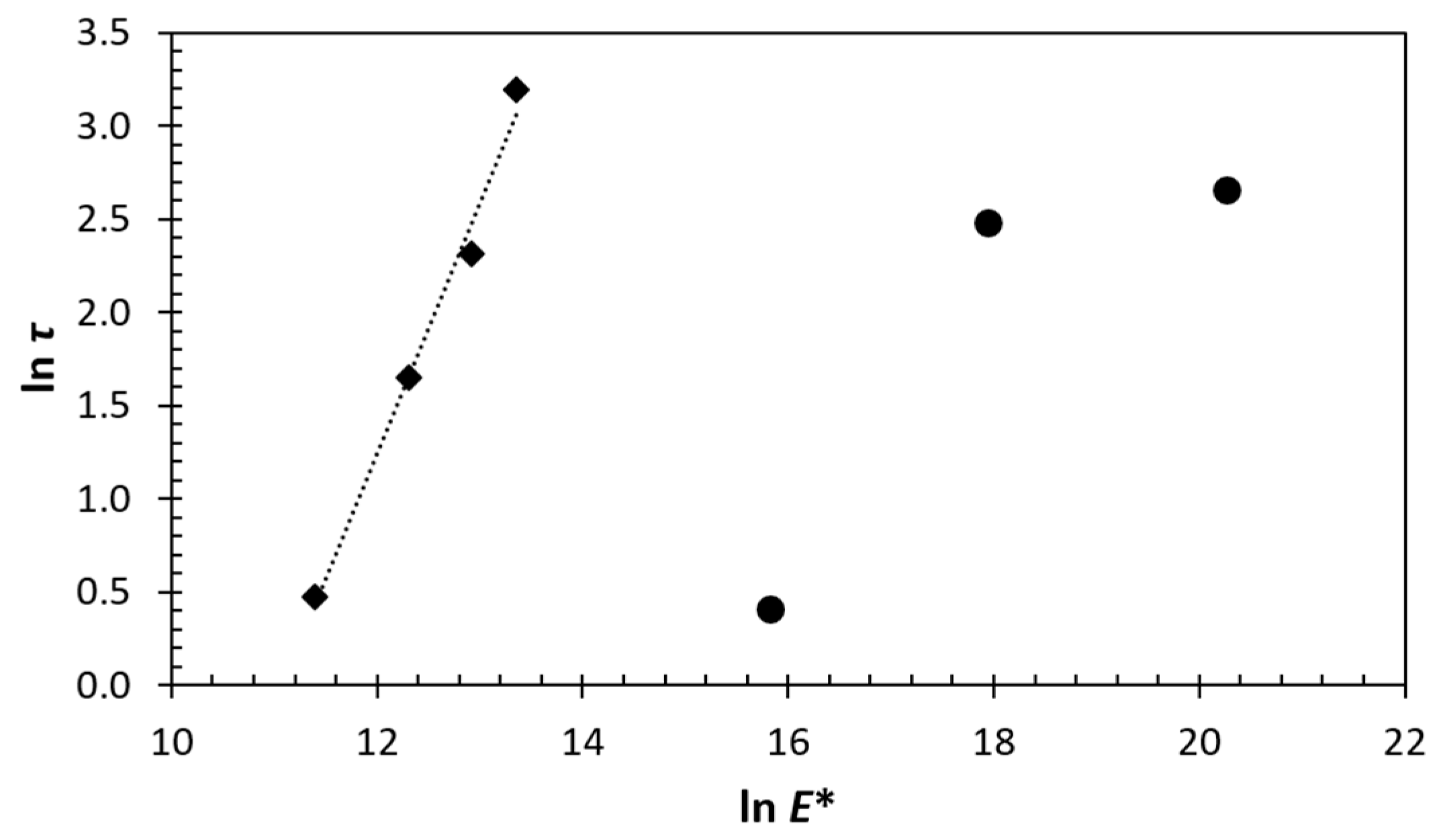
3.4. Structure-Property Relation of the Sealing Mechanism
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Kinetic Parameter | Endo Isomer | Exo Isomer |
|---|---|---|
| ln ADA (kg·mol−1·s−1) | 15.8 | 16.4 |
| EDA (kJ·mol−1) | 65.1 | 73.7 |
| ln ArDA (s−1) | 27.9 | 37.1 |
| ErDA (kJ·mol−1) | 101.3 | 137.1 |
| ΔrH° (kJ·mol−1) | −36.2 | −63.4 |
| ΔrS° (kJ·mol−1·K−1) | −100.5 | −172.3 |



References
- Esteves, C. Self-healing functional surfaces. Adv. Mater. Interfaces 2018, 5, 1800293. [Google Scholar] [CrossRef]
- Shchukin, D.G.; Möhwald, H. Self-repairing coatings containing active nanoreservoirs. Small 2007, 3, 926–943. [Google Scholar] [CrossRef] [PubMed]
- Cho, S.H.; White, S.R.; Braun, P.V. Self-healing polymer coatings. Adv. Mater. 2009, 21, 645–649. [Google Scholar] [CrossRef]
- Samadzadeh, M.; Boura, S.H.; Peikari, M.; Kasiriha, S.M.; Ashrafi, A. A review on self-healing coatings based on micro/nanocapsules. Prog. Org. Coat. 2010, 68, 159–164. [Google Scholar] [CrossRef]
- Toohey, K.S.; Sottos, N.R.; Lewis, J.A.; Moore, J.S.; White, S.R. Self-healing materials with microvascular networks. Nat. Mater. 2007, 6, 581–585. [Google Scholar] [CrossRef] [PubMed]
- Torre-Muruzabal, A.; Daelemans, L.; van Assche, G.; de Clerck, K.; Rahier, H. Creation of a nanovascular network by electrospun sacrificial nanofibers for self-healing applications and its effect on the flexural properties of the bulk material. Polym. Test. 2016, 54, 78–83. [Google Scholar] [CrossRef]
- Wietor, J.L.; Dimopoulos, A.; Govaert, L.E.; van Benthem, R.A.T.M.; de With, G.; Sijbesma, R.P. Preemptive healing through supramolecular cross-links. Macromolecules 2009, 42, 6640–6646. [Google Scholar] [CrossRef]
- Li, Y.; Fang, X.; Wang, Y.; Ma, B.; Sun, J. Highly transparent and water-enabled healable antifogging and frost-resisting films based on poly(vinyl alcohol)-Nafion complexes. Chem. Mater. 2016, 28, 6975–6984. [Google Scholar] [CrossRef]
- Wouters, M.; Craenmehr, E.; Tempelaars, K.; Fischer, H.; Stroeks, N.; van Zanten, J. Preparation and properties of a novel remendable coating concept. Prog. Org. Coat. 2009, 64, 156–162. [Google Scholar] [CrossRef]
- Scheltjens, G.; Brancart, J.; de Graeve, I.; van Mele, B.; Terryn, H.; van Assche, G. Self-healing property characterization of reversible thermoset coatings. J. Therm. Anal. Calorim. 2011, 105, 805–809. [Google Scholar] [CrossRef]
- Imbesi, P.M.; Fidge, C.; Raymond, J.E.; Cauët, S.I.; Wooley, K.L. Model Diels-Alder studies for the creation of amphiphilic cross-linked networks as healable, antibiofouling coatings. ACS Macro Lett. 2012, 1, 473–477. [Google Scholar] [CrossRef]
- Kötteritzsch, J.; Stumpf, S.; Hoeppener, S.; Vitz, J.; Hager, M.D.; Schubert, U.S. One-component intrinsic self-healing polymer for coatings based on reversible crosslinking by Diels-Alder-cycloaddition, macromol. Chem. Phys. 2013, 214, 1636–1649. [Google Scholar]
- Barthel, M.J.; Rudolph, T.; Teichler, A.; Paulus, R.M.; Vitz, J.; Hoeppener, S.; Hager, M.D.; Schacher, F.H.; Schubert, U.S. Self-healing materials via reversible crosslinking of poly(ethylene oxide)-block-poly(furfuryl glycidyl ether) (PEO-b-PFGE) block copolymer films. Adv. Funct. Mater. 2013, 23, 4921–4932. [Google Scholar] [CrossRef]
- Turkenburg, D.H.; Durant, Y.; Fischer, H.R. Bio-based self-healing coatings based on thermo-reversible Diels-Alder reaction. Prog. Org. Coat. 2017, 111, 38–46. [Google Scholar] [CrossRef]
- Zheludkevich, M.L.; Tedim, J.; Ferreira, M.G.S. “Smart” coatings for active corrosion protection based on multi-functional micro and nanocontainers. Electrochim. Acta 2012, 82, 314–323. [Google Scholar] [CrossRef]
- Lutz, A.; van den Berg, O.; Wielant, J.; de Graeve, I.; Terryn, H. A Multiple-action self-healing coating. Front. Mater. 2016, 2, 73. [Google Scholar] [CrossRef]
- Andreeva, D.V.; Shchukin, D.G. Smart self-repairing protective coatings. Mater. Today 2008, 11, 24–30. [Google Scholar] [CrossRef]
- Chuo, T.W.; Liu, Y.L. Furan-functionalized aniline trimer based self-healing polymers exhibiting high efficiency of anticorrosion. Polymer 2017, 125, 227–233. [Google Scholar] [CrossRef]
- Diaz, M.M.; Brancart, J.; van Assche, G.; van Mele, B. Room-temperature versus heating-mediated healing of a Diels-Alder crosslinked polymer network. Polymer 2018, 153, 453–463. [Google Scholar] [CrossRef]
- Brancart, J.; Scheltjens, G.; Muselle, T.; van Mele, B.; Terryn, H.; van Assche, G. Atomic force microscopy-based study of self-healing coatings based on reversible polymer network systems. J. Intell. Mater. Syst. Struct. 2014, 25, 40–46. [Google Scholar] [CrossRef]
- Yoon, J.A.; Kamada, J.; Koynov, K.; Mohin, J.; Nicola, R.; Zhang, Y.; Balazs, A.C.; Kowalewski, T.; Matyjaszewski, K. Self-healing polymer films based on thiol-disulfide exchange reactions and self-healing kinetics measured using atomic force microscopy. Macromolecules 2012, 45, 142–149. [Google Scholar] [CrossRef]
- Kim, S.Y.; Lee, T.H.; Park, Y.I.; Nam, J.H.; Noh, S.M.; Cheong, I.W.; Kim, J.C. Influence of material properties on scratch-healing performance of polyacrylate-graft-polyurethane network that undergo thermally reversible crosslinking. Polymer 2017, 128, 135–146. [Google Scholar] [CrossRef]
- González-García, Y.; Santana, J.J.; González-Guzmán, J.; Izquierdo, J.; González, S.; Souto, R.M. Scanning electrochemical microscopy for the investigation of localized degradation processes in coated metals. Prog. Org. Coat. 2010, 69, 110–117. [Google Scholar] [CrossRef]
- González, S.; Santana, J.J.; González-García, Y.; Fernández-Mérida, L.; Souto, R.M. Scanning electrochemical microscopy for the investigation of localized degradation processes in coated metals: Effect of oxygen. Corros. Sci. 2011, 53, 1910–1915. [Google Scholar] [CrossRef]
- Scheltjens, G.; Diaz, M.M.; Brancart, J.; van Assche, G.; van Mele, B. A self-healing polymer network based on reversible covalent bonding. React. Funct. Polym. 2013, 73, 413–420. [Google Scholar] [CrossRef]
- Diaz, M.M.; van Assche, G.; Maurer, F.H.J.; van Mele, B. Thermophysical characterization of a reversible dynamic polymer network based on kinetics and equilibrium of an amorphous furan-maleimide Diels-Alder cycloaddition. Polymer 2017, 120, 176–188. [Google Scholar] [CrossRef]
- Cuvellier, A.; Verhelle, R.; Brancart, J.; Vanderborght, B.; van Assche, G.; Rahier, H. The influence of stereochemistry on the reactivity of the Diels-Alder cycloaddition and the implications for reversible network polymerization. Polym. Chem. 2019, in press. [Google Scholar] [CrossRef]
- Winter, H.; Chambon, F. Analysis of linear viscoelasticity of a crosslinking polymer at the gel point. J. Rheol. 1986, 30, 367–382. [Google Scholar] [CrossRef]
- Miller, D.R.; Macosko, C.W. A New derivation of post gel properties of network polymers. Macromolecules 1976, 9, 206–211. [Google Scholar] [CrossRef]

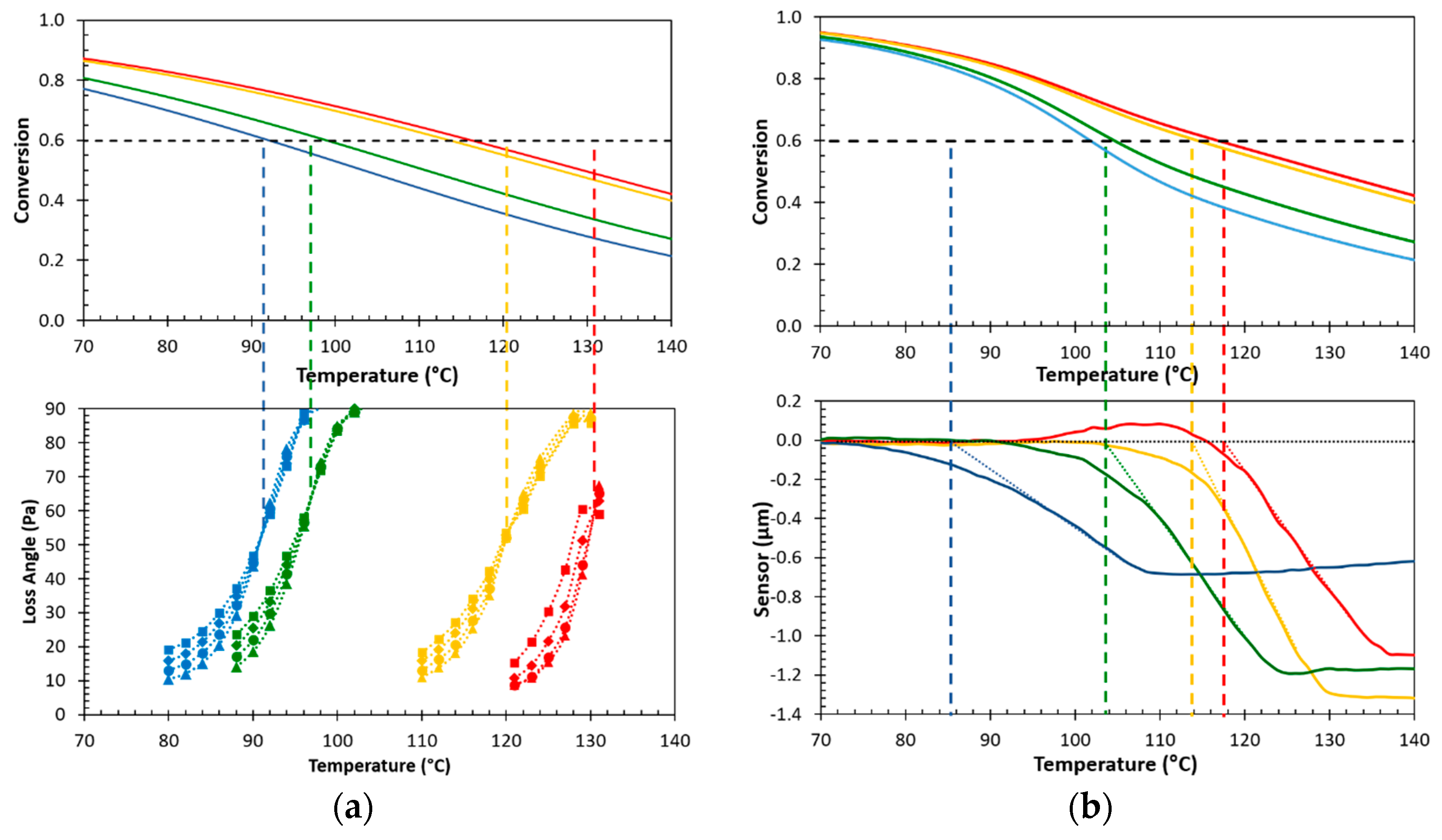
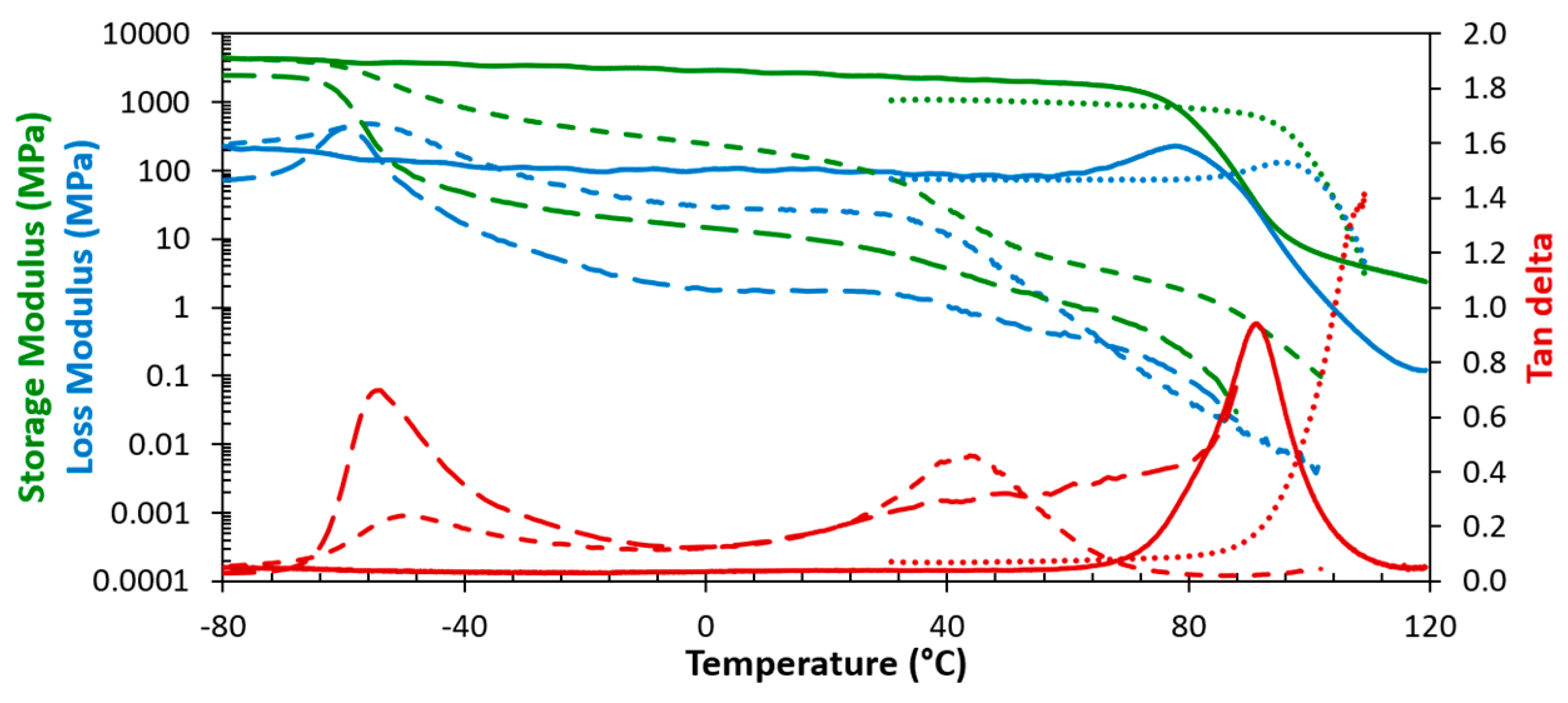


| Network | [M]0 (mol kg−1) | Tg (°C) 1 | E′ (MPa) 2 | Tgel,eq (°C) | Tgel (°C) 3 | Tsoft (°C) |
|---|---|---|---|---|---|---|
| DPBM-F230 | 2.52 | 95 | >2 × 103 | 116 | 130 | 118 |
| DPBM-F400 | 2.22 | 79 | 2.3 × 103 | 114 | 120 | 114 |
| DPBM-F2000 | 1.02 | −47 | 65 | 99 | 97 | 104 |
| DPBM-F4000 | 0.69 | −60 | 6.4 | 92 | 91 | 85 |
| DPBM-F400 | Model | Temperature | τseal (min) | η∞ | DPBM-F4000 | Model | Temperature | τseal (min) | η∞ |
|---|---|---|---|---|---|---|---|---|---|
| scratches | improved | 80 °C | 14.3 | 80.0% | scratches | improved | 70 °C | 24.4 | 37% |
| 90 °C | 12.0 | 88.4% | 75 °C | 10.1 | 71% | ||||
| 100 °C | 1.5 | 87.1% | 80 °C | 5.2 | 82% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brancart, J.; Verhelle, R.; Mangialetto, J.; Van Assche, G. Coupling the Microscopic Healing Behaviour of Coatings to the Thermoreversible Diels-Alder Network Formation. Coatings 2019, 9, 13. https://doi.org/10.3390/coatings9010013
Brancart J, Verhelle R, Mangialetto J, Van Assche G. Coupling the Microscopic Healing Behaviour of Coatings to the Thermoreversible Diels-Alder Network Formation. Coatings. 2019; 9(1):13. https://doi.org/10.3390/coatings9010013
Chicago/Turabian StyleBrancart, Joost, Robrecht Verhelle, Jessica Mangialetto, and Guy Van Assche. 2019. "Coupling the Microscopic Healing Behaviour of Coatings to the Thermoreversible Diels-Alder Network Formation" Coatings 9, no. 1: 13. https://doi.org/10.3390/coatings9010013
APA StyleBrancart, J., Verhelle, R., Mangialetto, J., & Van Assche, G. (2019). Coupling the Microscopic Healing Behaviour of Coatings to the Thermoreversible Diels-Alder Network Formation. Coatings, 9(1), 13. https://doi.org/10.3390/coatings9010013