ANN Laser Hardening Quality Modeling Using Geometrical and Punctual Characterizing Approaches
Abstract
:1. Introduction
2. Experimental Aspect
2.1. Experimental Conditions
2.2. Experimental Design
2.3. Experimental Set-Up
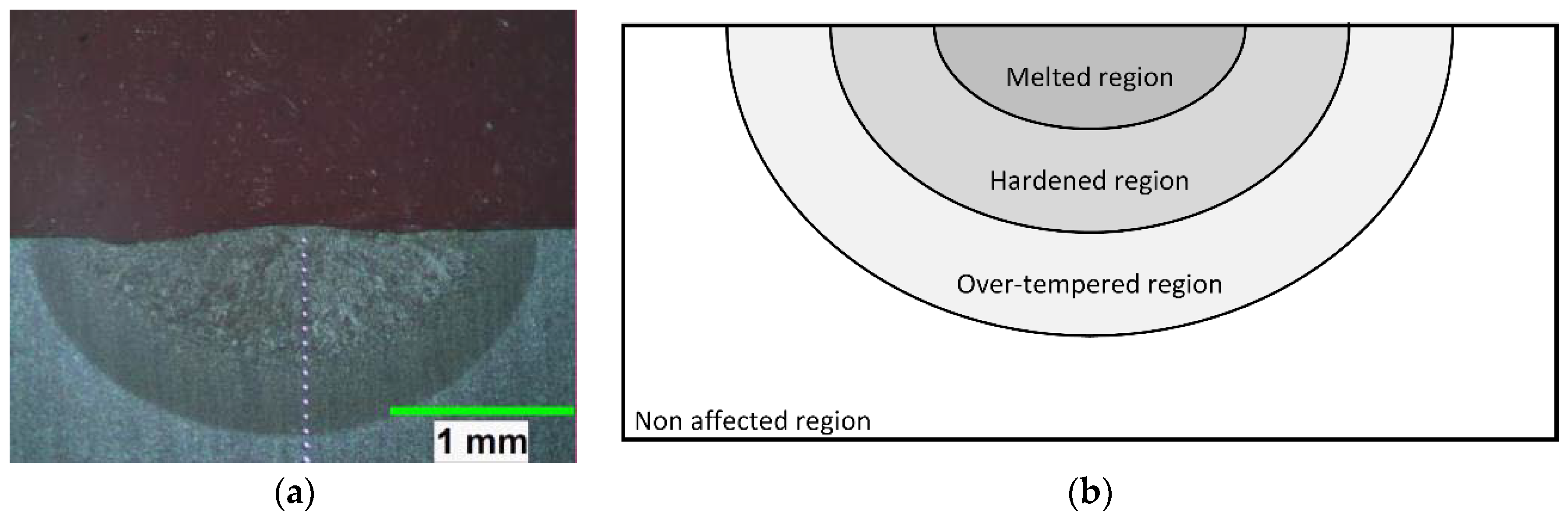
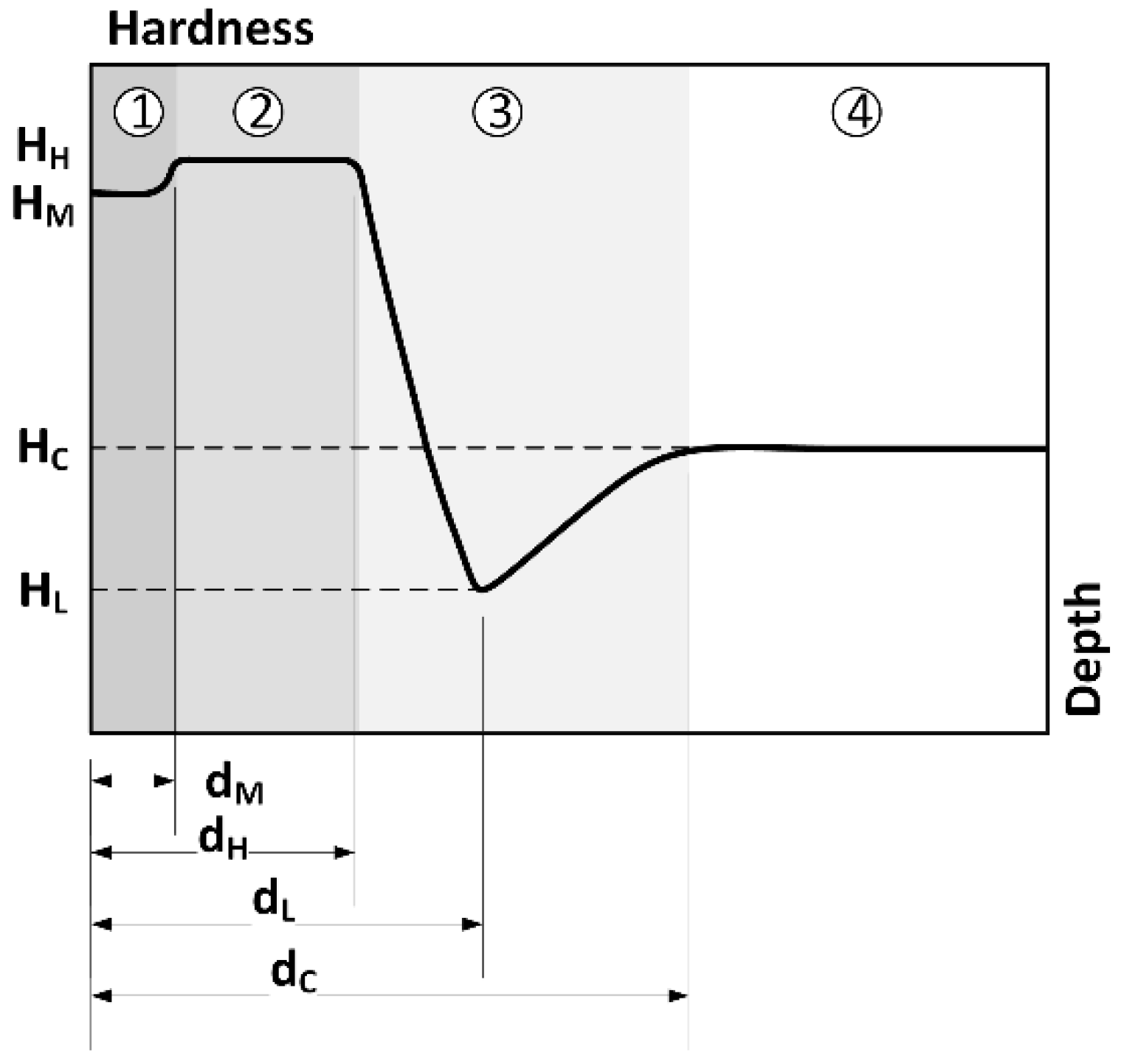
2.4. Experimental Results Analysis
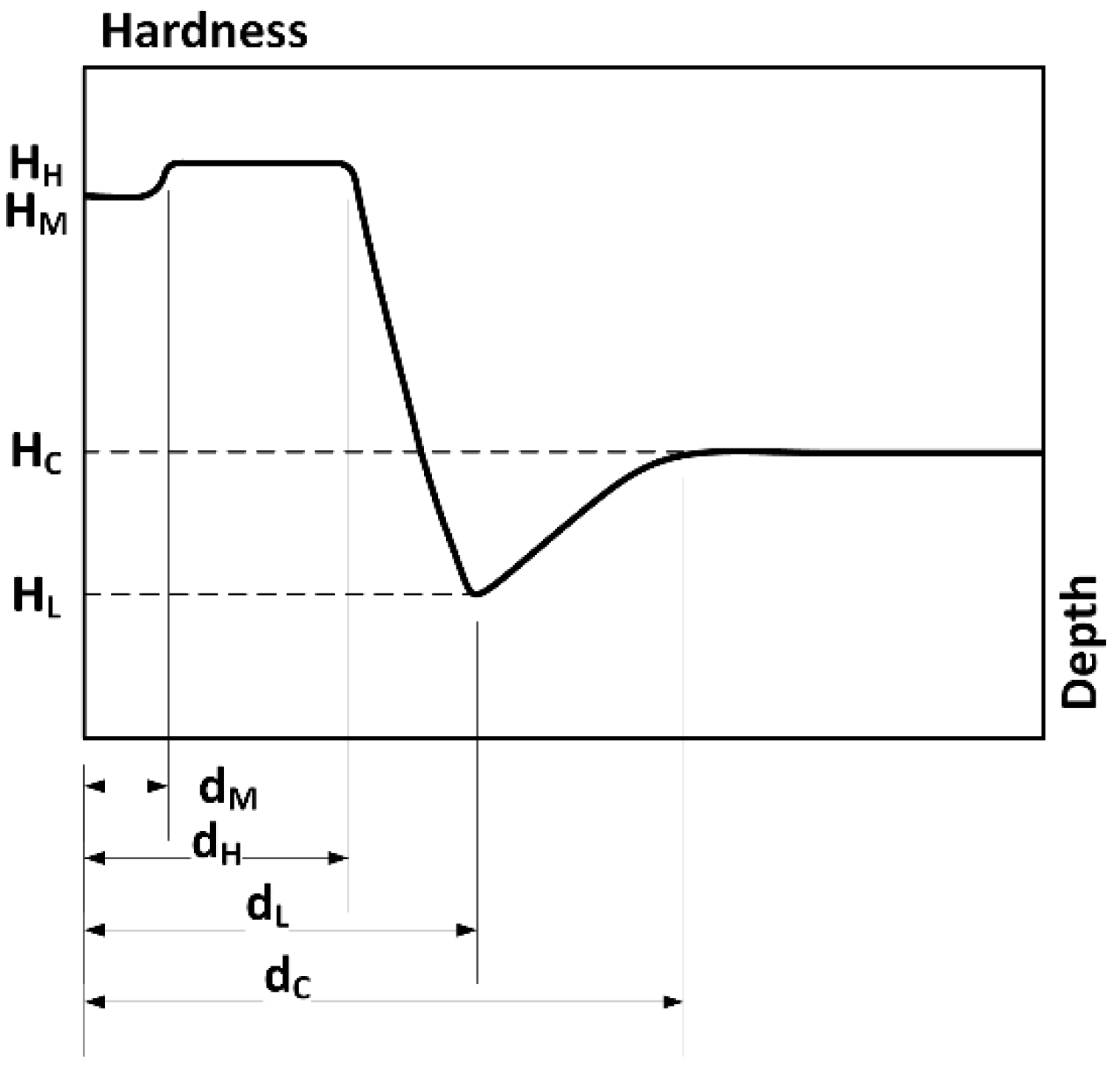
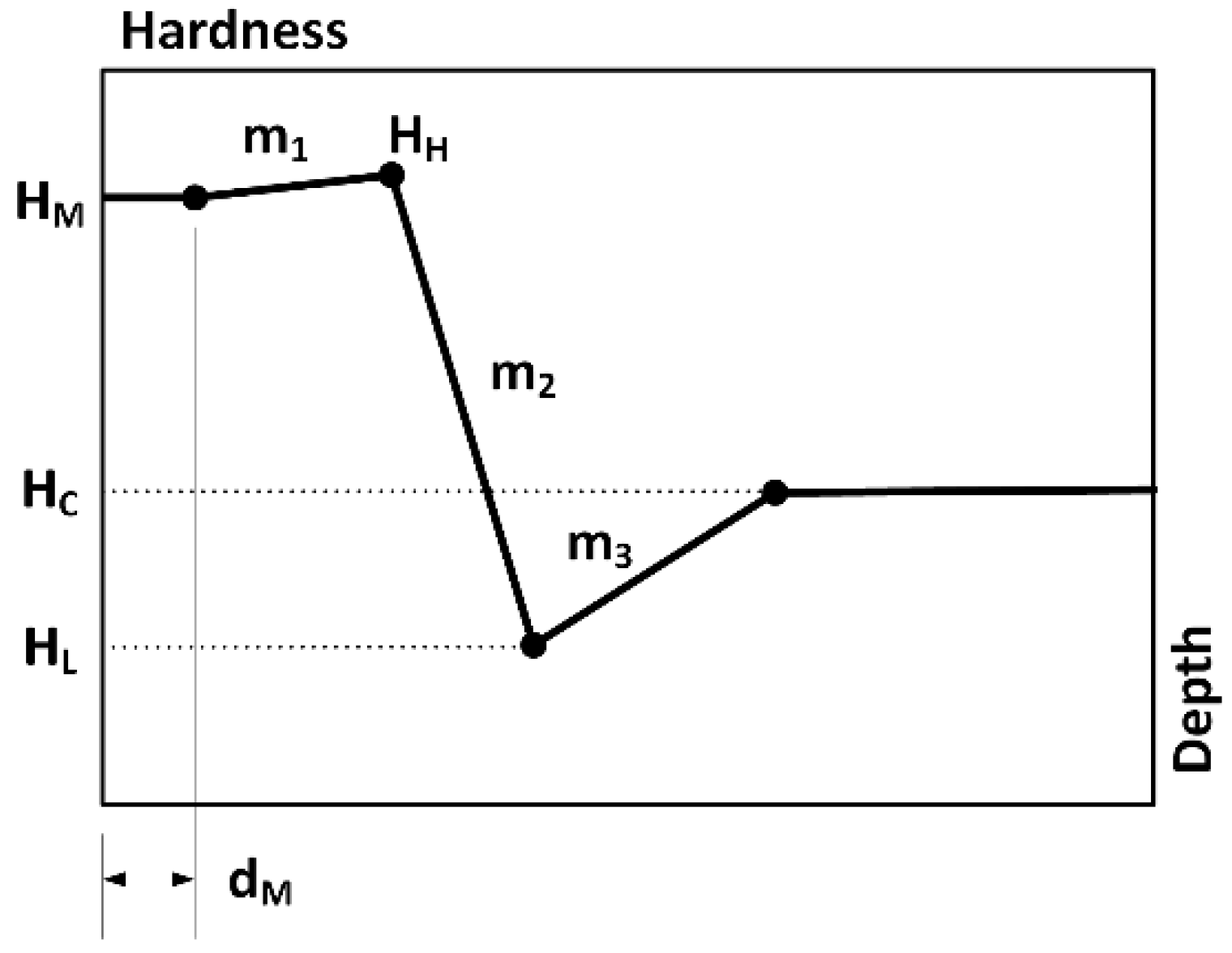
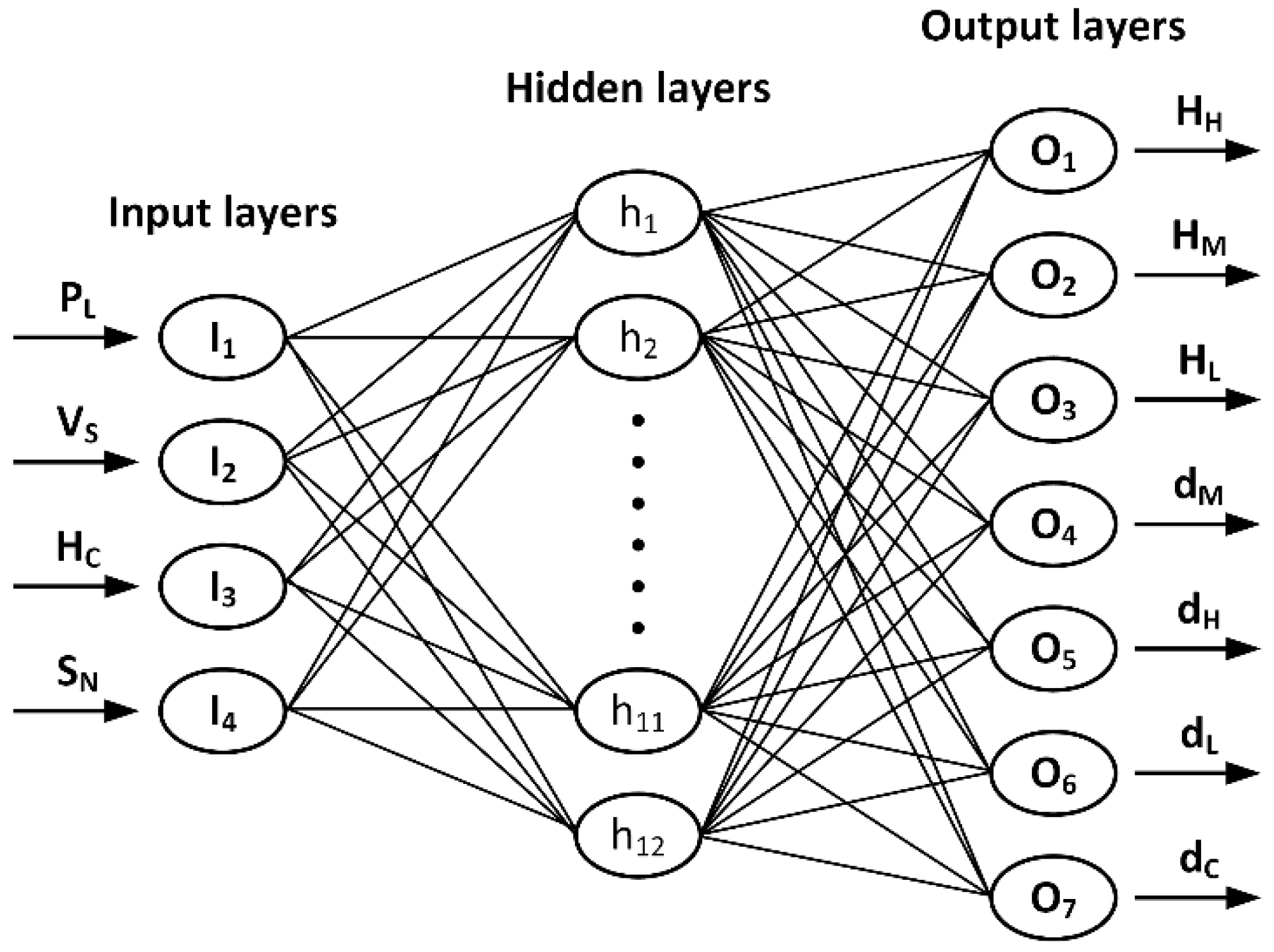
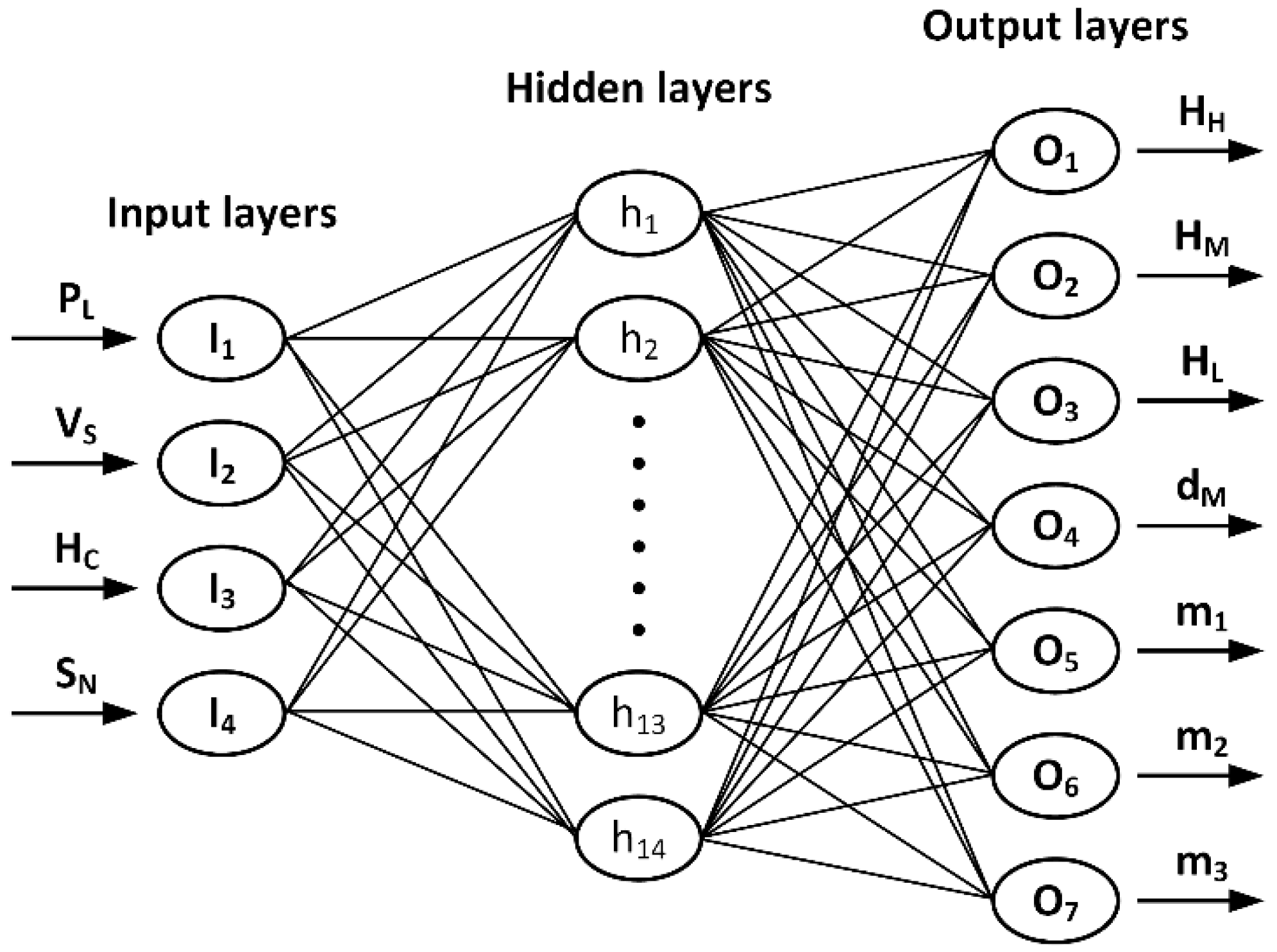
3. LHQ Assessment Model
Modeling Techniques
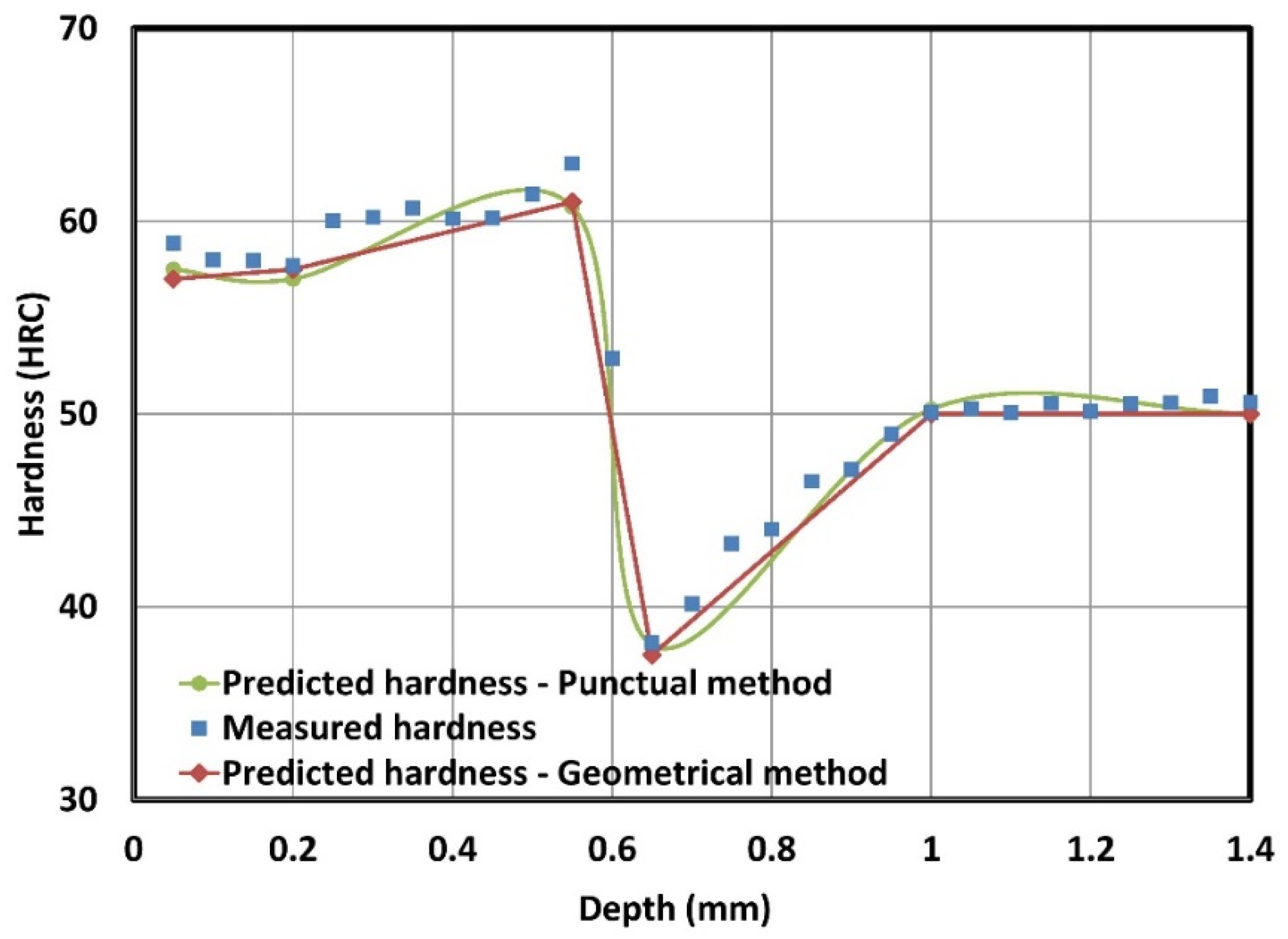
4. Results and Discussion
5. Conclusions
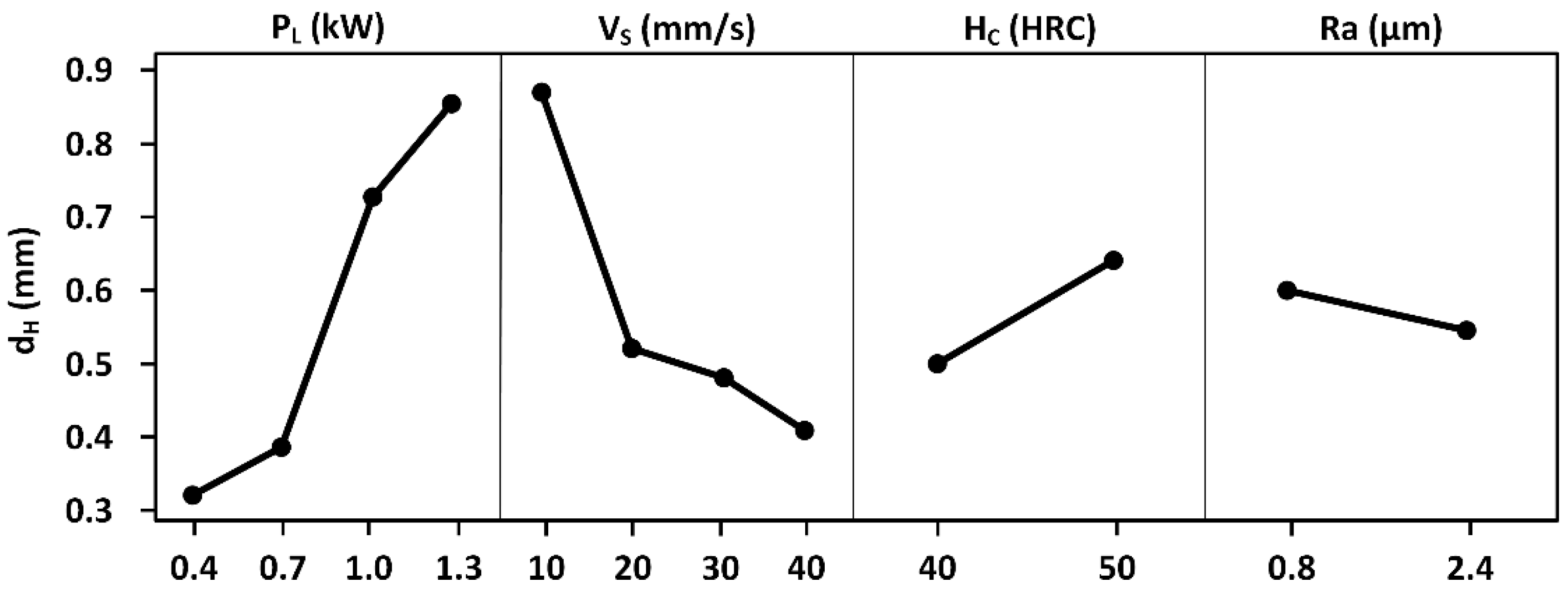
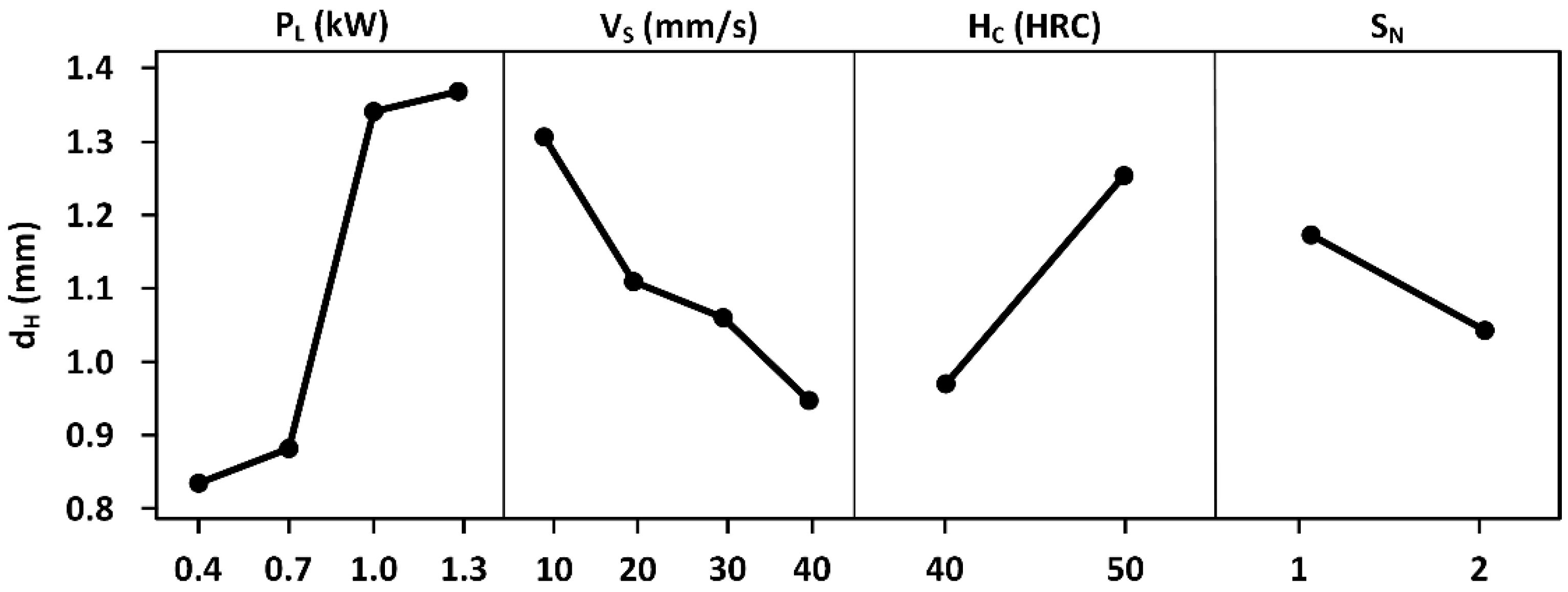
- Laser hardening processing was performed on 4340 steel during which the parameters of laser power, beam scanning speed, initial hardness and surface roughness were considered and for which the testing strategy was designed according to the Taguchi method (OA). The analysis of variance indicated that the machine parameters (laser power and beam scanning speed, in order of importance) have the greatest impact on process quality, followed by initial hardness.
- The impact of surface roughness was quite low compared to the rest of the variables. By repeating the same experimental process and exchanging the surface roughness variable for surface nature, it was determined that for a certain defined interval, surface nature has more of an impact than surface roughness; the experiment’s total error contribution decreased when surface nature was used. The results of the experiment’s second process were considered for the modeling process in this study.
- Structured approaches were adopted to model the LHQ variables according to the second experiment parameters using a multilayer perceptron ANN calculation model. The generated models were evaluated through performance evaluation criteria, and the results allowed us to conclude the following. Modeling the extracted attributes from the hardness profile curve using both approaches is an ingenious way to model LHQ elements with excellent accuracy.
- According to the accuracy of the generated models, the geometrical attributes are the most appropriate variables for LHQ modeling, rather than the punctual attributes. However, both approaches proposed are effective techniques that provide promising LHQ models.
Author Contributions
Funding
Conflicts of Interest
References
- Thomas, G.D.; Samuel, J.R.; Glenn, W.G. Heat Treatment and Properties of Iron and Steel; National Bureau of Standards Monograph 18, Supersedes Circular 495 and Monograph 18; National Bureau of Standards: Gaithersburg, MD, USA, 1966. [Google Scholar]
- Schneider, M.J.; The Timken Company; Chatterjee, M.S.; Bodycote. Introduction to Surface Hardening of Steels. In ASM Handbook, Volume 4A, Steel Heat Treating Fundamentals and Processes; Dossett, J., Totten, G.E., Eds.; ASM International: Almere, The Netherlands, 2013; pp. 389–398. [Google Scholar]
- Shang, H.M. On the width and depth of hardened zones during laser transformation hardening of tool steels. J. Mater. Proc. Technol. 1990, 23, 65–72. [Google Scholar] [CrossRef]
- Katsamas, A.; Zervaki, A.D.; Haidemenopoulos, G.N. Laser-beam surface transformation hardening of hypoeutectoid Ck-60 steel. Steel Res. Int. 1997, 68, 119–124. [Google Scholar] [CrossRef]
- Shiue, R.K.; Chen, C. Laser transformation hardening of tempered 4340 steel. Metall. Mater. Trans. A 1992, 23, 163–170. [Google Scholar] [CrossRef]
- Babu, P.D.; Buvanashekaran, G.; Balasubramanian, K.R. Experimental studies on the microstructure and hardness of laser transformation hardening of low alloy steel. Trans. Can. Soc. Mech. Eng. 2012, 36, 242–257. [Google Scholar] [CrossRef]
- Komanduri, R.; Hou, Z.B. Thermal analysis of the laser surface transformation hardening process. Int. J. Heat Mass Trans. 2011, 44, 2845–2862. [Google Scholar] [CrossRef]
- Grum, J.; Šturm, R. Laser surface melt-hardening of gray and nodular irons. Appl. Surf. Sci. 1997, 109, 128–132. [Google Scholar] [CrossRef]
- Lambiase, F.; Di Ilio, A.M.; Paoletti, A. Prediction of Laser Hardening by Means of Neural Network. In Proceedings of the 8th CIRP Conference on Intelligent Computation in Manufacturing Engineering, Ischia, Italy, 18–20 July 2012; pp. 181–186. [Google Scholar]
- Woo, H.G.; Cho, H.S. Estimation of hardened layer dimensions in laser surface hardening processes with variations of coating thickness. Surf. Coat. Technol. 1998, 102, 205–217. [Google Scholar] [CrossRef]
- Acherjee, B.; Mondal, S.; Tudu, B.; Misra, D. Application of artificial neural network for predicting weld quality in laser transmission welding of thermoplastics. Appl. Soft Comput. 2011, 11, 2548–2555. [Google Scholar] [CrossRef]
- Hitchens, D.M.W.N.; Clausen, J.; Fichter, K. Asian Productivity Organization. In International Environmental Management Benchmarks; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Mason, R.L.; Gunst, R.F.; Hess, J.L. Statistical Design and Analysis of Experiments: With Applications to Engineering and Science; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Alberdi, A.; Rivero, A.; López de Lacalle, L.N.; Etxeberria, I.; Suárez, A. Effect of process parameter on the kerf geometry in abrasive water jet milling. Int. J. Adv. Manuf. Technol. 2010, 51, 467–480. [Google Scholar] [CrossRef]
- Arnaiz-González, Á.; Fernández-Valdivielso, A.; Bustillo; López de Lacalle, L.N. Using artificial neural networks for the prediction of dimensional error on inclined surfaces manufactured by ball-end milling. Int. J. Adv. Manuf. Technol. 2016, 83, 847–859. [Google Scholar] [CrossRef]
- El Ouafi, A.; Belanger, R.; Guillot, M. Dynamic resistance based model for on-line resistance spot welding quality assessment. Mater. Sci. Forum 2012, 709–709, 2925–2930. [Google Scholar] [CrossRef]
| Parameters | Levels |
|---|---|
| Power (kW) | 0.4, 0.7, 1.0 and 1.3 |
| Speed (mm/s) | 10, 20, 30 and 40 |
| Initial hardness (HRC) | 40, 50 |
| Surface roughness (µm) | 0.8, 2.4 |
| Source | DF | Sum of Squares | Mean Square | f-Value | p-Value | Contributions (%) |
|---|---|---|---|---|---|---|
| PL (kW) | 3 | 0.81125 | 0.27042 | 14.09 | 0.002 | 52.76 |
| VS (mm/s) | 3 | 0.50625 | 0.16875 | 8.79 | 0.009 | 32.92 |
| HC (HRC) | 1 | 0.07562 | 0.07562 | 3.94 | 0.088 | 4.91 |
| Ra (µm) | 1 | 0.01000 | 0.01000 | 0.52 | 0.494 | 0.65 |
| Error | 7 | 0.13437 | 0.01920 | – | – | 8.73 |
| Total | 15 | 1.53750 | – | – | – | 100 |
| Characteristic | DoF | Sum of Squares | Mean Square | f-Value | p-Value | Contributions (%) |
|---|---|---|---|---|---|---|
| PL (kW) | 3 | 0.94092 | 0.31364 | 55.94 | 0 | 58.66 |
| VS (mm/s) | 3 | 0.25717 | 0.08572 | 15.29 | 0.002 | 16.03 |
| HC (HRC) | 1 | 0.30526 | 0.30525 | 54.45 | 0 | 19.03 |
| SN | 1 | 0.06126 | 0.06125 | 10.93 | 0.013 | 3.81 |
| Error | 7 | 0.03924 | 0.00560 | – | – | 2.47 |
| Total | 15 | 1.60384 | – | – | – | 100 |
| Variables | MAE | XRE | MSE | TSE | ||||
|---|---|---|---|---|---|---|---|---|
| T | V | T | V | T | V | T | V | |
| HH | 0.219 | 0.0640 | 1.149 | 0.497 | 0.0801 | 0.022154 | 1.2816 | 0.022154 |
| HM | 0.2656 | 0.1234 | 1.1 | 0.7709 | 0.099818 | 0.046141 | 1.5971 | 0.415267 |
| HL | 0.2219 | 0.0816 | 0.893 | 0.5932 | 0.0689 | 0.035358 | 1.1026 | 0.318228 |
| dM | 0.0131 | 0.0098 | 0.075 | 0.0493 | 0.000315 | 0.000187 | 0.00505 | 0.001688 |
| dH | 0.0295 | 0.012 | 0.141 | 0.0626 | 0.00138 | 0.000374 | 0.02208 | 0.003367 |
| dL | 0.0386 | 0.0117 | 0.173 | 0.0605 | 0.002342 | 0.000264 | 0.03747 | 0.002384 |
| dC | 0.0303 | 0.0065 | 0.137 | 0.0258 | 0.001444 | 0.000006 | 0.02311 | 0.000539 |
| Variables | MAE | XRE | MSE | TSE | ||||
|---|---|---|---|---|---|---|---|---|
| T | V | T | V | T | V | T | V | |
| HH | 0.1529 | 0.05290 | 0.81 | 0.3248 | 0.040455 | 0.008447 | 0.647286 | 0.076024 |
| HM | 0.2465 | 0.09083 | 1.56 | 0.3969 | 0.148896 | 0.013468 | 2.382342 | 0.121213 |
| HL | 0.2068 | 0.24019 | 1.14 | 1.4457 | 0.081355 | 0.154602 | 1.301689 | 1.391424 |
| dM | 0.0094 | 0.00844 | 0.06 | 0.0463 | 0.000191 | 0.000179 | 0.003058 | 0.001618 |
| m1 | 0.5264 | 0.41324 | 2.35 | 1.7062 | 0.411062 | 0.321390 | 6.577006 | 2.892513 |
| m2 | 0.00034 | 0.00031 | 0 | 0.0020 | 1.95 × 10−7 | 2.57 × 10−7 | 3.12 × 10−6 | 2.83 × 10−7 |
| m3 | 0.49373 | 0.25813 | 2.31 | 1.0456 | 0.359161 | 0.106389 | 5.746584 | 0.957505 |
| Q-Element | Geometrical Approach | Punctual Approach | |
|---|---|---|---|
| T | HH | 0.2537 | 0.3626 |
| dM | 3.7599 | 5.1309 | |
| dH | 0.9377 | 4.7073 | |
| dC | 0.9425 | 3.0091 | |
| V | HH | 0.08836 | 0.1080 |
| dM | 2.77873 | 3.1369 | |
| dH | 0.73379 | 1.9079 | |
| dC | 1.29508 | 0.6520 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maamri, I.; Barka, N.; El Ouafi, A. ANN Laser Hardening Quality Modeling Using Geometrical and Punctual Characterizing Approaches. Coatings 2018, 8, 226. https://doi.org/10.3390/coatings8060226
Maamri I, Barka N, El Ouafi A. ANN Laser Hardening Quality Modeling Using Geometrical and Punctual Characterizing Approaches. Coatings. 2018; 8(6):226. https://doi.org/10.3390/coatings8060226
Chicago/Turabian StyleMaamri, Ilyes, Noureddine Barka, and Abderrazak El Ouafi. 2018. "ANN Laser Hardening Quality Modeling Using Geometrical and Punctual Characterizing Approaches" Coatings 8, no. 6: 226. https://doi.org/10.3390/coatings8060226
APA StyleMaamri, I., Barka, N., & El Ouafi, A. (2018). ANN Laser Hardening Quality Modeling Using Geometrical and Punctual Characterizing Approaches. Coatings, 8(6), 226. https://doi.org/10.3390/coatings8060226






