2. Materials and Methods
Monodisperse polystyrene (PS) latex particles having a density of 1.05 g cm
−3 and an average diameter of 1.2 μm were synthesized at the Institute of Catalysis and Surface Chemistry (Krakow, Poland). They were washed by successive centrifugation and dispersion in ultrapure water. Zeta potential measurements show that they were negatively charged (−35 mV, in water pH 4, NaCl 10
−3 M). Two cationic cetyltrimethyl ammonium surfactants with different anions, bromide (CTAB, >99% pure, Merck, Fontenay sous Bois, France), chloride (CTAC, >98% pure, Fluka, Saint Quentin Fallavier, France) were used as received without further purification. The critical micelle concentration (cmc) value for CTAB and CTAC are 9.4 × 10
−4 M [
22] and 1.3 × 10
−4–1.6 × 10
−4 M respectively [
23]. The particle suspensions were prepared by adding the dispersion of particles into 250 mL of a surfactant solution (5 × 10
−4 M) to obtain a final concentration of 1.25 × 10
7 particles·cm
−3. This low particle concentration was chosen in order not to perturb the hydrodynamic flow. Indeed, Warszinski et al. [
24] demonstrate that the influence of particles on the colloid flow can be neglected if the volume fraction is below 5% (10
12 particles·cm
−3). All dispersions were adjusted to pH 4 with HCl and stirred for 12 h before experiments. The electrophoretic mobilities of the PS particles in water and in CTAB and CTAC solutions were measured with a microelectrophoresis cell (Mark II, Rank Brothers, Bottisham, UK) and the corresponding zeta potentials were then calculated using the Smoluchowski equation. The values of zeta potentials of PS particles dispersed in CTAB or CTAC solutions were equal to +33 mV and +54 mV, respectively. The electrodes were nickel disks of 12 mm diameter (99.0% pure, Goodfellow, Lille, France) that were mechanically polished with SiC emery paper and diamond powder down to 1 μm and cleaned by ultrasonication in ethanol. It has already been determined by electrochemical investigations that deposition takes place on nickel and not on a nickel oxide layer [
16]. The working electrode potential versus the reference electrode (Ag/AgCl) was monitored by means of a potentiostat (Voltalab PGP 201, Radiometer Analytical, Lyon, France).
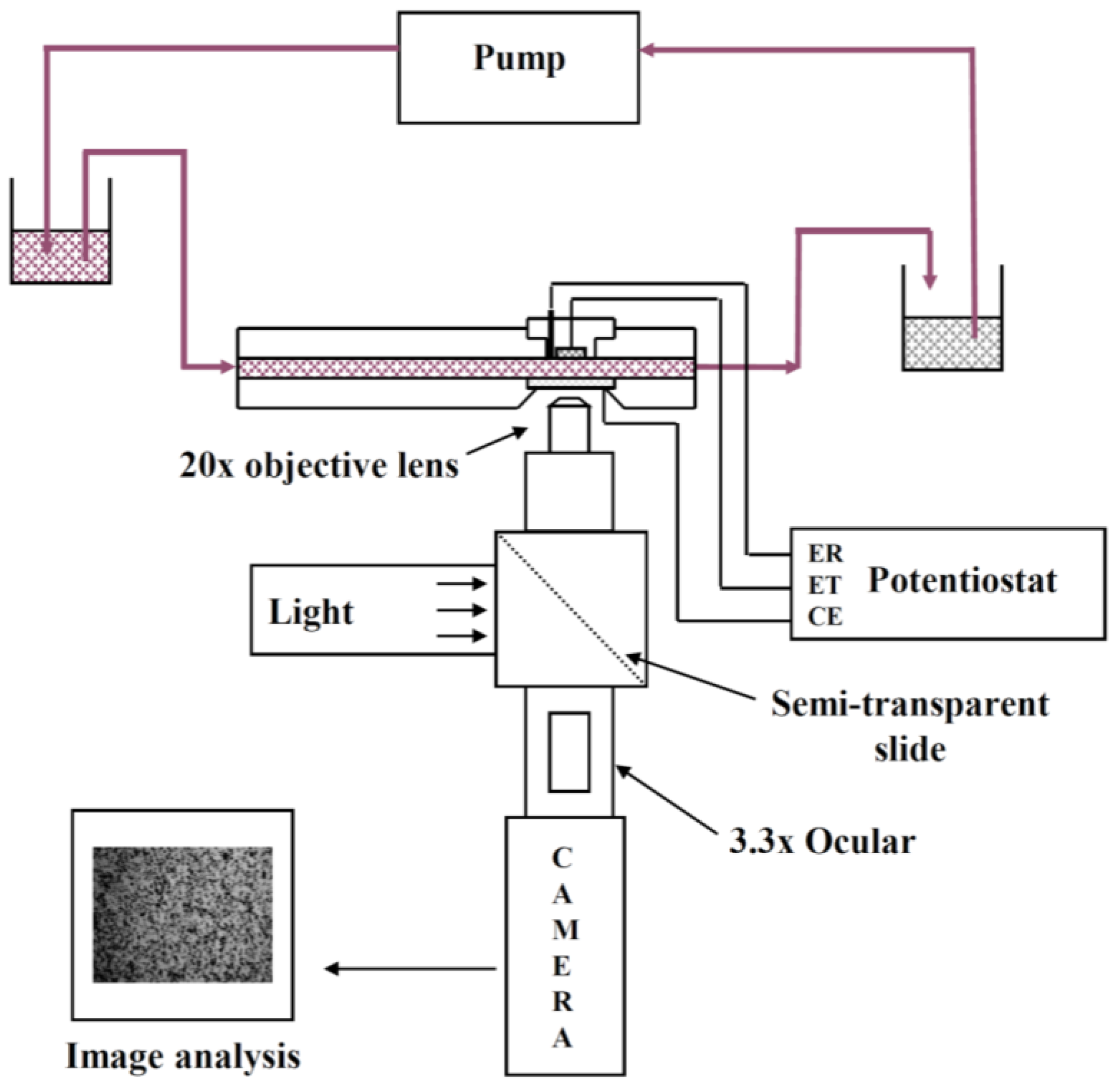
An EPD laminar flow cell was specifically designed for in situ investigation of electrophoretic deposition of micronic particles (of 0.8–100 μm) on a metallic substrate. The apparatus has been described previously [
16,
25]. Briefly, it contains a laminar flow cell combined with an optical set-up and an image analysis system (
Figure 1). This type of cell is of practical significance since it constitutes one of the technological geometries used for electrodeposition of materials and it allows the in-situ observation of the migration and deposition of a particle on an electrode. Moreover it allows continuous circulation of the suspension with constant particle concentration. A decrease in the number of particles due to particle deposition on the cathode is negligible under the experimental conditions of this study (<0.2%).
The suspension flows in a rectangular channel between two parallel plates made of poly(methyl methacrylate) (PMMA). In one plate acting as the cathode a removable plug comprising the circular metallic electrode (about 1 cm in diameter) is inserted. The other plate contains a conductive glass slide, coated with a tin oxide film, acting both as window and counter electrode. The distance between the two facing electrodes is 2 mm. A silver wire treated with hydrochloric acid (1 M) and saturated KCl solutions is inserted through the plug to act as the Ag/AgCl reference electrode. For all experiments the cathode and the glass window were placed vertically in front of the objective and the particles flowed tangentially to these electrodes. Steady flow in the channel is maintained by gravity. A peristaltic pump allowed recycling in order to maintain constant liquid levels between two vessels before and after the laminar flow cell. The conductivity of the suspension during deposition was measured in the vessel at the output of the cell with a conductivity meter (Mettler Seven Easy, Viroflay, France). The values were 190 and 102 μS cm
−1 for CTAB and CTAC solutions, respectively. An electrophoretic force ensures the particle flux to the electrode in this cell. A constant potential of −1.5 V (versus Ag/AgCl) was applied between the nickel and the tin oxide electrodes using a power supply (EG & G Princeton Applied Research, Elancourt, France). The electric potential and current across the cell were measured using a Generis digital multimeter (ESAO 4, Jeulin, Evreux, France). All experiments were performed at pH 4, at room temperature and at a constant flow rate of 3 mL min
−1 and repeated at least twice. These experimental conditions were chosen to compare the results with previous experiments [
26]. The optical set-up used to observe particle behavior was composed of a microscope (Olympus BH2-UMA, Olympus, Rungis, France) equipped with a long working distance objective (mag. 20×), a 3.3× intermediate lens, a cold light lamp, a camera, a video recorder and an image analysis system. The magnification power (mag. 1000×) was high enough to observe the movement of micrometric particles near the working electrode through the window (i.e., the counter electrode) and through the suspension. The camera focused on the center of the electrode to avoid any edge effects.
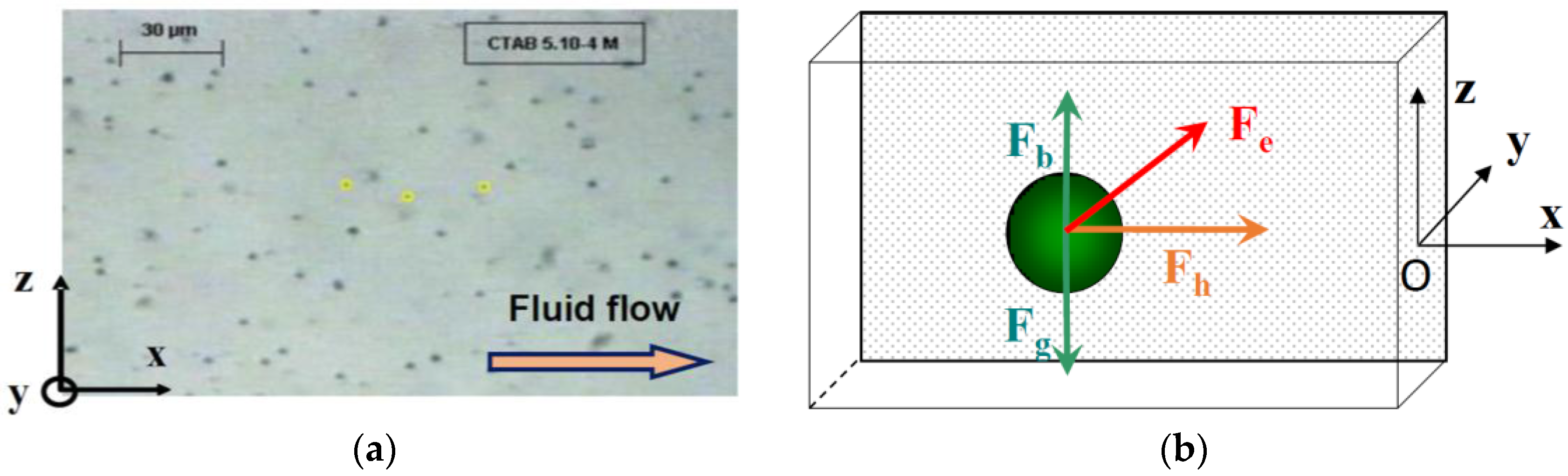
The measurements of particle velocity near the electrode were performed using Replay and Ellix softwares (MICROVISION Instruments, Evry, France). Replay software (Version 4.0) was used to capture an image from the video film every second. The particle position along the
x- and
z-axes were measured on each image using Ellix software (Version 5.0) (
Figure 2a). The measurements were done at different distances from the electrode along the
y-axis starting when particles were visible. For each
y distance, the
x-positions of about 15 particles were determined. We stopped the measurements when the particles stopped on the electrode or formed aggregates with other deposited particles or left the observed area.
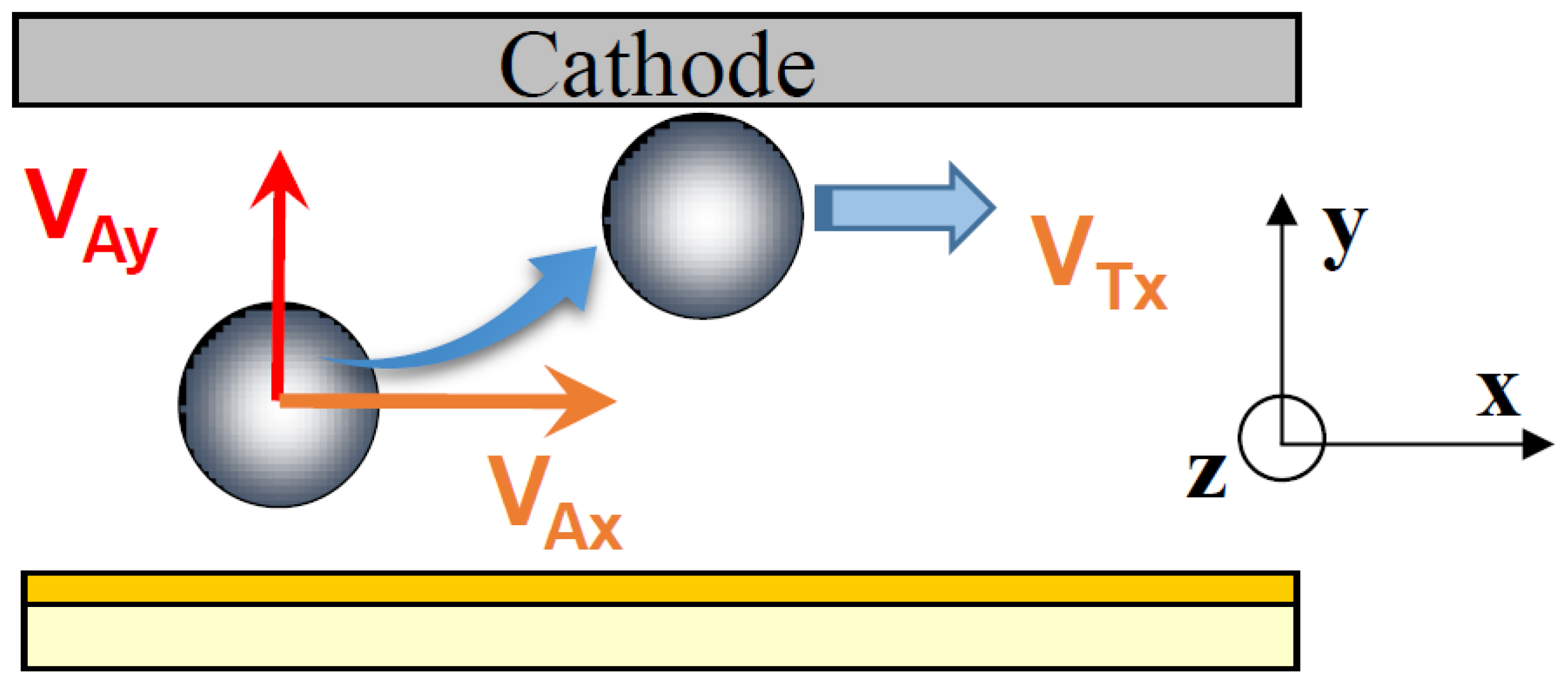
In this cell, the particles are subjected to three external forces (
Figure 2b) perpendicular to each other: the resultant of gravity and buoyancy forces (along the vertical
z-axis), the hydrodynamic force parallel to the electrode (along the longitudinal
x-axis) and the electrophoretic force directed toward the electrode (along the
y-axis). The migration to the cathode is the result of the sum of these external forces.
The resultant of the gravity and buoyancy forces is a function of the size
a and of the difference between the particle ρ
p and liquid ρ
f densities:
To determine the hydrodynamic force, we first checked that the fluid flow was laminar in this cell. The fluid velocity can be derived from the Navier-Stokes equation [
27] for an incompressible fluid and a stationary flow along one direction (
x-axis) which is the case for our experimental conditions. The fluid velocity profile between the two facing electrodes is then parabolic if the flow is laminar. We checked it by measuring the velocity of PS particles (4 μm in diameter) in the absence of an applied electric field and for different fluid flows up to 0.07 cm
3 s
−1 [
25]. This last value corresponds to a Reynolds number of about one. In this case, the hydrodynamic force exerted by the fluid on a particle can be calculated from the Stokes drag law. It is proportional to the particle size
a, the dynamic viscosity of the fluid η and to the particle velocity
Vx [
27]:
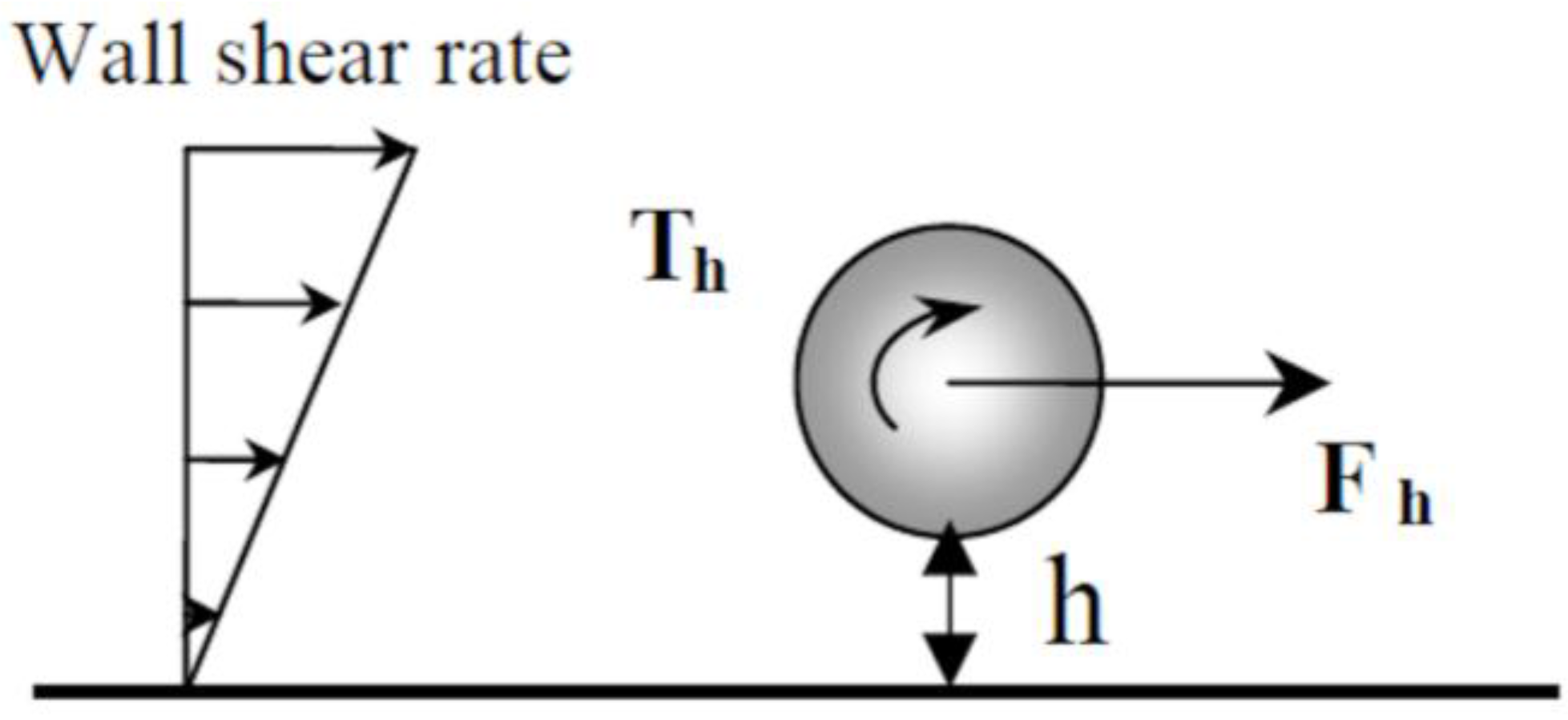
Due to the velocity gradient in the laminar flow cell, particles are also subjected to torque (
Figure 3). Recently, weakly adhesive nanoscale features were used to facilitate rolling of microparticles in shear flow [
20]. Using the EPD laminar flow cell, we observed the rotation of large particles (≈10 μm) but rolling was not visible for micronic particles.
The hydrodynamic force is modified near the wall [
27,
28] and becomes:
where
H is the dimensionless distance (particle-substrate distance
h/particle radius
a). In a laminar flow, the tangential velocity of the particles near the wall
VTx depends on the wall shear rate
G (s
−1) and is given as follows:
where
f(H) is the correlation function determined by [
28]
For particles having a radius of 600 nm, we consider that the condition (H << 1) is verified for a distance below 50 nm. In the laminar flow cell, the wall shear rate G is defined as G = 6Q/(L·l²) where L is the cell width (2 cm) and l is the cell thickness (2 mm). For a fluid flow equal to 3 mL min−1, the wall shear rate is equal to 3.7 s−1.
Close to the electrode, particles are also submitted to a lifting force [
29]. First-order equation was considered to evaluate its value:
Under our experimental conditions (ρf ≈ 1000 kg m−3, ηf ≈ 1 mPa·s, a = 600 nm) the hydrodynamic and lifting forces were calculated for different particle velocities Vx (1–100 μm s−1) using Equations (2) and (7). In the case of the highest value of the velocity, the lifting force is about one thousand times lower than the hydrodynamic force, therefore it is not considered significant.
The transport of particles in a solution is controlled by the hydrodynamic effects (convection) but also by the thermic effect (diffusion). The Peclet number (ratio of convection to diffusion rates) defined for wall shear flow as Pe// = G·a2/D is 3.3 where G = 3.7 s−1, a = 600 nm and D is the particle coefficient diffusion equal to 3.6 × 10−13 m2. Therefore, the transport by diffusion is considered negligible for our study.
The electrophoretic force depends on the applied electric field and on the size and zeta potential of the particles, so it will act on charged particles in low ionic strength solution. In an infinite liquid media and for a Debye layer having a thickness much lower than the particle size, the electrophoretic force derived from the Smoluchovski equation [
27] is:
where ε is the dielectric permittivity, ζ is the zeta potential of the particle and
E is the electric field applied to the particles.
When the particles approach the electrode, the electrophoretic force is also modified. Fransaer [
30] modelized this force and showed that for
H < 1 (i.e., for the distance below the particle radius), it is about 2–5 times higher than the electrophoretic force in the bulk suspension.
Calculations of the trajectory of a particle near the wall will also depend on the sum of the colloidal forces acting on it. Short range interactions (van der Waals, double layer, specific interactions) between particle and electrode take place near the cathode. The particle-electrode interaction potential was then calculated within the DLVO model considering the attractive (
VvdW) and repulsive (
VEDL) effects [
31].
The Czanercki equation [
32] was used for the retarded van der Waals contribution (
VvdW):
where
A123 is the Hamaker constant for the polystyrene particle-water-metal system (0.3 × 10
−21 J) and λ is the wavelength (100 nm).
The electrostatic double layer contribution (
VEDL) was calculated from the equation proposed by Ruckenstein and Prieve [
33] for an electrolyte 1:1.
with
k the Boltzmann constant,
T the temperature,
e the electronic charge,
z the electrolyte valence, ζ
1 the particle zeta potential, ζ
2 the electrode zeta potential and
k the inverse Debye length.
3. Results
Upon application of the potential, single particles were seen to migrate to the electrode. Most of them did not attach to the electrode but moved along the electrode. From the image analysis, the particle velocities along the
x- and
z- axes were determined.
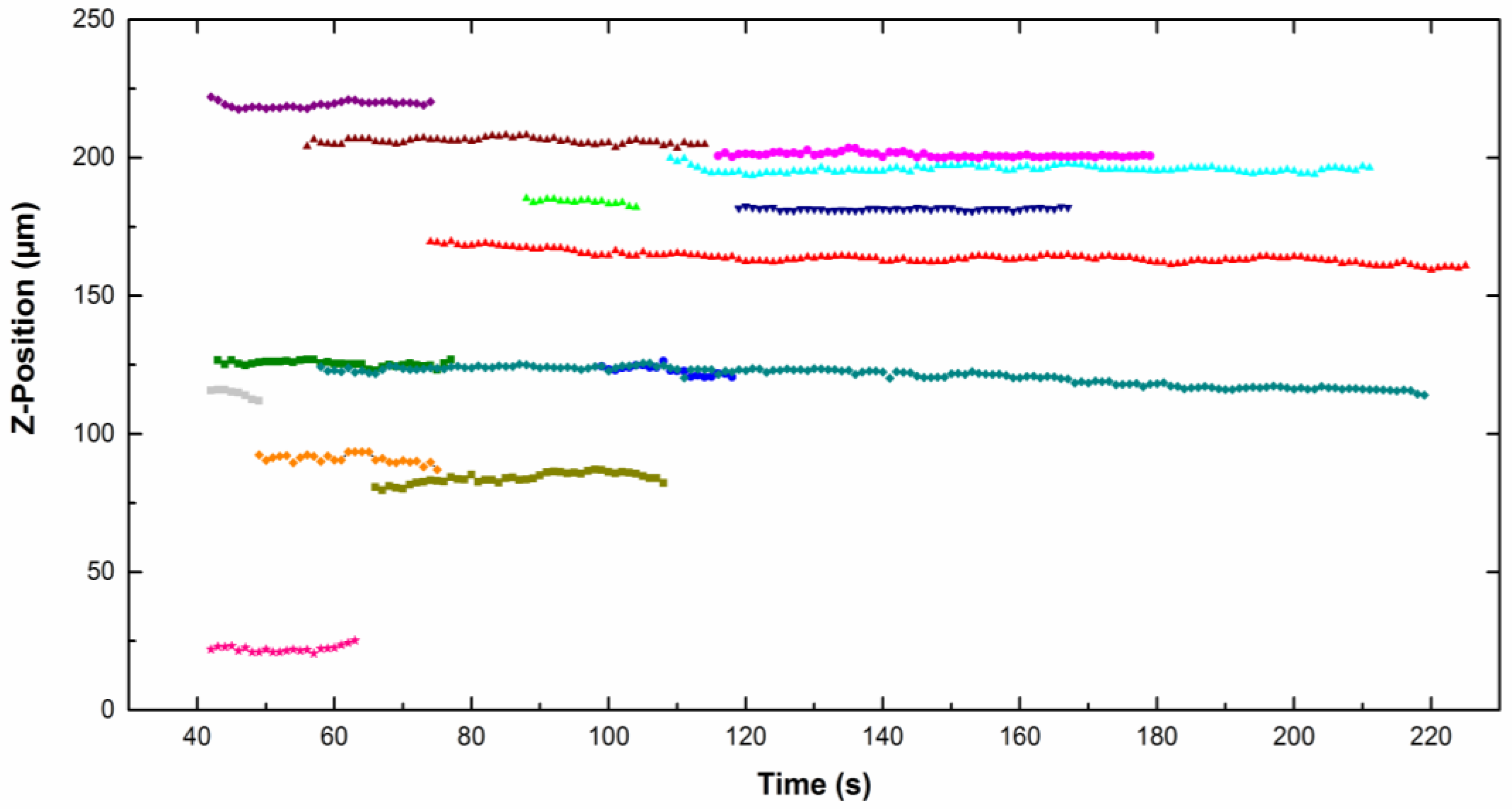
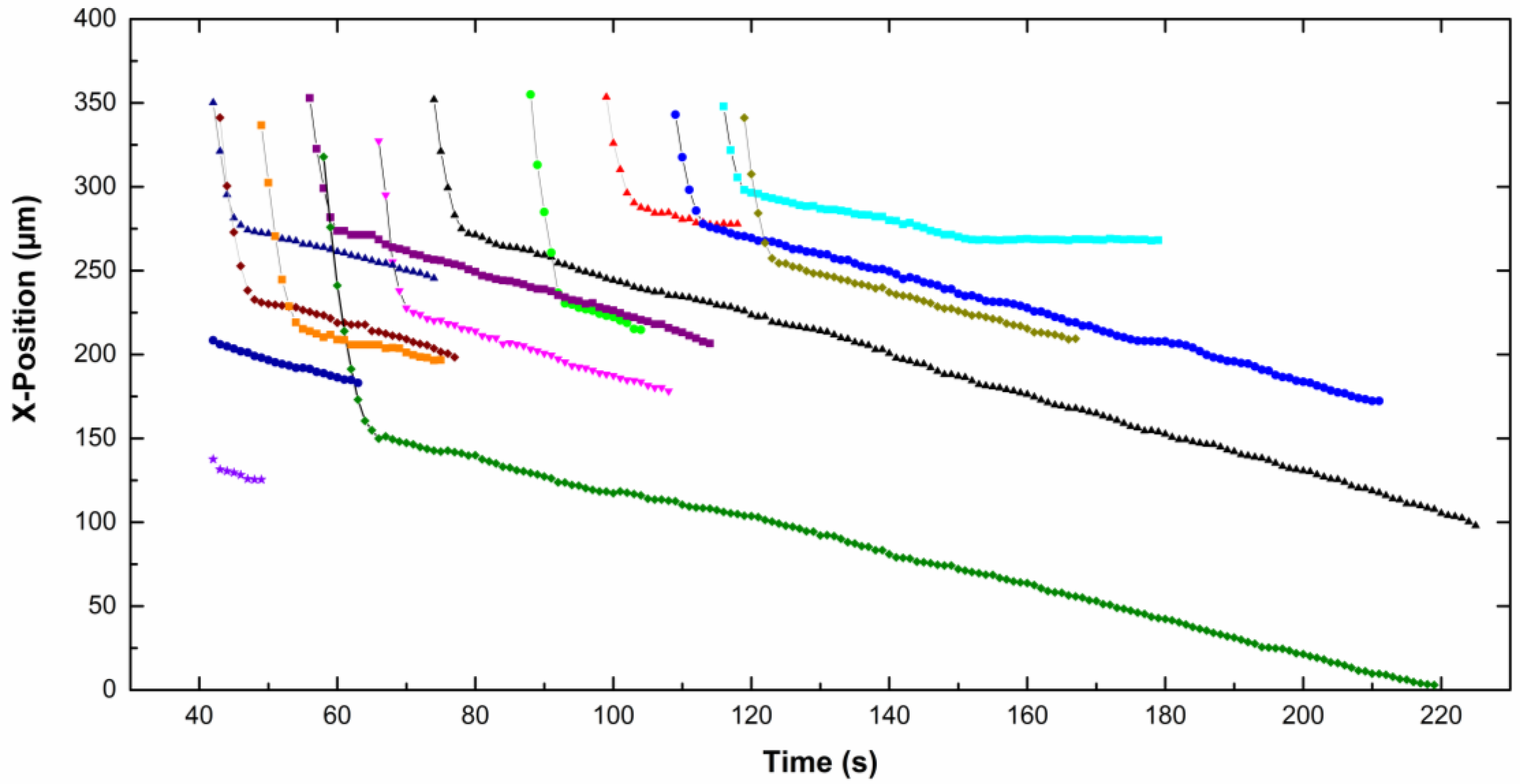
Figure 4 represents the
z-position of different particles moving along the cathode (placed vertically) as a function of time for particles dispersed in CTAB solution. The
z value is quite constant, which means that no sedimentation or flotation took place. The same trend was observed for particles in the CTAC solution. The particle density is close to the liquid density, therefore the result of the buoyancy and gravity forces is around zero (Equation (1)).
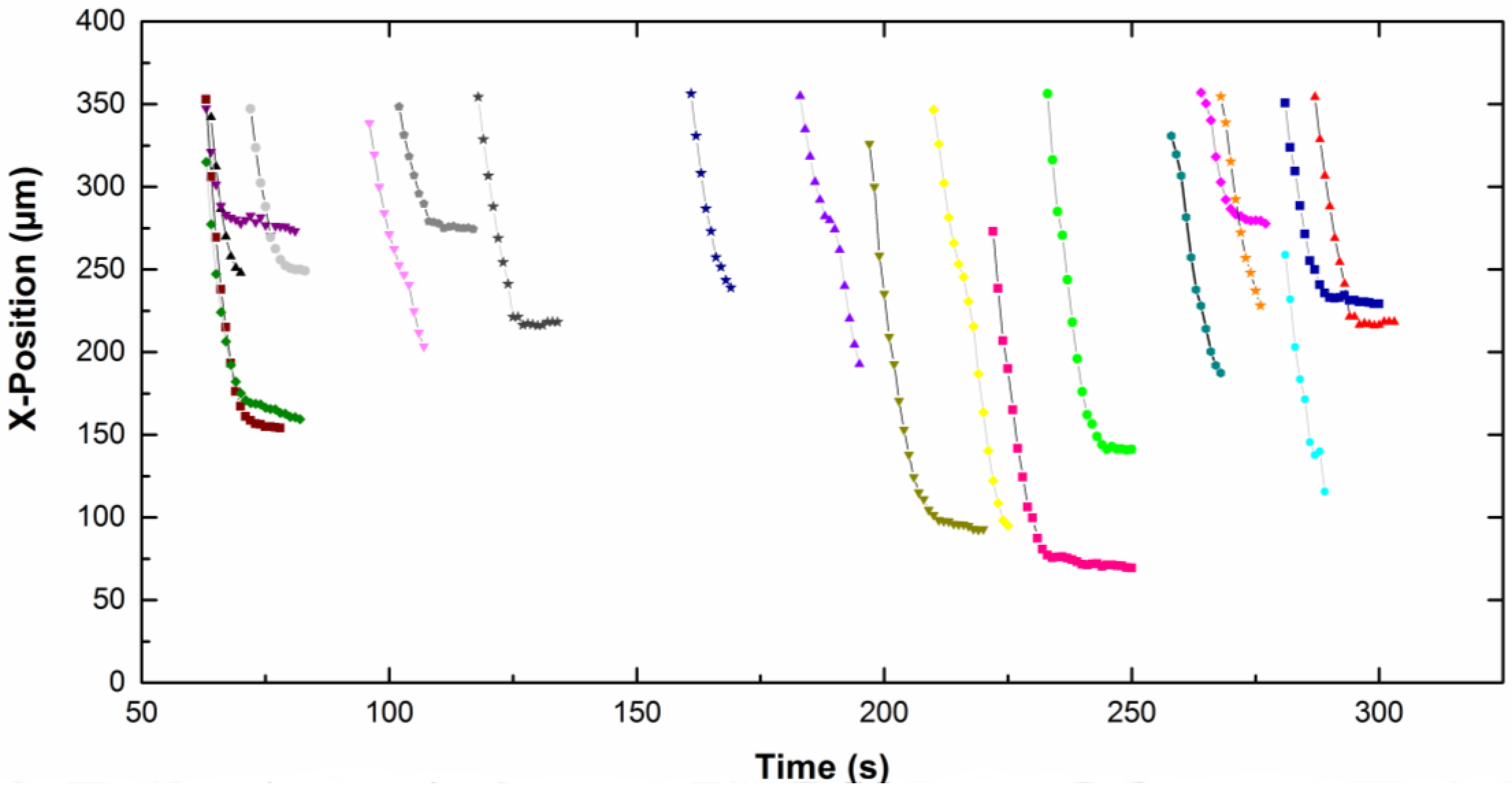
The
x-position of each particle, in focus on the screen, is given as a function of time on
Figure 5 for CTAB solution and
Figure 6 for CTAC solution. Note that the origin of the
x-axis was on the right part of the screen for particles moving from the left to the right, therefore the
x-position decreases with time. The upper part of the curves corresponds to particles approaching the electrode. Then the particles slow down and move slowly along the electrode (lower part of the curves). A net change of the slope is observed for all particles, which means a fall of the particle velocity. Depending on the type of surfactant counterion, particles exhibit different behavior near the electrode. In CTAC solution, particles stopped very quickly. Indeed they moved along the electrode for a few seconds, however in the presence of CTAB particles moved for up to 100 s.
From the curves (
Figure 5 and
Figure 6), we calculated the x-component of the approach velocity
VAx and of the tangential velocity
VTx along the electrode (see
Figure 7). Results are given in
Table 1. The
VAx approach velocity of particles migrating toward the electrode is about 20 μm s
−1. The velocity decreases in a few seconds to about 1 μm s
−1. We observed that both the approach velocity and the tangential velocity near the wall are a little bit lower for particles dispersed in CTAC solution compared to these ones in CTAB solution.
From the values of the tangential velocity VTx near the wall and using Equations (4) and (6), the distance between the particles and the electrode was found to be 18 nm and 0.5 nm for CTAB and CTAC, respectively. These calculations were done without considering external forces. Note that when the applied voltage was switched off, the particles in movement moved away from the cathode surface.
The V
Ay component of the approach velocity can not be measured, therefore we calculated its value from the following equation:
where μ is the electrophoretic mobility and
E the electric field applied to the particle.
The electrophoretic mobility in CTAB and CTAC solutions was equal to 2.337 × 10
−8 m
2 V
−1 s
−1 and 3.824 × 10
−8 m
2 V
−1 s
−1, respectively. The electric field in the suspension can be calculated considering the conductivity
Λ of the suspension, the current
I and the electrode surface area
Ae [
34].
The current after 3 min of deposition was equal to 0.46 and 0.33 mA in CTAB and CTAC suspensions, respectively. The surface area of the cathode was equal to 1.14 cm
2. In CTAB solution the value of the electric field was found to be 211 V m
−1 and 286 V m
−1 in CTAC solution. The calculated V
Ay values of electrophoretic velocities are given in
Table 1. The electrophoretic mobility of particles and the electric field in CTAB solution are lower than for particles in CTAC solution, so the electrophoretic velocity is lower.
Finally, the distance at which the electrophoretic force is equal to the hydrodynamic force was determined from Equations (2) and (8). The hydrodynamic force is higher than the electrophoretic force for most of the channel width. It reverses when particles are a short distance from the electrode, that is, about 50 μm for CTAB-coated particles and 125 μm for CTAC-coated particles. Under these experimental conditions most of the particles flow through the channel however more particles move toward the electrode in the CTAC solution than in the CTAB solution.
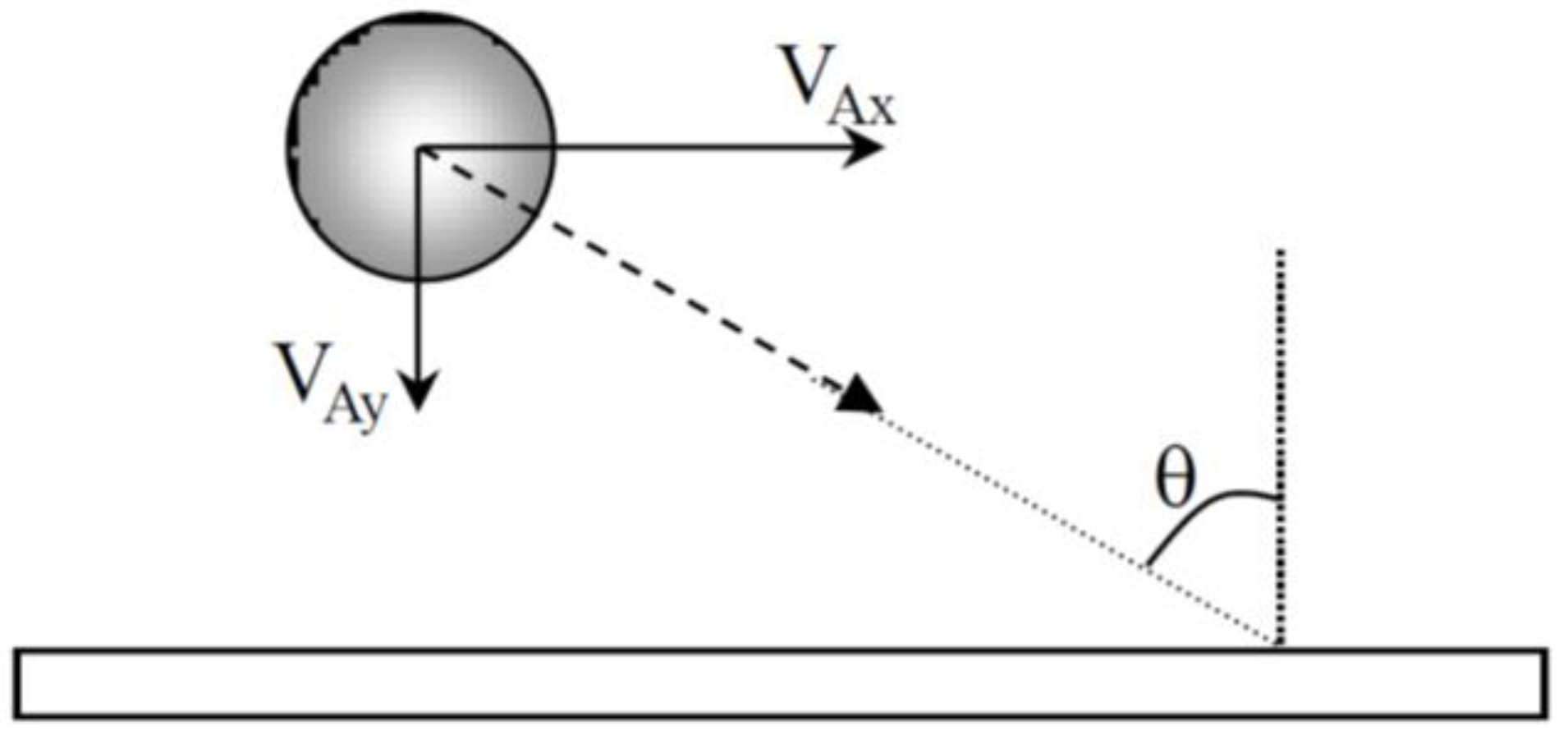
The approach angle of the particles may have an influence on the morphology of aggregates. When particles arrive near the cathode, the approach angle (
Figure 8) was then calculated from the ratio V
Ax/V
Ay of the experimental values given in
Table 1 and is about 80° for CTAB and 60° for CTAC.
Figure 9 shows the morphology of the aggregates after 10 min of deposition. Images were taken from the video film. When electrophoretic deposition of PS particles was done in the CTAB solution, dense structures were observed (
Figure 9a) while more open structures were visible in the CTAC solution (
Figure 9b).
4. Discussion
Using the EPD laminar flow cell, the migration of particles to the cathode as well as their movement along the electrode were observed. The components of particle velocity of functionalized micronic PS particles were measured in cationic CTAB or CTAC surfactant solutions in a constant applied voltage. The surfactant concentration (5 × 10
−4 M) was chosen close to the cmc. Surfactant molecules adsorb on surfaces and form aggregates above a surfactant concentration known as critical surface aggregation concentration (csac). The csac value is a little lower than the cmc above which micelles form in solution. For example, it is about 0.4× cmc for polymer substrates (polystyrene) [
35]. Under these conditions CTA
+ molecules present in the solution adsorb both onto the particles and the cathode forming two-layer aggregate structures (i.e., cylinders, surface micelles or bilayers) with positive head groups of the second layer pointing into the solution [
36]. Indeed zeta potentials of polystyrene particles and of mica sheets become positive at this surfactant concentration [
37]. An electrostatic repulsion arises between the positive particles and the surfactant bilayers adsorbed on the electrode. Moreover, functionalized particles and the electrode are hydrophilic. Both electrostatic and hydrophilic repulsions limit particle adhesion on the cathode. Moreover the surfactant adsorption depends on the type of counter-ions. On the one hand, the zeta potential of PS particles is more positive in CTAC solution (+54 mV) compared to the values in CTAB solution (+33 mV). Bromide ions have a larger radius than chloride ions and are less hydrated [
38]. So, they bind more closely to the CTA
+ head groups, leading to an efficient screening of the surfactant charge. On the other hand, counterions also influence the surfactant adsorption onto electrodes. The cathode is hydrophilic and becomes more or less positive at this surfactant concentration. Indeed, the open circuit potential of nickel electrodes was previously measured as a function of time in both the absence and presence of surfactant [
37]. The shift of the open circuit potential toward more positive values as compared to the case of water without a surfactant was higher for CTAB-coated electrode than for CTAC-coated electrode [
16]. This demonstrated the ability of the surfactant to form a protective layer on the nickel surface which seems more effective in the case of CTAB. An important increase of CTA
+ affinity for the electrode with the expected trend Cl
− < Br
− was also shown by electrocapillarity measurements on a mercury electrode [
39,
40]. The authors attributed the difference of adsorption to the formation of ion pairs between the surfactant molecule and its counterion, which forms only at the electrode surface or in its immediate vicinity and not in solution.
From the value of the
x-component of the tangential velocity near the wall the particle-electrode distance was calculated. We found a distance below 1 nm in the 5 × 10
−4 M CTAC solution and of about 20 nm in the 5 × 10
−4 M CTAB solution. These calculations were done taking only into account the hydrodynamic force acting on a particle moving freely along a smooth wall. Note that the origin of these distances is the distance from the shear wall (
Figure 3). Taking into account the thickness of the adsorbed surfactant bilayer, it should be localized at about 2 nm from the metallic surface. Moreover, particles are maintained near the electrode by the electrophoretic force and the electrode has a certain roughness (below 45 nm [
16]). Nevertheless, we can consider that these results indicate that the type of surfactant counter-ions influences the particle-electrode distance and that the particle-electrode distance is shorter in presence of CTAC than in presence of CTAB. In CTAC solution, the short particle-electrode distance and the rapid particle adhesion (in a few seconds) on the electrode indicate that particle-electrode interactions are attractive. Adsorption of CTAC molecules on the electrode is not sufficient to form a homogenous bilayer and to reverse the charge of the electrode, so attractive interactions should take place through van der Waals and electrostatic double layer interactions. The higher particle-electrode distance in CTAB solution and the longer time (about 100 s) for the particle to move along the electrode suggest repulsive interactions between the particles and the electrode. The interaction energy was then calculated using Equations (9) and (10) with a positive value for the zeta potential of the electrode. An electrode zeta potential of +5 mV was sufficient to obtain an energy barrier of about 3 kT at a distance of 15 nm and a secondary minimum at a distance of about 40–50 nm. So for a particle dragged along the electrode by the laminar flow and with a DC electric field, the electrode-particle distance ranges from a few nanometers to a few dozen nanometers depending on the type of surfactant.
Surfactant counter-ions also influence the distance at which the electrophoretic force predominates the hydrodynamic force and the approach angle of the particles near the cathode. The angle between the trajectory of the particle and the normal to the surface (
Figure 8) is lower in CTAC solution (≈60°) than in CTAB solution (≈80°). The approach angle, the time it takes for a particle to move along the electrode and the particle-electrode distance have an effect on the particle deposition and the growth of aggregates. In the presence of CTAB, particles have time during their tangential motion along the electrode to attach to each other to form aggregates. Other particles coming from the bulk suspension migrate to the immobilized aggregates due to the local electro-osmotic and electro-hydrodynamic flow. Moreover, the repulsive electrostatic interactions between particles are lower and so the particle-particle distance is also lower. Finally, dense aggregates were observed. In the presence of CTAC, the time it takes for a particle to move along the electrode is very short, particle aggregation due to the local flow around a deposited particle is limited and small aggregates are formed. But the distance from the electrode (
y-distance) at which the electrophoretic force predominates the hydrodynamic force is higher than for CTAB-coated particles, so more CTAC-coated particles migrate to the surface. Therefore smaller and more numerous aggregates were observed [
37]. Then they coalesce with each other leading to open structures.