Abstract
sp2 hybridized carbons constitute a broad class of solid phases composed primarily of elemental carbon and can be either synthetic or naturally occurring. Some examples are graphite, chars, soot, graphene, carbon nanotubes, pyrolytic carbon, and diamond-like carbon. They vary from highly ordered to completely disordered solids and detailed knowledge of their internal structure and composition is of utmost importance for the scientific and engineering communities working with these materials. Multiwavelength Raman spectroscopy has proven to be a very powerful and non-destructive tool for the characterization of carbons containing both aromatic domains and defects and has been widely used since the 1980s. Depending on the material studied, some specific spectroscopic parameters (e.g., band position, full width at half maximum, relative intensity ratio between two bands) are used to characterize defects. This paper is addressed first to (but not limited to) the newcomer in the field, who needs to be guided due to the vast literature on the subject, in order to understand the physics at play when dealing with Raman spectroscopy of graphene-based solids. We also give historical aspects on the development of the Raman spectroscopy technique and on its application to sp2 hybridized carbons, which are generally not presented in the literature. We review the way Raman spectroscopy is used for sp2 based carbon samples containing defects. As graphene is the building block for all these materials, we try to bridge these two worlds by also reviewing the use of Raman spectroscopy in the characterization of graphene and nanographenes (e.g., nanotubes, nanoribbons, nanocones, bombarded graphene). Counterintuitively, because of the Dirac cones in the electronic structure of graphene, Raman spectra are driven by electronic properties: Phonons and electrons being coupled by the double resonance mechanism. This justifies the use of multiwavelength Raman spectroscopy to better characterize these materials. We conclude with the possible influence of both phonon confinement and curvature of aromatic planes on the shape of Raman spectra, and discuss samples to be studied in the future with some complementary technique (e.g., high resolution transmission electron microscopy) in order to disentangle the influence of structure and defects.
1. Introduction
Raman spectroscopy is an inelastic light scattering process that allows to identify and characterize the structure of molecules from gas to solid phase, from amorphous to crystals. It is created by a fluctuating electric dipole caused by both the incident light beam and by the elementary excitations of the scattered media: E.g., ro-vibrations of free molecules, phonons in crystals, impurities, and local vibrational modes. In material sciences, it is used routinely, since the 1970s, to characterize carbon-based materials, ranging from very well organized carbons such as four coordinated diamond; to three coordinated aromatic carbons such as graphene [1,2], nanotubes [3], and nanoribbons, down to amorphous carbons [4]. The latter materials are disordered carbon solids containing a mixture of tri- and tetravalent bonds [5], with or without hetero atoms [6]. In between the two extremities of highly ordered and the very disordered three coordinated aromatic carbons, nanographites which display a local order at the nanometric scale (nanographites can refer here to soots, coals, pyrolitic graphite, implanted graphene/graphite, etc.), are also covered by this spectroscopic technique.
Researchers new to the field are in general astonished by the huge amount of papers found in a first raw bibliographic search. The main aim of this review paper is to help them in identifying how Raman spectroscopy aids in studying different forms of aromatic carbons containing defects. To emphasize the role of Raman spectroscopy played in this aromatic carbon community, a quick bibliographic search on Web of Science returns more than 1700 publications having the keyword “graphite” in the title and the keyword “Raman” in the topic. This number increases up to 9000 items when replacing “graphite” with “graphene” in the title, which makes a huge number of publications. The number of publications remains high (close to 900) if both “graphene” and “Raman” are considered as keywords in the title, implying that they are intrinsically correlated. This strong correlation is still significant for amorphous carbons as the amount of publications reaches 220 with the keywords “Raman + amorphous carbon” or “diamond like carbon” both in the title. We will detail the origin of this correlation below.
At this stage the most relevant questions are: How is Raman spectroscopy generally used (or how can it be used) for characterizing carbon-based materials, and what can we learn from the Raman spectra? The answer to these questions is not easy to give as it depends on the goal of the study: Basic characterization, or deeper fundamental study, or both. What is sure is that in all cases Raman spectroscopy gives information on defects. Most often in the scientific literature it is used to confirm that the good allotrope has been obtained after a given preparatory process (e.g., ion implantation, deposition varying relevant parameters like pressure or substrate temperature, mechanical modification by milling) or to quantify the amount of defects or structure deformation introduced after a given transformation of the pristine sample. It can also be used to give a rough estimation of the stored hydrogen content [6,7], to monitor chemical changes under some physicochemical process, to determine mechanical stress or stress release, to characterize the electronic properties, diameter of carbon nanotubes, coupling between a carbon phase and another environment, and so forth. Occasionally, Raman spectroscopy is employed to obtain more fundamental information on the material properties, such as the Grüneisen parameter [8]. In this paper, we review the most important uses of multiwavelength Raman spectroscopy of sp2 based carbon samples containing defects to answer the questions detailed above for these peculiar materials. We emphasize the role played by the laser wavelength used because of resonance effects that can be positive (i.e., allow to obtain additional information) or negative (i.e., introduction of unwanted experimental biases due to the wavelength dependency of the Raman cross sections for sp2 or sp3 carbons [9], merging of bands due to dispersion behavior caused by resonance effects, etc.).
In Section 2, we give an introductive and historical background of Raman spectroscopy in general and then applied to carbons. As the history of Raman spectroscopy starts at the same time as the beginnings of quantum mechanics, we have decided to give some details on the latter as well since generally it is skipped from specialized text books and review papers. Section 2 is split into three subparts, one giving the historical context, another giving some basics on the Raman effect, and the last one is more focused on Raman spectroscopy applied in the study of carbon solids. In Section 3, we give results (basically correlation between Raman spectroscopic parameters such as band intensity ratios, band position and band width, for different laser wavelength) related to different kinds of aromatic containing carbons that range from disordered graphene to amorphous carbons. The aim of Section 3 is to give a concrete and practical view on how Raman spectroscopy can be used to classify the nanostructure under investigation and its defectiveness. The guiding principle of this review section is the increase of complexity of the samples through the pages. In Section 4, we highlight the role of phonon confinement for a variety of nanocarbons and conclude our review.
2. Raman Spectroscopy of Carbon Solids: Basics
2.1. A Brief History of Raman Spectroscopy
The historical milestones (experimental, theoretical, and instrumental) on the Raman effect applied to carbon have been summarized in Figure 1. Below, we give more details. First light scattering experiments were performed in 1922 by Brillouin [10] and in 1923 by Compton, who used X-rays [11]. During the six following years, Raman was involved in 53 communications focused on scattering processes in liquids [12] that led him and his students to observe a new effect in the optical region. In 1928, Raman [13] finally realized he observed the analogue of the Compton effect: An inelastic light scattering process, but in the visible range of radiation. Two groups of unresolved bands were observed: One at a higher wavelength compared to the wavelength of the incident light (Stokes lines, more intense) and one at a lower wavelength (anti-Stokes lines, less intense). The denomination as Stokes or anti-Stokes lines is due to Woods [12] who noticed that, phenomenologically, this Raman effect gave a shift in wavelength as does fluorescence, a phenomenon discovered by Stokes in 1852 on fluorite, CaF2 [14]. Some German researchers doubted the discovery of the Raman effect as they failed to reproduce it, but Sommerfeld played a major role in the acceptance of the Raman effect by the international community [15,16]. The history of this discovery is discussed in detail in Singh et al. [17]. The inelastic scattering of light in the visible range was then found very promising for the study of molecular structures because the process allows to obtain infrared and far-infrared information (ro-vibrational states) using and detecting light in the visible range. Before the most efficient detector at that time (photography) was used, the Raman effect was first observed by coupling a spectroscope with the naked eye [15].
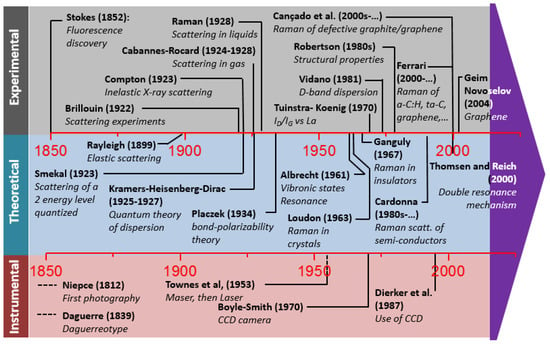
Figure 1.
Quick chronology of the Raman effect.
The theoretical background at the basis of the understanding of the Raman effect started to be established before the experimental discovery of the effect itself: In 1923, Smekal quantized a two-energy level system [18]. Two years later, Kramers and Heisenberg [19] obtained the expression of the scattering cross section of an electromagnetic wave by an atom described by quantum mechanics. In 1927, Dirac derived the same expression by quantizing both the matter and light, creating quantum electrodynamics [20]. Nowadays, the theory is generally labelled the Kramers–Heisenberg–Dirac (KHD) theory. In 1932, Breit reviewed this quantum theory of dispersion (Among other points, we learn in his paper the well-known fact that both the Schrödinger and matrix mechanics from Born, Heisenberg, and Jordan were tested to obtain the Kramers–Heisenberg formula of dispersion, and that they both lead to the same result.) [21]. In 1934, Placzek [22] introduced the bond-polarizability theory of Raman scattering. This approach is still useful nowadays as it allows “easy” manipulation of Raman intensities. It is based on a time-dependent perturbation theory and on some assumptions, among others that the nuclei of the molecules are fixed and that the system is in its ground electronic state, which prevent the theory from being used for resonance effects. The main advantages of this semi-classical theory is that point group theory can be used for deriving selection rules based on symmetry considerations. In 1961, Albrecht reported multiple hypothesis, introducing vibronic states and allowing his theory to be used for normal and resonance Raman scattering [23]. In 1956, Born, who is well known to first give the interpretation of the wave function squared absolute value, co-wrote a very detailed book about the dynamics of crystals in which some sections are dedicated to the Raman effect [24]. In 1964, Loudon reviewed the knowledge acquired on the theory adapted to crystals; the theory (he contributed to create in 1963) focusing in his paper on cubic, axial, and biaxial crystals, using the first order perturbation theory applied to a system with three systems interacting: The radiation, the electron, and the lattice (phonon) [25]. In his paper, he also reviewed crystal excitations involved in the Raman effect which are not only phonons. In 1967, Ganguly and Birman developed the theory of lattice Raman scattering in insulators [26]. Reviewing the period from the seventies to the present days is a complex task due to the increasing number of papers published in this period. This explosion of works related to Raman spectroscopy can be explained by the invention of the laser, which provides monochromatic intense photons. A bibliographic search with the key words “Raman + spectroscopy” in the title returns more than 21,000 papers. This number falls to 3200 if the research is restricted to the material science field only. In the 1970s, the number of papers published per year was just close to 5, whereas currently about 140 papers are published each year. The two series Light Scatterings in Solids [27] and Recent Advances in Linear and Non-Linear Raman Spectroscopy [28] will be helpful to the readers who want to follow the evolution of this field in more detail. The Journal of Raman Spectroscopy (published by John Wiley & Sons, Inc.) is a dedicated journal that publishes in the field. Raman spectroscopy is now routinely used in many labs to characterize many kinds of solids, transparent or absorbent, thick or monoatomically thin, and so forth. It is coupled with an optical microscope that focalizes the laser beam to a restricted sampling area/volume and helps in collecting light more efficiently after it got scattered with matter, at the micrometer lateral resolution. The reader will take advantage in reading the reference from Gouadec and Colomban [29] which is very well adapted to efficiently learn both the theoretical and experimental basics and which illustrates these basics on well-chosen examples.
The evolution of this field of research has been correlated to the evolution of the experimental techniques. It reached its apogee in the 1940s, studying first molecules in liquids and then in gas (first measurements where done unsuccessfully in gas phase from 1924 to 1928 by Rocard [30,31]). Due to both low Raman scattering cross sections (see below) and absorption of light, studying crystals was not easy until the advent of the laser in the 1960s (see Figure 1). Only transparent samples like diamond and CdS, with a large volume probed, are reported in the period 1930–1960 [32,33]. In 1928, Mandelstam and Landsberg intended to measure Brillouin spectra of quartz, but instead they observed faint new lines with an unexpected shift, which were in fact the corresponding Raman lines of quartz [34]. Lasers, contrary to the mercury lamp previously used, offered many advantages such as: High power, monochromaticity, and coherence, thus opening the era of studying solids. In parallel, progress had been made in electronics so that photomultipliers were used first before the CCD (charged coupled device) cameras [35] which were invented in 1970, based on semiconductors technology arranged in arrays. The CCD camera was applied first in the field of Raman spectroscopy for solids in 1987 for characterizing ultrathin organized layers of organic films [36] without using specific molecules in which resonance effects enhance the Raman signature, as was done before by Rabolt et al. [37]. More information on the instrumental aspect can be found in the work by Adar et al. [38]. The early history of the Raman effect can also be found in a review by Long [39]. Laser coupling to nanometric metal nanoparticles or atomic force microscopy tips [40] allows reaching nanometric resolution, but this is another topic and will not be covered in this paper. Before discussing more details on the use of Raman spectroscopy for characterizing carbon allotropes, we first provide some basic theoretical knowledge on Raman spectroscopy.
2.2. Basic Knowledge on Raman and Resonance Raman Spectroscopy
The aim of the following section is to give the main physical ideas behind normal and resonant Raman scattering, and not to give a complete lesson on Raman spectroscopy theory, including cross section calculations/band intensities in the case of normal and resonant Raman scattering. For a deeper learning, we refer to the works of Rocard and Long [30,41] for the basics and applications in material sciences and [41] for the full quantum theory applied to free molecules. The review by Born and Huang [24] displays, among other useful developments, a full description of calculations leading to the Placzek’s formalism. For solids, the studies by Cardona et al. [42,43] are highly recommended.
2.2.1. Experimental Set-Up
The typical experimental set-up applied for Raman spectroscopy measurements, with a backscattering geometry, is presented in Figure 2a. Briefly, a laser beam is aligned by a set of mirrors and driven to an objective that focalizes it on the sample placed on a motorized XY stage. Depending on the set-up, different laser sources (laser wavelength from λ0 = 244–1064 nm) with their corresponding optics can be found. Depending on the community, either the wavelength or the laser energy is used to display spectroscopic data. They are related by the expression (see Equation (1)):
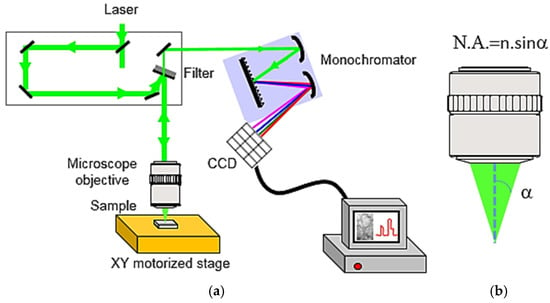
Figure 2.
Experimental set-up with a backscattering geometry: (a) Details of the system; (b) Definition of the numerical aperture (N.A.), with n the index of refraction of the medium in which the lens is working and α the maximal half-angle of the cone of light that can enter or exit the lens.
After light and matter have interacted in the sample, the photons (either reflected, elastically scattered, inelastically scattered, or other photons coming from competing processes such as fluorescence) are collected by the same objective and driven to a filter that diminishes the intensity of the elastic photons. Generally, the cut-off frequency of this filter is close to 50–100 cm–1, meaning that modes with a lower wavenumber will not be detected. Photons other than the elastic ones are then driven to a monochromator in which light dispersion occurs. Light is finally spread on a CCD camera, converted in an electronic signal that is recorded on a computer. The spot radius on the sample, R, is , where λ0 is the laser wavelength and N.A. the numerical aperture as defined in Figure 2b, n being the refractive index separating the sample and the optics. According to the Rayleigh criterion, R is also the lateral resolution, as it is the smallest distance between two points that can be probed. The XY stage is generally motorized in order to work in a mapping mode: The stage moves to different x,y-positions at which spectra are recorded to check spatial inhomogeneity at the micron scale. The vertical resolution, labelled Δz, is generally of the order of the micron, if the material is transparent. In addition, it can be adjusted using confocal mode. Note that it can be lower if the material under investigation is absorbing the laser light. More details on the experimental operation of Raman spectroscopy can be found in the paper by Gouadec and Colomban [29].
2.2.2. Conservation Rules
Raman photons are created by a fluctuating electric-dipole in the scattering medium, by the simultaneous action of the incident light beam and the elementary excitations of the solid, leading to an induced polarization moment . To describe this interaction, three ways can be used. The easiest one describes classically both electromagnetic field and matter. The second one describes, classically, the electromagnetic field but quantifies matter. The third one quantifies both.
Let us start by introducing the classical monochromatic electric field of the incident laser , E0 being its amplitude, ω0 its frequency, its plane wave propagation vector (which is in vacuum, c being the speed of light) and the 3D position in space. The elementary excitation of the crystal, called the phonon, has a crystal momentum called , and a corresponding frequency ωq, for each value of . As the system is isolated, two conservation rules (on total energy and momentum) occur, leading respectively to Equation (2) and (3):
where ωs and are the scattered light frequency and wavevector, respectively. Due to these conservation rules, the geometry of the experiment normally determines orientation and magnitude of the scattering wave vector. In current experiments, the backscattering geometry (i.e., θ = 180°, see Figure 3 for the definition of this angle) is one of the mostly routinely used in labs. The displacement of a peculiar ion in the unit cell around its rest position is given by , where is the phonon coordinate. The phonon coordinate is a linear combination of bond lengths and bond angles and is associated to the normal modes of vibration. Whatever the crystal symmetry, varies from 0 to a value which is of the order of 1/a, a being the typical lattice parameter, close to 1 . In the visible range of radiation, considering the conservation rule on momentum, and whatever the value of θ, as the ratio between and is close to 100, it means that necessarily the phonon that will satisfy the conservation rule will be close to , i.e., close to the center of the Brillouin zone. For higher order processes (i.e., involving more than just one phonon), the wave vector conservation rule becomes Equation (4):
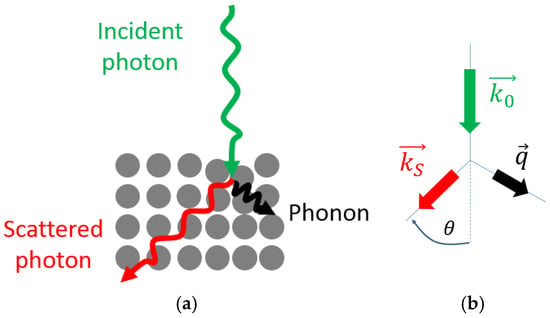
Figure 3.
Scattering geometry: (a) Photon/phonon interaction; (b) Corresponding momentum.
As a consequence, not only phonons at the center of the Brillouin zone can contribute now.
2.2.3. Classical Expressions for Molecules
Before considering the more complex case of solids, we introduce some basics of Raman theory for molecules. The incident electromagnetic field induces a dipolar momentum in an electronic system, the ρ-component ( being given by , with the polarizability tensor αρσ, (higher order terms, related to hyper-Raman spectroscopy, are not mentioned here). The components of αρσ can be approximated by a Taylor expansion. For simplicity, let us forget about the ρ and σ indexes coding for directions in space, and let us assume we consider a linear molecule with a normal vibrational coordinate Q(t) characterized by an intrinsic vibrational frequency ωvib. Then, . The term is sometimes noted R and called the first order Raman tensor. It gives the coupling strength of the nuclear and electronic coordinates. By including both the expression of the incident electric field and the polarizability elements expansion, one obtains by using the product of two cosines the following expression (see Equation (5)):
in which we have omitted the term, for simplicity, and the random phase of the nuclear mode of vibration acquired during the scattering process. This expression contains three terms: The first one has the same frequency as the incident laser and is interpreted as due to elastic Rayleigh scattering, the second and third ones having their frequencies lowered or increased by the frequency ωvib. These latter terms are respectively interpreted as due to the inelastic Stokes and anti-Stokes Raman scattering. These processes are represented in an energy diagram in Figure 4a–c, respectively. For the Stokes photon, and far from the oscillating dipole, the amplitude of the electric field is given by classical electrodynamics as (see Equation (6)):
ϕ being the orientation given from the dipole axis and ε0 the permittivity of vacuum. The outgoing flux of energy is given by the Poynting vector: . Integrating over the unit sphere, this flux gives the total energy radiated by the Stokes induced dipole (see Equation (7)):
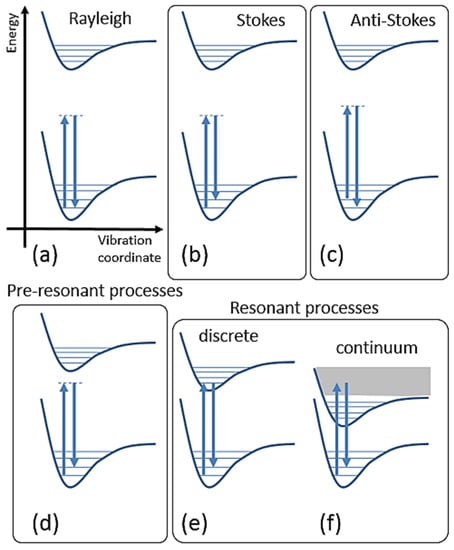
Figure 4.
Jablonski diagram of Rayleigh scattering (a), non-resonant Stokes (b) and anti-Stokes (c) Raman scattering, and pre-resonant (d) and resonant Raman scatterings (e,f).
The classical theory then predicts the fourth power (sign − is replaced by + if we consider anti-Stokes), the incident beam intensity and the dependencies. However, it fails to reproduce resonance effects, Stokes, and anti-Stokes intensity ratio behavior with temperature, etc.
2.2.4. Semi-Classical Expression for Molecules
When matter is treated quantum mechanically, some of these behaviors are better reproduced. We only consider the first order induced dipole here. During the scattering process, one incident photon (of energy ℏω0, ℏ being the Planck constant divided by 2π) is annihilated, and one photon and one phonon are created. Below, all the results are obtained in the framework of time-dependent perturbation theory applied for a molecule (details in Chapter 4 of [41]), limited here to the first order of expansion [22]. Let us define the unperturbed initial and final states of the molecule considered: and respectively. The ρ-component ( of the first order induced dipole is , where is the transition polarizability, as given in Equation (8):
The summation r runs over all the states of the molecule. , ℏωi and ℏωf being the energies of the initial and final states, respectively. Γr is related to the lifetime of the level r (damping factor). The numerator is the product of two transition electric dipole terms: One for a transition from to (absorption) and one from to (emission). Term one and two under the sum will not play the same role depending on the comparison between ω0 and ωri,f: The first term can increase a lot if , being predominant in the case of resonance condition, whereas this is not the case for the second one that is still present even far from resonance conditions. In general, all the pathways connecting and with non-null transition electric dipole terms must be considered in the summation. Representing this scattering in an energy diagram is simplified by introducing a virtual state and its corresponding virtual level of energy (i.e., not a stationary state coming from the resolution of the Schrodinger’s equation), as it is done in Figure 4b,c (the virtual level is marked by a dashed line). The case where is represented in Figure 4b (Stokes) and c (anti-Stokes), whereas the case is represented in Figure 4d–f corresponding respectively to pre-resonance, discrete resonance and continuum resonance Raman scatterings. By considering the Born–Oppenheimer condition (electron and nucleus motions are not coupled), one has the vibronic wavefunction that can be written with the corresponding quantum number for vibration and the energy . In the ground electronic state, the expression of (see Equation (8)) does not change a lot. It is labelled “the A-term” in the Albrecht denomination [23]. However, if one introduces a perturbation calculated by considering electron–nucleus interaction (i.e., the electronic Hamiltonian is expanded in the nuclear displacements around the equilibrium position Q0), then other additional terms (called B, C, and D terms) appear in the previous expression of . More information about the meaning of these terms can be found in the paper by Long [41].
As the electric dipole moments can be expanded in a Taylor series over the normal vibrational coordinates, one can obtain the following expression (Equation (9)):
with if , if , or 0 in the other cases, noting the elements of the Raman tensor as . We can notice that the vibrational mode will be Raman active only if this last term is different from zero. This condition defines the so-called “selection rules”. They are directly related to the symmetry of the system. See [44] for further details. Considering that the molecule is not oriented preferentially, the total energy radiated by the Raman effect is given by the expression (Equation (10)):
where is composed of k products in the form of for Stokes and for anti-Stokes processes.
2.2.5. Raman Effect in Crystals
For well oriented crystals, the same kind of expressions holds but with some changes. First, the vibrational quantum number is replaced by the Bose factor , k being the Boltzmann constant and T the temperature expressed in K. Second, for monocrystals, one must take care of the incident and scattered polarization directions. In general, one has the differential cross section expressed as (Equation (11)):
where dΩ is a solid angle, e0ρ and esσ are the ρth and σth components of respectively the incident and scattered elementary polarization vectors. It sometimes can be found as: ,, or . For single crystals, by measuring the dependence of the scattered intensity on and , one can deduce the symmetry of the Raman tensor and hence the symmetry of the corresponding Raman-active phonon [45].
To determine the cross sections experimentally, one needs first a reference with a known Raman cross section. In order to deduce the cross section relatively to the reference material, one has to correct from electromagnetic biases such as reflection losses which can be different from the reference material and the sample to analyze (due to specific refractive index) or interference effects [46,47,48]. The reader interested in the method can read the detailed work of Klar et al. that was performed on graphene [49].
2.3. Basic Properties of Graphene and Related Materials
Due to its valency, carbon exists under several allotropic forms—such as diamond, graphite, graphene, nanotubes, and fullerene—and many other forms will likely be discovered in the future [50]. Plasma and nanoscale plasma/surface interactions are processes responsible for a large number of them (we do not pretend to list all these interactions; they can be found in the review by Ostrikov et al. [51]). Roughly speaking, two families exist: The “sp3 family” (with the tetra-coordinated diamond), and the “sp2 family” with the graphene as the model of aromatics, with many possibilities in between the two families [52]. Amorphous carbons can mix aromatic sp2 and sp3 carbons, as well as heteroatoms.
Graphene is a monolayer thick crystal organized as displayed in Figure 5a. The hybridization between one s-orbital and two p-orbitals leads to a trigonal planar structure with three in-plane sp2 σ bonds and one out-of-plane π bond. The σ bonds are responsible of the robustness of the lattice, whereas the π bond, by binding covalently with a neighbor π bond, is responsible of the electronic conduction. Two atoms per unit cell are necessary to reproduce the crystal, and the two vectors, and , with a = 1.42 , are displayed in Figure 5a [53]. The reciprocal-lattice vectors are b1 and b2. In this momentum space, three specific points of the Brillouin zone are the Г, M and K points. The lower part of Figure 5b represents the electronic structure in vicinity of the K point, where the π and π* bands meet with a zero-gap energy. The dispersion of the π and π* bands is , where is the Fermi velocity, and q the momentum measured relatively to the K point [54]. The shape of the electronic bands forms a cone which is called a Dirac cone, because of the linear dispersion curve. It is because of this peculiar point that graphene is called a semi-metal. A review by Neto et al. presents the basic theoretical aspects of graphene’s peculiar electronic properties [53]. Note that the sp2 behavior can be partially modified by some mechanisms, such as chemical adsorption of hydrogen on top of C atoms, that modify curvature and then induce a mixed sp2/sp3 state [55].
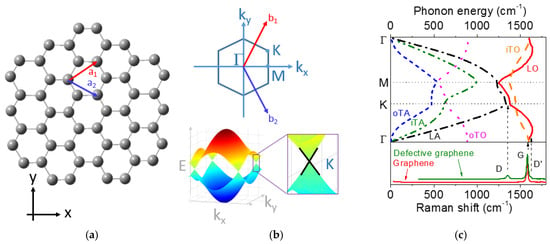
Figure 5.
Honeycomb lattice of graphene. (a) Unit-cell vectors (a1 and a2). (b) Electronic structure in the reciprocal lattice. Г, K, and M are high symmetry points in this space. (c) Phonon dispersion curve and Raman spectra (LO, LA, iTO, iTA, oTO, and oTA. O and A refer to optic and acoustic phonon branches, L and T refer to longitudinal and transversal, and i and o refer to in plane or out of plane, respectively).
The upper part of Figure 5c displays the phonon dispersion [56] for a Г-M-K-Г trajectory in the Brillouin zone (the figure is generally presented with the phonon energy horizontally). As there are two atoms in the unit cell, there are 3 × 2 phonon branches. “O” and “A” stand for optical (three branches) and acoustic (three branches) phonon branches, acoustic branches being close to zero at the center of the Brillouin zone. “L” and “T” stand for lateral or transverse vibrations and “i-” or “o-” stand for in plane or out of plane. The lower part of Figure 5c displays a typical Raman spectrum for defect free and defective graphene. In this spectral range, one can observe the presence of one band (called the G band) at 1582 cm−1 for the defect free sample, whereas one can see two extra bands (the D and D’ bands) for the defective sample. As it has been discussed in Section 2.2.2, not all the phonons give rise to a band in the Raman spectrum. We give more information about the Raman spectra of graphene related materials in the next section.
2.4. Raman Spectra of Graphene, Graphite, and Disordered Carbons
This section is separated in two subsections. The first one gives usable information about the origin and behavior of the bands often encountered for aromatic based materials. The second section deals with a historical overview of the findings about Raman spectroscopy in the field, in a linear way.
2.4.1. Basics of Raman Spectroscopy for Graphene and Graphite
Raman spectra of a wide variety of disordered carbons are displayed in Figure 6 in order to overview what varies and how much in terms of band intensities, width, position, etc. The Raman spectra displayed in Figure 6 are obtained from a highly oriented pyrolytic graphite, nanographites, and amorphous carbon (we do not specify the kind of synthesis here as we consider only the main trends in the Raman spectra). Note that a complete discussion about what is called “intensity” in the literature when speaking about band fitting procedures, is given in Section 2.6.
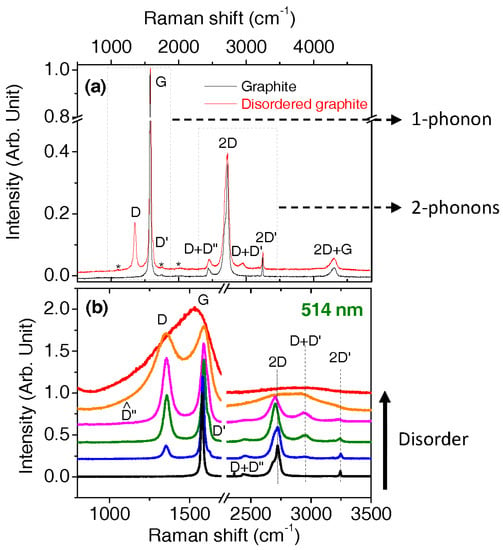
Figure 6.
Raman spectra of graphite and disordered carbons recorded at 514 nm. (a) Attribution of the main bands in the first, second, and third order regions. (b) Same for a variety of more disordered carbons.
Graphite belongs to the P63/mmc () space group. If considering only a graphene plane, at the Г point of the Brillouin zone, there are six normal modes that possess only one mode (doubly degenerate in plane) with a E2g representation, which is Raman active (see [57]). Its wavenumber is at 1582 cm−1 and it gives rise to the so-called “G band”. Its width is close to 15 cm−1 and it is mainly due to an electron–phonon coupling interaction [58]. By combining two graphene planes to build graphite, one can obtain another Raman active mode that gives rise to a band at 42 cm−1, which cannot be measured by standard set-ups as the one presented here. Then for standard set-up operation, only one band should be detected. However, this is not the case: For pure graphite, for example (see Figure 6a), one extra band with a high intensity is detected (one-third of the G band intensity, at 2720 cm−1). This band is composed of several bands for graphite and few layers graphene, but has a Lorentzian shape for monolayer graphene and disordered graphite in which stacking in the c direction is not like in graphite [1,59]. Its intensity, compared to the G band can vary from 3 to 1/3 from graphene to graphite, respectively. When disorder increases, this band broadens, overlapping with other bands and nearly disappears. For amorphous carbon, the intensity compared to that of the G band is lower than 6% (see Figure 6b). There are also several weaker bands (2–5% of the G band intensity, at 2450, 3240, 4300 cm−1) and even weaker bands, marked by stars (0.4% of the G band intensity at 1750 cm−1). Most of the weak bands are listed in the paper by Kawashima and Katagiri [60]. As proposed by the international consensus, these bands are due to the double resonance mechanism which is described in detail in Section 2.5. A defective graphite presents other bands that can be as intense as the G band at 1350 and 1615 cm−1 (see Figure 6). These bands are activated by defects due to the breaking of the crystal symmetry that relax the Raman selection rules. They are called the “D and D’ bands”, respectively. The “D” stands for “defect” and has nothing to do with the diamond band that lies at 1332 cm−1. The intense bands lying below 1640 cm−1 are due to first order phonons (see the phonon relation dispersion in Figure 5c). In the range 2000–3000 cm−1, they are due to two-phonon processes and named 2D, D + D’, 2D’, and so forth. For higher wavenumbers, they are due to third order processes, etc. When increasing the order of the process, the intensity is generally diminished because of the cross section which becomes less and less probable. Considering the less intense bands, the D” band is present in the shoulder of the D band of very defective samples. It is always needed when fitting (see Section 2.6). Other bands are the 2450 cm−1 band, which has been attributed recently to a D + D” band by Couzi et al. [61], the D + D’ (in literature, the wrong D + G label is often found [62]), the 2D’ bands and the 2D + G band. Even weaker bands are present and marked by stars in Figure 6a. The 1750 cm−1 band is called the M band and has been understood in the framework of the double resonance mechanism [63].
In Figure 6b, one can see that when disorder increases, the bands broaden, and the relative intensity of the bands changes: The D band increases with disorder and then decreases when being close to an amorphous carbon. These two behaviors have been related to the coherence length La (obtained from structural analysis), with the two historical formulae (Equations (12) [64] and (13) [4,5]):
c and c’ are parameters that depend on the fourth power of the laser wavelength [4,65,66] and that can vary from one sample to the other [65,67]. Why ID/IG behaves like for La > 2 nm is also justified in Section 3.1. Since 2010, an upgrade was published that allows a better understanding of the information retrieved from the intensity ratio. It is presented in Section 3.3. Note that instead of ID/IG, another spectral parameter that is often used is proportional to ID/IG × E0(eV)4, E0 being the laser energy. This is because the c and c’ parameters evolve as the fourth power of the laser wavelength [66,68]. It allows to compare results from different wavelength on a same plot.
One important fact about band parameters behavior is that some bands disperse, which normally does not happen according to constant eigenenergy’s values obtained by quantum mechanics. This, again, is due to the double resonance mechanism, detailed in Section 2.5. Here, we briefly describe what is observed. The D band disperses linearly with the energy of the laser used, the slope being close to 50 cm−1·eV−1. This is a consequence of the double resonance mechanism. This has been observed for many aromatic based carbons, with different amounts of disorder (see Figure 7), an offset being present from one sample to the other (in the range ± 15 cm−1). The D-band dispersion is useful for differencing an aromatic based sample from a diamond based sample because the 1332 cm−1 band in the latter case does not disperse. The D’ band also displays a dispersion (not shown here) but it is less significant than that of the D band.
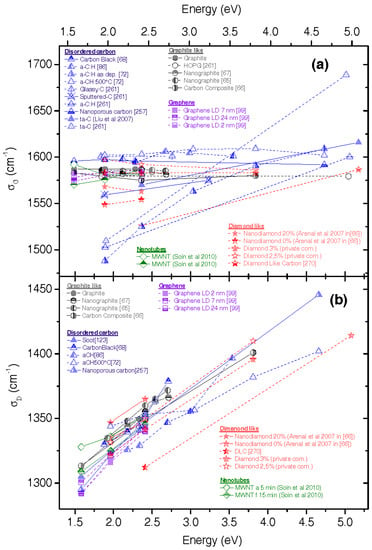
Figure 7.
Dispersion relations of the (a) G band and (b) D band for many disordered samples (data derived from literature as indicated).
The 2D band has twice the slope of the D band (not shown here). Several other weaker bands also display a dispersive behavior, which can be explained by the double resonance mechanism [61,69]. The G band is not due to the so called double resonance mechanism and for perfect graphite and graphene, it does not display dispersion, lying at 1582 cm−1. However, its position can change with the state of disorder in the material, in the range 1590–1600 cm−1 (for nanocrystalline graphite) down to 1520 cm−1 for amorphous carbons. This band position is sensitive to clustering of the sp2 phase, bond disorder, presence of sp2 rings and/or chains, presence of sp3 carbons and the way they are coupled to aromatic carbons [70]. Due to the electronic resonance Raman process (see Figure 4e,f), the G band can display a dispersion behavior, as displayed in Figure 7b, driven by the size of the aromatic domains (from roughly 0.5 eV up to few eVs for few aromatic carbon clusters [71]). This is particularly true for amorphous carbons. To our knowledge, this dispersion parameter is generally not used to better characterize amorphous carbons with small aromatic size skeleton, but should be used more often such as was done in the work by Lajaunie et al. [72].
The width of the G band (ГG) can be used to have an idea about the amount of defects (even if depending on the sample there are some differences, as can be seen in Part 3 with doped graphene, for example). It varies generally from 10 up to 200 cm−1 from graphene to amorphous carbons, but can be influenced by doping. It was found to vary roughly as a power law of La [5] for a large variety of samples, but it was found to vary as 1/La for samples with La in the range 20–65 nm [65]. Using only ГG is not enough to better characterize the sample analyzed, since the ID/IG parameter can be different for two kinds of samples whereas ГG is the same.
2.4.2. Historical Aspects
The following section is meant to provide an intermezzo, but detailed description of historical highlights in Raman spectroscopy of aromatic carbons. This section is less essential to the general reading of this paper, and therefore we refer to Section 2.5 on the double resonance mechanism for a continued subject reading.
Figure 8 displays the most important historical breakthroughs in Raman spectroscopy of aromatic carbons. First Raman spectra from a carbon were obtained on diamond in 1930. A band was observed at 1332 cm−1 [73], with a better understanding of the first and second orders reported in 1970 [74]. The phonon spectrum of graphite was modelled and obtained for the first time in 1965 [75,76]. Only two modes are Raman active according to the point group symmetry analysis. In 1970, Tuinstra and Koenig [64] detected with Raman spectroscopy only one band at 1575 cm−1 for graphite and attributed it to a doubly degenerate deformation vibration of hexagonal rings, corresponding to the E2g mode (The true frequency admitted today is 1582 cm−1 [77], but at that time the authors did not realize they used a high power (300 mW instead of the few mW or even less for absorbent materials) that can increase the equilibrium temperature of the sample, resulting in a downshift of the bands.) Moreover, they compared graphite with more disordered carbons (i.e., activated charcoal, lampblack, and vitreous carbon) and found a new band close to 1355 cm−1. They noted that this band is close to the 1332 cm−1 band of diamond, but ruled out the fact that the 1355 cm−1 band is due to sp3 carbons. They also showed that the relative height ratio between the 1355 cm−1 band (labelled D band, for “defect-induced band”) and the 1575 cm−1 band (labelled G band for “graphite allowed band”) is correlated to the crystallite size, La, retrieved from X-ray diffraction measurements. This is the so called Tuinstra–Koenig relation. In 1978, Tsu et al. observed three behaviors that are nowadays used to characterize defects and electronic structure of aromatic carbons [77]. First, they observed a new mode at 1627 cm−1 that they attributed wrongly to a splitting of the E2g mode. Then, they saw a high shift of the 1575 cm−1 band (up to 1590 cm−1) and finally they observed the presence of a band at 2742 cm−1, twice the frequency of the 1370 cm−1 band (also high shifted) even if the 1370 cm−1 band is not present in the spectrum. Nowadays, we label the 1627 and 2742 cm−1 bands as the D’ and 2D band, respectively. Using a different polarization configuration, Vidano et al. [78] related the D, G, D’, and 2D bands to in-plane vibrations and noticed the composite behavior of the 2D band, prophesying that once well understood, this behavior could help in better characterizing disorder and structural imperfection. Indeed, the shape and intensity of this 2D band was found to be very dependent on the electronic structure and the number of stacked layers in a multilayer graphene sample [1], and to the quality of the layer stacking in nano graphite by Cançado et al. [59], for example. The spectroscopic parameters of all these bands were noticed to be very dependent on the structure of the samples and then, to give a quick and good idea of the degree of graphitization, a thermal treatment was performed on different carbon fibers, coals, and pyro carbons between 450 and 3000 °C [78,79,80] and later, on amorphous carbons by Ferrari and Robertson [5].
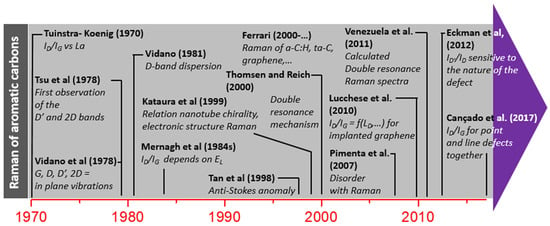
Figure 8.
Chronology of the Raman effect applied to aromatic carbon.
D Band and Combination Band Dispersions
In 1979, Nemanich and Sollins attributed the 2D band plus weaker bands appearing at 2450 and 3248 cm−1 to vibrational density of states features, using calculated phonon dispersion curves of graphite [81]. However, this was not completely satisfactory as the 2D band, even when the graphite sample is defect free, is of the same order of magnitude as the G band, whereas it should depend on the defect density according to this hypothesis (Before the physical origin of the 2D band was well understood, it was named the G’ band, exactly because it was always observed in the spectra together with the Raman allowed G band. The D* band can also be found in the literature. Be careful, the denomination D* is used since 2016 for another band. See in the paragraph text for details.). Part of the problem was solved when Vidano, in 1981, noticed that the D and 2D-band frequencies were dependent on the laser wavelength (the D band varying from 1360 down to 1330 cm−1 when using laser wavelengths from 488 nm up to 647 nm, and a slope which is twice for the 2D band) [82], hiding a vibronic resonance behavior. The same kind of dispersion for the D and 2D bands was observed on other graphites [83,84], carbon blacks [68], hydrogenated amorphous carbons [85], and later on carbon nanotubes [86,87] and most recently on graphene [62] (and references therein). The slope is close to 50 cm−1/eV for the D band and close to the double for the 2D band. Dispersion of weaker bands, mainly due to combination modes such as 2D + G, 2D + 2G, etc., were also reported in [4,5,60].
In 1984, Mernagh et al. also noticed that the ratio was depending on the laser wavelength [68], which is another proof that the D band arises from a resonant effect (if not, the ratio should be constant because of the dependency in the non-resonant Raman cross section affecting all non-resonant bands). In 1989, Knight and White determined the c value appearing in the Tuinstra and Koenig relation at 4.4 nm and that was done with 514 nm lasers [88] before the work of Cançado et al. [65]. In 1998, Tan et al. studied thermal effects on graphite and ion implanted graphite [89]. By comparing Stokes and anti-Stokes spectra, the D and 2D bands were found shifted differently for a given temperature, without clear explanation [89]. The origin of the dispersive effect of the D and 2D band were tentatively given by Pócsik et al. [90] and Matthews et al. [91] in 1998 and 1999, respectively. The slopes of the dispersions were reproduced in their work by considering a coupling between electrons and phonons with the same wave vector near the K point of the Brillouin zone (and called the quasi selection rule). However, this coupling was introduced ad hoc and moreover the authors failed to reproduce the puzzling anti-Stokes behavior. Thomsen and Reich went a step further by calculating the Raman cross section of graphite in a double resonance process [92] (completed by Saito et al. [93]), and were able to reproduce both the D and 2D dispersion relations together with the Stokes/anti-Stokes shifts. This double resonance mechanism is due to a heritage of the way Raman spectroscopy is treated in semiconductors and in which Cardonna played a major role [27,42,45]. Because of conservation rules of energy and momentum, the double resonance process, involving photons, electron-hole pairs and phonons, and described a little bit more in Section 3, selectively enhances a peculiar phonon wavevector (close to the K-point in the Brillouin zone) and then a phonon frequency [57]. For the D-band, a phonon and a defect are involved. For the 2D-band, only two phonons (without defect) are necessary. This explains why the 2D-band is always visible, even for defect free samples. The Stokes/anti-Stokes differences were understood, as the double resonance mechanism does not involve the same phonons during creation (Stokes) or annihilation (anti-Stokes) processes. In 2007, Pimenta et al. published a paper prophesying that being able to reproduce the resonant Raman behaviors will allow to better characterize disorder in nano-graphite based systems [94].
Graphene was experimentally first obtained in 2004 [95] and most of its fantastic electronic properties, related to the Dirac cone, were reviewed soon after [53,96]. The ability of Raman spectroscopy to study these properties is presented in the work by Ferrari and Basko [62]. Jorio, Cançado, and Lucchese et al., in a series of papers [97,98,99,100,101,102], were able to characterize and distinguish the influence of 0D and 1D defects on graphene. Venezuela et al. published a theoretical paper in 2011 [69] in which they calculated the double resonant Raman spectra of defective graphene, and reproduced the dispersion of D, D’, 2D bands and weaker ones (which are combination bands but not necessarily, some bands being attributed to acoustic branches). (The names of the bands do not necessarily respect the names given by other authors in the literature. For example, on the one hand the D” band in their paper can be labelled D4 in other papers such as [61]. On the other hand, Venezuela et al. labelled bands D3, D4, D5, etc. Note that we did not use their labelling here. The supplementary information of [62] gives (among other things) valuable information on the history of this nomenclature.) Weaker bands, due to two phonon scatterings, were also observed and understood in the framework of the double resonance mechanism [103,104]. In 2012, Eckmann et al. showed that the intensity of the D’ band compared to the D band, which is not sensitive to the amount of defects, is however sensitive to the nature of the defect (sp3, vacancy, edge) [105]. A bibliometric search with the key words “double resonance” + “graphite” + “Raman” in the abstract returns at present 122 papers, concerning not only graphene but also other allotropes like carbon nanotubes, meaning this double resonance mechanism is well established. In fact, it is so well established that it is now used on other isoelectronic and structural analogs of graphene such as 2D dichalcogenides (ME2, M = metal, E = S, Se or Te) to interpret multiwavelength Raman spectra [106,107,108].
However, two things have to be noticed at this point about understanding Raman cross sections: First, we have to mention the existence of an alternative approach and second we need to introduce a possible recent breakthrough. Thus, first: Another approach was performed to model the Raman spectrum of graphite based materials. It started in 2002 by Castiglioni et al. [109,110,111,112,113,114,115,116]. This approach is based on calculating resonant Raman cross sections of disconnected aromatic molecules of different sizes, governed by interactions between π electrons and the nuclei. This approach is also able to reproduce the D-band dispersion. Even if the double resonant mechanism is now commonly used and admitted, it does not mean the molecular approach has ceased today. For example, the group of Castiglioni recently published a paper on a polycyclic aromatic hydrocarbon resembling a longitudinally confined graphene ribbon with armchair edge [117]. Their technique could be applied in the future because it can help in studying confined and nanoshaped graphene. As a proof, the authors were able to reproduce the intensity of the G + D combination band which could be used as an experimental measure of confinement in graphitic materials, as they claimed. The second thing to be noticed, the possible breakthrough mentioned above, is that in 2016 the group of Heller et al. re-interpreted the theory of graphene Raman scattering using the Kramers–Heisenberg–Dirac theory without needing to introduce the double resonance mechanism [118]. Therefore, the authors were able to describe with a second order perturbation theory (double resonance mechanism is a fourth order perturbation theory [45]) the following characteristics: The bands’ dispersive behavior, defect sensitivity, Stokes/anti-Stokes anomalies, intensities, etc. Many other effects have now to be reproduced in the framework of this theory, especially concerning recent advances on UV Raman to probe the dispersion of graphene far away from the K point of the Brillouin zone (see at the end of Section 3.1), before being able to admit that this theory is better than the double resonance mechanism theory. We have to mention that Placzeck’s theory also works fine to reproduce coupling effects between layers in a multi-layer graphene, being able to reproduce the out-of-plane mode variation with the number of stacked layers, in the range 10–50 cm−1 [119].
For more defective samples (such as carbon blacks, soots, nanographite, and amorphous carbons) other bands were reported many times in the literature, already since 1985. The D3 and D4 bands are examples of such bands. (In that nomenclature, the D1 and D2 bands are the D and D’ bands lying at 1350 and 1620 cm−1. In the literature, the D3 band is sometimes called the A-band and the D4 band is occasionally referred to as the TPA band (which stands for transpolyacetylene). They are found at 1500 and 1200 cm−1, respectively [66,120,121,122,123]. They are generally difficult to observe as they fall in the D-G region, and for very defective materials, the D and G bands are broad (100 cm−1 or so), so that only the D4 band can be seen as a shoulder on the overall spectrum. The D4 band has been recently understood in the framework of the double resonance mechanism too [61]. More precisely, using a large variety of disordered graphitic carbon materials, Couzi et al. [61] have shown with the help of multiwavelength spectroscopy that this band is in fact composed of three sub-bands (the D*, D**, and D’’) that disperse differently. However, the authors failed in relating the intensity of these sub-bands to the La parameter, essentially because the main factors governing the resonant Raman process (and thus the corresponding band intensities) are related to the nature of defects (point defect, edge defect, staking fault, curved or twisted planes, etc.). Note that the D” at 1100 cm−1 in the visible range has been introduced by Venezuela et al. [69] in 2011. We give more information on the D” band in the last paragraph of Section 3.4. The Raman spectra of amorphous carbons can be seen as simpler, because only a broad asymmetric band is seen close to 1500 cm−1. However, this is incorrect, and for several reasons. First, many different kinds of amorphous carbon exist: sp2 dominated ones (a-C), sp3 dominated ones (ta-C, t referring to tetrahedral), one containing hetero-atoms such as H (a-C:H, ta-C:H, …) or N. Their structure and properties are related but widely varying [124,125,126]. Second, as there is some aromatic carbon embedded in their structure, some resonance occurs [127]. Ferrari and Robertson studied and reviewed the Raman behavior of such materials in the 2000s [4,5,128]. Contrary to the Tuinstra and Koenig relation, the Ferrari’s relation says that when the size of the aromatic domains is large, then the D band is intense. This relation was supposed to be connected to the Tuinstra and Koenig relation for an L value of 2 nm, imposing a relation between c and c’, but this connection was found empirically. More than a decade later, the evolution of on a large scale of L was understood, and the change of slope was found close to 1 nm [101]. It was done by bombarding a graphene layer varying the flux of incident ions creating the surface coverage of “0D” defects in the honey comb structure. The average distance between these 0D defects, LD, was then introduced and a relation between and LD found. Very recently, the group of Cançado et al. disentangled the contribution of graphene samples containing 0D (point) and 1D (line) defects, by giving in function of La and LD [97]. More details on the way ion bombardment can help to better understand Raman spectra are given in Section 3.3. Just note that very recent improvements have been done by the same group in order to distinguish point defects and line defects using multiwavelength Raman spectroscopy [97].
The historical approach in this review is mainly focused on Raman spectroscopy of graphene based samples. However, one should note that other allotropes played an important role in the historical development of Raman spectroscopy of carbons as well, which we rapidly cite here. C60 has been discovered by Kroto in 1985 [129]. Vibronic resonance effects in C60 were evidenced 5–6 years later (taking into account only the A term from Albrecht’s theory and reproducing the two orders of magnitude enhancement) [130,131,132]. Carbon nanotubes (CNT) were studied intensively since 1991, after their discovery (or rediscovery [133]) by Iijima [134]. Raman spectra of CNT not only contain G, D, and 2D bands, but also the well-known radial breathing modes (RBM). As Raman spectroscopy is a resonant process, these RBM frequencies and intensities depend on the nanotube electronic structure which is itself driven by the way the graphene plates are rolled. The Kataura plot is a tool that can give the intensity of a given mode in function of the laser used to perform the Raman spectroscopic measurements [135]. Raman spectroscopy can thus be seen as a power tool to distinguish between different nanotubes, the symmetry aspects of which are reviewed in the review paper by Barros et al. [136].
2.5. Brief Introduction to the Double Resonance Mechanism
Below, we give the basics of the double resonance mechanism which is a fourth order perturbation theory. The reader who also wants to learn about the details of this mechanism is referred to the following papers [2,137,138,139].
The Raman cross section contains sums of terms like the following one in Equation (14) ( terms, accounting for relaxations processes, have been omitted in the denominator, for simplicity):
Here, He–Radiation and He–phonon or defect are the Hamiltonians describing the interaction between electrons and light, and electron and phonons (or defects), respectively. and are the initial and final electronic states, , , and are intermediate states corresponding to the intermediate steps of the double resonance mechanism. In the reciprocal space, when the valence and conduction bands cross at the K-point (see Figure 5b), an incoming photon with the energy and wave vector can always excite an electron/hole pair in the vicinity of this crossing point. This is how the double resonance mechanism starts: An electron-hole pair is excited by the incoming photon that is absorbed. Then, the electron is scattered by a phonon or a defect with a vibrational energy and wavevector .
Many different scatterings can occur (see Figure 9), however only the resonant one will modify the Raman cross section by minimizing its denominator. Other scatterings are possible (not displayed on Figure 9, see Figure 2 of [62] for a complete description). After the scattering process between the excited electron and the phonon, the electron has a wavevector. The electron is then scattered back by a phonon or a defect, and finally the electron-hole pair recombines, emitting a new photon with the energy , if one considers the Stokes process. The first resonances occur from to , and the second resonance occurs from to . The third and fourth steps are not resonant. Changing the energy of the incident photon will select another phonon that will maximize the Raman cross section, leading to the dispersion of the D and 2D bands. The intravalley process, using a scattering with a defect and with a phonon, will give rise to the D’ band. The intervalley process between K and K’ points in the Brillouin zone will give rise to the D band if the excited electron is scattered by a phonon and a defect, or to the 2D band if the scattering by the defect is replaced by a scattering back with another phonon.
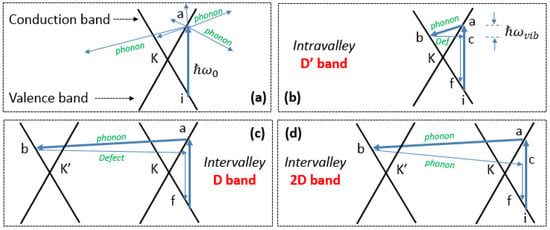
Figure 9.
Double resonant scattering for the valence and conduction bands, adapted from [92]. (a) Electron-hole excitation followed by non-resonant phonon scattering. (b) Intravalley process giving rise to the D’ band: Phonon (resonant) + defect scattering. (c,d) Intervalley processes giving rise to D and 2D processes with phonon (resonant) + defect and double phonon processes, respectively.
Then, for the bands appearing because of the intervalley process, we have a set of two coupled quantities (electron and phonon momentums + dispersion relation) that obey the quasi selection rule , meaning the phonon with wavevector q will couple preferentially with the electronic state that has the 2 k wavevector measured from the K point. Using multiwavelength Raman spectroscopy data allows to follow the iLO and iTO phonon energies along the dispersion relations, exploring the Brillouin zone, which is strictly forbidden for conventional Raman spectroscopy (see for example Section 3.1 and Figure 12 in the article by Malard et al. [139]).
The quasi selection rule cited above can be very useful for quantum calculations: A procedure for calculations can be to identify first the different scattering configurations between electrons and phonons by using analytical laws describing the electronic structure and phonon dispersion relation in order to perform Density Functional calculations in a second step, as they are more time consuming. 2D integration in the Brillouin zone is then necessary to take into account contributions from all the directions. Quantum interferences can occur, as the cross section is proportional to the square of the absolute value of a sum of terms integrated on the Brillouin zone (see [140]).
2.6. Intensity, Band Profiles, and Models for Fitting Spectra of Aromatic Carbons
If we do not take into account the instrumental transfer function that can be negligible in many cases (If the natural width is comparable to the width of the instrumental transfer function, which is generally a Gaussian function, then the intensity of the band is a convolution between the natural line shape and the instrumental function. Depending on the grating used, the instrumental width varies but is in general close to 1 cm−1.), the total intensity of one phonon mode with a wavevector and a frequency , in a perfect crystal, is spread on a symmetric profile which is Lorentzian, see Equation (15): (If one considers only the dominant term of (αρσ)fi (Equation (8) in Section 2.2.4) and applies the square of the modulus to calculate the Raman intensity, one will find: |1/(ωri − ω0 − iΓr)|2 = 1/[(ωri − ω0)2 + (Γr)2])
The full width at half maximum of this band, , is the inverse of the phonon lifetime, with electron–phonon and electron–electron interactions that can contribute. For the G band of graphene it was shown that the dominant term that determines the width is the electron–phonon coupling that leads to 11 cm−1 at room temperature [58,141]. At the other extreme, the material is amorphous. The analysis of the profile of Raman modes of amorphous carbon has led to many studies [142,143] (and references from Ferrari et al., see Section 3.6). The profile of a Raman mode is related to the neighboring of the vibrating molecule or atoms. Any variation in this neighboring will affect the width of the Raman mode. For single crystals, all atoms have equivalent environment and the associated Raman bands are sharp. This is evidently not the case for an amorphous material where each atom has a specific environment and the ranges of values of bond angles and bond distances are wider than in a crystalline material. This leads to a broadening of the bands, which is effectively observed for amorphous carbons. Usually, a Gaussian function is used to fit the Raman bands, even if, as mentioned by Wang et al. [144], there is no clear justification for using this function.
In between amorphous materials and perfect crystals, defects play a role in the disturbed Raman scattering process. The double resonance mechanism involving defects is an example, but it is not the only one. Another mechanism that can influence the inelastic scattered light is confinement at the nanoscale. Defects can localize the wavefunction of the phonon, leading to a delocalization of its momentum in the Brillouin zone, due to the Heisenberg principle, relaxing the rule. Then, because of the phonon dispersion relation , it allows to explore away from the Г point, new frequencies appearing in the Raman spectrum. Richter et al. [145] succeeded in understanding asymmetric profiles observed on the band at 520 cm−1 in silicon by following this approach, the phonon confinement model. They proposed to multiply the phonon wavefunction by a Gaussian function that localizes the phonon [145]. It can account for linewidth increase and wavenumber decrease. The intensity of the band is written as (see Equation (16)):
By choosing a good weighting function W, and by describing correctly the phonon branches in the Brillouin zone (BZ) and integrating the above expression, one can obtain the influence of phonon confinement on the shape of the spectrum. This was done for graphene by Puech et al. in 2016 [146]. LO and TO phonons introduced a second G band component at a lower wavelength (close to 1550 cm−1), but also broadened all the bands
Another kind of profile, which is asymmetric, has to be mentioned: The Breit–Wigner–Fano (BWF) profile (see Equation (17)):
where the q parameter is a real number (here, q has nothing to do with the momentum, not enough letters being possible to choose in the many alphabets usable). 1/q accounts for an interaction between a phonon and a continuum of states. It is generally used to fit the G bands of metallic nanotubes. Sometimes it can be used just because it is convenient to use it, e.g., to account for confinement effects or an unresolved band lying in the wing of the G band. Then, the term 1/q has no physical meaning.
2.7. Procedures for Fitting of the First Order Region
To fit what is often called the first order region (1000–1700 cm−1), a large variety of procedures have been reported in the literature. Here, we just mention some of them (more details will be given in the corresponding sub sections of Section 3):
- One band: The G band is fitted by a Lorentzian if symmetric, and by a BWF if not symmetric.
- Three bands: The G, D, and D’ bands are fitted by Lorentzians. D and D’ bands are sometimes labelled D1 and D2, respectively. The D’ band is less intense than the D band by an order of magnitude and can be forgotten when the D and is much less intense than the G band.
- Four bands: The G, D, and D’ bands are fitted by Lorentzians and a Gaussian band is added in the redshift wing of the G band (close to 1500 cm−1). This band is sometimes called the D3 band, in other cases it is called the A band.
- Five bands: Same as the four bands model, but adding another band around 1200 cm−1, which is sometimes found Lorentzian, otherwise found Gaussian. This band is called the D4 band, or D” since the theoretical work of Venezuela et al. [69].
- Six bands: Same as the five bands model, but with another distinct band close to 1150 cm−1. This band is generally more easily seen using red laser (633/785 nm) instead of green/blue lasers.
- Recent developments [61] have revealed that the bands around 1100–1200 cm−1 are in fact three bands (D”, D*, and D**) with different dispersion behavior (see Figure 6).
- Occasionally, no D’ band is observed (possibly merged with the G band so that authors do not try to decompose each component).
- Sometimes, the D and G bands which are Lorentzian are accompanied by two other broader bands (Gaussian or of different line shape) that are red-shifted compared to the D and G bands. The term amorphous component can often be found as well.
We advise the reader to carefully check for the relative intensity ratio notation used in the literature. In some papers, for example, the ratios of two band intensities are the area ratios (noted A), sometimes it is the maximum intensity (noted I) and elsewhere it is reported without fitting (noted H). Jorio et al. [147] performed a comparison between AD/AG and ID/IG for bombarded graphene and found that ID/IG should be used instead of AD/AG.
2.8. Examples of How Comparison with First-Principle Calculations Can Help
Systems are sometimes so complex that the use of first-principle calculations are more than needed, helping in retrieving quantitative data of the structure or kind of defects. Lattice-dynamic behavior of a crystal affects physical properties such as phonon dispersion, which (as we know) can be compared to Raman spectra for some points of the Brillouin zone. Our aim in this part is not to detail the theory from the first-principle, but to illustrate the use of the theory and which information can be retrieved. The reader who is interested in more details about the basics of the lattice vibration theory is advised to read the seminal paper by Born and Huang [24], and the reader who would like to know more about the density functional (perturbation) theory, the methodology, and its approximations could read the review paper by Baroni et al. [148]. Such theories are implemented in open source codes like QUANTUM-ESPRESSO [149] or licensed codes like the Vienna Ab Initio Simulation Package (VASP).
As a first example, Mohiuddin et al. applied an external strain on a graphene plane both experimentally (observing the splitting of the E2G Raman active mode) and theoretically [8]. The good match between both experiment and theory strengthens the physical description of the graphene on the basis of the calculation. Going a step further is possible as well: Bonini et al. [141] were able to determine from first principle the thermal properties of graphene and graphite, enhancing the role of electron–phonon and phonon–phonon interactions and compared them with the band shift and band width (σG and ГG) evolution with temperature. ГG being essentially due to electron-phonon coupling at room temperature, whereas the band width of the infrared active mode is narrower, only caused by phonon–phonon interactions. Next example is about identifying defects signature, which is a holy grail in the field [69], and will be discussed in much more detail in Section 3.3, Section 3.4, Section 3.5 and Section 3.6 (some issues can be found in the review article by Ferrari and Basko [62]). Here, we mention the fact that for carbon nanotubes, the works by Saidi et al. [150] have revealed that di-vacancies and other defects influence the non-resonant G bands more than the radial breathing modes. These defects can also affect the intensity of the resonant Raman bands, allowing them to be identified by this way [151,152]. As a final example, we would like to mention graphene oxide, which is a heavily oxidized carbon. The G band of graphene oxide has been found blue shifted experimentally, compared to graphene. Its explanation was obtained with the help of first principles [153]: Graphene oxide can be composed of sp2 areas surrounded by an alternating pattern of single-double carbon bonds.
3. Raman Spectroscopy of Different Aromatic Carbons
In this section, we review the way multiwavelength Raman spectroscopy is used in literature to better characterize aromatic based carbons, by focusing on more and more disordered aromatic carbons. The aim is to give a concrete and practical view on how Raman spectroscopy can be used to classify the nanostructure. Figure 10 displays the Raman cross sections of typical graphene based materials compared to some other relevant molecules or reference materials.
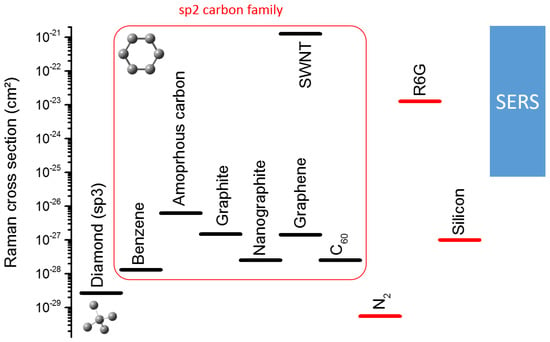
Figure 10.
Raman cross section for carbonaceous materials compared to reference materials. Sources: Diamond [154], graphene [49], nanographite [65], benzene [155], silicon [156], SERS [157]. Note that Raman cross section of solids can sometimes be difficult to obtain because of substrate effects that can give rise to interference effects that depend on the thicknesses and optical indexes, as it was shown for graphene [48,158] and earlier for amorphous carbon [46].
We start with graphene in Section 3.1, and will continue with what we call nanographenes in Section 3.2 (nanotubes, nanohorns, nanocones, nanofibers), followed by bombarded graphene in Section 3.3, very defective carbons (e.g., coal, soot, black carbons) in Section 3.4 and graphite intercalated compounds in Section 3.5. We will finish with amorphous carbons in Section 3.6.
3.1. Graphene
Graphene has many astonishing properties (that are reviewed by Peres [159]). One of them is the existence of Dirac cones crossing at the Fermi level at the K point of the Brillouin zone (see Figure 5b), and that determine mostly the transport properties in graphene. As there is some electronic resonance with incoming photons, these cones also determine the properties of Raman spectra, which can appear counterintuitively. The main thing to keep in mind about Raman spectroscopy of graphene is that it is then driven by the electron properties—how they move, interfere, and interact—affects the Raman spectra. Disorder can modify the electronic properties, and then can find finger prints in the Raman spectra because of the resonance mentioned above. Among other defects, one can find: Adsorbed species, folded regions, rippling, vacancies, topological defects (such as Stone–Wales defects), charged impurities on wafer [159], and so forth.
Graphene is the building block of nanocarbons: Staking individual (graphene) layers will give rise to multi-layer graphene and eventually graphite. Rolling it, results in the formation of carbon nanotubes. Creating point defects or linear defects (edge or grain boundaries) can account for different processes such as ion implantation or crystal growth under thermal treatment of amorphous carbons, for example. If one wants to understand the Raman spectrum of aromatic carbon containing samples, one has to understand first the Raman spectrum of graphene. Many reviews can be found on Raman spectroscopy applied to graphene, but we advise the reader to first use the work of Ferrari [62] and its useful 13 pages of supplementary information, or the work of Beams et al. [160]. Below, we give some trends before focusing, in Section 3.2, on some specific nanoforms and on few kinds of defective graphene samples.
Graphene without defect gives rise to two main bands: The symmetry allowed G band and another band, the 2D band. For multilayer graphene, useful information can be found in the work of Malard et al. [139]. The G band is due to the E2g phonon at the center of the Brillouin zone (and called the Г-point). The 2D band is due to TO phonons around the K point in the Brillouin zone, and is active due to the double resonance mechanism [57], as presented briefly in Section 2.5. As an illustration, multi-layer graphene was found to display characteristic Raman spectra, especially in the 2D spectral region [1]. As it has different electronic structures close to the K point, and because the double resonance mechanism connects phonons to the electronic structure, the position, shape (composed of several overlapped bands), and intensity of the 2D band(s) can be used to distinguish from monolayer up to 5–10 stacked layers. The relative intensity ratio between the 2D and G bands was also found to be dependent on the number of layers: I2D/IG is close to 3 for monolayer graphene, and falls down to 0.3 for highly oriented pyrolytic graphite (HOPG). Then, the Raman plot σ2D versus I2D/IG can be used to rapidly have an idea of the quality of the graphene samples handled. Figure 11 gives such an illustration for two wavelengths: 514 and 633 nm. The HOPG samples have been cleaved by the tape method to obtain multilayer graphene flakes that were deposited on a silicon substrate. Raman spectra have been obtained from all the flakes. For 514 nm, HOPG is situated at (2725; 0.3) and the monolayer is situated at (2686; 3). One can see that, with this method, many intermediates are obtained. The broadening around the guide for the eyes lines can be due to stacking faults that modify the electronic structure of the multilayers, and thus the 2D shape and intensity [161,162,163]. One has to note that σG slightly depends also on the number of layers but the shift compared to HOPG is no more than 5–6 cm−1 [164]. The width of the G band, due to electron–phonon coupling has been evaluated to be 11.5 cm−1 [58], phonon–phonon scattering being responsible to 4–5 cm−1 extra broadening found experimentally. For graphite and multilayer graphene, we mention the existence of a C band, which is sensitive to coupling between layers: It lies at 44 cm−1 for graphite and shifts regularly down to 31 cm−1 for bilayer graphene [165].
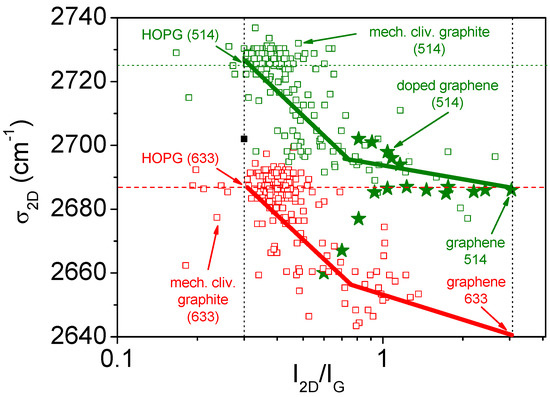
Figure 11.
2D band position as function of I2D/IG for laser wavelengths of 514 and 633 nm. Graphene frequencies were obtained from [1]. Empty squares are from mechanically cleaved graphene flakes (original data). Stars are from [160] (doped with carrier density from −3 × 1013 cm−2 to +4 × 1013 cm−2), the downshift corresponds to positive doping, whereas upshift corresponds to negative doping.
As another example, dopant impurities can modify the Raman spectrum of graphene [166,167,168]. Playing with the electron doping (i.e., changing the position of the Fermi level) modifies the Raman spectrum: The band positions and intensities are modified [169]. In Figure 11, the doping effect on a single layer graphene has been added: Doping with electrons or holes can increase or decrease σ2D, and both diminish I2D/IG. The effects of doping have been reviewed in 2007 [137] and in 2015 [160]. We report that changing the carrier density also affects the D band spectroscopic parameters [170]. Impurities adsorbed on graphene can also modify carrier mobility and thus the Raman spectrum of graphene [171], changing the D band intensity.
Substrate effects on the position of the 2D and G bands (downshift, splitting) have been reported in the works of Das and Calizo et al. [164,172,173]. Strain can be such effect [174]. If that is the case, Frank et al. demonstrated that using different wavelength gives very different 2D band shape. Among others, doping can be an important and unintentional effect as it can change the position of the 2D band, as shown by Yang et al., [175], for graphene grown on SiC, or by Das et al., [176], for other substrates. However, as doping also affects the G band position and width, checking G band anomalies can be used to detect such an unwanted effect. Roughly, for electron or hole concentrations higher than 1013 cm−2, the G band width is diminished by a factor of 2 (i.e., close to 7–8 cm–1) [176]. G band splitting and intensity enhancement (i.e., Surface Enhanced Raman Scattering) were observed for multilayer graphene in contact with Ag and Au [177]. The splitting and intensity enhancement were found to be higher for single layers. As the 2D band intensity was found diminished by the Ag deposition, an n-type doping effect was concluded. A p-doping effect was deduced for Au deposition because of the 2D band shift. If the reader is interested in the detection of graphene combined with the SERS effect, a further reading of the 2013 review can be found in the work of Xu et al. [178]. A good way to differentiate between doping effect and subtract effect is to plot σG versus σ2D of the analyzed samples (this differentiation is possible because strain affects the band position by changing bond length and angles between bonds, whereas doping affects the electron–phonon coupling [179]).
Depending on the optical constants of the substrate on which the graphene layer is deposited, the substrate (layer) thickness, the numerical aperture of the objective used or the wavelength of light used for performing the micro Raman spectroscopy analysis, the absolute intensity of the G and 2D bands can be altered due to electromagnetic interference effects so that their relative intensity ratio is changed in appearance [48,158]. For example, for a SiO2 substrate layer thickness in the range of 225–375 nm, I2D/IG appears to vary from 2 to 8 instead of being constant at 3. A refined analysis was performed by Klar et al. [49] who were interested in the absolute intensities of the G and 2D bands for multilayer graphene, checking numerical aperture effects, wavevector polarization, substrate effect, etc.
We have to mention a breakthrough due to deep UV Raman spectroscopy that has been used only since very recently (2015) on graphene [180]. The advantage is that, due to the double resonance mechanism, one gets far away from the K point in the Brillouin zone, exploring a larger part of the dispersion relations, for example near the M point of the Brillouin zone. The ()4 wavelength dependency of the G band intensity was confirmed for 266 nm (4.7 eV), but a surprising ()−1 relationship was found for the 2D band. It would lead to the conclusion that I2D/IG is proportional to ()5. On nanographites [65], Cançado et al., who observed a La dependency, did not observe any () dependency, but their data were recorded in the visible range, in a small range of wavelength. Tyborski et al. observed that when the 2D band disappears, the two phonon density of states rises in the 2600–3300 cm−1 spectral region [181]. Among the many things they deduced from their analysis, taking into account symmetry arguments, they were able to deduce from this spectral region, the maximum frequency of the LO phonon at 1626 cm−1, and its frequency at the M point at 1408 cm−1. Saito et al. performed predictive calculations up to 177 nm (7 eV) [182]. They also determined the asymmetry parameter evolution with , appearing in the Breit–Wigner–Fano profile of metallic nanotubes (see Section 3.2.3 for more details) what has never been down before, to our knowledge. Finally, Raman spectroscopic measurements from UV up to 325 nm were performed on multilayer graphene in order to test the model predictions on the number of bands shaping the 2D band of multilayer graphene (due to the complex electronic structure close to the K point). The 2D band profile was found to change: For monolayer graphene, three sub bands appear at 325 nm [183]. The one with the lowest frequency (2800 cm−1), supposed to have the same origin as the G* band, has an intensity enhanced when the number of layer increases, whereas the one with the highest frequency (2900 cm−1) display another behavior. This experimental result is found to be in agreement with previous calculations announcing three strong bands and a weak band caused by four electron-hole scattering processes involved in the double resonance mechanism [184]. To conclude about UV Raman spectroscopy, it allows deeper exploration of the Brillouin zone.
Finally, Raman spectroscopy can also be used to determine mechanical properties [185], study strain effects [186], and characterize grain boundaries [187,188] of graphene grown on a substrate. In addition, it is used to deduce the thermal conductivity of suspended graphene [189], and to monitor electrostatic deflection of suspended graphene [190].
3.2. Graphene based Nanoforms
3.2.1. Nomenclature
A huge number of different carbon nanoforms are now produced around the world such as single and multiwall nanotubes, bamboo nanotubes, nanotube forests, fullerenes, nano-onions, nanocones, stacked nanocones, scrolled graphene, nanofibers, nanowalls, nanosheets, and nanoplates. Graphene is definitely their building block, and by applying a transformation, such as stacking, cutting, circularly wrapping, scrolling, coiling, screwing, etc., all the other forms can be obtained. In 2012, the editors of the journal Carbon decided to propose a nomenclature to classify all these sp2 carbon nanoforms [191]. To help researchers in their bibliographic studies, they proposed to classify all the known forms in three families: Molecular forms (0D), cylindrical nanoforms (1D), layered nanoforms (2D). Another family should be included, to our opinion, and called “graphenic carbon materials”, as was reported in [192]. This fourth family contains graphite, carbon fibers, and could also include all amorphous carbons that are based on aromatic rings, but at a local order. If one considers the addition of oxygen to the carbon nanoforms, an alternative approach to categorize them was proposed in the work of Wick et al. [193], based on their toxicologic identification.
For some of these families, the state of the art is not yet enough advanced to propose a bijection between all the members of the above families and their Raman spectra. Below, we present the understanding and main trends about Raman spectroscopy of some of the nanoforms and, where possible, the links between different kinds of nanoforms.
3.2.2. Nanodomains, Nanoribbons
Graphene edges, labelled as 1D defects, exist in two configurations which are named zigzag and armchairs, related to the shape of the terminal carbons of the hexagons (see Figure 12a). Nanoribbons are delimited by these edges, which give them peculiar electronic properties (See for example Section 7 in the work of Mohr et al. [140].), forming gaps in the electronic dispersion relations due to spatial confinement of the electron wavefunction. This can affect their Raman spectra, again due to resonance.
Figure 12.
Nanoribbons. (a) Zigzag and armchair nanoribbons; (b) Typical spectra of a real nanoribbon, as studied by Casiraghi et al. [204].
The first Raman study on edges was performed by Cançado et al. in 2004 on step-like edges on graphite [194]. Roughly 2 microns away from a step, no D band was observed whereas a D band and a D’ band were observed on both zigzag and armchair configurations. The intensity of the D’ band was found non-sensitive to these two configurations, whereas the D band was found to be more intense for armchair edges than zigzag edges. The explanation of these two behaviors is that as the D’ band is an intravalley process (see Section 2.4), momentum conservation upon the double resonance mechanism can be satisfied whatever the direction in the Brillouin zone, whereas for the D band, which is an intervalley process, it cannot be satisfied for zigzag edges (see [139,194] for more details). You et al. [195] have also investigated this point in 2008. They observed that a piece of graphene with two edges separated by 90° have necessarily different chirality (this is the case if the angles are 30°, 90°, or 150°, whereas when it is 60° or 120° the chirality is the same, due to geometry). They also observed that the D band intensity is weaker for zigzag edges. Note that because graphene edges are sometimes not perfect at the micrometric scale (the size of the laser beam once focalized on the surface of a sample), especially when graphene is obtained by mechanical cleavage, it can be difficult to always conclude on the zigzag or armchair edge origin with Raman spectroscopy [196]. In 2014, Islam et al. took into account non-ideal edges orientation at a scale smaller than the micrometric size of the spot (see Figure 1 of [197]). Raman spectroscopy is now used to control the properties of edges of individual grains grown by chemical vapor deposition on large scales (few tens of microns) [187].
Because of a lack of translation symmetry, the edges do not have the same environment as in between edges of the ribbons, thus their vibrational frequencies should be different. Bands lying at 1450 and 1530 cm−1 have been observed in 2010 by Ren et al. and attributed to localized edge phonon modes of zigzag and armchair configurations terminated by H atoms [198]. These bands were observed only with red laser but not with green laser, meaning a resonance behavior may happen. Vibrational density of states calculations taking into account different sizes and shapes of nanoribbons were performed by Mazzamuto et al. in 2011 [199]. Among other features, out of plane edge localized modes were predicted at 630 cm−1 for armchair nanoribbons, whereas in plane edge localized modes were found at 480 cm−1 for zigzag nanoribbons [199]. Non-resonant Raman spectra were also studied in the same period by Saito et al. [200]. They found that, depending on the edge configuration and polarization directions of the incident and scattered photons relatively to the edge orientation, a symmetry selection rule for phonons appeared. Very recently, the group of Castiglioni published a paper on a polycyclic aromatic hydrocarbon resembling a longitudinally confined graphene ribbon with armchair edge and found the presence of G and D bands, low wavenumber bands, and combination modes in the 2500–3250 cm−1 spectral region like in graphene, with intensity very sensitive to laser wavelength due to resonance effect [117]. Radial breathing like modes, looking like the one found in nanotubes (see Section 3.2.3), have also been predicted and detected [201,202]. Verzhbitskiy et al. have shown that below 1000 cm−1, the spectral region is very sensitive to the edge morphology and functionalization [203], as can be seen in Figure 12b, as is found for the radial breathing modes of carbon nanotubes (see below) or poly aromatic hydrogenated molecules [117]. Moreover, the D band dispersion is found to vary from 10 to 30 cm−1/eV, lower than the classical 50 cm−1/eV, allowing to use multiwavelength Raman spectroscopy as a detector of such nanostructures. Very recently, the Raman spectroscopy of nanoribbons has been reviewed by Casiraghi and Prezzi [204].
3.2.3. Nanotubes
Basically, a single wall carbon nanotube (SWNT) can be seen as a rolled piece of graphene (see inset of Figure 13). The way this piece is rolled is named the chirality of the tube [205,206]. This chirality defines several properties of the tube: Its geometry (diameter) but also its electronic properties (band gap). Due to their quasi unidimensional structure (quantum confinement) the electronic density of states of SWNTs exhibits Van Hove singularities, which are singularities associated to a very high density of electronic states. Therefore, the chirality defines the allowed electronic transition between Van Hove singularities with a photonic excitation. In addition, the chirality also governs the band gap and a tube can be either metallic or semi-conductor. As a result, it is possible to plot all the allowed electronic transitions with the diameter of the SWNT. This plot is called the Kataura plot [135]. As Raman scattering for SWNTs obeys a resonant mechanism, the Kataura plot directly indicates which kind of tube is resonant for a given excitation wavelength. The final recorded Raman signal will come only from the resonating tubes. As a consequence, the Raman cross section of SWNTs is extremely high (contrary to their IR signal) [207], and since the pioneering work by Rao et al. [87], Raman spectroscopy has been extensively used for the study of SWNTs [208]. The typical first order Raman spectrum of SWNTs is divided in three parts:
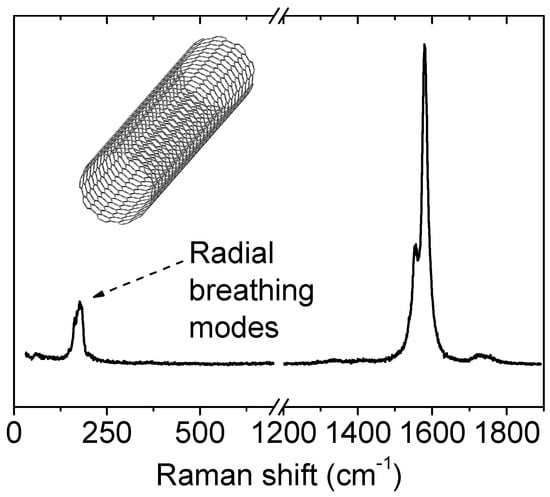
Figure 13.
Example of carbon nanotube Raman spectrum (λ0 = 514 nm).
- The low frequency region (typically between 100 and 300 cm−1), which is associated to radial breathing modes (RBM), see Figure 13. The frequency of these modes is directly related to the diameter of the tubes. One can find a review on RBM not only limited to nanotubes published recently by Ghavanloo et al. [209];
- The D band (around 1300 cm−1), related to defects (as for graphite and graphene);
- The G band (around 1550 cm−1), also similar to the G band of graphite and graphene.
Nevertheless, in the case of SWNTs the profile is related to their electronic properties. As mentioned above, it is possible to determine which kind of tube is resonant for a given excitation wavelength using the Kataura plot, and then resonance allows to identify the kind of nanotube probed [210]. If the resonant tubes are metallic, the G band exhibits an asymmetric profile named Breit–Wigner–Fano (BWF). This feature is not present for semi-conducting tubes and is coming from a specific interaction between the phonons and the electronic continuum [211]. Saito et al. performed calculations on the shape of the Breit–Wigner–Fano profile for different excitation energies, taking into account the double resonance mechanism and found that the shape is modified [182].
To conclude this part, rings of single nanotubes with different diameters have been synthetized since 2006 [212]. Ring size-dependent Raman G-band splitting in carbon nanotubes has been reported and attributed to the resonance condition changes caused by additional curvatures in rings instead of attributed to bond length change induced by curvature/strain (ring diameter ranging from 129 to 372 nm generates strain in the range 0.3–1.3%) [213]. When deconvoluted, the sub bands were found to lie at σG1 = 1535 cm−1, σG2 = 1553 cm−1, σG3 = 1563 cm−1, σG4 = 1575 cm−1, σG5 = 1593 cm−1 and σG6 = 1603 cm−1. This splitting rises for strains up to roughly 1%. Such splitting was found on strained graphene as well [8].
3.2.4. Fullerenes
Here we briefly review the main papers dealing about the Raman spectroscopy of fullerenes. First, fullerene are mixture of pentagonal and hexagonal rings which leads to a curved shape, like a soccer ball, the name of footballene being encountered sometimes, referring to C60. Since their discovery in 1985, once vaporizing graphite using laser light [129], fullerenes have been extensively studied using Raman spectroscopy. Among others, C60, C70, C80, C84 have been detected, up to C400 [214]. The paper of Dresselhaus in 1996 [215], and then the one of Kuzmany et al. in 2004 [216] both review the Raman spectroscopy of C60 and related materials, from pristine C60 up to peapods, which are single wall nanotubes filled by C60 molecules [216]. Contrary to the other sp2 carbon forms presented in our review, fullerenes exhibit specific Raman modes that can be easily identified. For example, as shown in Figure 14, in the case of C60, the modes labelled Hg(1) to Hg(8) rise at 272, 433, 709, 772, 1099, 1252, 1425, and 1575 cm−1, respectively, and the modes labelled Ag(1) and Ag(2) rise at 496 and 1470 cm−1. The intensity of the Ag(2) mode at 1470 cm−1 is much more intense than the other modes due to a vibronic coupling that enhances its Raman intensity for E0 close to 2.6 eV [130]. This band intensity can be used as a probe of the coupling between C60 and its environment, like was shown by Bardelang et al. [217], where C60 has been introduced in an open framework. Due to different selection rules, the corresponding modes for C70 are different [218]. Both C60 and C70 can be polymerized under UV radiation [219], leading to the rise of low vibrational modes at 118 cm–1, which correspond to bonds between C60 in the solid phase. Note that heating C60 thin films can lead to the formation of highly disordered nanographites [220].
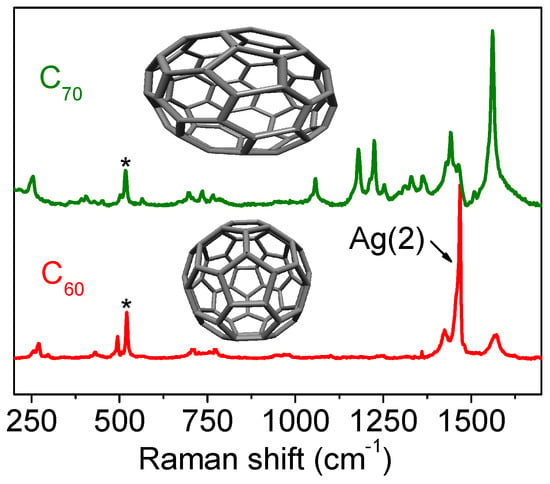
Figure 14.
Raman spectra obtained from fullerenes C60 and C70. The band at 520 cm−1 and marked by a star is due to the underlying silicon wafer. λ0 = 514 nm.
3.2.5. Nanocones
Nanocones, also called nanohorns, are typically 2–5 nm in diameter and 40–50 nm in length, looking like needles, the number of pentagons at their tips piloting their shape, as for fullerenes [221]. They were first obtained by Iijima et al. in 1999 [222], and Raman spectra performed at that time were looking like Raman spectra in between nanographite and amorphous carbons. Depending on the synthesis conditions, four different types have been identified, and labelled because of their shape observed by transmission electron microscopy: Dahlia-like, bud-like, seed-like, and petal-like [223]. A typical spectrum of a nanocone is displayed in Figure 15. By increasing the pressure up to 8 GPa, some types debundle whereas others change from one type to the other, and new promising configurations, of interest for future functionalization, have been found [223]. Calculations by Sasaki et al. [224] predict the existence of a topological D band, shifted by 50 cm−1 and being non dispersive with the incoming photon energy. However, to our knowledge, such a shift has not yet been observed.
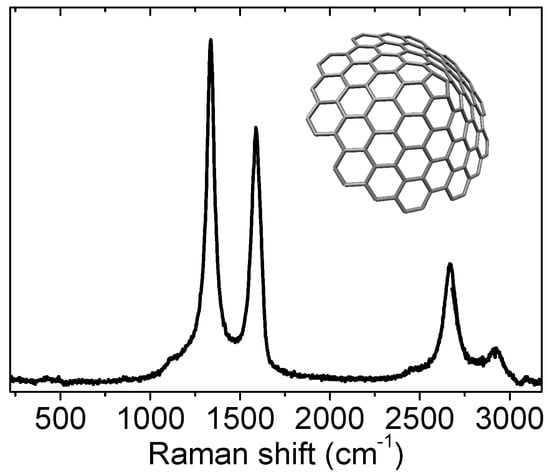
Figure 15.
Typical Raman spectrum of a nanocone. The insert is an illustration.
In situ Raman spectroscopy reported done by Pena-Alvarez et al. [223], has revealed several interesting things: The G band high shifts with stress, a band rises close to 1510 cm−1 (looking like the G band of an amorphous carbon), all the bands increase their width, and the most important thing: The width of the D band increases much more than the G band. Exactly all these effects have been found in a large variety of disordered samples that are not nanocones (ranging from nanographite to amorphous carbon) exhibiting very typical, similar, and often encountered Raman spectra, looking like the orange one in Figure 6b [66].
In a previous study [66], we have used a simple parametric model to describe the relation between the spectroscopic parameters ID/IG, ГG, ГD, and the presence of a band close to 1500 cm−1, for a huge variety of disordered carbons and using three wavelengths from 325 to 633 nm (based on empirical laws relating these parameters to La plus the assumption that the ()4 dependency affecting ID/IG also prevails for the Ferrari relation). To reproduce the spectra well, an unknown source of broadening of the D band was absolutely needed for 514 and 633 nm, but not for 325 nm, highlighting a resonance effect. Except the resonance effect which was not studied by Pena-Alvarez et al. [223], exactly all these effects have been observed in stressed nanocones as can be seen in Figure 16. In this figure, we compare the width of the G band (ГG) versus ID/IG scaled by the laser wavelength (λ0) for the large variety of samples analyzed by Pardanaud et al. [66], (referred here to “disordered carbons”), heated amorphous carbons (work of Pardanaud et al. [225,226]), bombarded graphite (work of Niwase et al. [227]) and the nanocones from the work of Pena-Alvarez et al. [223]. The grey lines are the models based on the Tuinstra and Ferrari relations (see the work of Pardanaud et al. [66], for more details) and stand for disordered graphite and amorphous carbons, respectively. All these data draw a common pattern that has to do with the so-called “amorphization trajectory” of Ferrari [4], presented in more details in Section 3.6. Briefly, starting from a perfect graphite, on the left corner of the figure, both ГG and ID/IG increase, ГG being linear with ID/IG. At a certain point (in the range ID/IG = 0.6–3), ID/IG starts to decrease whereas ГG continues to increase, changing the trajectory in this plot. This happens when
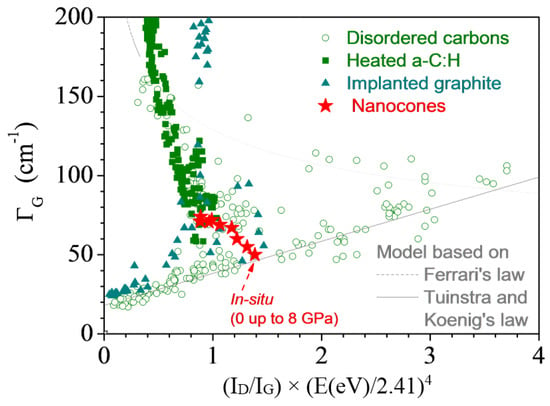
Figure 16.
ГG vs. ID/IG plot for a large variety of disordered graphitic samples. Grey lines are obtained from a fit (more explanation in the work of Pardanaud et al. [66]. Data obtained from disordered carbons (514 and 325 nm data) were also obtained from this paper. Data of implanted HOPG (triangles) were taken from [230] and from [231], respectively, and those of thermally heated amorphous carbons were taken from [225]. Data belonging to nanocones under high pressure are given in green stars, and were extracted from [223].
- both the Ferrari relation and Tuinstra and Koenig’s law meet, and/or
- a new set of bands close to 1200 and 1500 cm−1 appears, and/or
- the D bands broaden more than excepted.
This change of trajectory is observed for both disordered carbons and nanocones where the compressive stress has been increased up to 8 GPa.
Widths are generally related to lifetimes, here the decay lifetime of the iTO phonon involved in the D band, due to confinement effect induced by external compressive stress, can be the cause of the band width increase. The rise of the 1510 cm−1 band when increasing the compressive stress, can be understood qualitatively as a phonon confinement effect too [146]. Note that for La = 2 nm, Puech et al. were able to produce a peak which is close to 1550 cm−1, 40 cm−1 away from the detected position. However, in their calculations they used flat graphite, whereas nanocones are not flat. Bonds, and then of course band positions, are however affected by curvature [8] so that a combined effect of phonon confinement plus curvature may explain the existence of this band at 1510 cm−1. That band was not observed on disordered samples studied by Pardanaud et al. [66], using UV, due to resonance effects. We believe that in situ multiwavelength Raman spectroscopy coupled to skeleton analysis of TEM images (like the one performed by Oschatz et al. [228], or by Da Costa et al. [229]) performed on stressed nanocones could be the next insight to pave the way between 2D ordered and 3D disordered aromatic carbons, especially by taking advantage of resonance effects.
3.3. Disordered Graphene as a Reference for More Disordered Carbons
Structural defects that may appear during a growth process or some processing can modify local properties and make new properties varying from one kind of defect to another [232]. As an example, defective graphenes composed of randomly oriented domains, called amorphous 2D materials, have been observed in 2011 under electron beams [233]. Here, we focus on the Raman spectra of point defects (0D), line defects (1D), and Stone–Wales defects. Writing “disorder”, or “defect”, one immediately thinks about the D and D’ bands, not only the G and 2D bands. Even though the shape of the G and 2D bands can also be changed by disorder (we will see that in Section 3.4), we will now focus on the D and D’ bands that become activated by defects, whereas they are forbidden by selection rules for perfect graphene planes. We just mention that the rise of these bands subsequently to ion irradiation was first studied in the 1980s and 1990s on graphite [227,234,235,236,237,238], giving an insight to the production and behavior of defects in graphite.
Coming back to graphene, in 2012 Eckmann et al. [105] showed that the intensity of the D’ band compared to the D band (ID/ID’) is very effective to discriminate between different kinds of defects: ID/ID’ = 3.5, the minimum value, is found for boundaries, whereas ID/ID’ is close to 7 for vacancy like defects and up to 13 for sp3 defects. The ID/ID’ ratio is interesting because, according to the resonance Raman theory, it is not sensitive to the number of defects but only to the type of defects. Until today, we do not know if all defects activate these D and D’ bands. To answer this question, one has to introduce in a controlled way many kinds of defects in graphene and record their corresponding Raman spectra. Since 2006, this task has been challenged mainly by the group of Jorio and Cançado by studying 0D [98,99,101] and 1D [65,67] defects of graphene separately, and together very recently [97], and also with 0D defects in multilayer graphene [99,100]. Eckmann et al. also challenged this point, by comparing sp3-C, vacancies, and substitutional boron atoms, thereby highlighting the role played by the D’ band [239].
In 2006 and 2007, Cançado et al. worked first on nanographites with crystallites delimited by 1D defects (and obtained by heating diamond like carbons), and clarified the Tuinstra and Koenig relation, highlighting the ()4 dependency of the ID/IG ratio for 1D defects [65,67,240]. Moreover, they have shown that the width of the D, G , D’, and 2D bands verify a relation which is: Г = A + B/La, A and B being constants (A = 11 cm−1 for the G band, for example, close to the 11.5 cm–1 calculated for the perfect graphite crystal [58]). As a direct consequence, ID/IG and Г are linear if plotted one against the other for these nanographites, with La in the range 20–65 nm. This is what is evidenced in the bottom of Figure 16. Another direct consequence is that ГG and ГD evolve linearly too, with a slope close to 1.
In 2010, Lucchese et al. [101] introduced their well-known “local activation model” in order to reproduce the spectra obtained on graphene samples bombarded at different fluences by 90 eV Ar+ ions. They found the following expression (see Equation (18)) for 0D defects by writing the evolution equation of the S and A regions as shown in Figure 17a,b
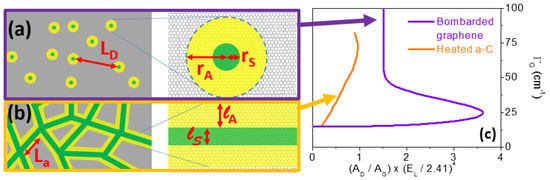
Figure 17.
0D and 1D local activation models. (a,b) Definition of the structurally damaged regions and activated regions, with LD, the distance between defects, and La, the size of crystallites surrounded by edges, for respectively the 0D and 1D defects; (c) ГG as a function of AD/AG.
Here, rS (see Figure 17a) is the radius of the structurally disordered area around the defect, and rA the radius of the activated region (i.e., the region in which the selection rules are broken leading to the intervalley double resonance mechanism and giving rise to a D band). CA and CS are constants whose origins are discussed in [101] (CA is related to the Raman cross sections, CS is related to the geometry of the defect), LD is the average distance between defects. In the regime where the quantity of defects is small (i.e., when the mean distance between defects is large compared to rA − rS), a first order Taylor expansion of the above equation reduces to Equation (19):
In their study [101], the defect was a vacancy and the parameters found were: rA = 3 nm, rS = 1 nm, CA = 4.2, and CS 0. For a low number of defects, the ID/IG ratio behaves like 1/LD2, which better fits the data than the Tuinstra and Koenig 1/La relation. In another study [239], no dependency with the type and number of defects (such as vacancy and sp3-C) was obtained using this ratio (but a difference was noticed from 3D materials, see Figure 3 and its discussion in that study). However, comparing D and D’ intensities with the type and number of defects leads to a strong correlation. In the low concentration regime, one can find Equation (20):
with the subscript D or D’ to refer to the D or D’ bands. One can see that the ID/ID’ ratio strongly depends on the CS,D’ coefficient, which is found to be equal to 0.1 for sp3 defects whereas it is 1.2 for vacancy defects.
Ribeiro-Soares et al. studied 1D defects in graphene [102]. They heated a diamond-like carbon from 1200 to 2800 °C. They obtained an expression for the ID/IG intensity ratio [102], by noting that two sets of two bands have to be considered: A first set of D and G bands occurring from the activated region, and one set of D and G bands, downshifted due to softening of the phonon modes, occurring from highly disordered areas. Let us thus consider a structurally damaged ribbon (width lS), and activated region (width lA) and the mean size of a crystallite La (see Figure 17b). The evaluation of the intensity coming from the structurally damaged ribbon is purely geometric, whereas that of the ones from the activated region is geometric plus an exponential function introduced to account for the localization of the scattering giving rise to the D band. The final expression is then (see Equation (21):
The C constants are related to the cross sections and contain the wavelength dependency. The values of lS and lA were found to be 1.4 nm and 4 nm, respectively, and in very good agreement with Scanning Tunneling Microscopy (STM) data. When La >> lS (i.e., the size of the structurally disordered region is negligible compared to the size of the crystallites), one obtains Equation (22):
which perfectly reproduces the Tuinstra and Koenig expression obtained experimentally in 1970. The group of Jorio and Cançado produced recently a work that aims to disentangle the contribution of 0D and 1D defects coexisting on graphene related materials [97]. Figure 17c displays for both 0D and 1D defects the plot of ГG as function of the AD/AG ratio scaled with the laser energy, A being the band area (see comment in Section 2.7).
We now focus on another kind of defects named topological defects. These are non-hexagonal arrangements of carbon atoms in the graphene lattice. They are reported for most of the graphene based materials such as SWNTs, graphene [241,242] and graphite [243]. This kind of defect introduces a curvature in the flat geometry of a graphene layer. Probably one of the most studied topological defects is displayed in Figure 18: The Stone–Thrower–Wales (STW) defect (44 papers found using a bibliometric tool focused on abstracts), which corresponds to two pentagon-heptagon pairs. It is not easy to determine the precise frequency associated to the Raman signature of these defects. Theoretical calculations with SWNTs reported that the characteristic frequency of the STW defects should lie between 1820 and 1962 cm−1, depending on the local curvature of the tube [244]. On the other hand, SERS measurements performed with SWNTs have shown two modes at 1139 and 1183 cm−1 associated to STW defects [245]. Theoretical calculations predict, among other things, a softening of the G band by −26 cm−1, and a hardening of the D band by +13 cm−1 [246]. A way to detect their Raman signature would be to use SERS, as suggested in the work of Itoh et al. [247].
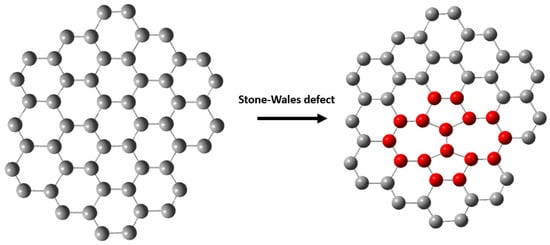
Figure 18.
Stone–Wales defect.
3.4. Very Defective Carbons: Pyrocarbons, Coals, and Soots
The first reported work on very defective carbons is from Tuinstra and Koenig who found the relation relating the intensities of the D and G bands for activated charcoal, lampblack, and vitreous carbon, as reported above. In 1984, Lespade et al. [79] reported the Raman spectra of many disordered carbons such as pyrocarbons and fibers, using heat treatment to change the structure of these materials that were found to be graphitizable and not graphitizable. Four graphitization indexes were found: The frequency of the G band, its width, the intensity ratio ID/IG, and the width of the 2D band. Among others, they introduced a graphitization trajectory in the Г2D vs. ГG plot, distinguishing between 2D and 3D order [79]. The behavior of the 2D band according to a 3D order (related to the stacking order) was elucidated in more details 24 years later by Cançado et al. who heated diamond-like carbons in the range 2200–2700 °C [59]. Among other things, they evidenced a contribution of the band coming from 3D graphite and a contribution from graphene, and were able to relate their relative intensity ratio to the size of the crystallites in the c direction up to roughly 200 nm. Today, the number and origin of the 2D sub-bands have been understood for multilayer graphene [1] in the framework of the double resonance mechanism and more complex things can occur such as folding [248], misorientation [162], and stacking faults that can modify the intensities and shape. All these processes may also contribute to the intensity ratio spreading displayed in Figure 11. Table 1 in the paper by Larouche et al. [249] resumes the main spectral indicators that are used in the literature to deduce information about the structure of very defective carbons. They presented the influence of curvature by introducing the distance parameter Leq, which is the average continuous graphene length including tortuosity of graphenic planes (see Figure 19). They showed that this tortuosity is very well correlated to the 2D band width. Note that they defined tortuosity as the number of phonons produced at the K point divided by the number of phonons produced at the Г point of the Brillouin zone. We advise the reader that tortuosity is generally derived differently, from the analysis of HRTEM images [250,251]. The main message of this paper though is that the 2D band width is a good parameter to gain an insight into the tortuosity.

Table 1.
Characteristics of ta-C:H and various a-C:H sub-types.
Figure 19.
Tortuosity as defined by Larouche et al. [249]. The domains represented by red arrows (La) are aromatic domains without defects. The domains represented by purple arrows (Leq) are composed of several aromatic domains, in-between there are curved graphene sites.
We now focus on soots and pyrocarbons (see a typical Raman spectrum on Figure 20). First of all, what is the difference between soots and pyrocarbons? When processing hydrocarbons (varying pressure, P, and temperature, T, in the reactor), gas phase nucleation leads to soots, whereas heterogeneous nucleation on the substrate leads to the formation of pyrocarbons, which can contain up to 5 at. % of hydrogen [252]. The Raman spectroscopy of soots (e.g., diesel soots, spark discharge soots, commercial black carbons) has been investigated in detail in 2005 [122]. To fit all the data in the 1000–1700 cm−1 spectral region, five bands were necessary: D (called D1), D’ (called D2), and G bands, plus two less intense bands, the D3 and D4 bands, lying at 1500 and close to 1180 cm−1 (dependent on the wavelength of the laser), respectively. The best fit found was a four Lorentzian fit plus a Gaussian lineshape for the D3 band. The need of such a band was first proposed by Rouzaud et al. [253]. In 2009, Brunetto et al. bombarded some aliphatic and aromatic dominated soots produced in flames to mimic the effect of irradiation encountered in the primitive solar nebulae [254]. The authors used a σG vs. ГG plot to compare their Raman spectra to the one collected on meteorites, interplanetary dusts and the grains collected from the Wild 2 comets. They found them very similar, allowing them to suppose that the irradiation played a major role in the processing of the carbon materials at the beginning of the solar system. Recently, the multiwavelength analysis is being used more than in the past to give better refined information on soots. For example, in 2011, combining temperature programmed oxidation and multiwavelength Raman spectroscopy (514–785 nm), Schmidt et al. noticed that a structure/reactivity relation from different soots can be obtained [255]. In 2015, in the framework of soot formation, Russo et al. evidenced that by changing the wavelength of the laser they were able to relate the origin of the fuel molecule and the structure of the soot [256]. The G band was found to display an asymmetric profile, and a D5 band (attributed to the presence of olefinic chains lying in grain boundaries), in the range 1100–1200 cm−1, was found to be more intense using 633 nm instead of green or blue lasers. Ess et al. were able to relate the structural change of soots under heating under oxygen atmosphere up to 600 °C and relate it to the organic carbon content [257].
Figure 20.
Raman spectrum obtained from a pyrocarbon. The inset represents a rough laminar pyrocarbon with defects (black bonds), sp3 bonds (blue), sp bonds (red), and hydrogen bonds (green). (λ0 = 633 nm).
Pyrocarbons are generally deposited on substrates by cracking hydrocarbons at temperatures higher than 900 °C, using chemical vapor deposition processes. Using infiltration process, pyrocarbons are used mainly in carbon/carbon fiber composites, whose aim is to withstand mechanical stress at high temperature [252]. A large variety of pyrocarbon textures exist. Among them, we can cite rough laminar (columnar structures), smooth laminar, and regenerative laminar [258]. High resolution TEM shows columnar and wavy structures (produced by pentagons during the deposition process [259]). Their TEM fringes length was found to be 1.6, 2.3, and 2.6 nm, respectively. In particular, the Raman D band width was found to be a good spectroscopic criterion to distinguish them. Bourrat et al. [258] found ГD = 80, 85, and 110 cm−1 for rough, smooth, and regenerative laminar pyrocarbon, respectively. The ranges were refined later: ГD = 80–90 cm−1 for rough laminar, ГD = 90–130 cm−1 for smooth laminar, and ГD = 170–200 cm−1 for regenerative laminar [123,260]. The interpretation is that ГD is sensitive to curvature effects, as is suggested by TEM analysis. ГG is spread on a narrower range, i.e., from 55 to 70 cm−1.
We finish this section by focusing on the D” band, sometimes called D4 band and lying in between 1100 and 1200 cm−1. It has been used for a long time to fit spectra of disordered samples (especially soot materials) and amorphous carbons with some local order (i.e., those containing sp2 aromatic domains). It is sometimes called the TPA band (for trans-polyacetylene), as it lies close to the mode found in nanodiamonds [261]. It has been recently considered in the fitting procedure of nanoporous carbons [262]. The history of this band and its relation to the 2450 cm−1 band, first reported in the work of Nemanich, [81], for defectless graphite, is important to mention here because it illustrates the fact that studying disordered materials helps in understanding the spectra of well-ordered materials. The D” band origin has been understood by Venezuela et al. [69] in 2011 on perfect graphene (it is mainly due to phonons associated to the KГ direction in the Brillouin zone). In 2013, May et al. [263] were able to calculate the shape of the 2450 cm−1 band in the framework of the double resonance mechanism on perfect graphene involving TO and LA phonons close to the K point. They were able to reproduce its dispersion and change of shape depending on the laser wavelength. In 2016, Zhou et al. [183] observed on perfect graphene the laser sensitivity of the D” and D + D” bands in the UV range. In 2014, Herzinger et al. [264] created defective graphene and nanotubes by bombardment with high energy ions, and characterized the dispersion behavior of this D” band. Couzi et al. [61] determined on defective aromatic carbons (graphite nanoplatelets, heat-treated glassy carbons, pyrograph nanofilaments, and multiwall nanotubes) the behavior of the D” band, identifying two new bands (D* and D**) lying close to the D” band, but with positive dispersion behavior, and reproduced the dispersion of the D + D” in the near UV. We have to note that the D*, D**, and D” bands do overlap, creating the well-known D4 band often used to fit Raman spectra of soots. Very recently, the D4 and D3 bands were observed on nanotubes and partially exfoliated by acid treatment [265].
3.5. Graphite Intercalated Compounds
In this part, we briefly present some results about a kind of material that must be cited because it displays a large variety of structures and because it has great application potential in different fields (such as energy storage, superconductivity, nano-medicine, etc. [266] and references therein): Graphite intercalated compounds (GICs). GICs are multilayered materials sufficiently ordered to exhibit staging in which the number of graphitic layers in between adjacent intercalants can be varied in a controlled way. The interlayer spacing can be tuned from 0.34 up to 1 nm [267]. The denomination n-stage GICs can be found in [268], n defining the constant number of graphene layers between any nearest pair of intercalant layers. More details about the staging can also be found in [266]. The diminution of the interlayer spacing distance reduced the van der Waals interaction between planes so that it can be envisaged as a route to form graphene and nano-ribbons [269]. The list of metals and small molecules that can be embedded in between graphene planes is huge and not exhaustive here: Alkali-metals (K, Li, Cs, Rb); alkali-earth-metals (Be, Ca, Ba); halogens; C60 [270]; FeCl3 [271]; H2SO4 and HSO4− [272]; AsF5, HNO3, and SbCl5 [273]; etc. Intercalants can be electron donors or electron acceptors. Thus, charge transfer and strain are intrinsic effects in GICs, and Raman spectroscopy is sensitive to both. Raman study of highly staged GICs allowed to disentangle both effects [274]. A seminal work by Solin presenting an overview of the Raman spectroscopy of these compounds was published in 1980 [275]. A more recent work on a combination of Raman spectroscopy and ab initio calculations of GICs by Chacon-Torres et al. was reported in 2014 [266]. Inner graphene layers (also called interior layers) and outer graphene layers (also called graphene layers bounded by intercalants) can be differentiated by the G line splitting, with σG of the blue component that can reach values as high as 1636 cm−1 [266,273]. Superconductivity has been observed in many GICs (with the highest critical temperature found at a relatively high temperature, 11.5 K, for CaC6, see references [266]) and multiwavelength Raman spectroscopy is a central characterization tool because superconductivity may be due to electron–phonon interaction and mediated by phonons [276]. Multiwavelength Raman spectroscopy also allows a direct measurement of the Fermi level by observing the Pauli blocking (which results in the 2D band intensity vanishing by tuning the wavelength of the laser) [271].
3.6. Amorphous and Diamond-Like Carbons
Most of the work cited on Raman spectroscopy of amorphous carbons [277] comes from the thousands of times cited papers by Ferrari et al. Their four landmark papers were published from 2000 to 2005 and combine all together a comprehensive view of the understanding about Raman spectroscopy of amorphous carbons [4,5,6,70], based on many other papers that we will not cite all here. The study of Raman spectroscopy of amorphous carbons was completed in 2015 by the work of Zhang et al. [278], as we will see soon hereafter.
To begin with, amorphous carbons are generally containing sp3, sp2 carbons, and heteroatoms (such as hydrogen). sp3 carbons determine the mechanical properties (hardness, density), whereas the sp2 aromatic clusters determine the optical properties (energy gap), mainly due to the π/π* bonds with the energy gap in the IR–visible–UV range, depending on their size. Adding hydrogen, and organizing the structure by heating the sample, can change the optical properties together with the structure [7,124,125,126,225,279,280,281,282] and Raman spectroscopy can help in checking the changes. For example, hydrogen changes the electronic structure, which leads to a Raman resonance mechanism that can be observed, helping in quantifying the amount of hydrogen in the amorphous carbons [283]. Depending on the amount of aromatic/aliphatic sp2/sp3 carbons and hydrogen atoms, several kinds of amorphous carbons can be distinguished: a-C, ta-C, a-C:H, and ta-C:H. The t stands for tetracoordinated as these carbons contain generally close to 70% of sp3 carbons. A basic scheme of the ternary phase diagram for amorphous carbons is displayed in Figure 21. More information can be found in [70,124]. The classification is however more complex, with even more variety of samples. a-C:H types are themselves split in subgroups with different properties: PLCH (polymer-like a-C:H), DLCH ( diamond-like a-C:H), GLCH (graphite-like a-C:H) and GLCHH (graphite-like a-C:H with extra hydrogen subtype), as displayed in Table 1, adapted from [278].
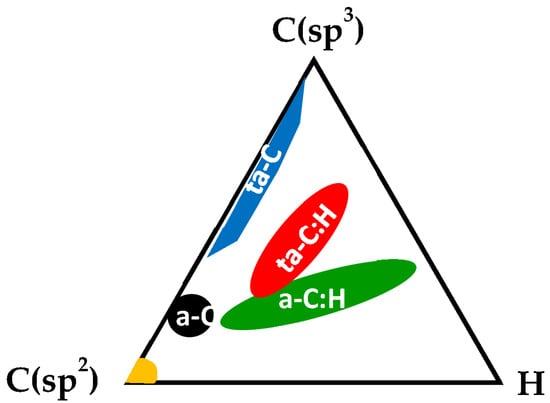
Figure 21.
Basic ternary phase diagram of amorphous carbons.
Except PLCH, which only displays a photoluminescence background, Raman spectra of amorphous carbons generally display two broad overlapped G and D bands, the D band being less intense, or disappearing when the amount of sp3 carbons is higher. The D band position displays the wavelength dispersion as in graphene but shifted depending on the kind of amorphous carbon, as shown in Figure 7b. For the G band, it depends on the local degree of order, as already displayed in Figure 7a. Figure 22 displays the Raman spectra of one a-C:H film (H being close to 30 at.%) but recorded with five different laser wavelengths, ranging from 266 to 633 nm [72]. The dependence of the shape with the laser wavelength [284] can be explained mainly by the fact that the sample is composed of a distribution of aromatic domains which display local electronic structures. The wavelength used is resonant with one kind of environment that appears stronger in the spectrum. Ferrari et al. proposed a “three stage” model that can explain the ordering of the sp2 phase going from nanocrystalline graphite (nc-G) to highly disordered amorphous carbon, explaining the changes in the spectroscopic parameters [4]. The parameters followed are the ID/IG and σG parameters, and their changes with the laser wavelength. For example, at 514 nm, the G band position is at 1582 cm−1 for graphite, it upshifts to 1600 cm−1 for nanographite composed of only sp2 aromatic clusters, whereas it can shift up to 1630 cm−1 for other forms of sp2 carbons (chains), where sp3 carbons are present. Then, when starting amorphization, σG diminishes down to 1520 cm−1. In Figure 23, we illustrate that starting from an amorphous carbon, we obtain a nanographite. We plot σG for an a-C:H (DLCH) film that has been heated at a 15 K·min−1 rate, under a 1-bar Ar atmosphere, Raman spectra being recorded in situ, with ramp 1 stopped at 900 °C. A typical evolution is drawn [225] that informs us that the amorphous carbon is organizing when temperature is increased, by growth of the size of the carbon aromatic clusters. A plateau is reached at 600 °C. Ramp 2 is made on the same sample after it has first been cooled down to room temperature. One can see that the G band at room temperature is now lying at 1592 cm−1. The second ramp informs us that now it behaves like graphite and no more like an amorphous carbon, with an upshift of about 10 cm−1, which is typical for a nanocrystalline graphite. The diminution of σG with T for graphite and graphene is reversible and can be used as a contact less thermometer [172,173].
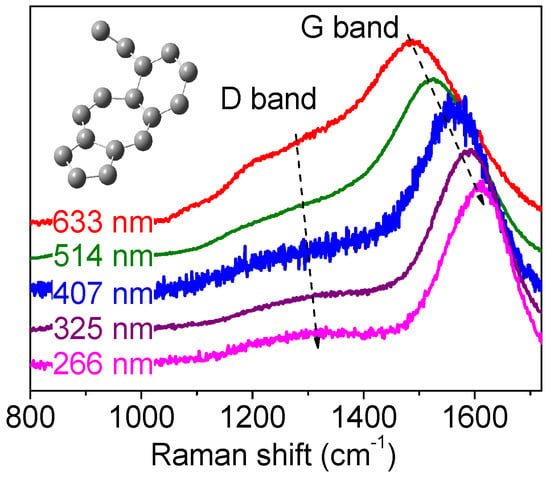
Figure 22.
Raman spectra of amorphous carbon (a-C:H with about 30 at.% H) obtained with different laser wavelengths.
Figure 23.
Temperature evolution of σG for a DLCH sample (H/H + C = 29%). In situ measurement is done in an environmental cell, under argon atmosphere to avoid oxidation.
Next, we ask “what are the other spectroscopic parameters that can be used to characterize amorphous carbons?” The 2D band cannot be used in general as it is very low in intensity and very broad, as can be seen in Figure 6b, except when the amorphous carbon is heated. Another spectroscopic parameter has been found useful to help in determining the amount of hydrogen bonded in a-C:H: the so-called m/IG parameter, which is the ratio between the slope of the photoluminescence background, m, in the range 800–1800 cm−1 divided by the G band intensity. This spectroscopic parameter gives certain qualitative information, as presented in the work of Casiraghi et al. [6], and in the work of Buijnsters et al. [285], but is also sensitive to other defects meaning it cannot be used systematically (see the analysis on a heated a-C:H performed by comparing Raman spectroscopy with thermal desorption spectroscopy and ion beam analysis [7], and calculations at the end of the work of Rose et al. [282]). It has been found that the G band width, ГG, is correlated to the sp3 content and the linear dispersion of σG of as deposited samples correlates to the H content [286]. Then, a good way to represent the data is to plot σG as a function of ГG, as was done for several wavelengths in [72,282]. Figure 24 displays such a plot for different kinds of heated amorphous carbons plus nanocrystalline graphite (for nc-G, ta-C, and ta-C:H data, see [66]). If one uses ГG as an indicator of local disorder close to sp2 bonds in the material (which can be related to the size of the clusters [5,65] and/or to the sp3 content close to sp2 bonds [286]), one can use this parameter in order to have an idea of where is the sample situated in Ferrari’s “three stage model”. With this in mind, nc-G is more ordered than a-C:H/D which are themselves more ordered than ta-C:H and ta-C. Each kind of carbon draws its own line when heated, but all these lines tend to converge in a region close to 100 cm−1. a-C, a-C:H, and a-C:D data were recorded in-situ, contrary to ta-C, ta-C:H, and nc-G, and thus appear down shifted due to dilatation and multi-phonon processes [172,173]. The presence of hydrogen systematically diminishes the position of the G band (for ta-C/ta-C:H and a-C/ta-C:H). The systematic frequency shift between a-C:H and a-C:D that tends to diminish when decreasing ГG (i.e., ordering the material) is partially due to an isotopical shift of C-H/C-D bonds, as the difference is in the same order as for C6H6 and C6D6 molecules [287].
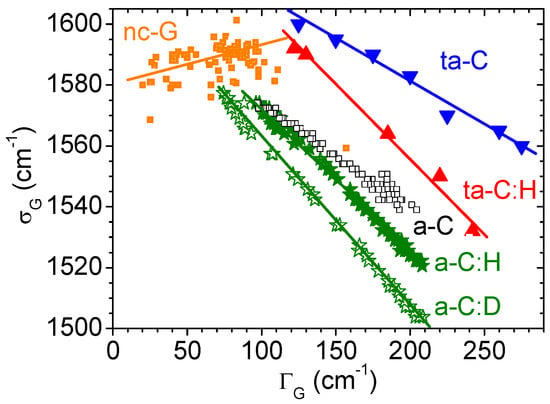
Figure 24.
Plots of σG vs. ГG for nc-G and different amorphous carbons. Data were recorded with λL = 514 nm.
In 2015, a phenomenological model based on dispersion was proposed by Zhang et al. [278] in order to better characterize amorphous carbons by analyzing their Raman spectra recorded with several wavelengths. This model starts with the statement that the G band intensity is the sum of three kinds of sp2 clusters (see Equation (23)):
where ω is the Raman frequency, λL the laser wavelength, and Ig, Ir and Ic are the intensities of the nc-G, fused aromatic rings and olefinic chain clusters, respectively. Without going into details here (the model is detailed in Section 2 and in the appendixes of [278]), this shows that σG is a weighted average of the resonant frequencies for the three types of sp2 carbons (see Equation (24)):
where ng, nr, and nc are the amount of different kind of carbons that satisfy ng + nr + nc = 1. As ωg, ωr, and ωc display a linear dispersion with λL [278], and as the parameters for these linear relations have been tabulated, one can in principle deduce ng, nr, and nc from the G band dispersion.
4. Discussion
4.1. Role of Resonance
The resonance mechanisms at play in the Raman process of aromatic based carbons allow us to have a better insight in the study of graphenic materials, making multiwavelength Raman spectroscopy a relevant tool. So far, the well-known double resonance mechanism, based on scattering of an incoming photon by a phonon followed by a second scattering by a defect or another phonon, is the best option to explain most of the behaviors reported in the literature since the 1970s (such as the rising of bands like D*, D**, D”, D, D’, and 2D and combinations thereof), as we mentioned in this review. This mechanism can probe the phonon dispersion curve of graphene away from the gamma point of the Brillouin zone. The dispersion and intensity behaviors of these bands (i.e., the dependency of the D/D’ relative intensity ratio to the kind of defects, the relative D/G intensity ratio sensitivity to the amount of defects), the Stokes/anti-Stokes anomalies, the zigzag/armchair dependency, the doping effects are all explained in the framework of this double resonance mechanism. It must be noticed that mechanisms alternative to double resonance are also under consideration [118] but still need to be confirmed. So far, the double resonance mechanism remains considered as the most efficient model.
4.2. Role of Defects
Because of defects implied in this model, Raman spectroscopy can be used to characterize how a graphenic material is far from its crystalline state. As an illustration, Figure 25a displays the width of the D band (ГD) in function of the width of the G band (ГG), which is similar to focusing on the ГD/ГG that was done in [288]. Data shown are obtained for many graphenic materials (Another way that has already been used, is to display the ГD/ГG ratio as function of ГG. We then observe that the ratio evolves from 2 at ГG = 25 cm−1 down to 1 at ГG = 75 cm−1, and following it increases up to 2.3 at ГG = 93 cm−1, and finally stays constant till ГG = 150 cm−1. Mallet et al. observed such a variation of ГD/ГG with La, reaching the lowest value at La = 8 nm (see Figure 13 in the work of Zhao et al. [271]).) (carbon fibers [289], soots [122,290,291], pyrocarbons [123,252,260], nanocones [223], a large variety of disordered carbons collected from the Tore Supra tokamak [66], nanographites from Cançado et al. [65], geothermic carbons from [292], and ion implanted graphites taken from [231]). Depending on the characteristic size of the aromatic domain, the data are grouped in three different areas: the lowest rectangle with La higher than roughly 10 nm, the intermediate region with La in the range of few to 10 nm, and the higher one with La close to 1 nm. Below ГG = 50 cm−1 the evolution is linear, with a slope close to 1 that was found by Cançado et al. for nanographites [65]. When ГG is close to 75 cm−1, the slope changes drastically: D, with ГD = 50 cm−1, broadens extremely fast up to ГD = 120–150 cm−1, whereas G only evolves from 50 to 75 cm−1. This behavior was previously observed in [66,292] and is now also evidenced for pyrocarbons and nanocones. Note that some materials do not display the drastic change in slope, such as the data of graphite implanted by ions that are grouped around the line ГD = 2ГG − 35.
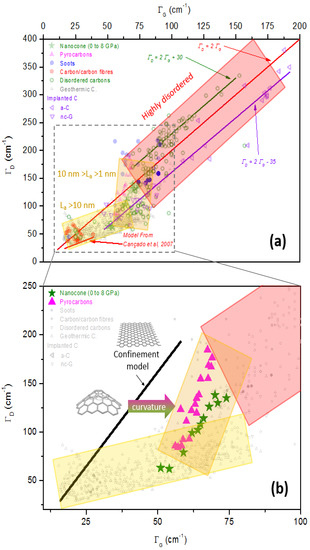
Figure 25.
ГD versus ГG plot. (a) For a large variety of disordered aromatic carbons; (b) Zoom with suggestion of both phonon confinement and curvature effects.
4.3. Other Effects: Our Propositions
The strategy adopted to deals with this apparent complexity, has been to study graphene with controlled defects. Creating point defects [101] and/or linear defects [97,102] and controlling their influence on the Raman spectrum of graphene have been the milestones of a bottom-up approach aiming at understanding the Raman spectra of more complex aromatic carbons. It has been one of the best progresses made over the last few years in order to overcome the old Tuinstra and Ferrari relations that were found to give more or less the order of magnitude/trends. Nowadays, other crucial steps have to be made in order to be closer to real materials. Among other effects that must be taken into account in the understanding of the Raman spectra, there are:
- curvature effects;
- phonon confinement effects (due to poor coupling between different aromatic planes, porosities, etc.);
- and combinations thereof.
The influence of these effects on Raman spectra should be studied in detail in the future on graphene samples containing point defects and/or linear defects with controlled amounts in order to disentangle the origin of all the effects. Three good material systems for that hypothetical study could be:
- heated C60;
- bombarded nanoribbons of different shapes and sizes deposited on deformable surfaces;
- in situ measurements of nanocones in high pressure/temperature cells.
For the second kind of materials, we believe that in situ multiwavelength Raman spectroscopy analysis could be coupled to skeleton analysis of high resolution TEM images (like reported in Da Costa, Pre, and Farbos et al. [229,251,293] respectively) in order to relate the skeleton and the kind of defects produced under constraint and to check their influence on the Raman spectrum, via resonance effects.
Concerning what already exists in the literature about curvature and/or phonon confinement fingerprints in the Raman spectra, the analysis of pyrocarbons, which can be composed of tortuous planes of varying length, has revealed that the width of the D band is sensitive to curvature effects of the graphene sheets [123,260]. Nanocones submitted to a pressure increase up to 8 GPa display some morphological changes that are accompanied by a change in the Raman spectrum too [223]. The corresponding data are displayed in Figure 25b. Among other changes, the increase of the D band width with the pressure increase is more pronounced than for the G band leading to a rapid evolution of the D band width compared to the G band width. This rapid evolution is not seen for implanted graphite samples on which two kinds of signatures (amorphous and nanocrystalline) have been observed together [231]. An explanation may be that a synergetic effect hinders curvature of graphene planes, preferring the formation of sp3 defects. This could be due to a characteristic of phonon confinement as evidenced by Puech et al. (data extracted from Figure 6 and Figure 7 of the work of Puech et al. [146]). However, we know that both nanocones and pyrocarbons can be composed of curved aromatic planes and the question remains open: How can curvature affect the spectrum too? Part of the answer was obtained by observing a band shift of the G band [8], but none was obtained for defective graphene concerning the D band widths. The arrow in Figure 25b starts from the line of the confinement model and suggests that curvature produces an extra broadening of the G band. Recently, an additional source of broadening for the G band was revealed by studying pressurized graphene membranes and it was attributed to strain (if strain is higher than 1%) [294]. This should be investigated in more detail, and the question of how curvature can lead to phonon confinement answered too.
5. Conclusions
Based on the observation that many procedures are available to fit the complex Raman spectra of very defective aromatic carbons (such as soots, pyrocarbons, coals, and amorphous carbons), we decided to review the Raman spectroscopic characteristics of these materials. Basically, if someone wants to perform a structural analysis of a carbon-based sample using only Raman spectroscopy he/she has to focus on, at least:
- the ratio intensity between the D and G bands;
- the presence of additional bands (e.g., 2D, D’, etc.);
- the width of all bands.
The combination of all these parameters will give a first basic idea of the structure, namely if the sample is well-structured or strongly disordered. Nevertheless, with only a basic Raman measurement (notably if a single excitation wavelength is used) it is clear that at the present moment a more detailed analysis of the structural defects will require other complementary experimental tools, such as high-resolution transmission electron microscopy, which is a pity as Raman spectroscopy is probably the most simple, fast, and non-destructive analysis method. If possible, we therefore suggest the use of multiwavelength Raman spectroscopy, since it allows for a better characterization of defects, looking at band position, relative intensities, and width.
We can reasonably assume that each type of defect has a Raman spectral signature. The point up to now is to identify each spectral signature, which is a real experimental challenge as in most samples the different structural defects combine, thus giving rise to a complex Raman spectrum. As suggested in Figure 25 where curvature effects are evidenced in carbon nanocones and pyrocarbons, the solution is to work with well controlled samples with specific defects. This systematic approach will pave the way towards a complete guide for a multiwavelength analysis of all aromatic carbon-based species.
Acknowledgments
Cedric Pardanaud wants to thank Gerard Vignoles and Jean-Marc Leyssale for providing spectra and inset related to pyrocarbons; Miriam Peña Alvarez for the spectra obtained from nanohorns; Cinzia Casiraghi and Deborah Prezzi for spectra and inset related to nanoribbons; and Gregory Giacometti for providing Figure 5b. Finally, Cedric Pardanaud wants to acknowledge Pascale Roubin for previous scientific discussions and for being at the origin of the carbon thematic in the PIIM Lab in 2007.
Author Contributions
Cedric Pardanaud as last and corresponding author conducted the literature search. Alexandre Merlen and Cedric Pardanaud performed and analyzed own Raman measurements/data and contributed equally to the figures building. All three authors were involved in the writing and editing of the manuscript. Josephus Gerardus Buijnsters performed a deep reading at several steps of the writing process.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| σx (expressed in cm−1): Band position of the band labelled x (x could be G, D, 2D, D’, …). |
| Γx (expressed in cm−1): Full width at half maximum of the band labelled x. |
| Ix (expressed in arbitrary units related to the number of counts on the detector): height of the band labelled x. |
| Ax (expressed in arbitrary units related to the number of counts on the detector): integrated area of the band labelled x. |
References
- Ferrari, A.C.; Meyer, J.C.; Scardaci, V.; Casiraghi, C.; Lazzeri, M.; Mauri, F.; Piscanec, S.; Jiang, D.; Novoselov, K.S.; Roth, S.; et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006, 97, 187401. [Google Scholar] [CrossRef] [PubMed]
- Elias, D.C.; Nair, R.R.; Mohiuddin, T.M.G.; Morozov, S.V.; Blake, P.; Halsall, M.P.; Ferrari, A.C.; Boukhvalov, D.W.; Katsnelson, M.I.; Geim, A.K.; et al. Control of graphene’s properties by reversible hydrogenation: Evidence for graphane. Science 2009, 323, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Dresselhaus, M.S.; Jorio, A.; Saito, R. Characterizing graphene, graphite, and carbon nanotubes by Raman spectroscopy. Annu. Rev. Condens. Matter Phys. 2010, 1, 89–108. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Robertson, J. Resonant Raman spectroscopy of disordered, amorphous, and diamondlike carbon. Phys. Rev. B 2001, 64, 075414. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Robertson, J. Raman spectroscopy of amorphous, nanostructured, diamond-like carbon, and nanodiamond. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2004, 362, 2477–2512. [Google Scholar] [CrossRef] [PubMed]
- Casiraghi, C.; Ferrari, A.C.; Robertson, J. Raman spectroscopy of hydrogenated amorphous carbons. Phys. Rev. B 2005, 72, 085401. [Google Scholar] [CrossRef]
- Pardanaud, C.; Martin, C.; Roubin, P.; Giacometti, G.; Hopf, C.; Schwarz-Selinger, T.; Jacob, W. Raman spectroscopy investigation of the H content of heated hard amorphous carbon layers. Diam. Relat. Mater. 2013, 34, 100–104. [Google Scholar] [CrossRef]
- Mohiuddin, T.M.G.; Lombardo, A.; Nair, R.R.; Bonetti, A.; Savini, G.; Jalil, R.; Bonini, N.; Basko, D.M.; Galiotis, C.; Marzari, N.; et al. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Grüneisen parameters, and sample orientation. Phys. Rev. B 2009, 79, 205433. [Google Scholar] [CrossRef]
- Piscanec, S.; Mauri, F.; Ferrari, A.C.; Lazzeri, M.; Robertson, J. Ab initio resonant Raman spectra of diamond-like carbons. Diam. Relat. Mater. 2005, 14, 1078–1083. [Google Scholar] [CrossRef]
- Brillouin, L. Diffusion de la lumière et des rayons X par un corps transparent homogène. Influence de l’agitation thermique. Ann. Phys. 1922, 17, 88–122. (In French) [Google Scholar] [CrossRef]
- Compton, A. A quantum theory of the scattering of X-rays by light elements. Phys. Rev. 1923, 21, 483. [Google Scholar] [CrossRef]
- Krishnan, R.S.; Shankar, R.K. Raman effect: History of the discovery. J. Raman Spectrosc. 1981, 10, 1–8. [Google Scholar] [CrossRef]
- Raman, C.V. A new radiation. Ind. J. Phys. 1928, 2, 387–398. [Google Scholar]
- Stokes, G.G. On the change of refrangibility of Light. Philos. Trans. R. Soc. 1852, 142, 463–562. [Google Scholar] [CrossRef]
- Ramaseshan, S. The Raman effect. Curr. Sci. 1998, 75, 6. [Google Scholar]
- Singh, R.; Riess, F. Seventy years ago—The discovery of the Raman effect as seen from German physicists. Curr. Sci. 1998, 74, 1112–1115. [Google Scholar]
- Singh, R.C.V. Raman and the discovery of the Raman effect. Phys. Perspect. 2002, 4, 399–420. [Google Scholar] [CrossRef]
- Smekal, A. The quantum, theory of dispersion. Naturwissenschaften 1923, 11, 873–878. [Google Scholar] [CrossRef]
- Kramers, H.A.; Heisenberg, W. Über die streuung von strahlung durch atome. Z. Phys. 1925, 31, 681–708. (In German) [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of dispersion. Proc. R. Soc. Lond. A 1927, 114, 710–728. [Google Scholar] [CrossRef]
- Breit, G. Quantum theory of dispersion. Rev. Mod. Phys. 1932, 4, 504. [Google Scholar] [CrossRef]
- Placzek, G. Rayleigh-Streuung und Raman-Effekt. In Handbuch der Radiologie; Marx, E.A., Ed.; Akademische Verlagsgesellschaft: Leipzig, Germany, 1934; Volume 6, p. 205. (In German) [Google Scholar]
- Albrecht, A.C. On the theory of Raman intensities. J. Chem. Phys. 1961, 34, 1476–1484. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; The International Series of Monographs on Physics; Oxford University Press: Oxford, UK, 1956. [Google Scholar]
- Loudon, R. The Raman effect in crystals. Adv. Phys. 1964, 13, 423–482. [Google Scholar] [CrossRef]
- Ganguly, A.K.; Birman, J.L. Theory of Lattice Raman Scattering in Insulators. Phys. Rev. 1967, 162, 806–816. [Google Scholar] [CrossRef]
- Cardona, M.; Güntherodt, G. Light-Scattering in Solids; Topics in Applied Physics; Springer-Verlag: Berlin, Germany, 1989; Volume 66, pp. 2–12. [Google Scholar]
- Nafie, L.A. Recent advances in linear and non-linear Raman spectroscopy. Part X. J. Raman Spectrosc. 2016, 47, 1548–1565. [Google Scholar] [CrossRef]
- Gouadec, G.; Colomban, P. Raman spectroscopy of nanomaterials: How spectra relate to disorder, particle size and mechanical properties. Prog. Cryst. Growth Charact. Mater. 2007, 53, 1–56. [Google Scholar] [CrossRef]
- Rocard, Y. Role des vibrations des atomes dans les molécules dans le phénomène de diffusion de la lumière. Compt. Rend. 1927, 185, 1026–1028. (In French) [Google Scholar]
- Rocard, Y. Les nouvelles radiations diffusées. Compt. Rend. 1928, 186, 1107–1109. (In French) [Google Scholar]
- Raman, C.V. The scattering of light in crystals and the nature of their vibration spectra. Proc. Indian Acad. Sci. 1951, 34, 61–71. [Google Scholar]
- Poulet, H.; Mathieu, J.P. Détermination des vibrations fondamentales du sulfure de cadmium cristallisé. Ann. Phys. 1964, 13, 549–552. (In French) [Google Scholar] [CrossRef]
- Landsberg, G.; Mandelstam, L. Über die lichtzerstreuung in kristallen. Z. Phys. 1928, 50, 769–780. (In German) [Google Scholar] [CrossRef]
- Boyle, W.S.; Smith, G.E. Charge coupled semiconductors devices. Bell Syst. Tech. J. 1970, 49, 587–593. [Google Scholar] [CrossRef]
- Dierker, S.B.; Murray, C.A.; Legrange, J.D.; Schlotter, N.E. Characterization of order in langmuir-blodgett monolayers by unenhanced raman-spectroscopy. Chem. Phys. Lett. 1987, 137, 453–457. [Google Scholar] [CrossRef]
- Rabolt, J.F.; Santo, R.; Swalen, J.D. Raman measurements on thin polymer-films and organic monolayers. Appl. Spectrosc. 1980, 34, 517–521. [Google Scholar] [CrossRef]
- Adar, F.; Delhaye, M.; DaSilva, E. Evolution of instrumentation for detection of the Raman effect as driven by available technologies and by developing applications. J. Chem. Educ. 2007, 84, 50–60. [Google Scholar] [CrossRef]
- Long, D.A. Early history of the Raman effect. Int. Rev. Phys. Chem. 1988, 7, 317–349. [Google Scholar] [CrossRef]
- Langeluddecke, L.; Singh, P.; Deckert, V. Exploring the nanoscale: Fifteen years of tip-enhanced Raman spectroscopy. Appl. Spectrosc. 2015, 69, 1357–1371. [Google Scholar] [CrossRef] [PubMed]
- Long, D.A. The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules; John Wiley & Sons, Ltd.: Chichester, UK, 2002. [Google Scholar]
- Cardona, M. Resonance phenomena. Top. Appl. Phys. 1982, 50, 19–178. [Google Scholar]
- Cantarero, A.; Tralleroginer, C.; Cardona, M. Excitons in one-phonon resonant Raman scattering: Deformation-potential interaction. Phys. Rev. B 1989, 39, 8388–8397. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Jorio, A. Applications of Group Theory to the Physics of Solids; Springer: New York, NY, USA, 2008. [Google Scholar]
- Yu, P.Y.; Cardona, M. Fundamentals of Semiconductors, Physics and Materials Properties, 4th ed.; Springer: Berlin, Germany, 2010. [Google Scholar]
- Ramsteiner, M.; Wild, C.; Wagner, J. Interference effects in the raman-scattering intensity from thin-films. Appl. Opt. 1989, 28, 4017–4023. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Y.; Ni, Z.H.; Yu, T.; Shen, Z.X.; Wang, H.M.; Wu, Y.H.; Chen, W.; Wee, A.T.S. Raman studies of monolayer graphene: The substrate effect. J. Phys. Chem. C 2008, 112, 10637–10640. [Google Scholar] [CrossRef]
- Yoon, D.; Moon, H.; Son, Y.W.; Choi, J.S.; Park, B.H.; Cha, Y.H.; Kim, Y.D.; Cheong, H. Interference effect on Raman spectrum of graphene on SiO2/Si. Phys. Rev. B 2009, 80, 125422. [Google Scholar] [CrossRef]
- Klar, P.; Lidorikis, E.; Eckmann, A.; Verzhbitskiy, I.A.; Ferrari, A.C.; Casiraghi, C. Raman scattering efficiency of graphene. Phys. Rev. B 2013, 87, 205435. [Google Scholar] [CrossRef]
- Hirsch, A. The era of carbon allotropes. Nat. Mater. 2010, 9, 868–871. [Google Scholar] [CrossRef] [PubMed]
- Ostrikov, K.; Neyts, E.C.; Meyyappan, M. Plasma nanoscience: From nano-solids in plasmas to nano-plasmas in solids. Adv. Phys. 2013, 62, 113–224. [Google Scholar] [CrossRef]
- Bernier, P.; Lefrant, S. Le Carbone Dans Tous Ses Etats; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1998. [Google Scholar]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Wallace, P. The band theory of graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Ivanovskaya, V.V.; Zobelli, A.; Teillet-Billy, D.; Rougeau, N.; Sidis, V.; Briddon, P.R. Hydrogen adsorption on graphene: A first principles study. Eur. Phys. J. B 2010, 76, 481–486. [Google Scholar] [CrossRef]
- Wirtz, L.; Rubio, A. The phonon dispersion of graphite revisited. Solid State Commun. 2004, 131, 141–152. [Google Scholar] [CrossRef]
- Reich, S.; Thomsen, C. Raman spectroscopy of graphite. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2004, 362, 2271–2288. [Google Scholar] [CrossRef] [PubMed]
- Lazzeri, M.; Piscanec, S.; Mauri, F.; Ferrari, A.C.; Robertson, J. Phonon linewidths and electron-phonon coupling in graphite and nanotubes. Phys. Rev. B 2006, 73, 155426. [Google Scholar] [CrossRef]
- Cancado, L.G.; Takai, K.; Enoki, T.; Endo, M.; Kim, Y.A.; Mizusaki, H.; Speziali, N.L.; Jorio, A.; Pimenta, M.A. Measuring the degree of stacking order in graphite by Raman spectroscopy. Carbon 2008, 46, 272–275. [Google Scholar] [CrossRef]
- Kawashima, Y.; Katagiri, G. Fundamentals, overtones, and combinations in the raman-spectrum of graphite. Phys. Rev. B 1995, 52, 10053–10059. [Google Scholar] [CrossRef]
- Couzi, M.; Bruneel, J.L.; Talaga, D.; Bokobza, L. A multi wavelength Raman scattering study of defective graphitic carbon materials: The first order Raman spectra revisited. Carbon 2016, 107, 388–394. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Basko, D.M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Brar, V.W.; Samsonidze, G.G.; Dresselhaus, M.S.; Dresselhaus, G.; Saito, R.; Swan, A.K.; Unlu, M.S.; Goldberg, B.B.; Souza, A.G.; Jorio, A. Second-order harmonic and combination modes in graphite, single-wall carbon nanotube bundles, and isolated single-wall carbon nanotubes. Phys. Rev. B 2002, 66, 155418. [Google Scholar] [CrossRef]
- Tuinstra, F.; Koenig, J.L. Raman spectrum of graphite. J. Chem. Phys. 1970, 53, 1126–1130. [Google Scholar] [CrossRef]
- Cançado, L.G.; Jorio, A.; Pimenta, M.A. Measuring the absolute Raman cross section of nanographites as a function of laser energy and crystallite size. Phys. Rev. B 2007, 76, 064304. [Google Scholar] [CrossRef]
- Pardanaud, C.; Martin, C.; Roubin, P. Multiwavelength Raman spectroscopy analysis of a large sampling of disordered carbons extracted from the Tore Supra tokamak. Vib. Spectrosc. 2014, 70, 187–192. [Google Scholar] [CrossRef]
- Cancado, L.G.; Takai, K.; Enoki, T.; Endo, M.; Kim, Y.A.; Mizusaki, H.; Jorio, A.; Coelho, L.N.; Magalhaes-Paniago, R.; Pimenta, M.A. General equation for the determination of the crystallite size La of nanographite by Raman spectroscopy. Appl. Phys. Lett. 2006, 88, 163106. [Google Scholar] [CrossRef]
- Mernagh, T.P.; Cooney, R.P.; Johnson, R.A. Raman-spectra of graphon carbon-black. Carbon 1984, 22, 39–42. [Google Scholar] [CrossRef]
- Venezuela, P.; Lazzeri, M.; Mauri, F. Theory of double-resonant Raman spectra in graphene: Intensity and line shape of defect-induced and two-phonon bands. Phys. Rev. B 2011, 84, 035433. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Robertson, J. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B 2000, 61, 14095–14107. [Google Scholar] [CrossRef]
- Robertson, J.; Oreilly, E.P. Electronic and atomic-structure of amorphous-carbon. Phys. Rev. B 1987, 35, 2946–2957. [Google Scholar] [CrossRef]
- Lajaunie, L.; Pardanaud, C.; Martin, C.; Puech, P.; Hu, C.; Biggs, M.J.; Arenal, R. Advanced spectroscopic analyses on a:C–H materials: Revisiting the EELS characterization and its coupling with multi-wavelength Raman spectroscopy. Carbon 2017, 112, 149–161. [Google Scholar] [CrossRef]
- Ramaswamy, C. Raman effect in diamond. Nature 1930, 125, 704. [Google Scholar] [CrossRef]
- Solin, S.A.; Ramdas, A.K. Raman spectrum of diamond. Phys. Rev. B 1970, 1, 1687. [Google Scholar] [CrossRef]
- Yoshimori, A.; Kitano, Y. Theory of the lattice vibration of graphite. J. Phys. Soc. Jpn. 1956, 2, 352. [Google Scholar] [CrossRef]
- Young, J.A.; Koppel, J.U. Phonon spectrum of graphite. J. Chem. Phys. 1965, 42, 357. [Google Scholar] [CrossRef]
- Tsu, R.; Gonzalez, J.; Hernandez, I. Observation of splitting of E2g mode and two-phonon spectrum in graphites. Solid State Commun. 1978, 27, 507–510. [Google Scholar] [CrossRef]
- Vidano, R.; Fischbach, D.B. New lines in raman-spectra of carbons and graphite. J. Am. Ceram. Soc. 1978, 61, 13–17. [Google Scholar] [CrossRef]
- Lespade, P.; Marchand, A.; Couzi, M.; Cruege, F. Characterization of carbon materials with Raman microspectrometry. Carbon 1984, 22, 375–385. [Google Scholar] [CrossRef]
- Nakamizo, M.; Kammereck, R.; Walker, P.L. Laser Raman studies on carbons. Carbon 1974, 12, 259–267. [Google Scholar] [CrossRef]
- Nemanich, R.J.; Solin, S.A. 1st-order and 2nd-order raman-scattering from finite-size crystals of graphite. Phys. Rev. B 1979, 20, 392–401. [Google Scholar] [CrossRef]
- Vidano, R.P.; Fischbach, D.B.; Willis, L.J.; Loehr, T.M. Observation of raman band shifting with excitation wavelength for carbons and graphites. Solid State Commun. 1981, 39, 341–344. [Google Scholar] [CrossRef]
- Baranov, A.V.; Bekhterev, A.N.; Bobovich, Y.S.; Petrov, V.I. Interpretation of some singularities in raman-spectra of graphite and glass carbon. Opt. I Spektrosk. 1987, 62, 1036–1042. [Google Scholar]
- Wang, Y.; Alsmeyer, D.C.; McCreery, R.L. Raman-spectroscopy of carbon materials—Structural basis of observed spectra. Chem. Mater. 1990, 2, 557–563. [Google Scholar] [CrossRef]
- Ramsteiner, M.; Wagner, J. Resonant raman-scattering of hydrogenated amorphous-carbon—Evidence for pi-bonded carbon clusters. Appl. Phys. Lett. 1987, 51, 1355–1357. [Google Scholar] [CrossRef]
- Kastner, J.; Pichler, T.; Kuzmany, H.; Curran, S.; Blau, W.; Weldon, D.N.; Delamesiere, M.; Draper, S.; Zandbergen, H. Resonance Raman and infrared-spectroscopy of carbon nanotubues. Chem. Phys. Lett. 1994, 221, 53–58. [Google Scholar] [CrossRef]
- Rao, A.M.; Richter, E.; Bandow, S.; Chase, B.; Eklund, P.C.; Williams, K.A.; Fang, S.; Subbaswamy, K.R.; Menon, M.; Thess, A.; et al. Diameter-selective Raman scattering from vibrational modes in carbon nanotubes. Science 1997, 275, 187–191. [Google Scholar] [CrossRef] [PubMed]
- Knight, D.S.; White, W.B. Characterization of diamond films by Raman-spectroscopy. J. Mater. Res. 1989, 4, 385–393. [Google Scholar] [CrossRef]
- Tan, P.H.; Deng, Y.M.; Zhao, Q. Temperature-dependent Raman spectra and anomalous Raman phenomenon of highly oriented pyrolytic graphite. Phys. Rev. B 1998, 58, 5435–5439. [Google Scholar] [CrossRef]
- Pocsik, I.; Hundhausen, M.; Koos, M.; Ley, L. Origin of the D peak in the Raman spectrum of microcrystalline graphite. J. Non Cryst. Solids 1998, 227, 1083–1086. [Google Scholar] [CrossRef]
- Matthews, M.J.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S.; Endo, M. Origin of dispersive effects of the Raman D band in carbon materials. Phys. Rev. B 1999, 59, R6585–R6588. [Google Scholar] [CrossRef]
- Thomsen, C.; Reich, S. Double resonant Raman scattering in graphite. Phys. Rev. Lett. 2000, 85, 5214–5217. [Google Scholar] [CrossRef] [PubMed]
- Saito, R.; Jorio, A.; Souza, A.G.; Dresselhaus, G.; Dresselhaus, M.S.; Pimenta, M.A. Probing phonon dispersion relations of graphite by double resonance Raman scattering. Phys. Rev. Lett. 2002, 88, 027401. [Google Scholar] [CrossRef] [PubMed]
- Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S.; Cancado, L.G.; Jorio, A.; Saito, R. Studying disorder in graphite-based systems by Raman spectroscopy. Phys. Chem. Chem. Phys. 2007, 9, 1276–1290. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Cançado, L.G.; da Silva, M.G.; Ferreira, E.H.M.; Hof, F.; Kampioti, K.; Huang, K.; Penicaud, A.; Achete, C.A.; Capaz, R.B.; Jorio, A. Disentangling contributions of point and line defects in the Raman spectra of graphene-related materials. 2D Mater. 2017, 4, 015039. [Google Scholar]
- Cançado, L.G.; Jorio, A.; Martins Ferreira, E.H.; Stavale, F.; Achete, C.A.; Capaz, R.B.; Moutinho, M.V.O.; Lombardo, A.; Kulmala, T.S.; Ferrari, A.C. Quantifying defects in graphene via Raman spectroscopy at different excitation energies. Nano Lett. 2011, 11, 3190–3196. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, E.H.M.; Moutinho, M.V.O.; Stavale, F.; Lucchese, M.M.; Capaz, R.B.; Achete, C.A.; Jorio, A. Evolution of the Raman spectra from single-, few-, and many-layer graphene with increasing disorder. Phys. Rev. B 2010, 82, 125429. [Google Scholar] [CrossRef]
- Giro, R.; Archanjo, B.S.; Martins Ferreira, E.H.; Capaz, R.B.; Jorio, A.; Achete, C.A. Quantifying defects in N-layer graphene via a phenomenological model of Raman spectroscopy. Nucl. Instrum. Methods Phys. Res. Sec. B Beam Interact. Mater. Atoms 2014, 319, 71–74. [Google Scholar] [CrossRef]
- Lucchese, M.M.; Stavale, F.; Ferreira, E.H.M.; Vilani, C.; Moutinho, M.V.O.; Capaz, R.B.; Achete, C.A.; Jorio, A. Quantifying ion-induced defects and Raman relaxation length in graphene. Carbon 2010, 48, 1592–1597. [Google Scholar] [CrossRef]
- Ribeiro-Soares, J.; Oliveros, M.E.; Garin, C.; David, M.V.; Martins, L.G.P.; Almeida, C.A.; Martins-Ferreira, E.H.; Takai, K.; Enoki, T.; Magalhaes-Paniago, R.; et al. Structural analysis of polycrystalline graphene systems by Raman spectroscopy. Carbon 2015, 95, 646–652. [Google Scholar] [CrossRef]
- Cong, C.X.; Yu, T.; Saito, R.; Dresselhaus, G.F.; Dresselhaus, M.S. Second-order overtone and combination Raman modes of graphene layers in the range of 1690–2150 cm−1. Acs Nano 2011, 5, 1600–1605. [Google Scholar] [CrossRef] [PubMed]
- Popov, V.N. Two-phonon Raman bands of bilayer graphene: Revisited. Carbon 2015, 91, 436–444. [Google Scholar] [CrossRef]
- Eckmann, A.; Felten, A.; Mishchenko, A.; Britnell, L.; Krupke, R.; Novoselov, K.S.; Casiraghi, C. Probing the nature of defects in graphene by Raman spectroscopy. Nano Lett. 2012, 12, 3925–3930. [Google Scholar] [CrossRef] [PubMed]
- Pimenta, M.A.; del Corro, E.; Carvalho, B.R.; Fantini, C.; Malard, L.M. Comparative study of Raman spectroscopy in graphene and MoS2-type transition metal dichalcogenides. Accounts Chem. Res. 2015, 48, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, B.R.; Wang, Y.X.; Mignuzzi, S.; Roy, D.; Terrones, M.; Fantini, C.; Crespi, V.H.; Malard, L.M.; Pimenta, M.A. Intervalley scattering by acoustic phonons in two-dimensional MoS2 revealed by double-resonance Raman spectroscopy. Nat. Commun. 2017, 8, 14670. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.H.; Yang, T.; Yamamoto, M.; Zhou, L.; Ishikawa, R.; Ueno, K.; Tsukagoshi, K.; Zhang, Z.D.; Dresselhaus, M.S.; Saito, R. Double resonance Raman modes in monolayer and few-layer MoTe2. Phys. Rev. B 2015, 91, 205415. [Google Scholar] [CrossRef]
- Castiglioni, C.; Di Donato, E.; Tommasini, M.; Negri, F.; Zerbi, G. Multi-wavelength Raman response of disordered graphitic materials: Models and simulations. Synth. Met. 2003, 139, 885–888. [Google Scholar] [CrossRef]
- Castiglioni, C.; Negri, F.; Tommasini, M.; Di Donato, E.; Zerbi, G. Raman spectra and structure of sp2 carbon-based materials: Electron-phonon coupling, vibrational dynamics and Raman activity. Carbon 2006, 100, 381–402. [Google Scholar]
- Castiglioni, C.; Tommasini, M.; Zerbi, G. Raman spectroscopy of polyconjugated molecules and materials: Confinement effect in one and two dimensions. Philos. Trans. R. Soc. 2004, 362, 2425–2459. [Google Scholar] [CrossRef] [PubMed]
- Di Donato, E.; Tommasini, M.; Fustella, G.; Brambilla, L.; Castiglioni, C.; Zerbi, G.; Simpson, C.D.; Mullen, K.; Negri, F. Wavelength-dependent Raman activity of D2h symmetry polycyclic aromatic hydrocarbons in the D-band and acoustic phonon regions. Chem. Phys. 2004, 301, 81–93. [Google Scholar] [CrossRef]
- Negri, F.; Castiglioni, C.; Tommasini, M.; Zerbi, G. A computational study of the Raman spectra of large polycyclic aromatic hydrocarbons: Toward molecularly defined subunits of graphite. J. Phys. Chem. A 2002, 106, 3306–3317. [Google Scholar] [CrossRef]
- Negri, F.; di Donato, E.; Tommasini, M.; Castiglioni, C.; Zerbi, G.; Mullen, K. Resonance Raman contribution to the D band of carbon materials: Modeling defects with quantum chemistry. J. Chem. Phys. 2004, 120, 11889–11900. [Google Scholar] [CrossRef] [PubMed]
- Tommasini, M.; Di Donato, E.; Castiglioni, C.; Zerbi, G.; Severin, N.; Bohme, T.; Rabe, J.P. Resonant Raman spectroscopy of nanostructured carbon-based materials: The molecular approach. In Electronic Properties of Synthetic Nanostructures; Kuzmany, H., Fink, J., Mehring, M., Roth, S., Eds.; American Institute of Physics: College Park, MD, USA, 2004; Volume 723, pp. 334–338. [Google Scholar]
- Tommasini, M.; Castiglioni, C.; Zerbi, G. Raman scattering of molecular graphenes. Phys. Chem. Chem. Phys. 2009, 11, 10185–10194. [Google Scholar] [CrossRef] [PubMed]
- Maghsoumi, A.; Brambilla, L.; Castiglioni, C.; Mullen, K.; Tommasini, M. Overtone and combination features of G and D peaks in resonance Raman spectroscopy of the C78H26 polycyclic aromatic hydrocarbon. J. Raman Spectrosc. 2015, 46, 757–764. [Google Scholar] [CrossRef]
- Heller, E.J.; Yang, Y.; Kocia, L.; Chen, W.; Fang, S.A.; Borunda, M.; Kaxiras, E. Theory of graphene Raman scattering. Acs Nano 2016, 10, 2803–2818. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Lu, X.; Cong, C.X.; Yu, T.; Xiong, Q.H.; Quek, S.Y. Stacking sequence determines Raman intensities of observed interlayer shear modes in 2D layered materials—A general bond polarizability model. Sci. Rep. 2015, 5, 14565. [Google Scholar] [CrossRef] [PubMed]
- Benybassez, C.; Rouzaud, J.N. Characterization of carbonaceous materials by correlated electron and optical microscopy and raman microspectroscopy. Scanning Electron Microsc. 1985, 1, 119–132. [Google Scholar]
- Jawhari, T.; Roig, A.; Casado, J. Raman-spectroscopic characterization of some commercially available carbon-black materials. Carbon 1995, 33, 1561–1565. [Google Scholar] [CrossRef]
- Sadezky, A.; Muckenhuber, H.; Grothe, H.; Niessner, R.; Poschl, U. Raman micro spectroscopy of soot and related carbonaceous materials: Spectral analysis and structural information. Carbon 2005, 43, 1731–1742. [Google Scholar] [CrossRef]
- Vallerot, J.M.; Bourrat, X.; Mouchon, A.; Chollon, G. Quantitative structural and textural assessment of laminar pyrocarbons through Raman spectroscopy, electron diffraction and few other techniques. Carbon 2006, 44, 1833–1844. [Google Scholar] [CrossRef]
- Jacob, W.; Moller, W. On the structure of thin hydrocarbon films. Appl. Phys. Lett. 1993, 63, 1771–1773. [Google Scholar] [CrossRef]
- Hopf, C.; Angot, T.; Areou, E.; Duerbeck, T.; Jacob, W.; Martin, C.; Pardanaud, C.; Roubin, P.; Schwarz-Selinger, T. Characterization of temperature-induced changes in amorphous hydrogenated carbon thin films. Diam. Relat. Mater. 2013, 37, 97–103. [Google Scholar] [CrossRef]
- Schwarz-Selinger, T.; von Keudell, A.; Jacob, W. Plasma chemical vapor deposition of hydrocarbon films: The influence of hydrocarbon source gas on the film properties. J. Appl. Phys. 1999, 86, 3988–3996. [Google Scholar] [CrossRef]
- Wagner, J.; Ramsteiner, M.; Wild, C.; Koidl, P. Resonant raman-scattering of amorphous-carbon and polycrystalline diamond films. Phys. Rev. B 1989, 40, 1817–1824. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Li Bassi, A.; Tanner, B.K.; Stolojan, V.; Yuan, J.; Brown, L.M.; Rodil, S.E.; Kleinsorge, B.; Robertson, J. Density, sp3 fraction, and cross-sectional structure of amorphous carbon films determined by X-ray reflectivity and electron energy-loss spectroscopy. Phys. Rev. B 2000, 62, 11089–11103. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Matus, M.; Kuzmany, H.; Kratschmer, W. Resonance raman-scattering and electronic-transitions in C60. Solid State Commun. 1991, 80, 839–842. [Google Scholar] [CrossRef]
- Sinha, K.; Menendez, J.; Hanson, R.C.; Adams, G.B.; Page, J.B.; Sankey, O.F.; Lamb, L.D.; Huffman, D.R. Evidence for solid-state effects in the electronic-structure of C60 films—A resonance-Raman study. Chem. Phys. Lett. 1991, 186, 287–290. [Google Scholar] [CrossRef]
- Vanloosdrecht, P.H.M.; Vanbentum, P.J.M.; Verheijen, M.A.; Meijer, G. Raman-scattering in single-crystal C60. Chem. Phys. Lett. 1992, 198, 587–595. [Google Scholar] [CrossRef]
- Monthioux, M.; Kuznetsov, V.L. Who should be given the credit for the discovery of carbon nanotubes? Carbon 2006, 44, 1621–1623. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Kataura, H.; Kumazawa, Y.; Maniwa, Y.; Umezu, I.; Suzuki, S.; Ohtsuka, Y.; Achiba, Y. Optical properties of single-wall carbon nanotubes. Synth. Met. 1999, 103, 2555–2558. [Google Scholar] [CrossRef]
- Barros, E.B.; Jorio, A.; Samsonidze, G.G.; Capaz, R.B.; Souza, A.G.; Mendes, J.; Dresselhaus, G.; Dresselhaus, M.S. Review on the symmetry-related properties of carbon nanotubes. Phys. Rep. Rev. Sec. Phys. Lett. 2006, 431, 261–302. [Google Scholar] [CrossRef]
- Ferrari, A.C. Raman spectroscopy of graphene and graphite: Disorder, electron-phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007, 143, 47–57. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Jorio, A.; Souza, A.G.; Saito, R. Defect characterization in graphene and carbon nanotubes using Raman spectroscopy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2010, 368, 5355–5377. [Google Scholar] [CrossRef] [PubMed]
- Malard, L.M.; Pimenta, M.A.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectroscopy in graphene. Phys. Rep. Rev. Sec. Phys. Lett. 2009, 473, 51–87. [Google Scholar] [CrossRef]
- Mohr, M.; Maultzsch, J.; Thomsen, C. Splitting of the Raman 2D band of graphene subjected to strain. Phys. Rev. B 2010, 82, 201409. [Google Scholar] [CrossRef]
- Bonini, N.; Lazzeri, M.; Marzari, N.; Mauri, F. Phonon anharmonicities in graphite and graphene. Phys. Rev. Lett. 2007, 99, 176802. [Google Scholar] [CrossRef] [PubMed]
- Schwan, J.; Ulrich, S.; Batori, V.; Ehrhardt, H.; Silva, S.R.P. Raman spectroscopy on amorphous carbon films. J. Appl. Phys. 1996, 80, 440–447. [Google Scholar] [CrossRef]
- Chu, P.K.; Li, L.H. Characterization of amorphous and nanocrystalline carbon films. Mater. Chem. Phys. 2006, 96, 253–277. [Google Scholar] [CrossRef]
- Wang, Q.; Allred, D.D.; Knight, L.V. Deconvolution of the Raman spectrum of amorphous carbon. J. Raman Spectrosc. 1995, 26, 1039–1043. [Google Scholar] [CrossRef]
- Richter, H.; Wang, Z.P.; Ley, L. The one phonon raman-spectrum in microcrystalline silicon. Solid State Commun. 1981, 39, 625–629. [Google Scholar] [CrossRef]
- Puech, P.; Plewa, J.M.; Mallet-Ladeira, P.; Monthioux, M. Spatial confinement model applied to phonons in disordered graphene-based carbons. Carbon 2016, 105, 275–281. [Google Scholar] [CrossRef]
- Jorio, A.; Ferreira, E.H.M.; Moutinho, M.V.O.; Stavale, F.; Achete, C.A.; Capaz, R.B. Measuring disorder in graphene with the G and D bands. Phys. Status Solidi B 2010, 247, 2980–2982. [Google Scholar] [CrossRef]
- Baroni, S.; de Gironcoli, S.; Dal Corso, A.; Giannozzi, P. Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 2001, 73, 515–562. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Saidi, W.A. Effects of topological defects and diatom vacancies on characteristic vibration modes and Raman intensities of zigzag single-walled carbon nanotubes. J. Phys. Chem. A 2014, 118, 7235–7241. [Google Scholar] [CrossRef] [PubMed]
- Saidi, W.A.; Norman, P. Probing single-walled carbon nanotube defect chemistry using resonance Raman spectroscopy. Carbon 2014, 67, 17–26. [Google Scholar] [CrossRef]
- Saidi, W.A.; Norman, P. Spectroscopic signatures of topological and diatom-vacancy defects in single-walled carbon nanotubes. Phys. Chem. Chem. Phys. 2014, 16, 1479–1486. [Google Scholar] [CrossRef] [PubMed]
- Kudin, K.N.; Ozbas, B.; Schniepp, H.C.; Prud’homme, R.K.; Aksay, I.A.; Car, R. Raman spectra of graphite oxide and functionalized graphene sheets. Nano Lett. 2008, 8, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Aggarwal, R.L.; Farrar, L.W.; Saikin, S.K.; Andrade, X.; Aspuru-Guzik, A.; Polla, D.L. Measurement of the absolute Raman cross section of the optical phonons in type Ia natural diamond. Solid State Commun. 2012, 152, 204–209. [Google Scholar] [CrossRef]
- Skinner, J.G.; Nilsen, W.G. Absolute Raman scattering cross-section measurement of the 992 cm−1 line of benzene. J. Opt. Soc. Am. 1968, 58, 113–119. [Google Scholar] [CrossRef]
- Aggarwal, R.L.; Farrar, L.W.; Saikin, S.K.; Aspuru-Guzik, A.; Stopa, M.; Polla, D.L. Measurement of the absolute Raman cross section of the optical phonon in silicon. Solid State Commun. 2011, 151, 553–556. [Google Scholar] [CrossRef]
- Pettinger, B.; Picardi, G.; Schuster, R.; Ertl, G. Surface-enhanced and STM-tip-enhanced Raman spectroscopy at metal surfaces. Single Mol. 2002, 3, 285–294. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Ni, Z.H.; Shen, Z.X.; Wang, H.M.; Wu, Y.H. Interference enhancement of Raman signal of graphene. Appl. Phys. Lett. 2008, 92, 043121. [Google Scholar] [CrossRef]
- Peres, N.M.R. Colloquium: The transport properties of graphene: An introduction. Rev. Mod. Phys. 2010, 82, 2673–2700. [Google Scholar] [CrossRef]
- Beams, R.; Cancado, L.G.; Novotny, L. Raman characterization of defects and dopants in graphene. J. Phys. Condens. Matter 2015, 27, 083002. [Google Scholar] [CrossRef] [PubMed]
- Bayle, M.; Reckinger, N.; Huntzinger, J.R.; Felten, A.; Bakaraki, A.; Landois, P.; Colomer, J.F.; Henrard, L.; Zahab, A.A.; Sauvajol, J.L.; et al. Dependence of the Raman spectrum characteristics on the number of layers and stacking orientation in few-layer graphene. Phys. Status Solidi B 2015, 252, 2375–2379. [Google Scholar] [CrossRef]
- Poncharal, P.; Ayari, A.; Michel, T.; Sauvajol, J.L. Raman spectra of misoriented bilayer graphene. Phys. Rev. B 2008, 78, 113407. [Google Scholar] [CrossRef]
- Poncharal, P.; Ayari, A.; Michel, T.; Sauvajol, J.L. Effect of rotational stacking faults on the Raman spectra of folded graphene. Phys. Rev. B 2009, 79, 195417. [Google Scholar] [CrossRef]
- Das, A.; Chakraborty, B.; Sood, A.K. Raman spectroscopy of graphene on different substrates and influence of defects. Bull. Mater. Sci. 2008, 31, 579–584. [Google Scholar] [CrossRef]
- Tan, P.H.; Han, W.P.; Zhao, W.J.; Wu, Z.H.; Chang, K.; Wang, H.; Wang, Y.F.; Bonini, N.; Marzari, N.; Pugno, N.; et al. The shear mode of multilayer graphene. Nat. Mater. 2012, 11, 294–300. [Google Scholar] [CrossRef] [PubMed]
- Araujo, P.T.; Terrones, M.; Dresselhaus, M.S. Defects and impurities in graphene-like materials. Mater. Today 2012, 15, 98–109. [Google Scholar] [CrossRef]
- Casiraghi, C. Doping dependence of the Raman peaks intensity of graphene close to the Dirac point. Phys. Rev. B 2009, 80, 233407. [Google Scholar] [CrossRef]
- Casiraghi, C.; Pisana, S.; Novoselov, K.S.; Geim, A.K.; Ferrari, A.C. Raman fingerprint of charged impurities in graphene. Appl. Phys. Lett. 2007, 91, 233108. [Google Scholar] [CrossRef]
- Kalbac, M.; Reina-Cecco, A.; Farhat, H.; Kong, J.; Kavan, L.; Dresselhaus, M.S. The influence of strong electron and hole doping on the Raman intensity of chemical vapor-deposition graphene. ACS Nano 2010, 4, 6055–6063. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.K.; Li, Q.Q.; Zou, Y.; Qian, Q.K.; Jin, Y.H.; Li, G.H.; Jiang, K.L.; Fan, S.S. The dependence of graphene Raman D-band on carrier density. Nano Lett. 2013, 13, 6170–6175. [Google Scholar] [CrossRef] [PubMed]
- Ni, Z.H.; Ponomarenko, L.A.; Nair, R.R.; Yang, R.; Anissimova, S.; Grigorieva, I.V.; Schedin, F.; Blake, P.; Shen, Z.X.; Hill, E.H.; et al. On resonant scatterers as a factor limiting carrier mobility in graphene. Nano Lett. 2010, 10, 3868–3872. [Google Scholar] [CrossRef] [PubMed]
- Calizo, I.; Ghosh, S.; Bao, W.Z.; Miao, F.; Lau, C.N.; Balandin, A.A. Raman nanometrology of graphene: Temperature and substrate effects. Solid State Commun. 2009, 149, 1132–1135. [Google Scholar] [CrossRef]
- Calizo, I.; Bao, W.Z.; Miao, F.; Lau, C.N.; Balandin, A.A. The effect of substrates on the Raman spectrum of graphene: Graphene-on-sapphire and graphene-on-glass. Appl. Phys. Lett. 2007, 91, 201904. [Google Scholar] [CrossRef]
- Frank, O.; Mohr, M.; Maultzsch, J.; Thomsen, C.; Riaz, I.; Jalil, R.; Novoselov, K.S.; Tsoukleri, G.; Parthenios, J.; Papagelis, K.; et al. Raman 2D-band splitting in graphene: Theory and experiment. Acs Nano 2011, 5, 2231–2239. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Huang, Q.S.; Chen, X.L.; Zhang, G.Y.; Gao, H.J. Substrate doping effects on Raman spectrum of epitaxial graphene on SiC. J. Appl. Phys. 2010, 107, 034305. [Google Scholar] [CrossRef]
- Das, A.; Pisana, S.; Chakraborty, B.; Piscanec, S.; Saha, S.K.; Waghmare, U.V.; Novoselov, K.S.; Krishnamurthy, H.R.; Geim, A.K.; Ferrari, A.C.; et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 2008, 3, 210–215. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Novoselov, K.S.; Shin, H.S. Interaction between metal and graphene: Dependence on the Layer number of graphene. Acs Nano 2011, 5, 608–612. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.G.; Mao, N.N.; Zhang, J. Graphene: A platform for surface-enhanced Raman spectroscopy. Small 2013, 9, 1206–1224. [Google Scholar] [CrossRef] [PubMed]
- Bronsgeest, M.S.; Bendiab, N.; Mathur, S.; Kimouche, A.; Johnson, H.T.; Coraux, J.; Pochet, P. Strain relaxation in CVD graphene: Wrinkling with shear lag. Nano Lett. 2015, 15, 5098–5104. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.L.; Siregar, S.; Hasdeo, E.H.; Kumamoto, Y.; Shen, C.C.; Cheng, C.C.; Li, L.J.; Saito, R.; Kawata, S. Deep-ultraviolet Raman scattering studies of monolayer graphene thin films. Carbon 2015, 81, 807–813. [Google Scholar] [CrossRef]
- Tyborski, C.; Herziger, F.; Gillen, R.; Maultzsch, J. Beyond double-resonant Raman scattering: Ultraviolet Raman spectroscopy on graphene, graphite, and carbon nanotubes. Phys. Rev. B 2015, 92, 041401. [Google Scholar] [CrossRef]
- Saito, R.; Nugraha, A.R.T.; Hasdeo, E.H.; Siregar, S.; Guo, H.H.; Yang, T. Ultraviolet Raman spectroscopy of graphene and transition-metal dichalcogenides. Phys. Status Solidi B 2015, 252, 2363–2374. [Google Scholar] [CrossRef]
- Zhou, W.; Zeng, J.W.; Li, X.F.; Xu, J.; Shi, Y.; Ren, W.; Miao, F.; Wang, B.G.; Xing, D.Y. Ultraviolet Raman spectra of double-resonant modes of graphene. Carbon 2016, 101, 235–238. [Google Scholar] [CrossRef]
- Herziger, F.; Calandra, M.; Gava, P.; May, P.; Lazzeri, M.; Mauri, F.; Maultzsch, J. Two-dimensional analysis of the double-resonant 2D Raman mode in bilayer graphene. Phys. Rev. Lett. 2014, 113, 187401. [Google Scholar] [CrossRef] [PubMed]
- Zandiatashbar, A.; Lee, G.-H.; An, S.J.; Lee, S.; Mathew, N.; Terrones, M.; Hayashi, T.; Picu, C.R.; Hone, J.; Koratkar, N. Effect of defects on the intrinsic strength and stiffness of graphene. Nat. Commun. 2014, 5, 3186. [Google Scholar] [CrossRef] [PubMed]
- Ferralis, N. Probing mechanical properties of graphene with Raman spectroscopy. J. Mater. Sci. 2010, 45, 5135–5149. [Google Scholar] [CrossRef]
- Yu, Q.K.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.F.; Su, Z.H.; Cao, H.L.; Liu, Z.H.; Pandey, D.; Wei, D.G.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.Y.; Lee, J.H.; Kim, M.J.; Dash, J.K.; Lee, C.H.; Joshi, R.; Lee, S.; Hone, J.; Soon, A.; Lee, G.H. Direct observation of grain boundaries in chemical vapor deposited graphene. Carbon 2017, 115, 147–153. [Google Scholar] [CrossRef]
- Chen, S.S.; Moore, A.L.; Cai, W.W.; Suk, J.W.; An, J.H.; Mishra, C.; Amos, C.; Magnuson, C.W.; Kang, J.Y.; Shi, L.; et al. Raman measurements of thermal transport in suspended monolayer graphene of variable sizes in vacuum and gaseous environments. Acs Nano 2011, 5, 321–328. [Google Scholar] [CrossRef] [PubMed]
- Metten, D.; Froehlicher, G.; Berciaud, S. Monitoring electrostatically-induced deflection, strain and doping in suspended graphene using Raman spectroscopy. 2D Mater. 2017, 4. [Google Scholar] [CrossRef]
- Suarez-Martinez, I.; Grobert, N.; Ewels, C.P. Nomenclature of sp2 carbon nanoforms. Carbon 2012, 50, 741–747. [Google Scholar] [CrossRef]
- Bianco, A.; Cheng, H.M.; Enoki, T.; Gogotsi, Y.; Hurt, R.H.; Koratkar, N.; Kyotani, T.; Monthioux, M.; Park, C.R.; Tascon, J.M.D.; et al. All in the graphene family—A recommended nomenclature for two-dimensional carbon materials. Carbon 2013, 65, 1–6. [Google Scholar] [CrossRef]
- Wick, P.; Louw-Gaume, A.E.; Kucki, M.; Krug, H.F.; Kostarelos, K.; Fadeel, B.; Dawson, K.A.; Salvati, A.; Vazquez, E.; Ballerini, L.; et al. Classification framework for graphene-based materials. Angew. Chem. Int. Ed. 2014, 53, 7714–7718. [Google Scholar] [CrossRef] [PubMed]
- Cancado, L.G.; Pimenta, M.A.; Neves, B.R.A.; Dantas, M.S.S.; Jorio, A. Influence of the atomic structure on the Raman spectra of graphite edges. Phys. Rev. Lett. 2004, 93, 247401. [Google Scholar] [CrossRef] [PubMed]
- You, Y.M.; Ni, Z.H.; Yu, T.; Shen, Z.X. Edge chirality determination of graphene by Raman spectroscopy. Appl. Phys. Lett. 2008, 93, 163112. [Google Scholar] [CrossRef]
- Casiraghi, C.; Hartschuh, A.; Qian, H.; Piscanec, S.; Georgi, C.; Fasoli, A.; Novoselov, K.S.; Basko, D.M.; Ferrari, A.C. Raman spectroscopy of graphene edges. Nano Lett. 2009, 9, 1433–1441. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.S.; Tamakawa, D.; Tanaka, S.; Makino, T.; Hashimoto, A. Polarized microscopic laser Raman scattering spectroscopy for edge structure of epitaxial graphene and localized vibrational mode. Carbon 2014, 77, 1073–1081. [Google Scholar] [CrossRef]
- Ren, W.C.; Saito, R.; Gao, L.B.; Zheng, F.W.; Wu, Z.S.; Liu, B.L.; Furukawa, M.; Zhao, J.P.; Chen, Z.P.; Cheng, H.M. Edge phonon state of mono- and few-layer graphene nanoribbons observed by surface and interference co-enhanced Raman spectroscopy. Phys. Rev. B 2010, 81, 035412. [Google Scholar] [CrossRef]
- Mazzamuto, F.; Saint-Martin, J.; Valentin, A.; Chassat, C.; Dollfus, P. Edge shape effect on vibrational modes in graphene nanoribbons: A numerical study. J. Appl. Phys. 2011, 109, 064516. [Google Scholar] [CrossRef]
- Saito, R.; Furukawa, M.; Dresselhaus, G.; Dresselhaus, M.S. Raman spectra of graphene ribbons. J. Phys. Condens. Matter 2010, 22, 334203. [Google Scholar] [CrossRef] [PubMed]
- Yu, F.; Zhou, H.Q.; Zhang, Z.X.; Tang, D.S.; Chen, M.J.; Yang, H.C.; Wang, G.; Yang, H.F.; Gu, C.Z.; Sun, L.F. Experimental observation of radial breathing-like mode of graphene nanoribbons. Appl. Phys. Lett. 2012, 100, 101904. [Google Scholar] [CrossRef]
- Zhou, J.; Dong, J. Vibrational property and Raman spectrum of carbon nanoribbon. Appl. Phys. Lett. 2007, 91, 173108. [Google Scholar] [CrossRef]
- Verzhbitskiy, I.A.; De Corato, M.; Ruini, A.; Molinari, E.; Narita, A.; Hu, Y.; Schwab, M.G.; Bruna, M.; Yoon, D.; Milana, S.; et al. Raman fingerprints of atomically precise graphene nanoribbons. Nano Lett. 2016, 16, 3442–3447. [Google Scholar] [CrossRef] [PubMed]
- Casiraghi, C.; Prezzi, D. Raman spectroscopy of graphene nanoribbons: A review. In GraphITA: Selected papers from the Workshop on Synthesis, Characterization and Technological Exploitation of Graphene and 2D Materials Beyond Graphene; Carbon Nanostructures; Morandi, V., Ottaviano, L., Eds.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Reich, S.; Thomsen, C.; Maultzsch, J. Carbon Nanotubes: Basic Concepts and Physical Properties; Wiley-VCH: Weinheim, Germany, 2004. [Google Scholar]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
- Bohn, J.E.; Etchegoin, P.G.; le Ru, E.C.; Xiang, R.; Chiashi, S.; Maruyama, S. Estimating the Raman cross sections of single carbon nanotubes. Acs Nano 2010, 4, 3466–3470. [Google Scholar] [CrossRef] [PubMed]
- Sauvajol, J.-L.; Anglaret, E.; Rols, S.; Stephan, O. Spectroscopies on carbon nanotubes. In Understanding Carbon Nanotubes: From Basics to Applications; Loiseau, A., Launois, P., Petit, P., Roche, S., Salvetat, J.-P., Eds.; Springer: Berlin, Germany, 2006; Volume 677, pp. 277–334. [Google Scholar]
- Ghavanloo, E.; Fazelzadeh, S.A.; Rafii-Tabar, H. Analysis of radial breathing-mode of nanostructures with various morphologies: A critical review. Int. Mater. Rev. 2015, 60, 312–329. [Google Scholar] [CrossRef]
- Jorio, A.; Pimenta, M.A.; Souza, A.G.; Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Characterizing carbon nanotube samples with resonance Raman scattering. New J. Phys. 2003, 5, 139. [Google Scholar] [CrossRef]
- Brown, S.D.M.; Jorio, A.; Corio, P.; Dresselhaus, M.S.; Dresselhaus, G.; Saito, R.; Kneipp, K. Origin of the Breit-Wigner-Fano lineshape of the tangential G-band feature of metallic carbon nanotubes. Phys. Rev. B 2001, 63, 155414. [Google Scholar] [CrossRef]
- Song, L.; Ci, L.J.; Sun, L.F.; Jin, C.H.; Liu, L.F.; Ma, W.J.; Liu, D.F.; Zhao, X.W.; Luo, S.D.; Zhang, Z.X.; et al. Large-scale synthesis of rings of bundled single-walled carbon nanotubes by floating chemical vapor deposition. Adv. Mater. 2006, 18, 1817–1821. [Google Scholar] [CrossRef]
- Ren, Y.; Song, L.; Ma, W.J.; Zhao, Y.C.; Sun, L.F.; Gu, C.Z.; Zhou, W.Y.; Xie, S.S. Additional curvature-induced Raman splitting in carbon nanotube ring structures. Phys. Rev. B 2009, 80, 113412. [Google Scholar] [CrossRef]
- Dunk, P.W.; Niwa, H.; Shinohara, H.; Marshall, A.G.; Kroto, H.W. Large fullerenes in mass spectra. Mol. Phys. 2015, 113, 2359–2361. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Eklund, P.C. Raman scattering in fullerenes. J. Raman Spectrosc. 1996, 27, 351–371. [Google Scholar] [CrossRef]
- Kuzmany, H.; Pfeiffer, R.; Hulman, M.; Kramberger, C. Raman spectroscopy of fullerenes and fullerene-nanotube composites. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2004, 362, 2375–2406. [Google Scholar] [CrossRef] [PubMed]
- Bardelang, D.; Giorgi, M.; Pardanaud, C.; Hornebecq, V.; Rizzato, E.; Tordo, P.; Ouari, O. Organic multishell isostructural host-guest crystals: Fullerenes C60 inside a nitroxide open framework. Chem. Commun. 2013, 49, 3519–3521. [Google Scholar] [CrossRef] [PubMed]
- Jishi, R.A.; Dresselhaus, M.S.; Dresselhaus, G.; Wang, K.A.; Zhou, P.; Rao, A.M.; Eklund, P.C. Vibrational-mode frequencies in C70. Chem. Phys. Lett. 1993, 206, 187–192. [Google Scholar] [CrossRef]
- Eklund, P.C.; Rao, A.M.; Zhou, P.; Wang, Y. Photochemical transformation of C60 and C70 films. Thin Solid Films 1995, 257, 185–203. [Google Scholar] [CrossRef]
- Brazhkin, V.V.; Lyapin, A.G.; Popova, S.V.; Voloshin, R.N.; Antonov, Y.V.; Lyapin, S.G.; Kluev, Y.A.; Naletov, A.M.; Melnik, N.N. Metastable crystalline and amorphous carbon phases obtained from fullerite C60 by high-pressuse-high-temperature treatment. Phys. Rev. B 1997, 56, 11465–11472. [Google Scholar] [CrossRef]
- Karousis, N.; Suarez-Martinez, I.; Ewels, C.P.; Tagmatarchis, N. Structure, properties, functionalization, and applications of carbon nanohorns. Chem. Rev. 2016, 116, 4850–4883. [Google Scholar] [CrossRef] [PubMed]
- Iijima, S.; Yudasaka, M.; Yamada, R.; Bandow, S.; Suenaga, K.; Kokai, F.; Takahashi, K. Nano-aggregates of single-walled graphitic carbon nano-horns. Chem. Phys. Lett. 1999, 309, 165–170. [Google Scholar] [CrossRef]
- Pena-Alvarez, M.; del Corro, E.; Langa, F.; Baonza, V.G.; Taravillo, M. Morphological changes in carbon nanohorns under stress: A combined Raman spectroscopy and TEM study. RSC Adv. 2016, 6, 49543–49550. [Google Scholar] [CrossRef]
- Sasaki, K.; Sekine, Y.; Tateno, K.; Gotoh, H. Topological Raman band in the carbon nanohorn. Phys. Rev. Lett. 2013, 111, 116801. [Google Scholar] [CrossRef] [PubMed]
- Pardanaud, C.; Martin, C.; Giacometti, G.; Mellet, N.; Pegourie, B.; Roubin, P. Thermal stability and long term hydrogen/deuterium release from soft to hard amorphous carbon layers analyzed using in-situ Raman spectroscopy. Comparison with Tore Supra deposits. Thin Solid Films 2015, 581, 92–98. [Google Scholar] [CrossRef]
- Pardanaud, C.; Martin, C.; Giacometti, G.; Roubin, P.; Pegourie, B.; Hopf, C.; Schwarz-Selinger, T.; Jacob, W.; Buijnsters, J.G. Long-term H-release of hard and intermediate between hard and soft amorphous carbon evidenced by in situ Raman microscopy under isothermal heating. Diam. Relat. Mater. 2013, 37, 92–96. [Google Scholar] [CrossRef]
- Niwase, K.; Tanabe, T.; Sugimoto, M.; Fujita, F.E. Modification of graphite structure by D+ and He+ bombardment. J. Nucl. Mater. 1989, 162, 856–860. [Google Scholar] [CrossRef]
- Oschatz, M.; Pre, P.; Dorfler, S.; Nickel, W.; Beaunier, P.; Rouzaud, J.N.; Fischer, C.; Brunner, E.; Kaskel, S. Nanostructure characterization of carbide-derived carbons by morphological analysis of transmission electron microscopy images combined with physisorption and Raman spectroscopy. Carbon 2016, 105, 314–322. [Google Scholar] [CrossRef]
- Da Costa, J.P.; Weisbecker, P.; Farbos, B.; Leyssale, J.M.; Vignoles, G.L.; Germain, C. Investigating carbon materials nanostructure using image orientation statistics. Carbon 2015, 84, 160–173. [Google Scholar] [CrossRef]
- Niwase, K. Irradiation-induced amorphization of graphite. Phys. Rev. B 1995, 52, 15785–15798. [Google Scholar] [CrossRef]
- Pardanaud, C.; Martin, C.; Cartry, G.; Ahmad, A.; Schiesko, L.; Giacometti, G.; Carrere, M.; Roubin, P. In-plane and out-of-plane defects of graphite bombarded by H, D and He investigated by atomic force and Raman microscopies. J. Raman Spectrosc. 2015, 46, 256–265. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. Acs Nano 2011, 5, 26–41. [Google Scholar] [CrossRef] [PubMed]
- Kotakoski, J.; Krasheninnikov, A.V.; Kaiser, U.; Meyer, J.C. From point defects in graphene to two-dimensional amorphous carbon. Phys. Rev. Lett. 2011, 106, 105505. [Google Scholar] [CrossRef] [PubMed]
- Elman, B.S.; Dresselhaus, M.S.; Dresselhaus, G.; Maby, E.W.; Mazurek, H. Raman-scattering from ion-implanted graphite. Phys. Rev. B 1981, 24, 1027–1034. [Google Scholar] [CrossRef]
- Compagnini, G.; Puglisi, O.; Foti, G. Raman spectra of virgin and damaged graphite edge planes. Carbon 1997, 35, 1793–1797. [Google Scholar] [CrossRef]
- Nakamura, K.; Fujitsuka, M.; Kitajima, M. Finite size effect on raman-scattering of graphite microcrystals. Chem. Phys. Lett. 1990, 172, 205–208. [Google Scholar] [CrossRef]
- Nakamura, K.; Kitajima, M. Real-time raman measurements of graphite under Ar+ irradiation. Appl. Phys. Lett. 1991, 59, 1550–1552. [Google Scholar] [CrossRef]
- Nakamura, K.; Kitajima, M. Ion-irradiation effects on the phonon correlation length of graphite studies by raman-spectroscopy. Phys. Rev. B 1992, 45, 78–82. [Google Scholar] [CrossRef]
- Eckmann, A.; Felten, A.; Verzhbitskiy, I.; Davey, R.; Casiraghi, C. Raman study on defective graphene: Effect of the excitation energy, type, and amount of defects. Phys. Rev. B 2013, 88, 035426. [Google Scholar] [CrossRef]
- Sato, K.; Saito, R.; Oyama, Y.; Jiang, J.; Cancado, L.G.; Pimenta, M.A.; Jorio, A.; Samsonidze, G.G.; Dresselhaus, G.; Dresselhaus, M.S. D-band Raman intensity of graphitic materials as a function of laser energy and crystallite size. Chem. Phys. Lett. 2006, 427, 117–121. [Google Scholar] [CrossRef]
- Meyer, J.C.; Kisielowski, C.; Erni, R.; Rossell, M.D.; Crommie, M.F.; Zettl, A. Direct imaging of lattice atoms and topological defects in graphene membranes. Nano Lett. 2008, 8, 3582–3586. [Google Scholar] [CrossRef] [PubMed]
- Ng, T.Y.; Yeo, J.J.; Liu, Z.S. A molecular dynamics study of the thermal conductivity of graphene nanoribbons containing dispersed Stone-Thrower-Wales defects. Carbon 2012, 50, 4887–4893. [Google Scholar] [CrossRef]
- Thrower, P.A. The study of defects in graphite by transmission electron microscopy. In Chemistry and Physics of Carbon; Walker, P.L., Jr., Ed.; Marcel Dekker: New York, NY, USA, 1969. [Google Scholar]
- Wu, G.; Dong, J.M. Raman characteristic peaks induced by the topological defects of carbon nanotube intramolecular junctions. Phys. Rev. B 2006, 73, 245414. [Google Scholar] [CrossRef]
- Fujimori, T.; Radovic, L.R.; Silva-Tapia, A.B.; Endo, M.; Kaneko, K. Structural importance of Stone-Thrower-Wales defects in rolled and flat graphenes from surface-enhanced Raman scattering. Carbon 2012, 50, 3274–3279. [Google Scholar] [CrossRef]
- Shirodkar, S.N.; Waghmare, U.V. Electronic and vibrational signatures of Stone-Wales defects in graphene: First-principles analysis. Phys. Rev. B 2012, 86, 165401. [Google Scholar] [CrossRef]
- Itoh, T.; Yamamoto, Y.S.; Biju, V.; Tamaru, H.; Wakida, S. Fluctuating single sp2 carbon clusters at single hotspots of silver nanoparticle dimers investigated by surface-enhanced resonance Raman scattering. AIP Adv. 2015, 5, 127113. [Google Scholar] [CrossRef]
- Podila, R.; Rao, R.; Tsuchikawa, R.; Ishigami, M.; Rao, A.M. Raman spectroscopy of folded and scrolled graphene. Acs Nano 2012, 6, 5784–5790. [Google Scholar] [CrossRef] [PubMed]
- Larouche, N.; Stansfield, B.L. Classifying nanostructured carbons using graphitic indices derived from Raman spectra. Carbon 2010, 48, 620–629. [Google Scholar] [CrossRef]
- Yehliu, K.; Vander Wal, R.L.; Boehman, A.L. Development of an HRTEM image analysis method to quantify carbon nanostructure. Combust. Flame 2011, 158, 1837–1851. [Google Scholar] [CrossRef]
- Pre, P.; Huchet, G.; Jeulin, D.; Rouzaud, J.N.; Sennour, M.; Thorel, A. A new approach to characterize the nanostructure of activated carbons from mathematical morphology applied to high resolution transmission electron microscopy images. Carbon 2013, 52, 239–258. [Google Scholar] [CrossRef]
- Bourrat, X.; Langlais, F.; Chollon, G.; Vignoles, G.L. Low temperature pyrocarbons: A review. J. Braz. Chem. Soc. 2006, 17, 1090–1095. [Google Scholar] [CrossRef]
- Rouzaud, J.N.; Oberlin, A.; Benybassez, C. Carbon-films—Structure and microtexture (optical and electron-microscopy, raman-spectroscopy). Thin Solid Films 1983, 105, 75–96. [Google Scholar] [CrossRef]
- Brunetto, R.; Pino, T.; Dartois, E.; Cao, A.T.; d’Hendecourt, L.; Strazzulla, G.; Brechignac, P. Comparison of the Raman spectra of ion irradiated soot and collected extraterrestrial carbon. Icarus 2009, 200, 323–337. [Google Scholar] [CrossRef]
- Schmid, J.; Grob, B.; Niessner, R.; Ivleva, N.P. Multiwavelength Raman microspectroscopy for rapid prediction of soot oxidation reactivity. Anal. Chem. 2011, 83, 1173–1179. [Google Scholar] [CrossRef] [PubMed]
- Russo, C.; Ciajolo, A. Effect of the flame environment on soot nanostructure inferred by Raman spectroscopy at different excitation wavelengths. Combust. Flame 2015, 162, 2431–2441. [Google Scholar] [CrossRef]
- Ess, M.N.; Ferry, D.; Kireeva, E.D.; Niessner, R.; Ouf, F.X.; Ivleva, N.P. In situ Raman microspectroscopic analysis of soot samples with different organic carbon content: Structural changes during heating. Carbon 2016, 105, 572–585. [Google Scholar] [CrossRef]
- Bourrat, X.; Fillion, A.; Naslain, R.; Chollon, G.; Brendle, M. Regenerative laminar pyrocarbon. Carbon 2002, 40, 2931–2945. [Google Scholar] [CrossRef]
- Bourrat, X.; Lavenac, J.; Langlais, F.; Naslain, R. The role of pentagons in the growth of laminar pyrocarbon. Carbon 2001, 39, 2376–2380. [Google Scholar] [CrossRef]
- Vallerot, J.M. Matrice de Pyrocarbone: Propriétés, Structure et Anisotropie Optique. Ph.D. Thesis, Université de Bordeaux 1, Bordeaux, France, 2004. (In French). [Google Scholar]
- Prawer, S.; Nemanich, R.J. Raman spectroscopy of diamond and doped diamond. Philos. Trans. R. Soc. 2004, 362, 2537–2565. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.; Sedghi, S.; Silvestre-Albero, A.; Andersson, G.G.; Sharma, A.; Pendleton, P.; Rodriguez-Reinoso, F.; Kaneko, K.; Biggs, M.J. Raman spectroscopy study of the transformation of the carbonaceous skeleton of a polymer-based nanoporous carbon along the thermal annealing pathway. Carbon 2015, 85, 147–158. [Google Scholar] [CrossRef]
- May, P.; Lazzeri, M.; Venezuela, P.; Herziger, F.; Callsen, G.; Reparaz, J.S.; Hoffmann, A.; Mauri, F.; Maultzsch, J. Signature of the two-dimensional phonon dispersion in graphene probed by double-resonant Raman scattering. Phys. Rev. B 2013, 87, 075402. [Google Scholar] [CrossRef]
- Herziger, F.; Tyborski, C.; Ochedowski, O.; Schleberger, M.; Maultzsch, J. Double-resonant LA phonon scattering in defective graphene and carbon nanotubes. Phys. Rev. B 2014, 90, 45431. [Google Scholar] [CrossRef]
- Chernyak, S.A.; Ivanov, A.S.; Maslakov, K.I.; Egorov, A.V.; Shen, Z.X.; Savilov, S.S.; Lunin, V.V. Oxidation, defunctionalization and catalyst life cycle of carbon nanotubes: A Raman spectroscopy view. Phys. Chem. Chem. Phys. 2017, 19, 2276–2285. [Google Scholar] [CrossRef] [PubMed]
- Chacon-Torres, J.C.; Wirtz, L.; Pichler, T. Raman spectroscopy of graphite intercalation compounds: Charge transfer, strain, and electron-phonon coupling in graphene layers. Phys. Status Solidi B 2014, 251, 2337–2355. [Google Scholar] [CrossRef]
- Allen, M.J.; Tung, V.C.; Kaner, R.B. Honeycomb carbon: A review of graphene. Chem. Rev. 2010, 110, 132–145. [Google Scholar] [CrossRef] [PubMed]
- Dresselhaus, M.S.; Dresselhaus, G. Intercalation compounds of graphite. Adv. Phys. 2002, 51, 1–186. [Google Scholar] [CrossRef]
- Abdelkader, A.M.; Cooper, A.J.; Dryfe, R.A.W.; Kinloch, I.A. How to get between the sheets: A review of recent works on the electrochemical exfoliation of graphene materials from bulk graphite. Nanoscale 2015, 7, 6944–6956. [Google Scholar] [CrossRef] [PubMed]
- Gupta, V.; Scharff, P.; Risch, K.; Romanus, H.; Muller, R. Synthesis of C60 intercalated graphite. Solid State Commun. 2004, 131, 153–155. [Google Scholar] [CrossRef]
- Zhao, W.J.; Tan, P.H.; Liu, J.; Ferrari, A.C. Intercalation of few-layer graphite flakes with FeCl3: Raman determination of fermi level, layer by layer decoupling, and stability. J. Am. Chem. Soc. 2011, 133, 5941–5946. [Google Scholar] [CrossRef] [PubMed]
- Salvatore, M.; Carotenuto, G.; de Nicola, S.; Camerlingo, C.; Ambrogi, V.; Carfagna, C. Synthesis and characterization of highly intercalated graphite bisulfate. Nanoscale Res. Lett. 2017, 12, 167. [Google Scholar] [CrossRef] [PubMed]
- Eklund, P.C.; Falardeau, E.R.; Fischer, J.E. Raman-scattering in low stage compounds of graphite intercalated with AsF5, HNO3 and SbCl5. Solid State Commun. 1979, 32, 631–634. [Google Scholar] [CrossRef]
- Chacon-Torres, J.C.; Wirtz, L.; Pichler, T. Manifestation of charged and strained graphene layers in the Raman response of graphite intercalation compounds. ACS Nano 2013, 7, 9249–9259. [Google Scholar] [CrossRef] [PubMed]
- Solin, S.A. Raman and IR studies of graphite intercalates. Phys. B+C 1980, 99, 443–452. [Google Scholar] [CrossRef]
- Calandra, M.; Mauri, F. Theoretical explanation of superconductivity in C6Ca. Phys. Rev. Lett. 2005, 95, 237002. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J. Diamond-like amorphous carbon. Mater. Sci. Eng. R Rep. 2002, 37, 129–281. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, X.; Lin, Y.; Wang, F. A ternary phase diagram for amorphous carbon. Carbon 2015, 94, 202–213. [Google Scholar] [CrossRef]
- Dillon, R.O.; Woollam, J.A.; Katkanant, V. Use of raman-scattering to investigate disorder and crystallite formation in as-deposited and annealed carbon-films. Phys. Rev. B 1984, 29, 3482–3489. [Google Scholar] [CrossRef]
- Peter, S.; Guenther, M.; Gordan, O.; Berg, S.; Zahn, D.R.T.; Seyller, T. Experimental analysis of the thermal annealing of hard a-C:H films. Diam. Relat. Mater. 2014, 45, 43–57. [Google Scholar] [CrossRef]
- Mangolini, F.; Rose, F.; Hilbert, J.; Carpick, R.W. Thermally induced evolution of hydrogenated amorphous carbon. Appl. Phys. Lett. 2013, 103, 161605. [Google Scholar] [CrossRef]
- Rose, F.; Wang, N.; Smith, R.; Xiao, Q.-F.; Inaba, H.; Matsumura, T.; Saito, Y.; Matsumoto, H.; Dai, Q.; Marchon, B.; et al. Complete characterization by Raman spectroscopy of the structural properties of thin hydrogenated diamond-like carbon films exposed to rapid thermal annealing. J. Appl. Phys. 2014, 116, 123516. [Google Scholar] [CrossRef]
- Casiraghi, C. Effect of hydrogen on the UV Raman intensities of diamond-like carbon. Diam. Relat. Mater. 2011, 20, 120–122. [Google Scholar] [CrossRef]
- Wagner, J.; Wild, C.; Koidl, P. Resonance effects in raman-scattering from polycrystalline diamond films. Appl. Phys. Lett. 1991, 59, 779–781. [Google Scholar] [CrossRef]
- Buijnsters, J.G.; Gago, R.; Jimenez, I.; Camero, M.; Agullo-Rueda, F.; Gomez-Aleixandre, C. Hydrogen quantification in hydrogenated amorphous carbon films by infrared, Raman, and X-ray absorption near edge spectroscopies. J. Appl. Phys. 2009, 105, 093510. [Google Scholar] [CrossRef]
- Cui, W.G.; Lai, Q.B.; Zhang, L.; Wang, F.M. Quantitative measurements of sp3 content in DLC films with Raman spectroscopy. Surf. Coat. Technol. 2010, 205, 1995–1999. [Google Scholar] [CrossRef]
- Wu, A.; Cremer, D. Correlation of the vibrational spectra of isotopomers: Theory and application. J. Phys. Chem. A 2003, 107, 10272–10279. [Google Scholar] [CrossRef]
- Mallet-Ladeira, P.; Puech, P.; Toulouse, C.; Cazayous, M.; Ratel-Ramond, N.; Weisbecker, P.; Vignoles, G.L.; Monthioux, M. A Raman study to obtain crystallite size of carbon materials: A better alternative to the Tuinstra-Koenig law. Carbon 2014, 80, 629–639. [Google Scholar] [CrossRef]
- Martin, C.; Pegourie, B.; Ruffe, R.; Marandet, Y.; Giacometti, G.; Pardanaud, C.; Languille, P.; Panayotis, S.; Tsitrone, E.; Roubin, P. Structural analysis of eroded carbon fiber composite tiles of Tore Supra: Insights on ion transport and erosion parameters. Phys. Scr. 2011, 2011, 01024. [Google Scholar] [CrossRef]
- Ruiz, M.P.; de Villoria, R.G.; Millera, A.; Alzueta, M.U.; Bilbao, R. Influence of the temperature on the properties of the soot formed from C2H2 pyrolysis. Chem. Eng. J. 2007, 127, 1–9. [Google Scholar] [CrossRef]
- Chen, P.W.; Huang, F.L.; Yun, S.R. Optical characterization of nanocarbon phases in detonation soot and shocked graphite. Diam. Relat. Mater. 2006, 15, 1400–1404. [Google Scholar] [CrossRef]
- Beyssac, O.; Goffe, B.; Petitet, J.P.; Froigneux, E.; Moreau, M.; Rouzaud, J.N. On the characterization of disordered and heterogeneous carbonaceous materials by Raman spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2003, 59, 2267–2276. [Google Scholar] [CrossRef]
- Farbos, B.; Weisbecker, P.; Fischer, H.E.; da Costa, J.P.; Lalanne, M.; Chollon, G.; Germain, C.; Vignoles, G.L.; Leyssale, J.M. Nanoscale structure and texture of highly anisotropic pyrocarbons revisited with transmission electron microscopy, image processing, neutron diffraction and atomistic modeling. Carbon 2014, 80, 472–489. [Google Scholar] [CrossRef]
- Shin, Y.Y.; Lozada-Hidalgo, M.; Sambricio, J.L.; Grigorieva, I.V.; Geim, A.K.; Casiraghi, C. Raman spectroscopy of highly pressurized graphene membranes. Appl. Phys. Lett. 2016, 108, 221907. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).