Strain Energy Effects in the Spinodal Decomposition of Cu-Ni(Fe) Nanolaminate Coatings

Abstract

A model for spinodal decomposition must account for interface effects that include gradient and strain energy terms. The measurement of diffusion in the Cu-Ni(Fe) alloy for the special case of nanolaminate structured coatings is considered wherein the composition fluctuation is one-dimensional along <111>. An analytic approach is taken to model the kinetics of the transformation process that provides quantification of the strain energy dependence on the composition wavelength, as well as the intrinsic diffusivities and higher-order gradient-energy coefficients. The variation of the wave amplification factor R with wavenumber is modeled first to incorporate the boundary condition for growth at infinite wavelength. These results are used next to determine the gradient energy coefficients K_μ by modeling the interdiffusion coefficient Ď_B variation with wavenumber, where a unique determination of the diffusion coefficient Ď is made. The value of the strain energy component that originates from interface strains associated with the epitaxial growth between layers is then determined by assessing the variation of wavelength-dependent amplification factors. A peak value of 9.4 × 10⁷ J·m⁻³ for the strain energy is computed for Cu-Ni(Fe) nanolaminate coatings with 2–4 nm composition wavelengths.

1. Introduction

The diffusional transformation of spinodal decomposition [1,2,3,4,5,6,7,8,9,10] proceeds by the growth of a periodic composition fluctuation as the α-phase matrix decomposes at temperatures within the spinodal into α' and αʺ phases, without a change in the crystal structure. The evolution continues of the linear Cahn-Hilliard model for spinodal decomposition. The effect of nonlinear relaxation dynamics [11] is considered with respect to the interaction of phase boundaries and their motion. The case for multilayered structures is investigated wherein it can be modeled that the motion of an interface is affected by interactions with second nearest interfaces, leading towards the tendency of doubling the composition wavelength over time. Mossbauer measurements [12] evidence the continued decomposition of Cu-Ni(Fe) at room temperature.

The relevance of lattice coherency effects are seen in material behaviors of Cu-Ni(Fe) alloys including mechanical and magnetic. Numerous spinodal decomposition studies use the processing of bulk alloys. Mechanical alloying [13] provides a route to produce nanostructured powder precursors as well. The effect of coherency strains is evident in the yield strength [14,15] of age-hardened alloys where maximum strength was achieved for lower aging temperatures. An advantage of spinodal decomposition for mechanical hardening [16] is that excellent dimensional stability can be maintained since no crystallographic changes take place. A giant magnetoresistance behavior was introduced [17] by aging a bulk alloy through processing via spinodal decomposition with uniaxial deformation to produce local superlattice-type nanostructures. Coatings [18] on low-carbon steels have been evaluated for improved corrosion behavior. In multilayered form, a more recent investigation [19] of ferromagnetic nanostructured multilayers considers the effect of growth conditions to superparamagnetic contributions to magnetoresistance behavior that result from composition-rich regions.

This study considers the effects of strain energy from a one-dimensional modulation in nanolaminate structures on the kinetics of the spinodal decomposition process.

2. Background

The free energy f at a temperature T_i is considered for an alloy system composed of elements A and B. The compositions c_α' and c_αʺ indicate the lower and upper bounds, respectively, for the composition c_B of element B within the miscibility gap. The local minima in the free energy curve, i.e., at f′ = ∂f/∂c = 0, provide the locus of points at temperatures T_i that form the miscibility gap.

The phase transformation process of spinodal decomposition [1,2,3,4,5,6,7,8,9,10] proceeds via uphill diffusion when the second-order derivative of the Helmholtz free energy f with respect to composition c is less than zero, i.e., fʺ = ∂²f/∂c² <0. The locus of points for those compositions at temperatures that are between the bounds defined by fʺ = 0 is the chemical spinodal. There is no barrier for decomposition for temperatures within the spinodal T_i < T_s. Decomposition for one-dimensional diffusion is found [20] where satellite reflections are observed about the Bragg peaks in X-ray diffraction patterns for a heat treated Cu-Ni-Fe alloy. An initial explanation considers an interfacial energy term [1] between adjacent atomic planes. The additional consideration of a gradient energy term [3,4] provides the identification of a critical wavenumber β_c to the composition fluctuation where the wavenumber-dependent interdiffusivity Ď_B equals zero. The decomposition stops and decay occurs beyond a critical wavenumber, i.e., β > β_c, where maximum growth occurs at a wavenumber β_m (classically, equal to β_c/$\sqrt{2}$).

The presence of coherency effects [5] from a strained lattice will further depress the transformation temperature of the chemical spinodal T_s to a coherent spinodal T_s*. The decrease of the spinodal temperature, i.e., T_s – T_s*, can be significant [21] for some alloy systems such as Au-Ni with a large lattice misfit, whereas it is potentially smaller for bulk alloy systems such as Cu-Ni(Fe) that have a smaller misfit strain. Along with a composition gradient energy, the presence of interfaces provides a strain energy term that evidences maximum growth of a characteristic composition wavelength along elastically soft directions. Consequently, an applied stress [8] during aging affects the evolving morphology of the composition fluctuation.

The linear theory of diffusion for spinodal decomposition [1,2,3,4,5,8,21,22,23,24] provides for the accommodation of energy associated with new evolving surfaces and interface strain for the composition fluctuations. The wavenumber dependent interdiffusivity Ď_B is linearly proportional to the square of the wavenumber β² where the amplification factor R of growth to the composition wave equals −β²·Ď_B. The values of β_c and β_m will change with the depression of the coherent spinodal temperature for the aging process.

The consideration of additional gradient-energy terms K_μ as (e.g., from the effects of distant interface interactions) is used in a further modified formulation [25] of diffusion. In concept, this allows for fitting a higher-order, non-quadratic relationship between the interdiffusivity Ď_B and wavenumber, i.e., as can be directionally quantified using the dispersion relationship B. This has been accomplished by simultaneous determination [25,26] of K_μ and Ď. However, uncertainty is introduced without direct use of the long-wavelength boundary condition.

A condition arises during decomposition that the presence of strain energy will always decrease the amplification factor R. The effect is to increase the magnitude of interdiffusivity Ď_B outside the spinodal, but decrease its magnitude within the spinodal. This requires use of higher-order terms in a polynomial expansion that should meet the requirement for establishing an upper bound to the amplification factor variation with the dispersion relation and, consequently, a lower bound for the value of measured diffusion behavior.

The magnitude of the 2η²·Y (the elastic modulus Y) strain energy depends upon the accommodation of strain η within the crystal structure, and its variation with the dispersion relation. As the wavenumber, i.e., dispersion relation, decreases towards zero the strain through the nanolaminate structure will decay in magnitude. This represents the conditions for a bulk-diffusion couple. Maximum strain is often seen experimentally in metallic superlattices as Cu-Ni(Fe) at relatively small composition wavelengths of 2–3 nm that correspond with a decrease in wavenumber to 3–2 nm⁻¹. Therefore, a variation in the 2η²·Y term with composition wavelength is anticipated.

3. Experimental Section

Nanolaminate structures consist of an alternating sequence of constituent components that form a composition fluctuation. Nanolaminate thin films of Cu_0.53/Ni_0.40Fe_0.07 are prepared [26] by alternating the vapor flux between Cu and Ni-Fe sources onto a heated substrate. The deposition chamber is evacuated to a base pressure of 20 μPa (0.2 μTorr) with use of a liquid-nitrogen cooled Meissner trap. The source metals are >0.99995 pure and are thermally evaporated from 7 cm³ crucibles at 0.1–1 nm·s⁻¹ evaporation rates to produce a 0.5–0.9 μm film thickness. The source-to-substrate separation of 30 cm enables thickness control with use of 6 MHz gold-coated quartz crystal microbalances to produce a coating composition to within ±1 at.%. The nanolaminates coatings are deposited onto 4 cm × 8 cm sheets of both cleaved mica and polished Si wafers (with the native oxide intact). A 20–40 nm thick buffer layer of pure Cu is deposited initially to introduce (111) film growth. The substrate is an oxygen-free Cu plate that is heated with a quartz lamp for a growth temperature of 350 ± 5 °C. The deposition process produces a dense columnar structure with a single habit plane of dense packed growth. The growth of (111) is typical for face-center-cubic metal alloys such as Cu-Ni(Fe). The alternating layers of Cu and Ni(Fe) grow epitaxial with one another.

The growth or decay in amplitude Q of an A/B composition fluctuation with wavelength (λ_A/B) for layer pairs of components A and B is accomplished again [26] using anneal treatments within a turbo-molecular pumped, quartz tube at temperatures of 320, 345, and 400 °C. Samples are annealed to reduce the amplitude of the composition fluctuation from which growth or decay of the composition wave is assessed. A series of X-ray diffraction patterns are taken in the θ/2θ mode, as shown in Figure 1 and Figure 2 using a Rigaku Miniflex II diffractometer (Rigaku Americas Corp., The Woodlands, TX, USA) equipped with a graphite monochromator. A monochromatic Cu k_α radiation is used to measure the amplitude and wavelength of the composition fluctuation where a 25 kV-10 mA current was applied to the Cu anode. For a sample rotation θ, the X-ray detector is rotated 2θ. Each increment Δ2θ of rotation is 0.02° with a 5–10 s dwell time. The integrated intensity of each reflection is computed from digitized X-ray reflectivity spectra using the diffraction peak de-convolution software provided with the Rigaku Miniflex II diffractometer. Satellite peaks (±) about the superlattice peak of the (111) Bragg reflection correspond with the short-range order for the composition modulation in the nanolaminate growth direction. A change in the satellite intensity (I) will occur as the sample is annealed at time (t) intervals that range from 20 to 1000 min. The calculation of the composition profile is made wherein the satellite peak intensity I^± is proportional with the wave amplitude. Homogenization of the structure and decay in the composition wave amplitude result for anneal treatments above the spinodal temperature, whereas growth occurs within the chemical spinodal.

4. Method of Analysis

A review is presented of the formulations [1,2,3,4,5,6,7,8,9,10] for spinodal decomposition that relate to use of the X-ray diffraction method for experimental measurement [21,22,23,24,25,26,27,28,29,30,31,32,33,34] of the time-temperature dependent changes in the composition wave. In particular, reference to formulations and the equations are shown which comprise the basis to compute the higher-order gradient energy coefficients, the diffusion coefficients, and the strain energy variation with nanolaminate spacing. The Background contains equations [25,26,27,28,32,33] that are now adapted for analysis of spinodal decomposition in the Cu-Ni(Fe) alloy system, and as modified to determine strain energy effects in the Current Approach.

4.1. Modified Diffusion Formulation

The stability of a nanolaminate interface with respect to diffusion along the A/B fluctuation at time t can be considered using the discrete theory in terms of a static concentration wave [32]. The composition wavelength λ_A/B of the fluctuation between A-rich and B-rich regions, i.e., layer pair spacing for nanostructures, is equated to the wavenumber β as 2π/λ_A/B. The microscopic theory of diffusion [10,25,29] is used to quantify the interdiffusivity coefficient Ď_B of each nanolaminate as dependent on its composition wavelength at temperature T_i. The macroscopic diffusion coefficient Ď for the alloy system corresponds with an infinite composition wavelength. The relative decay in satellite intensity I^±(t) for the composition fluctuation is normalized to the Bragg peak intensity, and this value is used to determine [22,23,24,25,26,33] the amplification factor R as

ln{[I^± (t)]/[I^±(0)]} = 2R·t

(1)

The measured intensity I_m of the Bragg peak and satellite reflections are normalized to compute corrected values I_c with respect to the 2θ peak positions. Details of the X-ray intensity formulations are provided in Appendix. The amplification factor R is related to the generalized Ď_B through the dispersion relationship B²(β) according to the expression

R = −B²(β)·Ď_B

(2)

The B²(h) expression [32] derived for face-centered-cubic [100] or [111] growth is

B²(h) = 2{1 − cos(2πh)}/d_(hkl)²

(3)

The interplanar spacing is d_(hkl) and h equals d_(hkl)/λ_A/B. The use of a curvilinear fit to the variation of Ď_B with B²(h) yields the value of Ď at B²(h) = 0. That is, a nanolaminate with an infinite composition wavelength is the equivalent of a macroscopic diffusion couple. A generalized expression for Ď_B is presented in terms of its energetic components to account for potential nonlinear effects. The Ď coefficient is related to Ď_B through [25,26] the Fourier transform F_e(h) of the elastic strain energy for the distorted lattice, the second derivative fʺ of the Helmholtz free energy (per atom volume N_v), and the gradient-energy coefficients K_μ as

Ď_B = Ď·{1 + F_e(h)/fʺ + (2/fʺ)·Σ[K_μ·B^2μ(h)]}

(4)

For a face-center cubic system, N_v equals 4/a³ for an alloy lattice parameter a. The order of the polynomial is µ, and the diffusion coefficient Ď is related [21] to the mobility M according to the expression

Ď = (M/N_v)·fʺ

(5)

The fʺ and K_μ terms in Equation (4) are identical with expressions [3,4,29,30,31,32] that appear in both the continuous and discrete theories of spinodal decomposition. The expression for the diffusion coefficient used in Equation (5) includes only the Helmholtz free energy term fʺ because the presence of strain energy is not a prerequisite, but it varies with each nanolaminate sample—An original criterion of the modified diffusion equation [21] for spinodal decomposition. A direct series expansion of the Ď_B with B²(h) relationship is now used to fit the experimental data as

Ď_B = Ď·[1 + Σ K'_μ·B^2μ(h)]

(6)

Accordingly, from Equations (5) and (6), the coefficients K'_μ are used to compute the gradient energy coefficients K_μ, where K'_μ is now equal to 2K_μ/fʺ. Equation (6) will be used in this analysis to determine the diffusion coefficient Ď, and finalize the values for both the K'_μ and K_μ gradient energy coefficients. The B(h) value is equal to β in the long wavelength approximation. The F_e(h) quantity is equated [21] with strain energy and is, therefore, a function of B(h). The strain energy term equals 2η²·Y, where η is the compositionally dependent variation of strain that equals (1/a)·(∂a/∂c), and Y is the <hkl> orientation-dependent biaxial modulus.

The diffusivity is zero at the coherent spinodal (T_s*). From the linear theory using Equation (4) where only one gradient energy coefficient is considered, the following condition is found.

fʺ + 2η²·Y + 2K·B² = 0

(7)

The gradient energy coefficient K can be determined from Equation (7) with respect to the critical wavenumber where there is no growth or decay. Where the wavenumber B equals zero, i.e., for a macroscopic diffusion couple where the wavelength goes to infinity, Equation (7) reduces to

fʺ + 2η²·Y = 0

(8)

This relationship indicates that the fʺ = 0 condition for the chemical spinodal is changed with a suppression to the condition of fʺ = –2η²·Y for the coherent spinodal. From an experimental estimate of the chemical spinodal temperature T_s, the value of fʺ for any temperature can then be computed [21] using Boltzmann’s constant k_B as

fʺ = N_v·k_B·(T – T_s)/[c·(1 − c)]

(9)

The amount that the coherent spinodal temperature is suppressed below the chemical spinodal, i.e., T_s – T_s*, can be determined using the Equation (8) equivalence where the temperature T is now equated as T_s*.

4.2. Current Approach

In order to uniquely determine the diffusion coefficient Ď and the unknown effect of strain energy on diffusion, the higher-order gradient-energy coefficients are now included in the expansion of the modified linear theory as seen in Equations (4) and (6). To reiterate, the suppression of the coherent spinodal described in Equations (7)–(9) will vary from sample to sample since the wavenumber-dependent Fourier transform F_e(h) of the elastic strain energy is equal to 2[η(h)]²·Y(h). Simulated curves are used to establish baseline behavior without inclusion of the strain energy term. This approach is taken since it has been well established for nanolaminate structures that both the strain η and modulus Y components can vary with the wavenumber, i.e., these are not constant values. In this approach, the difference between the measured data and simulated values will be used to quantify the effect of strain energy.

The value of the temperature-dependent diffusion coefficient Ď, representative of diffusion behavior for the long-wavelength equivalent, has been extrapolated previously [25,26,27,28] from the behavior of composition fluctuations with shorter wavelengths, i.e., longer wavenumbers, by fitting the variation of the interdiffusion coefficient Ď_B with B². Without a known boundary condition, modeling of the gradient energy coefficient K'_μ terms and the diffusion coefficient Ď from the Ď_B variation with B² behavior has introduced some uncertainty. Since all diffusion coefficients are derived from the direct measurement of the amplification factor R as seen in Equation (2), the computation of the gradient energy coefficients using the microscopic theory of diffusion will now be approached by, first, using the R variation with B rather than the Ď_B variation with B². The value of R value approaches zero for the infinite wavelength case, i.e., B = 0, providing a boundary condition that will be used in the interpolative analysis of data to follow.

The sign conventions are reviewed to distinguish the effects of the strain energy during diffusion. Growth of the composition fluctuation when T < T_s requires that the diffusivity is negative (Ď_B < 0) for uphill diffusion, and the amplification factor is positive (R > 0). Similarly, decay of the composition fluctuation when T > T_s requires that the interdiffusivity is positive (Ď_B > 0) for downhill diffusion, and the amplification factor is negative (R < 0). Accordingly, from Equations (2), (4) and (5), growth of the composition wave amplitude within the spinodal occurs when fʺ < 0 and K > 0, whereas decay outside the spinodal occurs when fʺ > 0 and K < 0.

For growth of the fluctuation, and to be consistent with the sign requirements of the model formulation reviewed in the Background, the variation of R with B is simulated using a new higher-order polynomial expansion,

R_s = Σ k'_μ·B^μ(h)

(10)

From Equations (2) and (4), it follows that the difference ΔR between the simulated value of the amplification factor R_s and the experimental value R_e, i.e., ΔR = R_s – R_e, will be positive for all temperatures and attributable as a sole consequence of strain energy. It has been shown [21] that the strain energy accelerates diffusion outside the spinodal, but hinders it within the spinodal. So, the simulated variation of R with B must now envelope all experimental data as an upper bound. In addition, for decay it is already seen from Equation (10) that ∂R/∂B < 0 as evaluated at B = 0, and for growth that ∂R/∂B > 0. These ∂R/∂B requirements guide the fitting procedure to determine the order μ of the polynomial to appropriately provide the correct (±) sign of the first k'_μ term from Equation (10), i.e., k'₁ < 0 for decay and k'₁ > 0 for growth. The k'_μ terms as determined from Equation (10) are then used to compute the simulated values for interdiffusivity Ď_Bs that correspond with Equation (2) as

Ď_Bs = −R_s/B²(h)

(11)

The simulated Ď_Bs values are then curve fit using Equation (6) to evaluate the K'_μ values corresponding to the fit of the R variation with B. Since K'_μ is equal to 2K_μ/fʺ from Equations (5) and (6), it follows that a condition for growth is K'₁ >0 (since fʺ <0, Ď <0 and K₁ >0 within the spinodal), whereas the condition for decay is K'₁ <0 (since fʺ >0, Ď >0 and K₁ <0 outside the spinodal). From Equations (4)–(6), it follows that the difference ΔĎ_B between the experimental value of the interdiffusion coefficient Ď_Be and the simulated value Ď_Bs, i.e., ΔĎ_B = Ď_Be – Ď_Bs, will be positive for all temperatures and is a sole consequence of strain energy. Again, strain energy [21] accelerates diffusion outside the spinodal and hinders it within the spinodal. So, the simulated variation of the magnitude of the interdiffusivity |Ď_B| with B must envelope all experimental data as a lower bound. The predetermined K'_μ values that follow from evaluating Equation (6), as consistent with the Equation (10) data fit, are used to determine the one remaining, unknown diffusion parameter, i.e., Ď, at each temperature.

The determination of the K'_μ values by curve fitting both the amplification factor and interdiffusivity variation with wavenumber, allows for the computation of the strain energy term consistent with previous [21] derivation. The strain energy is determined in the solution by equating the difference between Equations (4) and (11) as

F_e(h) = 2η(h)²·Y(h) = ΔĎ_B·[fʺ(h)/Ď]

(12)

A plot of the strain energy term 2η²·Y can then be made to evaluate its variation with composition wavelength λ.

5. Results and Discussion

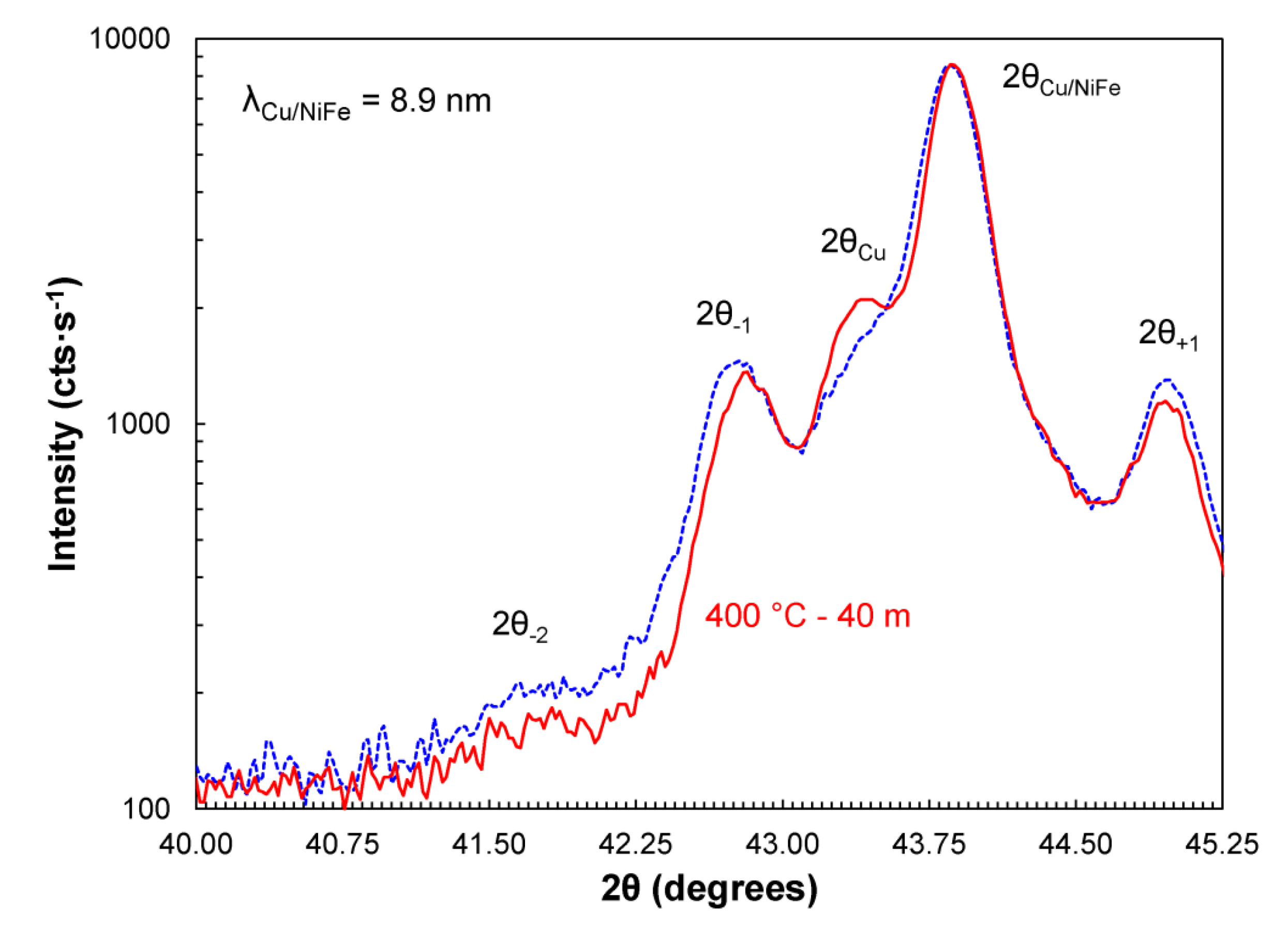
The growth of structures with longer wavelengths, i.e., smaller wavenumbers, occurs in the α-phase for temperatures within the spinodal to produce phase separated regions of α' and αʺ with dissimilar lattice spacing. The consequence for a bulk α-phase alloy will be a tendency to split the Bragg X-ray reflection, decrease its intensity, and broaden its shoulder as is consistent with the growth of long wavelength components. However, for nanolaminate structures, there is an initial composition wavelength along a specific crystallographic direction. With annealing, the Cu/Ni(Fe) superlattice Bragg peak may first narrow in width due to the effects of nanocrystalline grain growth, and split due to phase separation where a 2θ_Cu peak may appear, as seen in Figure 1 and Figure 2 for 2.1 and 8.9 nm wavelength samples annealed at 400 °C for 40 min. The satellite peaks that correspond with the composition fluctuation are indicated in the subscript of the 2θ_i peak position in Figure 1 and Figure 2.

Figure 1. The intensity I^± of the Bragg and satellite peak variation with 2θ position for the Cu/Ni(Fe) nanolaminate coating with a 8.9 nm wavelength λ before (dashed line) and after (solid line) a 40 min at 400 °C anneal treatment.

Figure 1. The intensity I^± of the Bragg and satellite peak variation with 2θ position for the Cu/Ni(Fe) nanolaminate coating with a 8.9 nm wavelength λ before (dashed line) and after (solid line) a 40 min at 400 °C anneal treatment.

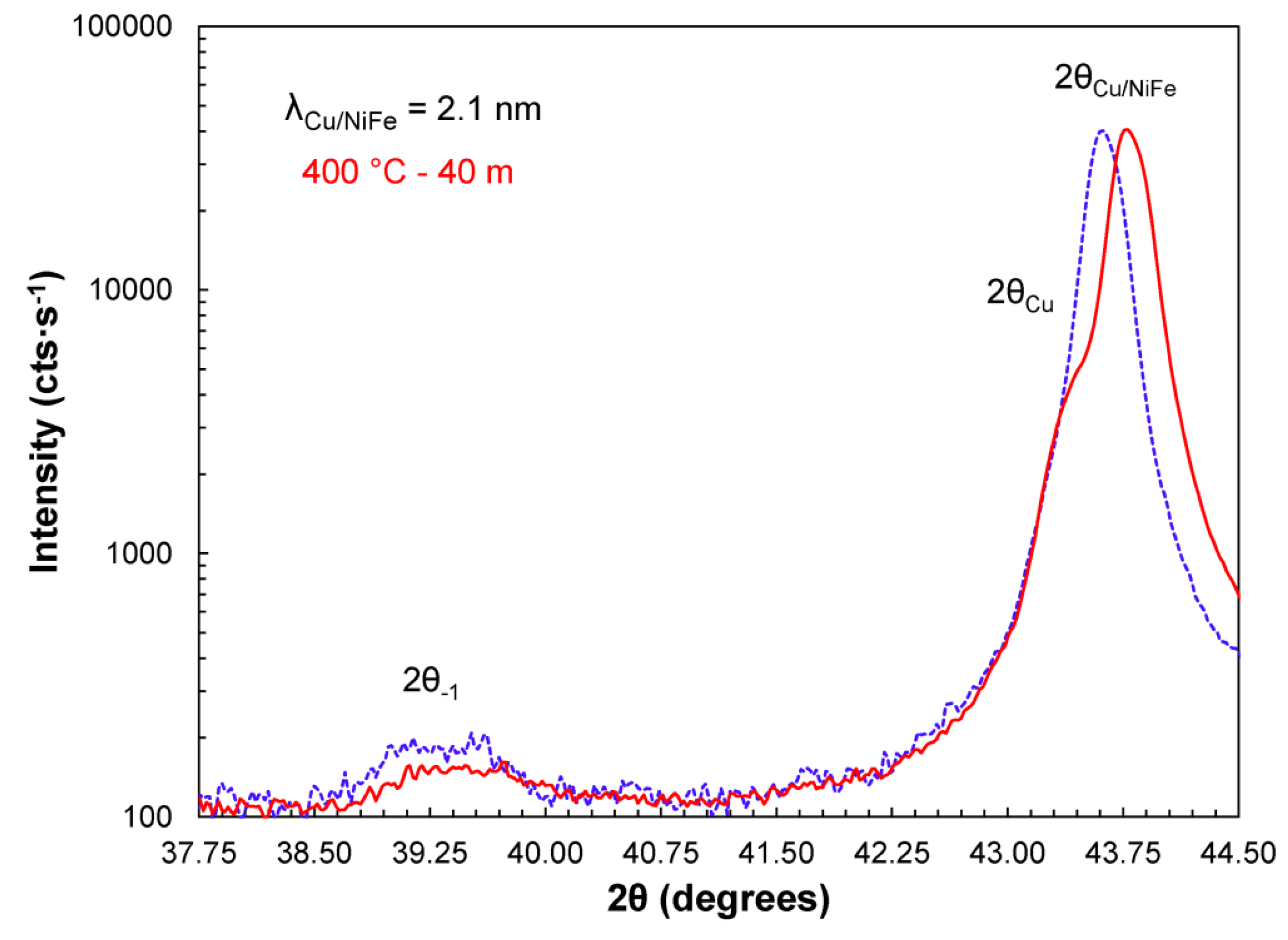
Figure 2. The intensity I^± of the Bragg and satellite peak variation with 2θ position for the Cu/Ni(Fe) nanolaminate coating with a 2.1 nm wavelength λ before (dashed line) and after (solid line) a 40 min at 400 °C anneal treatment.

Figure 2. The intensity I^± of the Bragg and satellite peak variation with 2θ position for the Cu/Ni(Fe) nanolaminate coating with a 2.1 nm wavelength λ before (dashed line) and after (solid line) a 40 min at 400 °C anneal treatment.

The relaxation of lattice strain (when present) can shift the Bragg peak position as seen for the 2.1 nm nanolaminate sample of Figure 2. In addition, enhanced diffusivity for an artificial composition wave during the early stages of annealing [24,25,26] causes an initial, nonlinear decay of satellite peak intensity with time.

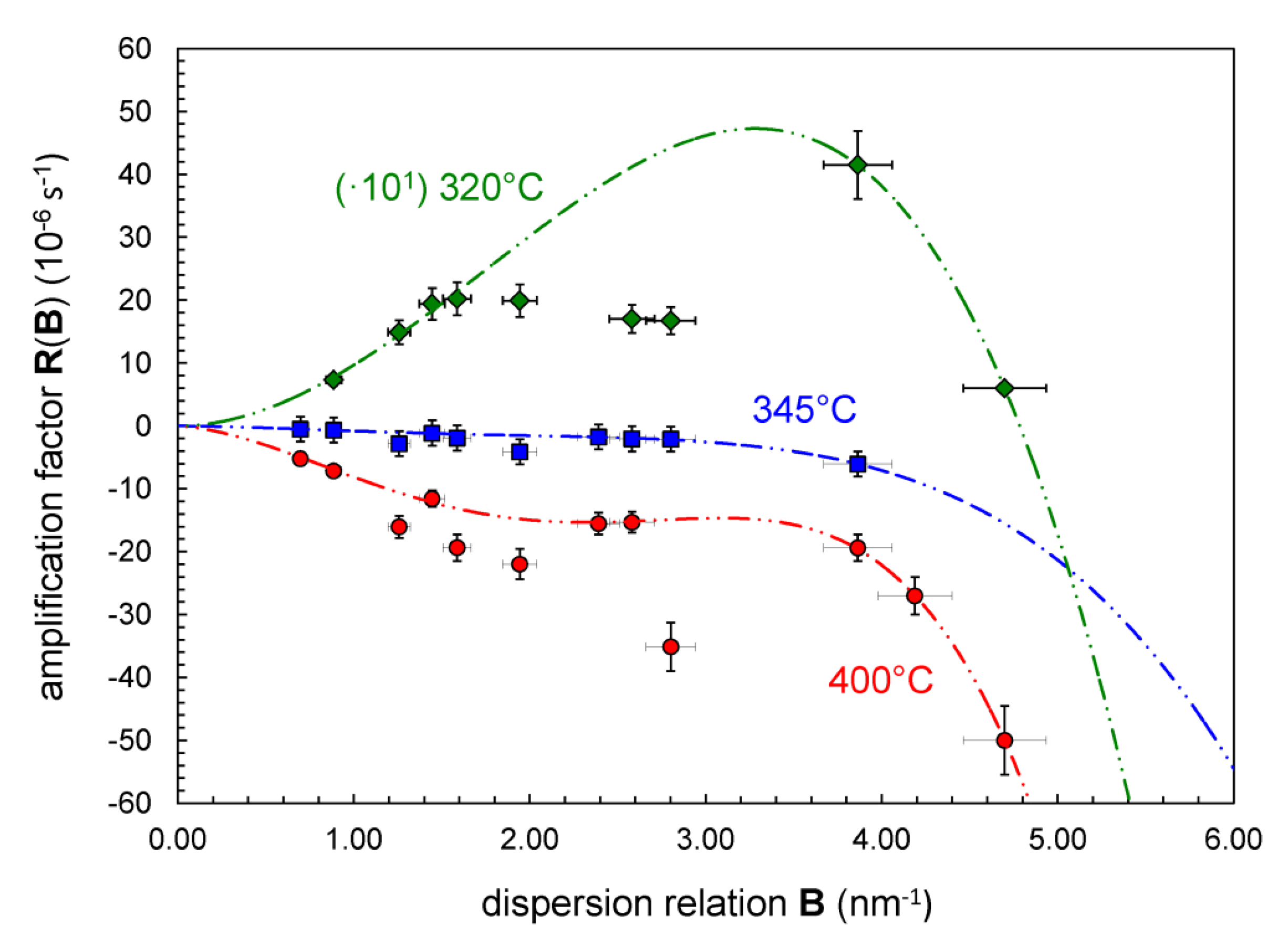
The amplification factor R variation for the nanolaminates (at each anneal temperature) is computed from the integrated peak intensities of the diffraction spectra as shown in Figure 1 and Figure 2 using Equation (1). The R-values are plotted in Figure 3 as a function of the dispersion relation B which is computed using Equation (3) for a (111) growth of the Cu/Ni(Fe) structure. Decay of the composition fluctuation occurs above 345 °C and growth below 320 °C, providing an interpolated estimate for the chemical spinodal of 335 °C. There is insufficient temperature-dependent data in this study to detail the effects of composition wavelength on the depression of the spinodal due to coherency effects. However, a critical wavelength λ_c of 1.26 nm is found for growth at 320 °C, i.e., the coherent spinodal temperature T_s* is 320 °C for a 1.26 nm composition wavelength. This corresponds with the B_c value of 4.78 nm−1 where R_λ equals zero as determined from the Equation (10) fitting of the R-values in Figure 3. This λ_c-value corresponds with a composition wavelength for maximum growth λ_m of 1.78 nm at 320 °C, where [21] λ_m equals λ_c·$\sqrt{2}$.

Figure 3. The amplification factor R (10⁶ s⁻¹) variation with the dispersion-relation wavenumber B (nm⁻¹) as computed from the decay or growth of the first-order satellite intensity I⁻ at peak position of 2θ₋₁ for Cu/Ni(Fe) nanolaminate samples annealed at 320 °C (diamond) as scaled by a factor of 10, at 345 °C (squares), and 400 °C (circles).

Figure 3. The amplification factor R (10⁶ s⁻¹) variation with the dispersion-relation wavenumber B (nm⁻¹) as computed from the decay or growth of the first-order satellite intensity I⁻ at peak position of 2θ₋₁ for Cu/Ni(Fe) nanolaminate samples annealed at 320 °C (diamond) as scaled by a factor of 10, at 345 °C (squares), and 400 °C (circles).

The fʺ values can next be computed, as listed in Table 1, using Equation (9) where T_s equals 335 °C for Cu_0.53/Ni_0.40Fe_0.07 using a N_v value of 86.1 atom·nm⁻³ as computed for 4 atoms in a unit cell volume with a 0.3595 nm lattice parameter. A positive fʺ value is consistent with the heat of mixing wherein unlike atoms cluster as opposed to having the tendency for long-range ordering for systems with a negative heat of mixing. The baseline R behavior for growth or decay is modeled as a function of B using a fourth-order polynomial expansion of Equation (10). This is the minimum order of expansion required to meet the sign criteria for the modeled k'_μ values that is described in the Current Approach Section 4.2.

Table 1. Diffusion and gradient energy coefficients for Cu/Ni(Fe) nanolaminates.

Diffusion and Gradient Energy Coefficients	Cu/Ni(Fe)			Cu/Ni
T (°C)	320	345	400	400
Ď (10−6 nm2·s−1)	−1.065	1.208	11.27	4.846
M (10+16 nm2·J−1·s−1)	0.1285	0.2187	0.3139	0.1350
fʺ (10−19 J·nm−3)	−0.7134	0.4756	3.091	3.078
K1 (10−20 J·nm−1)	0.3496	−0.9311	−4.494	−2.650
K2 (10−21 J·nm)	−0.2735	1.890	5.752	2.582
K3 (10−22 J·nm3)	0.1496	−1.702	−3.991	−0.9814
K4 (10−23 J·nm5)	−0.0295	0.5397	0.6091	0.1309

Table 1. Diffusion and gradient energy coefficients for Cu/Ni(Fe) nanolaminates.

Diffusion and Gradient Energy Coefficients	Cu/Ni(Fe)			Cu/Ni
T (°C)	320	345	400	400
Ď (10−6 nm2·s−1)	−1.065	1.208	11.27	4.846
M (10+16 nm2·J−1·s−1)	0.1285	0.2187	0.3139	0.1350
fʺ (10−19 J·nm−3)	−0.7134	0.4756	3.091	3.078
K1 (10−20 J·nm−1)	0.3496	−0.9311	−4.494	−2.650
K2 (10−21 J·nm)	−0.2735	1.890	5.752	2.582
K3 (10−22 J·nm3)	0.1496	−1.702	−3.991	−0.9814
K4 (10−23 J·nm5)	−0.0295	0.5397	0.6091	0.1309

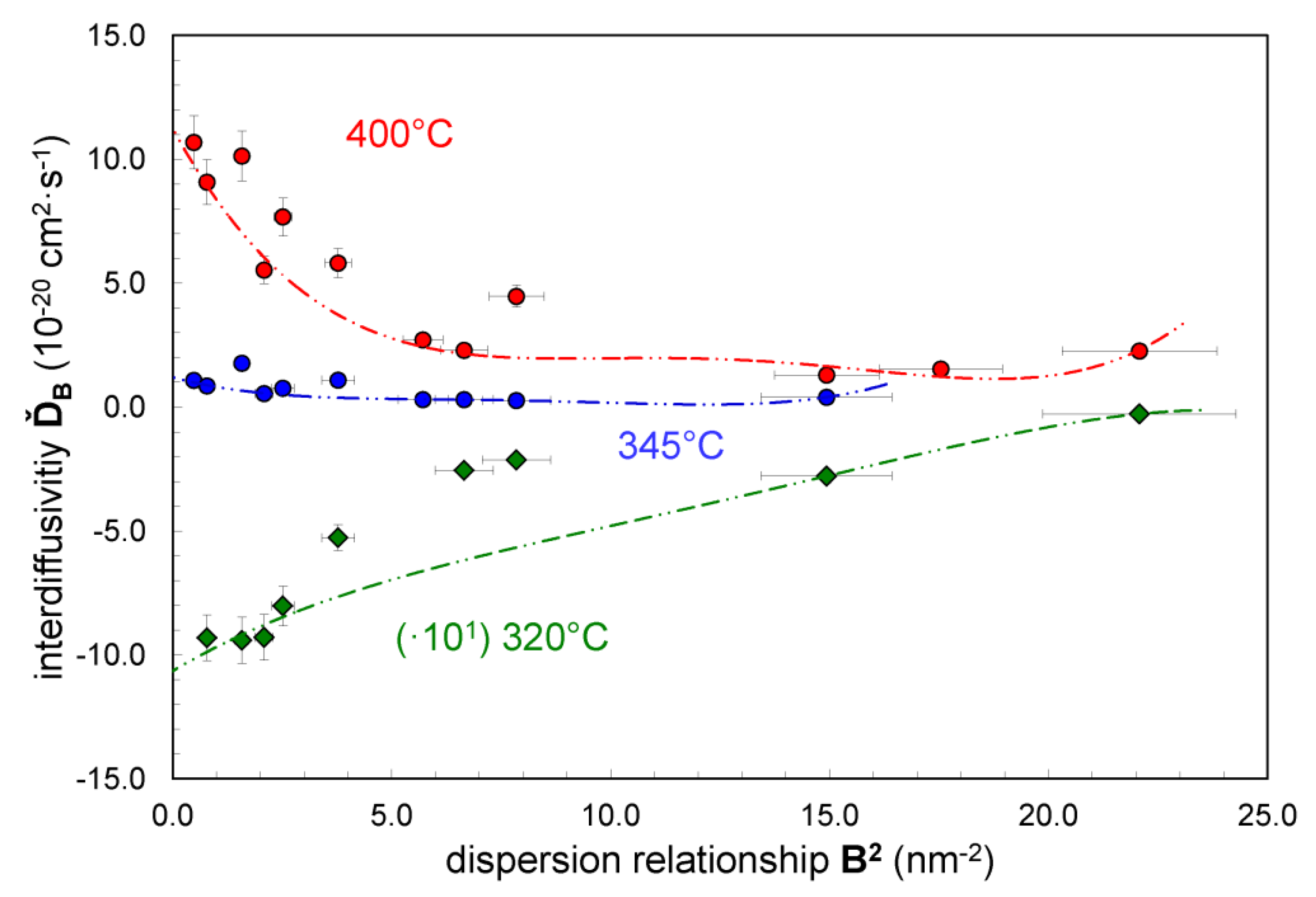
The corresponding Ď_B-values that correspond to the measured R-values are computed using Equation (2) and are plotted in Figure 4. The baseline Ď_B behavior for growth or decay is computed as a function of B² using the k'_μ coefficients. The K'_μ coefficients are determined by using a fourth-order expansion of Equation (6) to fit the baseline Ď_B-values. This is the minimum order needed to meet the sign criteria for the modeled K'_μ values as described in the Current Approach Section 4.2. From this data fit that prescribes conversion of k'_μ into K'_μ coefficients, the remaining unknown, i.e., the intercept value for Ď, is uniquely determined. The corresponding K_μ values of Equation (4) are listed in Table 1, where it has been noted previously that K'_μ equals 2K_μ/fʺ. The mobility M values at each temperature are listed in Table 1 as computed using Equation (5). In general, the mobility M will decrease with a decreasing value of the Ď/fʺ ratio.

Figure 4. The interdiffusivity Ď_B (cm²·s⁻¹) variation with the square of the dispersion relation wavenumber B² (nm⁻²) as computed from the amplification factor R for Cu/Ni(Fe) nanolaminate samples annealed at 320 °C (diamond) as scaled by a factor of 10, at 345 °C (squares), and 400 °C (circles).

Figure 4. The interdiffusivity Ď_B (cm²·s⁻¹) variation with the square of the dispersion relation wavenumber B² (nm⁻²) as computed from the amplification factor R for Cu/Ni(Fe) nanolaminate samples annealed at 320 °C (diamond) as scaled by a factor of 10, at 345 °C (squares), and 400 °C (circles).

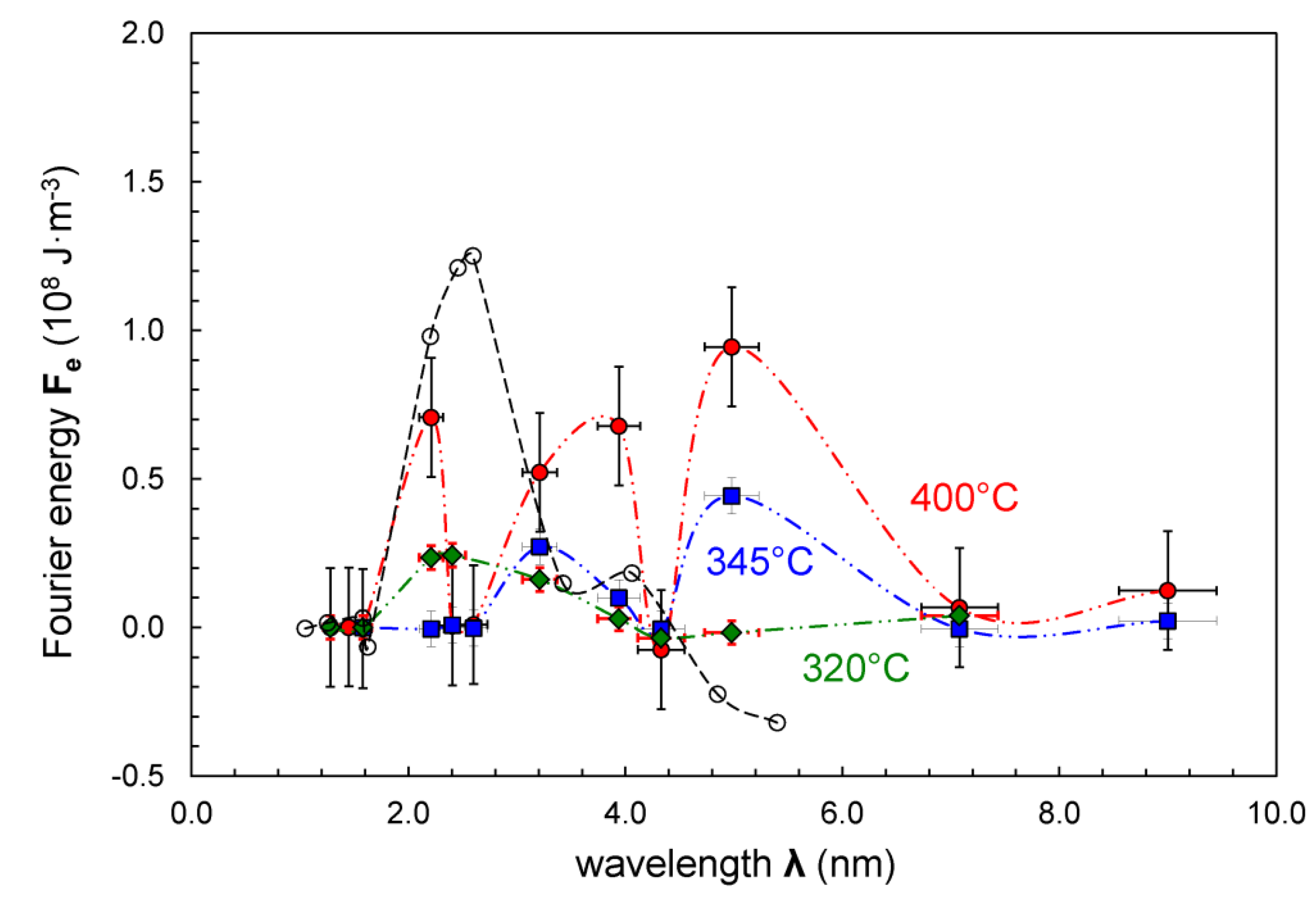
The strain energy component, that primarily constitutes [21] the Fourier energy F_e, is computed using Equation (12). The energy variation with composition wavelength is plotted in Figure 5. It is clear that a strain energy contribution provides a significant effect in some nanolaminates by enhancing the decay of the composition fluctuation outside the spinodal and hindering its decay within the spinodal as seen in the results of Figure 3 and Figure 4. The peak (strain) energy computed for the Cu/Ni(Fe) nanolaminates has a value of 0.94 × 10⁸ J·m⁻³. The magnitude for this energetic component as seen in Figure 5 is comparable to the values of the Helmholtz free-energy term fʺ that are listed in Table 1. In comparison, a smaller 2η²·Y value of 0.43 × 10⁸ J·m⁻³ can be computed for Cu/Ni(Fe) using a rule-of-mixtures formulation with a biaxial modulus Y of 200 GPa and a 2η² strain term of 2.14 × 10⁻⁴ assuming a 1.03% interface misfit strain.

Figure 5. The Fourier energy F_e (10⁸ J·m⁻³) variation with composition wavelength λ (nm) as computed from the difference between experimental values and the modeled fit of the amplification factor R variation with the dispersion relation wavenumber B (nm⁻¹) for nanolaminate samples of: Cu/Ni(Fe) annealed at 320 °C (diamond), 345 °C (squares), and 400 °C (solid circles); as well as Cu/Ni annealed at 400 °C (open circles).

Figure 5. The Fourier energy F_e (10⁸ J·m⁻³) variation with composition wavelength λ (nm) as computed from the difference between experimental values and the modeled fit of the amplification factor R variation with the dispersion relation wavenumber B (nm⁻¹) for nanolaminate samples of: Cu/Ni(Fe) annealed at 320 °C (diamond), 345 °C (squares), and 400 °C (solid circles); as well as Cu/Ni annealed at 400 °C (open circles).

6. Analysis and Discussion

Single and multiple peaks in the interdiffusivity variation with wavenumber are reported [24,25,35] for the diffusion results of the Cu/Ni, Cu/Pd, Au/Cu, and Ag/Pd nanolaminate systems. The multiple fluctuations observed in both the amplification of Figure 3 and the interdiffusivity of Figure 4 are a potential consequence of: a shift towards longer wavelengths that can occur with aging time; and that strain energy will still enhance (outside the spinodal) or hinder (within the spinodal) diffusion at the shorter wavelengths. As introduced in Section 4.2, some data points in Figure 3 and Figure 4 will vary from the simulated curves that are used to fit and establish the baseline behavior without the strain energy term. Consequently a variation in the Fourier energy F_e, is an anticipated result, i.e., the strain energy dependence on composition wavelength as plotted in Figure 5. It is seen here that the magnitude of F_e measured for the Cu/Ni(Fe) nanolaminates decreases somewhat with reduced annealing temperature. In addition, computations of F_e for the Cu-Ni nanolaminate system from interdiffusion data reported at 400 °C [25] are plotted (with open circles) in Figure 5 using the present model approach for determining the gradient energy and diffusion coefficients as listed in Table 1. The Cu/Ni data shows a bimodal distribution with a peak value of 1.25·10⁸ J·m⁻³ at a composition wavelength of 2.6 nm. The strain energy effects will be lost for very-long composition wavelengths where strained-layer superlattice growth is difficult due to the introduction of threading dislocations, and for very short (<1 nm) wavelengths where there is elastic homogenization from interface mixing. Therefore, strain energy will vary with the composition wavelength from ~1 to 9 nm. Periodic or irregular variations in strain energy may result, as well, for nanolaminate structures that do not have a commensurate structure. A variety of X-ray techniques and analysis methods [36,37,38,39,40,41] are available to assess strain distributions through surface regions and strained-layer superlattices. However, a detailed assessment for profiling of elastic strains and the variation through the interface is beyond the scope of this present analysis.

The Arrhenius plot of Ď versus T⁻¹ in Figure 6 is used to compare the |Ď| values of the Cu_0.53/Ni_0.40Fe_0.07 nanolaminates to the bulk diffusion measurements of Cu_0.877Ni_0.107Fe_0.016 [42] and Cu_0.5Ni_(0.5−x)Fe_x where 0.02 < x < 0.08 [43,44] alloys. An activation energy Q of 51 ± 2 kcal/mol (215 ± 6 kJ/mol; 1.34 ± 0.06 eV/atom) is determined from the slope of a linear fit to the Cu_0.877Ni_0.107Fe_0.016 data. This linear fit provides an upper bound to the bulk measurements, and is consistent with the new |Ď| values for the nanolaminates as computed from Equations (6), (10) and (11). It has been postulated [21] that an asymptotic discontinuity is possible at the spinodal temperature, where the magnitude of the diffusion coefficient |Ď| vanishes since the composition fluctuation neither grows nor decays at T_c. Curvilinear (dashed) lines are constructed in Figure 6 where the diffusion values drop below the upper bound linear curve. A local depression in |Ď| is seen near a 10³/T value of ~1.6 which corresponds with a spinodal temperature of ~350 °C. This value for the spinodal temperature is close to the 335 °C assumed in the computation of fʺ using Equation (9), which is similar to the 333 °C result from a thermodynamic evaluation [45] of the Cu-Ni alloy system using the CALPHAD approach. In an assessment of the collective interdiffusion in both Fe- and Si-based nanolaminate structures [46], it has been proposed that a collective atomic jumping mechanism that governs interdiffusion involves at least 8–15 atoms.

Figure 6. The Arrhenius-type relationship is plotted for the log₁₀-scale variation of diffusion Ď (cm²·s⁻¹) with inverse temperature 10³·T⁻¹ (K⁻¹) for the Cu/Ni(Fe) nanolaminates (open circles) along with experimental data for Cu_0.877Ni_0.107Fe_0.016 (solid diamonds) [33] and Cu_0.5Ni_0.5−xFe_x (solid squares) [34,35].

Figure 6. The Arrhenius-type relationship is plotted for the log₁₀-scale variation of diffusion Ď (cm²·s⁻¹) with inverse temperature 10³·T⁻¹ (K⁻¹) for the Cu/Ni(Fe) nanolaminates (open circles) along with experimental data for Cu_0.877Ni_0.107Fe_0.016 (solid diamonds) [33] and Cu_0.5Ni_0.5−xFe_x (solid squares) [34,35].

7. Conclusions

The static concentration wave approach to diffusion is used to model the diffusivity behavior for the spinodal decomposition of Cu/Ni(Fe) nanolaminates. In a comparison of results for aging at 320, 345 and 400 °C, growth of the composition fluctuation is seen within the spinodal at temperatures below ~335 °C. A potential asymptote in an Arrhenius plot of the diffusion coefficients Ď (as modeled for the long-wavelength approximation) is consistent with drop off in diffusivity that would occur near the chemical spinodal temperature of ~335 °C. The gradient energy coefficient is expanded as a fourth-order polynomial function of the wavenumber for the composition fluctuation. A fitting procedure that starts with the variation of the amplification factor takes advantage of the boundary condition where growth or decay vanishes at infinite wavelength. The sign of the gradient-energy coefficient K_μ alternates with increasing μ-order, starting with a 1st-order coefficient that has: a negative value outside the chemical spinodal, and; a positive value within the spinodal in accordance with the Cahn-Hilliard theory for spinodal decomposition. The magnitude of the gradient-energy coefficients decrease with: the increasing μ-order of the interaction and; decreasing temperature. A maximum magnitude of 4.49 × 10⁻²⁰ J·nm⁻¹ for K₁ is found at 400 °C and a minimum magnitude of 0.03 × 10⁻²³ J·nm⁵ for K₄. Fluctuation in the strain energy 2η²·Y term is seen for nanolaminate structures with composition wavelengths λ less than 7 nm, where a peak value of 0.94 × 10⁸ J·m⁻³ is found from analysis of diffusion data at an aging temperature of 400 °C. A decrease in the strain energy for Cu/Ni(Fe) is found outside the 2–5 nm range of composition wavelengths—As is consistent with a typical loss in strained-layer superlattice growth for metallic nanolaminates as often attributed to intermixing at interfaces and the introduction of threading dislocations.