Thermal Analysis and Thermal–Mechanical Stress Simulation of Polycrystalline Diamond Compact Bits During Rock Breaking Process

Abstract

Polycrystalline diamond compact (PDC) bits are widely used in oil, gas, and geological exploration. During rock breaking, most of the work is converted into cutting heat, leading to a rise in cutter temperature and potential damage. However, the influence of formation temperature and rock properties on cutting temperature and thermal stress remains insufficiently understood. This study combined numerical simulation and experimental methods to investigate the temperature rise and thermal stress of a single PDC cutter during rock breaking, focusing on the effects of formation temperature (27–250 °C) and rock strength (sandstone, marble, and granite). The results show that the temperature rise of the PDC cutter adheres to the following three distinct stages: rapid increase, slow increase, and stabilization. Rock strength significantly affects the temperature rise rate and stress; when breaking granite, the cutter temperature reached approximately 131.4 °C, about 2–3 times higher than for marble and sandstone, while the rate of penetration (ROP) decreased by 70.6–75.6%. As formation temperature increased from 27 °C to 250 °C, the internal temperature difference within the cutter decreased from 72.6 °C to 35.6 °C, and the equivalent stress first increased and then decreased, peaking at 2.84 GPa at 50 °C. The ROP initially increased and then decreased with an increase in formation temperature. Numerical simulations and experimental findings are in good agreement. This study provides theoretical and technical guidance for optimizing cutter design and improving the rock-breaking efficiency and service life of PDC bits in deep and high-temperature formations.

1. Introduction

With the continuous exploitation of nonrenewable resources such as oil, natural gas, and coal, shallow resources have become increasingly scarce. Researchers have gradually shifted the target of energy exploration and development from conventional formations to deep and ultra-deep wells [1,2]. Polycrystalline diamond compact (PDC) bits are widely used in resource exploration and development owing to their good wear resistance and self-sharpness [3,4,5]. PDC bits are typically composed of a steel or matrix body on which multiple cutters are mounted. Each cutter consists of a polycrystalline diamond layer sintered onto a tungsten carbide substrate. The cutters are usually circular or slightly chamfered in shape, with typical diameters ranging from 13 mm to 19 mm. They are installed on the bit face in a patterned layout (e.g., spiral, blade, or roller-cone arrangements) and are rigidly fixed into pockets via brazing or mechanical pressing. This assembly allows the cutters to effectively engage and break rock under combined axial and rotational loads. According to statistics, PDC bits play an important role in society, and their share in the bit market has increased from 2% of the total footage of oil and gas wells in 1982 to 90% in 2019 [6,7,8]. However, with an increase in drilling depth in deep reservoirs, rocks that are poorly drillable, hard, and more abrasive are inevitably encountered during the drilling process, which intensifies the wear of the drill bit and leads to a lower ROP, reduced rock fragmentation efficiency, and increased drilling costs [9,10,11].

The main forms of failure of PDC cutters are tooth fracture, wear, and shedding; wear is the main cause of PDC cutter failure [12,13], accounting for approximately 50% of PDC cutter failures [14]. Most of the energy consumed by the PDC bits during rock breaking is converted into cutting heat, causing the temperature of the cutter to increase sharply. High temperatures (typically above 300–800 °C) cause changes in the physical and mechanical properties of the PDC cutter, thereby affecting the cutting process. Thermal damage and wear are the most common and important forms of failure in PDC cutter wear. When the cutters are excessively worn, not only will the ROP be reduced, but severe vibrations will also occur, which will seriously affect the service life of the downhole drilling tools. Therefore, it is important to study the temperature and stress changes and heat generation mechanism of the PDC cutter during the rock-breaking process. This will help to understand the wear mechanism of the PDC cutter and improve the rock-breaking performance of the PDC bits.

Because the PDC bit–rock interaction can be regarded as the sum of all the cutter–rock interactions on the bit, it is common practice to study the cutting behavior of a single PDC cutter [15], which typically includes measurable quantities such as cutting forces (normal and tangential), cutter temperature, wear volume, rate of penetration, and specific energy. Although scholars at home and abroad have conducted extensive research on the breaking mechanism of rock [16,17], relatively few studies have been conducted on the heat generation and temperature increase laws of PDC bits in rock drilling, particularly regarding how temperature evolves with drilling time, depth, and operational parameters. Glowka et al. [18,19,20] established a finite-element model for a single PDC cutter (13.44 mm diameter) to predict the average cutting temperature of a wear plane under steady-state and transient downhole conditions. Their simulated temperatures ranged from 200 °C to over 700 °C depending on the wear flat size and cutting conditions. The results showed that there was a correlation between the wear plane temperature and bit wear rate. Appl et al. [12] experimentally measured the temperature and wear rate of a 13.44 mm PDC cutter when cutting granite at a cutting speed of 2 m/s. They reported that the average wear plane temperature remained nearly constant at approximately 350 ± 20 °C under steady-state conditions, while the wear rate varied with changes in the normal load and rock properties. Che et al. [21] introduced the theory of heat generation in metal cutting, which assumes that nearly all plastic work during cutting is converted into heat. The model relates heat generation to cutting forces, speed, and material properties, and it was adapted to analyze the temperature rise in PDC cutters during rock breaking. Key variables include shear plane energy, friction work, and partition coefficients for heat flow into the cutter and rock. Beste et al. [22] concluded that there is considerable uncertainty in predicting the exact temperature of the bit during drilling due to variations in the contact conditions, cooling effects, and heterogeneous rock properties. Their experimental measurements indicated that the average cutter temperature could range between 300 and 500 °C under typical drilling conditions. Shao et al. [23] studied the contact surface temperature between the cutter and rock when cutting sandstone, and they found that the temperature of the cutter showed a positive correlation with the cutting depth and cutting speed. This is because larger cutting depths and higher speeds increase the volume of rock deformed per unit time and the frictional work at the cutter–rock interface, leading to greater heat generation and higher temperatures. Kim et al. [24] studied the influence of tooth shape on the temperature of a cutter and found that the effect on temperature was more evident when the contact area between the cutter and rocks was larger. This occurs because a larger contact area increases frictional resistance and reduces heat dissipation per unit area, resulting in higher interface temperatures. Liu et al. [25] investigated the thermal stability of PDC bits and developed a new three-layer structure for PDC bits that can withstand high temperatures of 820 °C. Zhang et al. [26] established a full-size PDC bit model using the finite element method to study the temperature and stress fields during the rock crushing process. Their simulation and experiments showed that the maximum cutter temperature reached 250 °C under typical drilling conditions. The study verified the accuracy of the finite element approach through laboratory measurements.

Most aforementioned studies focused on the effects of cutting speed, cutting depth, and cutter structure on the temperature of the cutter. However, the influence of formation temperature and rock strength on the temperature of the cutter is not yet clear, and the thermal stresses generated during the process of rock breaking by the PDC cutter have not been reported. Therefore, to understand the temperature and thermal stress field distribution rules of the PDC cutter during the rock-breaking process, this study aims to (1) investigate the influence of formation temperature (varied from 27 °C to 250 °C) and rock strength (represented by sandstone, marble, and granite) on the cutting temperature, temperature distribution, and thermal stress field of a single PDC cutter; and (2) analyze the evolution of the stress profile (e.g., equivalent von Mises stress) and rate of penetration (ROP) under these conditions. Using finite element simulation (Abaqus 2021) coupled with experimental validation, we focus on measurable outcomes, including the maximum/minimum cutter temperature, temperature gradient, stress magnitude at the crown and diamond–matrix interface, and ROP. This work addresses the identified gap by quantifying the thermo-mechanical response of PDC cutters to downhole temperature and formation strength, providing a basis for bit design in deep, high-temperature formations.

2. Rock Mechanics Parameters

Obtaining the physical and thermodynamic parameters (such as compressive strength and thermal conductivity) of granite under different temperature conditions forms the basis for studying the effect of formation temperature on rock breaking using a PDC cutter. These parameters were used in the nonlinear dynamic numerical simulation of the PDC cutter rock in Section 3 to provide theoretical support for the simulation to be close to the real situation.

A flowchart of the test is shown in Figure 1. First, the granite cores were drilled using an XY-1 drilling rig. Second, granite samples with a height-to-diameter ratio of 2:1, specifications of Φ50 mm × 100 mm, and parallelism of upper and lower end faces < 5‰ were prepared according to the international rock mechanics standard. Then, 12 granite samples with relatively good quality and homogeneous lithology were selected and placed in a drying oven and processed to 25, 50, 100, 150, 200, and 250 °C, respectively, according to an order of numbering from A–F. To ensure that the temperatures inside and outside the granite were consistent, the heating time was set to 2 h and the insulation was kept warm for 2 h. Subsequently, the heated granite was placed on a thermal conductivity tester to measure the thermal conductivities of the rock samples. Finally, the granite samples were placed in a universal testing machine to conduct uniaxial compression tests at a loading speed of 0.1 mm/s.

It can be observed from

Table 1. Physical and thermodynamic parameters for finite element analysis.

Temperature (°C)	Density (kg/m3)	Elastic Modulus (GPa)	Poisson’s Ratio	Compressive Strength (MPa)	Thermal Conductivity W/(m·°C)
27	2720	40	0.25	134.771	3.15
50	2680	38.6	0.23	140.13	3.04
100	2650	19.38	0.22	139.09	2.82
150	2670	13.76	0.20	128.275	2.64
200	2687	11.23	0.16	102.42	2.50
250	2650	10.51	0.15	75.15	2.38

that the average thermal conductivity of granite is 3.15 W/(m·°C) at room temperature, and after the rock samples were treated with high temperature at 250 °C, its average thermal conductivity decreased to 2.38 W/(m·°C), with a reduction of 24%. Overall, the thermal conductivity of the granite decreased with an increase in temperature. Seipold et al. [27] concluded that temperature is the most important factor affecting the thermal conductivity of dense rocks, such as granite.

As shown in Figure 2, the uniaxial compressive strength of granite was most affected by the heating temperature. Generally, with an increase in temperature, the uniaxial compressive strength of the heat-treated rock first increases and then decreases. When the heating temperature of the rock was 27 °C, the compressive strength of the granite sample was 134.771 MPa, and when the heating temperature was increased to 250 °C, the compressive strength was 75.145 MPa. When the heat treatment temperature is within the range of 27–50 °C, the compressive strength of the rock increases. This is because the mineral particles inside the granite sample expand due to the increase in heating temperature causing the original cracks to close, resulting in a decrease in porosity and an increase in rock strength. When the heating temperature is within the range of 100–250 °C, the compressive strength of the rock decreases. This is because the uneven expansion of mineral particles in the rock sample with increasing temperature causes the original microcracks to expand and develop, resulting in a decrease in rock strength. The fitting relationship between the uniaxial compressive strength of the granite samples and temperature is as follows:

$$\overline{\sigma }=-0.00207{\mathrm{T}}^2+0.2946\mathrm{T}+129.5692$$

(1)

where σ is the uniaxial compressive strength (MPa) and T is the temperature (°C).

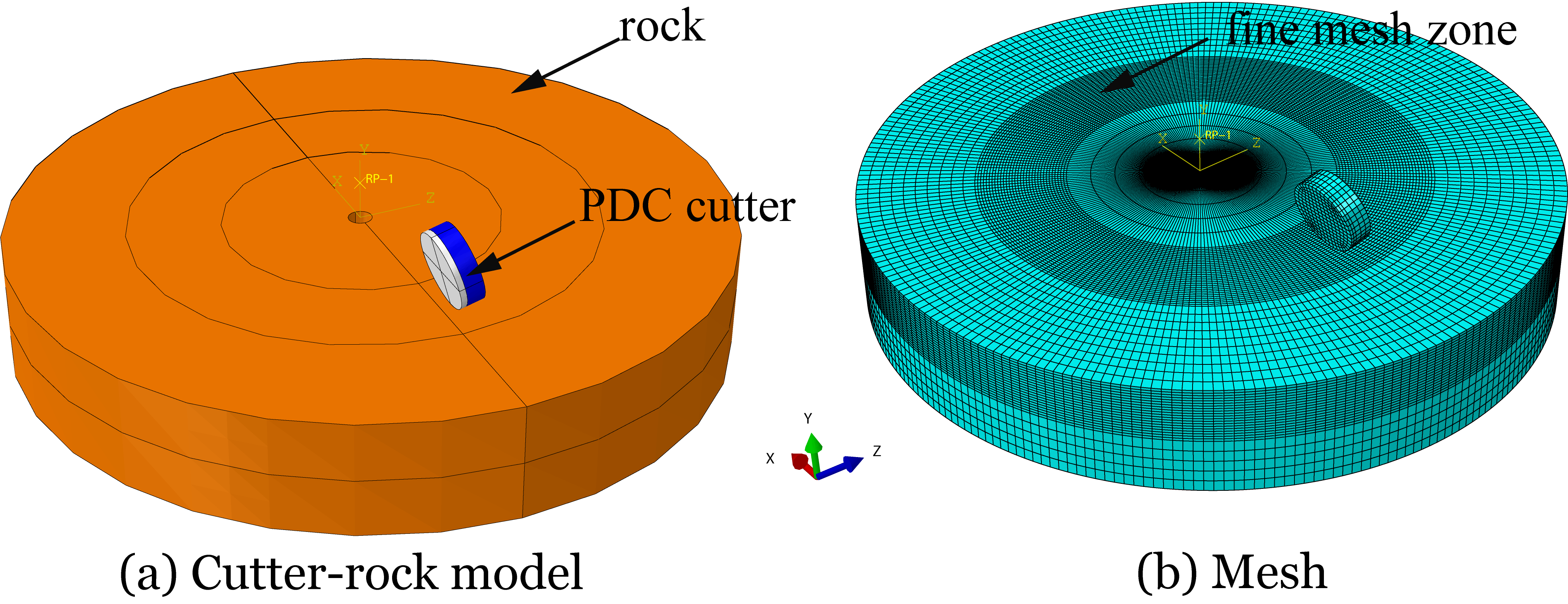
3. Finite Element Modeling of the Rock-Breaking Process

In the actual drilling process of PDC bits, the downhole working conditions are very complicated, and it is impossible to obtain temperature data accurately and in real time using measurement methods. In addition, it is difficult to experimentally observe and study thermal stress. Therefore, finite element simulations have become an important means of solving this problem.

3.1. Model Assumption

The cutter is the core unit of the bit, which is evenly distributed on the bit and mainly used to complete rock cutting. Therefore, the performance and life of the cutter often determine the cutting performance and life of the bit. To facilitate calculation and analysis, the following assumptions were made:

(1)

The PDC cutter and rock are homogeneous continuous media, and the effects of the pore medium were ignored.

(2)

Only vertical and rotary motions were considered in the rock-breaking process of the PDC cutter; lateral motions and oscillations were not considered without considering lateral and swinging movements.

(3)

The influence of the thermal convection and radiation between the bit, rock, and surrounding environmental medium were ignored.

3.2. Simulation Setup

A nonlinear dynamic model of the cutter rock was established, as shown in Figure 3. The diameter, thickness, rake angle, and rock sample size of the diamond layer were 13.44 mm, 8 mm, and 15°, and ø120mm ×30 mm , respectively. To improve computational efficiency, it is necessary to locally refine the mesh in the cutting area. The PDC cutter and rock samples were meshed with hexahedral solid elements, the eight-node trilinear displacement-temperature coupled reduced product (C3D8RT) was selected as the element type, and the number of rock sample model grids was 286,000 units. The numerical model adopted the international system of units (m-N-kg-s) and established a reference point (RP) to facilitate the application of displacement and rotational speed to the cutter. The PDC cutter, rock sample models, and divided meshes are shown in Figure 3.

3.3. Boundary and Load

In this section, the simulation is divided into two analysis steps as follows: (1) Step1: The cutter breaks the rock in the negative direction of the Y-axis. (2) Step 2: The cutter rotates around the Y-axis once. The boundary conditions were set in the load module, and the motion path of the cutter was first analyzed in Step 1 and moved linearly along the Y-axis. In Step 2 of the analysis, the speed is assigned, and the cutter rotates once around the Y-axis. For rock samples, it is necessary to completely restrict their movement; that is, the bottom and surrounding sides of the rock are completely fixed and constrained. The linear cutting speed of the cutter was set to 150 RPM and the initial formation temperature was 27 °C.

Rock is a nonlinear anisotropic material [28,29,30]; therefore, the widely adopted Drucker–Prager (D-P) criterion was employed for the rock constitutive model [31,32]. The material properties of the rock are listed in Table 1. The contact mode between the cutter and rock was general contact, and the friction coefficient between the rock sample and cutter was set to 0.3. The main parameters of the PDC cutter and rock used in the finite element analysis are listed in

Table 2. The main parameters of the PDC cutter and rock used in the finite element analysis.

Material	Density (kg/m3)	Elastic Modulus (GPa)	Poisson’s Ratio	Thermal Conductivity W/(m·°C)	Specific Heat J/(kg·°C)	Thermal Expansion Coefficient (×10−6 °C−1)
PCD	3510	897	0.07	543.0	790	2.5
WC-Co	15,000	579	0.22	100.0	230	5.2
Sandstone	2570	33.1	0.24	3.64	916.9	50
Marble	2750	42.2	0.21	3.50	800	4.6
Granite	2650	40	0.25	3.5	800	52.0

.

4. Simulation Results and Discussion

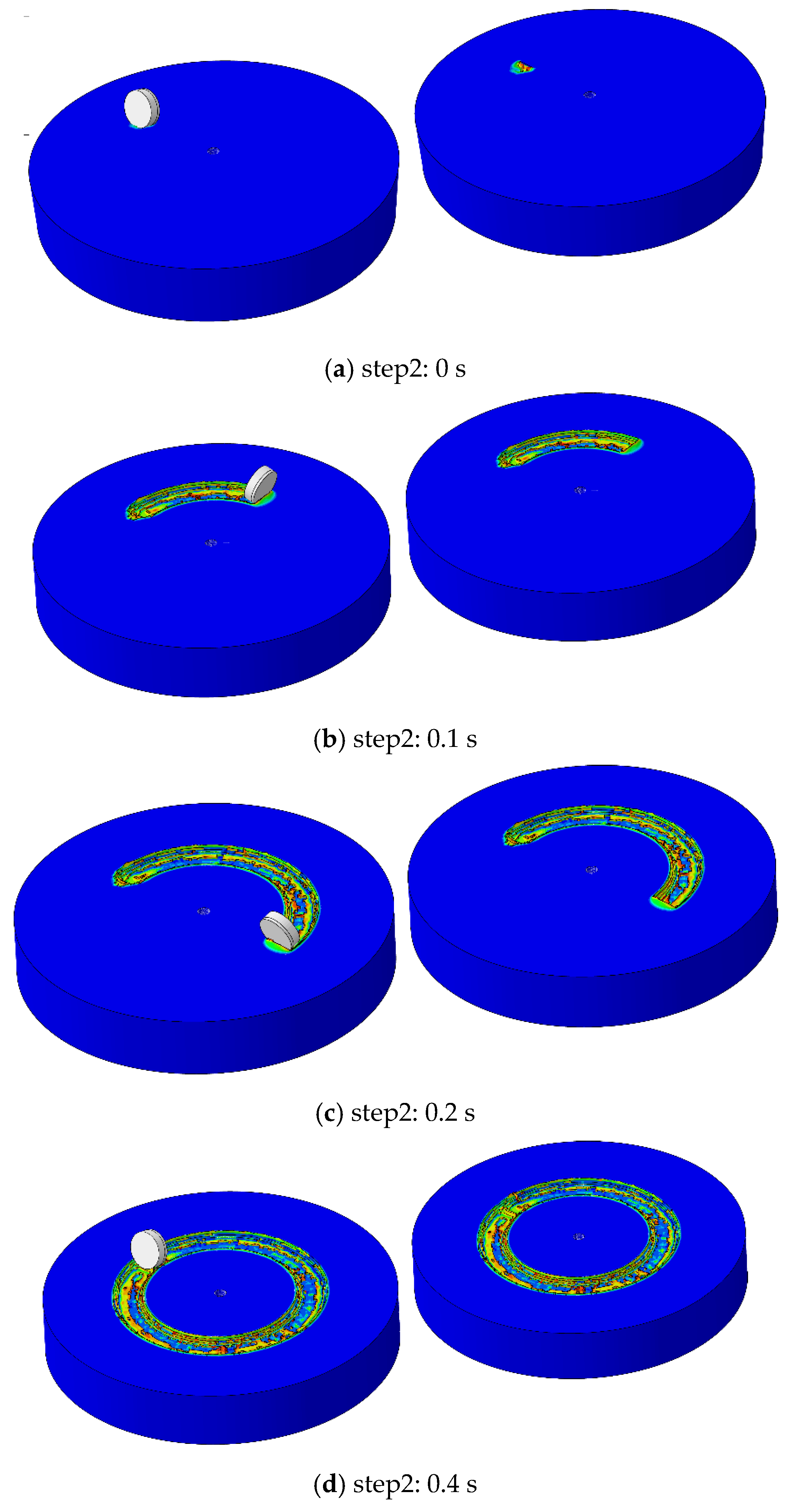
4.1. Analysis of Rock Breaking

As shown in Figure 4, in the second analysis step of the simulation, when the cutting time was 0 s, the top of the PDC cutter crown contacted the rock sample, causing damage to its surface and forming a stress concentration area on the rock, resulting in a crushing pit. When the damage strain of the rock exceeded its equivalent failure plastic strain, the rock unit was immediately destroyed and deleted and the crushing pit on the rock surface became larger at 0.2 s. With the progress of crushing, the volume of the crushing pit gradually increased, and at 0.4 s, the crushing pit formed a complete circular crushing pit.

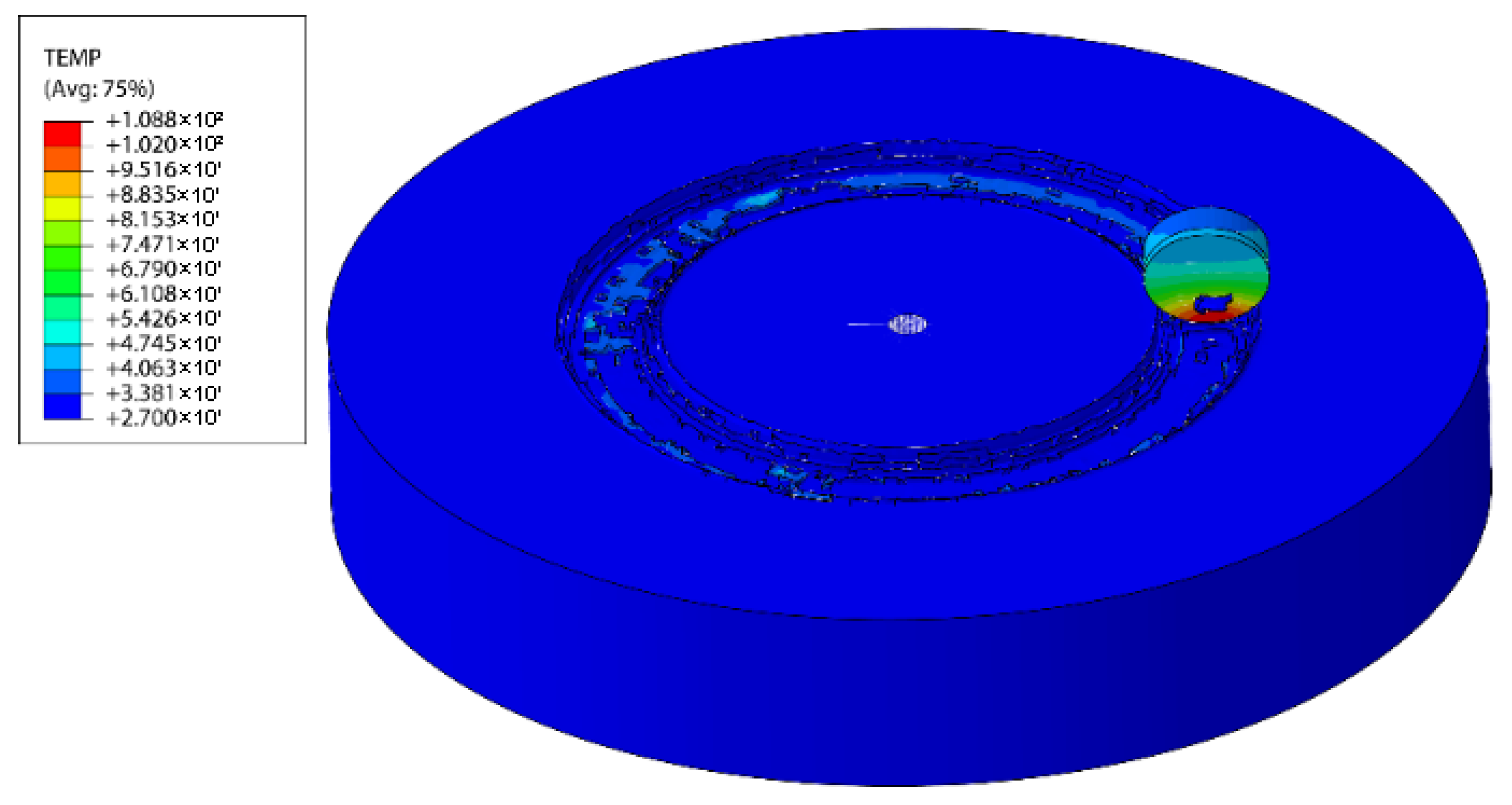
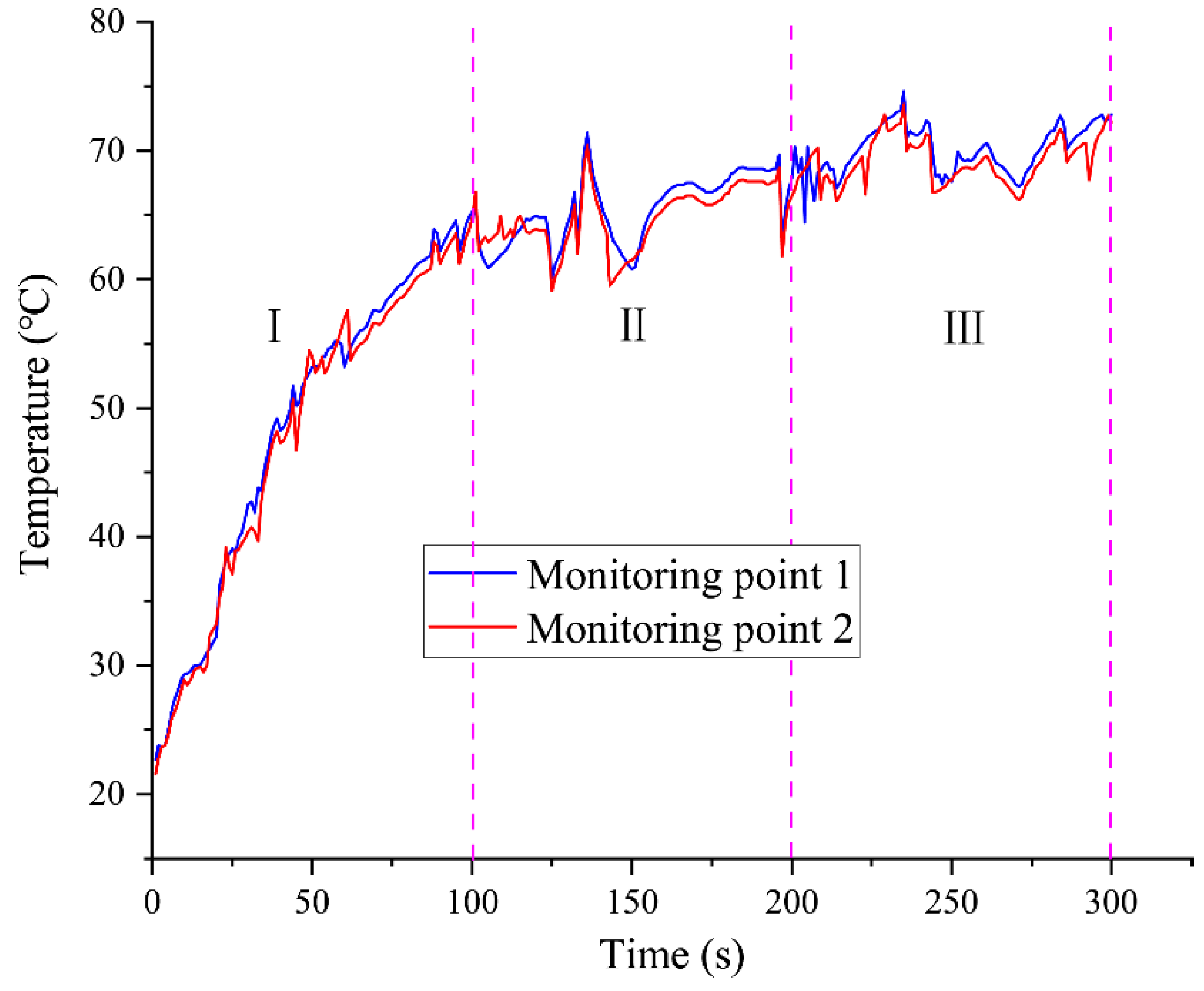
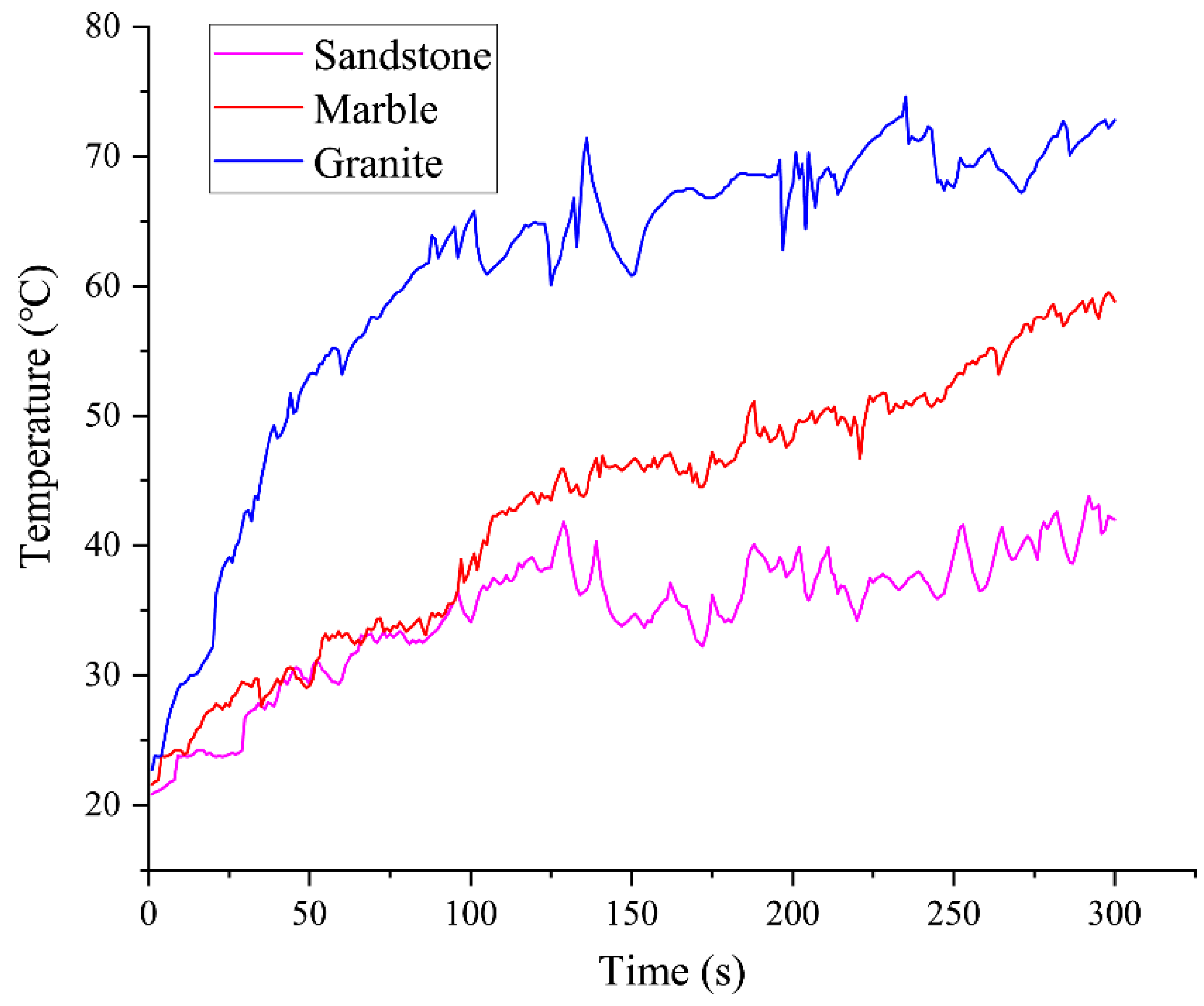
4.2. Temperature Field of the PDC Cutter

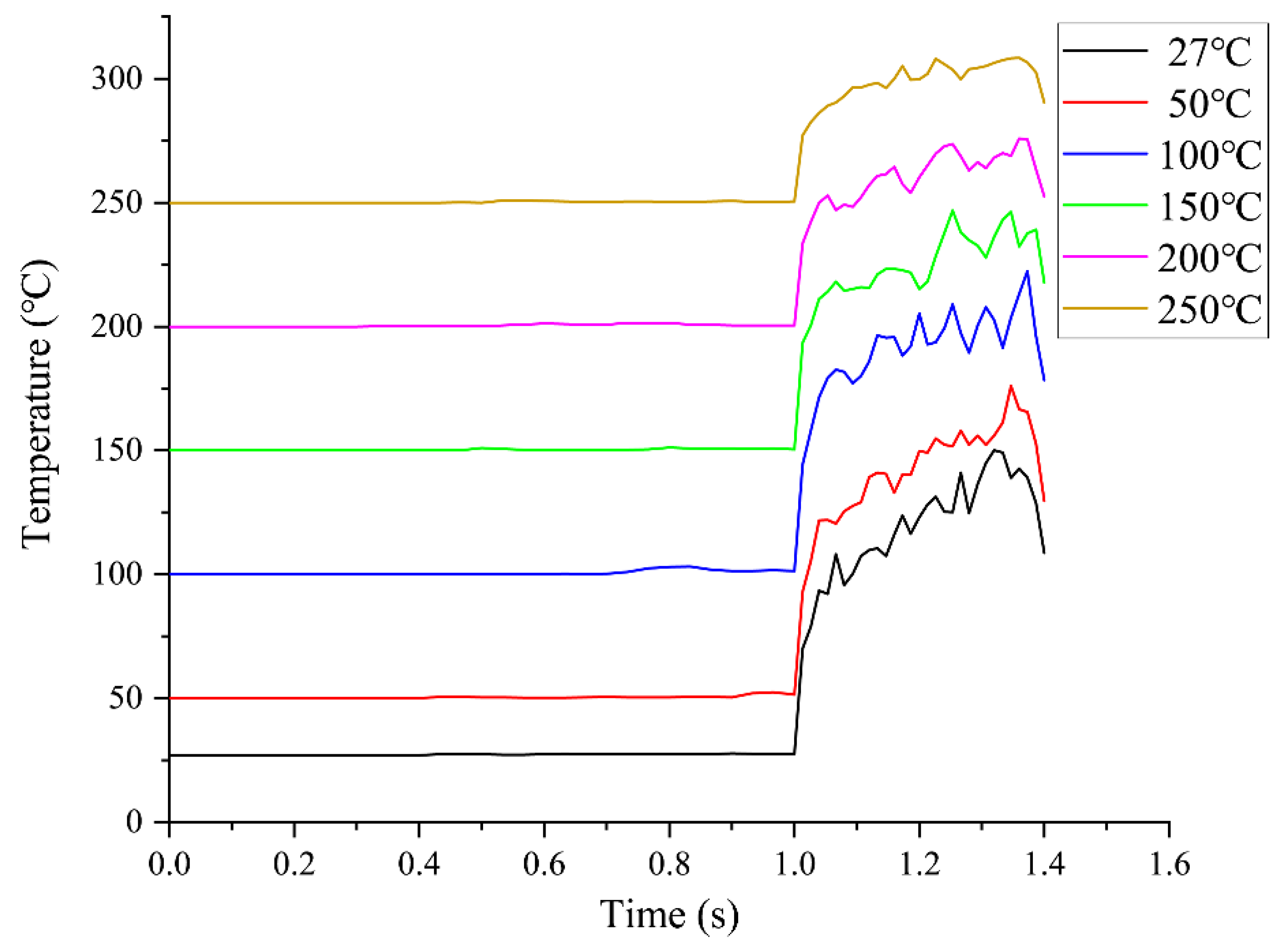
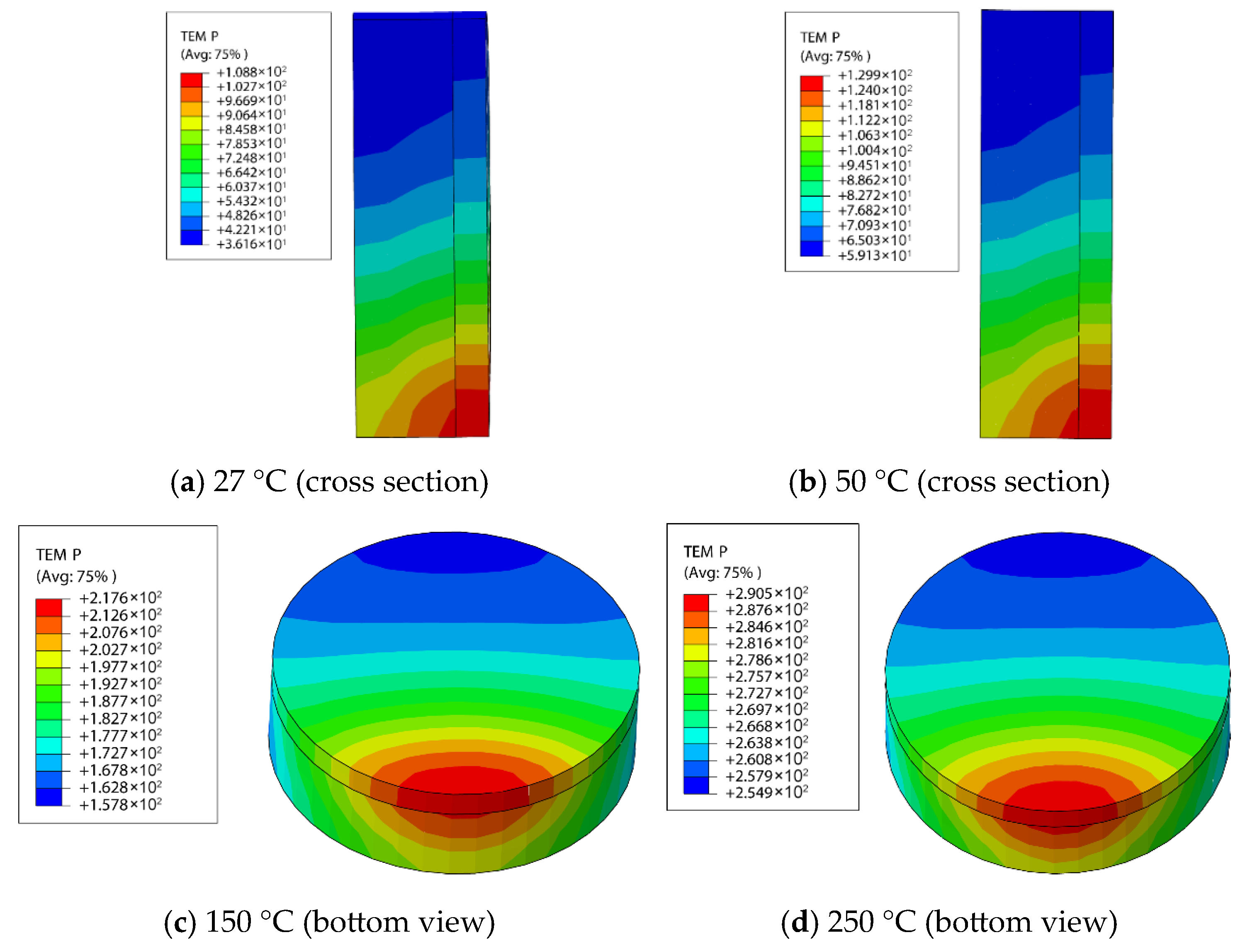
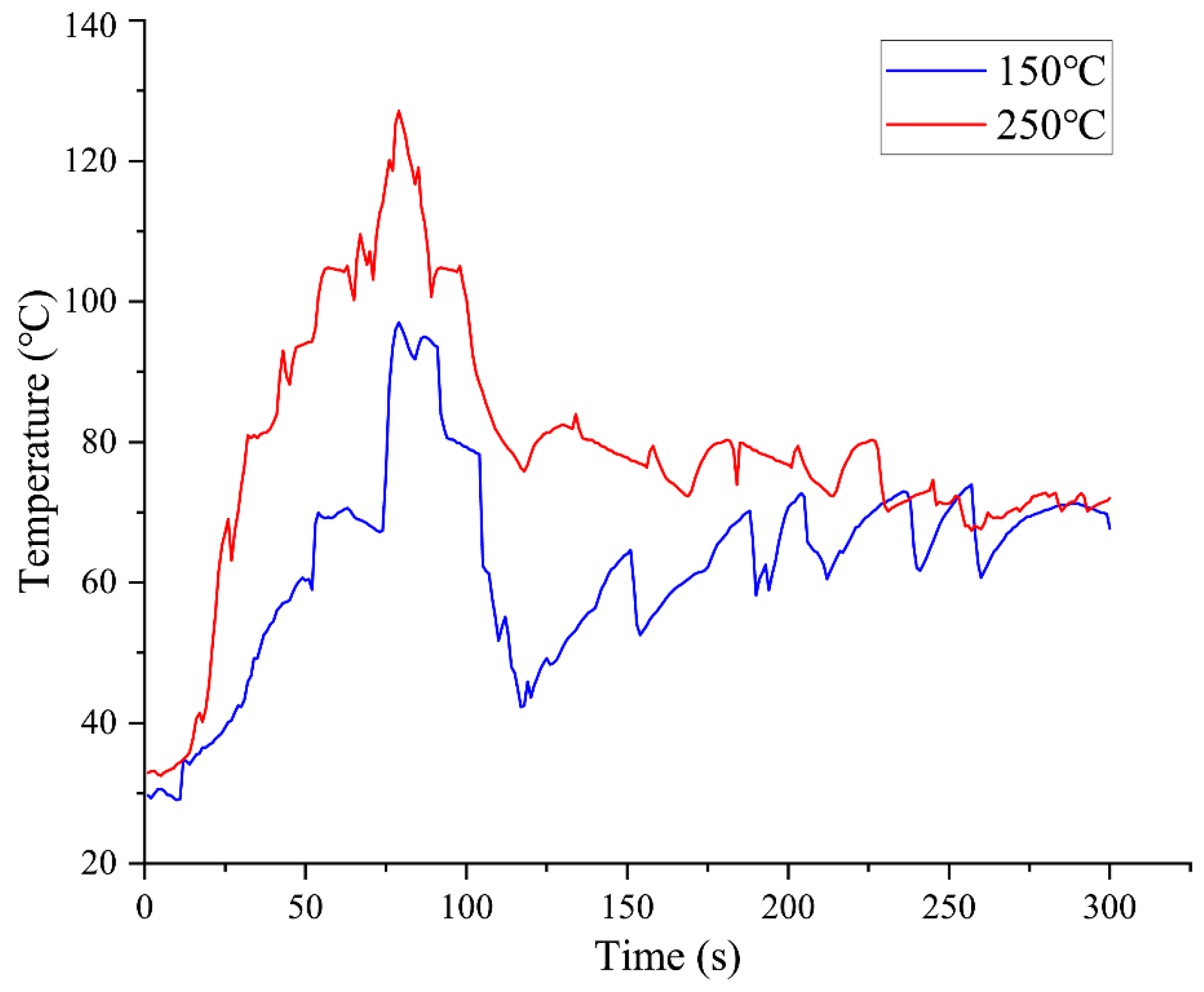
4.2.1. Effect of Formation Temperature

Figure 5 shows the temperature changes in the PDC cutter when crushing rocks at different formation temperatures. It can be observed that the temperature increase curves of the PDC cutter were approximately the same. At 0–1.0 s, the cutter penetrated 1.5 mm into the rock under the action of a vertical load. At this time, the cutter had a shallow penetration and did not produce intense friction with the rock; therefore, the temperature of the cutter remains unchanged from the initial temperature. The process during 1.0–1.4 s is rock breaking. It can be observed that the temperature rise of the PDC cutters can be divided into three stages as follows: a sharp rising period, slow rising period, and relatively stable period. The temperature of the cutter increases with an increase in the formation temperature because of the superposition of the cutting temperature produced by the friction between the cutter and the rock, and the formation temperature promotes the corresponding temperature rise in the cutter.

Figure 6 shows a nephogram of the temperature field distribution when breaking the rock using the PDC cutter. During the rock-breaking process of the PDC cutter, the high-temperature area on the surface of the cutter was primarily concentrated on the top of the crown of the cutter, which was distributed in a fan-shaped pattern. This is because of the intense friction between this part and the rock, which generates cutting heat. Heat is transferred inside the cutter by heat conduction; therefore, the temperature of the cutter gradually spreads from the contact area to the non-contact area with a gradient starting from the top of the crown, and the farther it was from the contact area, the lower the temperature was. A large temperature gradient distribution was generated inside the cutter.

Figure 7 shows the changes in the maximum and minimum temperatures of the PDC cutter and the temperature difference between them with respect to the formation temperature. When the formation temperature was 27 °C, the maximum and minimum temperatures of the cutter were 108.8 °C and 36.2 °C, respectively, and the temperature difference between the two was 72.6 °C. When the formation temperature was 250 °C, the maximum and minimum temperatures of the cutter were 290.5 °C and 254.9 °C, respectively, and the temperature difference was 35.6 °C. It can be observed that with an increase in the rock temperature, the internal temperature difference of the PDC cutter showed a decreasing trend.

4.2.2. Effect of Rock Strength

Figure 8 shows the temperature changes in the PDC cutter when breaking rocks with different strengths. The maximum temperatures of the PDC cutter when crushing sandstone, marble, and granite are 46.3, 75.2, and 131.4 °C, respectively. The temperature of the cutters when breaking granite under the same conditions was approximately two times that when breaking marble and three times that when breaking sandstone, and the influence of the rock strength on the temperature of the cutter was relatively large. This is because rock strength is an important factor affecting the cutting force; breaking rocks with high rock strength requires a large cutting force, and the increase in cutting force will lead to an increase in cutting heat production. It can also be observed that the temperature fluctuation of the cutter is relatively smooth when breaking sandstone, whereas the temperature fluctuation of the cutter is more severe when breaking granite. This is because there are differences in the failure mode of rocks with different strengths, and under the same cutting conditions, rocks in softer formations are plastically broken, whereas rocks in hard formations undergo brittle fracture. Furthermore, the fluctuation in the cutting force of the rocks in the softer formations was smaller, and the cutting force was the direct cause of the cutting heat and cutting temperature. Figure 9 shows a nephogram of the temperature field distribution of the granite broken by the PDC cutter.

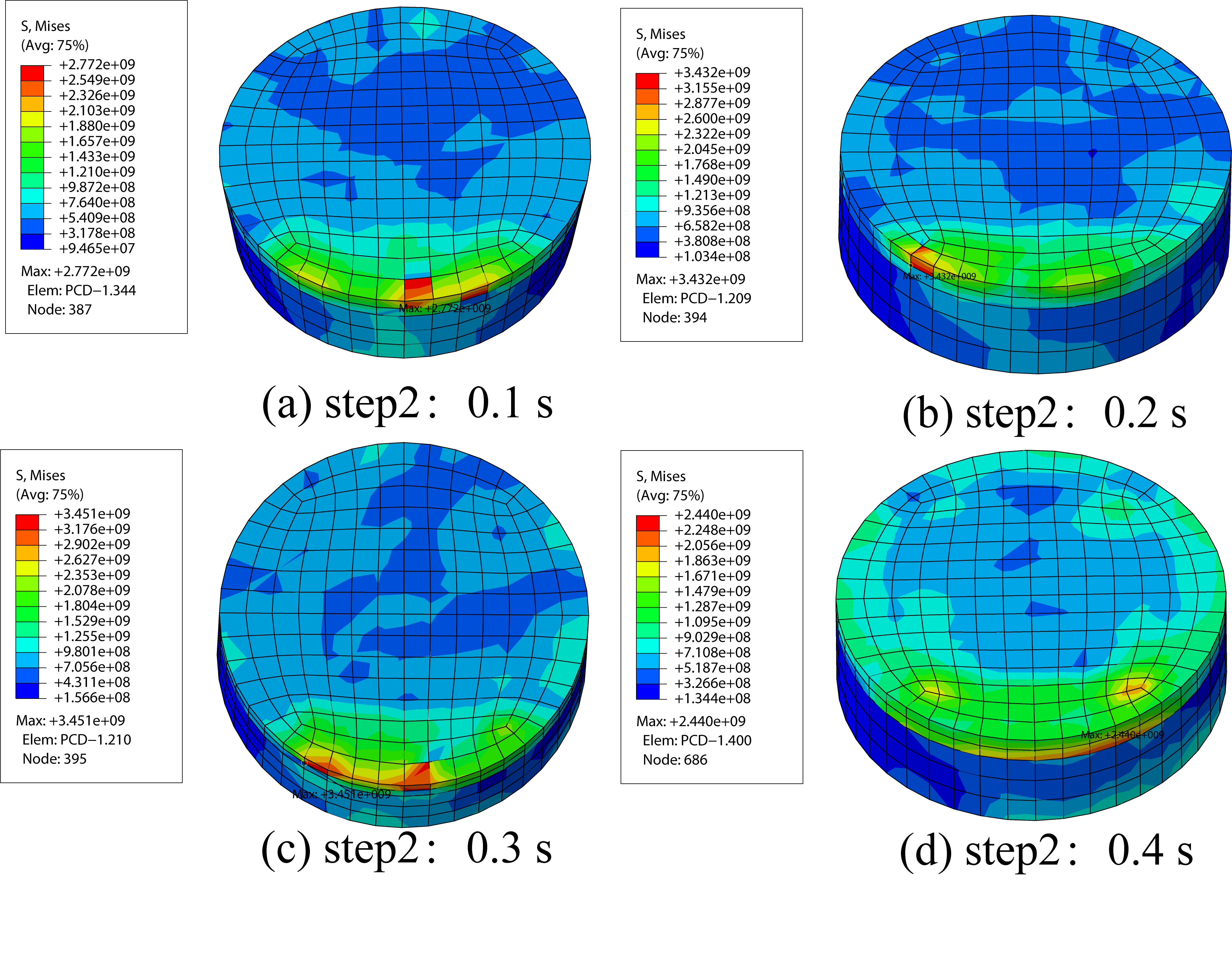
4.3. Thermal Stress Field of the PDC Cutter

The failure of the PDC cutter is mainly determined by the stress state inside the cutter, and the stress distribution on the surface of the PDC cutter can objectively reflect the stress situation of the cutter during rock breaking. Figure 10 shows the thermal stress contour of the PDC cutters. During the rock-breaking process, the stress on the PDC cutter is mainly concentrated near the crown of the cutter and at the junction surface between the diamond layer and tungsten carbide matrix. These areas are the main cutting parts of the PDC cutter for rock-breaking and play a decisive role in cutter damage.

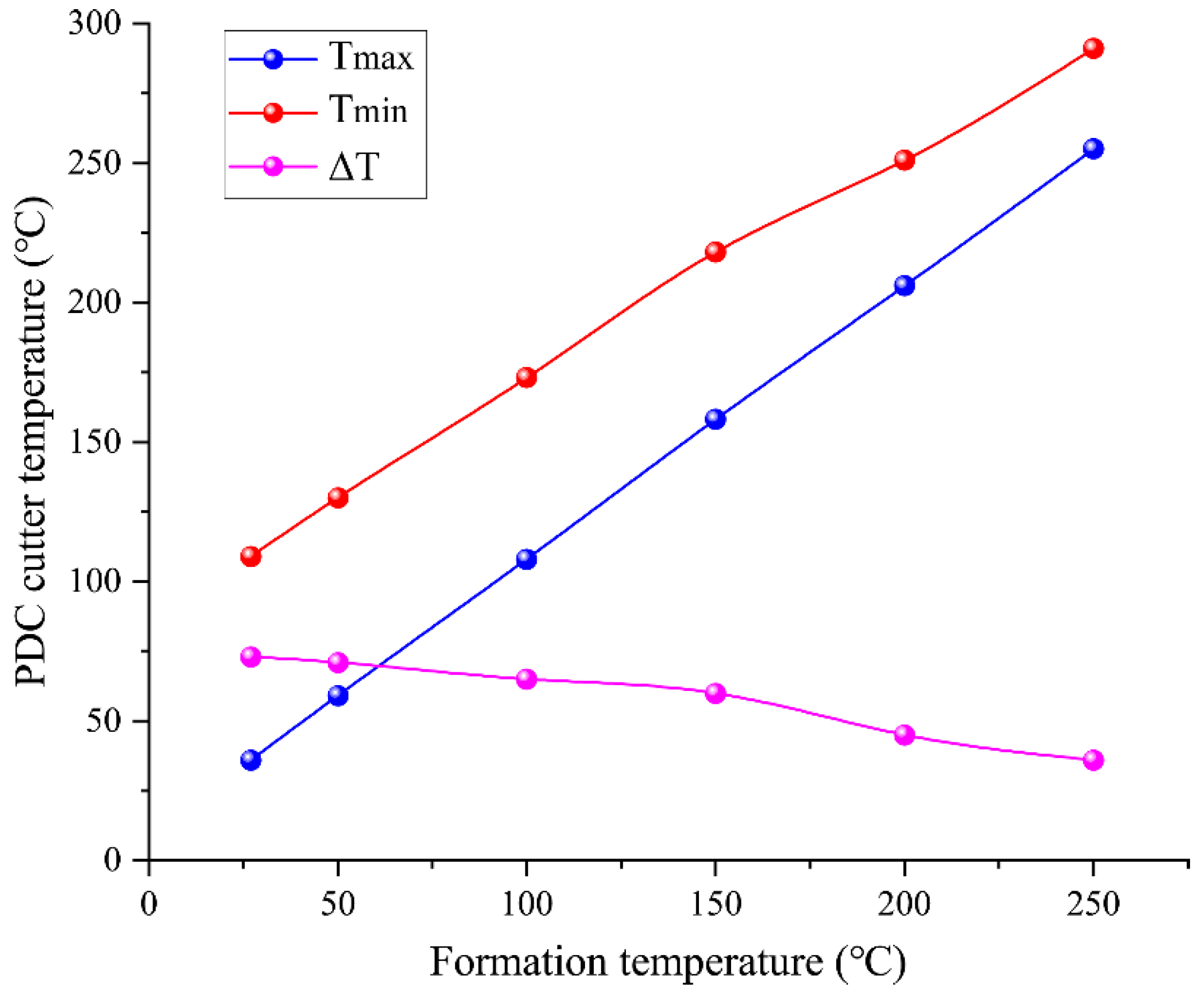
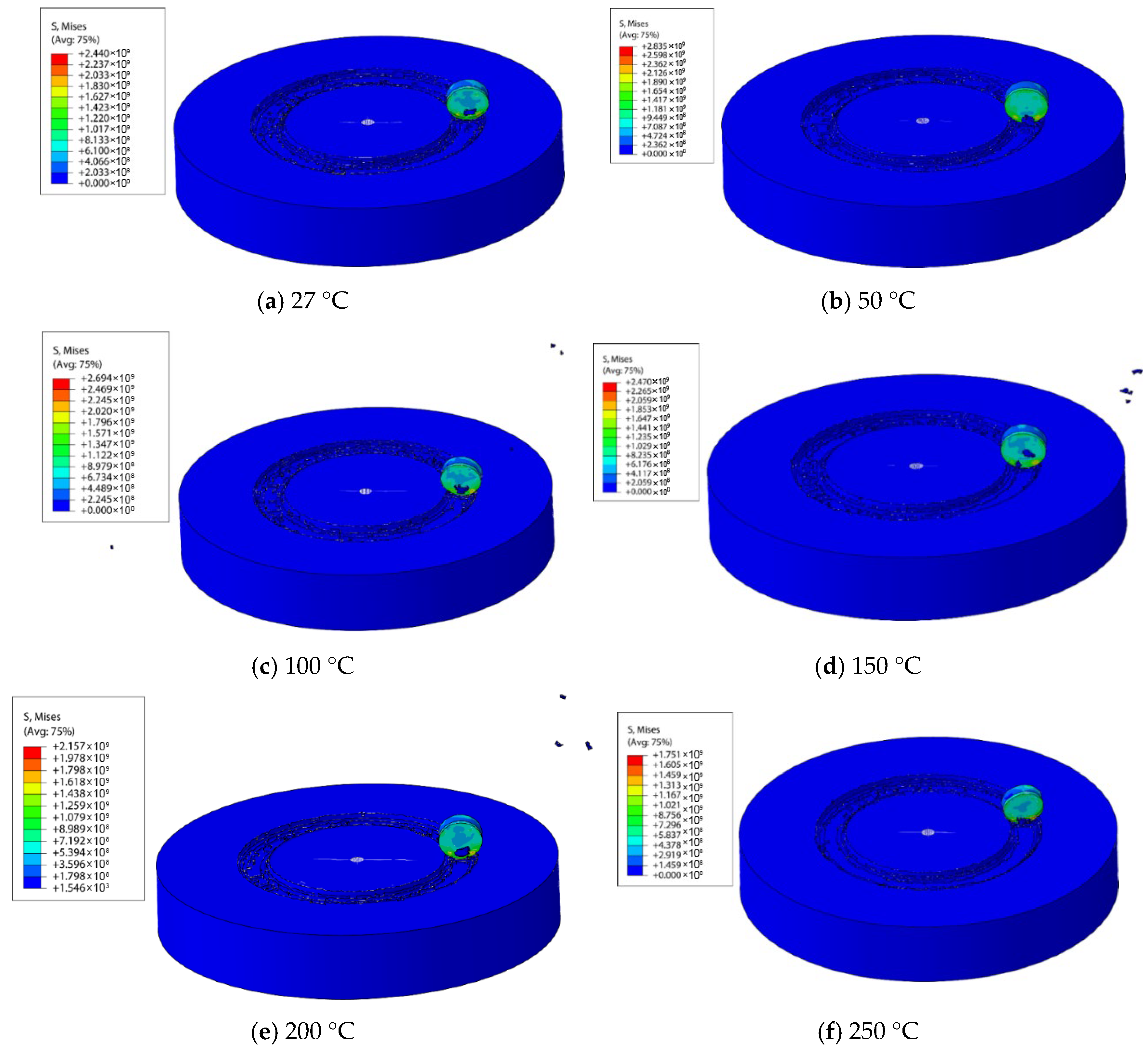
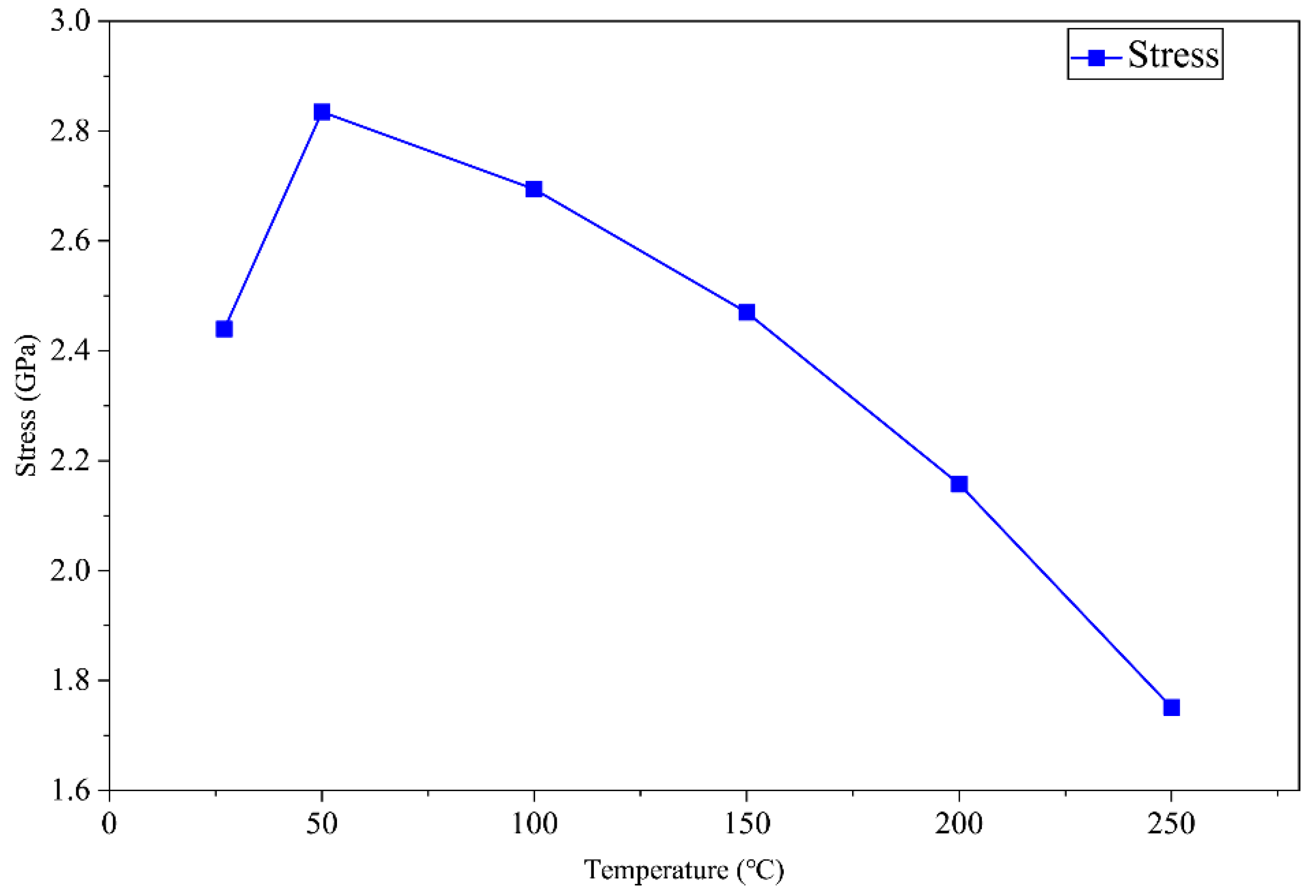
4.3.1. Effect of Formation Temperature

Figure 11 shows the nephogram of the stress field distribution of the PDC cutter breaking rocks at different temperatures. When breaking rocks with a formation temperature ranging from 27 to 250 °C, the maximum stress values of PDC cutters are 2.44, 2.84, 2.69, 2.47, 2.16, and 1.75 GPa, respectively. With an increase in the formation temperature, the equivalent stress of the PDC cutter first increased and then decreased (as shown in Figure 12). This is because within the range of 27–100 °C, when the temperature increases, the mineral particles inside the rock expand and cause the original cracks to close, resulting in a decrease in porosity and an increase in rock strength. At this time, a larger load was required to break the rock under the same conditions. Therefore, the stress of the PDC cutters exhibited an increasing trend with an increase in formation temperature. In the range of 100 to 250 °C, the increase in temperature causes the inconsistent expansion of mineral particles in the rock, leading to the expansion and development of the original microcracks, which results in a decrease in the strength of the rock.

The increase in formation temperature causes the rock to change from elastic–brittle to elastic–plastic, and the increase in rock plasticity reduces the probability of brittle breakage during the rock-breaking process of PDC bits. When PDC bits break rocks in high-temperature formations, the “rubber layer effect” occurs. At 250 °C, a softening effect occurred in the hard rock formations, resulting in a slight reduction in the stress of the PDC cutter.

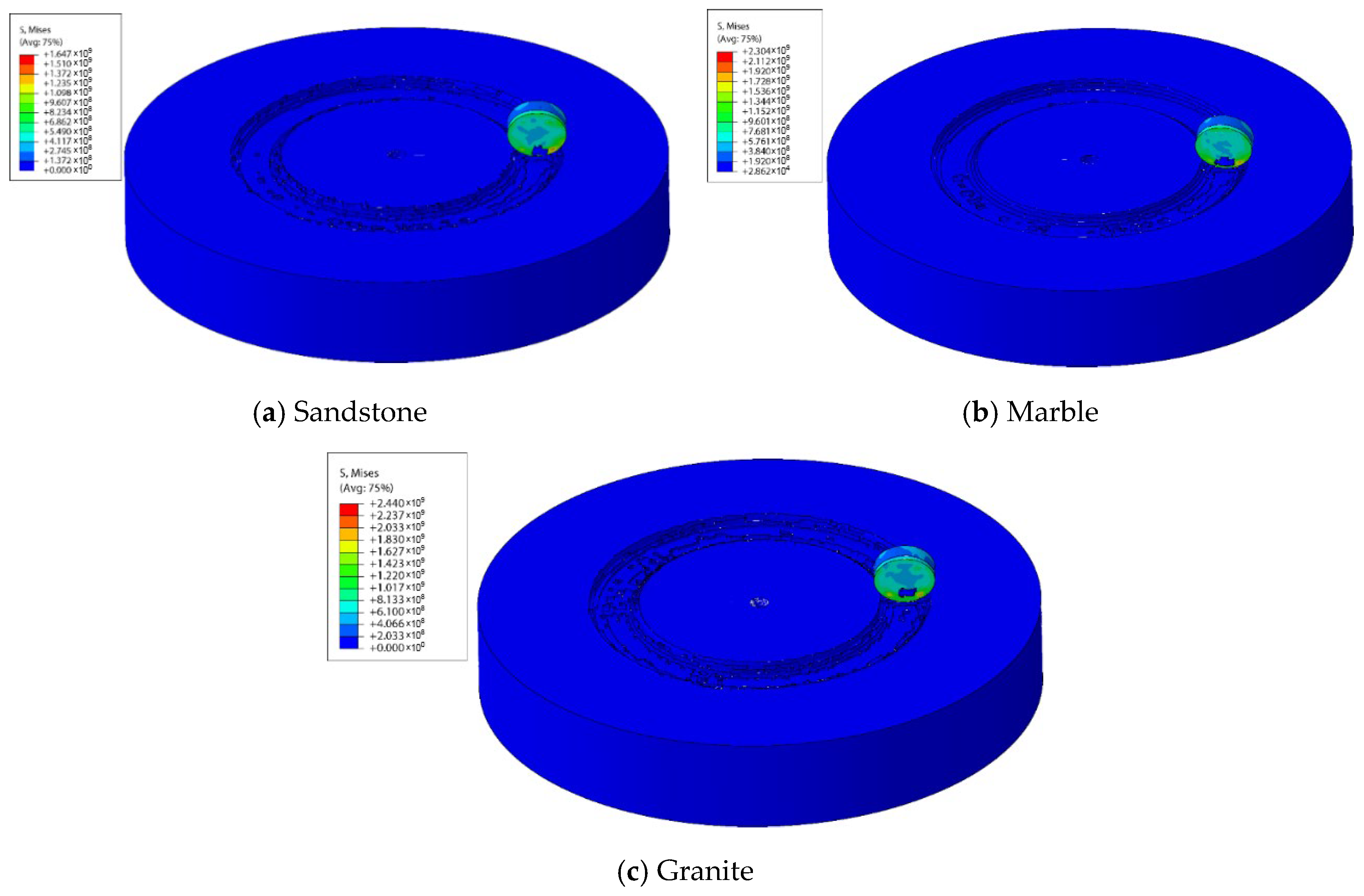
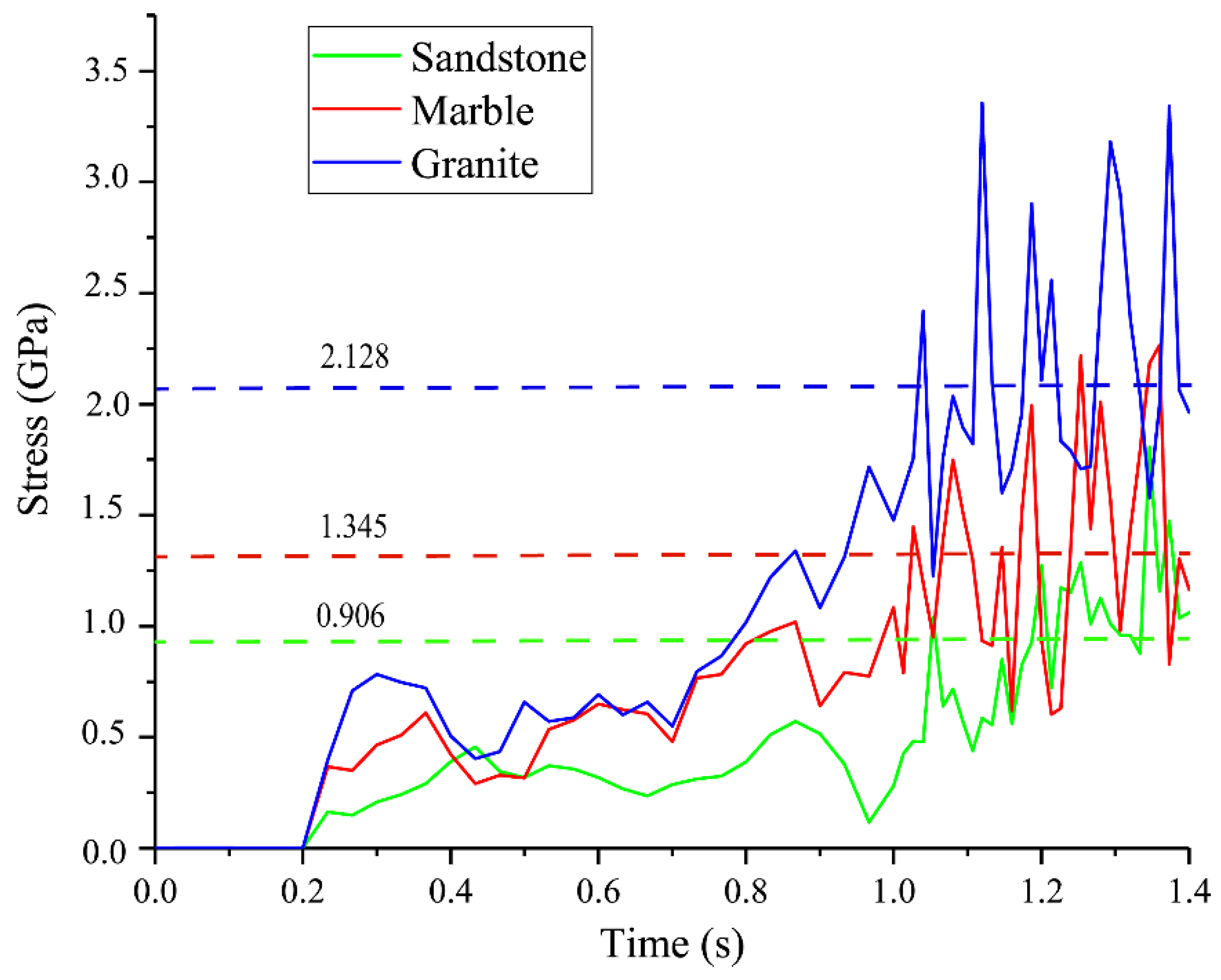
4.3.2. Effect of Rock Strength

Figure 13 shows the stress field distribution nephograms of the PDC cutters used for breaking the three types of rocks. The simulation results show that the rock strength has a significant influence on the overall stress distribution of the cutters. The maximum stress of PDC cutters when breaking sandstone, marble, and granite is 1.65, 2.304, and 2.44 GPa, respectively. These results were obtained at room temperature, with a weight-on-bit (WOB) of 2 kN and a rotational speed of 150 rpm. The stronger the rock, the greater the average stress of the cutter is. The crown of a cutter is prone to stress concentration, which can lead to excessive local stress.

The stress changes in the PDC cutters when breaking sandstone, marble, and granite are shown in Figure 14. It can be observed that the stress variation trend at the top of the cutter crown was almost the same for the three types of rocks when they were broken, which shows that the stress increases first and then fluctuates. The cutter breaks rocks of different strengths, resulting in different forces. The dashed line represents the average stress of the cutter when the three types of rocks were broken. It can be noted that the rock properties have a great influence on the stress of the cutter. The average stresses of the cutter when breaking sandstone, marble, and granite were 0.906, 1.345, and 2.128 GPa, respectively. The stress of the cutter when breaking granite was 58.2% higher than when breaking marble and 134.8% higher than when breaking sandstone.

During the period of 1.0–1.4 s, the fluctuation amplitude of cutter stress increases with the increase in rock strength. When the granite was broken, the stress fluctuation of the cutter increased significantly, indicating that the cutting stability gradually deteriorated, and the risk of impact failure increased. This is because the failure mode of rocks is related to the rock properties, there is a significant difference in the cutting depth of the cutter during the process of breaking rocks of different strengths, and the different cutting depth can change the rock fracture mode [17,28,29]. When the cutting depth did not exceed the critical cutting depth, the rock was plastically broken, and when the cutting depth exceeded the critical cutting depth, the rock underwent brittle fracture. When the granite breaks, brittle fractures occur with large stress fluctuations, whereas plastic failure occurs in marble and sandstone with small stress fluctuations [33,34].

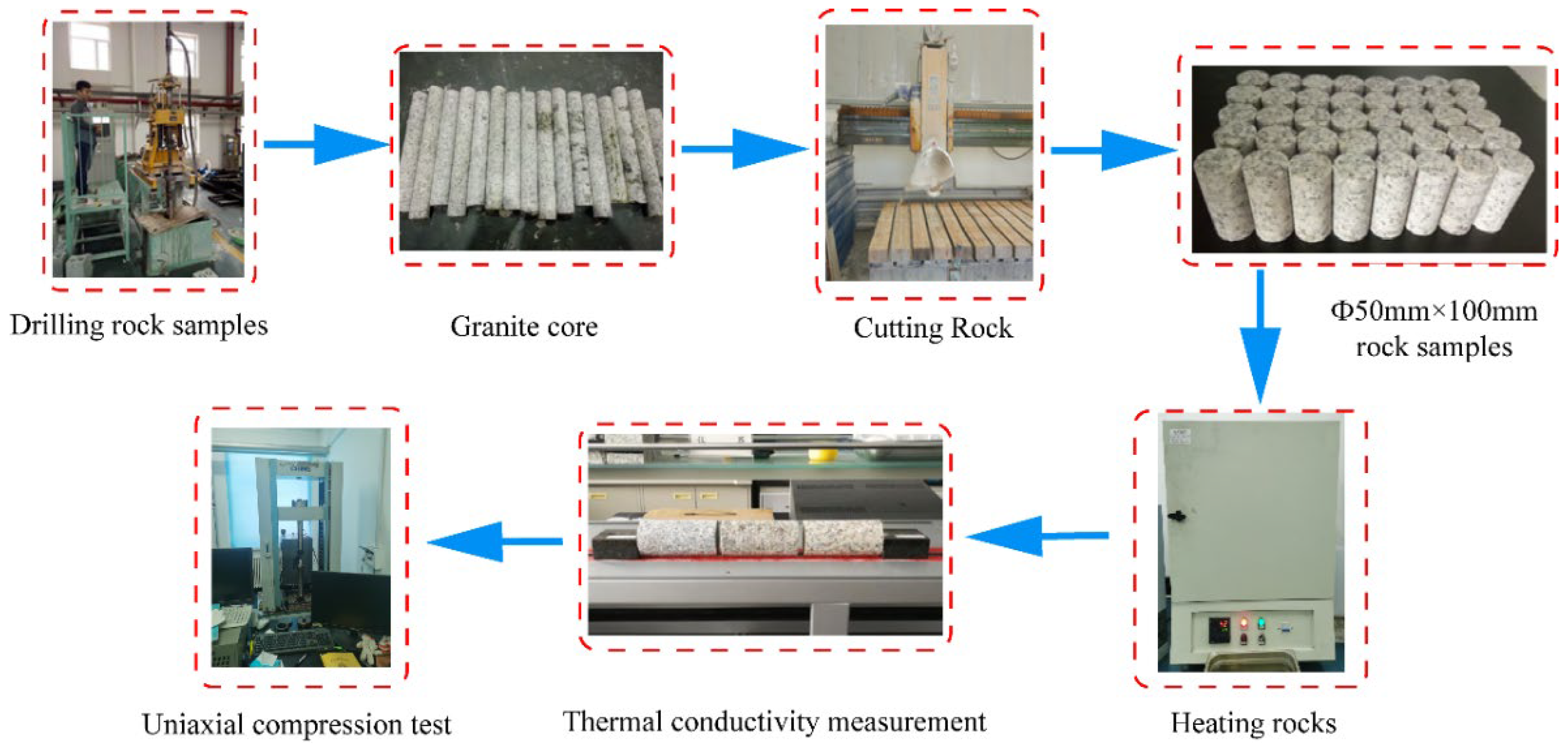
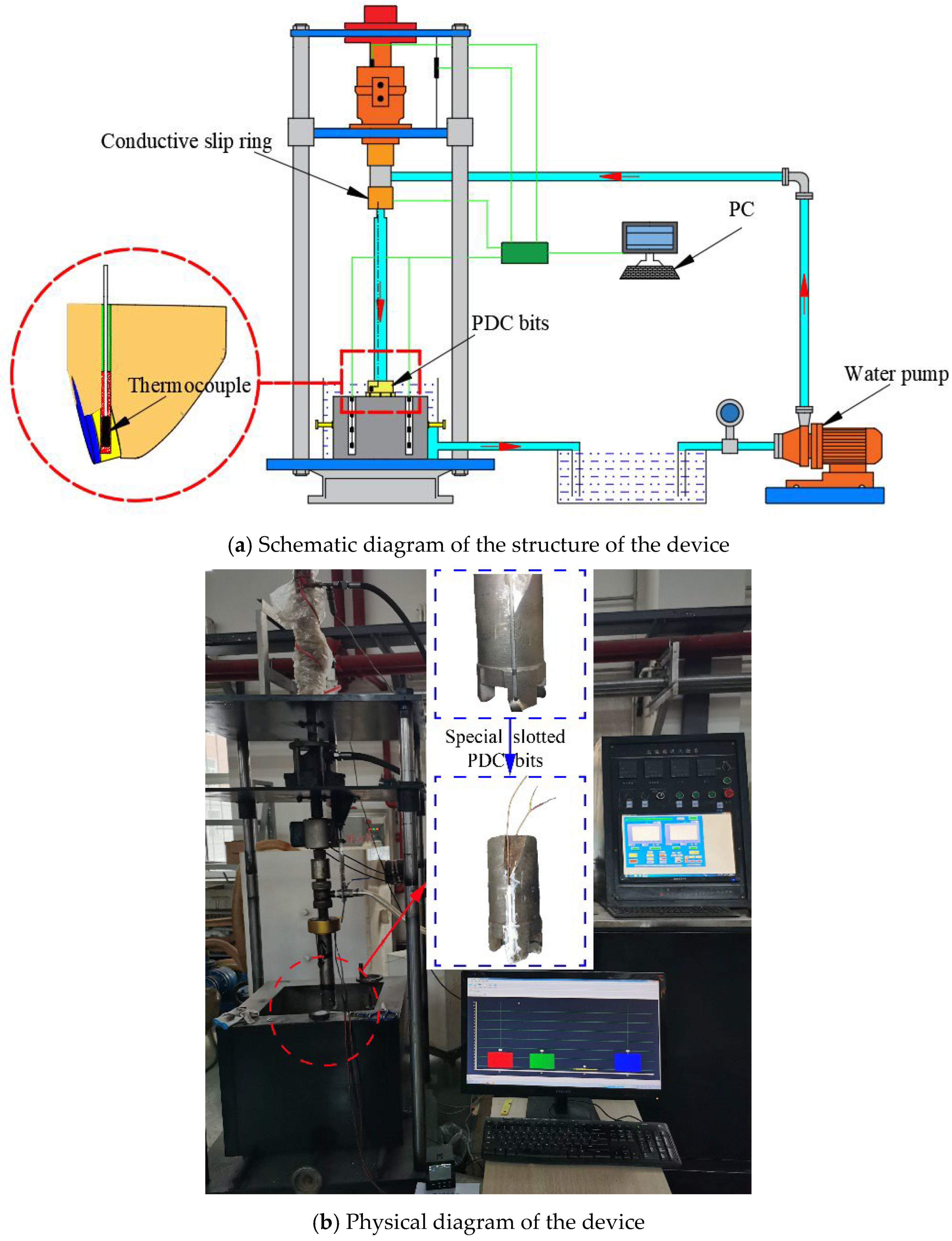
5. Experimental Setup

5.1. Experimental Devices

A schematic diagram of the experimental setup is shown in Figure 15a, which illustrates the arrangement of the drilling rig, PDC bit, thermocouple wiring, and data acquisition system. The device used in this experiment is a high-temperature thermal cycle drilling rig specially manufactured by a company in Hai’an City, Jiangsu Province, China, as shown in Figure 15b. The PDC bit used had an outer diameter of 49 mm, and each cutter had a diameter of 13.44 mm. The rock sample was prepared with dimensions of 150 mm × 100 mm × 240 mm. The heating chamber, which housed the sample during high-temperature tests, measured 450 mm × 400 mm × 390 mm. In order to accurately measure the temperature of PDC bits during rock breaking, some special treatments need to be applied to the drill bits. First, the two PDC cutters were drilled into 2 mm small round holes, and the wire grooves were prefabricated on the rigid body of the PDC bit and the wall of the drill pipe, which is convenient for laying the wires. Based on the working environment and measured temperature range of the test, a K-type thermocouple with a diameter of 1 mm was selected. The error of the thermocouple is 0.2 °C, and the measuring temperature range is 0–1300 °C.

To improve the intimate contact between the cutter and the thermocouple, thermal grease used for computer heat dissipation was used to fill the round hole densely to improve the accuracy of the temperature measurement. Glass cement was used to fill the round hole to prevent the drilling fluid from flowing into the round hole and affecting the measurement results. The MT60130-S06-VC through-hole thermocouple slip ring was selected for the test, which can avoid wire entanglement problems and complete signal transmission, and the MIK-R9600 multi-channel paperless recorder was selected for the temperature data acquisition storage. After each component was connected, the drilling rig was opened for the drilling test. The temperature changes during the rock-breaking process of the PDC bit were displayed on a paperless recorder and analyzed using software.

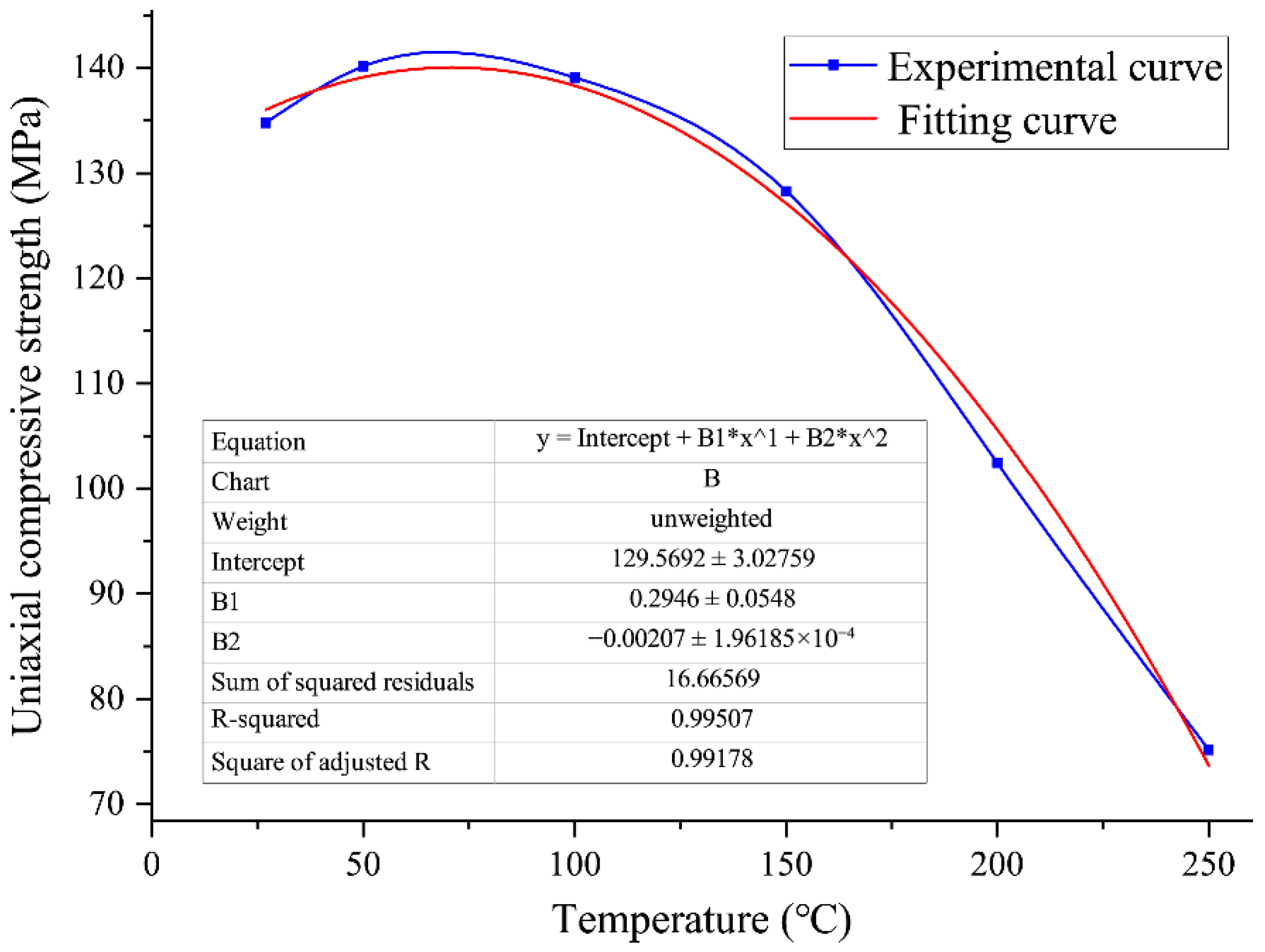
5.2. Experimental Results

Figure 16 shows the change in temperature rise of the PDC bit when the rotational speed is 200 rpm and weight-on-bit (WOB) is 2 kN. It can be observed from the figure that the temperature change trend of the two probes is the same as that of the simulation results, and there are three stages as follows: sharp rising (I), slow rising (II), and relatively stable (III) periods. From 0 to 100 s, the PDC bits and rocks instantaneously generated a large amount of heat owing to the friction and collision under the action of the WOB. Owing to the different thermal conductivities of the rocks and bits, heat cannot diffuse to the rocks in time, resulting in a rapid increase in the temperature of the bit. With the continuous drilling of rock breaking, the temperature continued to rise during the period of 100–200 s; however, the rate of temperature rise slowed significantly compared to that at 0–100 s. This is because, as the area between the bit and rock becomes progressively larger, heat conduction increases, and part of the heat is carried away by the drilling fluid, resulting in a decrease in the temperature rise rate of the bit. At the stage of 200–300 s, the heat generated by the bit was almost the same as that of convective heat transfer and heat loss, and the temperature finally reached a dynamic balance.

The tests of drilling sandstone, marble, and granite were conducted at a rotational speed of 200 rpm and a WOB of 2 kN, for a drilling time of 300 s, and the temperature change curve was obtained through the temperature acquisition system. It can be observed from Figure 17 that the temperature rise trend of the cutter is almost the same when drilling and breaking the three types of rocks. The temperature of the cutter first increases rapidly and then slowly, finally reaching a dynamically stable equilibrium state. The amplitude of the temperature fluctuation of the cutter during granite drilling was larger than that during marble and sandstone drilling. This was consistent with the temperature change rule of the simulation results.

As shown in

Table 3. Test records of the three kinds of rocks broken.

Type	Time (s)	Footage (mm)	ROP (mm/s)	Maximum Temperature (°C)	Temperature Rise Rate (°C/s)
Sandstone	300	54	0.18	42	0.067
Marble	300	45	0.15	59	0.123
Granite	300	13.2	0.044	75	0.177

, compared to drilling sandstone and marble, the ROP of drilling granite was lower by 75.6 and 70.6%, respectively, and the ROP decreased with an increase in rock strength. When drilling sandstone and marble, the temperature rise rates of the cutter were 0.067 °C/s and 0.123 °C/s, respectively, whereas when drilling granite, granite was relatively high, which was 0.177 °C/s. The temperature change in the cutter when drilling granite was greater than when drilling marble and sandstone.

5.3. Breaking Hig- Temperature Rock

In this section, the test of drilling high temperature granite at two different temperatures, 150 °C and 250 °C, respectively, was performed under the conditions of a rotational speed of 200 rpm, WOB of 2 kN, and drilling time of 300 s, to study the influence law of high temperature formations on the temperature of the PDC bit.

Figure 18 shows the relationship between the temperature of the bit and time when the rock temperature is 150 °C and 250 °C. It can be observed that when the PDC bit was drilling the rock at 150 °C and 250 °C, the temperature change trend of the bit was almost the same, which first increased, then decreased, and finally tended to a dynamic equilibrium state. From 0 to 100 s, the temperature of the rock was relatively high in the early stage of drilling, and the temperature of the PDC bit remained at room temperature. Owing to the relatively high thermal conductivity of the bit, the heat of the high-temperature rock was rapidly transferred to the bit, resulting in the temperature of the bit increasing in a short time. During the drilling process, the cooling effect of the drilling fluid was greater than the heat transfer effect, resulting in the temperature of the PDC bit decreasing during the period of 100–120 s. Finally, owing to the relative balance between the heat generated by the friction between the PDC bit and rock and the convective heat transfer and heat loss during the drilling process, the temperature of the bit finally reached a dynamic equilibrium state during 120–300 s.

It can be observed from

Table 4. Test records of the high-temperature rocks broken.

Type	Time (s)	Footage (mm)	ROP (mm/s)	Maximum Temperature (°C)
27	300	13.2	0.044	75
150	300	18	0.06	97
250	300	15.6	0.052	125.3

that when granite at 27, 150, and 250 °C was broken, the ROP of the PDC bit was 0.044, 0.06, and 0.052 mm/s, respectively. The ROP of the PDC bits for drilling 150 °C granite is greater than the other two cases. This is because when the rock temperature is 150 °C, the increase in temperature makes the various mineral particles within the granite undergo uneven expansion, leading to the development of the original fracture expansion, which produces thermal cracking and leads to a reduction in the strength of the rock. In addition, the use of normal-temperature water as the drilling fluid promoted the thermal cracking of granite under high-temperature conditions.

Notably, there is a significant difference between the rock fracture mechanism at room temperature and that under high-temperature formation conditions, and the damage mode of the rock changes from brittle to plastic failure with an increase in temperature. Although the strength of the granite decreases at 250 °C, it is still far from being weak enough for the PDC bit to easily penetrate it, and the increase in rock plasticity increases the probability of the PDC bit “slipping” at the bottom of the well, reducing its ROP.

6. Conclusions

This study systematically investigated the temperature and thermal stress evolution of PDC cutters during rock breaking through integrated numerical simulation and experimental validation, with a particular focus on the effects of formation temperature and rock strength. The main findings and their implications are summarized as follows:

(1)

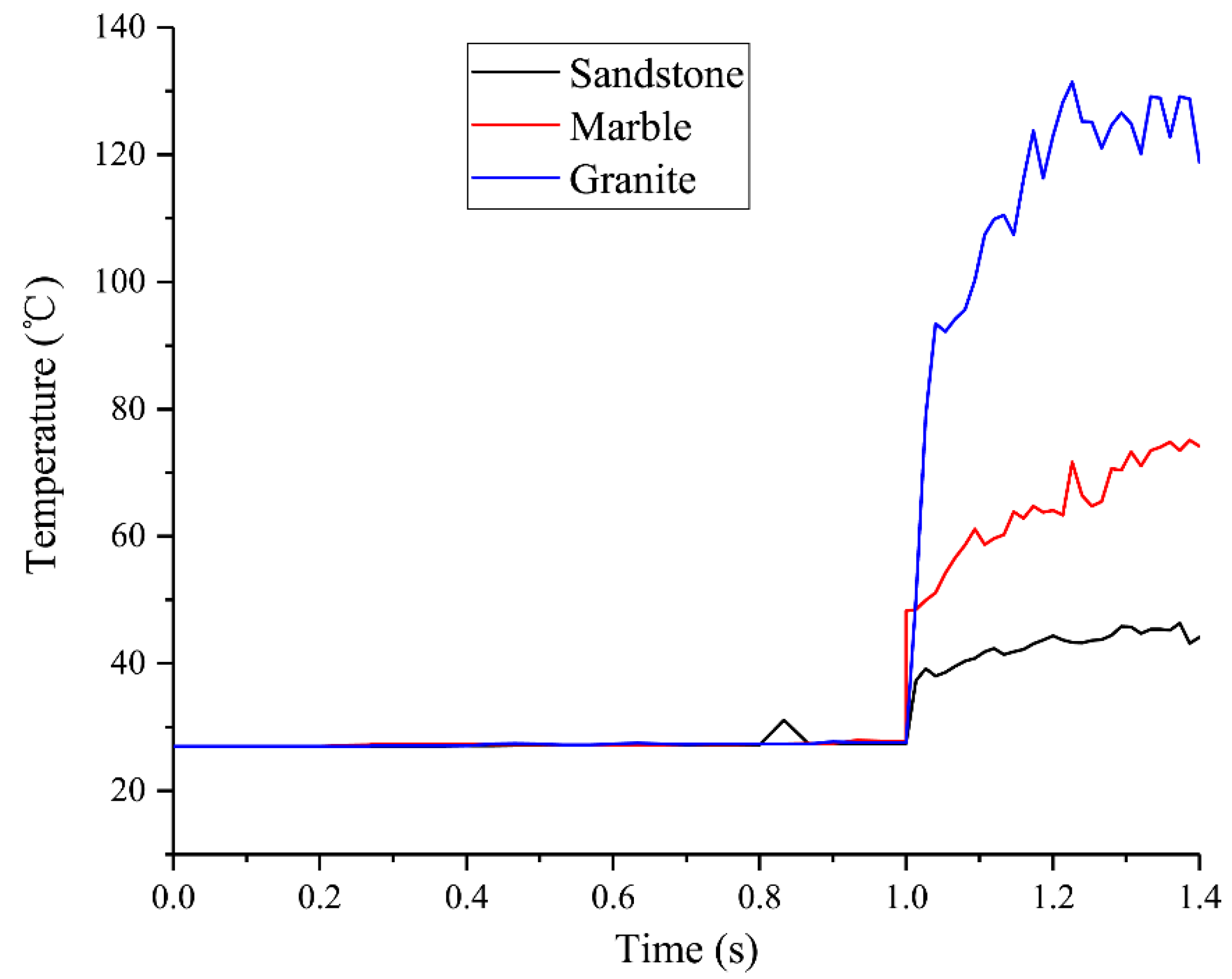
The temperature rise of a PDC cutter during rock breaking exhibits a consistent three-stage pattern as follows: rapid increase, slow increase, and stabilization. Rock strength is a dominant factor influencing the rate of temperature rise and the magnitude of cutter temperature. When breaking granite (uniaxial compressive strength ≈ 134.8 MPa at 27 °C), the cutter temperature reached approximately 131.4 °C, about two and three times higher than when cutting marble (≈75.2 °C) and sandstone (≈46.3 °C), respectively. Correspondingly, the rate of penetration (ROP) decreased by 70.6% and 75.6% when drilling granite compared to marble and sandstone.

(2)

Increasing formation temperature reduces the internal temperature gradient within the cutter, thereby mitigating thermal stress. As the formation temperature rose from 27 °C to 250 °C, the temperature difference between the maximum and minimum points on the cutter decreased from 72.6 °C to 35.6 °C. However, due to material heterogeneity and differential thermal expansion, significant thermal stress still develops, with the maximum equivalent stress (2.84 GPa) occurring at a formation temperature of 50 °C.

(3)

The stress distribution in the PDC cutter is highly concentrated at the crown and at the interface between the diamond layer and the tungsten carbide matrix. Both the magnitude and fluctuation amplitude of stress increase with rock strength. The average stress when breaking granite (2.128 GPa) was 58.2% and 134.8% higher than when breaking marble (1.345 GPa) and sandstone (0.906 GPa), respectively. Stress evolution during cutting shows an initial sharp increase followed by fluctuations, with greater instability observed in harder rocks.

(4)

High formation temperatures alter the rock failure mode from brittle to plastic, which affects cutting efficiency. Although rock strength decreases at elevated temperatures (e.g., granite compressive strength dropped from 134.8 MPa at 27 °C to 75.1 MPa at 250 °C), the increased plasticity can lead to a “rubber layer effect,” reducing the ROP. The highest ROP (0.06 mm/s) was observed at 150 °C, compared to 0.044 mm/s at 27 °C and 0.052 mm/s at 250 °C.