Quantifying Moisture Susceptibility in Asphalt Mixtures Using Dynamic Mechanical Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Mix Design
2.2. Experimental Methods
2.2.1. Test Procedures to Estimate the Work of Adhesion
2.2.2. DMA Test Procedures
- (1)
- Test Principle
- (2)
- Experimental Equipment and Methods
- Mounting: Each specimen was securely fixed onto a dual cantilever clamp using a specified torque.
- Equilibration: The furnace was switched off, and the temperature was reduced to −35 °C and held at this temperature for 10 min.
- Temperature Ramp: The temperature was then increased at a constant rate of 2 °C per minute.
- Dynamic Loading: Simultaneously during the temperature increase, a dynamic load was applied to the specimen.
- Data Acquisition: Various parameters, including the complex modulus, storage modulus, loss modulus, and phase angle, were continuously recorded.
- Replication: Four parallel specimens were tested for each asphalt mixture type to ensure result reliability.
- (3)
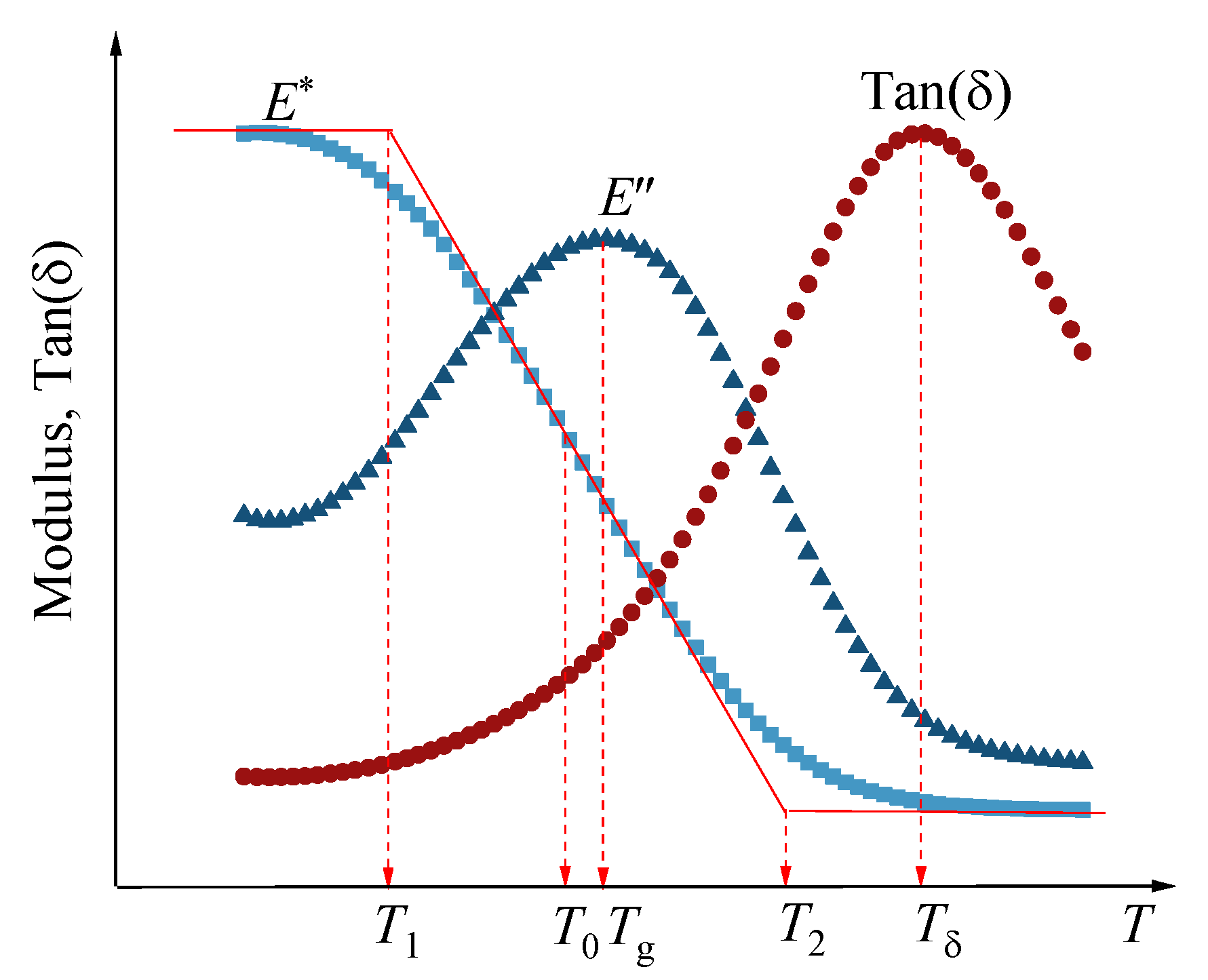
- Analysis Method
- The temperature corresponding to the midpoint () of the complex modulus curve is defined as , . This is also the temperature point where the complex modulus decreases the fastest with increasing temperature;
- The temperature corresponding to the intersection of the midpoint tangent of the complex modulus curve and the asymptote in the low-temperature zone is defined as , . is the temperature corresponding to the change in the asphalt mixture from a glassy to a rubbery state, which can be considered the glass transition temperature of the asphalt mixture;
- The temperature corresponding to the intersection of the midpoint tangent of the complex modulus curve and the asymptote in the high-temperature zone is defined as , . This temperature reflects the characteristics of the asphalt mixture in the high-temperature zone.
3. Results and Discussion
3.1. Adhesion Property
3.1.1. Surface Energy of the Asphalt Binder and Aggregate
3.1.2. Adhesion Work of the Asphalt Binder-Aggregate Combination
3.2. Moisture Susceptibility
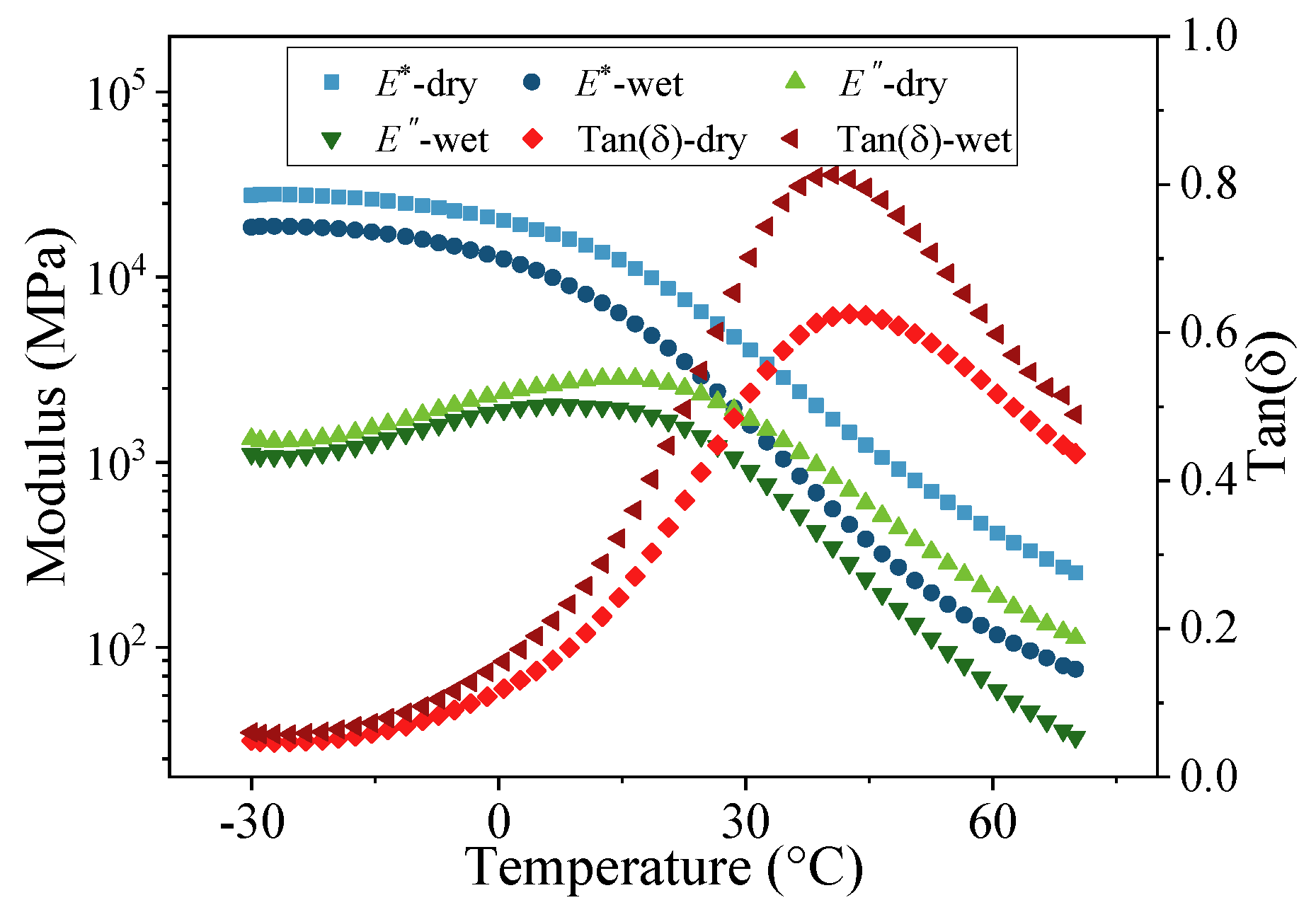
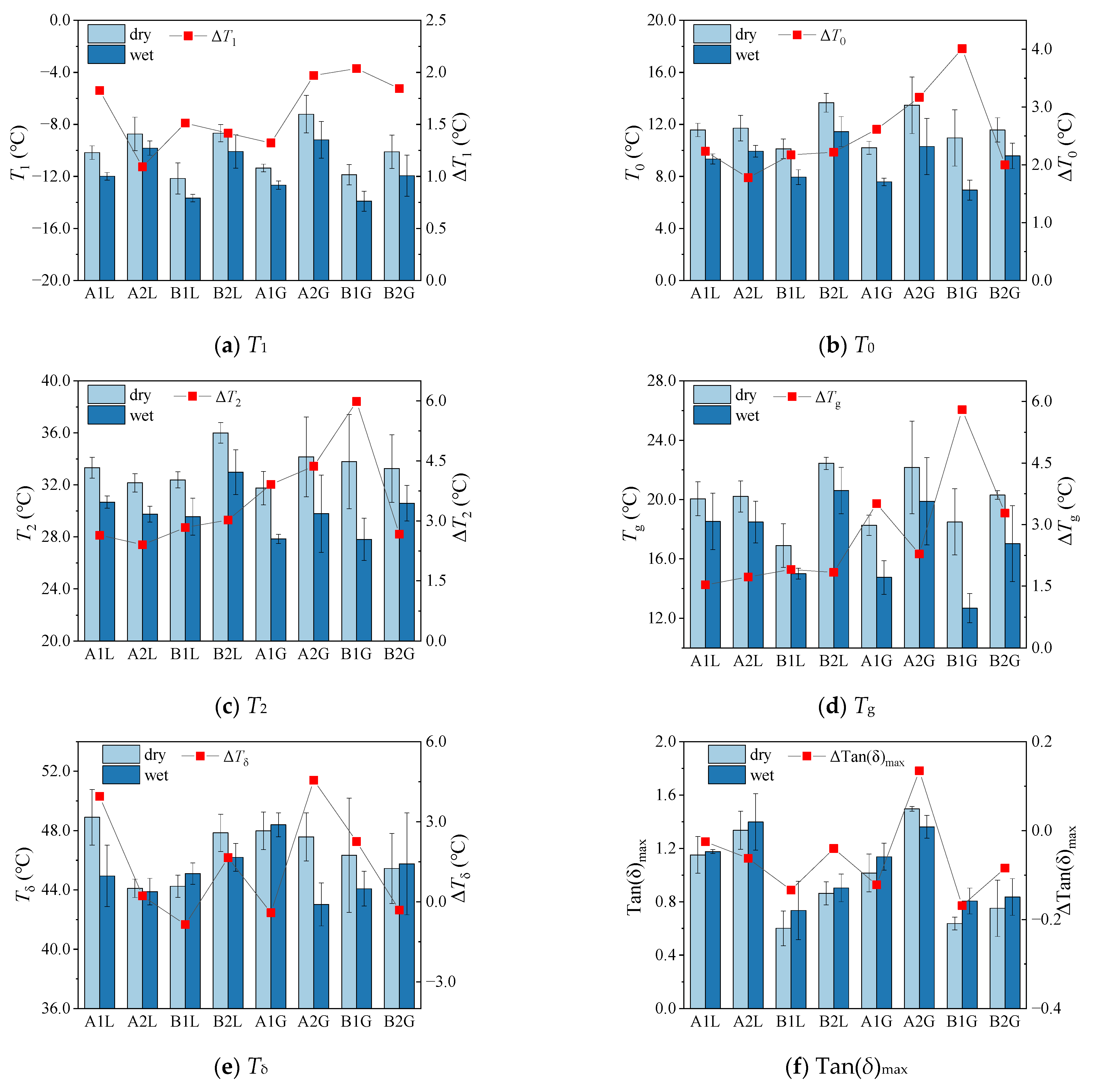
3.2.1. Characteristic Temperature
- Mixtures A1L (neat asphalt A1 with limestone), A2L (neat asphalt A2 with limestone), B1L (SBS-modified asphalt B1 with limestone), and B2L (SBS-modified asphalt B2 with limestone) decreased the characteristic temperatures T1, T0 and Tg by an average of 1.5 °C, 2.1 °C, and 1.7 °C after immersion, respectively, while the granite mixtures decreased by 1.8 °C, 2.9 °C, and 3.7 °C, respectively.
- The average reduction in T1 and T0 for the A1L and A1G mixtures formed by two types of aggregates and neat asphalt A1 after immersion is similar to that of asphalt A2.
- The Tg of the A1L and A1G mixtures decreases by an average of 2.5 °C, which is greater than the decrease of 2.0 °C observed for the A2L and A2G mixtures.
- The mixtures formed by modified asphalt B1 (i.e., B1L and B1G) exhibited average decreases of 1.8 °C, 3.1 °C, and 3.9 °C for T1, T0 and Tg, respectively, while the decreases for asphalt B2 (i.e., B2L and B2G) were 1.6 °C, 2.1 °C, and 2.6 °C, respectively.
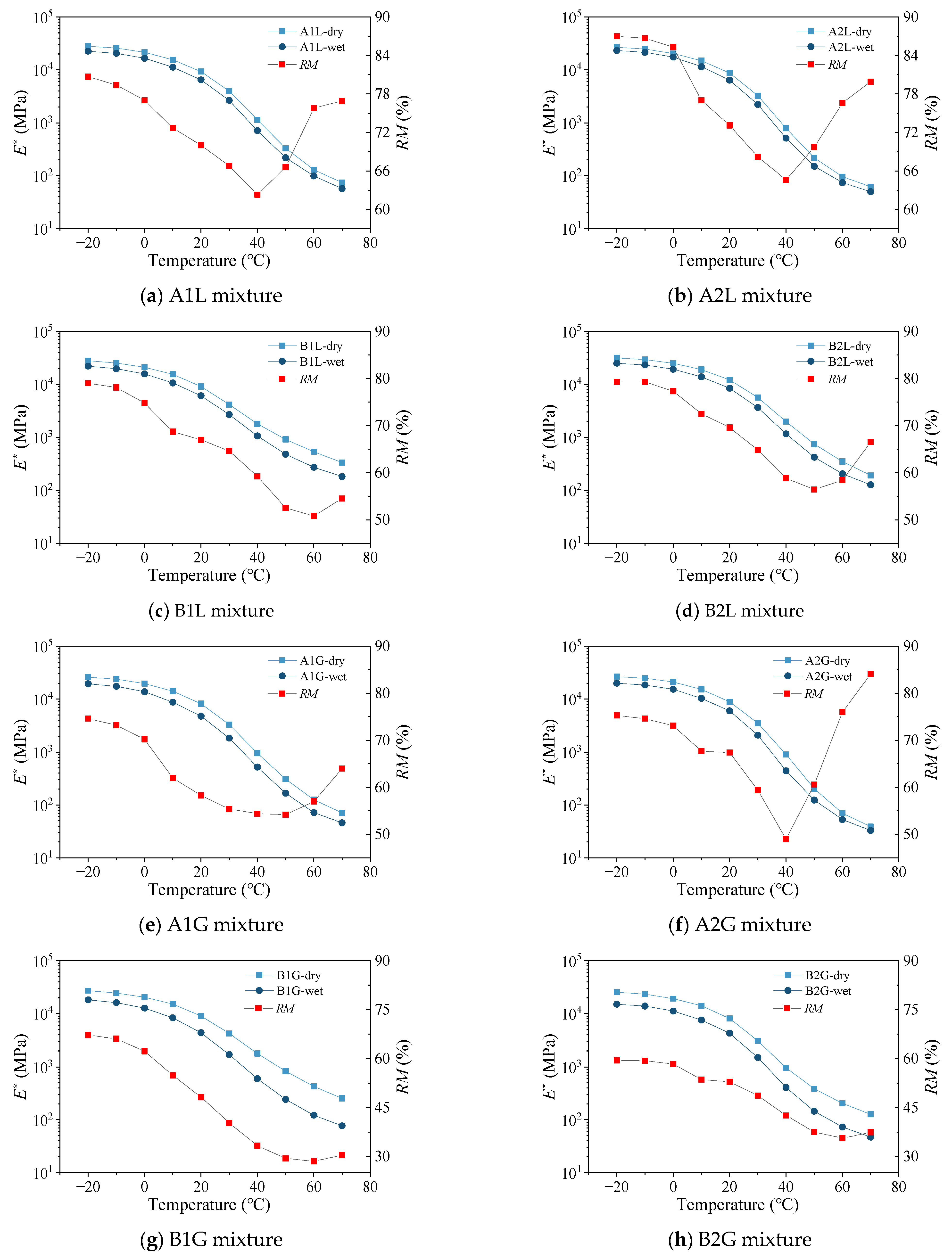
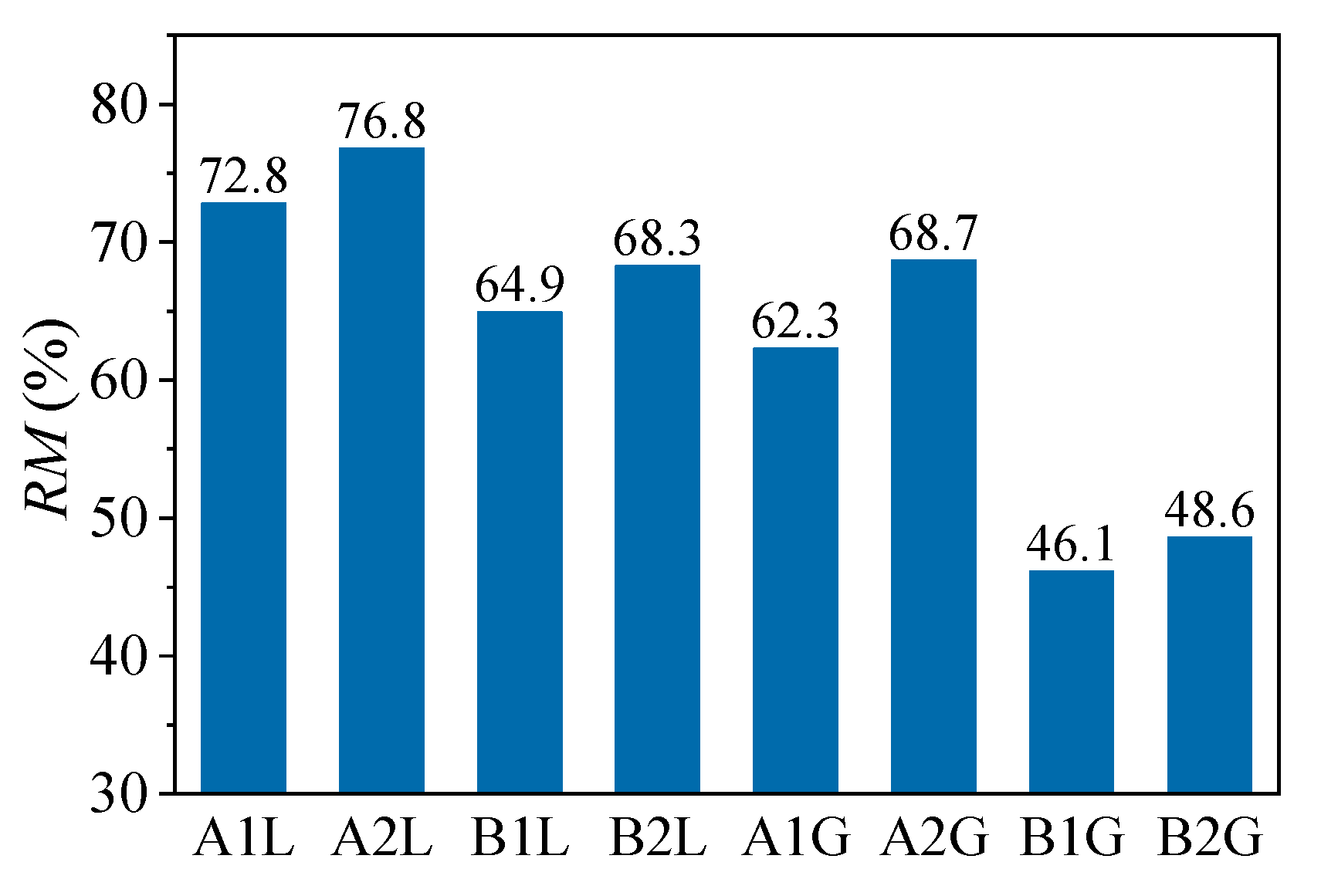
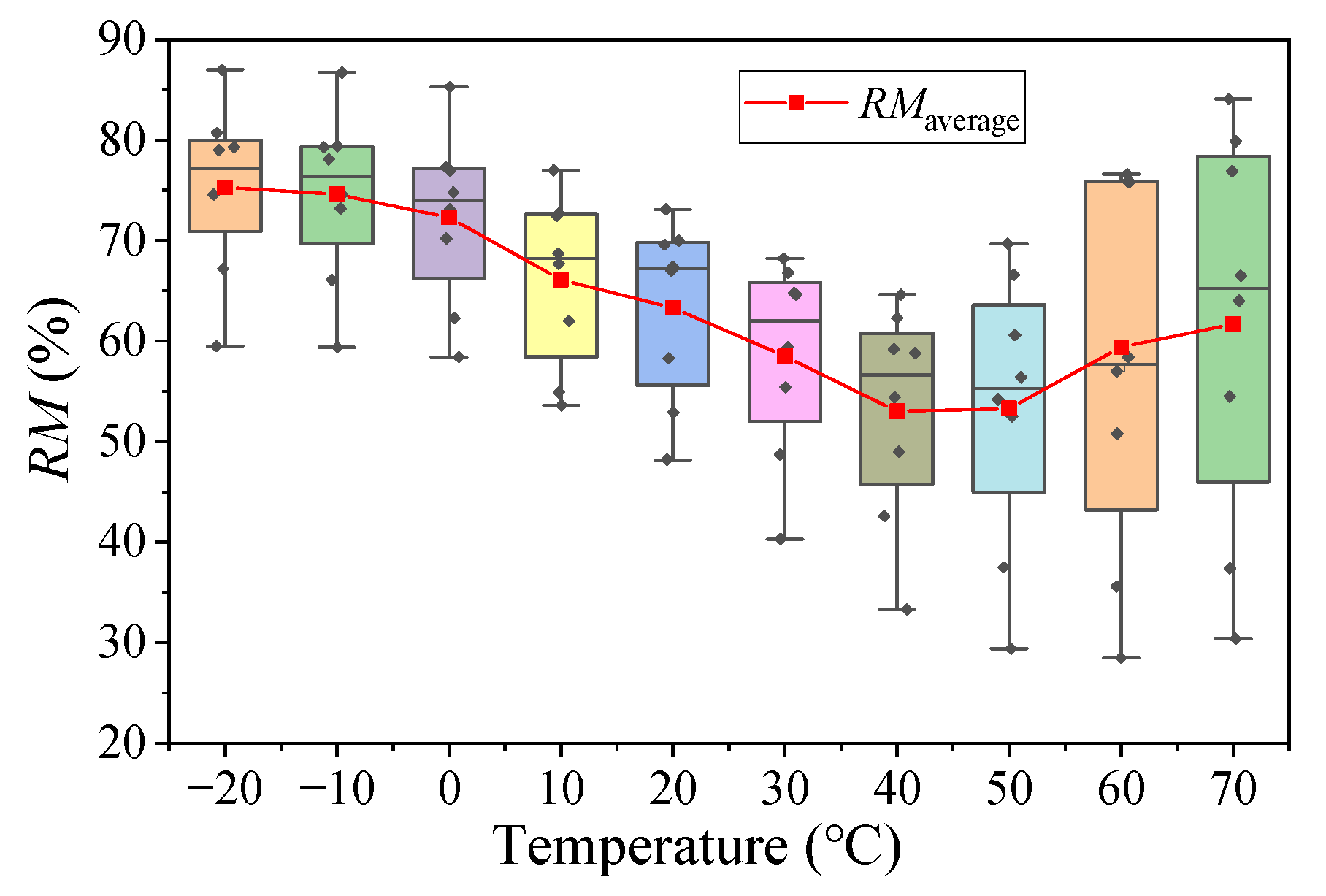
3.2.2. Residual Modulus
4. Conclusions
- The DMA method, utilizing thin-section specimens, proved to be an effective and efficient technique for assessing moisture-induced damage. It successfully captured the deterioration in performance through measurable decreases in the complex modulus and significant shifts in characteristic temperatures (T0, T1, T2, Tg) towards lower values after moisture conditioning.
- The derived indices, namely the residual modulus ratio (RM) and the characteristic temperature differentials, provided a reliable quantitative ranking of mixture susceptibility. Mixtures prepared with granite aggregate consistently demonstrated higher moisture sensitivity compared to those with limestone. Furthermore, among the binders tested, mixtures containing A1 (neat) and B1 (SBS-modified) asphalt exhibited greater performance loss than those with A2 and B2, respectively.
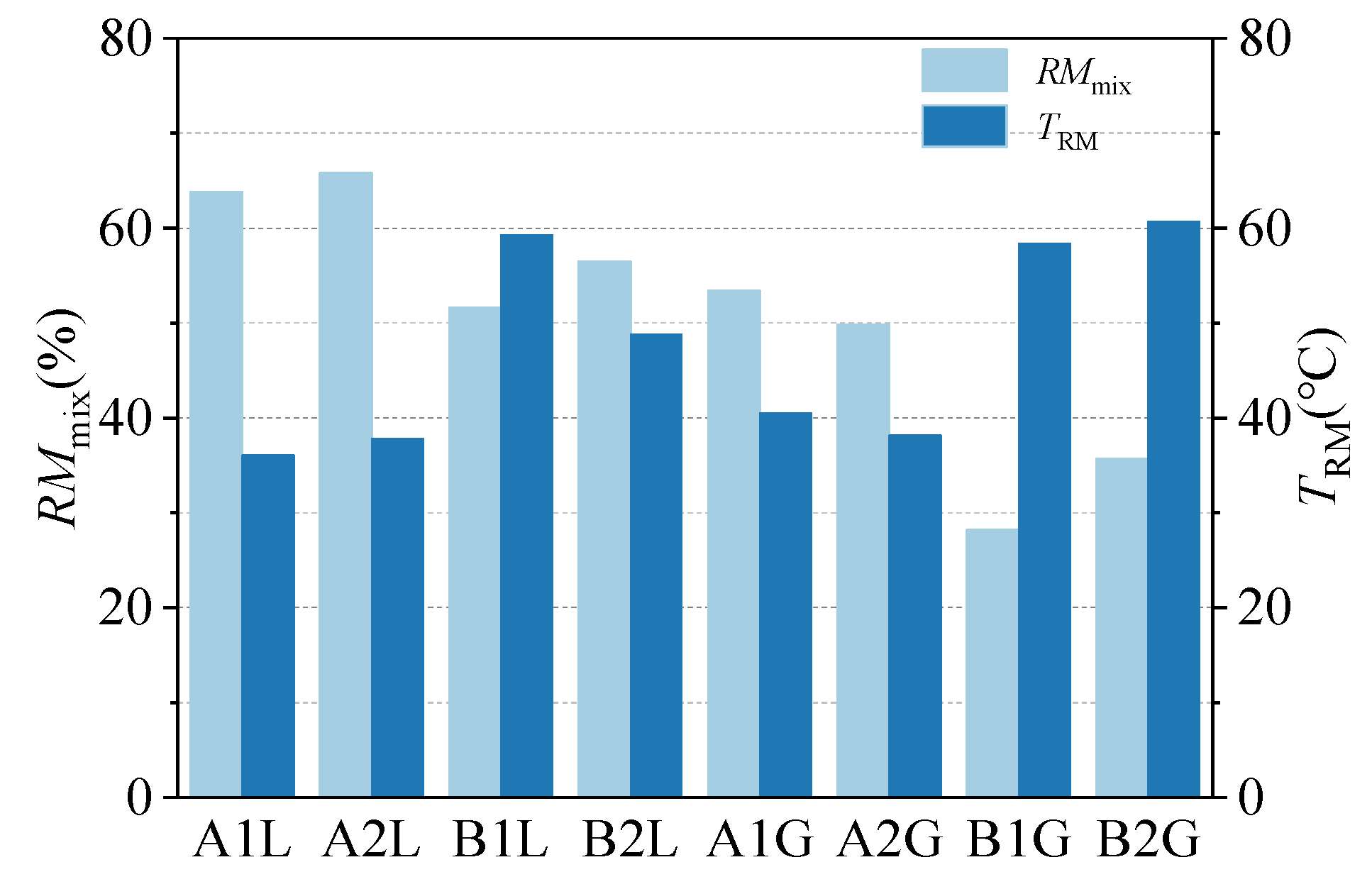
- A critical finding was the identification of the minimum residual modulus (RMmin) and its corresponding critical temperature (TRM). These parameters pinpointed the most severe conditions of moisture damage, with RMmin values which ranged from 28.2% to 65.8% and occurred at TRM values of approximately 40 °C for neat asphalt mixtures and 60 °C for SBS-modified asphalt mixtures. This indicates that the most unfavorable in-service temperature environment is higher for modified binders.
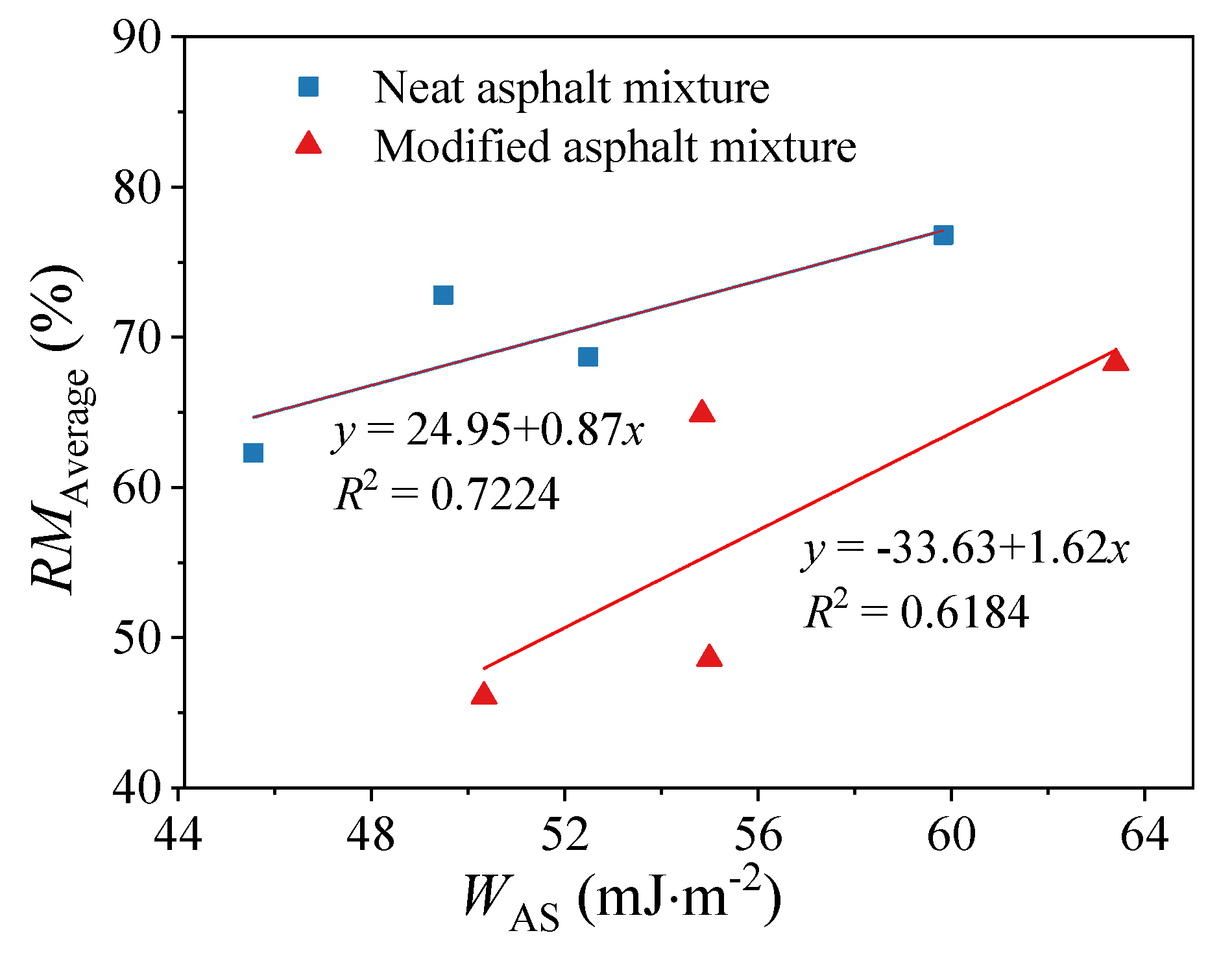
- The DMA-based evaluation of moisture susceptibility showed a correlative trend with the thermodynamic adhesion work (WAS) calculated from surface free energy components. However, the relationship was not absolute. While modified asphalts generally exhibited higher adhesion work, they showed inferior resistance to moisture damage compared to neat asphalts in the DMA tests. This highlights the complexity of moisture damage mechanisms and indicates that predictions based solely on surface energy theory should be approached with caution and require separate consideration for modified and neat binders.
- The comprehensive analysis underscores that the aggregate type is a primary governing factor in moisture susceptibility. The superior performance of limestone-based mixtures, quantified by all DMA indices, is attributed to its more favorable chemical interaction with asphalt binders, leading to stronger adhesion as evidenced by higher WAS values.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, B.; Shu, X.; Dong, Q.; Shen, J. Laboratory Evaluation of Moisture Susceptibility of Hot-Mix Asphalt Containing Cementitious Fillers. J. Mater. Civ. Eng. 2010, 22, 667–673. [Google Scholar] [CrossRef]
- Kok, B.V.; Yilmaz, M. The effects of using lime and styrene–butadiene–styrene on moisture sensitivity resistance of hot mix asphalt. Constr. Build. Mater. 2009, 23, 1999–2006. [Google Scholar] [CrossRef]
- Kakar, M.R.; Hamzah, M.O.; Valentin, J. A review on moisture damages of hot and warm mix asphalt and related investigations. J. Clean. Prod. 2015, 99, 39–58. [Google Scholar] [CrossRef]
- Das, B.P.; Siddagangaiah, A.K. Moisture damage analysis based on adhesive failure in asphalt mixtures. Int. J. Pavement Eng. 2022, 23, 2554–2564. [Google Scholar] [CrossRef]
- El-Hakim, R.T.A.; Epps, J.; Martin, A.E.; Arámbula-Mercado, E. Laboratory and field investigation of moisture susceptibility of hot and warm mix asphalts. Int. J. Pavement Eng. 2021, 22, 1389–1398. [Google Scholar] [CrossRef]
- Caro, S.; Masad, E.; Bhasin, A.; Little, D.N. Moisture susceptibility of asphalt mixtures, Part 2: Characterisation and modelling. Int. J. Pavement Eng. 2008, 9, 99–114. [Google Scholar] [CrossRef]
- Caro, S.; Masad, E.; Bhasin, A.; Little, D.N. Moisture susceptibility of asphalt mixtures, Part 1: Mechanisms. Int. J. Pavement Eng. 2008, 9, 81–98. [Google Scholar] [CrossRef]
- Mehrara, A.; Khodaii, A. A review of state of the art on stripping phenomenon in asphalt concrete. Constr. Build. Mater. 2013, 38, 423–442. [Google Scholar] [CrossRef]
- Usanga, I.N.; Okafor, F.O.; Ikeagwuani, C.C. Analysis of performance parameters based on surface free energy to evaluate moisture susceptibility of asphalt mixtures modified with calcined marl dust. Int. J. Pavement Eng. 2024, 25. [Google Scholar] [CrossRef]
- Hamedi, G.H.; Esmaeeli, M.R.; Gilani, V.N.M.; Hosseinian, S.M.; Lampropoulos, A. The Effect of Aggregate-Forming Minerals on Thermodynamic Parameters Using Surface Free Energy Concept and Its Relationship with the Moisture Susceptibility of Asphalt Mixtures. Adv. Civ. Eng. 2021, 2021, 8818681. [Google Scholar] [CrossRef]
- Elphingstone, G.M., Jr. Adhesion and Cohesion in Asphalt-Aggregate Systems; Texas A&M University: College Station, TX, USA, 1997. [Google Scholar]
- Cheng, D.; Little, D.; Lytton, R.; Holste, J. Surface energy measurement of asphalt and its application to predicting fatigue and healing in asphalt mixtures. Transp. Res. Rec. 2002, 1810, 44–53. [Google Scholar] [CrossRef]
- Hefer, A.W.; Bhasin, A.; Little, D.N. Bitumen Surface Energy Characterization Using a Contact Angle Approach. J. Mater. Civ. Eng. 2006, 18, 759–767. [Google Scholar] [CrossRef]
- Koc, M.; Bulut, R. Assessment of a Sessile Drop Device and a New Testing Approach Measuring Contact Angles on Aggregates and Asphalt Binders. J. Mater. Civ. Eng. 2014, 26, 391–398. [Google Scholar] [CrossRef]
- Tanzadeh, R.; Shafabakhsh, G. Surface free energy and adhesion energy evaluation of modified bitumen with recycled carbon black (micro-nano) from gases and petrochemical waste. Constr. Build. Mater. 2020, 245, 118361. [Google Scholar] [CrossRef]
- Liu, L.; Huang, W.; Liu, L.; Ye, F.; Chen, S.; Yang, R. Moisture susceptibility evaluation of asphalt mixture with account of horizontal loads: A novel test method. Constr. Build. Mater. 2024, 417, 135301. [Google Scholar] [CrossRef]
- Oldham, D.J.; Hajikarimi, P.; Fini, E.H. Introducing a New Test to Examine Moisture Susceptibility at the Interface of Bitumen and Stones. J. Transp. Eng. Part B Pavements 2022, 148, 4022029. [Google Scholar] [CrossRef]
- Aksoy, A.; Şamlioglu, K.; Tayfur, S.; Özen, H. Effects of various additives on the moisture damage sensitivity of asphalt mixtures. Constr. Build. Mater. 2005, 19, 11–18. [Google Scholar] [CrossRef]
- Rad, S.M.; Olagunju, M.; Elkashef, M. Impact of Binder and Aggregate Type on the Cracking, Rutting, and Moisture Susceptibility of Asphalt Mixes in Oklahoma: A BMD Approach. J. Mater. Civ. Eng. 2025, 37, 4024530. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, M.; Kaseer, F.; Arambula, E.; Lytton, R.L.; Martin, A.E. Prediction and evaluation of rutting and moisture susceptibility in rejuvenated asphalt mixtures. J. Clean. Prod. 2022, 333, 129980. [Google Scholar] [CrossRef]
- Akentuna, M.; Mohammad, L.N.; Sachdeva, S.; Cooper, S.B.; Cooper, S.B. Effectiveness of Loaded Wheel Tracking Test to Ascertain Moisture Susceptibility of Asphalt Mixtures. Transp. Res. Rec. 2022, 2676, 421–434. [Google Scholar] [CrossRef]
- Breakah, T.M.; Bausano, J.P.; Williams, R.C. Integration of Moisture Sensitivity Testing with Gyratory Mix Design and Mechanistic-Empirical Pavement Design. J. Transp. Eng. 2009, 135, 852–857. [Google Scholar] [CrossRef]
- Bausano, J.; Williams, R.C. Transitioning from AASHTO T283 to the Simple Performance Test Using Moisture Conditioning. J. Mater. Civ. Eng. 2009, 21, 73–82. [Google Scholar] [CrossRef]
- Brondani, C.; Vestena, P.M.; Faccin, C.; Schuster, S.L.; Specht, L.P.; Da Silva Pereira, D. Moisture susceptibility of asphalt mixtures: 2S2P1D rheological model approach and new index based on dynamic modulus master curve changes. Constr. Build. Mater. 2022, 331, 127316. [Google Scholar] [CrossRef]
- Kim, Y.; Little, D.N.; Lytton, R.L. Effect of moisture damage on material properties and fatigue resistance of asphalt mixtures. Transp. Res. Rec. J. Transp. Res. Board 2004, 1891, 48–54. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, X.; Wang, Y.; Zhou, X.; Wu, Y. Long-Term Performance Evolution of RIOHTrack Pavement Surface Layer Based on DMA Method. Materials 2022, 15, 6461. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Ma, Z.; Shan, L.; Zhang, C. Evaluation of the High- and Low-Temperature Performance of Asphalt Mortar Based on the DMA Method. Materials 2022, 15, 3341. [Google Scholar] [CrossRef] [PubMed]
- van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Monopolar surfaces. Adv. Colloid. Interface. Sci. 1987, 28, 35–64. [Google Scholar] [CrossRef] [PubMed]
- Fowkes, F.M. Additivity of intermolecular forces at interfaces. I. Determination of the contribution to surface and interfacial tensions of dispersion forces in various liquids. J. Phys. Chem. 1963, 67, 2538–2541. [Google Scholar] [CrossRef]
- Owens, D.K.; Wendt, R.C. Estimation of the surface free energy of polymers. J. Appl. Polym. Sci. 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- Kwok, D.Y.; Neumann, A.W. Contact angle measurement and contact angle interpretation. Adv. Colloid Interface Sci. 1999, 81, 167–249. [Google Scholar] [CrossRef]
- van Oss, C.J. Use of the combined Lifshitz-van der Waals and Lewis acid-base approaches in determining the apolar and polar contributions to surface and interfacial tensions and free energies. J. Adhes. Sci. Technol. 2002, 16, 669–677. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, M. Using surface free energy method to study the cohesion and adhesion of asphalt mastic. Constr. Build. Mater. 2013, 47, 254–260. [Google Scholar] [CrossRef]
- Habal, A.; Singh, D. Comparison of Wilhelmy plate and Sessile drop methods to rank moisture damage susceptibility of asphalt—Aggregates combinations. Constr. Build. Mater. 2016, 113, 351–358. [Google Scholar] [CrossRef]
- Ameri, M.; Ziari, H.; Yousefi, A.; Behnood, A. Moisture Susceptibility of Asphalt Mixtures: Thermodynamic Evaluation of the Effects of Antistripping Additives. J. Mater. Civ. Eng. 2021, 33, 4020457. [Google Scholar] [CrossRef]
- Zhang, J.; Bao, L. Determination of asphalt mixture’s viscoelastic constitutive parameters for pavement response analysis using dynamic modulus transformation. Constr. Build. Mater. 2022, 315, 125729. [Google Scholar] [CrossRef]
- Bi, Y.; Guo, F.; Zhang, J.; Pei, J.; Li, R. Correlation analysis between asphalt binder/asphalt mastic properties and dynamic modulus of asphalt mixture. Constr. Build. Mater. 2021, 276, 122256. [Google Scholar] [CrossRef]
- Fu, Q.; Xie, Y.; Long, G.; Niu, D.; Song, H. Dynamic mechanical thermo-analysis of cement and asphalt mortar. Powder Technol 2017, 313, 36–43. [Google Scholar] [CrossRef]
- Yang, G.; Wang, X.; Zhou, X.; Wang, Y. Experimental Study on the Phase Transition Characteristics of Asphalt Mixture for Stress Absorbing Membrane Interlayer. Materials 2020, 13, 474. [Google Scholar] [CrossRef] [PubMed]
- Soliman, H.; Shalaby, A. Characterizing the Low-Temperature Performance of Hot-Pour Bituminous Sealants Using Glass Transition Temperature and Dynamic Stiffness Modulus. J. Mater. Civ. Eng. 2009, 21, 688–693. [Google Scholar] [CrossRef]
- Tan, Y.; Guo, M. Study on the phase behavior of asphalt mastic. Constr. Build. Mater. 2013, 47, 311–317. [Google Scholar] [CrossRef]
- Arabani, M.; Hamedi, G.H. Using the Surface Free Energy Method to Evaluate the Effects of Polymeric Aggregate Treatment on Moisture Damage in Hot-Mix Asphalt. J. Mater. Civ. Eng. 2011, 23, 802–811. [Google Scholar] [CrossRef]
- Ghabchi, R.; Singh, D.; Zaman, M.; Tian, Q. Application of Asphalt-aggregates Interfacial Energies to Evaluate Moisture-induced Damage of Warm Mix Asphalt. Procedia Soc. Behav. Sci. 2013, 104, 29–38. [Google Scholar] [CrossRef]
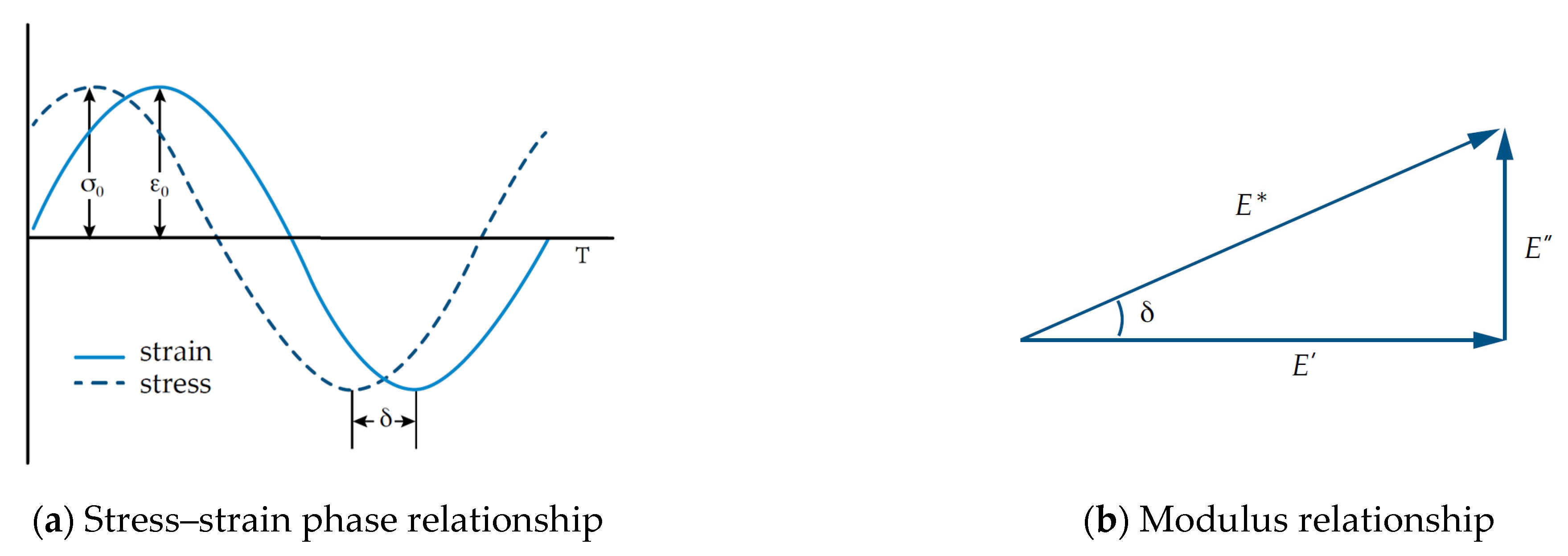

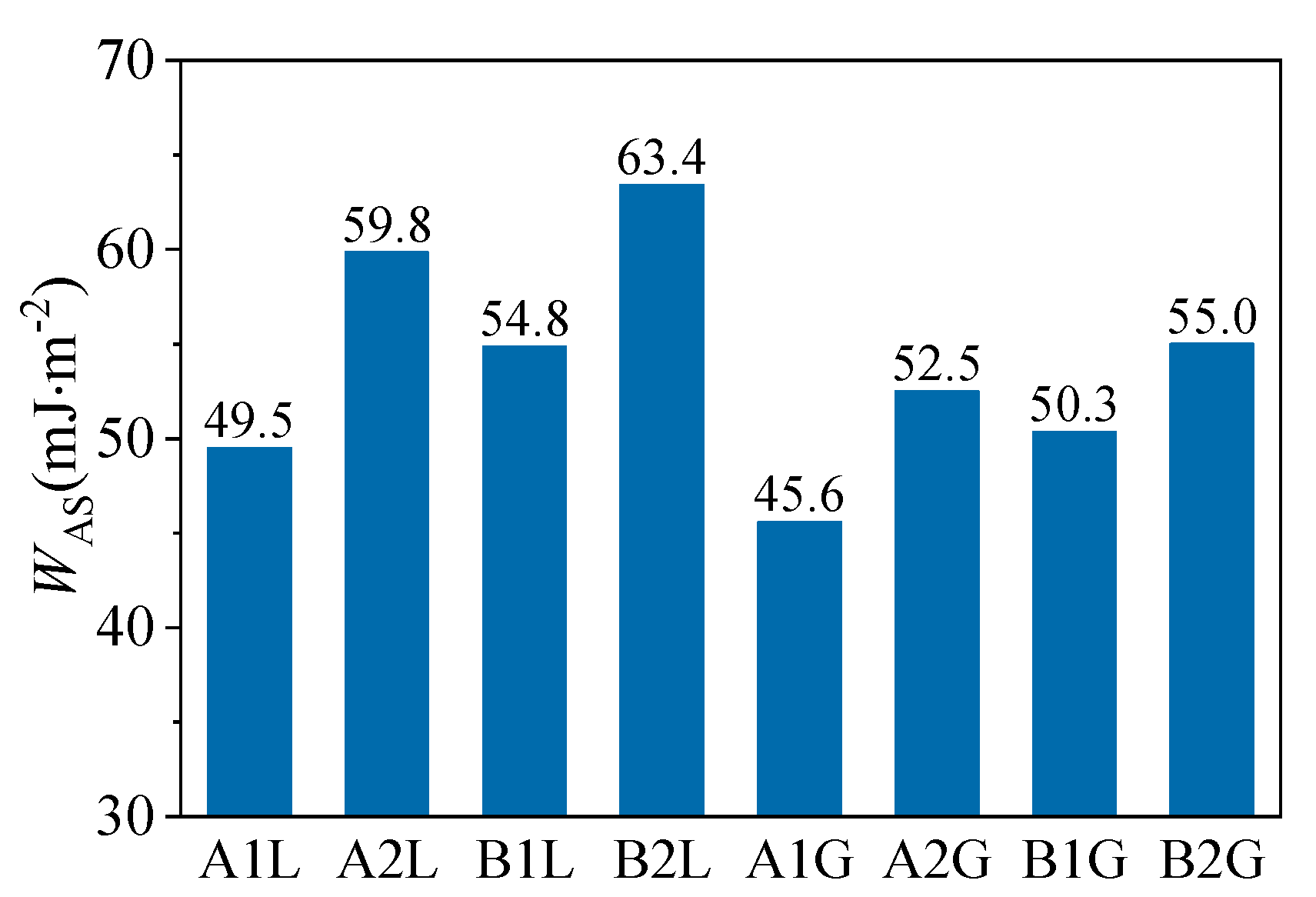

| Asphalts | Penetration (25 °C) /0.1 mm | Softening Point /°C | Ductility (10 °C) /cm | Viscosity (60 °C) /Pa·s | PG Grade |
|---|---|---|---|---|---|
| A1 | 69 | 46.9 | 88 | 258 | PG64-22 |
| A2 | 71 | 46.7 | >100 | 194 | PG64-22 |
| B1 | 51 | 76.7 | 58 | 14339 | PG76-22 |
| B2 | 49 | 64.4 | 68 | 3107 | PG70-22 |
| Sieve Size (mm) | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 |
| Passing rate (%) | 97.9 | 58.1 | 30.3 | 21.2 | 15.3 | 12.0 | 9.4 | 8.5 | 7.0 |
| Strain Amplitude | Frequency | Heating Rate | Temperature Range |
|---|---|---|---|
| 50 με | 1 Hz | 2 °C/min | −35 °C to 75 °C |
| Materials | SFE (mJ·m−2) | γd (mJ·m−2) | γp (mJ·m−2) | |
|---|---|---|---|---|
| Asphalt | A1 | 12.5 | 10.2 | 2.3 |
| A2 | 19.5 | 17.5 | 2.0 | |
| B1 | 15.5 | 12.7 | 2.7 | |
| B2 | 22.3 | 20.3 | 2.0 | |
| Aggregate | L | 51.0 | 32.2 | 18.8 |
| G | 57.3 | 16.9 | 40.4 |
| Asphalt Mixture | y0 | xc | w | A | R2 | RMmin/% | TRM/°C |
|---|---|---|---|---|---|---|---|
| A1L | 80.2 | 36.1 | 18.2 | −16.3 | 0.9383 | 63.8 | 36.1 |
| A2L | 87.9 | 37.8 | 20.8 | −22.0 | 0.9776 | 65.8 | 37.8 |
| B1L | 73.5 | 59.3 | 23.4 | −21.9 | 0.9673 | 51.6 | 59.3 |
| B2L | 77.2 | 48.8 | 19.9 | −20.7 | 0.9818 | 56.5 | 48.8 |
| A1G | 78.5 | 40.5 | 29.6 | −25.2 | 0.9809 | 53.4 | 40.5 |
| A2G | 75.5 | 38.2 | 10.5 | −25.6 | 0.8238 | 49.8 | 38.2 |
| B1G | 77.3 | 58.4 | 38.1 | −49.1 | 0.9994 | 28.2 | 58.4 |
| B2G | 58.1 | 60.7 | 24.2 | −22.4 | 0.9885 | 35.7 | 60.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhang, W.; Wei, J.; Xiong, Y.; Qiao, Y.; Wang, X. Quantifying Moisture Susceptibility in Asphalt Mixtures Using Dynamic Mechanical Analysis. Coatings 2025, 15, 1109. https://doi.org/10.3390/coatings15091109
Wang Y, Zhang W, Wei J, Xiong Y, Qiao Y, Wang X. Quantifying Moisture Susceptibility in Asphalt Mixtures Using Dynamic Mechanical Analysis. Coatings. 2025; 15(9):1109. https://doi.org/10.3390/coatings15091109
Chicago/Turabian StyleWang, Yanzhu, Wanguo Zhang, Jincheng Wei, Yuanshun Xiong, Yuanhui Qiao, and Xudong Wang. 2025. "Quantifying Moisture Susceptibility in Asphalt Mixtures Using Dynamic Mechanical Analysis" Coatings 15, no. 9: 1109. https://doi.org/10.3390/coatings15091109
APA StyleWang, Y., Zhang, W., Wei, J., Xiong, Y., Qiao, Y., & Wang, X. (2025). Quantifying Moisture Susceptibility in Asphalt Mixtures Using Dynamic Mechanical Analysis. Coatings, 15(9), 1109. https://doi.org/10.3390/coatings15091109





