Abstract
The composition design of asphalt mixtures plays a pivotal role in determining pavement performance and durability. To improve skeleton stability, paving uniformity, and mechanical strength, this research proposes a three-dimensional optimization framework for asphalt mixture design, focusing on aggregate gradation and optimum asphalt content. A skeleton-dense and anti-segregation gradation optimization method was developed by integrating a previously established skeleton-dense model with a segregation tendency prediction approach. In parallel, a mechanically driven method for determining optimum asphalt content was proposed by introducing the maximum migration shear stress as a performance-based alternative to the conventional Marshall stability parameter. Research results show that asphalt mixtures designed and compacted with the optimized gradation exhibit significantly enhanced high-temperature stability, while maintaining satisfactory low-temperature cracking resistance and moisture susceptibility. Field validation was conducted through the construction of a trial pavement section using the optimized gradation under recommended mixing and compaction temperatures. The resulting pavement demonstrated excellent compaction, strong resistance to segregation, and a highly stable spatial structure. These findings confirm the effectiveness of the proposed methodology in enhancing the high-temperature deformation resistance and overall structural integrity of asphalt mixtures.
1. Introduction
Early damage and insufficient durability of asphalt pavements have become prominent issues, with the service life of some expressways falling significantly short of their design expectations [1]. Asphalt mixture is a multi-scale and multi-phase material comprising aggregates, asphalt, and voids, and characterized by heterogeneity, discontinuity, and randomness. Its segregation behavior, compaction characteristics, and mechanical properties during construction and service directly influence the pavement performance and durability [2]. A fundamental solution to solve the above problem lies in further optimizing the aggregate gradation design from the perspective of the asphalt mixture itself. This approach aims to improve pavement uniformity, compaction quality, and mechanical performance.
Coarse and fine aggregates of varying sizes interact in specific proportions to form the aggregate gradation. An optimized aggregate gradation enables asphalt mixture to exhibit superior paving uniformity and a stable internal structure, which largely determines the pavement performance and service life of asphalt roads [3]. Extensive research has been conducted in the field of pavement engineering on aggregate gradation design methods. Representative approaches include the Marshall design method, the Superpave method, and the Bailey method [4]. The Marshall design method is a typical volumetric design approach, in which asphalt mixture specimens are prepared using a Marshall compactor. By measuring key physical and mechanical indicators, such as volume of air voids (VV), asphalt saturation, voids in mineral aggregate (VMA), Marshall stability, and flow value, this method determines a reasonable aggregate gradation [5]. Although the Marshall design method is widely adopted internationally, it relies heavily on empirical, coarse preliminary gradation selection based on specifications, without establishing a correspondence to the segregation behavior and compaction characteristics [6].
The Superpave design method utilizes control points and a restricted zone to design aggregate gradation, with particular emphasis on enhancing the high-temperature stability of asphalt mixtures. However, the definition of the restricted zone remains qualitative, lacking a quantitative evaluation criteria [7]. Rocha et al. [8] established the correlation between VMA, asphalt saturation, and the fatigue cracking and rutting resistance of asphalt mixtures. And then proposed a balanced mix design method that comprehensively considers both low-temperature crack resistance and high-temperature stability of asphalt mixtures. The Bailey method regards the skeleton structure formed by the interlocking and friction of coarse aggregates as the load-bearing framework of asphalt mixtures, thereby enhancing the high-temperature stability of asphalt pavements. However, it does not consider the aggregate segregation behavior of the asphalt mixture [9]. Sha et al. [10,11] proposed that coarse aggregates interlock to form a skeleton, while fine aggregates and mineral filler interact with asphalt to fill the skeleton voids. Based on this, they developed a gradation design method for Stone Asphalt Concrete (SAC). By controlling the boundary size between coarse and fine aggregates and the passing rates of key sieves, the asphalt mixture achieves low VV, high density, and impermeability, as well as excellent high-temperature stability. Zhang et al. [12,13] proposed the Coarse Aggregate Void Filling (CAVF) method for gradation design to enhance the high-temperature deformation resistance and low-temperature crack resistance of asphalt pavements.
Asphalt is a temperature-sensitive material. At relatively low temperatures, its viscosity increases substantially, enhancing its adhesive effect primarily between the mineral aggregates [14]. With temperature increasing, the viscosity of asphalt dramatically decreases, causing the asphalt film to gradually lose its adhesive function and transition into a lubricating effect at the aggregate interfaces [15]. Therefore, the asphalt content determines the thickness of the asphalt film on the aggregate surface, which significantly affects the mixing quality, compaction efficiency, and mechanical performance of asphalt mixture. Sun et al. [16] utilized a self-developed aggregate contact friction tester to investigate the influence of asphalt content on the interfacial interaction between asphalt and aggregates. Husain et al. [17] used the indirect tensile cracking test to evaluate the effect of asphalt content on the low-temperature cracking resistance of asphalt mixtures. Based on asphalt content, they predicted the cracking tolerance index using an artificial neural network model. Yan et al. [18] conducted variable-speed edge tests to investigate the effects of asphalt content and gradation characteristics on the workability of asphalt mixtures. The results showed that increasing asphalt content and coarser aggregate particles significantly raised the mixing resistance, thereby reducing construction workability. Wu et al. [19] explored the intrinsic relationship between the composition characteristics and pavement performance of asphalt mixtures and proposed a method for determining the mastic content in flowable mastic asphalt mixtures. Zhang et al. [20] employed atomic force microscopy and fluorescence microscopy to analyze the adhesion performance of epoxy asphalt prepared with varying base asphalt contents. They found that the epoxy asphalt exhibited the strongest bonding to aggregates when the base asphalt content was 40%. Li et al. [21] analyzed the rheological properties and low-temperature crack resistance of warm-mix recycled asphalt using dynamic shear rheometer (DSR) and low-temperature bending beam tests, and determined the optimum content of recycled asphalt. Kumar and Archilla [22] determined the optimum asphalt content by investigating the variation in VV and aggregate voids with asphalt content, thereby simplifying the Marshall design procedure. Li and Wang [23] reproduced the formation process of the skeleton structure and voids in asphalt mixtures using the discrete element method and estimated the optimum asphalt content based on the void ratio and skeleton stability. Hamzah et al. [24] applied the response surface methodology to analyze the coupled relationship among warm-mix additives, compaction temperature, and asphalt content, and determined the optimum asphalt content and warm-mix additive dosage.
In summary, most existing asphalt mixture design methods still rely on empirical and volumetric approaches, which lack mechanistic insight into how aggregate structure and asphalt content influence compaction behavior, segregation tendency, and long-term performance. As a result, these traditional approaches often fail to prevent construction defects such as segregation and insufficient compaction, which directly contribute to early pavement damage. A well-developed design method should not only target mechanical performance but also account for workability to ensure construction quality.
Based on this, this research proposes a three-dimensional optimization framework for asphalt mixture design, integrating segregation prediction and skeleton densification models to optimize gradation for both compaction quality and segregation resistance. Moreover, an optimum asphalt content determination method is developed based on mechanical parameters. The flowchart of the asphalt mixture composition optimization design is shown in Figure 1. By bridging the gap between material design and construction performance, the proposed method provides a practical and scalable tool for improving pavement durability, reducing maintenance frequency, and supporting quality control in real-world paving projects. It offers valuable guidance for highway engineers and decision-makers seeking to improve the reliability and longevity of asphalt pavements under increasingly demanding service conditions.
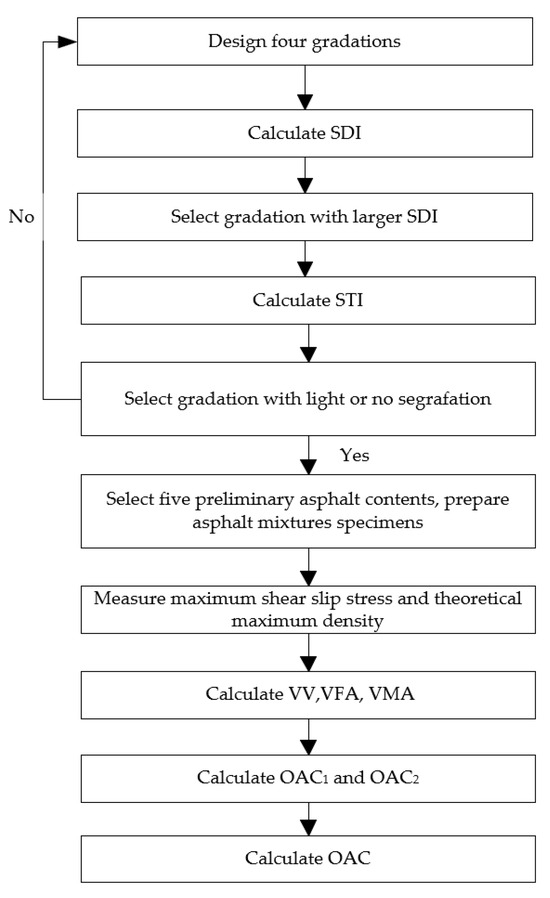
Figure 1.
The flowchart of the asphalt mixture composition optimization design.
2. Materials
2.1. Aggregate
The coarse aggregates and fine aggregates are made from limestone produced in Shaanxi, China. The bulk specific gravity of coarse and apparent specific gravity of fine aggregates were tested according to the test methods of aggregate for highway engineering (JTG E42-2005) [25], as shown in Table 1 and Table 2. The mineral powder is made of finely ground limestone, with main technical properties listed in Table 3.

Table 1.
The bulk specific gravity of coarse aggregate.

Table 2.
The apparent specific gravity of coarse aggregate.

Table 3.
The main technical index of mineral powder.
From Table 3, the main technical properties of the mineral powder meet the requirements specified in the Technical Specification for Construction of Highway Asphalt Pavements (JTG F40-2004) [26].
2.2. Gradation
The correlation between multi-dimensional geometric fusion characteristics and skeleton contact properties was studied using five AC asphalt mixture, as recommended in the Technical Specification for Construction of Highway Asphalt Pavements (JTG F40-2004), which is AC-13U, AC-13M, AC-13L, AC-16M, and AC-20M. The gradation curves are given in Figure 2.
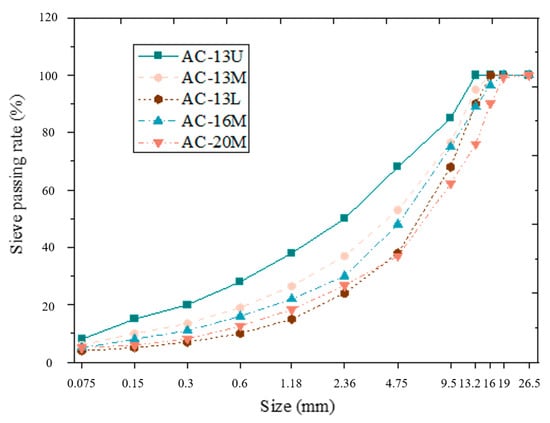
Figure 2.
The gradation curve.
2.3. Asphalt
The binder used is 90# base asphalt (Shell Bitumen, Beijing, China) and the physical and chemical performance indexes of the asphalt were tested in accordance with the Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering (JTJ 052-2000)) [27]. And its main technical indexes were shown in Table 4.

Table 4.
The requirements of asphalt technical indexes and test results.
3. Experiment Methods
3.1. Multi-Dimensional Geometric Fusion Characteristics
The AIMS II system is used to measure the sphericity (SP), texture index (TX), and angularity gradient (GA) of each aggregate size fraction. Based on the geometric parameters, relative density, volume, surface area, and perimeter of aggregates, a spread-reorganization principle is proposed to construct a composite geometric characteristics calculation model for characterizing the angularity, texture, and shape properties of graded mineral aggregates [28], as shown in Equations (1)–(3).
where CISP is the composite shape index; CITX is the composite texture index; gi is the relative volume density; GA is the angularity gradient; TX is the texture index; Vwi is the shape-weighted volume of aggregate particles; SAwi is the shape-weighted surface area of aggregate particles; Cwi is the shape-weighted perimeter of aggregate particles; and di is the weighted perimeter of aggregate.
Multi-dimensional geometric fusion characteristic (MGI) is proposed to characterize the comprehensive performance of graded aggregates in terms of geometric features, particle size, and aggregate quantity. The gray rational analysis is employed to evaluate the contributions of composite shape characteristics, composite texture characteristics, and composite angularity characteristics to multi-dimensional geometric fusion characteristics, thereby an establishing computational model for MGI, as presented in Equation (4):
MGI = 0.276 × CISP + 0.334 × CITX + 0.39 × CIGA
3.2. Three-Dimensional Dynamic Compaction Model
The surface morphology of aggregates was captured using three-dimensional blue light scanning, which bought from ZG Technology, Tianjin, China. The surface mesh was optimized in software Geomagic Studio (2013) and imported into discrete element software PFC (5.0 Suite) to establish an aggregate sieving model for verifying gradation accuracy. Microscopic parameters of contact model were determined based on dynamic modulus tests and uniaxial penetration tests. Considering the characteristics of gyratory compaction, a high-precision three-dimensional discrete element dynamic compaction model for asphalt mixtures was developed using wall servo control and a rigid clump-based loading plate, as shown in Figure 3 [29].
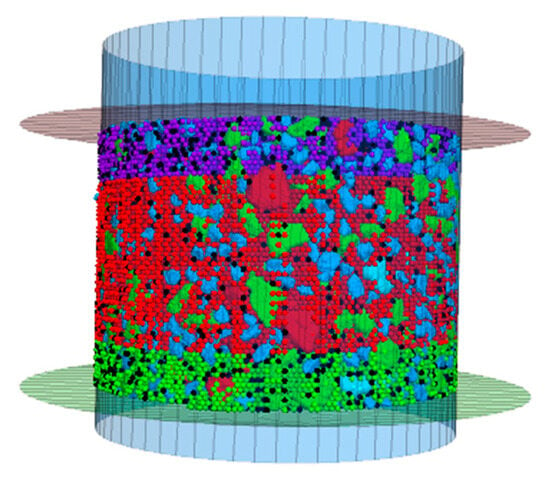
Figure 3.
Virtual gyratory compaction model.
3.3. Shear-Slip Test
To fully account for the migration status of aggregates in asphalt mixture under loading, a custom axial shear-slip resistance device is developed to investigate the shear-slip resistance of asphalt mixtures, as shown in Figure 4. Based on extensive testing and the force transmission mechanisms of aggregate particles, the maximum slip-induced shear stress was proposed as an index to evaluate the shear-slip deformation resistance of asphalt mixtures [30].

Figure 4.
Shear-slip resistance device for asphalt mixture.
4. Optimization Gradation Design Method for Skeleton Stability and Segregation Resistance
The macroscopic and mesoscopic performance variations in asphalt mixtures are primarily governed by intrinsic factors, including aggregate properties, asphalt binder characteristics, and gradation. In contrast, construction-related parameters—such as mixing and compaction temperatures, compaction equipment, and the number of roller passes exert a notable but secondary influence, acting as extrinsic factors. To isolate the effects of aggregate gradation, the inherent behavior of graded aggregates was evaluated under optimal mixing and compaction temperatures using identical aggregate and asphalt binder types, thereby simulating ideal construction conditions. Through appropriate gradation design, the stability of the coarse aggregate skeleton and the bonding–filling capability of the asphalt mastic can be effectively ensured.
4.1. Evaluation Method for Skeleton Compactness and Anti-Segregation Gradation
4.1.1. Prediction Method for Skeleton Compactness Strength
The mechanical strength of asphalt mixtures mainly originates from the contact network formed by the interlocking and friction of coarse aggregates, as well as the bonding–filling functions of the asphalt mastic. In previous studies, skeleton contact models of the coarse aggregate and bonding–filling models of the asphalt mastic were developed. Based on that, a skeleton-dense model was established to evaluate the high-temperature shear resistance of asphalt mixtures [31]. The calculation methods are presented in Equations (5)–(7).
where SCI is the skeleton contact index, FCITX is the bonding–filling index, SDI is the skeleton-dense index; F is the contact force between two coarse aggregates, mm; θ is the angle between the loading direction and the contact force, °; j and k are the two contacting aggregates; V, S, and R are the volume, surface area, and radius of two contacting aggregate, respectively, mm; Sm and Sv are the surface area of the asphalt mortar and voids, respectively, mm2.
The calculation of the skeleton-dense index (SDI) requires parameters such as contact force, contact length, and the surSface areas of asphalt mortar and voids, which must be obtained through a virtual compaction model of the asphalt mixture. However, establishing a virtual compaction model of asphalt mixtures requires professional researchers and involves a relatively high level of operational complexity in practical engineering. The multi-dimensional geometric fusion characteristics unify the geometric characteristics of shape, texture, and angularity with their particle size and mass fraction across different aggregate size fractions. As the primary source of interlocking and friction strength among aggregates, it fundamentally determines the skeleton stability of asphalt mixtures. This investigation calculates the multi-dimensional geometric fusion index (MDI) of AC-13U, AC-13M, AC-13L, AC-16M, and AC-20M mixtures, and measures the SCI of these five gradations using a three-dimensional dynamic compaction model. As presented in Figure 5, MDI exhibits a strong linear correlation with the SCI, with a R2 as high as 0.904. Therefore, MDI is used in place of SCI to calculate the skeleton compactness index of asphalt mixtures, as shown in Equation (8). The calculation of MDI requires only the physical and geometric parameters of aggregates, which not only reduces the complexity of engineering applications, but also enables the prediction of the skeleton compactness strength of asphalt mixtures at the design stage.
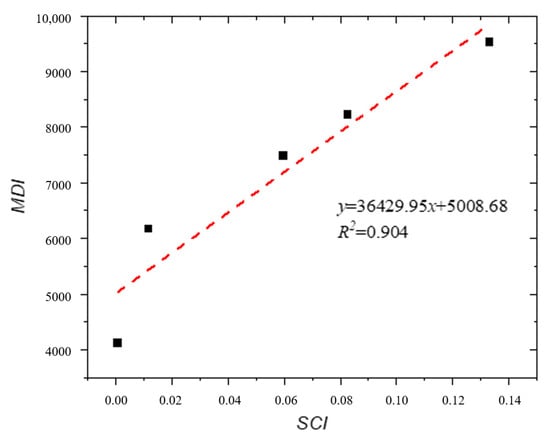
Figure 5.
The correlation between SCI and MDI.
4.1.2. Prediction Method for Gradation Segregation
The segregation tendency in asphalt mixtures is closely related to the interaction among coarse aggregates, particularly their contact and friction behavior during transportation and paving. To quantify this interaction, a composite angularity index (CIGA) was built, which combines the angularity, particle size, and mass fraction of coarse aggregates. This index was designed to reflect the combined contribution of each particle group to the overall contact strength of the mixture.
The composite angularity index of graded aggregates exhibits a strong linear correlation with the aggregate segregation index. Moreover, the composite angularity characteristics determine the segregation behavior of aggregates, thereby influencing the compaction properties and pavement performance of asphalt mixtures. To establish a scientifically robust method for predicting segregation in asphalt mixtures, transitioning from “post-evaluation” to “pre-prediction” of segregation issues, a model for predicting the segregation tendency of asphalt mixtures was developed using the composite angularity index, as shown in Equation (9).
where STI is the segregation tendency index of aggregates and CIGAmax is the maximum composite angularity index. According to the recommended gradation ranges for upper and middle layers in the Technical Specifications for Construction of Highway Asphalt Pavements (JTG F40-2004), the CIGAmax is adopted as that of SMA-20L.
Aggregate segregation causes changes in the particle size distribution, leading to variations in CIGA. The established composite angularity characteristic model requires only the input of the mass fraction of each aggregate size fraction to accurately calculate the composite angularity index for any gradation. During the optimization of asphalt mixture gradation, it is recommended to prioritize gradation types with no or slight segregation tendency, as indicated in Table 5.

Table 5.
Evaluation criteria for aggregate segregation in asphalt mixtures.
4.2. Optimization Design Method for Skeleton Compactness and Anti-Segregation Gradation
Considering the multi-scale and multi-phase particulate characteristics of asphalt mixtures, the segregation behavior and compaction characteristics were thoroughly analyzed based on the interface effects within the particle system. Accordingly, an aggregate segregation prediction model and a skeleton-dense model were developed to evaluate the segregation tendency and structural stability of asphalt mixtures. These two predictive models reflect the inherent properties of asphalt mixtures, namely the extent of segregation and structural strength under the conditions of optimal asphalt content and optimal mixing and compaction temperatures. However, the models are still in the preliminary stage of development and are applicable only to gradations using the same type of asphalt. Therefore, it is proposed to use the segregation tendency index and the skeleton-dense index to guide aggregate gradation optimization, focusing on minimizing segregation and enhancing the stability of the spatial structure.
Step 1: Select the gradation with optimal spatial structural stability, using the following method:
(1) Calculate the skeleton-dense index (SDI) of the designed gradation and rank the structural stability of both the designed gradation particle system and the corresponding median gradation particle system based on the SDI values.
(2) Selection criteria: ①A higher SDI indicates better structural stability of the gradation; ②The SDI of the selected gradation should be greater than that of the corresponding median gradation.
(3) If the gradation does not meet the criteria in Procedure (2), redesign the gradation until the SDI satisfies the selection requirements.
Step 2: Further optimize the anti-segregation gradation using the segregation tendency prediction model, as detailed below:
(1) Calculate the segregation tendency index of graded aggregates (STI) for each gradation.
(2) Evaluate the segregation tendency of each gradation; asphalt mixtures that tend to exhibit light or no segregation generally demonstrate better pavement performance.
(3) If the gradation that meets the spatial structural stability requirements does not satisfy the criteria in Procedure (2), redesign or adjust the gradation accordingly.
Taking the AC gradation as an example, the optimal selection of gradations with stable spatial structure and anti-segregation performance was conducted. It is generally considered that asphalt mixtures prepared with AC-type gradation exhibit a suspended dense structure, with an insignificant skeleton structure. This is also a key factor contributing to the generally good compactability of AC asphalt mixtures, while simultaneously accounting for their relatively limited resistance to high-temperature deformation. To address this issue, the proposed skeleton-dense model was applied to evaluate and analyze the AC-16 aggregate gradation, aiming to identify gradations with improved skeleton interlocking effect and compactness. Four gradation schemes were designed for comparative analysis, as shown in Table 6.

Table 6.
AC-16 designed gradation and gradation range values.
The skeleton-dense index (SDI) and the segregation tendency index of aggregates (STI) for Gradation 1, Gradation 2, Gradation 3, Gradation 4, and the median gradation were calculated using the skeleton-dense model and the segregation tendency prediction model, as presented in Table 7.

Table 7.
SDI and STI values of each designed gradation.
As shown in Table 7, the SDI values of the gradations follow the order: Gradation 1 > Gradation 2 > Median Gradation > Gradation 3 > Gradation 4. This indicates that the asphalt mixture formed with Gradation 1 exhibits the most stable internal structure, followed by Gradation 2 and the median gradation, while Gradation 3 and Gradation 4 show relatively poorer structural stability.
According to the calculated STI values, Gradation 1 and Gradation 2 are prone to slight segregation of coarse aggregates, while Gradation 3 and Gradation 4 tend to exhibit moderate segregation of coarse aggregates. The median gradation is more likely to experience segregation of fine aggregates. When slight segregation of coarse aggregates occurs, the skeleton–bonding system formed by the interaction between aggregate geometry and asphalt is the most stable, resulting in optimal rutting resistance, moisture stability, and low-temperature crack resistance of the asphalt mixture. In summary, Gradation 1 is identified as the optimal gradation.
The widely used Marshall method in practical engineering was adopted to optimize the selected AC-16 gradations, and a comparative analysis was conducted with the gradation optimized using the proposed skeleton compactness and anti-segregation design method. First, the initial asphalt content was selected, and the physical properties of asphalt mixtures for each gradation were measured, including bulk density, VV, VMA, and VCAmin. Among the gradations that met all the required physical indexes, the one with relatively high VMA and moderate VV was selected as the optimal gradation. The measured physical properties of the four designed gradations are presented in Table 8.

Table 8.
The calculation result and physical indexes of each designed gradation.
According to the Technical Specifications for Construction of Highway Asphalt Pavements (JTG F40-2004), the VV of AC-type asphalt mixtures should range between 3% and 6%. As shown in Table 8, Gradation 3 and Gradation 4 fail to meet the design requirements, while Gradation 1 and Gradation 2 fall within the specified range. In addition, the VMA must be greater than 17%, and VCAmin should be less than or equal to VCADRC. Both Gradation 1 and Gradation 2 satisfy these criteria.
Between them, Gradation 2 presents a more moderate air void content (VV) than Gradation 1, and is therefore selected as the optimal gradation according to the Marshall design method. However, this selection differs from the one identified using the method proposed in this study.
The Marshall method focuses primarily on volumetric parameters such as VV and bulk density, but does not establish a mechanistic link to high-temperature performance. Its indicators—such as stability and flow—are largely empirical, and cannot reliably reflect the actual mechanical strength of asphalt mixtures under service conditions.
In contrast, the gradation optimization method proposed in this study is grounded in mechanical principles, emphasizing skeleton compactness and resistance to segregation. It allows for the selection of gradations that form a more stable aggregate skeleton with stronger densification capacity, improving the internal structure of suspended dense mixtures and enhancing their high-temperature deformation resistance.
Moreover, the integration of a segregation tendency prediction model ensures that the selected gradation maintains structural stability throughout the entire construction process—including transportation, mixing, paving, and compaction. This contributes to better construction quality and long-term performance of asphalt pavements.
5. Method for Determining the Optimum Asphalt Content Based on Mechanical Parameters
5.1. The Applicability of Mechanical Parameters
Currently, the Marshall method is mainly used for asphalt mixture design in road engineering in China. However, with the continuous increase in traffic volume and the frequent occurrence of overloading, early damage of asphalt pavements has become increasingly prominent. As a result, asphalt mixtures designed using the Marshall method often fail to meet the quality standards required for modern road engineering. Relevant studies have shown that the stability index used in the Marshall design method has certain limitations and does not directly correlate with the performance of asphalt mixtures in actual pavement applications. In addition, the Marshall method relies solely on physical evaluation indicators, whereas the performance of asphalt mixtures is primarily characterized by mechanical parameters. Therefore, to address the limitations of the Marshall method, this study introduces mechanical parameters into the asphalt mixture design by conducting interface shear-slip tests, in which the maximum shear-slip stress is used to replace the traditional stability index. This approach directly links the mixture design with the high-temperature stability of asphalt pavements.
As shown in Figure 6, the Ꚍsl of asphalt mixtures with different gradations exhibits a similar trend with increasing asphalt content; it first increases and then decreases, showing a distinct peak. However, the asphalt content corresponding to the peak value varies across the different gradations, as listed in Table 9.
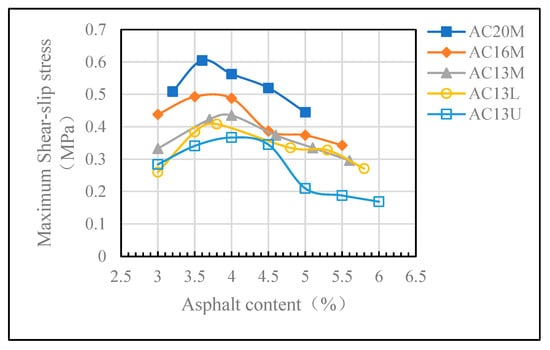
Figure 6.
The correlation between asphalt content and maximum shear-slip stress.

Table 9.
The asphalt content corresponding to the maximum shear-slip stress for each gradation.
The maximum shear-slip stress reflects the degree of contact among aggregate particles and the bonding strength within the asphalt mixture, indirectly indicating its resistance to deformation. The bonding strength of the mixture is closely related to the asphalt content.
As the asphalt content continues to increase, free asphalt begins to form and accumulate, which not only increases the voids between aggregates, but also reduces the bonding strength. As a result, the asphalt mixture becomes more susceptible to shear deformation, leading to a decrease in the maximum shear-slip stress. Therefore, under a given gradation, the asphalt mixture exhibits highest deformation resistance at the asphalt content corresponding to the peak shear-slip stress. Therefore, using the maximum shear-slip stress as a mechanical parameter in asphalt mixture design is both practical and feasible.
5.2. The Design Procedure for Asphalt Mixture Based on Mechanical Parameters
The design of asphalt mixtures involves both aggregate gradation and the determination of optimal asphalt content. In this study, the optimal asphalt content was determined through a combination of the Marshall method and interface shear-slip tests, incorporating both physical and mechanical performance indexes. The test results confirmed that the mechanical index is strongly correlated with the high-temperature rutting resistance of asphalt mixtures. Moreover, by introducing a mechanical parameter that reflects the contact and migration behavior of aggregate particles from a meso-scale perspective, the asphalt mixture design procedure becomes more precise and better aligned with the actual mechanical performance of the pavement.
According to the Technical Specification for Construction of Highway Asphalt Pavements (JTG F40-2004), the specific design steps are as follows:
(1) Specimen preparation.
Determine the amount of each aggregate size fraction based on the designed aggregate gradation.
Estimate an initial optimal asphalt content based on practical experience and then adjust it by ±0.5% and ±1.0% to obtain five different asphalt contents. Prepare Marshall specimens for each asphalt content accordingly.
(2) Test the physical and mechanical indexes.
① Test and calculate the physical indexes of mixtures with different asphalt–aggregate ratios using the conventional Marshall method, including density, VV, voids in mineral aggregate, and asphalt saturation.
② Measure the maximum shear-slip stress of asphalt mixtures with different asphalt–aggregate ratios using the localized load penetration migration test.
(3) Plot the relationship curves between each index and the asphalt content.
Plot the relationship curves between each performance index and the asphalt content. Based on these curves, determine the optimal asphalt content corresponding to the target value of each index. For example, let a1 be the asphalt content corresponding to the maximum density, a2 to the design air void content, a3 to the midpoint of the asphalt saturation range, and a4 to the maximum shear strength under slippage conditions.
(4) Calculate the optimal asphalt content.
① Calculate OAC1 according to Equation (10):
② According to the curves, determine the maximum and minimum asphalt content values, denoted as OACmax and OACmin. These values ensure that shear-slip stress, VV, VMA, and asphalt saturation meet the specified requirements. The design asphalt content OAC1 is then defined as the average of OACmax and OACmin.
③ Calculate the optimal asphalt content OAC.
The OAC represents the preliminarily determined optimum asphalt content for the given gradation. Based on this value, the asphalt mixture is further evaluated for its pavement performance, including high-temperature stability, low-temperature cracking resistance, moisture susceptibility, and durability.
The method of determining the optimum asphalt content by combining Marshall physical indices with micro-mechanical indexes offers the following advantages:
(1) The asphalt mixture design procedure can be directly linked to its high-temperature stability performance, enabling targeted improvements in pavement performance from the design stage.
(2) The interface shear-slip test for asphalt mixtures requires simple equipment, is cost-effective, provides rapid and convenient measurements, and ensures high accuracy.
(3) The method has a wide applicability range and can be used for various types of asphalt mixtures, such as AC, SMA, and OGFC. Additionally, the interface shear-slip test is compatible with specimens of any size, making it highly versatile.
5.3. Example of Asphalt Mixture Design Based on Mechanical Parameters
Based on the interface shear-slip test of asphalt mixtures, the maximum shear-slip stress is proposed as a design index. This index is used to replace the conventional Marshall stability value for determining the optimum asphalt content of the mixture. Using the selected AC16-S1 asphalt mixture, physical and mechanical indexes were measured at five different asphalt content levels, as shown in Table 10. The relationship curves between asphalt content and various physical and mechanical indexes for each gradation were plotted as shown in Figure 7.

Table 10.
The physical and mechanical indexes of AC-16 asphalt mixture.
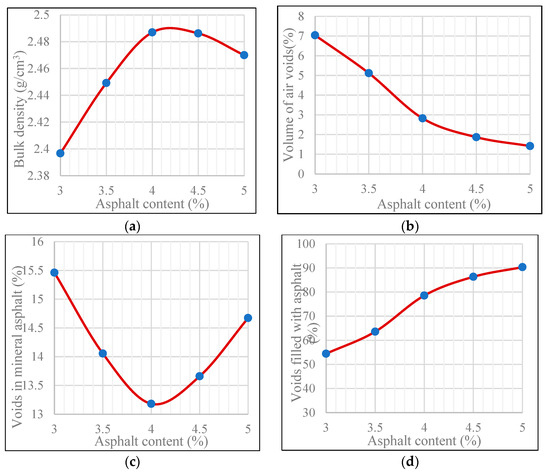

Figure 7.
The relationship between asphalt content and physical–mechanical indexes of AC-16 asphalt mixture. (a) Bulk density; (b) Volume of air voids; (c) Voids in mineral asphalt; (d) Voids filled with as-phalt; (e) Maximum shear-slip stress.
According to the experimental curves, the optimum asphalt content is determined using the maximum shear-slip stress as the mechanical index, following the conventional Marshall design method. The specific procedure is as follows:
(1) Determine the optimal asphalt content of asphalt mixture OAC1.
According to the relationship curves of each index, the asphalt contents corresponding to the maximum bulk density, the design VV, the midpoint of the asphalt saturation range, and the maximum shear-slip stress are determined as a1, a2, a3, and a4, respectively. The optimum asphalt content values that meet the specified criteria for each index are as follows:
Bulk density a1: The optimal asphalt content corresponding to maximum bulk density is 4.15%.
Volume of air voids a2: The optimal asphalt content corresponding to VV 4% is 3.72%.
Voids filled with asphalt a3: The optimal asphalt content corresponding to midpoint of VFA range is 3.71%.
Maximum shear-slip stress a4: The optimal asphalt content corresponding to maximum shear-slip stress is 3.75%.
Based on Equation (13), determine the average asphalt content OAC1, corresponding to the four indexes:
(2) Determine the optimal asphalt content of asphalt mixture OAC2.
According to the relationship curves, the maximum and minimum asphalt contents, denoted as OACmax and OACmin, are determined based on the requirement that the shear-slip stress, VV, VMA, and asphalt saturation all meet their specified limits. The design asphalt content OAC2 is defined as the average of OACmax and OACmin. The minimum asphalt content corresponding to the lowest limit of VMA (13.5%) is 3.76%, thus OACmax = 3.76% and OACmin = 3.71%.
(3) Determination of optimum asphalt content for asphalt mixture.
The optimum asphalt content is generally taken as the average of OAC1 and OAC2.
After verification, the VMA corresponding to the selected OAC fits the minimum required limit and falls within the lean asphalt region, to the left of the asphalt content corresponding to the lowest VMA.
Through the above procedure, the optimum asphalt content of the AC-16 graded asphalt mixture was finally determined to be 3.78%. Compared with the value obtained using the conventional Marshall design method (4.0%), the optimum asphalt content based on the maximum shear-slip stress is lower. Therefore, using the maximum shear-slip stress in place of Marshall stability for determining the optimum asphalt–aggregate ratio can result in significant asphalt savings.
6. Performance Evaluation
6.1. Laboratory Evaluation of Pavement Performance
To verify the reliability of the proposed gradation optimization method for skeleton densification and anti-segregation, as well as the determination of optimum asphalt content based on mechanical parameters, mixtures with Gradation 1 and Gradation 2 were selected and compacted at their respective optimum asphalt contents to form asphalt mixture specimens. Then, the pavement performances of the two mixtures were compared and analyzed through high-temperature, low-temperature, and moisture susceptibility tests.
High-temperature performance was evaluated through rutting tests and interface shear-slip tests. Low-temperature performance was assessed by low-temperature bending tests. Moisture susceptibility was tested using immersed Marshall tests and freeze–thaw splitting tests. The results are presented in Table 11, Table 12 and Table 13.

Table 11.
Test results of high-temperature performance evaluation.

Table 12.
Low-temperature bending test results.

Table 13.
Moisture susceptibility test results.
Two AC-16 asphalt mixtures were prepared using Gradation 1 and Gradation 2, referred to as AC-16-1 and AC-16-2, respectively. Performance test results indicate that AC-16-1 exhibits superior high-temperature deformation resistance compared to AC-16-2, while its low-temperature crack resistance and moisture stability are slightly lower. Nonetheless, both mixtures satisfy the relevant specification limits. These findings demonstrate that gradation optimized via the proposed skeleton-dense model effectively improves the rutting resistance of asphalt mixtures without compromising other key performance indicators. This confirms the applicability and engineering significance of the proposed method in enhancing high-temperature stability.
6.2. Evaluation of Pavement Non-Uniformity
A trial pavement section was constructed using the recommended AC-16-1 gradation to evaluate the paving uniformity of the asphalt surface. The mixing temperature of the asphalt mixture was 170 °C, with initial compaction at 150 °C and final compaction at 135 °C, using full-width paving. Utilizing the advantages of the PQI device for rapid, non-destructive, and large-sample testing, the variability in pavement density caused by aggregate segregation during construction was assessed. A statistical approach was then applied in the procession to quantitatively evaluate the paving uniformity and the anti-segregation performance of the asphalt mixture.
Table 14 presents the PQI test data for the intermediate asphalt layer. The sampling intervals were set as follows: 1.5 m in the transverse direction with 0.75 m from the pavement edge, and 2 m in the longitudinal direction. The collected PQI density data are shown in Table 14.

Table 14.
PQI pavement density test results (kg/m3).
The compaction degree at each measurement point in Table 14 was calculated, and the results are presented in Table 15.

Table 15.
Compaction degree data at measurement points (%).
As shown in Table 15 and Table 16, the compaction degree at most field measurement points falls within 94% to 97%, with a coefficient of variation of only 0.67%, well below the 1% threshold. This reflects good construction uniformity and consistent compaction quality across the trial pavement section. The results verify that the proposed gradation design method, which integrates skeleton densification and anti-segregation principles, is both practical and reliable. Moreover, the asphalt mixture exhibits favorable segregation resistance, further supporting its suitability for engineering application.

Table 16.
Statistical analysis of compaction parameters.
7. Conclusions
This study addressed the issues of uneven asphalt pavement paving and insufficient high-temperature deformation resistance by applying the previously proposed aggregate segregation tendency prediction method and the asphalt mixture skeleton-dense structure prediction model. The skeleton-dense and anti-segregation gradation optimization design method was then investigated. The main conclusions are summarized as follows:
- The skeleton-dense index (SDI), calculated using the skeleton-dense structure prediction model, is utilized to optimize gradations with stronger skeleton effects and higher densification capacity. Furthermore, the segregation tendency index (STI) is calculated to further select gradations with low segregation tendency or weak segregation potential. This ensures that the asphalt mixture maintains good high-temperature deformation resistance throughout different construction stages.
- A design method was proposed in which mechanical parameters are used to replace Marshall stability for determining the optimum asphalt content. A comparative analysis of the pavement performance between asphalt mixtures designed by the proposed method and those designed using the Marshall method revealed that the mixture prepared with the optimized gradation exhibited superior high-temperature stability, while its low-temperature cracking resistance and moisture stability still met specification requirements. These findings demonstrate that the proposed gradation design method effectively enhances the high-temperature deformation resistance of asphalt mixtures.
- A trial pavement section was constructed using the optimized gradation under the recommended mixing and compaction temperatures. The anti-segregation capability of the selected gradation was validated by evaluating the paving uniformity of the trial section. The results showed that the pavement exhibited a high degree of compaction with a low coefficient of variation, indicating that the optimized gradation not only possesses strong resistance to segregation but also forms a highly stable spatial structure.
In future research, the relationship between composite geometric characteristics and volumetric parameters obtained through the Marshall test method will be investigated, aiming to provide a technical foundation for developing a more scientific and effective asphalt mixture design methodology.
Author Contributions
Project administration, J.S.; funding acquisition, S.D. and J.S.; writing—original draft preparation, J.S.; investigation, L.F.; software, L.Z.; methodology, S.D. and S.H.; formal analysis, J.X.; validation, G.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Basic Research Plan in Shandong Province [grant number ZR2023QE122, ZR2024QE025], the Fundamental Research Funds for the Central Universities [grant number 300102213530], and the Open Research Project of Shandong Key Laboratory of Highway Technology and Safety Assessment [grant number SH202302].
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Abbreviation | Definition | Unit |
| CISP | Composite shape index | -- |
| CITX | Composite texture index | -- |
| CIGA | Composite angularity index | -- |
| MGI | Multi-dimensional geometric fusion characteristic | -- |
| SCI | Skeleton contact index | -- |
| FCITX | Bonding-filling index | -- |
| SDI | Skeleton-dense index | -- |
| STI | Segregation tendency index of aggregates | -- |
| VV | Volume of Air voids | % |
| VMA | Voids in mineral aggregate | % |
| VFA | Voids filled with asphalt | % |
| Ꚍsl | Maximum shear-slip stress | Mpa |
References
- Yang, J.J.; Huang, W.; Lü, S.T.; Qian, G.P.; Zheng, J.L. Strength theory and structural failure characteristics of asphalt pavement. J. Traffic Transp. Eng. 2024, 24, 131–143. [Google Scholar]
- Zhang, K.; Zhang, Z.Q.; Luo, Y.F.; Huang, S.Y. Accurate detection and evaluation method for aggregate distribution uniformity of asphalt pavement. Constr. Build. Materials. 2017, 152, 715–730. [Google Scholar]
- Gao, J.F.; Wang, H.N.; Bu, Y.; You, Z.P.; Zhang, X.; Irfan, M. Influence of Coarse-Aggregate Angularity on Asphalt Mixture Macroperformance: Skid Resistance, High-Temperature, and Compaction Performance. J. Mater. Civ. Eng. 2020, 32, 655–693. [Google Scholar]
- Liu, Z.Y.; Dong, Z.J.; Zhou, T.; Shan, L.Y.; Ma, X.Y. Review and prospects of performance enhancement of asphalt mixtures based on material informatics. China J. Highw. Transp. 2024, 37, 98–120. [Google Scholar]
- Coase, R.H. Marshall on method. J. Law Econ. 1975, 18, 25–31. [Google Scholar]
- Wang, X.; Zhou, Y.T.; Lan, J.R.; Cao, T.W.; Tang, N.; Ma, T.L. Study on gradation characteristics of Superpave asphalt concrete. J. Wuhan Univ. Technol. 2007, 29, 12–14. [Google Scholar]
- McGennis, R.B.; Anderson, R.M.; Kennedy, T.W.; Solaimanian, M. Background of SUPERPAVE Asphalt Mixture Design and Analysis; Federal Highway Administration, Office of Technology Applications: Washington, DC, USA, 1995. [Google Scholar]
- Rocha, M.L.; Aragao, F.T.S.; Nascimento, L.; Underwood, S. Balanced Mixture Design Framework for Asphalt Mixtures Based on Index-and Performance-Volumetrics Relationships. Transp. Res. Record. 2023, 2677, 233–245. [Google Scholar]
- Lü, W.J.; Chen, A.W.; Hao, P.W.; Dai, J.L. Influence of the parameter CA in the Bailey method on the performance of asphalt mixture. J. Chang’an Univ. Nat. Sci. Ed. 2005, 25, 5–8. [Google Scholar]
- Sha, Q.L. Design and Construction of Multi-Fractured Aggregate Asphalt Concrete (SAC) Series; People’s Traffic Press: Beijing, China, 2005; 272. [Google Scholar]
- Sha, Q.L. Aggregate gradation design methods of SAC and other coarse aggregate gap-graded mixtures. Highway 2005, 1, 143–150. [Google Scholar]
- Zhang, X.N.; Guo, Z.X.; Wu, K.H. Volume-based design method of asphalt mixtures. J. Harbin Univ. Civ. Eng. Archit 1995, 28, 28–36. [Google Scholar]
- Zhang, X.N.; Wang, S.H.; Wu, K.H.; Wang, D.Y. CAVF method for composition design of asphalt mixture. Highway 2001, 12, 17–21. [Google Scholar]
- Sun, X.; Qin, X.; Liu, Z.; Yin, Y.M. Damaging effect of fine grinding treatment on the microstructure of polyurea elastomer modifier used in asphalt binder. Measurement 2025, 242, 115984. [Google Scholar]
- Sun, X.; Xu, H.; Zheng, X.; Qin, X.; Guo, T.; Gao, J. Microscopic effect and mechanism of spray polyurea modifier on the asphalt binder: Experimental characterization and molecular dynamics simulations. Polymer 2025, 316, 127807. [Google Scholar]
- Sun, S.F.; Li, P.L.; Cheng, L.D.; Xiao, W.; Zhang, W.Q. Analysis of skeleton contact stability of graded aggregates system and its effect on slip creep properties of asphalt mixture. Constr. Build. Mater. 2022, 316, 125911. [Google Scholar]
- Husain, S.F.; Nazzal, M.D.; Manasreh, D.; Abbas, A.; Quasem, T.; Mansour, M. Using artificial neural networks to predict the cracking resistance change due to asphalt binder content variation. J. Mater. Civ. Eng. 2023, 35, 306–308. [Google Scholar]
- Yan, X.L.; Jing, H.J.; You, Q.L.; Ai, T. Mixing flow characteristics and workability index of asphalt mixtures. China Civ. Eng. J. 2019, 52, 120–128. [Google Scholar]
- Wu, K.H.; Wu, C.H.; Nie, G.H.; Cai, X.; Xu, X.Q.; Zheng, Y.Q.; Huang, W.K.; Wang, Z.X.; Huang, J.D. Theory and design method of flowable mastic asphalt mixture (FMA). China J. Highw. Transport. 2025, 38, 102–113. [Google Scholar]
- Zhang, F.L.; Yao, P.F.; Guo, X.X.; Zhang, L.; Huang, K. Study on the performance of epoxy asphalt with different matrix asphalt contents. J. Mater. Civ. Eng. 2023, 35. [Google Scholar] [CrossRef]
- Li, Z.X.; Guo, T.T.; Chen, Y.Z.; Bian, X.W. Study on rheological properties of warm mix large proportion recycled asphalt. Mater. Res. Express 2022, 9, 105101. [Google Scholar]
- Kumar, J.K.R.; Archilla, A.R. Simple Analytical Procedure to Estimate Optimum Asphalt Content. J. Test. Eval. 2025, 53, 414–429. [Google Scholar]
- Li, Y.M.; Ma, R.; Wang, X.; Cheng, P.; Chen, Y. Improvement effect of different modifiers on storage stability of high content SBS modified asphalt. Case Stud. Constr. Mater. 2024, 20, e02820. [Google Scholar]
- Hamzah, M.O.; Golchin, B.; Tye, C.T. Determination of the optimum binder content of warm mix asphalt incorporating Rediset using response surface method. Constr. Build. Mater. 2013, 47, 1328–1336. [Google Scholar]
- JTG E42-2005; Test Methods of Aggregate for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2005.
- JTG F40-2004; Technical Specifications for Construction of Highway Asphalt Pavements. Ministry of Transport of the People’s Republic of China: Beijing, China, 2004.
- JTJ 052-2000; Test Methods of Asphalt and Asphalt Mixtures for Highway Engineering. Ministry of Transport of the People’s Republic of China: Beijing, China, 2000.
- Su, J.F.; Li, P.L.; Sun, S.F.; Cheng, L.D.; Bi, J.Y.; Zhu, D.J. Effects of Composite Geometric Characteristics of coarse particles on Interface Interactions of Aggregate-asphalt System. Constr. Build. Mater. 2021, 287, 122750. [Google Scholar]
- Su, J.F.; Li, P.L.; Dong, S.H.; Su, H.F. Accurately Tracking Migration of Particles Based on Discrete-Element Simulation during Compaction Process. J. Mater. Civ. Eng. 2024, 36, 181–184. [Google Scholar]
- Su, J.F.; Li, P.L.; Wei, X.F.; Sun, S.F.; Zhu, L.; Dong, C. Analysis of interface interaction of aggregate-asphalt system and its effect on shear-slip behavior of asphalt mixture. Constr. Build. Mater. 2020, 264, 120680. [Google Scholar]
- Su, J.F.; Li, P.L.; Zhang, Y.L.; Dong, S.H.; Sun, S.F.; Jin, L. Aggregate migration and self-organisation properties of asphalt mixtures during compaction process. Road Mater. Pavement Des. 2024, 25, 1245–1264. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).