Abstract
Temperature dependence of the deformation behavior and the residual stress in 304 stainless steel beams with single-sided Al2O3 coatings of varying thicknesses are analyzed using the image relative method. The results demonstrate that, due to the mismatch of thermal expansion coefficient between the coating and substrate, residual stresses were produced, which caused the bending deformation of the single-side coated specimens. Moreover, coating thickness significantly influences the deformation behavior of specimens. Within the elastic deformation regime, the single-side coated specimens would exhibit alternating bending and flattening deformations in response to the fluctuations of temperature. The higher ratio of the coating thickness to the substrate thickness is, the smaller bending curvature of specimens becomes, and the lower residual compressive stresses in the coating are. For the specimens undergoing elastic deformation, residual stresses can be effectively calculated through the Stoney’s formula. However, as the thickness of coating is close to that of substrate (the corresponding specimens would be regarded as the laminated composites), plastic deformation occurs. And the residual stresses in those specimens vary along the direction of the thickness and the length. In addition, the residual stress decreased with increasing temperature because of the stress relaxation.
1. Introduction
Due to the mismatch of coefficient of thermal expansion (CTE) between the substrate and coating, residual stresses were inevitably be produced in the coated composites, which directly determines the reliability, stability and service life of the coated components [1,2,3]. A vast amount of literatures exist on the topic that suitable residual stress is helpful to improve the mechanical properties of the coated components, but too large residual stress causes the failure [4,5,6]. Consequently, exact measurement of residual stress is critically important to the coated components.
Stoney’s formula has long been one of the most important tools for understanding residual stress of the coated composites with bilayer structures [7,8,9]. Nevertheless, several assumptions were made to derive the Stoney’s formula. Actually, it is impossible to satisfy all assumptions of Stoney’s formula because of the complicated coating deposition. Among those assumptions, the most important requirement is that the coating and substrate must be in the elastic deformation regime, that is, there is no plastic deformation or fracture appeared in the composites. Therefore, residual stress of the single-faced coating samples with elastic deformation could be approximatively evaluated through the Stoney’s formula. According to this formula, the key of calculating residual stress is to measure the bending curvature radius of specimens at different temperatures. In this work, the image relative method, which is based on the comparation of photographs at different experimental conditions, was used to achieve the bending curvature radius of a specimen at elevated temperature. By taking images of the same sample at room and high temperatures, an increase in the deflection of the test piece can be achieved by comparing the two images. After that, the temperature dependence of residual stress in the coating could be clarified [10,11].
However, as the thickness of substrate is close to that of coating, the assumption of the Stoney’s formula is violated [7]. Those composites with thick coating can be regarded as the laminate composites. Since the residual stress in the laminated layer result from the interface stress, it varies along the direction of the thickness and the length. Bao et al. [12] proposed an analytical formula to calculate residual stress in the laminates with unsymmetrical structure. Results indicate that the residual stress changing along the length and the normal direction of interface. Additionally, both tensile stress and compressive stress exist in the same layer of the unsymmetrical laminates due to the existence of residual bending stress. F. Kroupa [13] investigated the residual macrostresses in thick, nonhomogeneous planar coating by using the methods of the isotropic theory of elasticity. It was observed that the residual macrostresses were related to the ratio of the coating thickness to the substrate thickness, the shapes of samples, the position and the temperature. Ghasemi et al. [14] calculated non-uniform residual stresses trapped in composite laminates by employing the integral hole drilling method. The results demonstrated that the residual stress of each ply has effect on the released strains of its underneath ply during hole drilling process and its effect on the released strains of the other plies is negligible. As presented above, stresses in the laminate composites are not material constant, which vary as the function of the position [15,16].
However, what is the critical coating-to-substrate thickness ratio that the single-side coated specimens maintain elastic deformation? And how are the residual stresses and the elastic deformation change with the variations of temperature? Otherwise, with the increase of coating thickness, plastic deformation may appeared. Then, how to calculate the residual stresses? And how are those bilayer samples deform with the increasing temperature? In order to clarify those questions, three different thicknesses of Al2O3 coating, 0.2 mm, 0.7 mm and 1.0 mm, were adopted to deposit on each 304 stainless steel bars through single-face coating method. Due to the mismatch of CTE between the substrate and coating, the one-side coated 304 stainless steel beams bent with different bending curvature radius. In this work, the image relative method was used to observe the detailed deformation process during the heating and the cooling process. And temperature dependence of the deformation behavior and the residual stress of 304 stainless steel beams single-face coated with different thickness of Al2O3 coatings are also analyzed.
2. Experimental
2.1. Sample Preparation
In this work, the degreased 304 stainless steel bars with the size of 5.0 mm × 70.0 mm × 1.0 mm and the γ-Al2O3 (Tianjin Kemiou Chemical Reagent Co., Ltd., Tianjin, China) were employed as the original crude materials. By using DH-2080 plasma spraying equipment (Shanghai Dahao Ruifa Thermal Spray Machinery Co., Ltd. Shanghai, China), Al2O3 coatings were deposited on one face (5.0 mm × 70.0 mm) of 304 stainless steel bars with different thickness of 0.2 mm, 0.7 mm and 1.0 mm, respectively. Consequently, the corresponding samples were noted as S1, S2 and S3, respectively. A mixture of argon and hydrogen was used as the plasma gas. And the detailed phase composition of Al2O3 coating deposited on 304 stainless steel bars was shown in Figure 1, which indicated that the main phases were α-Al2O3 and γ-Al2O3.
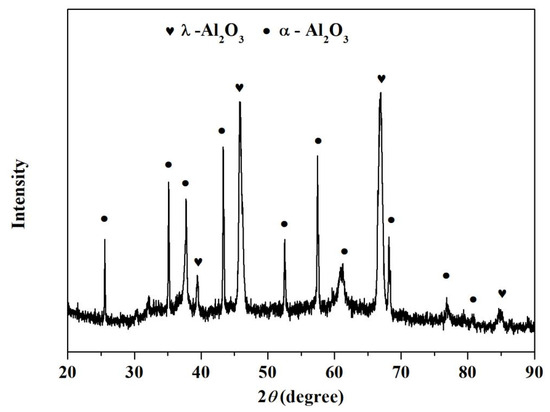
Figure 1.
XRD patterns of the Al2O3 coating fabricated in this work.
2.2. Characterization
Thickness of the coating and the substrate of all specimens in this work was identified by VHX digital microscope. The morphology was studied by scanning electron microscopy (SEM, Merlin, Zeiss, Oberkochen, Germany). To record the deformations of samples at elevated temperatures, Visual in-situ Tester (TianJin ZhongHuan Electric Furnace Co., Ltd., Tianjin, China) coupled with photography technology was used. In the process of testing shown in Figure 2, samples were heat-treated with a heating rate of 8 °C/min. And then, they were cooled to the room temperature (RT) with the rate of 8 °C/min. Based on the photos of the specimens under different experimental conditions, the temperature dependence of curvature radius were obtained.

Figure 2.
The flowchart of test procedure.
3. Results and Discussion
The single-side coated 304 stainless steel bars with different thickness of Al2O3 coatings were shown in Figure 3a–c. As shown in those figures, Al2O3 coatings with the thickness of 0.2 mm, 0.7 mm and 1.0 mm were deposited on each 304 stainless steel bar through single-face coating method, respectively. The ratio of the coating thickness to the substrate thickness (h/H) is chosen as 0.2, 0.7 and 1.0, respectively. In addition, the continuous and tight interface in Figure 3d illustrates that a good interface bonding was successfully achieved between the coating and substrate. Generally, few pores can be found in the Al2O3 coatings, which indicates that specimens prepared in this work have high density.

Figure 3.
The single faced coating composites with different thickness of Al2O3 coating: (a–c) optical photographs; (d) SEM image of S1 sample.
Figure 4 shows the deformation behavior of samples during the heating process. Owing to the CTE of Al2O3 coating is lower than that of 304 stainless steel substrate, the specimens exhibit apparent convex deformation which revealed that the residual stress in the Al2O3 layer (which is located on the convex surface of specimen) is compressive in nature. It’s worth noting that the temperature at which the bent beam specimens deformed into the flat shape completely was defined as the zero-stress temperature (Tzero, at which the residual stress in the coating is near zero) [17]. As illustrated in Figure 4a–c, due to the stress relaxation, the bending curvature radius of bent samples increased as the temperature rose from RT to Tzero. And it can be concluded that the Tzero of S1 sample and S2 sample was 280 °C and 540 °C, respectively. As the temperature reached to Tzero, the bent S1 and S2 samples deformed into the flat shape. However, the deformation could not be found in S3 sample until 304 stainless steel substrate melted completely. This can be attributed to the residual stress generated at the interface caused the plastic deformation behavior in S3 sample. Here, S3 sample can be regarded as unsymmetric laminate composite containing two layers in this study. Therefore, unlike S1 and S2 samples, the S3 sample can not deform into the flat shape as the temperature exceeds Tzero.
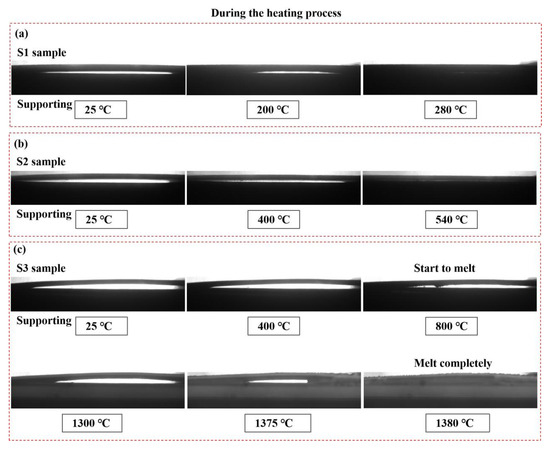
Figure 4.
In-situ recorded images of the single-sided coating samples during the heating process: (a) S1 sample; (b) S2 sample; (c) S3 sample.
The curvature radius (R) of S1 and S2 samples were determined from the deflection and the span of the one-side coated specimens shown in Figure 4. Based on the value of R, residual stress in the coating of S1 and S2 samples can be calculated by using Stoney’s formula. The material parameters required for the Stoney’s formula are the elastic modulus (Es, 200 GPa) and the Poisson’s ratio (, 0.29) of substrate. As the calculated results plotted in Figure 5, residual stresses in the coating of S1 and S2 samples decrease with the increasing temperature because of the relaxation of stress caused by high temperature [18]. Simultaneously, the residual stress of S1 sample was higher than that of S2 sample at the room temperature, which means that the thinner of coating is, the higher of residual stresses are. This is agree with the results of Ref. [19].
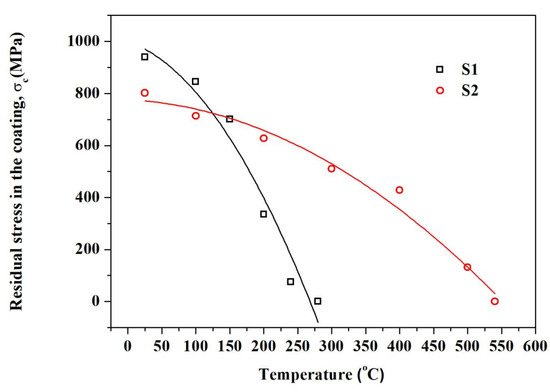
Figure 5.
Temperature dependence of the residual stress in the coating of S1 and S2 samples during the heating process.
However, due to the plastic deformation in S3 sample, the Stoney’s formula was limited in evaluating the residual stress of S3 specimens. According to our previous work [14,20], for a laminate composite composed of 2n (n = 1, 2, 3 …) homogeneous layers, the interface stresses are the source of residual stress in each layer. Since the interface stresses are not constant, which varies along the direction of the thickness and the length, the formula for the residual stresses in the coating () can be simplified to:
Here, h1 = h2 = 1.0 mm. y is the distance from the tensile surface to the neutral axis, −1 ≤ y ≤ 1. ΔT is the temperature difference from sintering temperature to testing temperature. x/L, 0 ≤ ≤1. Here, x is the distance from the testing position to the middle (x = 0) of the specimen; L is the half length of the bar.
From Equation (1), it can be concluded that the maximum absolute stress is at the middle of the bar. And it decreases from the maximum value at the middle of the specimen to zero at the ends of the specimen.
In Figure 6, the constantly changing of S1 and S2 samples during the secondary cooling process was exhibited. Due to the shrinkage distortion and stresses balance, the flat beam specimens gradually deformed into the circular arc shape again as the temperature fell from Tzero to RT, as demonstrated in Figure 6. Therefore, it can be assumed that the residual compressive stress was generated again during the secondary cooling process because of the dismatch of CTE between the coating and substrate. And the residual compressive stress increased with increasing the temperature difference from Tzero to testing temperature. Moreover, the tightly bound Al2O3 coating on 304 stainless steel substrates indicates perfect interface bonding. The above observations suggest that, in the elastic limit range, the one-side coated 304 stainless steel bars would repeat the deformation from straightening (during the heating process) to bending (during the cooling process) because of the varied residual stress generated in different temperature. However, in the specimens with thick coating, large residual stress would cause the irrecoverable plastic deformation.

Figure 6.
Deformations of S1 sample and S2 sample during the secondary cooling process: (a) S1 sample; (b) S2 sample.
The residual stress in the coating of S1 and S2 samples during the secondary cooling process can also be confirmed by the Stoney’s formula. As illustrated in Figure 7, the residual stress increases with the decreasing temperature. The result indicates that, owing to the difference of thermal expansion coefficient between the coating and substrate, residual stresses generated during the cooling process. And the bigger temperature difference (ΔT= Tzero − Ttesting) from zero-stress temperature (Tzero) to testing temperature (Ttesting) is, the higher the residual stresses are. As the temperature drops down to the room temperature for the second time, the maximum residual stresses of S1 and S2 samples were 803.3 MPa and 780.3 MPa, which are 14.5% and 2.7% lower than that in the first cooling process, respectively. This was attributed to the defect and interfacial failure caused by the repeated heating and cooling process.
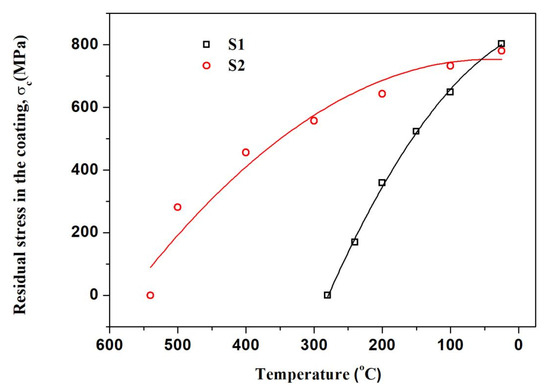
Figure 7.
Changes of residual stress in the coating (σc) of (a) S1 sample and (b) S2 sample during the secondary cooling process.
4. Conclusions
- In this work, the image relative method combined with Stoney’s formula were used to evaluate 304 stainless steel beams single face coated with different thickness of Al2O3 coatings at elevated temperature. Results show that the residual stress decreased with the increasing temperature because of the stress relaxation. Additionally, due to the defect and interfacial failure caused by the repeated heating and cooling process, the residual stress in Al2O3 coating damped after the secondary cooling process.
- The coating thickness may lead to different deformation behavior of specimens. As for S1 and S2 samples, elastic deformation generated in the single faced specimens. With the fluctuations of temperature, the single faced specimens exhibit alternating bending and flattening deformations. Moreover, the thinner the coating is, the bigger the bending curvature radius becomes, and the higher the residual stresses are.
- As the thickness of coating is close to that of substrate, plastic deformation would appear in the samples with lamellar structure. The residual stress in the coating of those specimens decreases from the maximum value at the middle of the specimen to zero at the ends of the specimen.
Author Contributions
Conceptualization: H.L. and D.W.; methodology: Y.B.; validation: L.Z. and Y.M.; data curation: J.Z.; writing—original draft preparation: H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Beijing Natural Science Foundation, Grant Number 2254097 and the Young Elite Scientists Sponsorship Program by Bast.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting the findings of the current study are available from the corresponding authors upon request.
Conflicts of Interest
The authors declare no conflict of interest. Author Haiyan Li, Lei Zhang, Yudi Mao, Jinlun Zhang, Detian Wan and Yiwang Bao were employed by China Testing & Certification International Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CTE | Coefficient of thermal expansion |
| R | The curvature radius |
| SEM | Scanning electron microscopy |
| Tzero | Zero-stress temperature |
| RT | Room temperature |
| Es | The elastic modulus |
| Vs | The Poisson’s ratio |
| Ttesting | Testing temperature |
References
- Zhang, X.; Xu, B.; Wang, H.; Wu, Y. Effects of oxide thickness, Al2O3 interlayer and interface asperity on residual stresses in thermal barrier coatings. Mater. Des. 2006, 27, 989–996. [Google Scholar] [CrossRef]
- Hsueh, C.; Fuller, E. Analytical modeling of oxide thickness effects on residual stresses in thermal barrier coatings. Scr. Mater. 2000, 42, 781–787. [Google Scholar] [CrossRef]
- Rabiei, A.; Evans, A.G.; Nusier, S.Q.; Ahmed, T. Failure mechanisms associated with the thermally grown oxide in plasma-sprayed thermal barrier coatings. Acta Mater. 2000, 48, 3963–3976. [Google Scholar] [CrossRef]
- Yao, X.; Olsson, E.; Wang, M.; Wang, J.; Cai, Q.; Peng, N.; Webb, R.; Zhao, Y. Xenon Ion Implantation Induced Surface Compressive Stress for Preventing Dendrite Penetration in Solid-State Electrolytes. Small 2022, 18, 2108124. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Guo, C.; Dai, W.; Li, Z.; Yue, H.; Li, Q.; Zhang, J.; Shang, Z. Effects of coating porosity, thickness and residual stress on stress and fatigue behavior of micro-arc oxidation coated aero Al alloys. J. Mater. Res. Technol. 2024, 31, 4139–4152. [Google Scholar] [CrossRef]
- Qi, Y.; Ban, C.; Harris, S.J. A New General Paradigm for Understanding and Preventing Li Metal Penetration through Solid Electrolytes. Joule 2020, 4, 2599–2608. [Google Scholar] [CrossRef]
- Stoney, G. The tensions of metalic films deposited by electroplating. Proc. R. Soc. 1909, 82, 172–177. [Google Scholar]
- Chen, P.-Y.; Wang, W.-C.; Wu, Y.-T. Experimental investigation of thin film stress by Stoney’s formula. Measurement 2019, 143, 39–50. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.-P. Applicability range of Stoney’s formula and modified formulas for a film/substrate bilayer. J. Appl. Phys. 2006, 99, 053513. [Google Scholar] [CrossRef]
- Li, H.Y.; Zhang, X.; Liu, X.G.; Wan, D.; Bao, Y. A way to control sintering deformation of Al2O3 components by gradient shrinkage. Ceram. Int. 2024, 50, 44716–44721. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Bao, Y. Fast evaluation of the temperature dependence of residual stress in ceramic coatings via an image relative method. Int. J. Appl. Ceram. Technol. 2024, 21, 3583–3589. [Google Scholar] [CrossRef]
- Bao, Y.; Su, S.; Yang, J.; Huang, Z. Residual stress analysis in unsymmetrical laminated ceramics by non-uniform strain model. J. Chin. Ceram. Soc. 2002, 30, 579–584. [Google Scholar]
- Kroupa, F. Residual stresses in thick, nonhomogeneous coatings. J. Therm. Spray Technol. 1997, 6, 309–319. [Google Scholar] [CrossRef]
- Ghasemi, A.; Taheri-Behrooz, F.; Shokrieh, M. Determination of non-uniform residual stresses in laminated composites using integral hole drilling method: Experimental evaluation. J. Compos. Mater. 2014, 48, 415–425. [Google Scholar] [CrossRef]
- Perreux, D.; Lazuardi, D. The effects of residual stress on the non-linear behaviour of composite laminates Part I. Experimental results and residual-stress assessments. Compos. Sci. Technol. 2001, 61, 167–175. [Google Scholar] [CrossRef]
- Tabatabaeian, A.; Ghasemi, A.R.; Asghari, B. Speciffcation of non-uniform residual stresses and tensile characteristic in laminated composite materials exposed to simulated space environment. Polym. Test. 2019, 80, 106147. [Google Scholar] [CrossRef]
- Li, H.-Y.; Hao, H.; Tian, Y.; Liu, X.-G.; Wan, D.; Bao, Y. Temperature dependence of flexural strength and residual stress of Al2O3 reinforced by kyanite coating. Ceram. Int. 2022, 48, 28745–28750. [Google Scholar] [CrossRef]
- Qi, B.; Absi, J.; Tessier-Doyen, N. Tessier-Doyen. Experimental and numerical study of the Young’s modulus vs temperature for heterogeneous model materials with polygonal inclusions. Comput. Mater. Sci. 2009, 46, 996–1001. [Google Scholar] [CrossRef]
- Li, H.; Hao, H.; Tian, Y.; Wang, C.; Bao, Y.; Wan, D. Effects of residual stresses on strength and crack resistance in ZrO2 ceramics with Alumina coating. J. Inorg. Mater. 2022, 37, 467–472. [Google Scholar] [CrossRef]
- Bao, Y.; Su, S.; Huang, J.-L. An uneven strain model for analysis of residual stress and interface stress in laminate composites. J. Compos. Mater. 2002, 36, 1769–1778. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).