Numerical and Experimental Study on Deposition Mechanism of Laser-Assisted Plasma-Sprayed Y2O3 Coating
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Assumptions
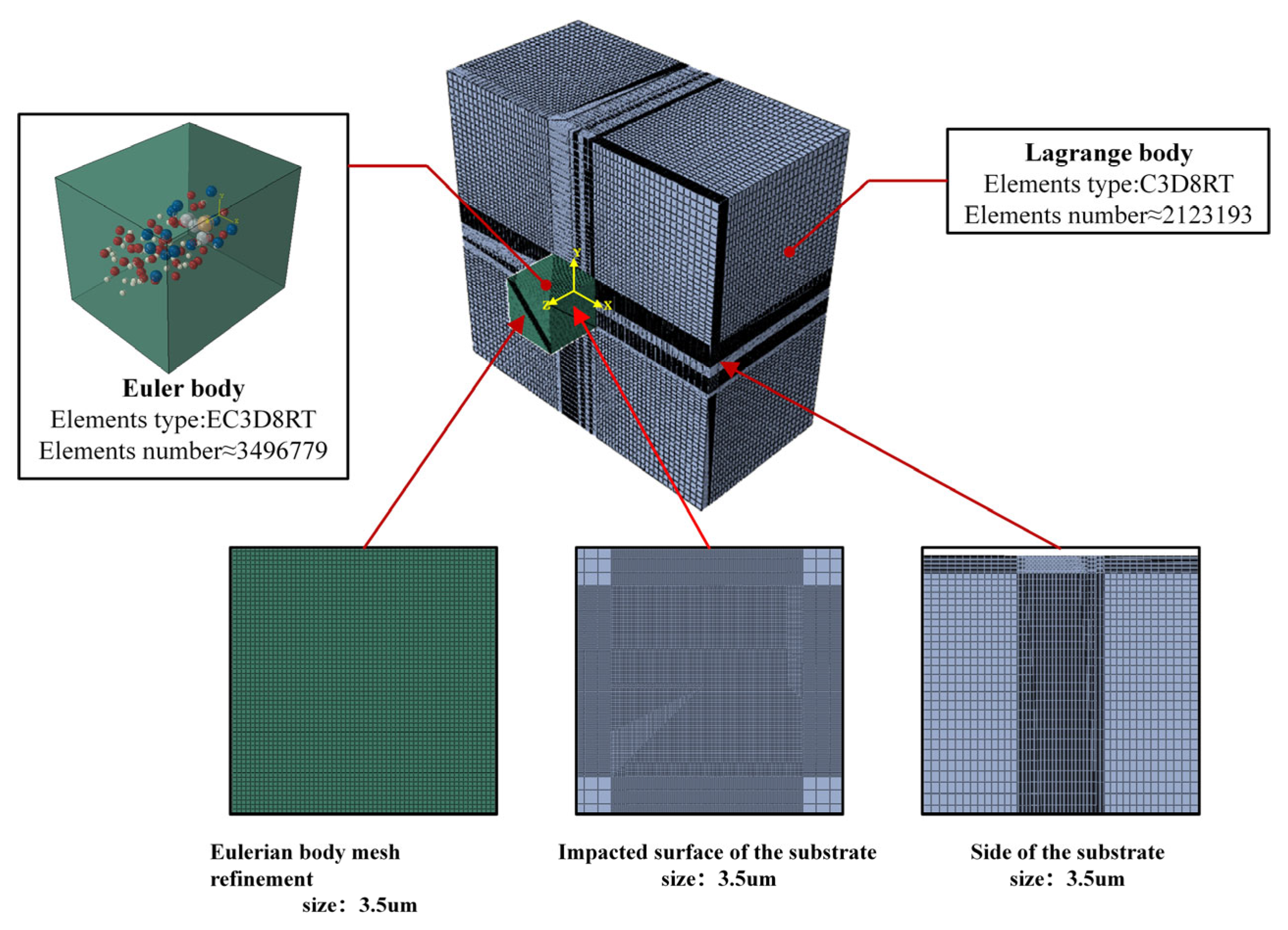
2.2. Computational Models and Methods
2.3. Material Model
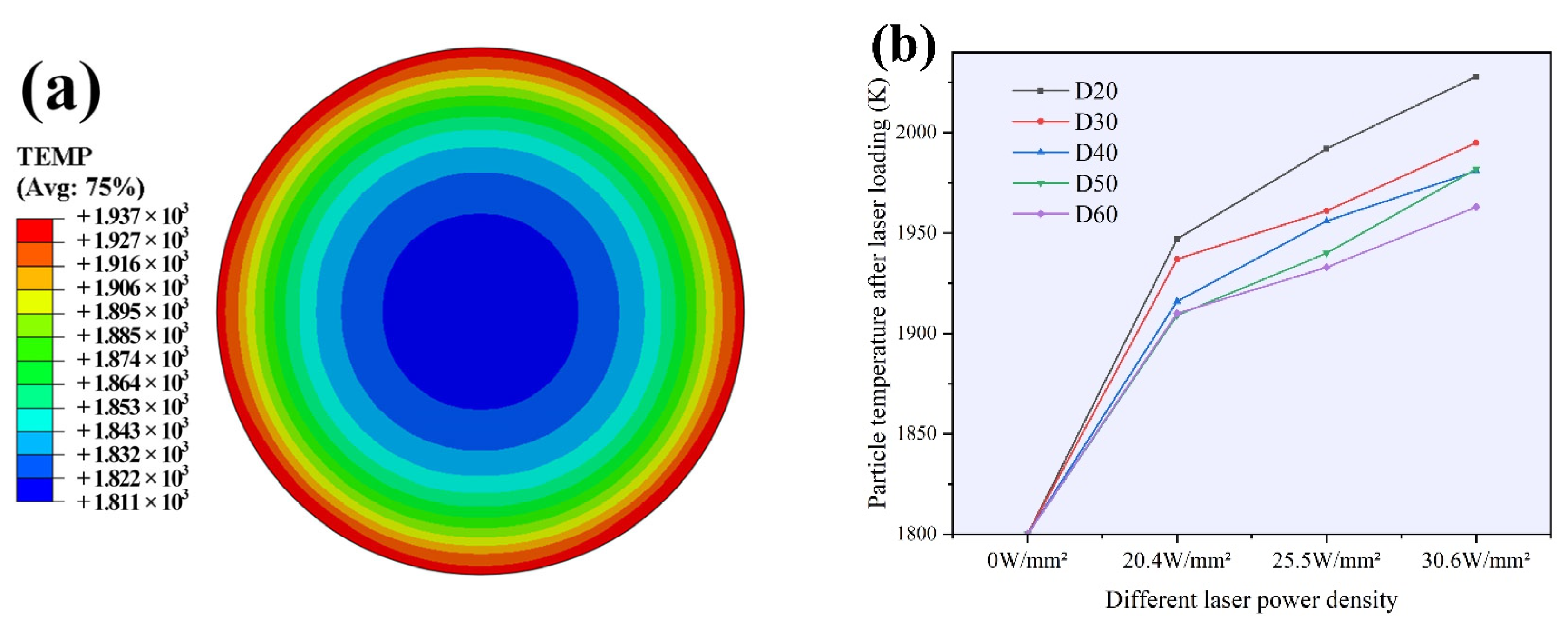
2.4. Laser Heat Source-Loading Model
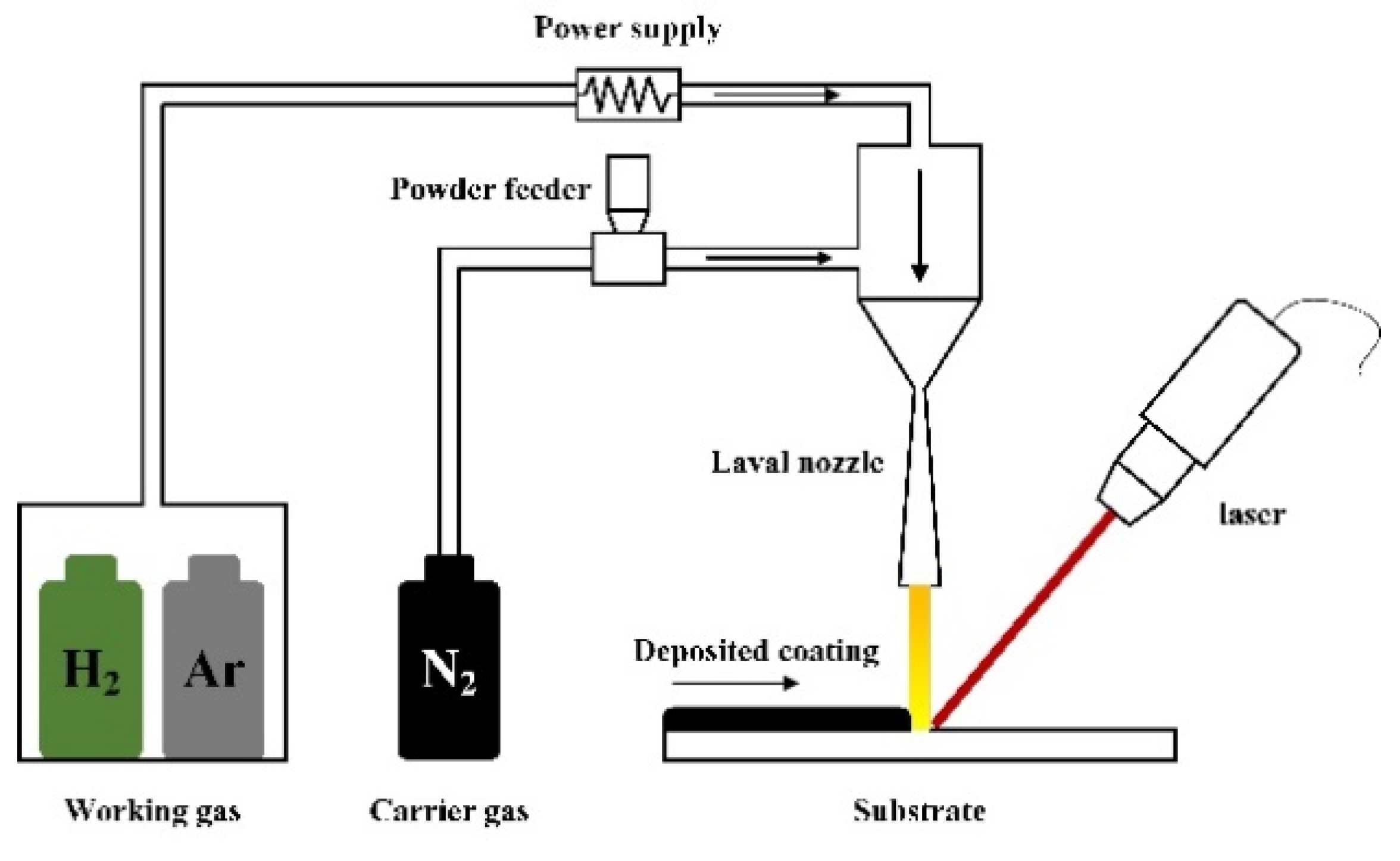
2.5. Experimental Methods
3. Numerical Simulation Results and Discussion
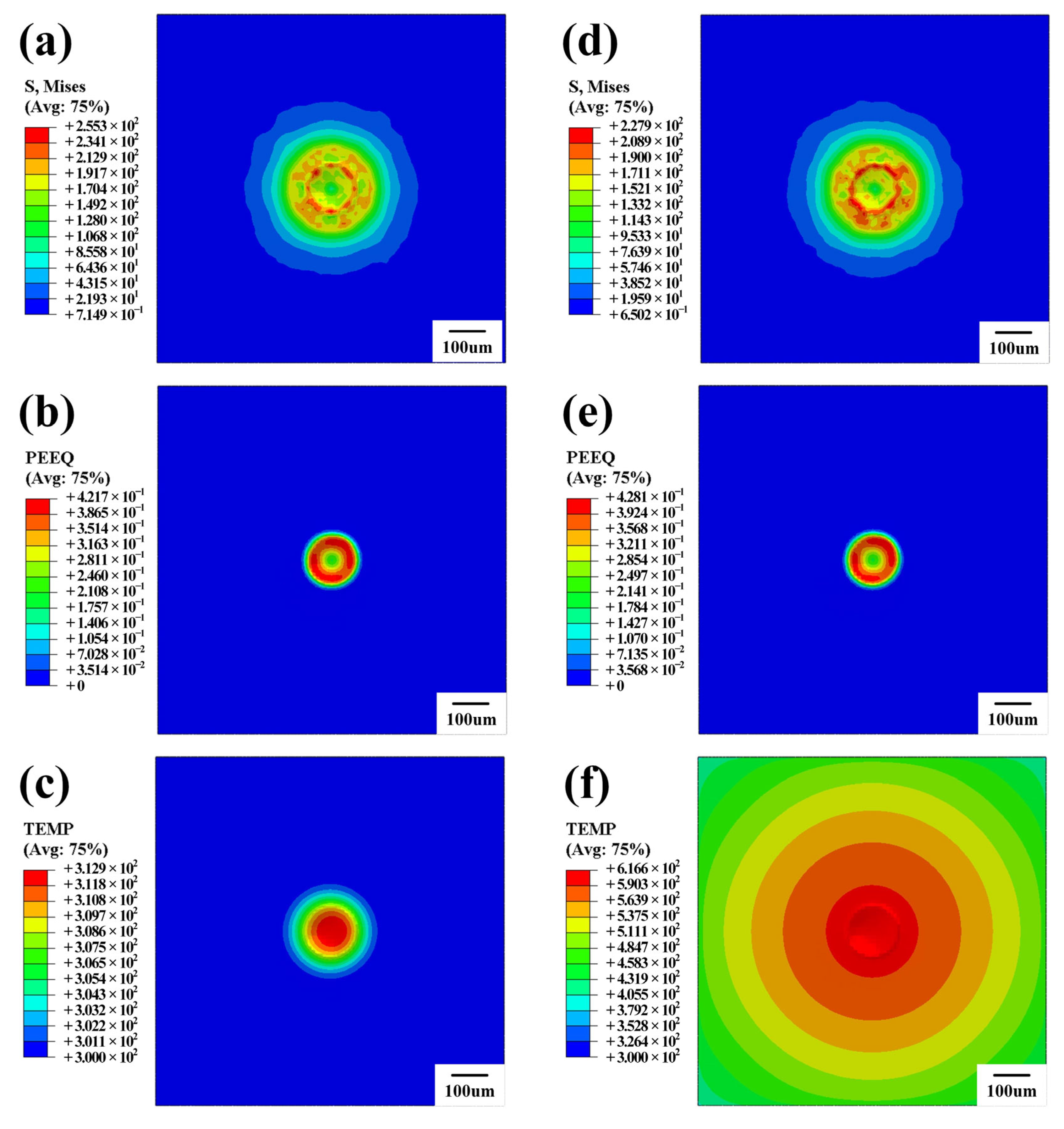
3.1. Single-Particle Laser Heat-Source Loading
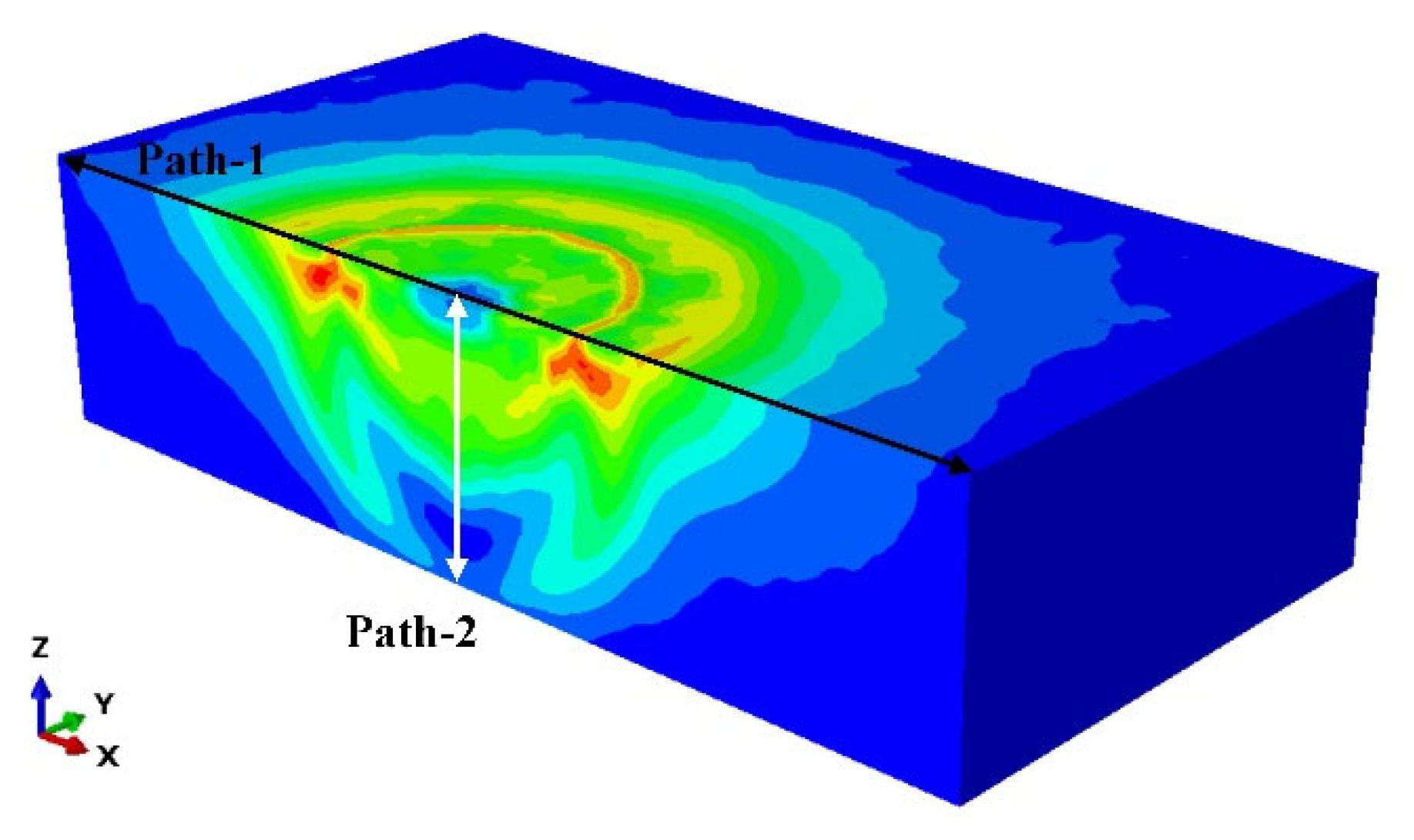
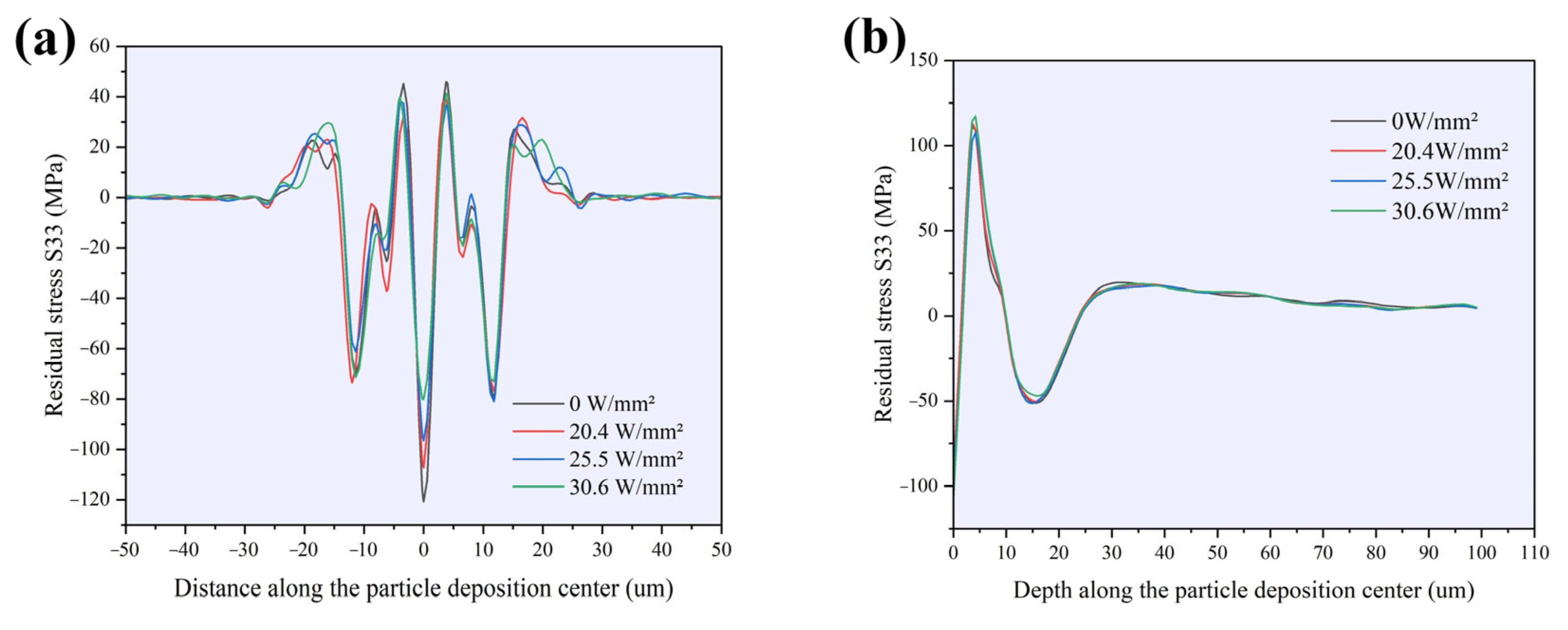
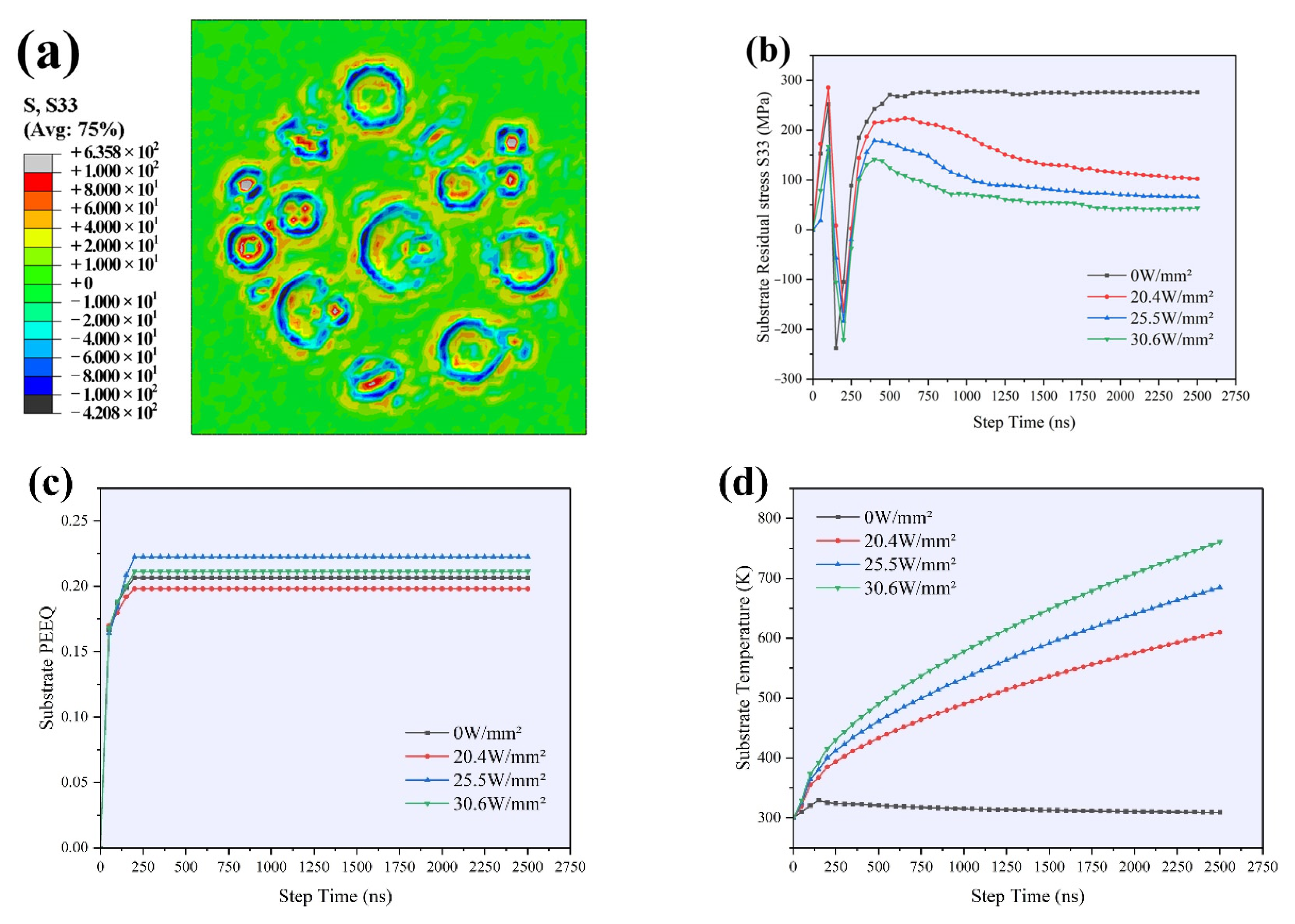
3.2. Multi-Particle Laser Thermal Source Loading
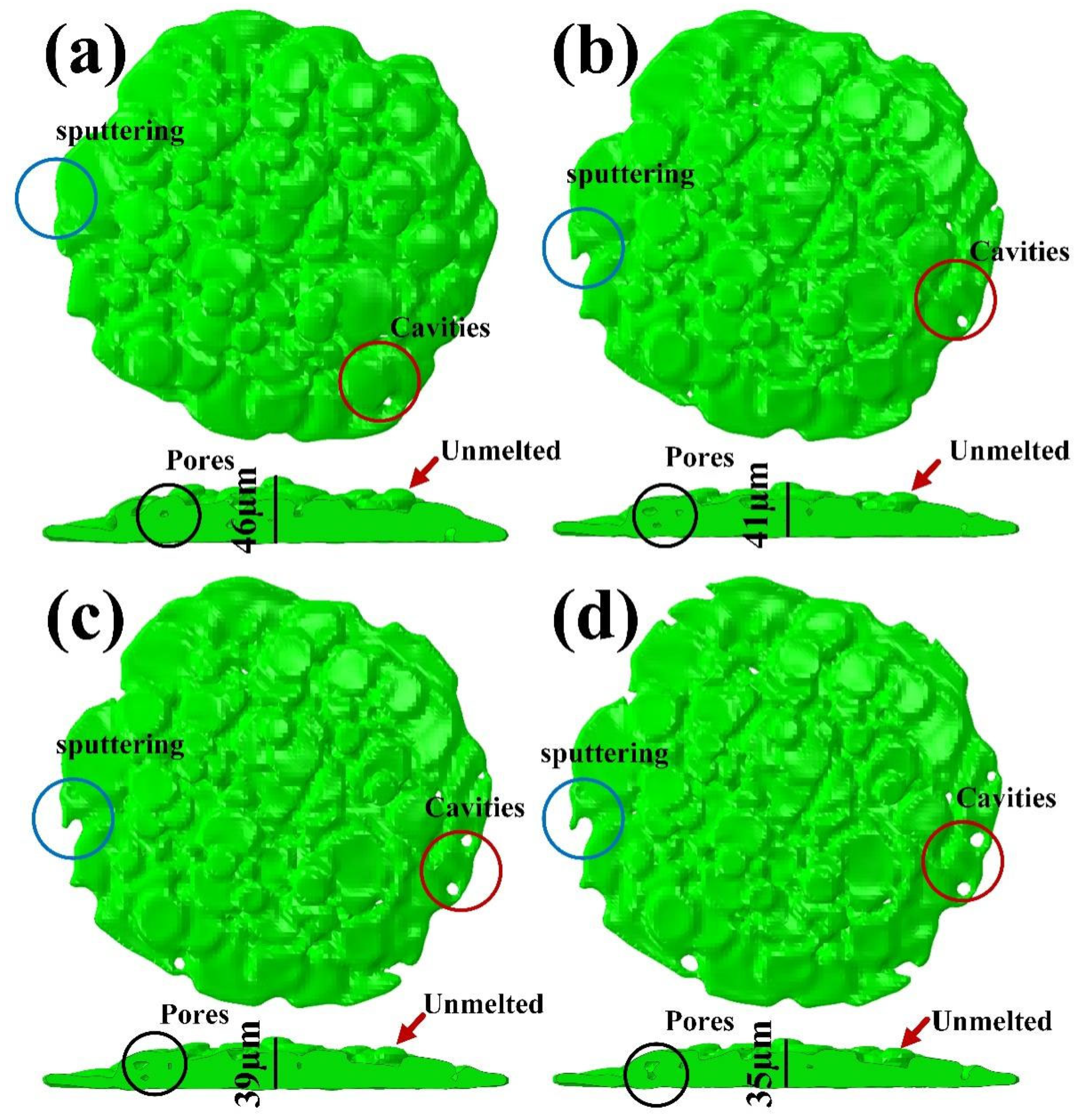
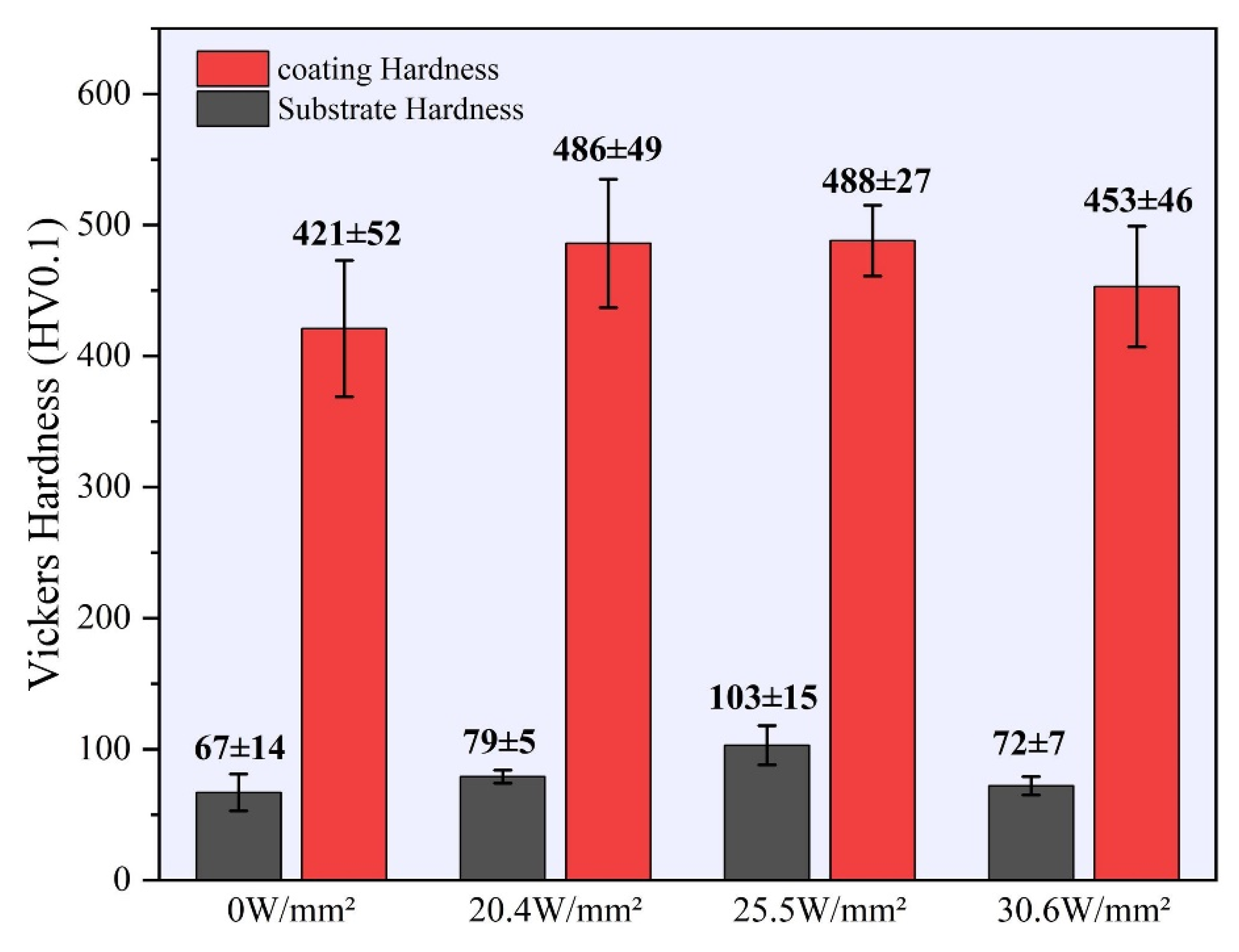
4. Experimental Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nunomura, S.; Tsutsumi, T.; Takada, N.; Fukasawa, M.; Hori, M. Radical, ion, and photon’s effects on defect generation at SiO2/Si interface during plasma etching. Appl. Surf. Sci. 2024, 672, 160764. [Google Scholar] [CrossRef]
- Choi, J.H.; Yoon, J.; Jung, Y.; Min, K.W.; Im, W.B.; Kim, H.J. Analysis of plasma etching resistance for commercial quartz glasses used in semiconductor apparatus in fluorocarbon plasma. Mater. Chem. Phys. 2021, 272, 125015. [Google Scholar] [CrossRef]
- Kreethi, R.; Hwang, Y.J.; Lee, H.Y.; Park, J.H.; Lee, K.A. Stability and plasma etching behavior of yttrium-based coatings by air plasma spray process. Surf. Coat. Technol. 2023, 454, 129182. [Google Scholar] [CrossRef]
- Cao, Y.C.; Zhao, L.; Luo, J.; Wang, K.; Zhang, B.P.; Yokota, H.; Yoshiyasu, I.; Li, J.F. Plasma etching behavior of Y2O3 ceramics: Comparative study with Al2O3. Appl. Surf. Sci. 2016, 366, 304–309. [Google Scholar] [CrossRef]
- Li, Q.; Hu, J.; Xie, J.; Wang, X.; Yu, C.; Jiang, S.; Jiang, X.; Li, E.; Deng, L. Influence of High-Enthalpy Atmospheric Plasma Spraying Process Parameters on Microwave Dielectric Properties of Y2O3 Coatings. J. Therm. Spray Technol. 2021, 30, 898–906. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Y.; Li, W.; Xu, S.; Zhong, N.; Liu, Y.; Yin, Z.; Zhang, J. Optimization on the bonding strength and microstructure of atmospheric plasma sprayed Y2O3 coatings by response surface methodology. Ceram. Int. 2024, 50, 20055–20067. [Google Scholar] [CrossRef]
- Lee, D.S.; Yun, S.; Han, J.W.; Song, M.; Kim, Y.; Lee, J.; Choi, J.; Chang, S.; Hong, S.; Kim, J. Microstructural evolution and mechanical properties of atmospheric plasma sprayed Y2O3 coating with state of in-flight particle. Ceram. Int. 2021, 47, 3853–3866. [Google Scholar] [CrossRef]
- Kim, M.; Choi, E.; Lee, D.; Seo, J.; Back, T.S.; So, J.; Yun, J.Y.; Suh, S.M. The effect of powder particle size on the corrosion behavior of atmospheric plasma spray-Y2O3 coating: Unraveling the corrosion mechanism by fluorine-based plasma. Appl. Surf. Sci. 2022, 606, 154958. [Google Scholar] [CrossRef]
- Madhura, B.; Patel, P.R.; Vetrivendan, E.; Rao, C.J.; Ningshen, S. Experimental study and numerical simulation of Y2O3 coatings deposited by plasma spraying at different torch powers. J. Therm. Spray Technol. 2023, 32, 2661–2682. [Google Scholar] [CrossRef]
- Sun, K.; Zhong, W.; Qiu, S.; Cai, W.; Xie, X.; Wang, H.; Zhang, S.; Li, W. Study on the microstructure, corrosion resistance and dielectric properties of atmospheric plasma-sprayed Y2O3 ceramic coatings. Coatings 2024, 14, 377. [Google Scholar] [CrossRef]
- Dong, T.; Liu, L.; Li, G.; Wang, R.; Yuan, J.; Feng, Y. Effect of induction remelting on microstructure and wear resistance of plasma sprayed NiCrBSiNb coatings. Surf. Coat. Technol. 2019, 364, 347–357. [Google Scholar] [CrossRef]
- Garcia-Alonso, D.; Serres, N.; Demian, C.; Costil, S.; Langlade, C.; Coddet, C. Pre-/during-/post-laser processes to enhance the adhesion and mechanical properties of thermal-sprayed coatings with a reduced environmental impact. J. Therm. Spray Technol. 2011, 20, 719–735. [Google Scholar] [CrossRef]
- Li, S.Y.; He, P.F.; Cheng, Y.H.; Liang, X.B.; Sun, C. Research Status of Ceramic-based Coatings Prepared by Laser-hybrid Thermal Spraying Technology. Surf. Technol. 2023, 52, 23–38. [Google Scholar]
- Schopphoven, T.; Gasser, A.; Wissenbach, K.; Poprawe, R. Investigations on ultra-high-speed laser material deposition as alternative for hard chrome plating and thermal spraying. J. Laser Appl. 2016, 28, 022501. [Google Scholar] [CrossRef]
- Zhao, X.; Xie, T.; Zhang, P.; Yao, Z.; Zhang, Q.; Deng, J.; Sui, Y.; Yao, J. The Effect of In Situ Laser-Assisted Plasma Spraying on the Plasma Etching Resistance of Yttrium Oxide Coating. Coatings 2024, 14, 1427. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, P.; Bai, S.; Qin, B.; Zhang, D. Influence of laser power on microstructure and properties of Al-Si+ Y2O3 coating. Coatings 2023, 13, 1289. [Google Scholar] [CrossRef]
- Jia, D.; Shi, W.; Zhang, H.; Wu, T.; Diao, Y.; Li, K.; Lu, C. Effects of Y2O3 content on wear resistance and corrosion resistance of 316L/TiC coating fabricated by laser cladding. Coatings 2023, 13, 1348. [Google Scholar] [CrossRef]
- Liu, X.Y.; Sui, Y.; Li, J.B.; Yue, J.Y.; Sun, X.H.; Yang, L.F.; Liu, C.S. Dimension effect of Y2O3 nanomaterial on microstructure and tensile properties of laser metal deposited stainless steel coatings. Surf. Coat. Technol. 2021, 419, 127259. [Google Scholar] [CrossRef]
- Gu, Y.; Pan, J.; Lu, H.; Xiao, J.; Ma, C.; Yu, N. Numerical and Experimental Study on the Deposition Mechanisms of Plasma Spraying on 7075 Aluminum Alloy. J. Mater. Eng. Perform. 2024, 33, 1071–1080. [Google Scholar] [CrossRef]
- Lin, E.; Chen, Q.; Ozdemir, O.C.; Champagne, V.K.; Müftü, S. Effects of interface bonding on the residual stresses in cold-sprayed Al-6061: A numerical investigation. J. Therm. Spray Technol. 2019, 28, 472–483. [Google Scholar] [CrossRef]
- Vincent, S.; Le Bot, C.; Sarret, F.; Meillot, E.; Caltagirone, J.P.; Bianchi, L. Penalty and Eulerian-Lagrangian VOF methods for impact and solidification of metal droplets plasma spray process. Comput. Fluids 2015, 113, 32–41. [Google Scholar] [CrossRef]
- Yang, X.; Meng, T.; Su, Y.; Chai, X.; Guo, Z.; Ma, T.; Yin, S.; Li, W. Particle deformation and coating deposition behavior in cold spray additive manufactured aluminum deposit on copper substrate by simulation and experiment. J. Mater. Res. Technol. 2024, 30, 2879–2890. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, X.; Tsutsumi, S.; Sasaki, T.; Li, C.; Ma, N. Measurement and analysis of cold spray residual stress using arbitrary Lagrangian-Eulerian method. Addit. Manuf. 2020, 35, 101296. [Google Scholar]
- Zhang, M.; Chen, L.; Shan, L.; Li, H. Analysis of semi-molten hollow particle spreading and deformation in plasma spraying. J. Phys. D Appl. Phys. 2024, 57, 235201. [Google Scholar] [CrossRef]
- Subedi, K.K.; Kong, S.C. Particle-based approach for modeling phase change and drop/wall impact at thermal spray conditions. Int. J. Multiph. Flow 2023, 165, 104472. [Google Scholar] [CrossRef]
- Xie, J.; Nélias, D.; Walter-Le Berre, H.; Ogawa, K.; Ichikawa, Y. Simulation of the cold spray particle deposition process. J. Tribol. 2015, 137, 041101. [Google Scholar] [CrossRef]
- Zhu, Z.; Kamnis, S.; Gu, S. Numerical study of molten and semi-molten ceramic impingement by using coupled Eulerian and Lagrangian method. Acta Mater. 2015, 90, 77–87. [Google Scholar] [CrossRef]
- Song, X.; Ng, K.L.; Chea, J.M.K.; Sun, W.; Tan, A.W.Y.; Zhai, W.; Li, F.; Marinescu, I.; Liu, E. Coupled Eulerian-Lagrangian (CEL) simulation of multiple particle impact during Metal Cold Spray process for coating porosity prediction. Surf. Coat. Technol. 2020, 385, 125433. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, J.; Li, Y.; Yu, B.; Zhao, J. Numerical simulation of the cold spray deposition of copper particles on polyether ether ketone (PEEK) substrate. J. Therm. Spray Technol. 2021, 30, 1792–1809. [Google Scholar] [CrossRef]
- Jang, T.J.; Kim, J.B.; Shin, H. Identification of plastic constitutive Johnson-Cook model parameters by optimization-based inverse method. J. Comput. Des. Eng. 2021, 8, 1082–1097. [Google Scholar] [CrossRef]
- Xiao, J.; Pan, J.; Gu, Y.; Lu, H.; Yu, N.; Lv, M.; Chen, X. Study on construction mechanism of ceramic-metal thermal barrier coating system by plasma spraying. Metall. Mater. Trans. A 2023, 54, 2827–2840. [Google Scholar] [CrossRef]
- Wang, G.W.; Ding, Y.; Guan, Y.C.; Wang, Y.; Yang, L.J. Model heat source using actual distribution of laser power density for simulation of laser processing. J. Cent. South Univ. 2022, 29, 3277–3293. [Google Scholar] [CrossRef]
- Li, B.; Du, J.; Sun, Y.; Zhang, S.; Zhang, Q. On the importance of heat source model determination for numerical modeling of selective laser melting of IN625. Opt. Laser Technol. 2023, 158, 108806. [Google Scholar] [CrossRef]
- Yan, S.; Zhang, A.; Liang, S.; Wang, T. Measurement of laser light absorptivity of commonly used metals in laser additive manufacturing technique. Aeronaut. Manuf. Technol. 2017, 536, 97–100. [Google Scholar]
- Wu, Y.; Du, J.; Choy, K.L.; Hench, L.L. Laser densification of alumina powder beds generated using aerosol assisted spray deposition. J. Eur. Ceram. Soc. 2007, 27, 4727–4735. [Google Scholar] [CrossRef]




| Property | Parameter, Symbol (Unit) | Al6061 | Y2O3 |
|---|---|---|---|
| General | Density, ρ ) | 2700 | 5010 |
| Specific heat, (J/kg•K) | 1009 | 656 | |
| Thermal conductivity, (W/m•K) | 155 | 2.32 | |
| Melting temperature, (K) | 925 | 2683 | |
| Inelastic heat fraction, β | 0.9 | 0.9 | |
| Coefficient of thermal expansion, (1/K) | 22.3 × 10−6 | 8 × 10−6 | |
| Elastic | Elastic modulus, (GPa) | 69.11 | 290 |
| Poisson’s ratio | 0.331 | 0.3 | |
| Plastic | Static yield strength, A (MPa) | 270 | 401 |
| Hardening modulus, B (MPa) | 154.3 | 288 | |
| Strain rate coefficient, C | 0.002 | 0.07 | |
| 0.239 | 0.2 | ||
| 1.42 | 0.09 | ||
| (1/s) | 1 | 1 | |
| (K) | 298 | 298 |
| Current (A) | Voltage (V) | Primary Gas, Ar (SLPM) | Primary Gas, H2 (SLPM) | Spraying Distance (mm) | Powder Feed Rate (g/min) | Gun Speed (mm/min) |
|---|---|---|---|---|---|---|
| 700 | 58 | 45 | 3 | 100 | 15 | 100 |
| 0 W/mm2 | 20.4 W/mm2 | 25.5 W/mm2 | 30.6 W/mm2 | |
|---|---|---|---|---|
| Laser power (W) | 0 | 400 | 500 | 600 |
| Average coating thickness (µm) | 355 ± 22 | 301 ± 18 | 259 ± 10 | 229 ± 14 |
| Porosity | 7.48 ± 0.51% | 4.21 ± 0.41% | 3.94 ± 0.37% | 5.29 ± 0.36% |
| Maximum pore size (µm) | 68 | 43 | 32 | 58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, H.; Zhao, X.; Fu, B.; Yang, H.; Sun, C. Numerical and Experimental Study on Deposition Mechanism of Laser-Assisted Plasma-Sprayed Y2O3 Coating. Coatings 2025, 15, 904. https://doi.org/10.3390/coatings15080904
Zou H, Zhao X, Fu B, Yang H, Sun C. Numerical and Experimental Study on Deposition Mechanism of Laser-Assisted Plasma-Sprayed Y2O3 Coating. Coatings. 2025; 15(8):904. https://doi.org/10.3390/coatings15080904
Chicago/Turabian StyleZou, Hui, Xutao Zhao, Bin Fu, Huabao Yang, and Chengda Sun. 2025. "Numerical and Experimental Study on Deposition Mechanism of Laser-Assisted Plasma-Sprayed Y2O3 Coating" Coatings 15, no. 8: 904. https://doi.org/10.3390/coatings15080904
APA StyleZou, H., Zhao, X., Fu, B., Yang, H., & Sun, C. (2025). Numerical and Experimental Study on Deposition Mechanism of Laser-Assisted Plasma-Sprayed Y2O3 Coating. Coatings, 15(8), 904. https://doi.org/10.3390/coatings15080904






