Performance Optimization of Stacked Weld in Hydrogen Production Reactor Based on Response Surface Methodology–Genetic Algorithm
Abstract
1. Introduction
2. Materials and Methods
2.1. Subsection
2.2. Experimental Design
2.3. Calculation of Mechanical Properties of Weld
- Tensile strength.
- Hydrogen embrittlement sensitivity index.
- Fatigue strain strength.
- Creep rate.
3. Results and Discussion
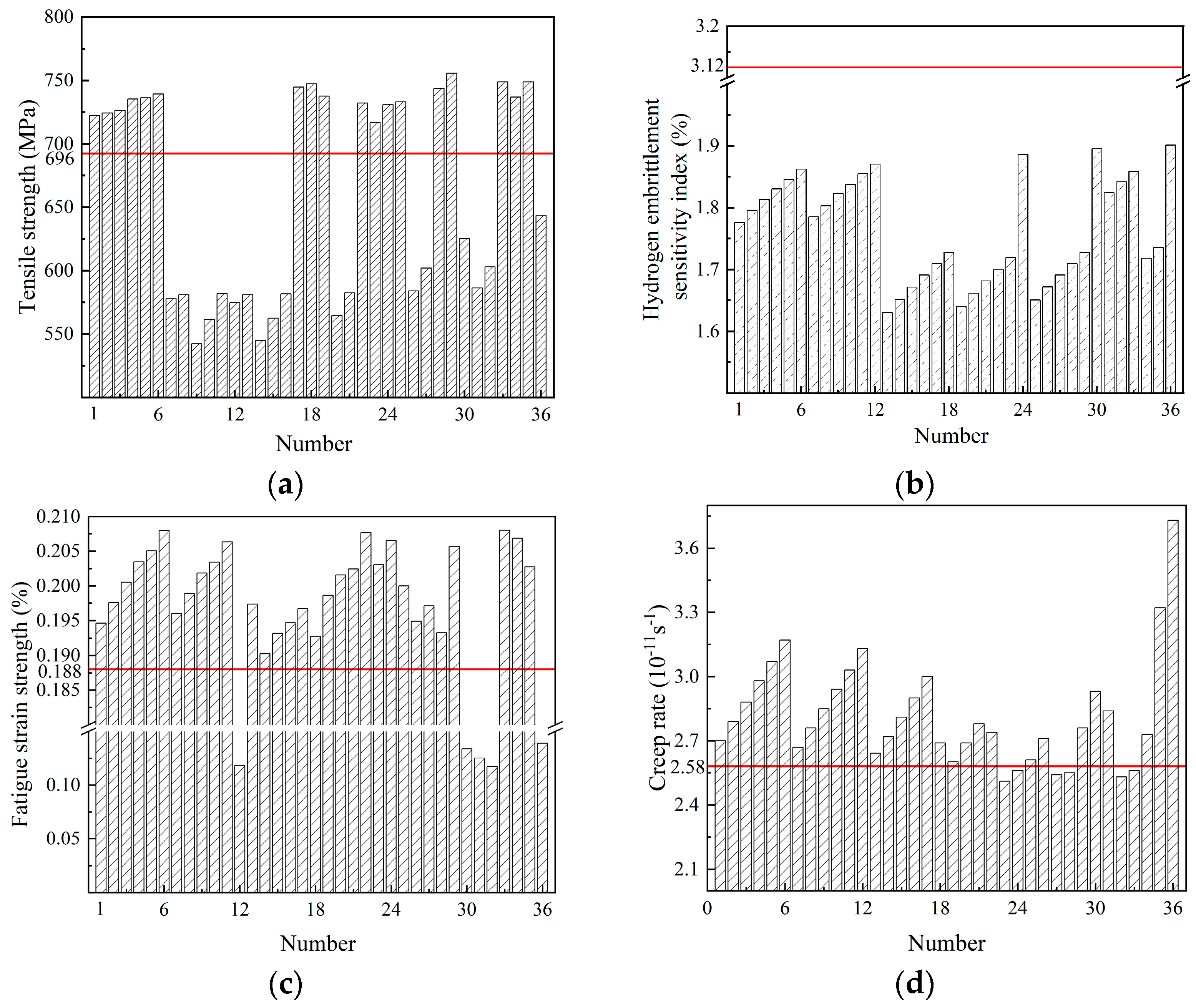
3.1. Calculation Results of Weld Properties
3.2. Establishment of Regression Model for Weld Performance and Variance Analysis
3.2.1. Tensile Strength
3.2.2. Hydrogen Embrittlement Sensitivity Index
3.2.3. Fatigue Strain Strength
3.2.4. Creep Rate
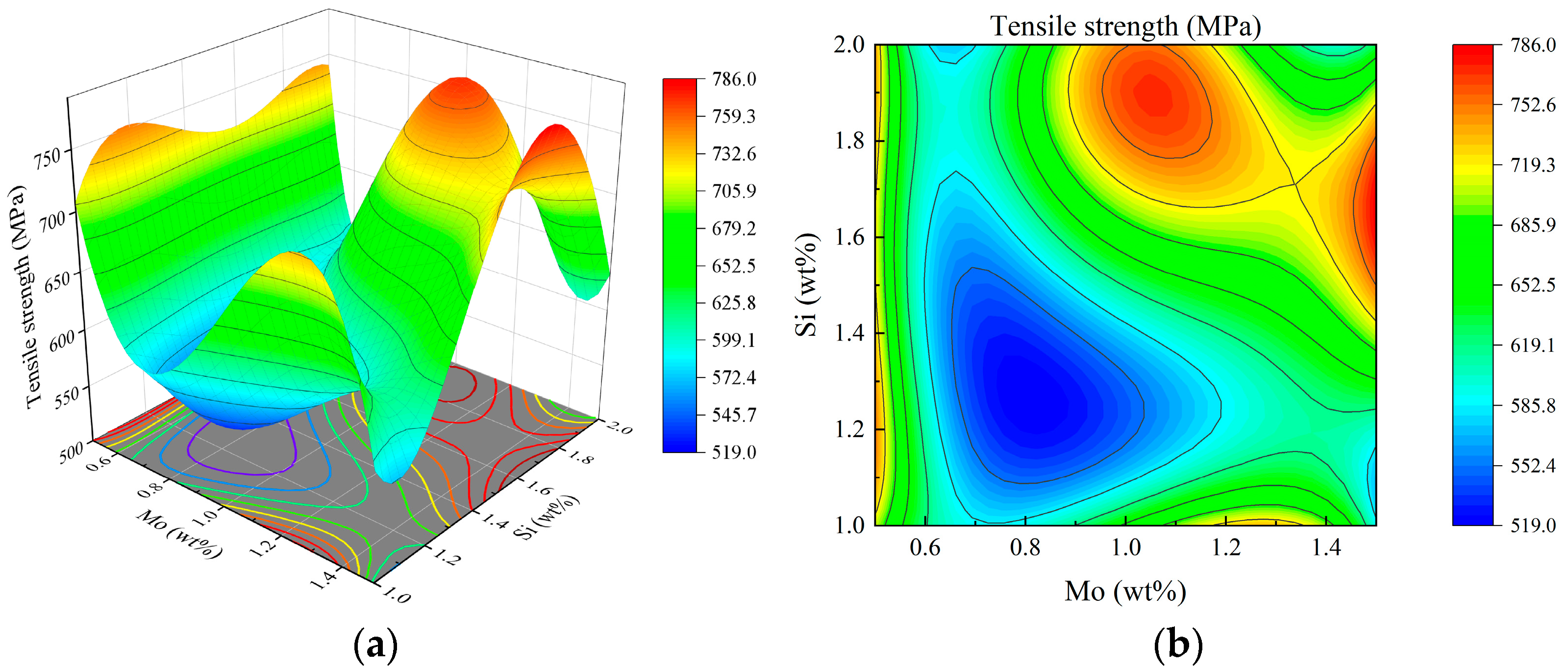
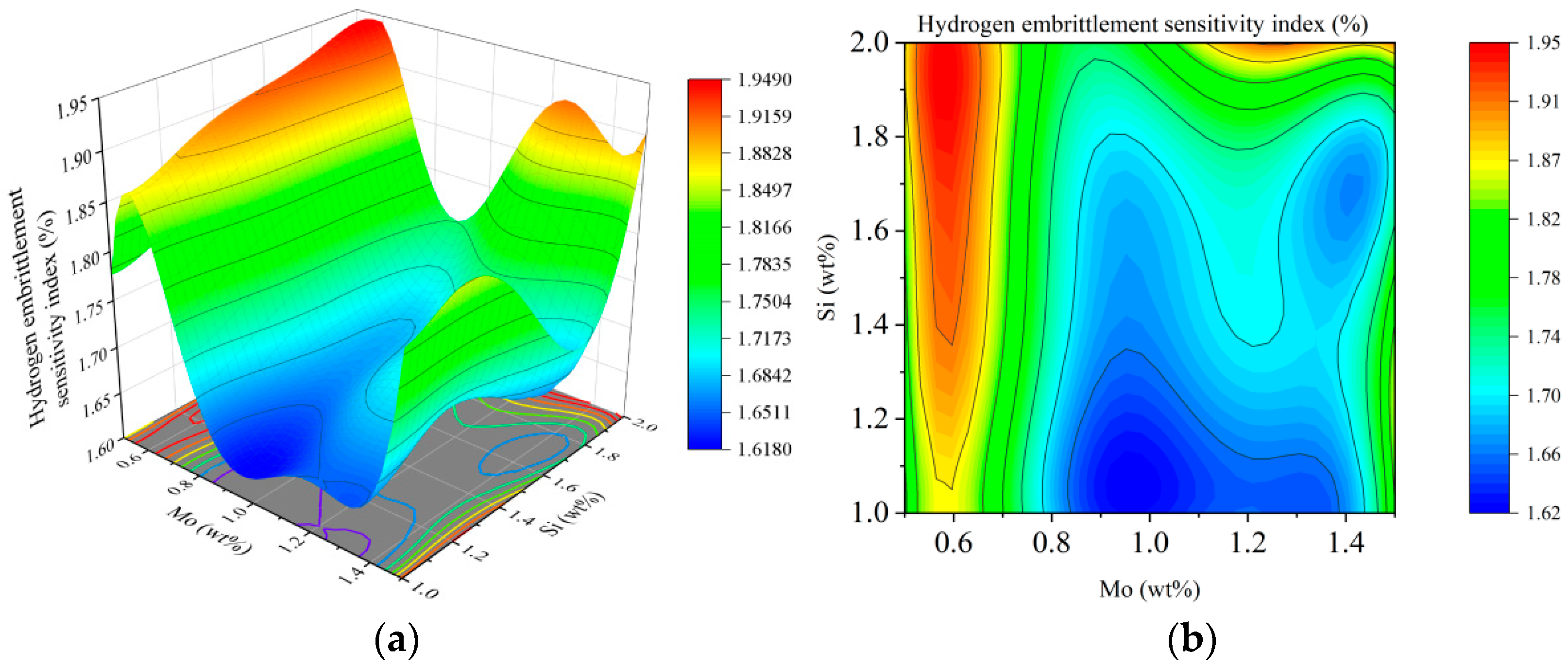
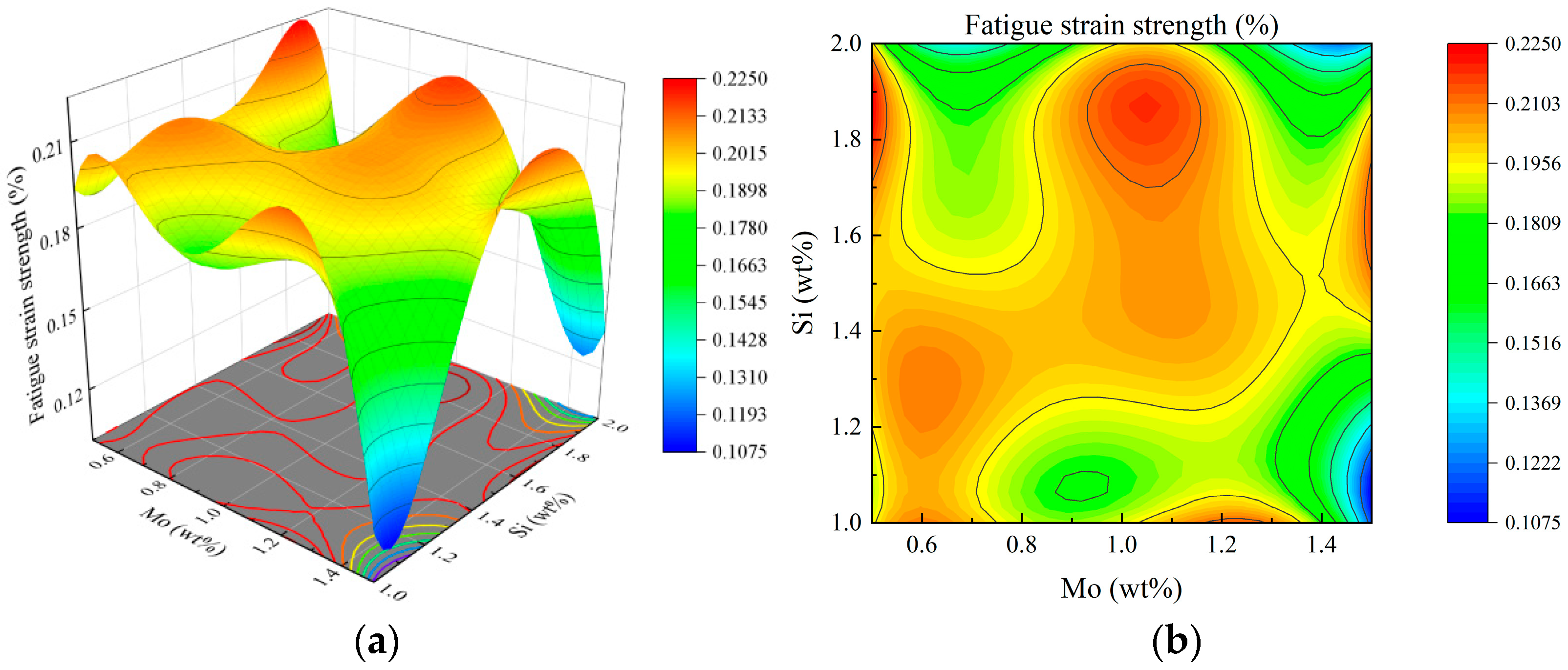
3.3. Response Surface Interaction Analysis
3.3.1. Tensile Strength
3.3.2. Hydrogen Embrittlement Sensitivity Index
3.3.3. Fatigue Strain Strength
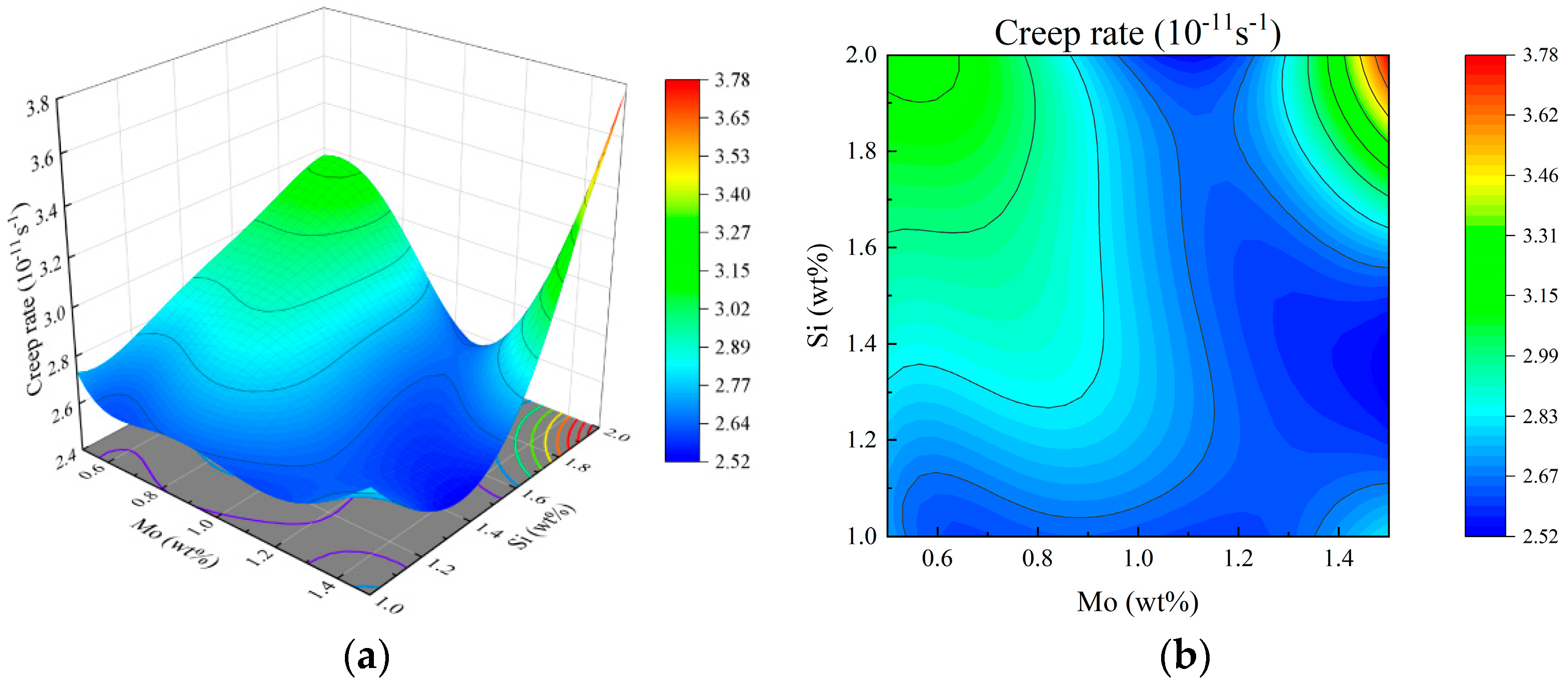
3.3.4. Creep Rate
4. Multi-Objective Optimization and Experimental Verification of Stacked Weld Performance
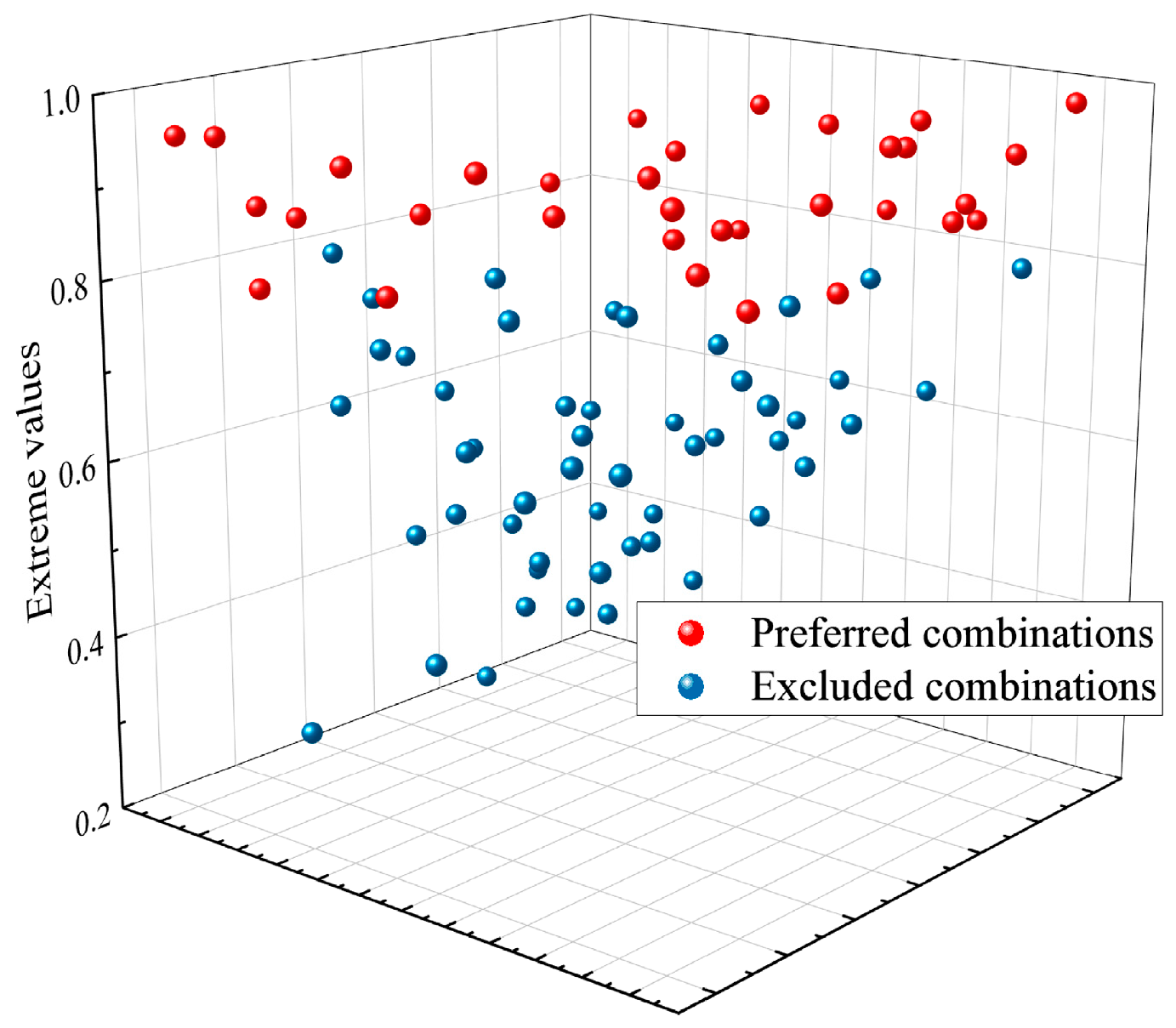
4.1. Determination of Combination of Weld Layer Performance Weight Coefficients
4.2. Multi-Objective Optimization of Stacked Weld Performance
4.2.1. Establishment of Mathematical Model for Multi-Objective Optimization
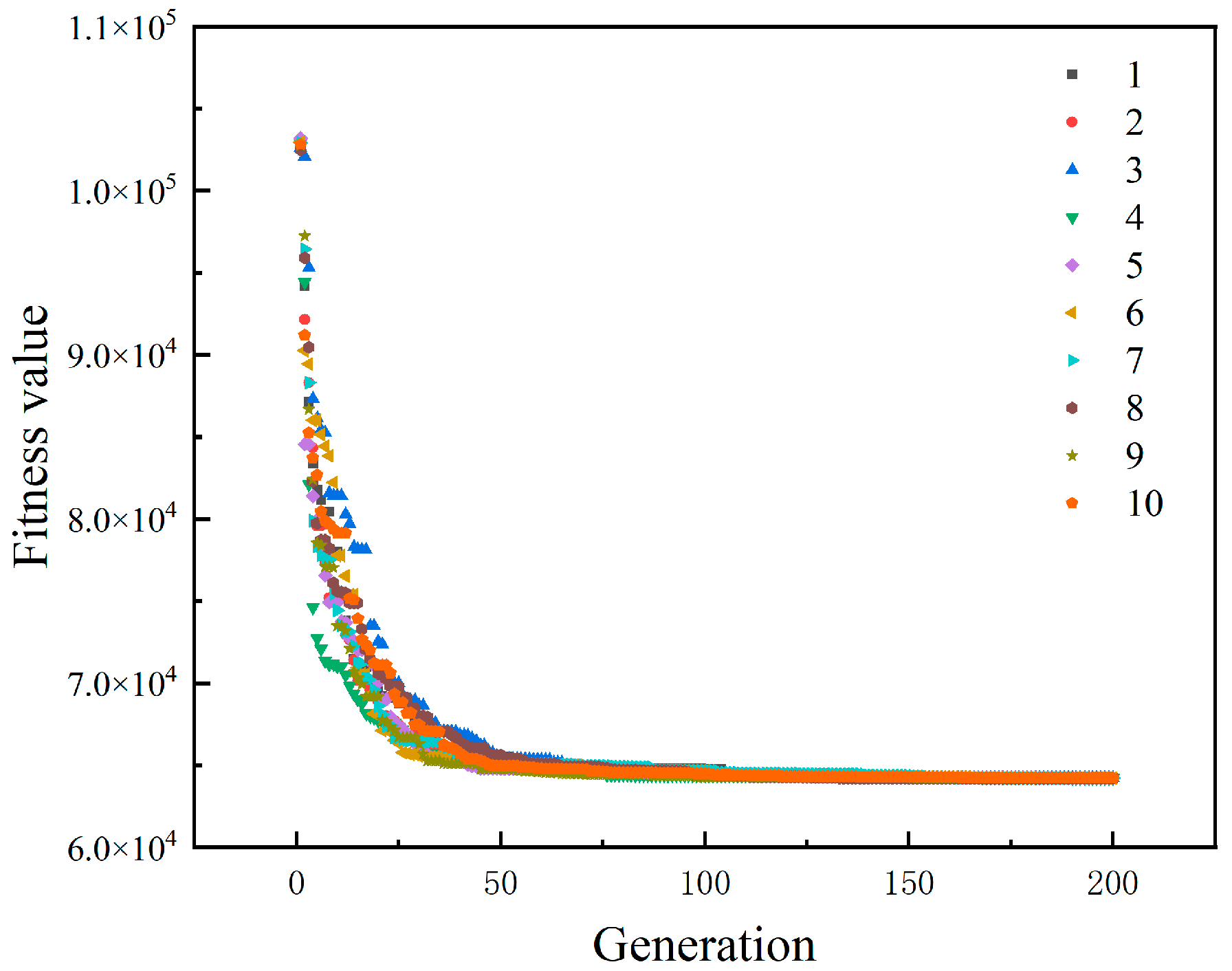
4.2.2. Multi-Objective Optimization Results
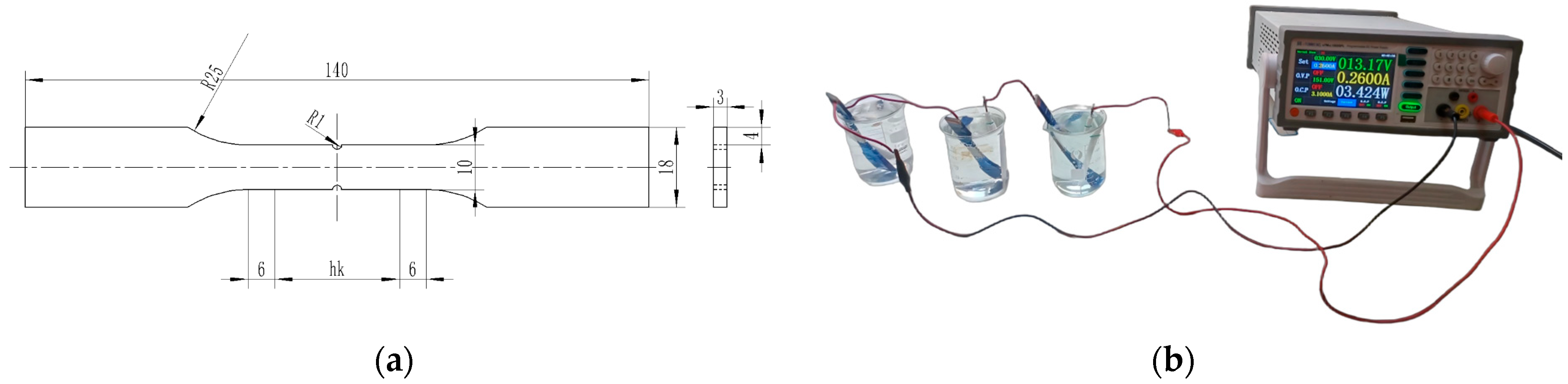
4.3. Welding Experiment Verification of Stacked Welds
4.3.1. Welding Experiment and Inspection
4.3.2. Performance Analysis of Stacked Weld
5. Conclusions
- The weld performance of 321 stainless steel under different combinations of Si and Mo content is calculated using JMatPro software. Through analysis of variance, high-precision regression models are established to describe the relationships between element content and tensile strength, hydrogen embrittlement sensitivity, fatigue strain strength and creep rate. These models can accurately predict weld performance. Response surface analysis further confirms that the interaction between Si and Mo has a significant effect on various weld properties.
- Based on the performance requirements of different weld layers, the exhaustive method is used to determine the optimal weight coefficient combinations for the performance evaluation indices of each weld layer. Combined with the response surface methodology results, a multi-objective optimization mathematical model for the gradient enhancement of the laminated weld is established. This model is solved using a genetic algorithm, yielding the optimal Si and Mo content combinations in the welding wire and the corresponding thickness of each weld layer.
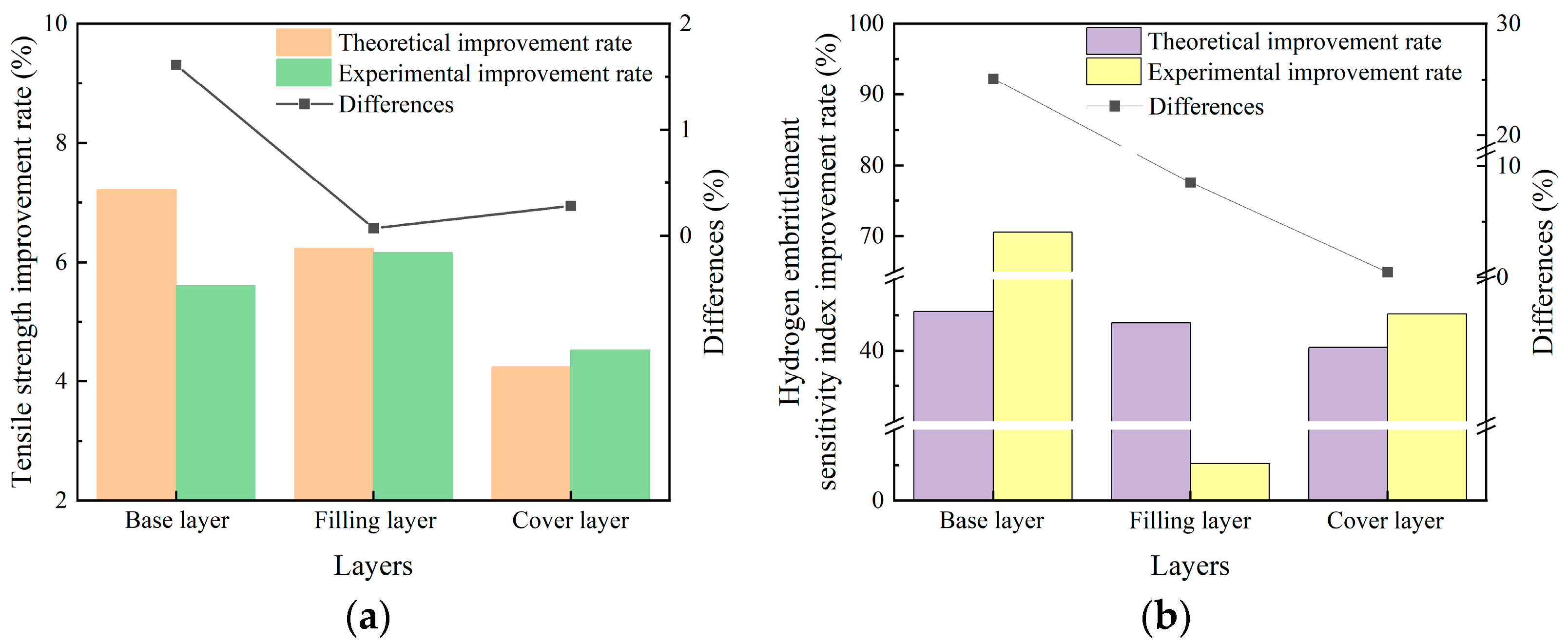
- Welding experiments are conducted on the stacked welds. The results show that, compared with the original stacked weld, the tensile strength of the base layer, filling layer and cover layer of the optimized weld increases by 5.60%, 6.16% and 4.53%, respectively, while the hydrogen embrittlement resistance improves by 70.56%, 52.40% and 45.16%, respectively. Additionally, the results indirectly confirm that the fatigue resistance and creep resistance of the optimized stacked weld are also enhanced. Overall, the comprehensive performance of the stacked weld meets the optimization objectives. Welding experiments verify the feasibility of the gradient performance optimization method for stacked weld in a hydrogen production reactor, based on the response surface methodology–genetic algorithm proposed in this study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ahad, M.T.; Bhuiyan, M.M.H.; Sakib, A.N.; Becerril, C.A.; Siddique, Z. An overview of challenges for the future of hydrogen. Materials 2023, 16, 6680. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Zhou, Q.; Yu, D. The future of hydrogen energy: Bio-hydrogen production technology. Int. J. Hydrogen Energy 2022, 47, 33677–33698. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Y. Hydrogen production by coal gasification in a supercritical water fluidized bed: Dynamic modeling of an industrial-scale reactor. Ind. Eng. Chem. Res. 2022, 61, 16153–16165. [Google Scholar] [CrossRef]
- Xie, X.; Wang, X.; Zhao, P.; Hao, Y.; Xie, R.; Liu, H. Learning time-aware multi-phase flow fields in coal-supercritical water fluidized bed reactor with deep learning. Energy 2023, 263, 125907. [Google Scholar] [CrossRef]
- Leng, Z.; Zhang, S.; Wang, W.; Gu, H.; Yin, J.; Wang, Z.; Liu, Y. Study on the influence of surface integrity on hydrogen permeation resistance of hydrogen production reactor materials. Appl. Sci. 2023, 13, 10461. [Google Scholar] [CrossRef]
- Liu, Y.; Gu, H.; Leng, Z.; Peng, C.; Wang, Z.; Zhang, S. Study on the Optimization of Process Parameters for Submerged Arc Welding of Hydrogen Production Reactor Material. Coatings 2024, 14, 1548. [Google Scholar] [CrossRef]
- Zhang, S.; Leng, Z.; Duan, Q.; Gu, H.; Lu, M.; Wang, Z.; Liu, Y. Experimental Determination and Simulation Validation: Johnson-Cook Model Parameters and Grinding Simulation of 06Cr18Ni11Ti Stainless Steel Welds. Machines 2024, 12, 660. [Google Scholar] [CrossRef]
- Davoodi, F.; Ashrafizadeh, F.; Atapour, M.; Rikhtehgaran, R. A novel approach for evaluation of load bearing capacity of duplex coatings on aluminum alloy using PLS and SVR models. Trans. Nonferrous Met. Soc. China 2022, 32, 1834–1851. [Google Scholar] [CrossRef]
- Lv, M.; Zhang, T.; Sun, W.; Ma, Q.; Shang, Z.; Zhang, J. Research on the optimal Design of the deposited metal alloy system for Welding with Design-Expert Ultra-High Strength steel powder core Welding Wire. Mech. Manuf. Abstr. Weld. Vol. 2020, 2, 7–16+21. [Google Scholar]
- Shalimov, M.P.; Votinova, E.B. Optimization of welding electrode coating composition based on simulation of interaction processes in metal-slag-gas system. Mater. Sci. Forum 2016, 870, 593–597. [Google Scholar] [CrossRef]
- Jindal, S.; Chhibber, R.; Mehta, N.P. Modeling flux chemistry for submerged arc weldments of high-strength low-alloy steel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 1259–1272. [Google Scholar] [CrossRef]
- Adeyeye, A.D.; Oyawale, F.A. Weld-metal property optimization from flux ingredients through mixture experiments and mathematical programming approach. Mater. Res. 2009, 12, 339–343. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, H.; Zeng, X.; Sun, G.; Ding, X.; Sun, Y. Influences of Si-Ti combined alloying on microstructures and properties of laser welded socket joints of molybdenum. Opt. Laser Technol. 2024, 175, 110749. [Google Scholar] [CrossRef]
- Li, D.; Liu, M.; Li, G.; Wang, H.; Jiao, L.; Xu, L. Effect of H on Mechanical Properties and Corrosion Resistance of Ferritic/Martensitic Steels with Different Si Contents. J. Mater. Eng. Perform. 2024. [Google Scholar] [CrossRef]
- Martin, M.; Weber, S.; Theisen, W.; Michler, T.; Naumann, J. Effect of alloying elements on hydrogen environment embrittlement of AISI type 304 austenitic stainless steel. Int. J. Hydrogen Energy 2011, 36, 15888–15898. [Google Scholar] [CrossRef]
- Ohmiya, S.; Fujii, H. Effects of Ni and Cr contents on fatigue crack growth properties of SUS316-based stainless steels in high-pressure gaseous hydrogen. ISIJ Int. 2012, 52, 247–254. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, Z.; Feng, S.; Jiang, K.; Yu, J.; Wu, H.; Shi, S.; Lin, Q. Improvement of low-cycle fatigue behavior of modified 9Cr-1Mo steels at 450 C in liquid LBE environment by the addition of Si element. Nucl. Eng. Des. 2023, 413, 112570. [Google Scholar] [CrossRef]
- Liu, T.; Chen, L.; Bi, H.; Che, X. Effect of Mo on high-temperature fatigue behavior of 15CrNbTi ferritic stainless steel. Acta Metall. Sin. (Engl. Lett.) 2014, 27, 452–456. [Google Scholar] [CrossRef]
- Liu, T.; Zhu, X.; Chen, L.; Bi, H.; Lin, Y.; Long, J. Fatigue-creep behavior of two ferritic stainless steels in simulated automotive exhaust gas and argon. J. Mater. Sci. 2020, 55, 3684–3699. [Google Scholar] [CrossRef]
- Lu, C.; Yi, H.; Chen, M.; Xu, Y.; Wang, M.; Hao, X.; Ma, Y. Effects of Si on the stress rupture life and microstructure of a novel austenitic stainless steel. J. Mater. Res. Technol. 2023, 25, 3408–3424. [Google Scholar] [CrossRef]
- Zhu, Y.; Kou, J.; Wang, S.; Zhu, Q.; Jiang, L.; Wang, J.; Li, Z. The effects of Si content in ERNiMo-2 deposited metals on deformation and fracture behavior during creep process. Mater. Sci. Eng. A 2025, 923, 147673. [Google Scholar] [CrossRef]
- Hirata, S.; Ito, T.; Mitsuhara, M.; Nishida, M. Effect of cold-working and Mo addition on creep behavior in high Mn austenitic stainless steels. Tetsu--Hagane/J. Iron Steel Inst. Jpn. 2015, 101, 51–58. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, D.; Wang, Q.; Zhang, X.; Li, Y. The influence of silicon on the microstructure and properties of ferritic heat-resistant stainless steel. Iron Steel 2021, 56, 71–76+110. [Google Scholar]
- Zhang, D.; Ma, D.; Wang, Y.; Xie, Q. The development of flux-cored welding wire for Super duplex stainless steel welding. Weld. Technol. 2022, 51, 78–83. [Google Scholar]
- Huang, Y. Research on the Strength, Toughness and Hydrogen Resistance of Weld Metals in Hydrogen-Adjacent Pressure Vessels. Master’s Thesis, Dalian Jiaotong University, Dalian, China, 2023. [Google Scholar]
- Chen, Z.; Yu, Y.; Hou, J.; Zhu, P.; Zhang, J. Microstructure and properties of iron-based surfacing layer based on JmatPro software simulation calculation. Vibroeng. Procedia 2023, 50, 180–186. [Google Scholar] [CrossRef]
- Su, F.; Wang, D.; Xue, J.; Deng, X.; Gong, Q.; Xia, X.; Shu, D. Data-driven optimization of material composition and casting processes for large ferritic nodular cast iron components in wind turbines. In Proceedings of the International Conference on Materials Engineering and Intelligent Manufacturing, Xiamen, China, 18–20 October 2024. [Google Scholar]
- Zhao, Z.; Zhang, P.; Li, S.; Zhang, J.; Shi, W.; Zhang, C.; Zhang, C. Fatigue-creep behaviors of Ni-Fe based superalloy under various testing conditions. J. Mater. Res. Technol. 2021, 15, 4694–4701. [Google Scholar] [CrossRef]
- Yang, W. Research on Abnormal Microstructure Analysis and Process Improvement of P355GH Welded Joints after Quenching. Weld. Technol. 2025, 54, 96–100. [Google Scholar]
- Ren, D.; Xiao., F.; Tian, P.; Wang, X.; Liao, B. Effects of welding wire composition and welding process on the weld metal toughness of submerged arc welded pipeline steel. Int. J. Miner. Metall. Mater. 2009, 16, 65–70. [Google Scholar] [CrossRef]
- Arniella, V.; Álvarez, G.; Belzunce, J.; Rodríguez, C. Hydrogen embrittlement of 2205 duplex stainless steel in in-situ tensile tests. Theor. Appl. Fract. Mech. 2023, 124, 103794. [Google Scholar] [CrossRef]
- Gutema, E.; Gopal, M.; Lemu, H. Tribological Study of Multi-Walled Carbon Nanotube-Reinforced Aluminum 7075 Using Response Surface Methodology and Multi-Objective Genetic Algorithm. J. Compos. Sci. 2025, 9, 137. [Google Scholar] [CrossRef]
- Al-Sabur, R. Tensile strength prediction of aluminium alloys welded by FSW using response surface methodology-Comparative review. Mater. Today Proc. 2021, 45, 4504–4510. [Google Scholar] [CrossRef]
- Ahmadi, A.; Rezaei, M.; Sadeghieh, S.M. Interaction effects of flotation reagents for SAG mill reject of copper sulphide ore using response surface methodology. Trans. Nonferrous Met. Soc. China 2021, 31, 792–806. [Google Scholar] [CrossRef]
- Sreenivasan, K.; Kumar, S.; Katiravan, J. Genetic algorithm based optimization of friction welding process parameters on AA7075-SiC composite. Eng. Sci. Technol. Int. J. 2019, 22, 1136–1148. [Google Scholar] [CrossRef]
- Geng, D.; Lan, X.; He, H.; Liu, C. Welding quality inspection method based on genetic algorithm to optimize BP neural network. In Proceedings of the IEEE 2nd International Conference on Big Data, Artificial Intelligence and Internet of Things Engineering, Nanchang, China, 26–28 March 2021. [Google Scholar]
- ISO 9692–2: 2024; Welding and Allied Processes-Joint Preparation-Part 2: Submerged arc Welding of Steels. ISO: Geneva, Switzerland, 2016.
- Pang, J.; Li, S.; Wang, Z.; Zhang, Z. Relations between fatigue strength and other mechanical properties of metallic materials. Fatigue Fract. Eng. Mater. Struct. 2014, 37, 958–976. [Google Scholar] [CrossRef]

| Chemical Composition | C | Si | Mn | Ni | Cr | Ti | P | S |
|---|---|---|---|---|---|---|---|---|
| Weight/(wt%) | ≤0.08 | ≤1.00 | ≤2.00 | 9~12 | 17~19 | 0.4~0.7 | ≤0.045 | ≤0.03 |
| Chemical Composition | C | Mn | Si | Cr | Ni | Mo | P | S |
|---|---|---|---|---|---|---|---|---|
| Weight/(wt%) | 0.038 | 1.72 | 0.61 | 19.7 | 10.6 | 0.007 | 0.023 | 0.001 |
| Chemical Composition | C | Mn | Si | Cr | Ni | Mo | P | S |
|---|---|---|---|---|---|---|---|---|
| Weight/(wt%) | 0.047 | 1.40 | 0.75 | 19.5 | 9.8 | 0.022 | 0.025 | 0.003 |
| Factors | Levels | |||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| Mo/(wt%) | 0.5 | 0.7 | 0.9 | 1.1 | 1.3 | 1.5 |
| Si/(wt%) | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
| No. | Content Combinations | No. | Content Combinations | No. | Content Combinations | No. | Content Combinations | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mo/(wt%) | Si/(wt%) | Mo/(wt%) | Si/(wt%) | Mo/(wt%) | Si/(wt%) | Mo/(wt%) | Si/(wt%) | ||||
| 1 | 0.5 | 1.0 | 10 | 0.7 | 1.6 | 19 | 1.1 | 1.0 | 28 | 1.3 | 1.6 |
| 2 | 0.5 | 1.2 | 11 | 0.7 | 1.8 | 20 | 1.1 | 1.2 | 29 | 1.3 | 1.8 |
| 3 | 0.5 | 1.4 | 12 | 0.7 | 2.0 | 21 | 1.1 | 1.4 | 30 | 1.3 | 2.0 |
| 4 | 0.5 | 1.6 | 13 | 0.9 | 1.0 | 22 | 1.1 | 1.6 | 31 | 1.5 | 1.0 |
| 5 | 0.5 | 1.8 | 14 | 0.9 | 1.2 | 23 | 1.1 | 1.8 | 32 | 1.5 | 1.2 |
| 6 | 0.5 | 2.0 | 15 | 0.9 | 1.4 | 24 | 1.1 | 2.0 | 33 | 1.5 | 1.4 |
| 7 | 0.7 | 1.0 | 16 | 0.9 | 1.6 | 25 | 1.3 | 1.0 | 34 | 1.5 | 1.6 |
| 8 | 0.7 | 1.2 | 17 | 0.9 | 1.8 | 26 | 1.3 | 1.2 | 35 | 1.5 | 1.8 |
| 9 | 0.7 | 1.4 | 18 | 0.9 | 2.0 | 27 | 1.3 | 1.4 | 36 | 1.5 | 2.0 |
| Tensile Strength /(MPa) | Hydrogen Embrittlement Sensitivity Index/(%) | Fatigue Strain Strength /(%) | Creep Rate /(10−11s−1) |
|---|---|---|---|
| 696.06 | 3.12 | 0.1880 | 2.58 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 2.014 × 105 | 20 | 10,071.39 | 5.90 | 0.0005 |
| Mo (xMo) | 5008.83 | 1 | 5008.83 | 2.94 | 0.1072 |
| Si (xSi) | 15,838.25 | 1 | 15,838.25 | 9.28 | 0.0082 |
| xMo xSi | 1689.45 | 1 | 1689.45 | 0.9904 | 0.3354 |
| xMo2 | 3341.27 | 1 | 3341.27 | 1.96 | 0.1820 |
| xSi2 | 1457.47 | 1 | 1457.47 | 0.8544 | 0.3699 |
| xMo2 xSi | 16,689.70 | 1 | 16,689.70 | 9.78 | 0.0069 |
| xMo xSi2 | 750.22 | 1 | 750.22 | 0.4398 | 0.5173 |
| xMo3 | 80.75 | 1 | 80.75 | 0.0473 | 0.8307 |
| xSi3 | 742.96 | 1 | 742.96 | 0.4355 | 0.5193 |
| xMo2 xSi2 | 2140.2 | 1 | 2140.2 | 12.55 | 0.0030 |
| xMo3 xSi | 2514.69 | 1 | 2514.69 | 1.47 | 0.2435 |
| xMo xSi3 | 9489.76 | 1 | 9489.76 | 5.56 | 0.0323 |
| xMo4 | 17,528.74 | 1 | 17,528.74 | 10.28 | 0.0059 |
| xSi4 | 15.19 | 1 | 15.19 | 0.0089 | 0.9261 |
| xMo3 xSi2 | 1667.3 | 1 | 1667.3 | 0.9774 | 0.3385 |
| xMo2 xSi3 | 4403.32 | 1 | 4403.32 | 2.58 | 0.1290 |
| xMo4 xSi | 10,427.69 | 1 | 10,427.69 | 6.11 | 0.0259 |
| xMo xSi4 | 1469.34 | 1 | 1469.34 | 0.8614 | 0.3681 |
| xMo5 | 114.44 | 1 | 114.44 | 0.0671 | 0.7991 |
| xSi5 | 0.5543 | 1 | 0.5543 | 0.0003 | 0.9859 |
| Residual | 25,587.35 | 15 | 1705.82 | ||
| Cor Total | 2.270 × 105 | 35 | |||
| R2 = 0.9273 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 0.2390 | 20 | 0.0119 | 13.01 | <0.0001 |
| Mo (xMo) | 0.0016 | 1 | 0.0016 | 6.49 | 0.0367 |
| Si (xSi) | 0.0002 | 1 | 0.0002 | 3.76 | 0.4874 |
| xMo xSi | 0.0000 | 1 | 0.0000 | 1.75 | 0.8038 |
| xMo2 | 0.0256 | 1 | 0.0256 | 17.40 | <0.0001 |
| xSi2 | 0.0001 | 1 | 0.0001 | 1.51 | 0.5052 |
| xMo2 xSi | 0.0002 | 1 | 0.0002 | 1.84 | 0.4822 |
| xMo xSi2 | 0.0001 | 1 | 0.0001 | 1.82 | 0.5370 |
| xMo3 | 0.0131 | 1 | 0.0131 | 27.44 | <0.0001 |
| xSi3 | 0.0003 | 1 | 0.0003 | 0.0767 | 0.3443 |
| xMo2 xSi2 | 0.0000 | 1 | 0.0000 | 2.28 | 0.8560 |
| xMo3 xSi | 0.0114 | 1 | 0.0114 | 14.92 | <0.0001 |
| xMo xSi3 | 0.0099 | 1 | 0.0099 | 4.48 | <0.0001 |
| xMo4 | 0.0120 | 1 | 0.0120 | 10.46 | <0.0001 |
| xSi4 | 0.0011 | 1 | 0.0011 | 0.7076 | 0.0769 |
| xMo3 xSi2 | 0.0012 | 1 | 0.0012 | 0.0305 | 0.0659 |
| xMo2 xSi3 | 0.0014 | 1 | 0.0014 | 2.50 | 0.0493 |
| xMo4 xSi | 0.0008 | 1 | 0.0008 | 0.0231 | 0.1175 |
| xMo xSi4 | 0.0007 | 1 | 0.0007 | 0.3054 | 0.1387 |
| xMo5 | 0.0176 | 1 | 0.0176 | 31.08 | <0.0001 |
| xSi5 | 0.0001 | 1 | 0.0001 | 0.0597 | 0.5385 |
| Residual | 0.0045 | 15 | 0.0045 | ||
| Cor Total | 0.2434 | 35 | |||
| R2 = 0.9817 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 0.0207 | 20 | 0.0010 | 5.07 | 0.0039 |
| Mo (xMo) | 0.0001 | 1 | 0.0001 | 0.2761 | 0.6069 |
| Si (xSi) | 1.759 × 10−8 | 1 | 1.759 × 10−8 | 0.0001 | 0.9935 |
| xMo xSi | 0.0003 | 1 | 0.0003 | 1.08 | 0.3146 |
| xMo2 | 0.0003 | 1 | 0.0003 | 1.05 | 0.3227 |
| xSi2 | 0.0000 | 1 | 0.0000 | 0.0628 | 0.8056 |
| xMo2 xSi | 0.0013 | 1 | 0.0013 | 5.12 | 0.0389 |
| xMo xSi2 | 8.088 × 10−6 | 1 | 8.088 × 10−6 | 0.0319 | 0.8607 |
| xMo3 | 0.0001 | 1 | 0.0001 | 0.2754 | 0.6074 |
| xSi3 | 0.0002 | 1 | 0.0002 | 0.6707 | 0.4256 |
| xMo2 xSi2 | 0.0009 | 1 | 0.0009 | 3.61 | 0.0769 |
| xMo3 xSi | 0.0000 | 1 | 0.0000 | 0.0861 | 0.7732 |
| xMo xSi3 | 0.0005 | 1 | 0.0005 | 1.78 | 0.2015 |
| xMo4 | 0.0003 | 1 | 0.0003 | 1.23 | 0.2856 |
| xSi4 | 3.449 × 10−6 | 1 | 3.449 × 10−6 | 0.0136 | 0.9088 |
| xMo3 xSi2 | 0.0012 | 1 | 0.0012 | 4.77 | 0.0453 |
| xMo2 xSi3 | 0.0002 | 1 | 0.0002 | 0.5959 | 0.4521 |
| xMo4 xSi | 0.0032 | 1 | 0.0032 | 12.67 | 0.0029 |
| xMo xSi4 | 0.0002 | 1 | 0.0002 | 0.9234 | 0.3518 |
| xMo5 | 0.0001 | 1 | 0.0001 | 0.2998 | 0.5920 |
| xSi5 | 0.0003 | 1 | 0.0003 | 1.09 | 0.3129 |
| Residual | 0.0038 | 15 | 0.0003 | ||
| Cor Total | 0.0245 | 35 | |||
| R2 = 0.9045 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 2.09 | 20 | 0.1046 | 13.54 | <0.0001 |
| Mo (xMo) | 0.0583 | 1 | 0.0583 | 7.56 | 0.0149 |
| Si (xSi) | 0.0013 | 1 | 0.0013 | 0.1626 | 0.6925 |
| xMo xSi | 0.0269 | 1 | 0.0269 | 3.49 | 0.0816 |
| xMo2 | 0.0002 | 1 | 0.0002 | 0.0245 | 0.8777 |
| xSi2 | 0.0002 | 1 | 0.0002 | 0.0234 | 0.8806 |
| xMo2 xSi | 0.0436 | 1 | 0.0436 | 5.65 | 0.0312 |
| xMo xSi2 | 0.0077 | 1 | 0.0077 | 0.9909 | 0.3353 |
| xMo3 | 0.0077 | 1 | 0.0077 | 0.9931 | 0.3348 |
| xSi3 | 0.0009 | 1 | 0.0009 | 0.1198 | 0.7340 |
| xMo2 xSi2 | 0.2393 | 1 | 0.2393 | 30.99 | <0.0001 |
| xMo3 xSi | 0.1053 | 1 | 0.1053 | 13.63 | 0.0022 |
| xMo xSi3 | 0.0003 | 1 | 0.0003 | 0.0403 | 0.8436 |
| xMo4 | 0.0001 | 1 | 0.0001 | 0.0151 | 0.9038 |
| xSi4 | 0.0046 | 1 | 0.0046 | 0.5969 | 0.4518 |
| xMo3 xSi2 | 0.0139 | 1 | 0.0139 | 1.80 | 0.1999 |
| xMo2 xSi3 | 0.0030 | 1 | 0.0030 | 0.3856 | 0.5439 |
| xMo4 xSi | 0.0074 | 1 | 0.0074 | 0.9541 | 0.3442 |
| xMo xSi4 | 0.0050 | 1 | 0.0050 | 0.6514 | 0.4322 |
| xMo5 | 0.0034 | 1 | 0.0034 | 0.4452 | 0.5147 |
| xSi5 | 0.0008 | 1 | 0.0008 | 0.1036 | 0.7520 |
| Residual | 0.1158 | 15 | 0.0077 | ||
| Cor Total | 2.21 | 35 | |||
| R2 = 0.9475 |
| Layers | Weight Coefficient | |||
|---|---|---|---|---|
| Tensile Strength | Hydrogen Embrittlement Sensitivity Index | Fatigue Strain Strength | Creep Rate | |
| Base layer | 0.5 | 0.3 | 0.1 | 0.1 |
| First filling layer | 0.5 | 0.2 | 0.1 | 0.2 |
| Second filling layer | 0.4 | 0.1 | 0.2 | 0.3 |
| Cover layer | 0.5 | 0.1 | 0.3 | 0.1 |
| Layers | Mo/(wt%) | Si/(wt%) | Thickness/(mm) |
|---|---|---|---|
| Base layer | 1.0 | 2.0 | 1.8 |
| First filling layer | 1.2 | 1.8 | 2.9 |
| Second filling layer | 1.4 | 1.6 | 2.5 |
| Cover layer | 1.5 | 1.5 | 2.8 |
| Layers | Tensile Strength /(MPa) | Hydrogen Embrittlement Sensitivity Index/(%) | Fatigue Strain Strength /(%) | Creep Rate /(10−11s−1) |
|---|---|---|---|---|
| Base layer | 746.28 | 1.70 | 0.1905 | 2.66 |
| First filling layer | 741.68 | 1.72 | 0.2035 | 2.56 |
| Second filling layer | 737.20 | 1.78 | 0.2017 | 2.53 |
| Cover layer | 725.64 | 1.87 | 0.2087 | 2.64 |
| Layers | Tensile Strength | Hydrogen embrittlement Resistance | Fatigue Resistance | Creep Resistance |
|---|---|---|---|---|
| Base layer | 7.21% | 45.51% | 4.26% | −3.10% |
| First filling layer | 6.55% | 44.87% | 8.24% | 0.78% |
| Second filling layer | 5.91% | 42.95% | 7.29% | 1.94% |
| Cover layer | 4.25% | 40.06% | 11.01% | −2.33% |
| Layers | Welding Current/(A) | Welding Voltage/(V) | Welding Speed/(cm/min) |
|---|---|---|---|
| Base layer | 440 | 30 | 38 |
| Filling layer | 470 | 32 | 40 |
| Cover layer | 420 | 30 | 34 |
| Layers | Optimized Stacked Weld | Original Stacked Weld | ||
|---|---|---|---|---|
| Tensile Strength /(MPa) | Hydrogen Embrittlement Sensitivity Index/(%) | Tensile Strength /(MPa) | Hydrogen Embrittlement Sensitivity Index/(%) | |
| Base layer | 718.2 | 0.63 | 680.1 | 2.14 |
| Filling layer | 697.2 | 0.99 | 656.7 | 2.08 |
| Cover layer | 680.9 | 1.36 | 651.4 | 2.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Gu, H.; Zhang, J.; Leng, Z.; Wang, Z.; Zhang, S. Performance Optimization of Stacked Weld in Hydrogen Production Reactor Based on Response Surface Methodology–Genetic Algorithm. Coatings 2025, 15, 889. https://doi.org/10.3390/coatings15080889
Liu Y, Gu H, Zhang J, Leng Z, Wang Z, Zhang S. Performance Optimization of Stacked Weld in Hydrogen Production Reactor Based on Response Surface Methodology–Genetic Algorithm. Coatings. 2025; 15(8):889. https://doi.org/10.3390/coatings15080889
Chicago/Turabian StyleLiu, Yu, Hongtao Gu, Jincheng Zhang, Zhiyi Leng, Ziguang Wang, and Shengfang Zhang. 2025. "Performance Optimization of Stacked Weld in Hydrogen Production Reactor Based on Response Surface Methodology–Genetic Algorithm" Coatings 15, no. 8: 889. https://doi.org/10.3390/coatings15080889
APA StyleLiu, Y., Gu, H., Zhang, J., Leng, Z., Wang, Z., & Zhang, S. (2025). Performance Optimization of Stacked Weld in Hydrogen Production Reactor Based on Response Surface Methodology–Genetic Algorithm. Coatings, 15(8), 889. https://doi.org/10.3390/coatings15080889






