Simple Strain Gradient–Divergence Method for Analysis of the Nanoindentation Load–Displacement Curves Measured on Nanostructured Nitride/Carbonitride Coatings
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of the NSC Samples
2.2. Developing the Stress–Strain Field Gradient–Divergence Method to Reveal Strain-Hardening and Strain-Softening Phenomena Caused by Nanoindentation
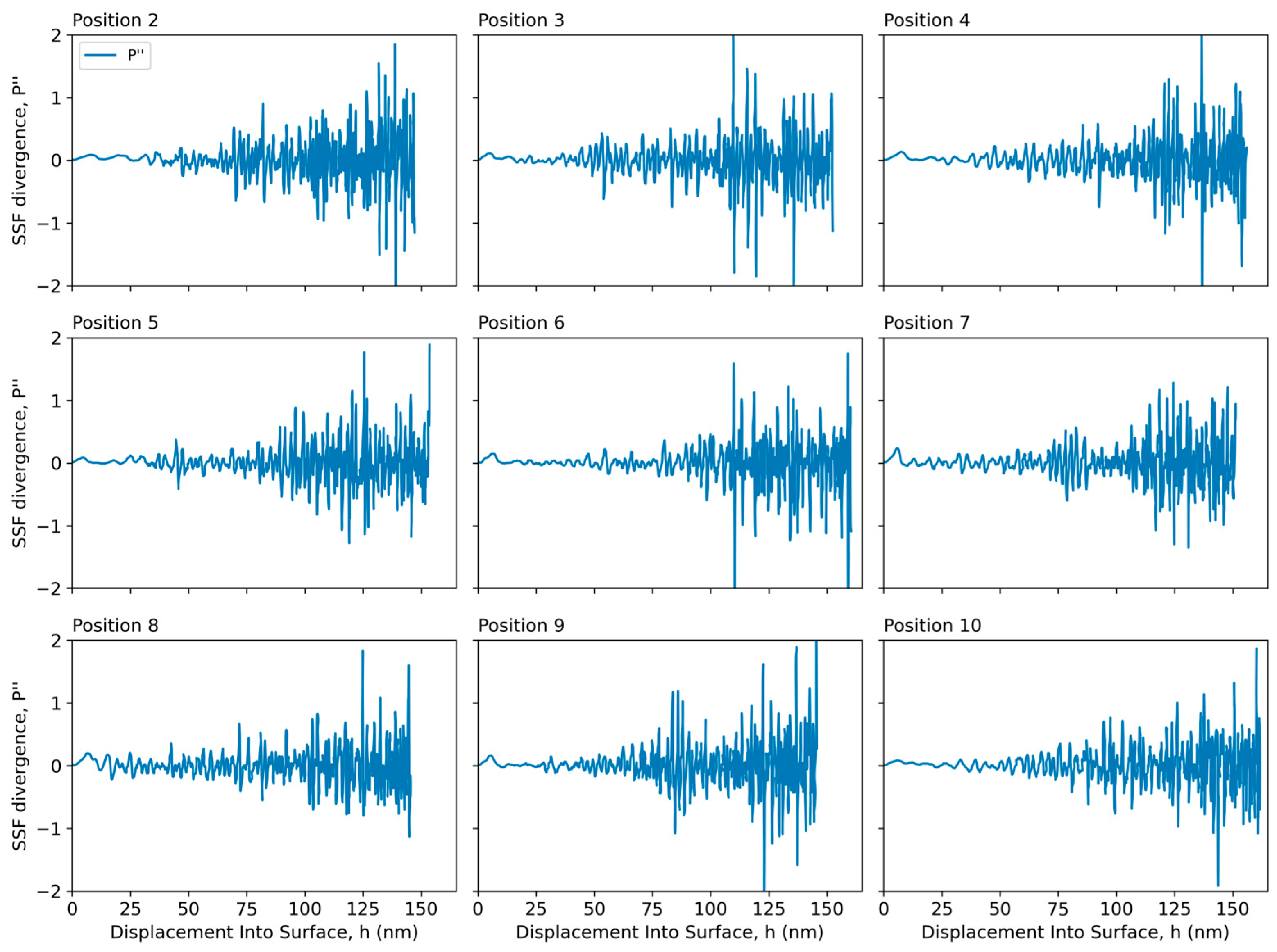
2.3. Strain Gradient and Divergence Oscillation Analysis of the Stress–Strain Field Caused by Incrementally Loaded Indenter
2.4. Nanoindentation Hardness Testing
2.5. Tribological Tests of the NSC Samples
2.6. Surface Roughness Evaluation Using Roughness Tester Mitutoyo AVANT
2.7. Electron Microscopy Examinations of the NSC Samples
3. Results and Discussion
3.1. Characterization of the NSC Film Samples
3.2. Scanning Electron Microscopy Study of the NSC Samples
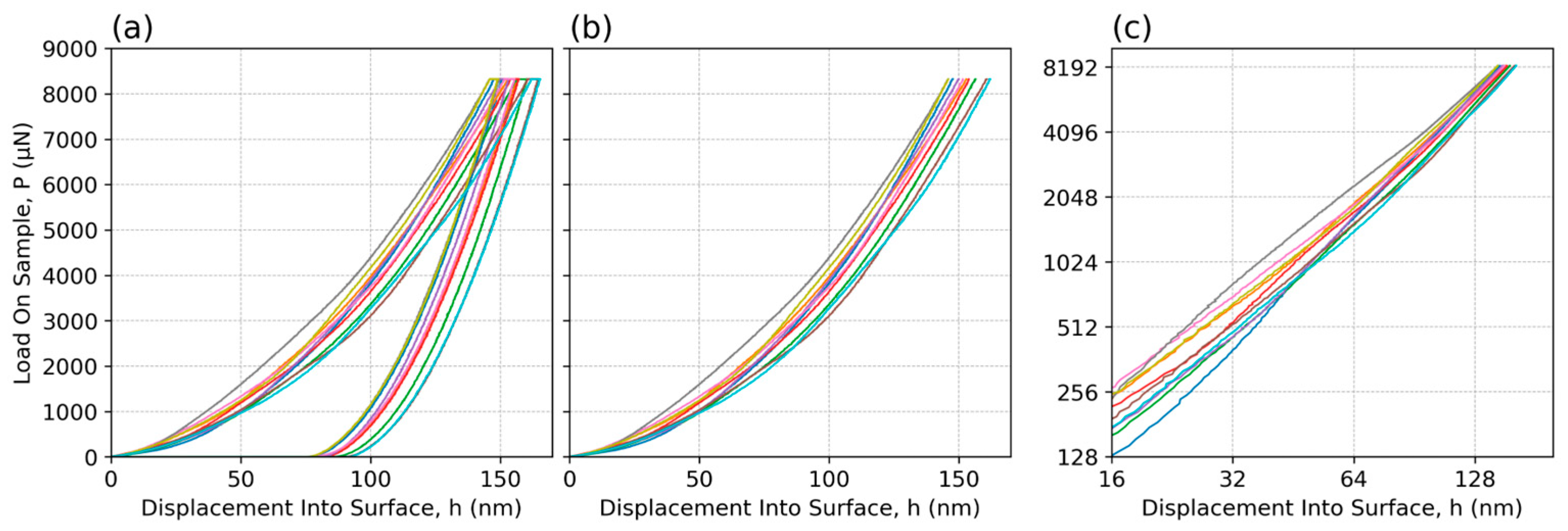
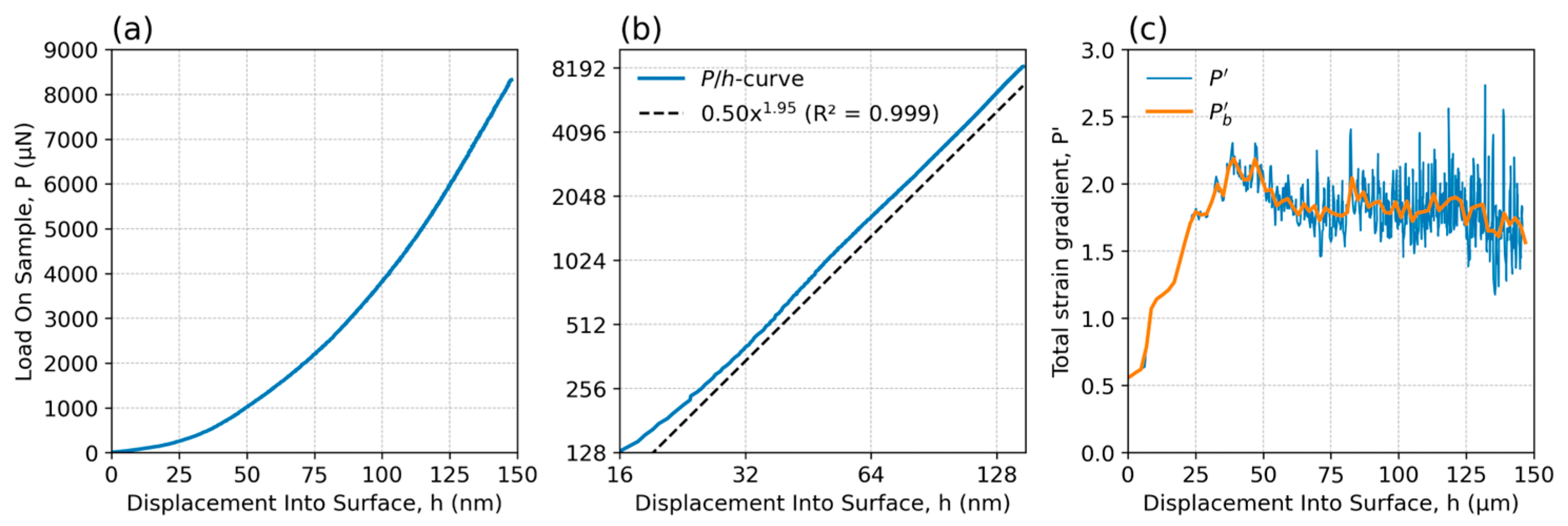
3.3. Nanoindentation Response Analysis Using the Loading Segment P/h-Curves Obtained at the Testing Peak Load of 8000 µN
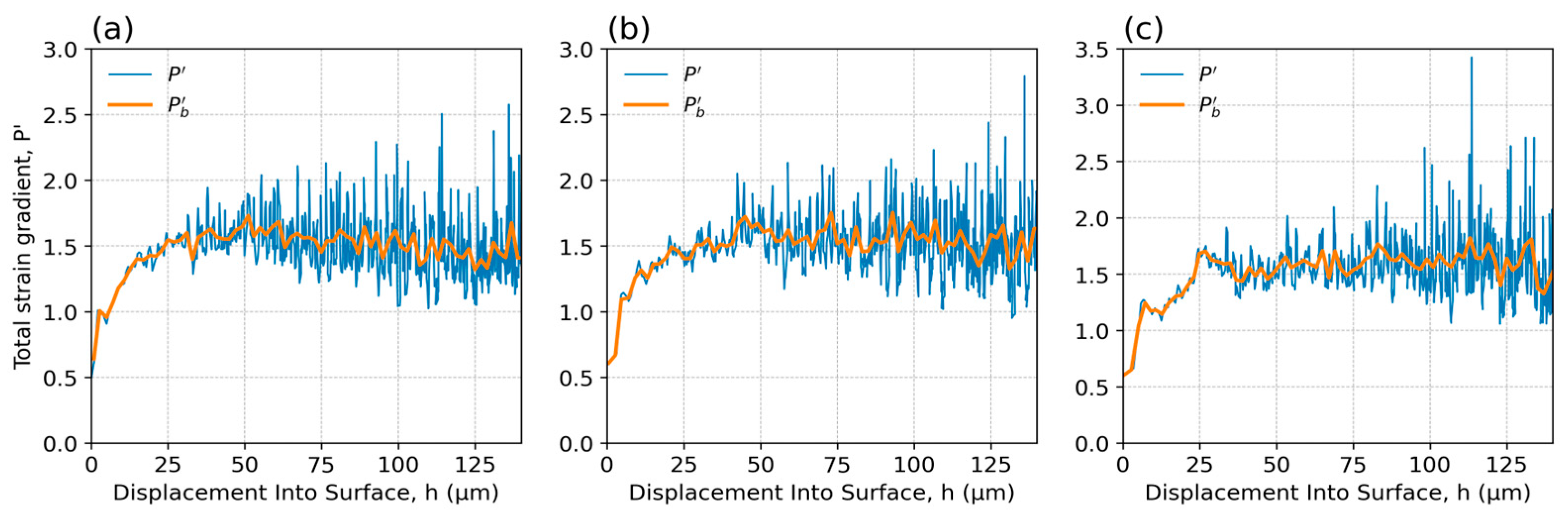
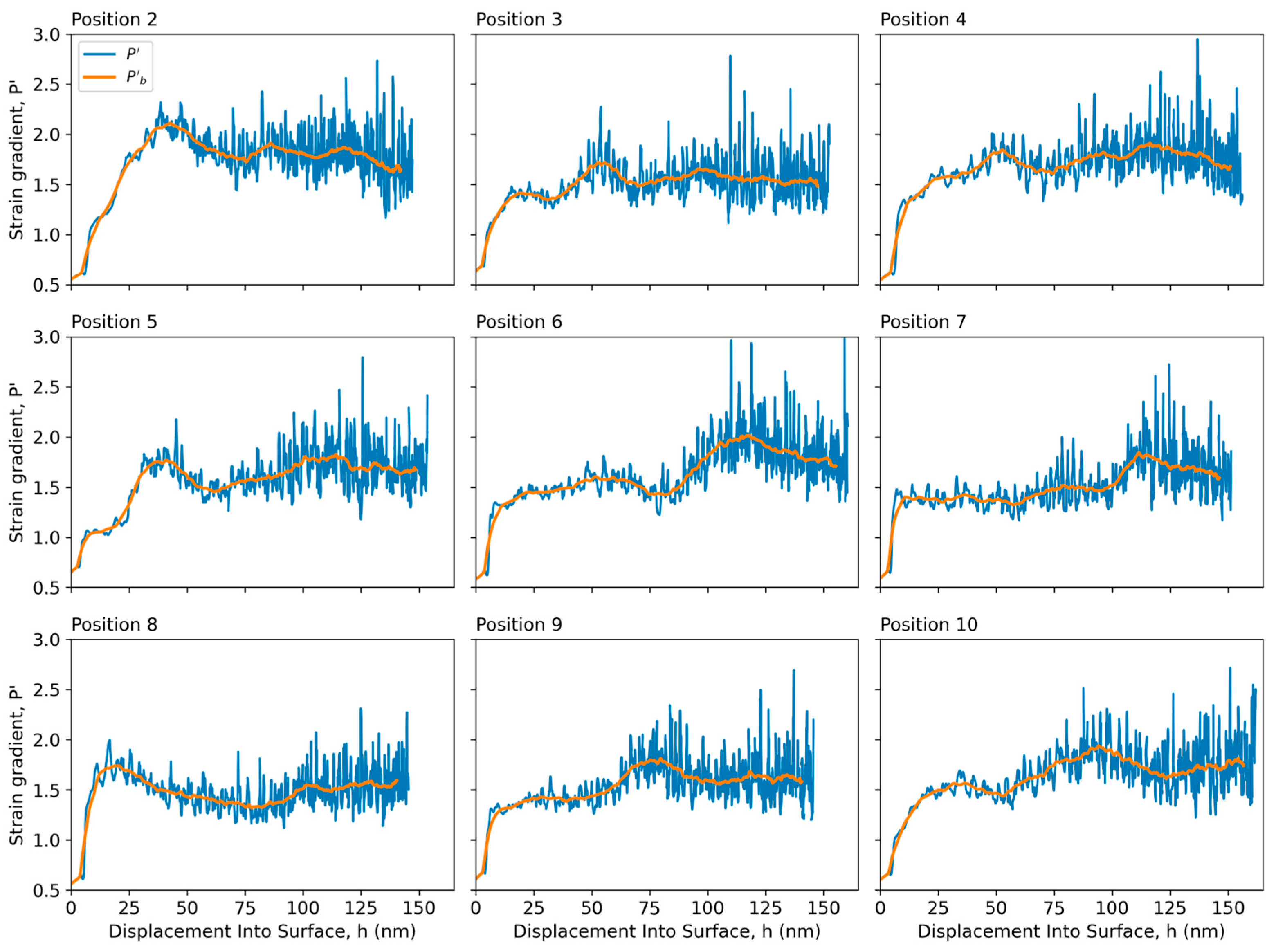
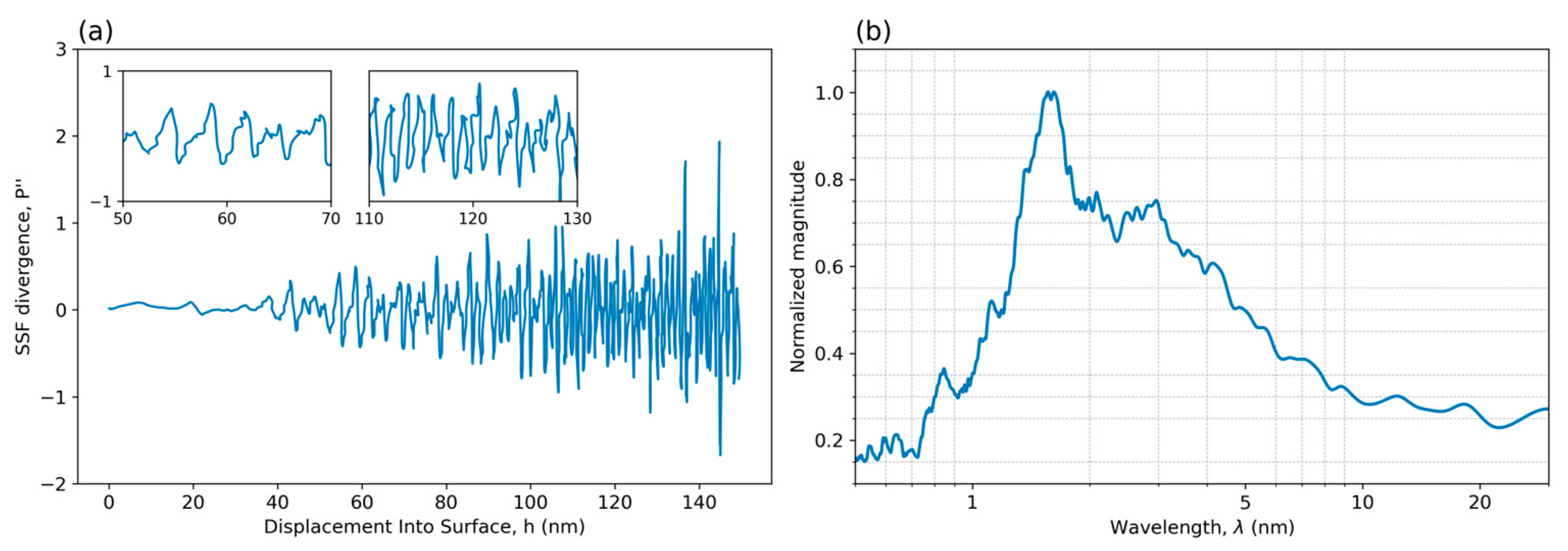
3.4. SSF Gradient P′/h-Profiles and Their Fine Structure
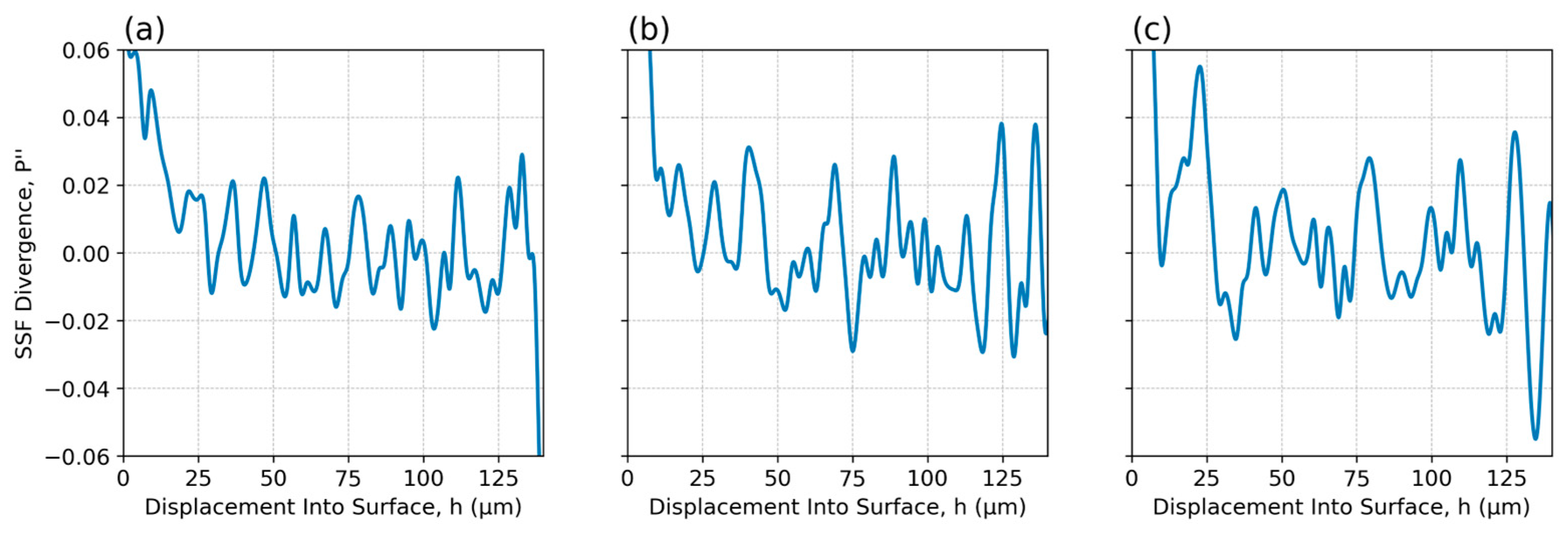
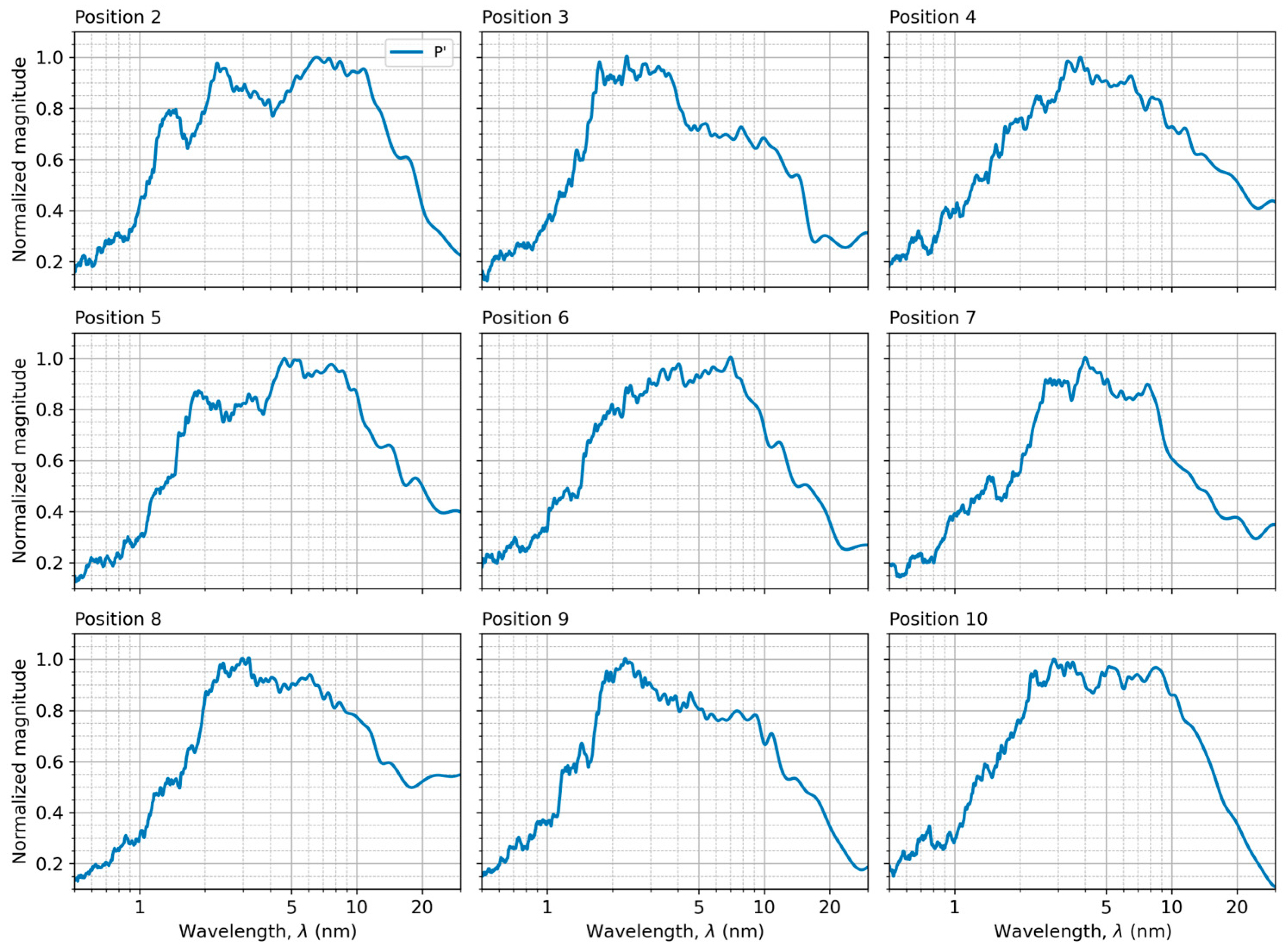
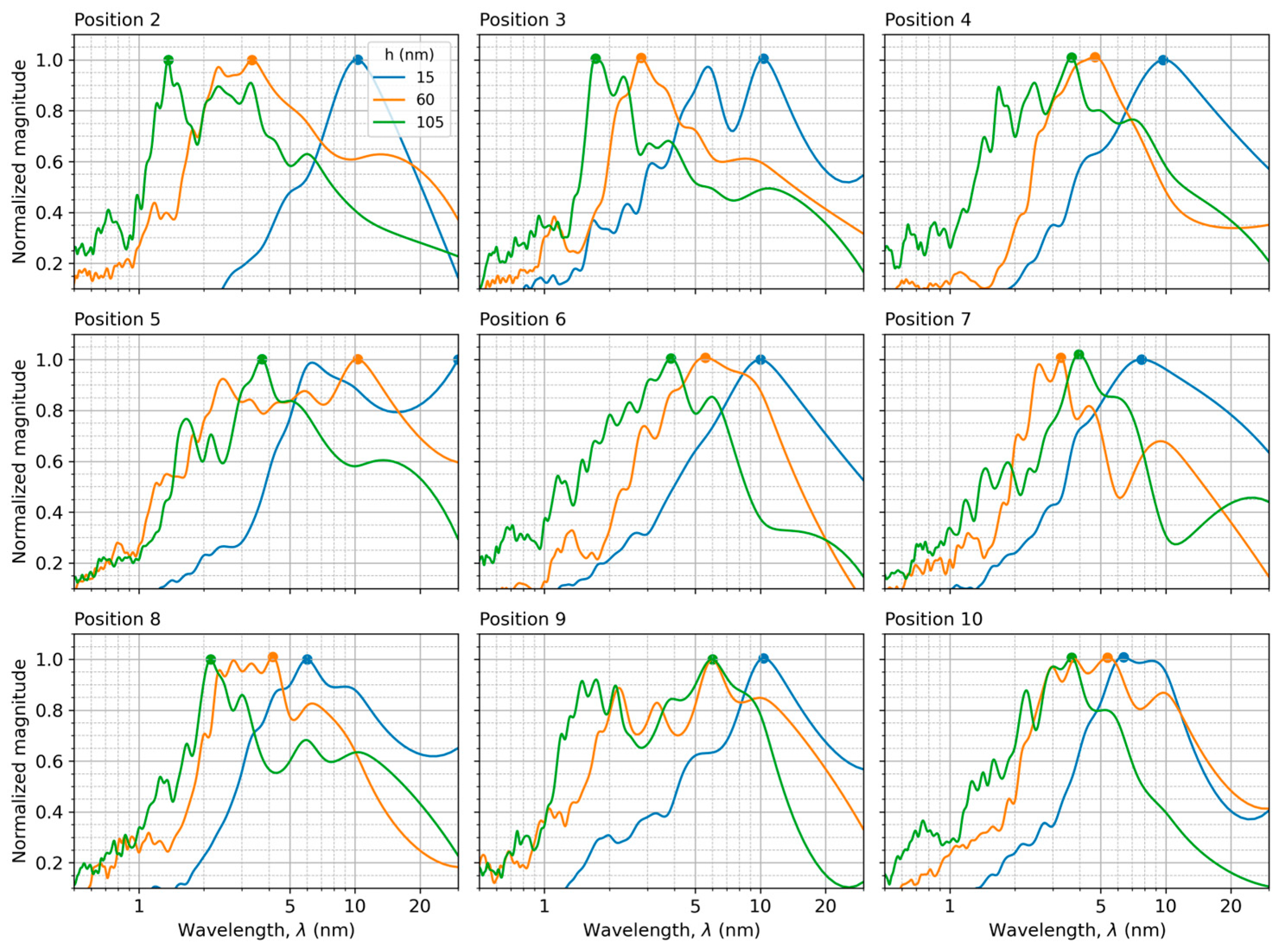
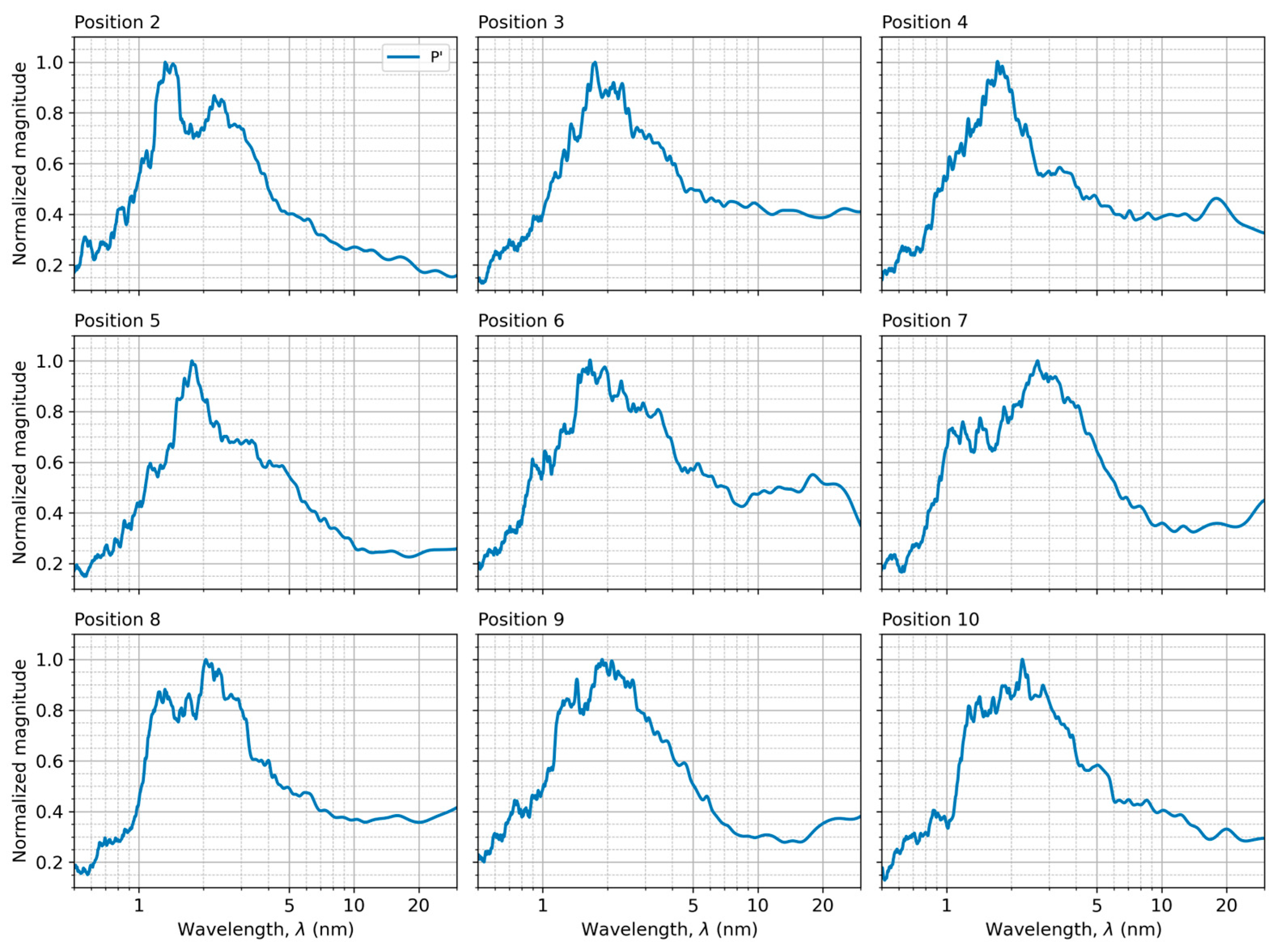
3.5. Fourier Frequency Analysis of the Total Strain Gradient’s Fine Structure
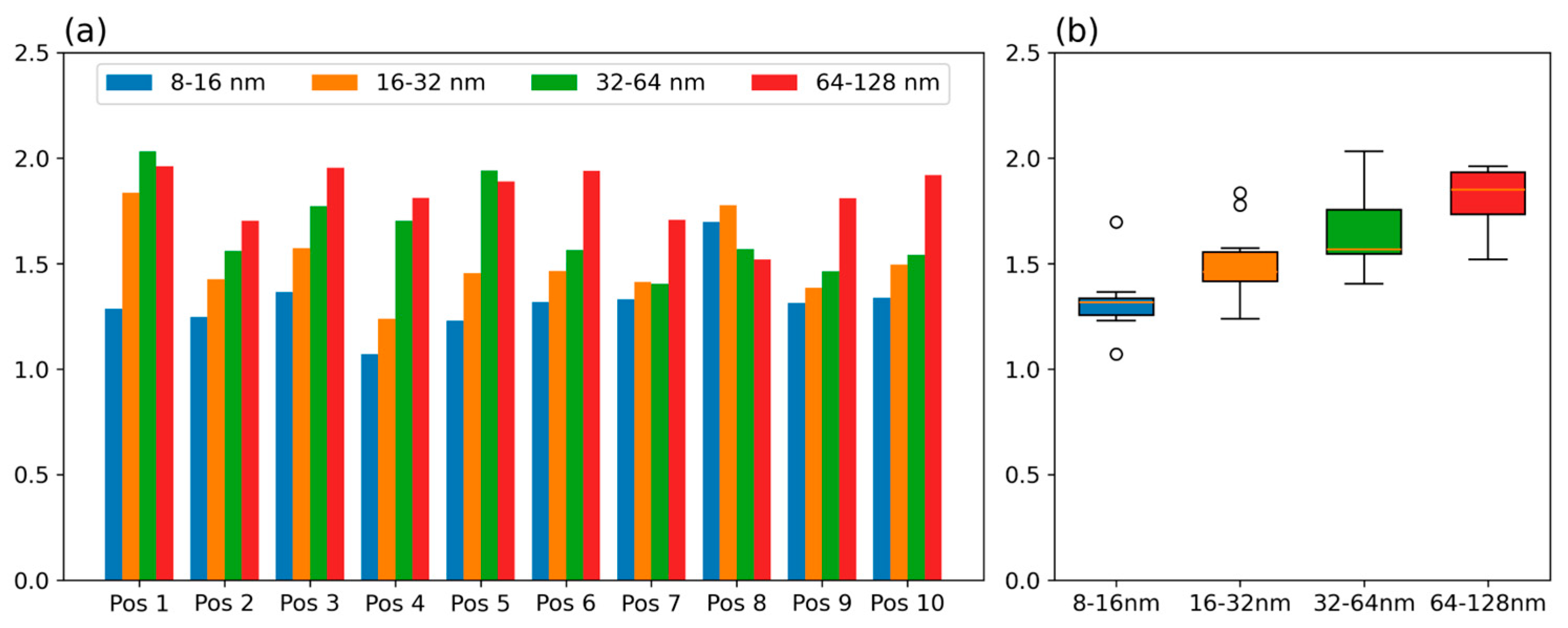
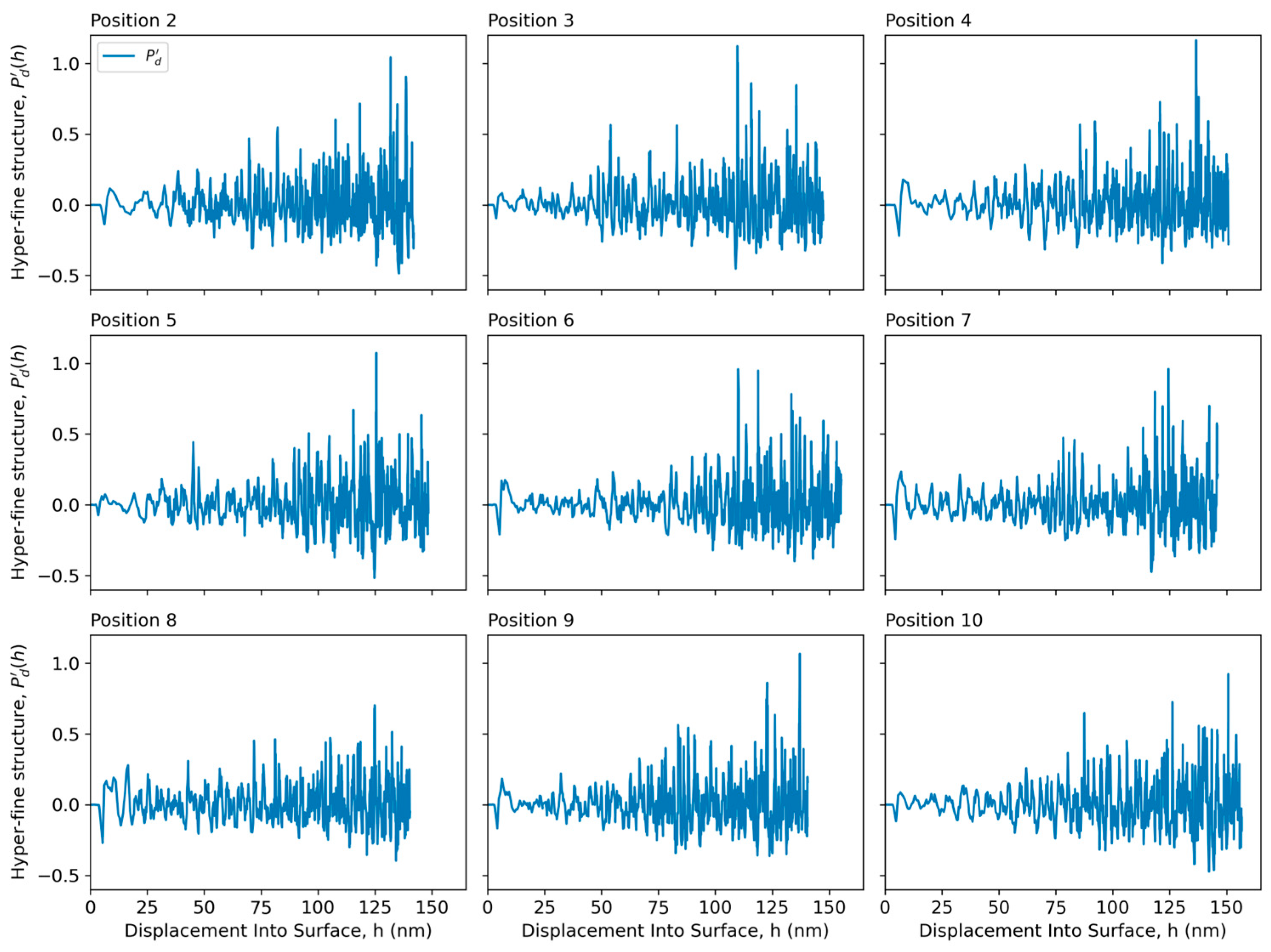
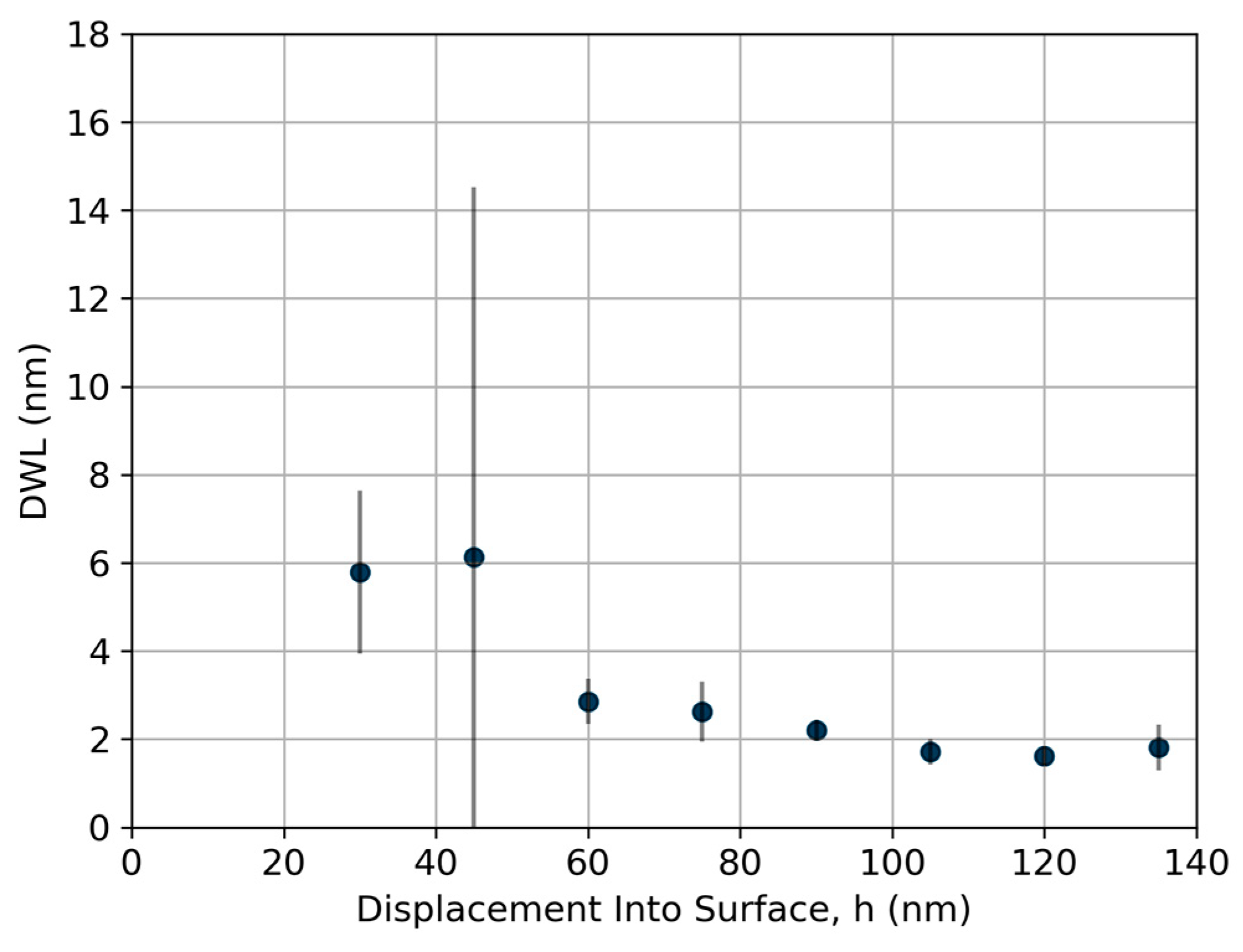
3.6. Fourier Frequency Analysis of the Total Strain Gradient’s Hyperfine Structure
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Surface Roughness Evaluation Using Roughness Tester Mitutoyo AVANT
| Raqz | NSC-1 | NSC-2 | NSC-3 | NSC-4 |
|---|---|---|---|---|
| Ra | 9.56 ± 0.89 | 13.17 ± 1.34 | 11.86 ± 1.15 | 10.41 ± 1.43 |
| Rq | 14.31 ± 1.12 | 19.47 ± 2.54 | 15.27 ± 1.19 | 13.52 ± 1.56 |
| Rz | 17.09 ± 1.91 | 23.65 ± 2.33 | 24.33 ± 2.54 | 19.64 ± 2.03 |
References
- Wu, W.-Y.; Ting, J.-M. Growth and Characteristics of Metal-Containing Diamond-like Carbon Using a Self-Assembled Process. Carbon 2006, 44, 1210–1217. [Google Scholar] [CrossRef]
- Persson, K.; Gåhlin, R. Tribological Performance of a DLC Coating in Combination with Water-Based Lubricants. Tribol. Int. 2003, 36, 851–855. [Google Scholar] [CrossRef]
- Zhang, S.; Sun, D.; Fu, Y.; Du, H. Recent Advances of Superhard Nanocomposite Coatings: A Review. Surf. Coat. Technol. 2003, 167, 113–119. [Google Scholar] [CrossRef]
- Musil, J. Hard and Superhard Nanocomposite Coatings. Surf. Coat. Technol. 2000, 125, 322–330. [Google Scholar] [CrossRef]
- Musil, J.; Vlček, J. Magnetron Sputtering of Hard Nanocomposite Coatings and Their Properties. Surf. Coat. Technol. 2001, 142–144, 557–566. [Google Scholar] [CrossRef]
- Pogrebnjak, A.; Smyrnova, K.; Bondar, O. Nanocomposite Multilayer Binary Nitride Coatings Based on Transition and Refractory Metals: Structure and Properties. Coatings 2019, 9, 155. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, Y.; Liu, J.; Tian, Y.; Chi, Y.; Yang, Y. Hardening Mechanism of Thick (Ti,Cr,V)N Composite Coatings with Multi-Layer Nano-Columnar Dendrites Microstructure. J. Eur. Ceram. Soc. 2024, 44, 2013–2025. [Google Scholar] [CrossRef]
- Gao, N.; Lu, D.; Zhao, Y.; Liu, X.; Liu, G.; Wu, Y.; Liu, G.; Fan, Z.; Lu, Z.; George, E.P. Strengthening of a CrMnFeCoNi High-Entropy Alloy by Carbide Precipitation. J. Alloys Compd. 2019, 792, 1028–1035. [Google Scholar] [CrossRef]
- Su, Y.L.; Kao, W.H.; Sung, K.H. Mechanical and Tribological Properties of NbAl, NbAlN, and NbAIN-CH Coatings Deposited Using Various Niobium Target Currents and Acetylene Flow Rates. J. Mater. Eng. Perform. 2022, 31, 3594–3610. [Google Scholar] [CrossRef]
- Leitans, A.; Jansons, E.; Lungevics, J.; Kundzins, K.; Boiko, I.; Kanders, U.; Kovalenko, V.; Linins, O. Tribological and Micromechanical Properties of the Nanostructured Carbonitride/Nitride Coatings of Transition Metals Alloyed by Hf and Nb. Coatings 2023, 13, 552. [Google Scholar] [CrossRef]
- Ul-Hamid, A. The Effect of Deposition Conditions on the Properties of Zr-Carbide, Zr-Nitride and Zr-Carbonitride Coatings—A Review. Mater. Adv. 2020, 1, 988–1011. [Google Scholar] [CrossRef]
- Musil, J.; Kunc, F.; Zeman, H.; Poláková, H. Relationships between Hardness, Young’s Modulus and Elastic Recovery in Hard Nanocomposite Coatings. Surf. Coatings Technol. 2002, 154, 304–313. [Google Scholar] [CrossRef]
- Donohue, L.A.; Smith, I.J.; Münz, W.D.; Petrov, I.; Greene, J.E. Microstructure and Oxidation-Resistance of Ti1 − x − y −zAlxCryYzN Layers Grown by Combined Steered-Arc/Unbalanced-Magnetron-Sputter Deposition. Surf. Coat. Technol. 1997, 94–95, 226–231. [Google Scholar] [CrossRef]
- Yang, Q.; Seo, D.Y.; Zhao, L.R. Multilayered Coatings with Alternate Pure Ti and TiN/CrN Superlattice. Surf. Coat. Technol. 2004, 177–178, 204–208. [Google Scholar] [CrossRef]
- Hahn, R.; Bartosik, M.; Soler, R.; Kirchlechner, C.; Dehm, G.; Mayrhofer, P.H. Superlattice Effect for Enhanced Fracture Toughness of Hard Coatings. Scr. Mater. 2016, 124, 67–70. [Google Scholar] [CrossRef]
- Yin, D.; Xu, Z.; Feng, J.; Qin, Y. Numerical Modelling of Multilayered Coatings—Latest Developments and Applications. Manuf. Rev. 2014, 1, 8. [Google Scholar] [CrossRef]
- Cabibbo, M.; Clemente, N.; El Mehtedi, M.; Hamouda, A.H.; Musharavati, F.; Santecchia, E.; Spigarelli, S. Constitutive Analysis for the Quantification of Hardness Decay in a Superlattice CrN/NbN Hard-Coating. Surf. Coat. Technol. 2015, 275, 155–166. [Google Scholar] [CrossRef]
- Vogli, E.; Tillmann, W.; Selvadurai-Lassl, U.; Fischer, G.; Herper, J. Influence of Ti/TiAlN-Multilayer Designs on Their Residual Stresses and Mechanical Properties. Appl. Surf. Sci. 2011, 257, 8550–8557. [Google Scholar] [CrossRef]
- Liew, W.Y.H.; Lim, H.P.; Melvin, G.J.H.; Dayou, J.; Jiang, Z.T. Thermal Stability, Mechanical Properties, and Tribological Performance of TiAlXN Coatings: Understanding the Effects of Alloying Additions. J. Mater. Res. Technol. 2022, 17, 961–1012. [Google Scholar] [CrossRef]
- Nie, X.-D.; Xu, J.-Y.; Zhang, Z.-C.; Wei, X.-L.; Xiao, J.-K.; Zhang, C. The Progress of Research on High-Entropy Ceramics in The Field of Tribology. Adv. Ceram. 2025, 46, 1–23. [Google Scholar] [CrossRef]
- Kanders, U.; Kanders, K.; Maniks, J.; Mitin, V.; Kovalenko, V.; Nazarovs, P.; Erts, D. Nanoindentation Response Analysis of Cu-Rich Carbon–Copper Composite Films Deposited by PVD Technique. Surf. Coat. Technol. 2015, 280, 308–316. [Google Scholar] [CrossRef]
- Das, J.; Linke, B. Evaluation and Systematic Selection of Significant Multi-Scale Surface Roughness Parameters (SRPs) as Process Monitoring Index. J. Mater. Process. Technol. 2017, 244, 157–165. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, S.; Shi, Q.; Ge, X.; Wang, W. Multilayer Coatings for Tribology: A Mini Review. Nanomaterials 2022, 12, 1388. [Google Scholar] [CrossRef] [PubMed]
- Kanders, U.; Kanders, K.; Jansons, E.; Boiko, I.; Kromanis, A.; Lungevics, J.; Leitans, A. Strain-Hardening and Strain-Softening Phenomena Observed in Thin Nitride/Carbonitride Ceramic Coatings During the Nanoindentation Experiments. Coatings 2025, 15, 674. [Google Scholar] [CrossRef]
- Fleck, N.; Hutchinson, J. Strain Gradient Plasticity. Adv. Appl. Mech. 1997, 33, 295–362. [Google Scholar]
- Gao, H.; Huang, Y.; Nix, W.D. Modeling Plasticity at the Micrometer Scale. Naturwissenschaften 1999, 86, 507–515. [Google Scholar] [CrossRef] [PubMed]
- Fischer-Cripps, A.C. Nanoindentation; Springer Nature: Berlin, Germany, 2004. [Google Scholar] [CrossRef]
- Johnson, K.L. The Correlation of Indentation Experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Mokios, G.; Aifantis, E.C. Gradient Effects in Micro-/Nanoindentation. Mater. Sci. Technol. 2012, 28, 1072–1078. [Google Scholar] [CrossRef]
- Kanders, U.; Kanders, K. Nanoindentation Response Analysis of Thin Film Substrates-I: Strain Gradient-Divergence Approach. Latv. J. Phys. Tech. Sci. 2017, 54, 66–76. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of Hardness and Elastic Modulus by Instrumented Indentation: Advances in Understanding and Refinements to Methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Sedlaček, M.; Podgornik, B.; Vižintin, J. Tribological Properties of DLC Coatings and Comparison with Test Results: Development of a Database. Mater. Charact. 2008, 59, 151–161. [Google Scholar] [CrossRef]
- Khun, N.W.; Lee, P.M.; Toh, W.Q.; Liu, E. Tribological Behavior of Nickel-Doped Diamond-Like Carbon Thin Films Prepared on Silicon Substrates via Magnetron Sputtering Deposition. Tribol. Trans. 2016, 59, 845–855. [Google Scholar] [CrossRef]
- Vicen, M.; Bronček, J.; Nový, F. Investigation of Tribological Properties of CarbonX Coating Deposited on 100Cr6 Steel. Prod. Eng. Arch. 2019, 25, 52–55. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall: Boca Raton, FL, USA, 1994. [Google Scholar] [CrossRef]
- Boiko, I.; Kanders, U.; Kundzins, K.; Leitans, A.; Lungevičs, J.; Jansons, E.; Linins, O. Nanostructured Smart Coatings Obtained by the High Power Magnetically Compresed Plasma Method. In Proceedings of the RTU 63rd International Scientific Conference Section Mechanical Engineering Technology and Heat Engineering, Riga, Latvia, 13 October 2022; RTU Press: Riga, Latvia, 2023; pp. 19–21. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar] [CrossRef]
- Attaf, M.T. Connection between the Loading Curve Models in Elastoplastic Indentation. Mater. Lett. 2004, 58, 3491–3498. [Google Scholar] [CrossRef]
- Meyer, E. Untersuchungen über Härteprüfung und Härte Brinell Methoden. Z. Ver. Deut. Ing. 1908, 52, 645–654. [Google Scholar]
- Fröhlich, F.; Grau, P.; Grellmann, W. Performance and Analysis of Recording Microhardness Tests. Phys. Status Solidi 1977, 42, 79–89. [Google Scholar] [CrossRef]
- Sneddon, I.N. The Relation between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
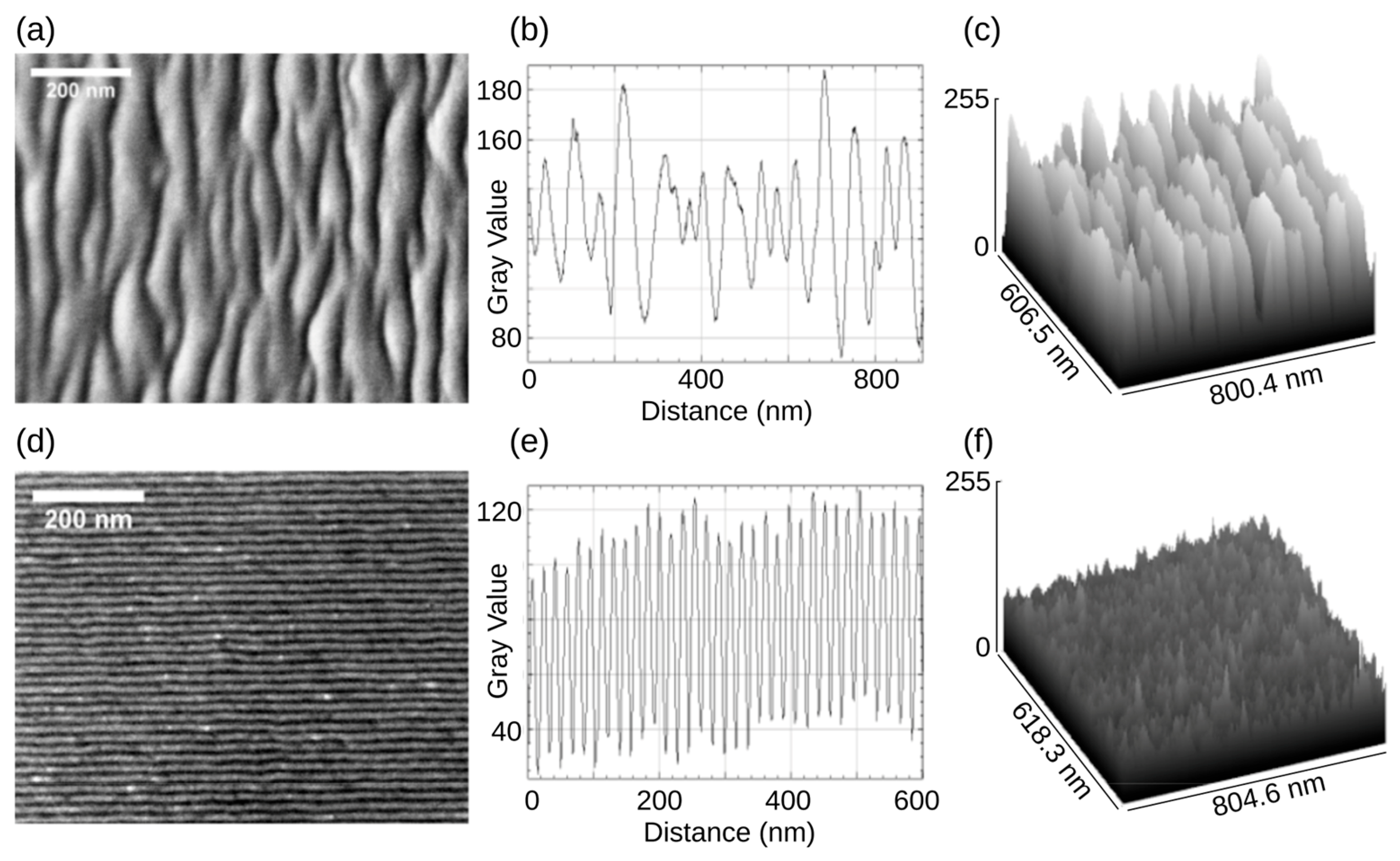
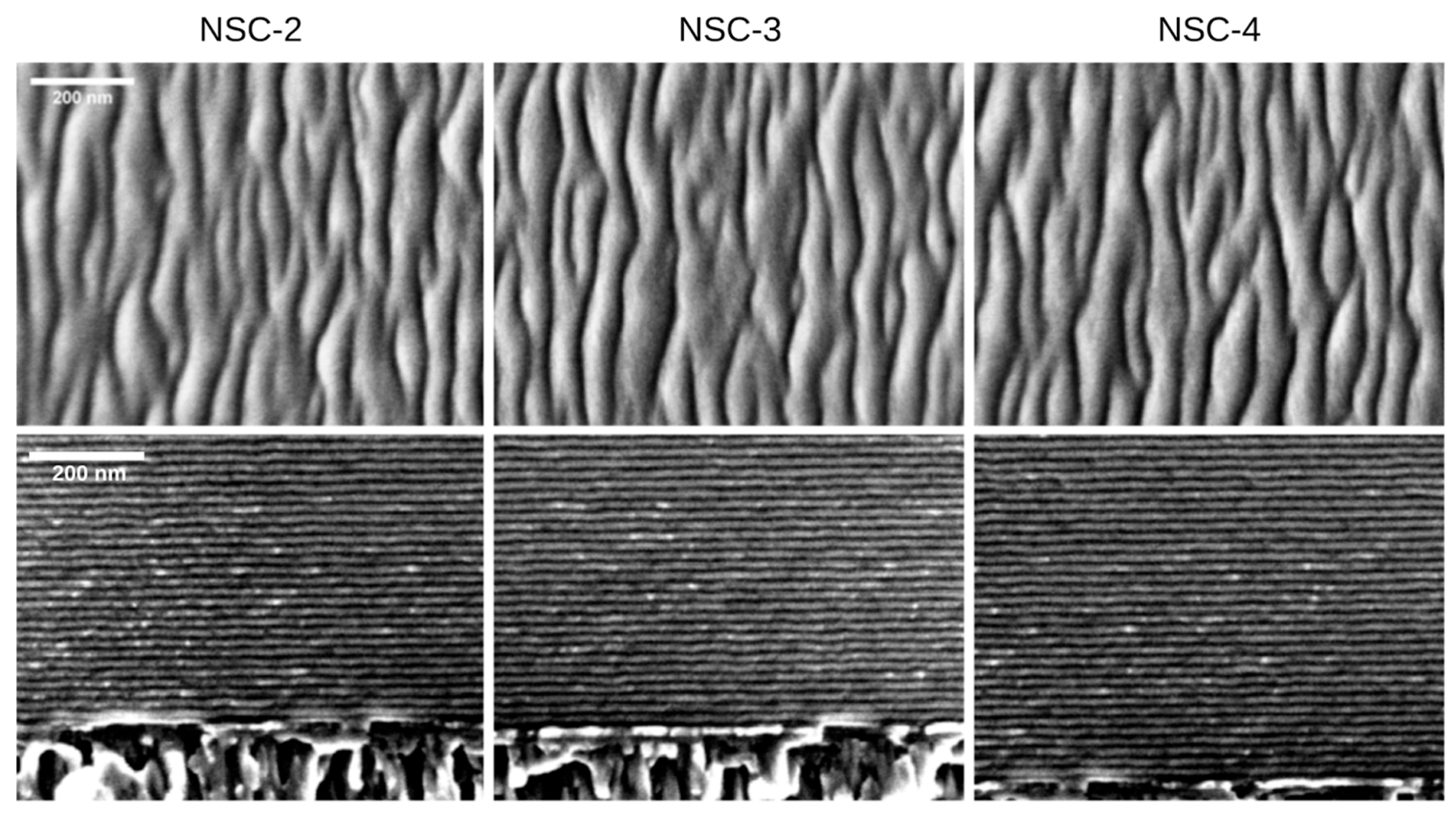


| Sample Label | Carbonitride/ Nitride Bilayer | Coating Total Thickness, t (nm) | PVD Process Duration, D (min) | Number of Periods, N | Sublayer (-N) Thickness, t1 (nm) | Sublayer (-CN) Thickness, t2 (nm) | Bilayer (-N/-CN) Thickness, t1 + t2 (nm) |
|---|---|---|---|---|---|---|---|
| NSC-1 | {TiAlSiNb-N/TiCr-CN} | 5470 | 104 | 311 | 11.7 | 5.9 | 17.6 |
| NSC-2 | {TiAlSiNb-N/TiCr-CN} | 5260 | 98 | 294 | 11.9 | 6.0 | 17.9 |
| NSC-3 | {TiAlSiNb-N/TiCr-CN} | 5680 | 103 | 310 | 12.2 | 6.1 | 18.3 |
| NSC-4 | {TiAlSiNb-N/TiCr-CN} | 5830 | 114 | 341 | 11.4 | 5.7 | 17.1 |
| Sample Label | Coating Thickness, t (nm) 1 | Substrate Temperature Ts, °C 2 | Nano- Hardness, H (GPa) 3 | Elastic-, Modulus, E (GPa) 3 | Steady-State Sliding Friction, CoF 4 | Wear Rate, Wr at Test Load of 3N (mm3/Nm) 5 |
|---|---|---|---|---|---|---|
| NSC-1 | 5470 ± 240 | 380 | 24.61 | 378.60 | 0.23 ± 0.07 | 4.3 × 10−6 |
| NSC-2 | 5260 ± 260 | 390 | 25.44 | 339.50 | 0.21 ± 0.06 | 4.7 × 10−6 |
| NSC-3 | 5680 ± 250 | 390 | 25.14 | 414.80 | 0.19 ± 0.02 | 3.9 × 10−6 |
| NSC-4 | 5830 ± 240 | 380 | 24.96 | 371.80 | 0.22 ± 0.06 | 4.5 × 10−6 |
| h-Intervals | Pos 1 | Pos 2 | Pos 3 | Pos 4 | Pos 5 | Pos 6 | Pos 7 | Pos 8 | Pos 9 | Pos 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| h ∈ (8–16) nm | 1.2844 | 1.2458 | 1.3652 | 1.0721 | 1.2289 | 1.3169 | 1.3313 | 1.6974 | 1.3138 | 1.3369 |
| h ∈ (16–32) nm | 1.8357 | 1.4250 | 1.5730 | 1.2388 | 1.4537 | 1.4655 | 1.4130 | 1.7765 | 1.3850 | 1.4953 |
| h ∈ (32–64) nm | 2.0331 | 1.5602 | 1.7733 | 1.7033 | 1.9404 | 1.5656 | 1.4038 | 1.5687 | 1.4623 | 1.5402 |
| h ∈ (64–128) nm | 1.9610 | 1.7029 | 1.9544 | 1.8105 | 1.8890 | 1.9382 | 1.7072 | 1.5198 | 1.8099 | 1.9186 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanders, U.; Kanders, K.; Kromanis, A.; Boiko, I.; Jansons, E.; Lungevics, J. Simple Strain Gradient–Divergence Method for Analysis of the Nanoindentation Load–Displacement Curves Measured on Nanostructured Nitride/Carbonitride Coatings. Coatings 2025, 15, 824. https://doi.org/10.3390/coatings15070824
Kanders U, Kanders K, Kromanis A, Boiko I, Jansons E, Lungevics J. Simple Strain Gradient–Divergence Method for Analysis of the Nanoindentation Load–Displacement Curves Measured on Nanostructured Nitride/Carbonitride Coatings. Coatings. 2025; 15(7):824. https://doi.org/10.3390/coatings15070824
Chicago/Turabian StyleKanders, Uldis, Karlis Kanders, Artis Kromanis, Irina Boiko, Ernests Jansons, and Janis Lungevics. 2025. "Simple Strain Gradient–Divergence Method for Analysis of the Nanoindentation Load–Displacement Curves Measured on Nanostructured Nitride/Carbonitride Coatings" Coatings 15, no. 7: 824. https://doi.org/10.3390/coatings15070824
APA StyleKanders, U., Kanders, K., Kromanis, A., Boiko, I., Jansons, E., & Lungevics, J. (2025). Simple Strain Gradient–Divergence Method for Analysis of the Nanoindentation Load–Displacement Curves Measured on Nanostructured Nitride/Carbonitride Coatings. Coatings, 15(7), 824. https://doi.org/10.3390/coatings15070824










