Numerical and Experimental Study of Enhanced Heat Dissipation Performance of Graphene-Coated Heating Cables
Abstract
1. Introduction
2. Materials and Methods
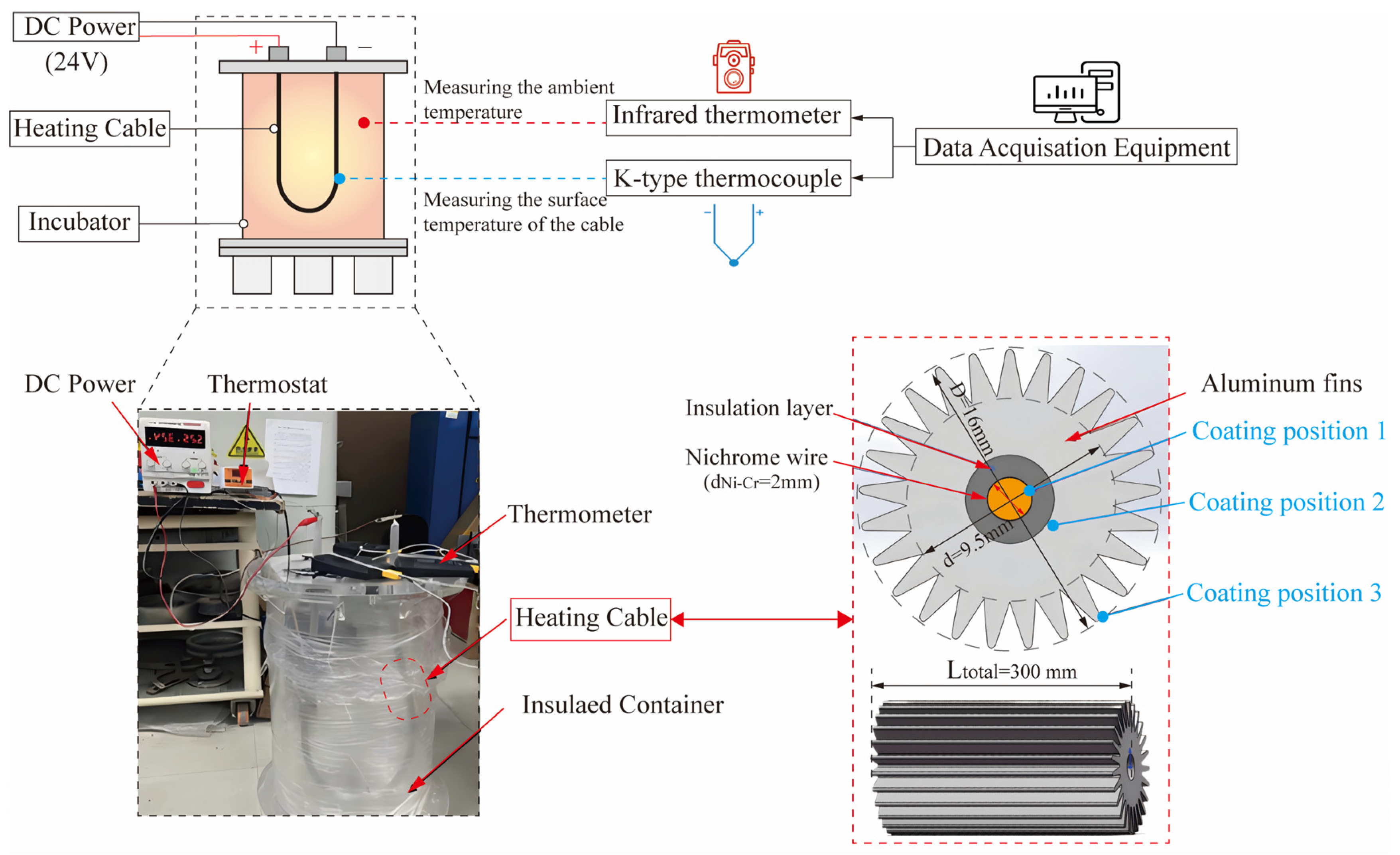
2.1. Experimental Apparatus
2.2. Experimental Testing Methodology
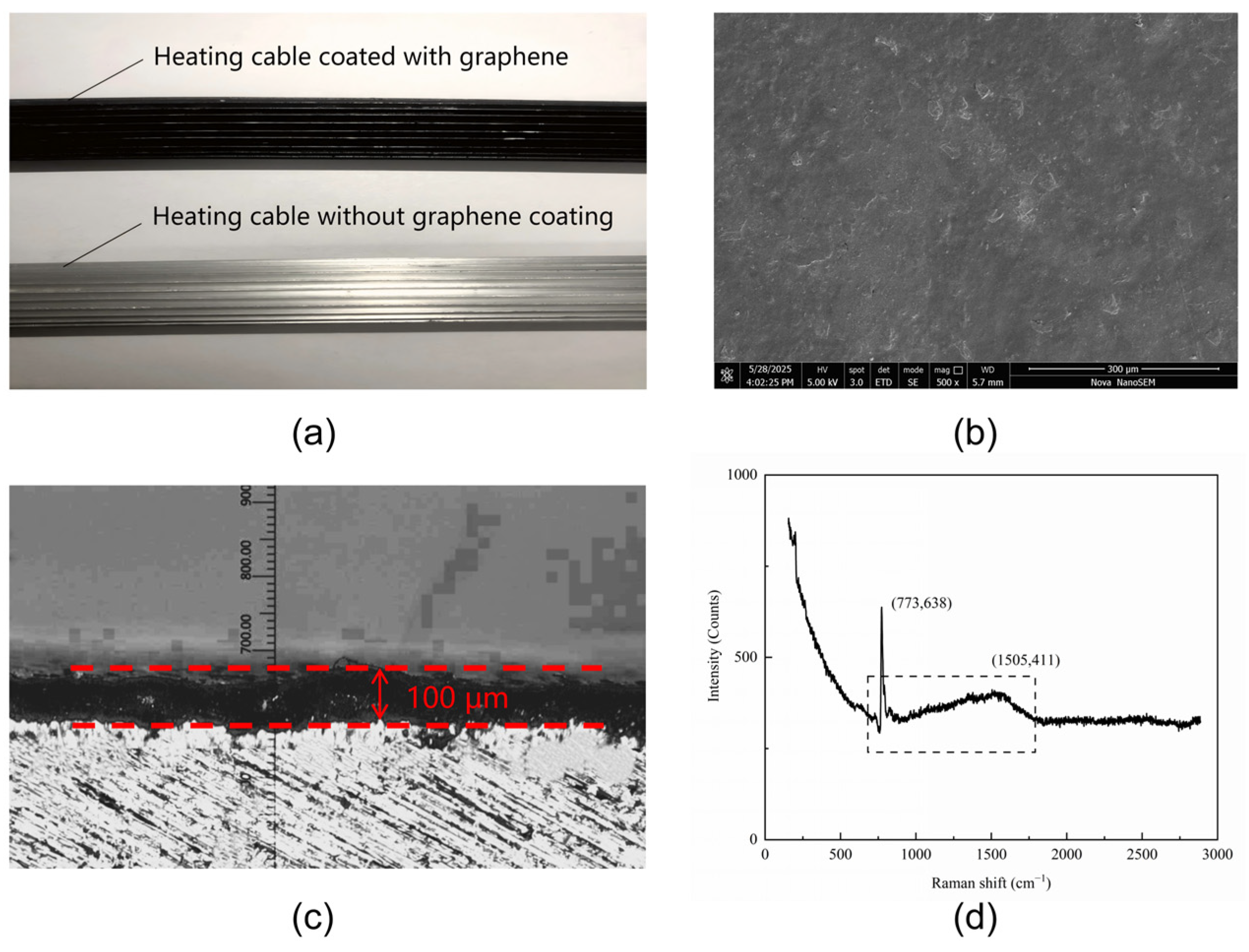
2.3. Preparation and Properties of Coatings
2.4. Surface Analysis of Graphene Coating
2.5. Comparison of Performance Indexes of Heating Cables
2.6. Temperature Measurement Error Analysis
3. Heat Transfer Numerical Simulation of Heating Cable
3.1. Heat Transfer Model of Heating Cables
3.2. Radiation Heat Transfer Solution Model
3.3. Three-Dimensional Model Development
3.4. Boundary Conditions and Meshing
4. Experimental Results and Discussion
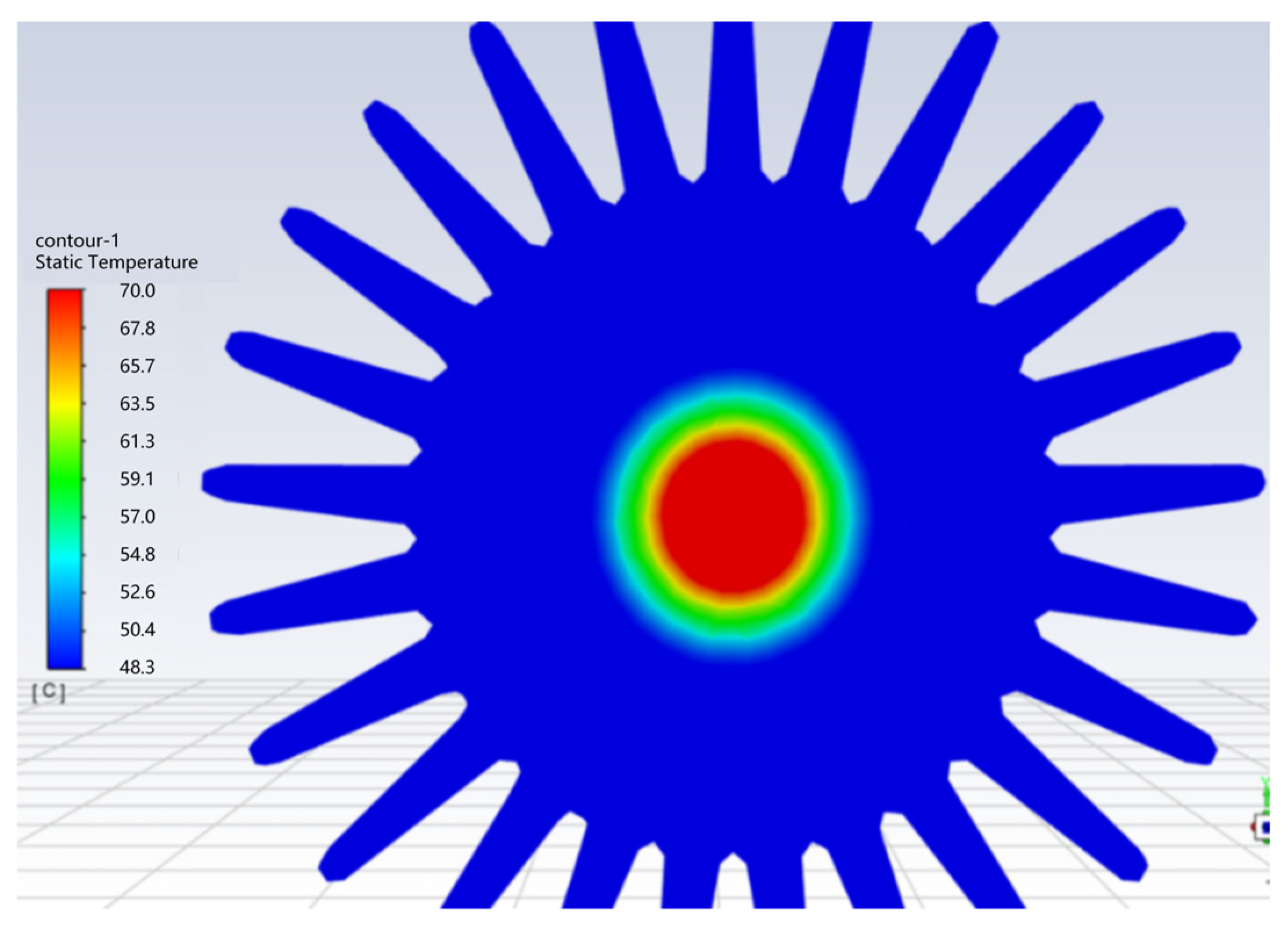
4.1. Numerical Simulation of Heat Dissipation Performance of Heating Cable with Different Coating Positions
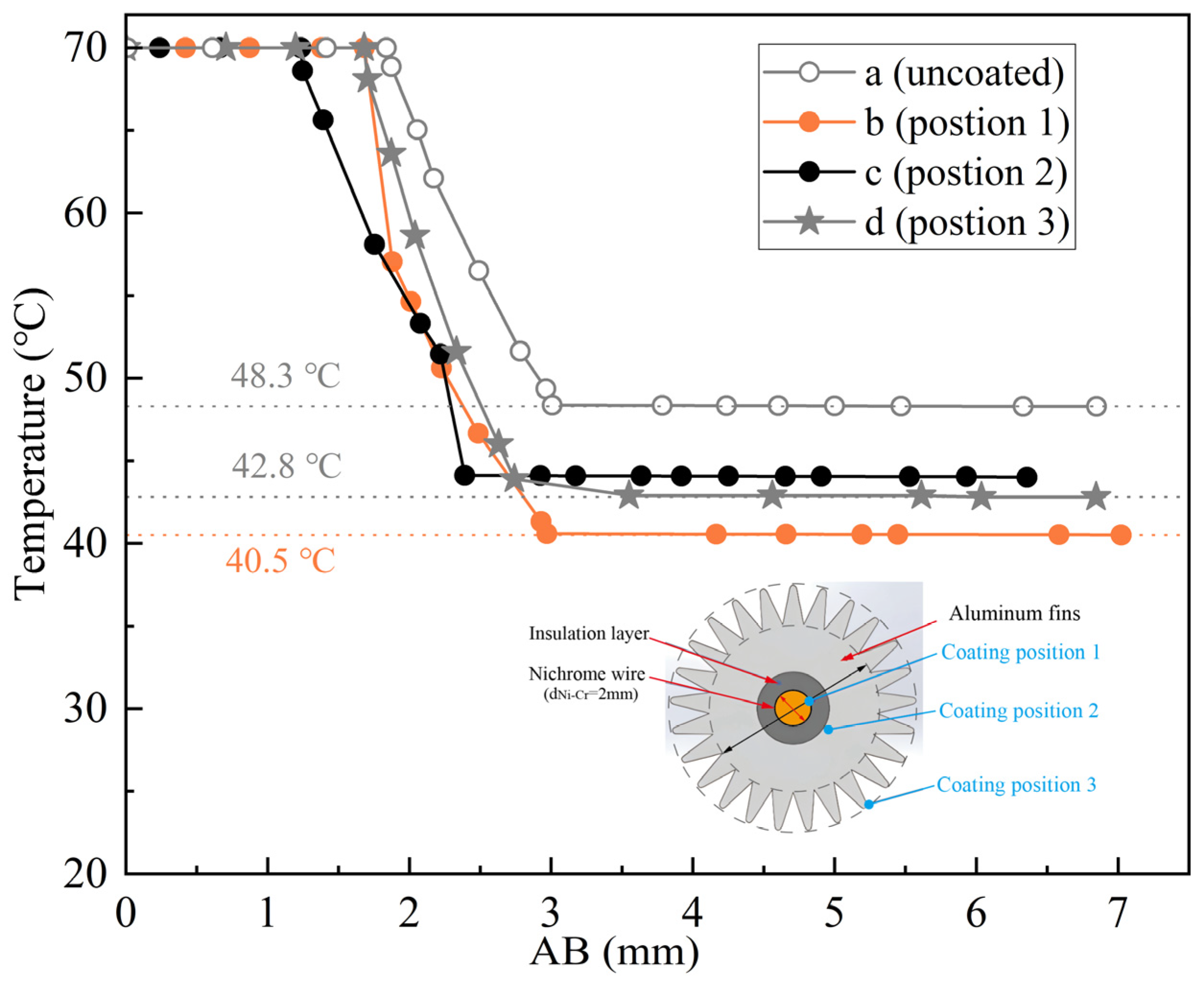
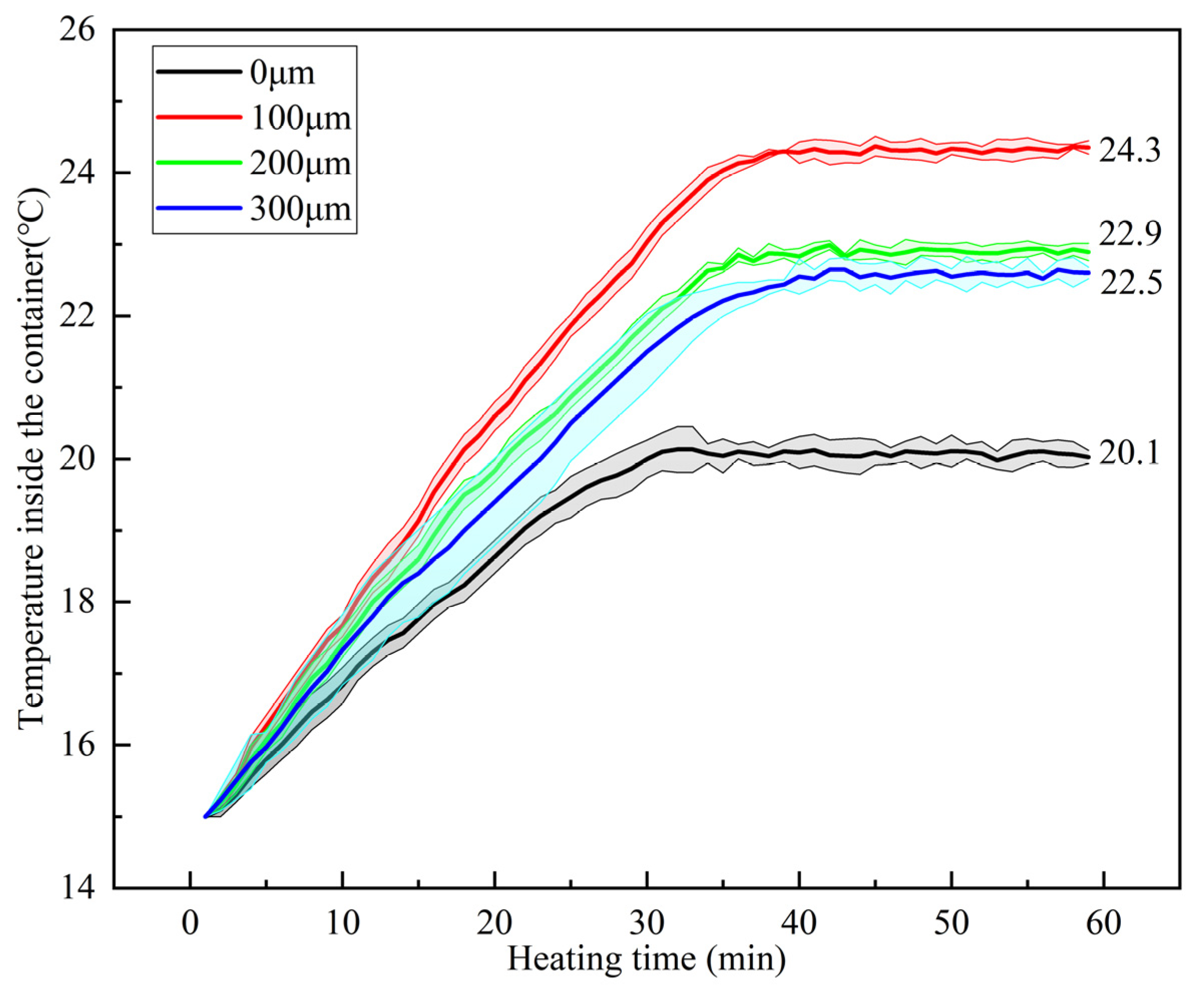
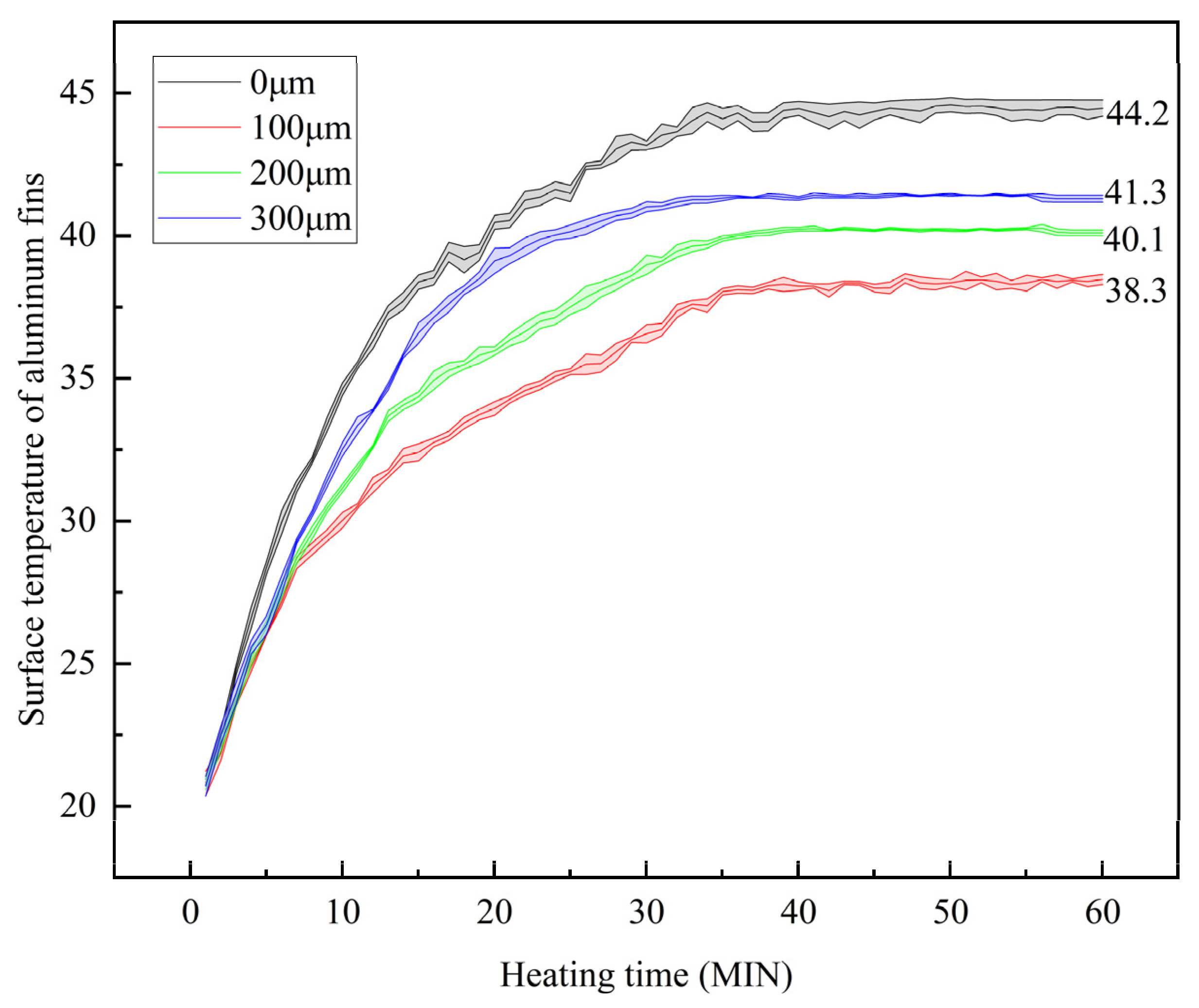
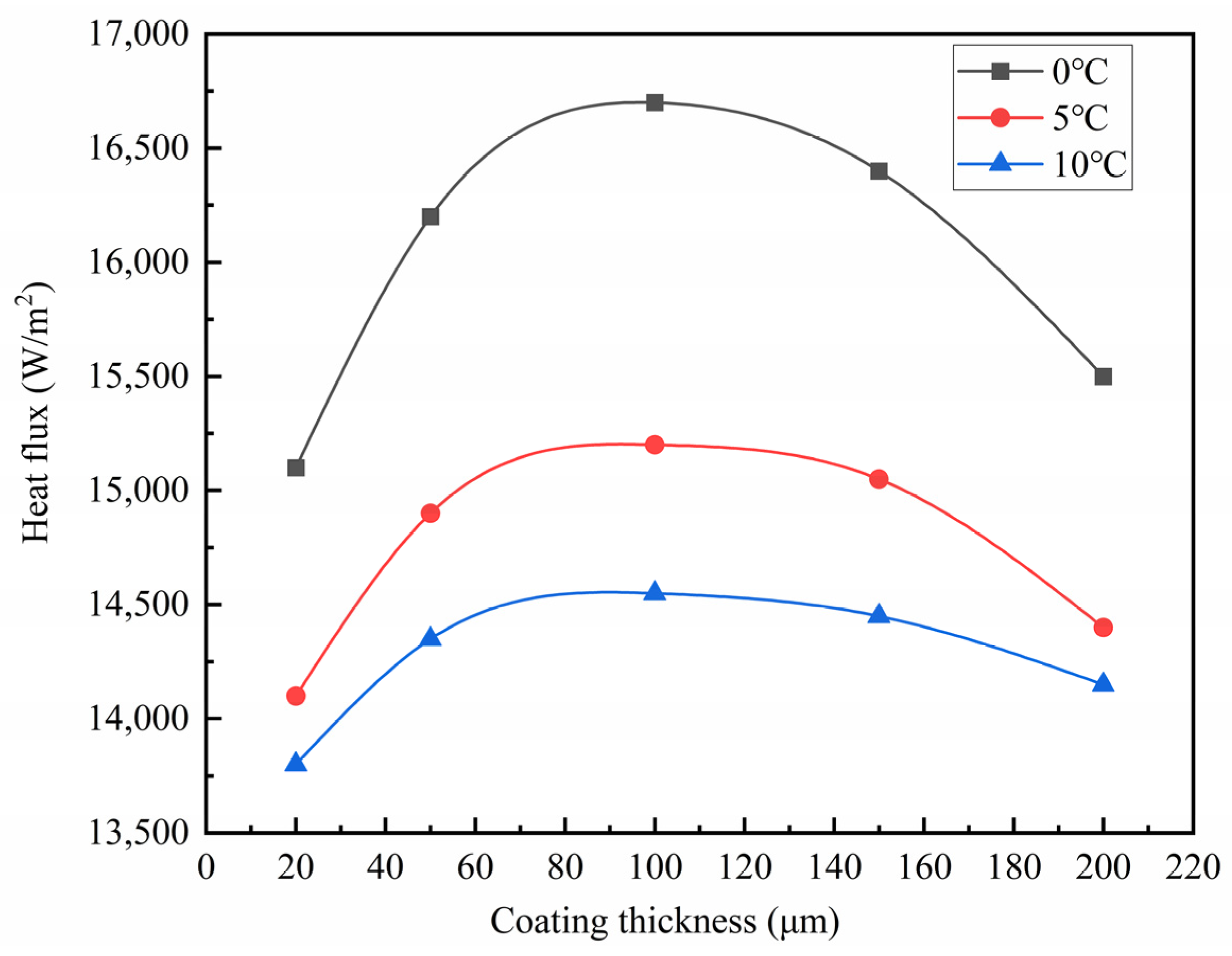
4.2. Effect of Coating Thickness on Temperature Rise of Heating Cable
4.2.1. Analysis of Coating Thickness Test Results
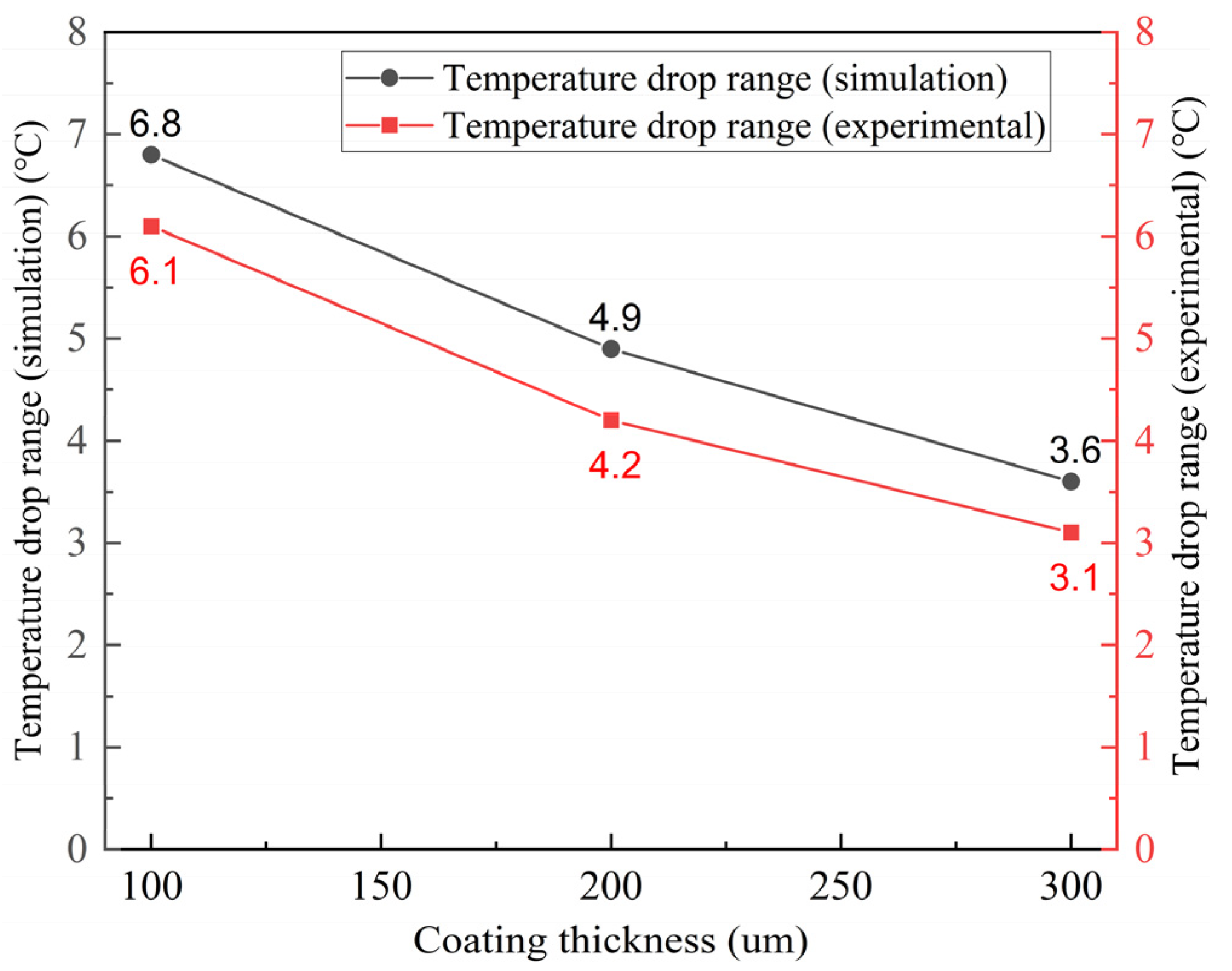
4.2.2. Correlation Between Simulation Value and Experimental Value of Coating Thickness
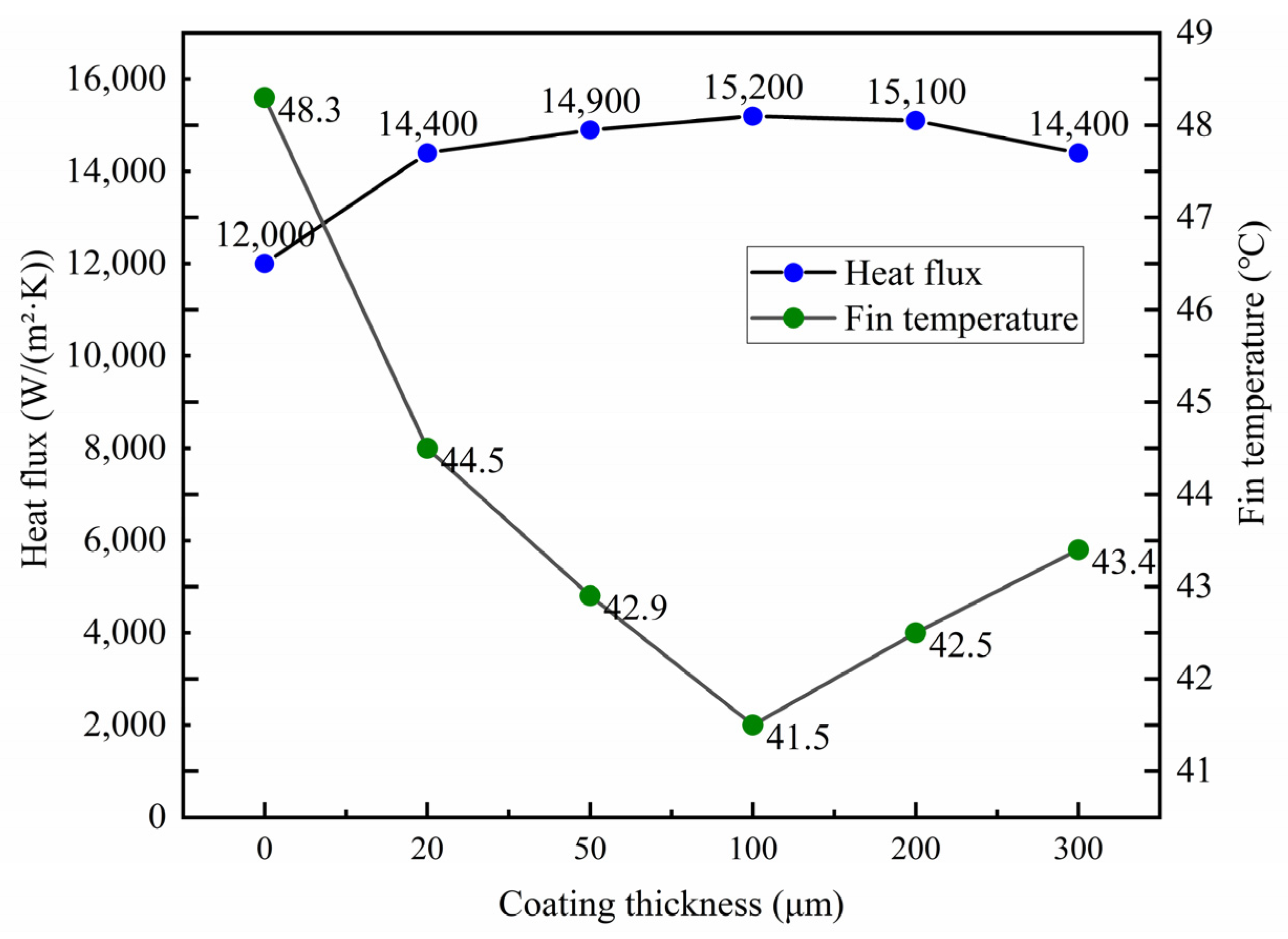
4.2.3. Mechanism Analysis of Heat Dissipation Performance with Respect to Coating Thickness
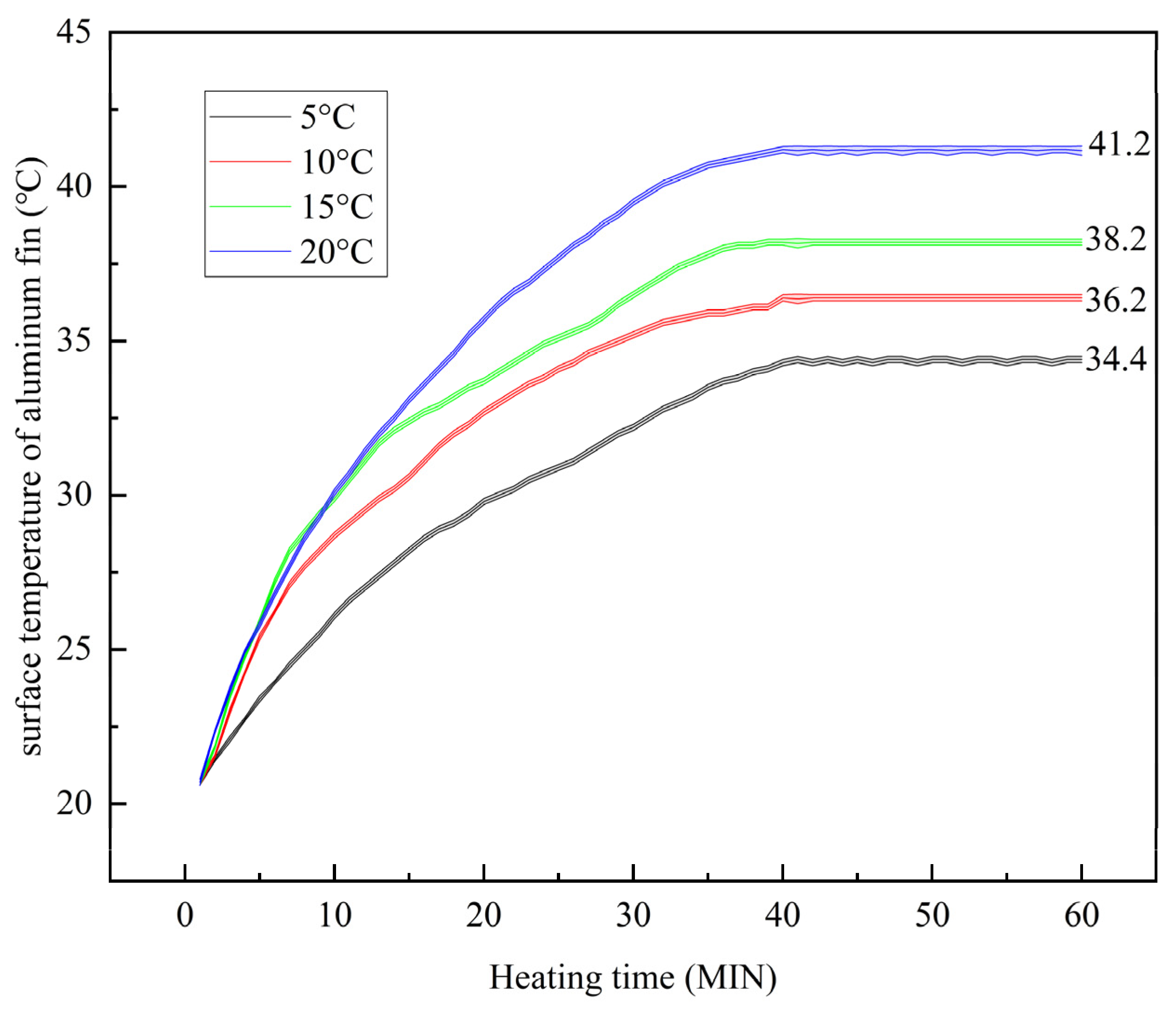
4.3. Effect of Ambient Temperature on Heating Cable Temperature-Rise Rate
4.3.1. Analysis of Ambient Temperature Experimental Results
4.3.2. Correlation Between Simulation Value and Experimental Value of Ambient Temperature
4.3.3. Analysis of the Mechanism of Different Heating Cable Heat Dissipation Efficiency in Different Ambient Temperatures
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Zhan, G.; Mao, W.; Lai, Y.; Luo, Y.; Liu, P. Numerical Simulation and Experimental Verification of Cu\Ni Dissimilar Metal Wire Deep Penetration Brazing. In Proceedings of the 2020 5th International Conference on Smart Grid and Electrical Automation (ICSGEA), Zhangjiajie, China, 13–14 June 2020; pp. 125–128. [Google Scholar] [CrossRef]
- Kim, J.-C.; Wi, J.-H.; Ri, N.-C.; Ri, S.-I. Thermal Conductivity of Graphene/Graphane/Graphene Heterostructure Nanoribbons: Non-Equilibrium Molecular Dynamics Simulations. Solid State Commun. 2021, 328, 114249. [Google Scholar] [CrossRef]
- Pyun, K.R.; Ko, S.H. Graphene as a Material for Energy Generation and Control: Recent Progress in the Control of Graphene Thermal Conductivity by Graphene Defect Engineering. Mater. Today Energy 2019, 12, 431–442. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, H.; Liu, J.; Bao, C. Measuring the Specific Surface Area of Monolayer Graphene Oxide in Water. Mater. Lett. 2020, 261, 127098. [Google Scholar] [CrossRef]
- Aacharya, A.; Koirala, R.; Khanal, S.; Baral, B. Comparative Analysis of Radiant and Radiator Heating System for a Residential Building. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1279, 012001. [Google Scholar] [CrossRef]
- Guan, Y.; Cui, H.; Fei, J. Study on Optimization of Copper to Aluminum for Locomotive Finned Tube Radiator. Energies 2023, 16, 2130. [Google Scholar] [CrossRef]
- Wang, F.; Li, Z.; Pang, D.; Li, Z.; Zhao, X.; Cheng, X.; Liu, M.; Zhang, Y.; Guo, W. Enhancing Heat Transfer of Photovolta-ic Panels with Fins. Int. J. Energy Res. 2024, 2024, 5180627. [Google Scholar] [CrossRef]
- Guan, Y.; Cui, H.; Li, M. Numerical Simulation Study on Air-Side of Diesel Locomotive Finned Tube Double Channel Radiator. J. Phys. Conf. Ser. 2021, 1746, 012048. [Google Scholar] [CrossRef]
- Majmader, F.B.; Hasan, M.J. Thermal Enhancement and Entropy Generation of an Air-Cooled 3D Radiator with Modified Fin Geometry and Perforation: A Numerical Study. Case Stud. Therm. Eng. 2023, 52, 103671. [Google Scholar] [CrossRef]
- Tran, N.; Wang, C.-C. Optimization of the Airside Thermal Performance of Mini-Channel-Flat-Tube Radiators by Using Composite Straight-and-Louvered Fins. Int. J. Heat Mass Transf. 2020, 160, 120163. [Google Scholar] [CrossRef]
- Habibian, S.H.; Abolmaali, A.M.; Afshin, H. Numerical Investigation of the Effects of Fin Shape, Antifreeze and Nanoparticles on the Performance of Compact Finned-Tube Heat Exchangers for Automobile Radiator. Appl. Therm. Eng. 2018, 133, 248–260. [Google Scholar] [CrossRef]
- Lipnický, M.; Brodnianská, Z.; Kotšmíd, S. Research of Geometrically Distinct Automobile Radiators in Terms of Thermal-Hydraulic Characteristics. Appl. Therm. Eng. 2023, 232, 121035. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Mo, S.; Jia, L.; Shao, X. Effect of Surface Modification on the Stability and Thermal Conductivity of Water-Based SiO2-Coated Graphene Nanofluid. Thermochim. Acta 2014, 595, 6–10. [Google Scholar] [CrossRef]
- Zhu, F.; Kan, Y.; Tang, K.; Liu, S. Investigation of Thermal Properties of Ni-Coated Graphene Nanoribbons Based on Molecular Dynamics Methods. J. Electron. Mater. 2017, 46, 4733–4739. [Google Scholar] [CrossRef]
- Manasoglu, G.; Celen, R.; Kanik, M.; Ulcay, Y. An Investigation on the Thermal and Solar Properties of Graphene-Coated Polyester Fabrics. Coatings 2021, 11, 125. [Google Scholar] [CrossRef]
- Wei, B.; Yang, N.; Tian, M.; Qu, L.; Zhu, S. Effect of Coating Methods on Thermal Conductivity of Graphene-Coated Fabrics for Welding Protective Clothing. Mater. Lett. 2022, 314, 131787. [Google Scholar] [CrossRef]
- Dong, P.; Long, C.; Peng, Y.; Peng, X.; Guo, F. Effect of coatings on thermal conductivity and tribological properties of aluminum foam/polyoxymethylene interpenetrating composites. J. Mater. Sci. 2019, 54, 13135–13146. [Google Scholar] [CrossRef]
- Almonti, D.; Ucciardello, N. Improvement of thermal properties of micro head engine electroplated by graphene: Experimental and thermal simulation. Mater. Manuf. Process. 2019, 34, 1612–1619. [Google Scholar] [CrossRef]
- Lv, F.; Qin, M.; Zhang, F.; Yu, H.; Gao, L.; Lv, P.; Wei, W.; Feng, Y.; Feng, W. High Cross-Plane Thermally Conductive Hierarchical Composite Using Graphene-Coated Vertically Aligned Carbon Nanotubes/Graphite. Carbon 2019, 149, 281–289. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, D. Improving Heat Dissipation and Temperature Uniformity in Radiative Cooling Coating. Energy Technol. 2020, 8, 1901362. [Google Scholar] [CrossRef]
- Perović, B.; Klimenta, D.; Tasić, D.; Raičević, N.; Milovanović, M.; Tomović, M.; Vukašinović, J. Increasing the Ampacity of Underground Cable Lines by Optimising the Thermal Environment and Design Parameters for Cable Crossings. IET Gener. Transm. Distrib. 2022, 11, 2309–2318. [Google Scholar] [CrossRef]
- Masnicki, R.; Mindykowski, J.; Palczynska, B. The Laboratory Stand for the Evaluation of Heat Dissipation from the Power Cable in a Casing Pipe. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Cvetković, D.; Nešović, A. Impact of heat source at radiant electric heating panel. Energy Build. 2021, 239, 110843. [Google Scholar] [CrossRef]
- Lu, X.; Cai, L.; Jia, Q.; Wang, J.; Sun, M.; Wang, L. Numerical Analysis of Cable Heat Output for Renewable Energy Transmission Lines. In Proceedings of the 2024 7th International Conference on Energy, Electrical and Power Engineering (CEEPE), Yangzhou, China, 26–28 April 2024; pp. 1500–1504. [Google Scholar] [CrossRef]
- Nie, Y.; Chen, D.; Zheng, S.; Xu, X.; Wang, X.; Wu, Z. Simulation and Calculation of Temperature Field and Current-Carrying Capacity of Power Cables under Different Laying Methods. Energies 2024, 17, 4611. [Google Scholar] [CrossRef]
- Xie, H.; Zhang, J.-q.; Liu, Y.-f.; Zhang, B.-s.; Wang, L.-f.; Fan, M.-h. Study on insulation failure time and failure temperature of the aged cables under external heating. Procedia Eng. 2018, 211, 1012–1017. [Google Scholar] [CrossRef]
- Lei, J.; Xiao, S.; Liu, Y.; Deng, X.; Tian, A.; Dong, l. Multi-Objective Optimisation of Heat Transfer and Structural Strength of Aero-Piston Air-Cooled Engine Cylinder Based on Orthogonal Test. Therm. Sci. Eng. Prog. 2024, 50, 102500. [Google Scholar] [CrossRef]
- Mallick, M.; Arunachalam, N. Effects of Electrophoretic Deposited Graphene Coating Thickness on the Corrosion and Wear Behaviors of Commercially Pure Titanium. Surf. Coat. Technol. 2022, 450, 128946. [Google Scholar] [CrossRef]
- Lanza, M.; Wang, Y.; Sun, H.; Tong, Y.; Duan, H. Morphology and performance of graphene layers on as-grown and transferred substrates. Acta Mech. 2014, 225, 1061–1073. [Google Scholar] [CrossRef]
- Fang, M.; Xiong, X.; Hao, Y.; Zhang, T.; Wang, H.; Cheng, H.-M.; Zeng, Y. Preparation of Highly Conductive Graphene-Coated Glass Fibers by Sol-Gel and Dip-Coating Method. J. Mater. Sci. Technol. 2019, 35, 1989–1995. [Google Scholar] [CrossRef]
- Zhang, H.; Ge, Y.; Pan, P.; Du, Y.; Fu, H.; Yan, M.; Li, P.; Long, H.; Zhang, C.; Cai, J.; et al. Suppression of Secondary Electron Emission on Oxygen-Free Copper Surface of Reduced Graphene Oxide Coatings Prepared by Electrophoretic Deposition. Appl. Surf. Sci. 2022, 603, 154490. [Google Scholar] [CrossRef]
- Ji, H.; Qiao, J.; Kang, N.; Wang, X.; Huang, J. Optimization of Hot Extrusion Process Parameters for 7075 Aluminum Alloy Rims Based on HyperXtrude. J. Mater. Res. Technol. 2023, 25, 4913–4928. [Google Scholar] [CrossRef]
- GB/T 1720-2020; Circle-Drawing Test of Coating Films. Standardization Administration of China: Beijing, China, 2020.



| Coating Thickness/μm | Thermal Conductivity/W/(m·K) | Emissivity | Adhesion Grade |
|---|---|---|---|
| 50 | 0.632 | 0.79 | 1 |
| 100 | 0.815 | 0.95 | 1 |
| 200 | 0.746 | 0.92 | 1 |
| 300 | 0.729 | 0.83 | 1 |
| Coating Thickness/μm | Environmental Temperature (°C) | Heat Flux (W/m2·K) | Aluminum Fin Surface Temperature (°C) | Container Temperature Rise ΔT (°C) |
|---|---|---|---|---|
| 0 | 15 | 12,000 | 44.3 | 5.1 |
| 100 | 15 | 15,200 | 38.9 | 9.3 |
| 200 | 15 | 13,900 | 40.1 | 7.9 |
| 300 | 15 | 13,500 | 41.2 | 7.5 |
| 100 | 5 | 18,500 | 34.4 | 13.5 |
| 100 | 20 | 12,700 | 40.5 | 7.3 |
| Mesh Size (mm) | Mesh Count (Million) | Tfin (°C) | q″ (W/m2·K) | GCI (%) |
|---|---|---|---|---|
| 0.5 | 0.8 | 52.0 ± 1.2 | 10,500 ± 200 | 7.3 |
| 0.2 | 1.2 | 50.1 ± 0.8 | 11,200 ± 150 | 4.7 |
| 0.1 | 3.0 | 48.3 ± 0.5 | 12,000 ± 100 | 1.2 |
| 0.05 | 6.5 | 48.1 ± 0.3 | 12,050 ± 80 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Xu, C.; Zhang, F.; Sun, T. Numerical and Experimental Study of Enhanced Heat Dissipation Performance of Graphene-Coated Heating Cables. Coatings 2025, 15, 777. https://doi.org/10.3390/coatings15070777
Chen Z, Xu C, Zhang F, Sun T. Numerical and Experimental Study of Enhanced Heat Dissipation Performance of Graphene-Coated Heating Cables. Coatings. 2025; 15(7):777. https://doi.org/10.3390/coatings15070777
Chicago/Turabian StyleChen, Zhenzhen, Chenchen Xu, Feilong Zhang, and Tao Sun. 2025. "Numerical and Experimental Study of Enhanced Heat Dissipation Performance of Graphene-Coated Heating Cables" Coatings 15, no. 7: 777. https://doi.org/10.3390/coatings15070777
APA StyleChen, Z., Xu, C., Zhang, F., & Sun, T. (2025). Numerical and Experimental Study of Enhanced Heat Dissipation Performance of Graphene-Coated Heating Cables. Coatings, 15(7), 777. https://doi.org/10.3390/coatings15070777





