Classification and Prediction of Unknown Thermal Barrier Coating Thickness Based on Hybrid Machine Learning and Terahertz Nondestructive Characterization
Abstract
1. Introduction
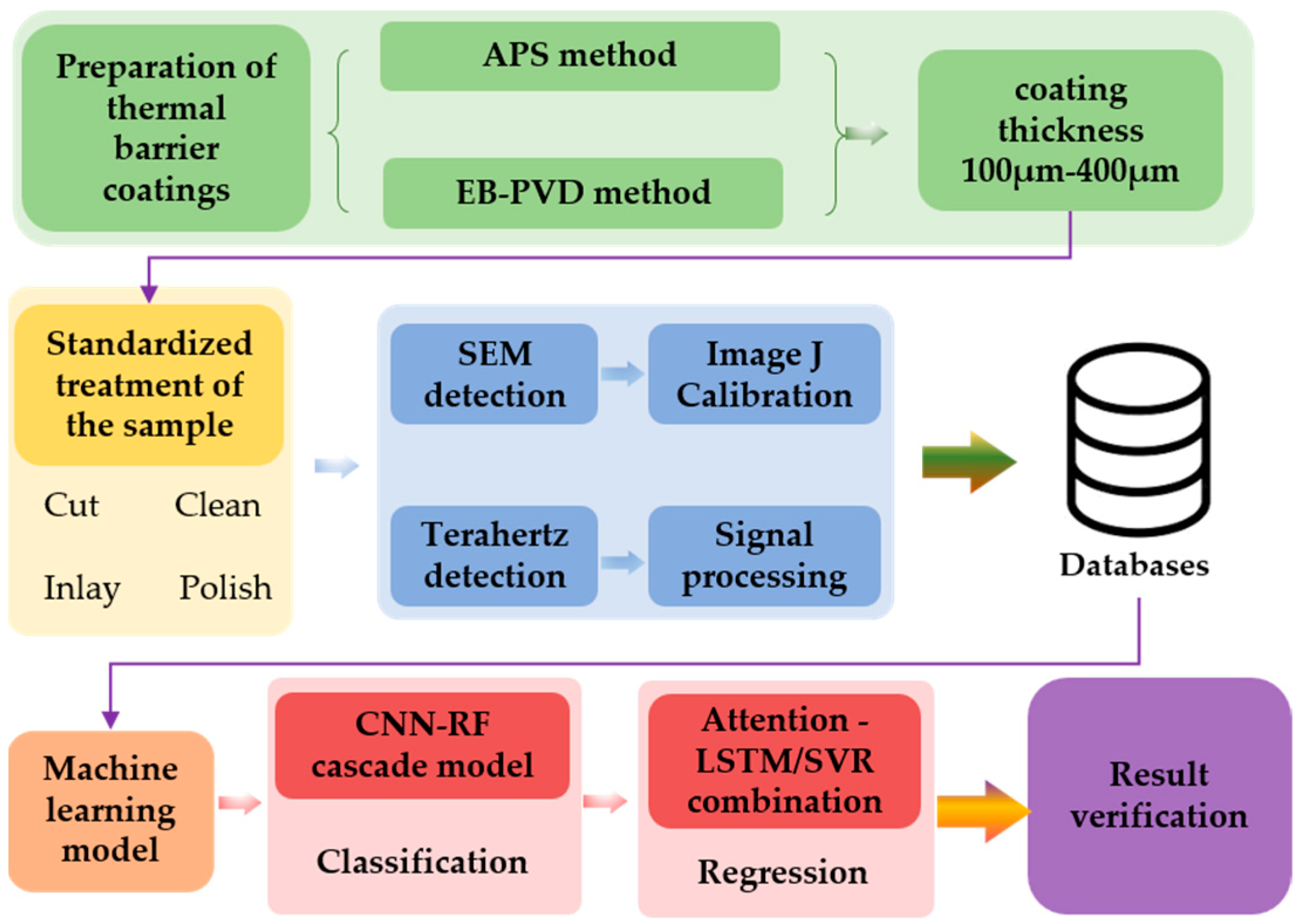
2. Materials and Methods
2.1. Sample Preparation and Characterization
2.2. Terahertz Detection Systems and Signal Processing
2.3. Machine Learning Model Building
3. Results and Discussion
3.1. Verification of Thickness Test Results
3.2. Terahertz Signal Feature Extraction and Analysis
3.3. Evaluation of Machine Learning Model Performance
4. Conclusions
- (1)
- Terahertz signal characteristics (time delay, frequency shift, energy attenuation) are significantly correlated with APS/EB-PVD coating thickness. Multi-modal feature fusion modeling reduces the root mean square error of thickness prediction to 8.9 μm, which is close to industrial tolerance requirements.
- (2)
- In classification and prediction tasks, the CNN-RF cascaded model achieves a classification accuracy of 96.8% for both processes, with feature importance screening enhancing model generalization. Additionally, the weighted fusion model combining attention-LSTM and SVR achieves an average absolute error of 7.1 μm, with dynamic weighting strategies effectively balancing local fluctuations and global trend modeling.
- (3)
- A hierarchical strategy based on coating type and thickness intervals further improves prediction accuracy, but computational costs increase, requiring a trade-off between accuracy and efficiency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sahith, M.S.; Giridhara, G.; Kumar, R.S. Development and analysis of thermal barrier coatings on gas turbine blades–A Review. Mater. Today Proc. 2018, 5, 2746–2751. [Google Scholar] [CrossRef]
- Vagge, S.T.; Ghogare, S. Thermal barrier coatings. Mater. Today Proc. 2022, 56, 1201–1216. [Google Scholar] [CrossRef]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 29, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Lakiza, S.M.; Grechanyuk, M.I.; Ruban, O.K.; Redko, V.P.; Glabay, M.S.; Myloserdov, O.B.; Dudnik, O.V.; Prokhorenko, S.V. Thermal barrier coatings: Current status, search, and analysis. Powder Metall. Met. Ceram. 2018, 57, 82–113. [Google Scholar] [CrossRef]
- Lan, Y.; Han, X.; Tong, M.; Huang, H.; Yang, Q.; Liu, D.; Zhao, X.; Zhong, C. Materials genomics methods for high-throughput construction of COFs and targeted synthesis. Nat. Commun. 2018, 9, 5274. [Google Scholar] [CrossRef]
- Shrestha, R.; Kim, W. Evaluation of coating thickness by thermal wave imaging: A comparative study of pulsed and lock-in infrared thermography–Part I: Simulation. Infrared Phys. Technol. 2017, 83, 124–131. [Google Scholar] [CrossRef]
- Shrestha, R.; Kim, W. Evaluation of coating thickness by thermal wave imaging: A comparative study of pulsed and lock-in infrared thermography–Part II: Experimental investigation. Infrared Phys. Technol. 2018, 92, 24–29. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, M.; Cao, B.; Ye, B.; Wen, D. Measurement of coating thickness using lift-off point of intersection features from pulsed eddy current signals. NDT E Int. 2020, 116, 102333. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, C.X.; Yang, L.; Zhou, Y.C.; Liu, Z.Y. Real-time detection of damage evolution and fracture of EB-PVD thermal barrier coatings under thermal shock: An acoustic emission combined with digital image correlation method. Surf. Coat. Technol. 2020, 399, 126151. [Google Scholar] [CrossRef]
- Guo, W.; Dong, L.; Wang, H.; Feng, F.; Xing, Z.; Ma, R.; Shao, H.; Gao, Z.; Wang, B.; Yang, J. Size estimation of coating disbonds using the first derivative images in pulsed thermography. Infrared Phys. Technol. 2020, 104, 103106. [Google Scholar] [CrossRef]
- Akbar, M.F.; Jawad, G.N.; Duff, C.I.; Sloan, R. Porosity evaluation of in-service thermal barrier coated turbine blades using a microwave nondestructive technique. NDT E Int. 2018, 93, 64–77. [Google Scholar] [CrossRef]
- Ma, X.; Ruggiero, P. Practical aspects of suspension plasma spray for thermal barrier coatings on potential gas turbine components. J. Therm. Spray Technol. 2018, 27, 591–602. [Google Scholar] [CrossRef]
- Fukuchi, T.; Fuse, N.; Okada, M.; Ozeki, T.; Fujii, T.; Mizuno, M.; Fukunaga, K. Topcoat thickness measurement of thermal barrier coating of gas turbine blade using terahertz wave. Electr. Eng. Jpn. 2014, 189, 1–8. [Google Scholar] [CrossRef]
- Kakuda, T.; Limarga, A.; Vaidya, A.; Kulkarni, A.; Bennett, T.D. Non-destructive thermal property measurements of an APS TBC on an intact turbine blade. Surf. Coat. Technol. 2010, 205, 446–451. [Google Scholar] [CrossRef]
- Zhong, S. Progress in terahertz nondestructive testing: A review. Front. Mech. Eng. 2019, 14, 273–281. [Google Scholar] [CrossRef]
- Chen, C.C.; Lee, D.J.; Pollock, T.; Whitaker, J.F. Terahertz characterization of interfacial oxide layers and voids for health monitoring of ceramic coatings. In Proceedings of the 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Republic of Korea, 21–25 September 2009. [Google Scholar]
- Chen, C.C.; Lee, D.J.; Pollock, T.; Whitaker, J.F. Pulsed-terahertz reflectometry for health monitoring of ceramic thermal barrier coatings. Opt. Express 2010, 18, 3477–3486. [Google Scholar] [CrossRef]
- Watanabe, M.; Kuroda, S.; Yamawaki, H.; ShiWa, M. Electromagnetic properties of plasma sprayed thermal barrier coatings in terahertz range. In Proceedings of the 2009 34th International Conference on Infrared, Millimeter, and Terahertz Waves, Busan, Republic of Korea, 21–25 September 2009. [Google Scholar]
- Watanabe, M.; Kuroda, S.; Yamawaki, H.; Shiwa, M. Terahertz dielectric properties of plasma-sprayed thermal-barrier coatings. Surf. Coat. Technol. 2011, 205, 4620–4626. [Google Scholar] [CrossRef]
- Schemmel, P.; Diederich, G.; Moore, A.J. Direct stress optic coefficients for YTZP ceramic and PTFE at GHz frequencies. Opt. Express 2016, 24, 8110–8119. [Google Scholar] [CrossRef]
- Schemmel, P.; Diederich, G.; Moore, A.J. Measurement of direct strain optic coefficient of YSZ thermal barrier coatings at GHz frequencies. Opt. Express 2017, 25, 19968–19980. [Google Scholar] [CrossRef]
- Luo, M.; Zhong, S.; Yao, L.; Tu, W.; Nsengiyumva, W.; Chen, W. Thin thermally grown oxide thickness detection in thermal barrier coatings based on SWT-BP neural network algorithm and terahertz technology. Appl. Opt. 2020, 59, 4097–4104. [Google Scholar] [CrossRef]
- Yin, X.X.; Hadjiloucas, S.; Zhang, Y. Complex extreme learning machine applications in terahertz pulsed signals feature sets. Comput. Methods Programs Biomed. 2014, 117, 387–403. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Ye, D.; Yin, C.; Wu, Y.; Chen, S.; Ge, X.; Wang, P.; Huang, X.; Liu, Q. Application of Machine Learning in Terahertz-Based Nondestructive Testing of Thermal Barrier Coatings with High-Temperature Growth Stresses. Coatings 2025, 15, 49. [Google Scholar] [CrossRef]
- Yan, C. A Review on Spectral Data Preprocessing Techniques for Machine Learning and Quantitative Analysis. iScience 2025, in press. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, C.; Bykhovsky, D.; Trigano, T.; Chen, Z.; Zheng, X.; Zhu, Y. Deep Learning Based Energy Spectrum Estimation for High Counting Rate Nuclear Spectrometry. IEEE Trans. Instrum. Meas. 2025, in press. [Google Scholar] [CrossRef]
- Traore, B.B.; Kamsu-Foguem, B.; Tangara, F. Deep convolution neural network for image recognition. Ecol. Inform. 2018, 48, 257–268. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, J.; Chang, L.; Zhao, J.; Cheng, J. Evaluating the thickness of thin-walled structures from ultrasound signals based on CNN-BILSTM model. Nondestr. Test. Eval. 2025, 1, 1–19. [Google Scholar] [CrossRef]
- Lv, Z.; Ding, Y.; Zhang, Y. Study on Long-Term Temperature Variation Characteristics of Concrete Bridge Tower Cracks Based on Deep Learning. Sensors 2025, 25, 207. [Google Scholar] [CrossRef]
- Elyan, E.; Gaber, M.M. A genetic algorithm approach to optimising random forests applied to class engineered data. Inf. Sci. 2017, 384, 220–234. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, L.; Zhang, Y.; Han, X.; Deveci, M.; Parmar, M. A review of convolutional neural networks in computer vision. Artif. Intell. Rev. 2024, 57, 99. [Google Scholar] [CrossRef]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wang, W.; Wang, G.; Tan, Q. Actual evapotranspiration estimation over the Tuojiang River Basin based on a hybrid CNN-RF model. J. Hydrol. 2022, 610, 127788. [Google Scholar] [CrossRef]
- Guo, J.; Xie, Z.; Qin, Y.; Jia, L.; Wang, Y. Short-term abnormal passenger flow prediction based on the fusion of SVR and LSTM. IEEE Access 2019, 7, 42946–42955. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, Z.; Kong, D.; Han, H.; Zhao, Y. EA-LSTM: Evolutionary attention-based LSTM for time series prediction. Knowl.-Based Syst. 2019, 181, 104785. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Shahnazar, A.; Bakhshandeh, A.H.; Jahed, A.D. Prediction of air-overpressure caused by mine blasting using a new hybrid PSO–SVR model. Eng. Comput. 2017, 33, 23–31. [Google Scholar] [CrossRef]
- Bobzin, K.; Bagcivan, N.; Parkot, D.; Schäfer, M.; Petković, I. Modeling and Simulation of Microstructure Formation for Po-rosity Prediction in Thermal Barrier Coatings Under Air Plasma Spraying Condition. J. Therm. Spray Technol. 2009, 18, 975–980. [Google Scholar] [CrossRef]














| Parameter Category | APS Process Parameters | EB-PVD Process Parameters |
|---|---|---|
| Substrate temperature | 700–900 °C | 900–1100 °C |
| Working pressure | atmospheric pressure | high vacuum (5 × 10−4–1 × 10−3 Pa) |
| Heat source parameters | Plasma power: 30–50 kW Working gas: Ar/H2 (60/15 SLPM) Voltage: 40–60 V Powder feed rate: 20 ± 2 g/min Carrier gas flow rate: Ar 40 ± 5 L/min | Electron beam voltage: 30–40 kV Beam current: 500–800 mA Focusing diameter: 2–5 mm Scanning speed: 200 mm/s |
| Process control parameters | Nozzle-substrate distance: 100 mm | Deposition angle: 90° |
| Coating material | 8YSZ (particle size 15–45 μm) | 8YSZ (purity ≥ 99.9%) |
| Deposition rate | 20–40 μm/min | 5–10 μm/min |
| Cooling method | Forced air cooling | Vacuum cooling (cooling rate ≤ 5 °C/min) |
| Typical thickness range | 100–500 μm | 50–400 μm |
| Model Component | Parameter Name | Parameter Value/Range | Optimization Method | Physical Significance |
|---|---|---|---|---|
| CNN feature extraction | Input Size | 128 × 128 × 3 | - | Time-frequency feature matrix dimensions |
| First Convolutional Kernel | 64 5 × 5 with step 1 | Grid Search | Capturing localized time-frequency patterns | |
| Second Convolutional Kernel | 128 × 3 × 3 with expansion 2 | Bayesian optimization | Enhanced sensory field | |
| Pooling method | 2 × 2 maximum pooling | - | Dimensionality reduction against overfitting | |
| Activation function | Leaky ReLU (α = 0.2) | Cross-validation | Mitigating gradient vanishing | |
| RF classifier | Number of decision trees | 200 | Early Stop Method | Balancing accuracy and efficiency |
| Maximum tree depth | 10 | Pruning Optimization | Prevent overfitting | |
| Minimum number of leaf samples | 5 | Lattice Search | Ensure statistical significance | |
| Feature filtering ratio | Top 30% | Importance Ranking | Remove redundant features | |
| LSTM prediction module | Number of hidden units | 64 | Hyperparametric Search | Temporal feature capacity |
| Dropout rate | 0.3 | Verification set tuning parameterization | Regularization | |
| Number of Attention Heads | 4 | Ablation Experiments | Multi-scale attention | |
| SVR module | Kernel function type | RBF | Performance Comparison | Nonlinear mapping |
| Penalty coefficient C | 1.0 | Grid Search | Controlling relaxation variables | |
| RBF kernel coefficient γ | 0.1 | Gradient descent | Determining the shape of decision boundaries | |
| Fusion strategy | Dynamic weight update frequency | Updates per epoch | Online Learning | Adapting to changes in data distribution |
| Weight smoothing coefficient | 0.8 | Sliding Average | Suppress weight oscillations |
| Kernel Function Types | MAE | Training Time/s | Memory Consumption/GB | Applicable Scenarios |
|---|---|---|---|---|
| Linear kernel | 12.4 ± 1.8 | 8.2 | 78% | Low-dimensional linear features |
| Polynomial kernel | 9.7 ± 1.2 | 23.5 | 65% | Medium complexity features |
| RBF kernel | 6.2 ± 0.8 | 15.7 | 42% | High-dimensional nonlinear features |
| Sigmoid kernel | 11.3 ± 1.5 | 18.9 | 71% | Special Classification Problems |
| Characteristic Parameters | Pearson’s Correlation Coefficient | RMSE | p-Value |
|---|---|---|---|
| Time delay, Δt | 0.991 | 4.8 | <0.001 |
| Frequency shift, Δf | 0.943 | 7.2 | <0.001 |
| Energy, η | 0.872 | 9.5 | <0.001 |
| Multi-feature fusion | 0.997 | 3.1 | <0.001 |
| Classification Standard | MAE | R2 | Training Time/s |
|---|---|---|---|
| Control group | 11.3 | 86.4% ± 1.9% | 650 |
| Standard I | 6.2 | 96.8% ± 0.4% | 592 |
| Standard II | 4.5 | 97.6% ± 0.3% | 716 |
| Standard III | 4.1 | 98.1% ± 0.35% | 1467 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Xu, J.; Wu, Y.; Yin, C.; Chen, S.; Liu, Q.; Ge, X.; Wan, L.; Ye, D. Classification and Prediction of Unknown Thermal Barrier Coating Thickness Based on Hybrid Machine Learning and Terahertz Nondestructive Characterization. Coatings 2025, 15, 725. https://doi.org/10.3390/coatings15060725
Xu Z, Xu J, Wu Y, Yin C, Chen S, Liu Q, Ge X, Wan L, Ye D. Classification and Prediction of Unknown Thermal Barrier Coating Thickness Based on Hybrid Machine Learning and Terahertz Nondestructive Characterization. Coatings. 2025; 15(6):725. https://doi.org/10.3390/coatings15060725
Chicago/Turabian StyleXu, Zhou, Jianfei Xu, Yiwen Wu, Changdong Yin, Suqin Chen, Qiang Liu, Xin Ge, Luanfei Wan, and Dongdong Ye. 2025. "Classification and Prediction of Unknown Thermal Barrier Coating Thickness Based on Hybrid Machine Learning and Terahertz Nondestructive Characterization" Coatings 15, no. 6: 725. https://doi.org/10.3390/coatings15060725
APA StyleXu, Z., Xu, J., Wu, Y., Yin, C., Chen, S., Liu, Q., Ge, X., Wan, L., & Ye, D. (2025). Classification and Prediction of Unknown Thermal Barrier Coating Thickness Based on Hybrid Machine Learning and Terahertz Nondestructive Characterization. Coatings, 15(6), 725. https://doi.org/10.3390/coatings15060725





