Multi-Objective Optimization of Laser Cleaning Quality of Composite Paint Layers Based on Response Surface

Abstract

To improve the laser cleaning surface quality of composite layers on Al alloy surfaces, a method of determining the optimal cleaning parameters is proposed that is based on the response surface methodology. It involves constructing a mathematical model of the input variables (laser power, scanning speed, repetition frequency, and defocusing amount). Laser cleaning experiments were conducted to analyze the effects of process parameters on paint removal performance. Using the response surface methodology (RSM), a relationship model was developed to link key factors, including paint layer removal thickness and surface roughness. The results indicate that the optimal process parameters are as follows: a laser power of 291 W, frequency of repetition of 166 kHz, scanning speed of 8425 mm/s, and defocusing amount of −17 mm. A verification test was performed to confirm the optimal parameters for the process. The error ranges for the thickness and roughness of the laser paint removal were within 1.9 μm~3.8 μm and −0.573 μm~−0.419 μm, respectively, indicating that the response surface method can be used to predict and optimize the quality of laser paint removal. These findings provide valuable insights into the laser treatment of composite paint layers on Al alloys and contribute to advances in surface treatment technology for Al alloys.

1. Introduction

Composite paint is usually used for the colored outer layer on large components, such as ships, aircraft, and tunnels. The layer of paint on the surface of the substrate is damaged by ageing, peeling, cracking, and rusting as the time spent in service increases [1,2]. The old layer of paint must be removed from the surface and a new layer applied. Taking into account maintenance costs and safety, the maintenance concept of removing the composite paint layer at the end of service has been progressively replaced by the maintenance concept of partial paint removal. Attention should be paid to the controllability of the removal of a multiple-layer superstructure [3,4]. Laser cleaning technology, as an effective and environmentally friendly method of removing paint, has significant advantages in the cleaning of composite paint layers [5,6,7]. The quality of the laser cleaning of composite paint layers (such as thickness of the removal layer and surface roughness) depends on the parameters of the laser process, such as laser power, scanning speed, and repetition rate. Controlled cleaning of the composite paint layer may be achieved by appropriate adjustment of the parameters of the laser cleaning process [8,9].

The effect of laser cleaning is mainly influenced by the parameters of the laser cleaning process. An adequate adjustment of process parameters can effectively remove attachments and ensure high surface quality. Mateo et al. [10] demonstrated that adjusting the appropriate pulse frequency and laser parameters could remove the paint layer without damaging the substrate. Hu et al. [11] found that appropriate laser cleaning parameters can remove surface contaminants and increase the surface efficiency of the substrate. Jasim [12], among others, showed that different strengths and frequencies of repeat testing affect the microscopic morphology of the cleaning sample, resulting in different hardnesses. Brygo et al. [13] found that laser energy density has a significant impact on the quality of laser paint removal. Razab et al. [14] performed laser cleaning on two different types of layers of pigment. The results showed that different elements in the paint layer also had a significant influence on the removal results of the stain. Shi et al. [15] found that cleaning efficiency can be improved by increasing the maximum laser power density, and that non-destructive cleaning of the substrate surface can be achieved by adjusting the intensity of spot overlap. Li et al. [16] pointed out that non-destructive cleaning of the paint layer of marine steel plates can be achieved by adjusting the pulsed laser parameters. Yang et al. [17] found that the degree of spot overlap had the greatest influence on the cleaning of acrylic resins on stainless steel, followed by laser power.

The parameters of laser cleaning are numerous and complicated to deal with. The cleaning quality of the paint layer is fully reflected by the combined action of several process parameters. Accordingly, Ding et al. [18] established a mathematical theorem focused on the parameters of the laser process and the quality of carbon black layer cleaning by the response surface method; they obtained a Pareto solution using an optimization algorithm that provides a choice of parameters for the technical requirements of carbon black layer cleaning. Yang [19] analyzed the influence of laser cleaning parameters on the controllability index based on the response surface method. The results showed that the influence of scanning time, laser power, and spot overlap rate on the thickness of the paint layer are positively correlated. The surface roughness increases with increasing laser power and decreases with an increasing degree of spot overlap. Sun et al. [20] used the response surface method and particle swarm optimization algorithm to optimize the laser cleaning parameters. The experiment showed that the optimized parameters could effectively remove corrosion from the surface of the pipe thread, and the cleaning effect was good without melting.

The literature cited above mainly examines the effect of process parameters on the cleaning effect of a single layer of paint, but the laser cleaning process of a composite layer of paint and the surface quality after layer cleaning are also worth further investigation. Liu et al. [21] carried out laser cleaning on the surface of a 2A12 aluminum alloy substrate coated with a composite paint layer. The results showed that changing the combination of laser process parameters could regulate the quality of laser cleaning, which verified the feasibility of laser layered cleaning. Zhang [22] developed a mathematical model focused on the parameters of the laser paint removal process, the amount of paint residue and deposition, the surface roughness, and the efficiency of paint removal by analyzing the surface response. After variance analysis and model validation, the proposed model was shown to effectively improve the quality and efficiency of the laser paint removal process.

A comprehensive representation of the laser cleaning performance of a composite paint layer under the combined action of several process parameters should be established, and the interaction between parameters should be further investigated. It is very important to undertake research with the objective of optimizing the quality of laser cleaning of composite paint layers. In this paper, two regression prediction models for the thickness of the paint removal and surface roughness were constructed using the response surface method, and the models’ reliability was assessed by means of a variance analysis. An analysis of the perturbation and response surface diagrams investigated the effects of the parameters of the laser cleaning process and their interactions on the thickness of the paint removal and the surface roughness. The laser cleaning process parameters for 30 μm paint removal thickness and large surface roughness were obtained. A validation test was performed using an optimized combination of parameters. The test results show that the response surface method can achieve the prediction and optimization of surface quality after laser paint removal.

2. Materials and Experimental Design

2.1. Preparation and Treatment of Experimental Materials

The test sample is a commonly used Al alloy for aircraft skin. The thickness is approximately 2 mm thick. The surface was uniformly sprayed with a white polyurethane topcoat (30 ± 3 μm) and a green epoxy primer (20 ± 3 μm thick). The surface roughness is Ra 4.35 μm. To facilitate the purification test and subsequent detection and analysis, a high-frequency electric spark wire cutting machine was used to cut the plate to a test sample of approximately 20 mm × 20 mm. The test sample is shown in Figure 1a and the diagram of the sample surface is shown in Figure 1b.

The composite-paint-layer laser cleaning system is described in Figure 2. The laser cleaning system consists essentially of two main components: a laser cleaning machine and a cleaning auxiliary device. A laser cleaning machine consists of a fiber-pulsed laser (QYCL-FP100, Qiangyuan Laser, Liaocheng, China), a human–machine interface display, a controller, a laser output head, a galvanometer, a motor, and an optical system (Figure 2a). The parameters of the laser cleaning process can be adjusted by means of an interface on the display screen, and parameters such as laser power, repetition frequency, and scanning speed can be adjusted. The key parameters of the laser cleaning machine are presented in

Table 1. The main parameters of the laser.

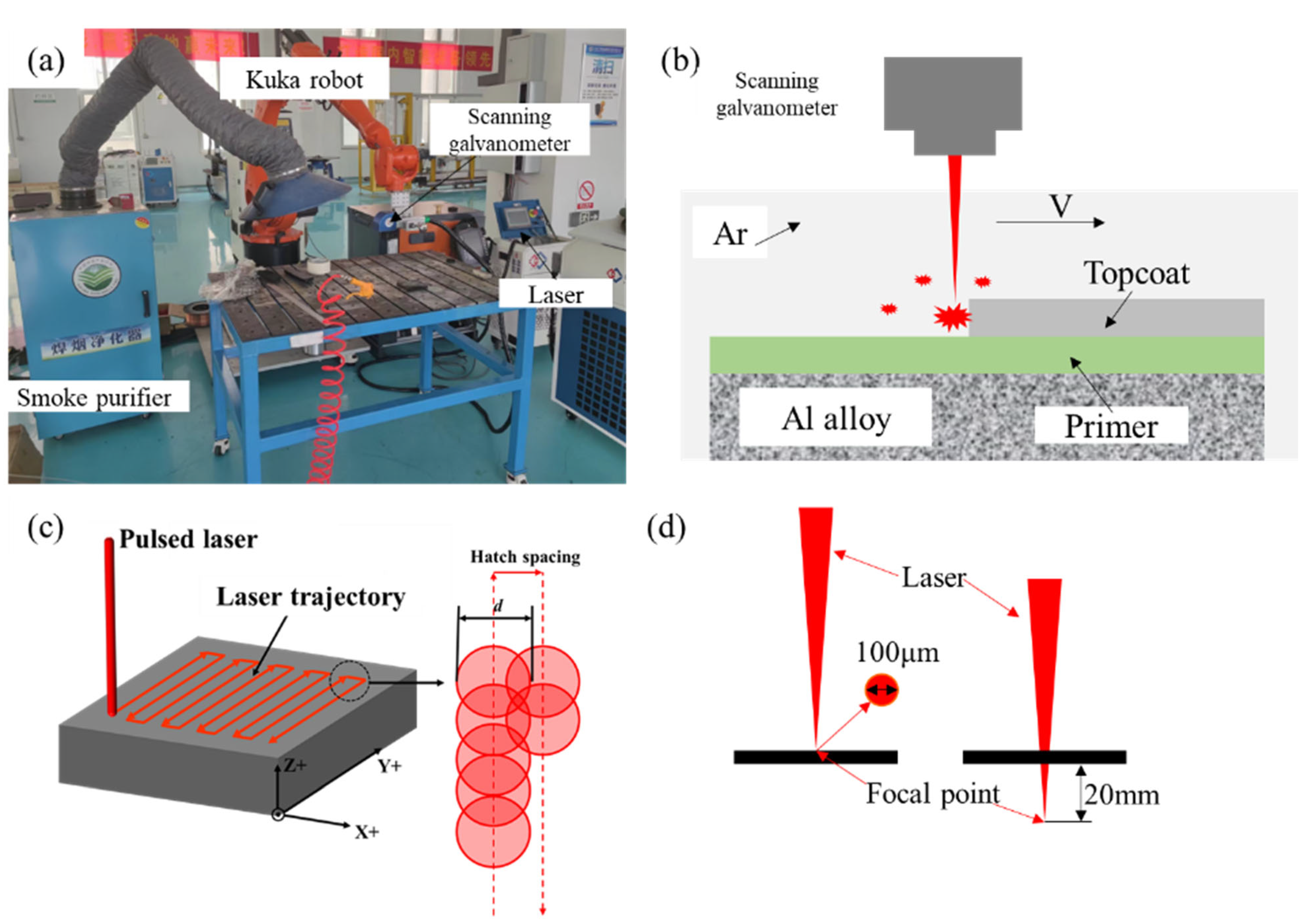
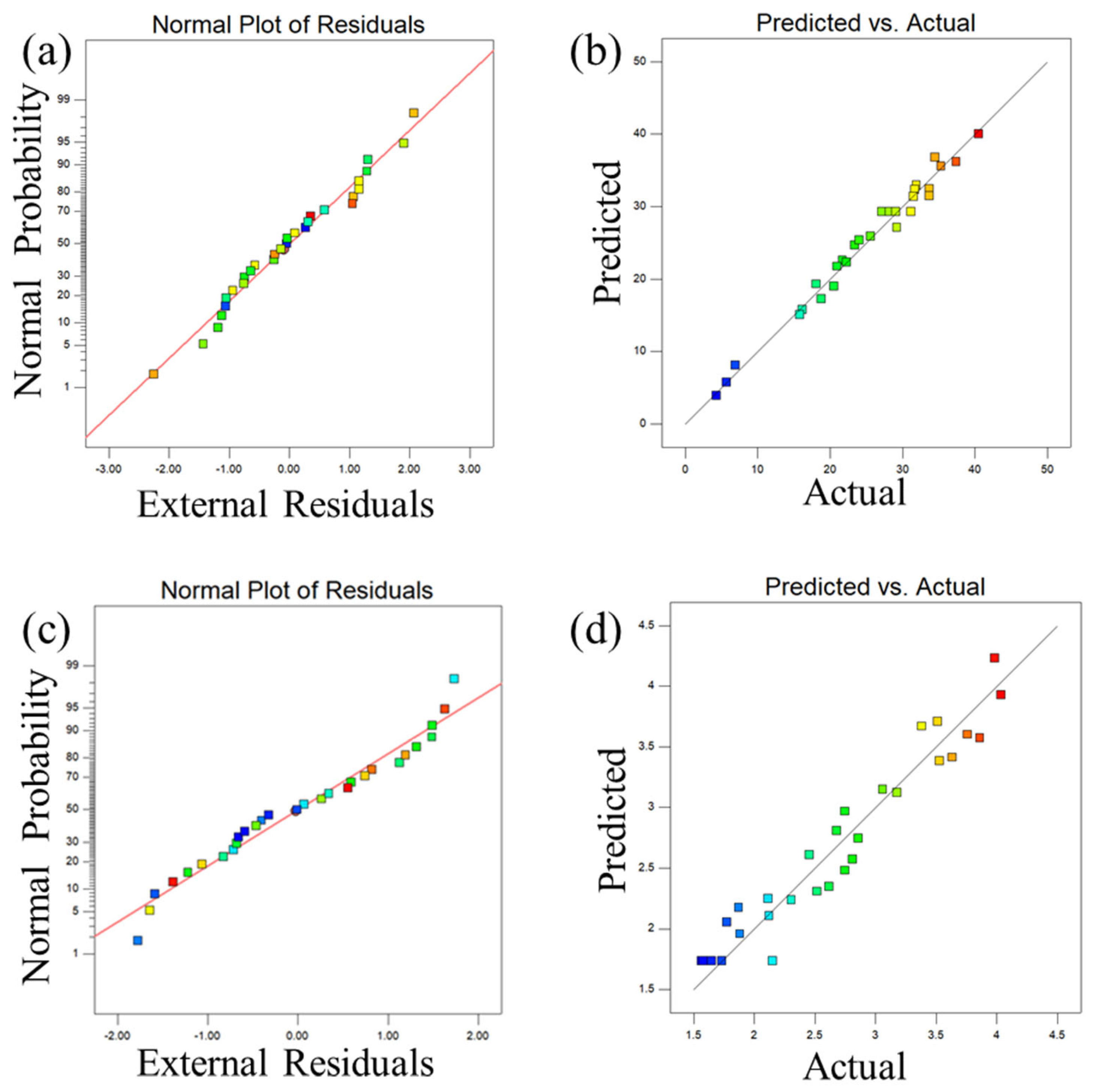
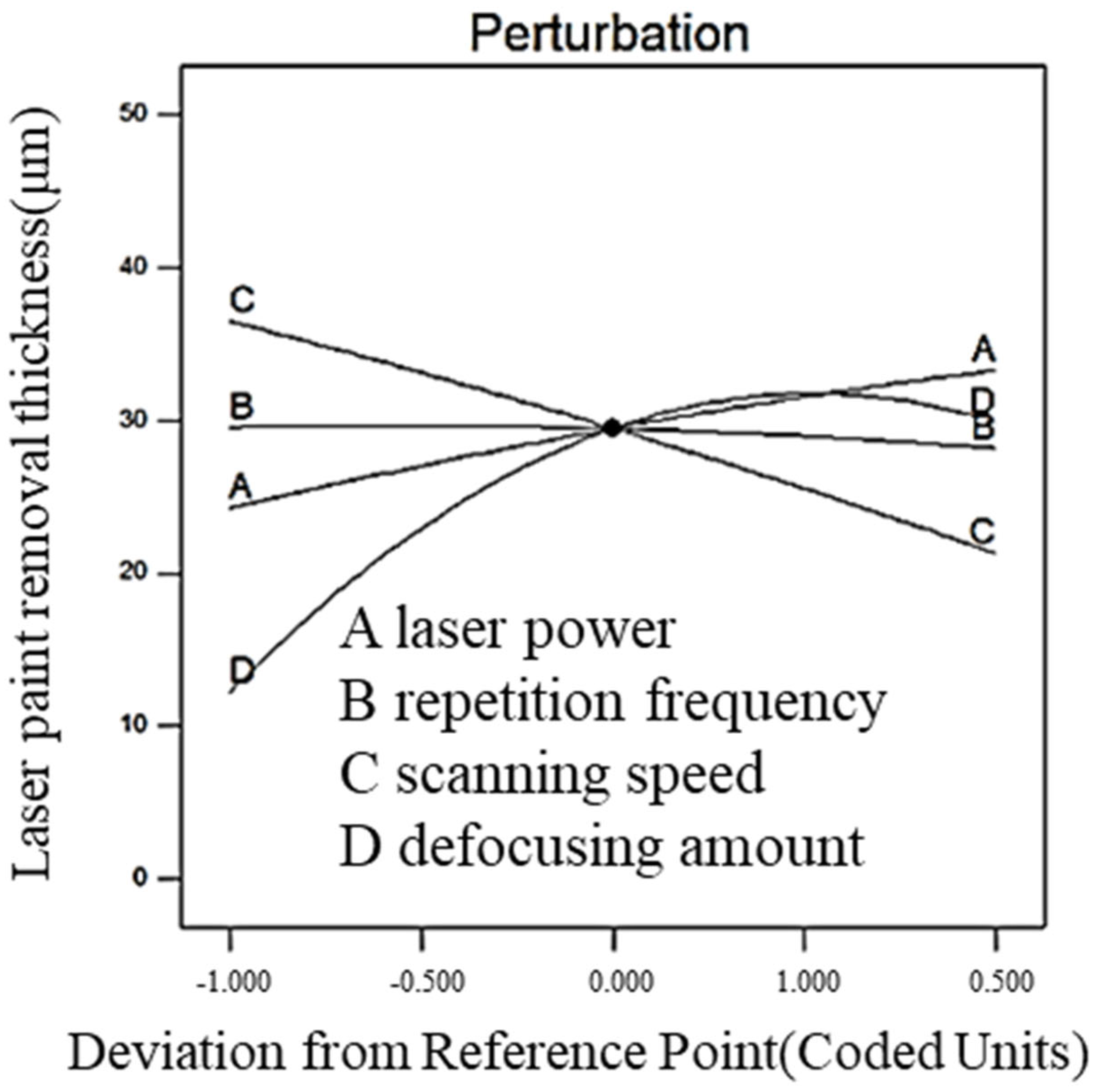
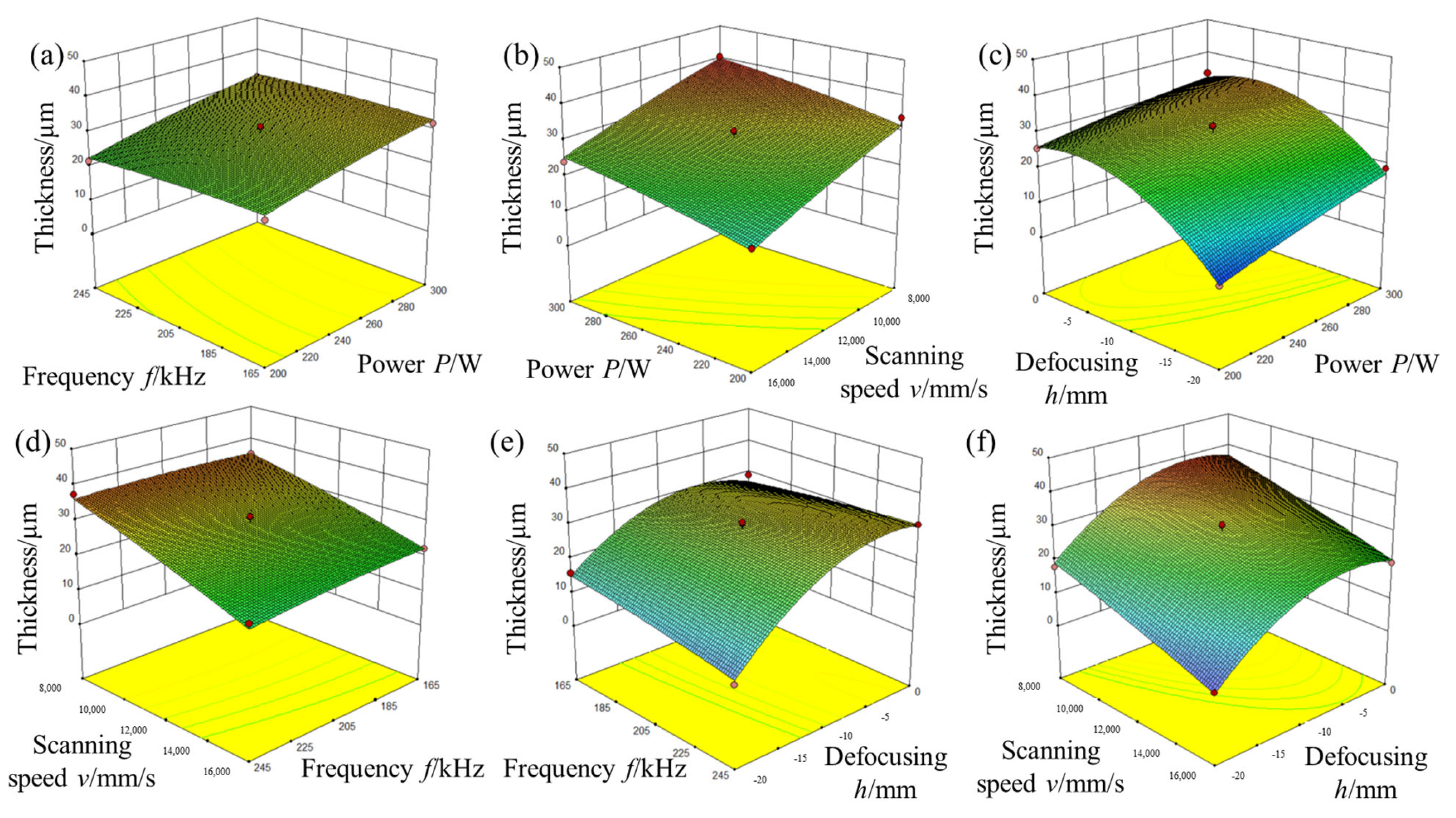
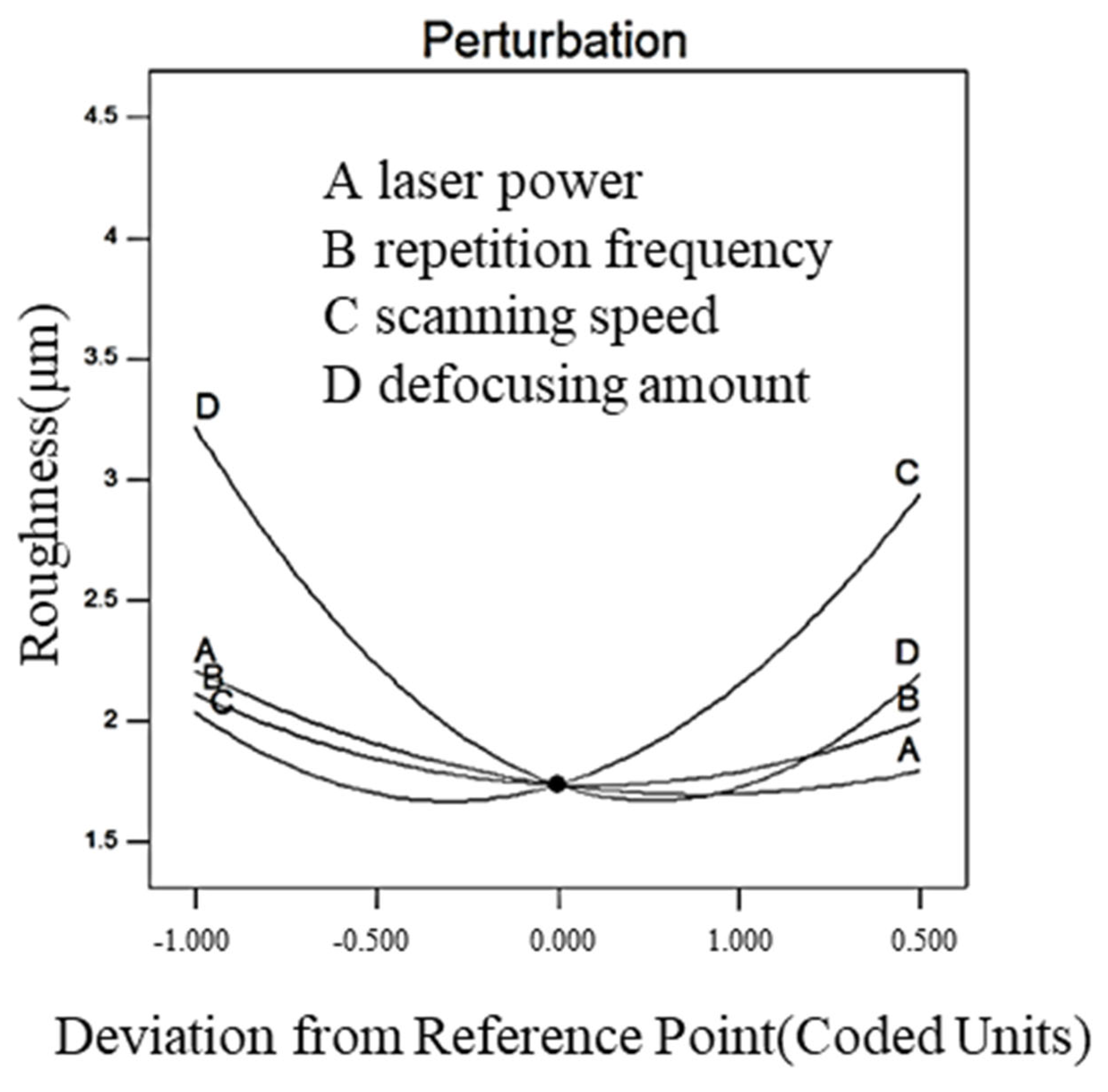
Symbol	Parameter	Value	Unit
λ	Laser wavelength	1060	nm
D	Spot diameter	100	μm
P	Laser power	0–300	W
f	Repetition frequency	0–300	kHz
n	Pulse width	70	ns
v	Scanning speed	0–20,000	mm/s

. The auxiliary part of the cleaning system includes key equipment, such as water coolant, protective gas, a vacuum cleaner, and a KUKA robot. A schematic diagram illustrating the laser cleaning of a composite paint layer is presented in Figure 2b.

2.2. Experimental Design

To better study the effect of the parameters of the laser cleaning process on the cleaning quality of the composite paint layer, the parameters were optimized using the response surface method (RSM) by applying a regression equation between each factor and the response [23,24].

$$f\left(x\right)={\alpha }_0+{\sum }_{i=1}^n{\alpha }_i{x}_i+{\sum }_{i=1}^n{\alpha }_{ii}{x_i}^2+{\sum }_{i=1,i,j}^n{\alpha }_{ij}{x}_i{x}_j+\epsilon$$

(1)

where f(x) is the predicted response value (exam factor), x_i and x_j are the examining factors, α₀, α_i, α_ii, and α_ij are regression coefficients, and ε is the noise or error term.

The RSM is more effective than other methods in establishing predictive models for inputs and outputs, is suitable for the precise optimization of continuous variables, and offers greater flexibility in the post-experimental phase. A four-factor, three-level Box–Behnken design (BBD) was used to design the experimental plan, and the RSM was applied to optimize the parameters of the laser cleaning process. The laser power (P), scanning speed (v), repetition frequency (f), and defocusing amount (h) were considered as independent variables for laser cleaning and composite paint removal. According to the results of previous experiments, the experiment levels were coded using the statistical software Design Expert, as shown in

Table 2. BBD experiment factors and level design.

Horizontal Coding of Each Factor/Factor	Level
	Low (−1)	Medium (0)	High (1)
Laser power P/W	200	250	300
Repetition frequency f/kHz	165	205	245
Scanning speed v/mm/s	8000	12,000	16,000
Defocusing h/mm	−20	−10	0

. The response value for optimization analysis comprised paint layer removal thickness (H) and surface roughness (Ra).

Table 3. Experimental design matrix and experimental results.

No	Process Parameters				Result
	P/W	f/kHz	v/mm/s	h/mm	H/µm	Ra/µm
1	250	205	12,000	−10	31.2	1.563
2	250	205	12,000	−10	29.1	1.650
3	250	245	16,000	−10	20.5	3.631
4	300	205	16,000	−10	24.0	2.859
5	300	245	12,000	−10	31.7	1.776
6	250	245	12,000	0	31.5	2.680
7	250	205	16,000	0	21.0	3.756
8	200	205	12,000	0	25.6	2.746
9	250	165	12,000	0	29.2	2.305
10	250	165	16,000	−10	22.3	3.175
11	250	165	12,000	−20	15.8	4.035
12	250	205	8000	−20	18.1	3.511
13	300	205	12,000	−20	18.8	3.859
14	200	205	8000	−10	33.7	2.113
15	250	205	12,000	−10	31.2	1.733
16	200	165	12,000	−10	23.4	2.811
17	250	205	12,000	−10	27.1	2.153
18	200	245	12,000	−10	21.7	2.748
19	250	205	16,000	−20	4.3	3.984
20	250	245	12,000	−20	6.9	3.059
21	200	205	16,000	−10	16.2	3.382
22	250	165	8000	−10	35.3	2.455
23	250	205	8000	0	34.5	2.517
24	200	205	12,000	−20	5.7	3.525
25	300	205	8000	−10	40.5	2.615
26	250	245	8000	−10	37.4	2.122
27	300	165	12,000	−10	31.9	1.871
28	300	205	12,000	0	33.7	1.882
29	250	205	12,000	−10	28.1	1.581

presents the design and results of the response surface test.

The surface morphology of the sample after cleaning is shown in the legend below (Figure 3). After cleaning, the thickness of the paint removal and the surface roughness of the paint layer were measured. The results of the tests are given in Table 3. Combined with the data in the table, it is apparent that when the thickness of the removal layer is low, as in samples (19), (20), and (24), the surface is red-brown, due to the small effect of the laser energy on the surface, which only removes the thinner coating. If the thickness of the paint is too thick, the top layer is removed, revealing a light green primer, as shown in the samples (1)~(6). There are also big differences in the surface finish of the different components. This shows that the quality of the laser cleaning process (other than the thickness of the paint and the roughness of the surface) can be adjusted by changing the parameters of the laser cleaning process.

3. Results and Discussions

3.1. Mathematical Modelling and Analysis of Variance

According to the paint removal data in Table 3, the Design-Expert response surface analysis software was used to perform polynomial regression fitting on the laser cleaning process parameters and paint layer removal thickness and surface roughness in Table 3. The regression prediction model of the laser cleaning process parameters and the paint layer removal thickness and surface roughness was obtained:

Y₁ = −11.024 + 0.138x₁ + 0.218x₂ − 1.708 × 10⁻⁴x₃ − 1.621x₄ + 1.875 × 10⁻⁴x₁x₂ + 1.25 × 10⁻⁶x₁x₃ − 2.5 × 10⁻³x₁x₄ − 6.093 × 10⁻⁶x₂x₃ + 7 × 10⁻³x₂x₄ + 1.875 × 10⁻⁶x₃x₄ − 2.513 × 10⁻⁴x₁² − 3.38 × 10⁻⁴x₂² − 3.224 × 10⁻⁸x₃² − 0.084x₄²

(2)

Y₂ = 22.165 − 0.047x₁ − 0.09x₂ − 9.029 × 10⁻⁴x₃ + 0.063x₄ − 4 × 10⁻⁶x₁x₂ − 1.281 × 10⁻⁶x₁x₃ − 5.99 × 10⁻⁴x₁x₄ + 1.233 × 10⁻⁶x₂x₃ + 8.444 × 10⁻⁴x₂x₄ + 4.788 × 10⁻⁶x₃x₄ + 1.052 × 10⁻⁴x₁² + 2.02 × 10⁻⁴x₂² + 4.716 × 10⁻⁸x₃² + 9.72 × 10⁻³x₄²

(3)

Y₁ is the paint removal thickness, Y₂ is the surface roughness, x₁ is the laser cleaning power, x₂ is the laser repetition frequency, x₃ is the scanning speed of laser cleaning, and x₄ is the defocusing amount. The variance analysis of the regression model of paint layer removal thickness and surface roughness is shown in

Table 4. Response values of the ANOVA.

Variance Source	Response Value
	Paint Layer Removal Thickness		Roughness
	F-Value	p-Value	F-Value	p-Value
Model	51.85	<0.0001	13.66	<0.0001
x1	74.64	<0.0001	6.11	0.0269
x2	1.7	0.2131	0.41	0.5335
x3	210.54	<0.0001	29.97	<0.0001
x4	283.88	<0.0001	37.33	<0.0001
x1x2	0.17	0.6856	3.095 × 10−3	0.9564
x1x3	0.076	0.7869	3.18	0.0965
x1x4	1.9	0.1899	4.34	0.0561
x2x3	1.16	0.3007	1.88	0.1918
x2x4	9.53	0.008	5.52	0.034
x3x4	0.006835	0.9353	1.77	0.2042
x12	0.78	0.3927	5.42	0.0354
x22	0.58	0.4604	8.19	0.0126
x32	0.52	0.481	44.65	<0.0001
x42	137.48	<0.0001	74.09	<0.0001
Lack of Fit	0.96	0.5659	1.57	0.3523
R2	0.9811		0.9318
Adjusted R2	0.9622		0.8636
Predicted R2	0.9143		0.6654
Adeq Precision	27.665		12.071

.

According to the results of the variance analysis in Table 4, the F-values of the regression model for the thickness of the paint removal and surface roughness are 51.32 and 13.66, respectively. The p-values were below 0.0001, indicating that the regression model was highly significant. The p-values for lack of fit are 0.5045 and 0.3523, both above 0.05, suggesting that the lack of fit is not significant. Moreover, the model R² values are 0.9816 and 0.9318, which are close to 1, respectively. The difference between the adjusted R² and predicted R² was less than 0.2. This demonstrates that the regression model is reliable and can be used to simulate the thickness of the paint removal and surface roughness data.

In Table 4, the p values for the paint removal thickness of the laser power P, scanning speed v, and defocusing amount h are all less than 0.0001. This shows that these three factors have a significant influence on the thickness of the paint layer removed.

The F-values for laser power P, repetition frequency f, scanning speed v, and defocusing amount h are 73.83, 1.73, 208.37, and 280.63, respectively. This shows that the order of the coefficients for the thickness of paint removal is as follows: h > v > p > f. The p-value of x₂x₄ in the variance analysis table is less than 0.05. This shows that the interaction between repetition frequency f and defocusing amount h also has a significant effect on the thickness of paint removal.

At the same time, the p-values for the surface roughness of the scanning speed v and the defocusing amount h are both less than 0.0001. The effect on roughness is very significant. The p-value of laser power P is less than 0.05, indicating that this factor is more significant. The F-values of laser power P, repetition frequency f, scanning speed v, and defocusing amount h are 6.11, 0.41, 29.97, and 37.33, respectively. This shows that the order of influence of each factor on roughness is as follows: h > v > p > f. The p-value of x₂x₄ in the analysis of variance table is less than 0.05. This shows that the interaction between repetition frequency f and defocusing amount h also has a significant effect on roughness.

To further test the reliability of the laser paint removal thickness regression model, the residual normal distribution diagram of the analysis model is shown in Figure 4a. The data points in the graph are evenly distributed around the fitting line and there are no outliers, indicating that the fitting is high. Meanwhile, the residual normal distribution diagram of the regression model is demonstrated, as shown in Figure 4c. The data points in the graph are evenly distributed along the fit line and there are no outliers, indicating that the regression model is highly fixable. A regression model was used to predict the paint removal thickness and roughness values in several sets of parameters of the laser cleaning process, and the predicted values were compared with experimental data. As shown in Figure 4b,d, most data points are close to the fitting line, suggesting that the regression predictor model considering the parameters of the laser cleaning process and the thickness of the paint and roughness is well formed. In summary, the regression predictor model considering the parameters of the laser cleaning process and the thickness of the paint removal and roughness is highly relevant and has high prediction accuracy, and it can be used to optimize the quality of paint removal thickness.

3.2. Influence of Process Parameters on the Amount of Paint Residue

To further investigate the influence of the process parameters of the laser cleaning process and their interaction on the thickness of the paint removal, the influence trends of the process parameters were analyzed using perturbation and response surface diagrams. The perturbation diagram is used to reflect the effect of one process parameter on the thickness of the paint removal and the response surface diagram is the result of the interaction of various process parameters.

Figure 5 shows a perturbation diagram of the thickness of the paint removal, where A is the laser power, B is the repetition frequency, C is the scanning speed, and D is the defocusing amount. As the laser output increases, the laser energy density increases and the energy absorbed by the substrate per square centimeter increases, which results in a stronger ablation and an increase in the thickness of the paint removal. The increase in repetition rate leads to a decrease in energy density and an increase in laser energy superposition per unit area. Therefore, the change in the frequency of repetitions does not have any apparent effect on the thickness of the paint removal. The parameter most influencing the thickness of the paint removal is the scanning speed. As the scanning speed increases, the superposition of the laser energy becomes less efficient and the absorption of the laser per unit area of substrate is reduced. The reduction in thickness of the paint removal thickness decreases accordingly. During the defocusing amount from −20 mm to 0 mm, the thickness of the paint removal increases first and then decreases. If the magnitude of the defocusing amount is 0 mm, the spot is smallest and the −20 mm spot is the largest. The size of the spot affects both the energy density and the spot overlap rate. The energy density of the spot increases as the spot decreases, and the spot overlap rate increases as the spot decreases. Both factors interact with one another. If the spot is approximately −5 mm, the interaction between the two is most significant and the thickness of the paint removal is the greatest.

The effect of the interaction of the different process parameters on the thickness of the paint removal is shown in Figure 6. According to the response surface diagram of the interactions of the process parameters, the thickness of the paint removal is significantly influenced by the interaction between the defocusing amount and repetition frequency, and the defocusing amount and scanning speed. As shown in Figure 6e, if the laser power and scanning speed are constant, the lower frequency of repetition and the lower defocusing amount (close to 0 defocusing amount) will cause the paint layer to absorb more laser energy, leading to a decrease in the thickness of the paint removal. This is because the spot is larger when it is far from the focal point, and the increase in the frequency of the repetition results in a reduction in the energy of the single pulse. Therefore, the thickness of the laser paint removal is reduced. From Figure 6f, it is apparent that the laser power and repetition frequency are constant, i.e., the laser single-pulse energy is constant. The smaller the defocusing amount (close to 0) and the slower the scanning speed, the more the laser energy is absorbed by the paint layer, resulting in a thicker layer of paint being removed. As the defocusing amount increases (away from the focus) and the scanning speed increases, the laser energy is less applied to the surface of the paint layer. The thickness of the laser paint removal is the smallest.

3.3. Effect of Process Parameters on Surface Roughness

In order to further investigate the influence of the laser cleaning process parameters and their interaction on the surface roughness of the paint layer after cleaning, the trends in the influence of the process parameters were analyzed using perturbation and response surface diagrams.

A perturbation diagram of the relationship between the surface roughness and the laser cleaning parameters is shown in Figure 7, where A is the laser power, B is the repetition frequency, C is the scanning speed, and D is the defocusing amount. If other parameters of the laser cleaning process are not changed and only the laser power or repetition frequency is adjusted, the effect on roughness is not apparent. Increasing the laser power and repetition frequency has a major effect on the energy density of the laser. Thus, the change in the energy density has a significant effect on the thickness of laser paint removal but does not have a significant effect on the surface roughness. As the scanning speed increases, the surface roughness of the layer of paint decreases slowly and then rapidly, reaching a maximum value of 10,000 mm/s. Generally, the faster the scanning speed, the rougher the surface layer is. As the defocusing amount approaches 0, the size of the spot decreases. After laser cleaning, the surface roughness of the layer of paint is first reduced rapidly, then slowly increased, with a general downward trend. The bigger the spot, the rougher the surface.

The effects of the interaction of the laser cleaning parameters on surface roughness are shown in Figure 8. According to the response surface diagram of the interaction of the process parameters, the surface roughness after laser cleaning is strongly influenced by the interactions between laser power and defocusing amount, and defocusing amount and repetition frequency. As shown in Figure 8c, when the defocusing amount is −10 mm and the power is about 250 W, the surface roughness is small after laser cleaning. Increased laser power and increased defocusing amount (close to −20 mm) will increase the roughness of the surface of the paint after laser cleaning. As shown in Figure 8e, the roughness is the smallest when the defocusing amount is −10 mm and the repetition frequency is 250 kHz. Higher frequencies of repetition and higher defocusing amounts (close to −20 mm) will result in increased surface roughness.

3.4. Evaluation Method for Laser Paint Removal from Al Alloy and Its Optimization

Based on the above analysis, the prediction results of both models for the thickness of the paint removal and roughness are in accordance with the requirements. Therefore, a double regression model may be used to optimize the laser cleaning quality. The optimization target for the laser cleaning quality of composite paint layers is given in

Table 5. Optimization criteria and weights.

Technical Parameter	Goal	Parameter	Weight
Laser power P/W	In range	200~300	1
Repetition frequency f/kHz	In range	165~245	1
Scanning speed v/mm/s	In range	8000~16,000	1
Defocusing h/mm	In range	−20~0	1
Paint layer removal thickness H/μm	Target	30	1
Surface roughness Ra/μm	Maximize	Max	1

. The target thickness for paint stripper removal is 30 μm; that is, only the top layer is removed. The goal of surface roughness optimization is a larger value, which results in a larger bonding force when the topcoat is reapplied after the removal of paint.

Using Design-Expert software to determine the optimal combination of process parameters, the optimization objectives encompassed the following: (a) Minimizing the values of both the amount of paint residue and paint deposited after ablation to ensure the cleanliness of the paint removal surface; (b) Attaining a surface roughness closely consistent with the original oxide film’s roughness of 8.49 µm. This alignment ensures that the paint removal surface exhibits a roughness similar to the original oxide film, meeting the requirements of industrial reuse; (c) Maximize paint removal efficiency to simultaneously ensure an effective paint removal and enhance overall efficiency. The optimization criteria and corresponding weights are detailed in Table 5.

The optimization objectives in Table 5 are solved using the Design-Expert software. Optimal parameters for the laser cleaning of composite paint layers with the highest reliability are selected from a number of sets of optimal parameters: laser power P = 291 W, repetition frequency f = 166 kHz, scanning speed v = 8425 mm/s, defocusing amount h = −17 mm, paint removal thickness H = 30 μm, surface roughness Ra = 4.051 um.

To demonstrate the reliability of the optimization results, we performed a follow-up test on laser composite paint removal using the parameters that were optimized. The results of three laser cleaning samples are shown in Figure 9. After the paint is removed, the sample is exposed to the primer, and the surface is light green. The topcoat is basically removed, meaning that the removal of the specified thickness of the composite paint layer is achieved, and the surface has a certain roughness, which is convenient for subsequent coating to increase the adhesion between the topcoat and primer.

The error analysis of the thickness of the paint removal and roughness results is given in

Table 6. Error analysis of paint removal thickness and roughness test results.

Sample	Paint Layer Removal Thickness H			Surface Roughness Ra
	Optimal	Actual	Relative Error	Optimal	Actual	Relative Error
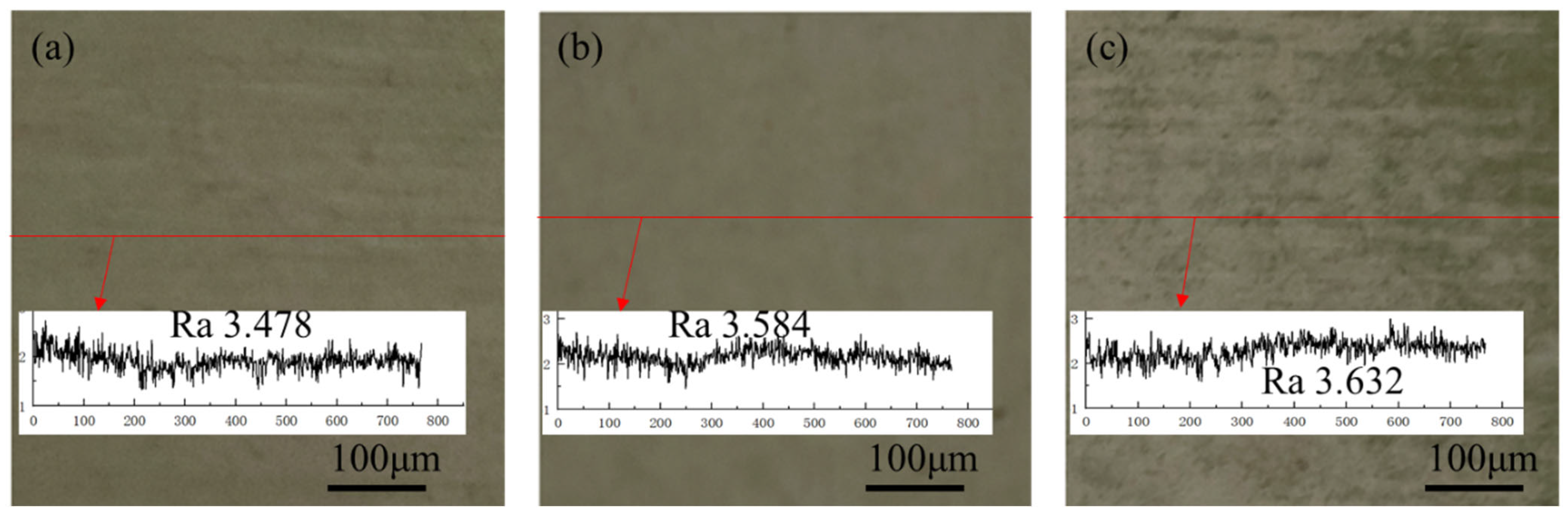
1	30 μm	32.6 ± 1.2 μm	2.6 μm	4.051 μm	3.478 ± 0.53 μm	−0.573 μm
2	30 μm	31.9 ± 2.4 μm	1.9 μm	4.051 μm	3.584 ± 0.75 μm	−0.467 μm
3	30 μm	33.8 ± 0.8 μm	3.8 μm	4.051 μm	3.632 ± 0.35 μm	−0.419 μm

. The table shows that the relative error of thickness is 1.9–3.8 μm and the relative error of roughness is 0.573–0.419 μm.

It was verified that the optimized process parameters take into account the layer cleaning of the composite paint primer and ensure a high surface roughness. There are some errors in the surface coating and there are also some errors in the cleaning process of the laser and in the measurements. Therefore, it is acceptable for there to be some errors between the measured values and the predicted target optimization values. This therefore demonstrates that the response surface method can realize the prediction and optimization of the laser cleaning quality of composite paint.

4. Conclusions

In the present research, a mathematical model focused on the parameters of the laser paint removal process and the thickness and surface roughness of the paint removal was determined using surface response analysis. After a variance analysis and model validation, the proposed model is shown to effectively improve the quality and efficiency of the laser cleaning process of the composite paint layer. Some conclusions may be drawn from this:

• Based on the response surface methodology (RSM), a regression prediction model was constructed for the paint layer removal thickness and surface roughness. A model variance analysis showed that both regression models are reliable. This approach can be used for simulating the laser cleaning quality data of composite paint layers.
• The effects of the parameters of the laser cleaning process and their interaction with the thickness of the laser paint removal and the surface roughness of the paint layer after cleaning were examined. The regression predictor model is analyzed and the order of influence on the thickness of the paint stripper is as follows: defocusing rate > scanning speed > laser power > repeat rate. The order of magnitude of the effect on sharpness is as follows: defocusing amount > scanning speed > laser power > repetition rate.
• To achieve the optimum values of laser paint removal thickness and surface roughness of the paint layer after cleaning, Design-expert software was used to solve the parameters of the laser cleaning process under the optimal target. The parameters for the laser cleaning process that are most reliable were selected: laser power P = 291 W, frequency of repetition f = 166 kHz, scanning speed v = 8425 mm/s, and refractive index h = −17 mm. The optimal parameters of the process were verified via randomization. The relative error for the thickness of the paint stripper is 1.9–3.8 m and the relative error for roughness is −0.573–−0.419 m. This demonstrates that the response surface method can be used to predict and optimize the surface quality of laser paint removal.