Research on Multi-Orbital Scanning Laser Bending Process of Polyvinyl Chloride Sheets
Abstract
1. Introduction
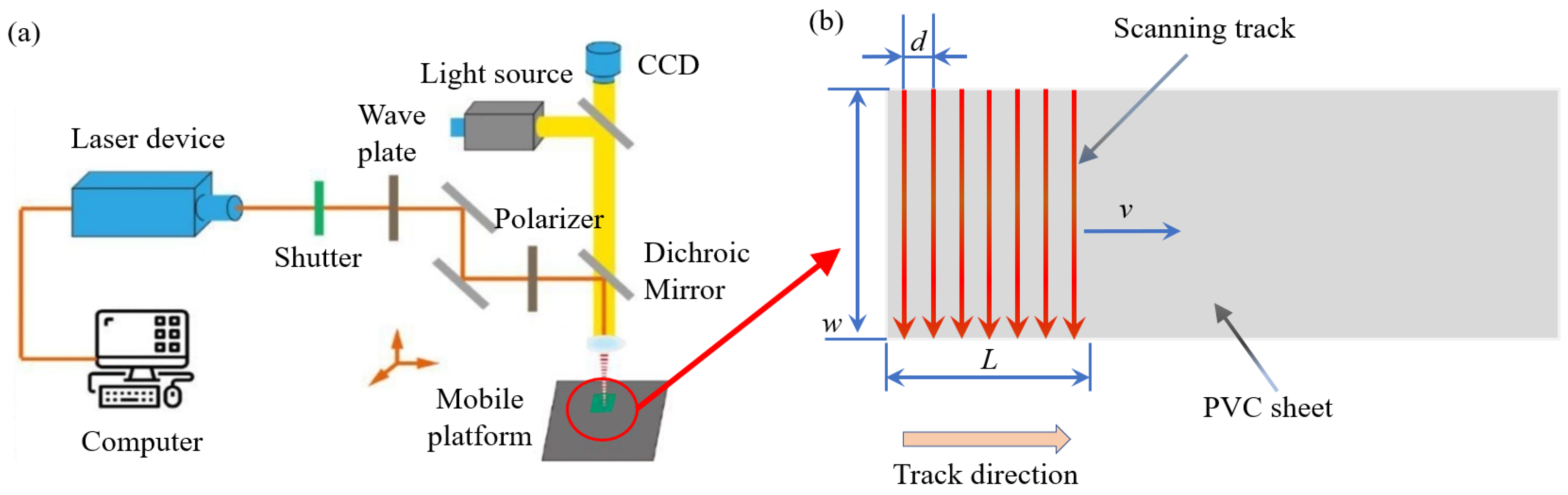
2. Experimental Design
2.1. Experimental Methods
2.2. Parametric Analysis
2.2.1. Processing Distance
2.2.2. Scanning Path Spacing
2.2.3. Illumination Length and Sheet Width
2.2.4. Scanning Speed
3. Simulation and Experiment
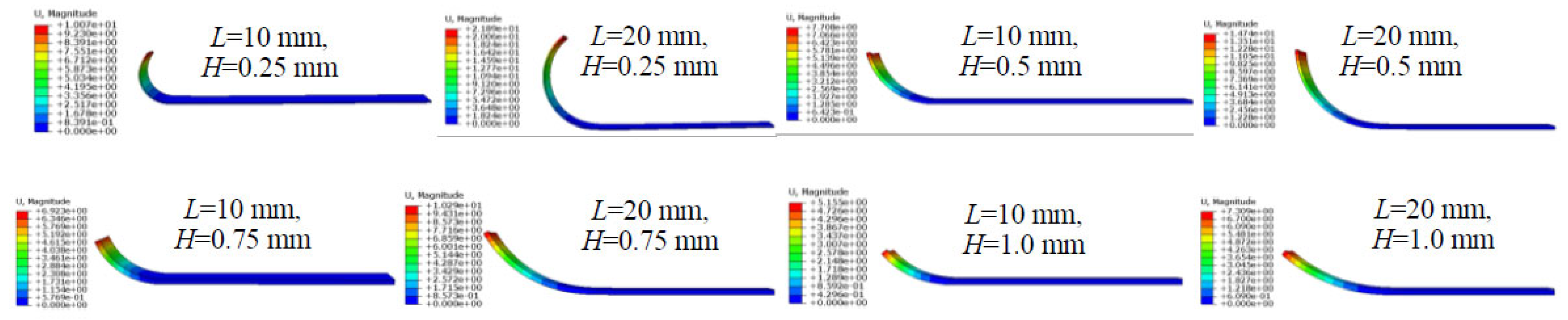
3.1. Simulation
3.2. Laser Application Experiments
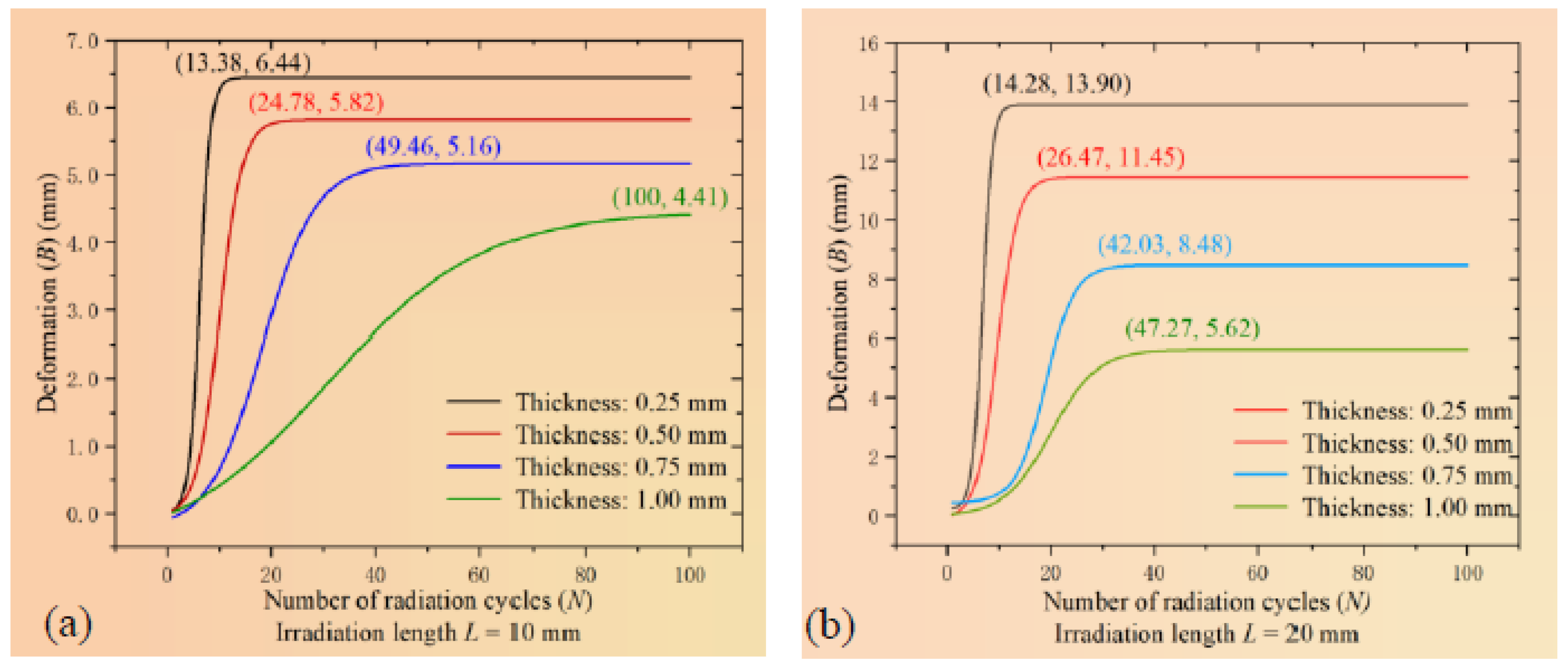
4. Result Analysis
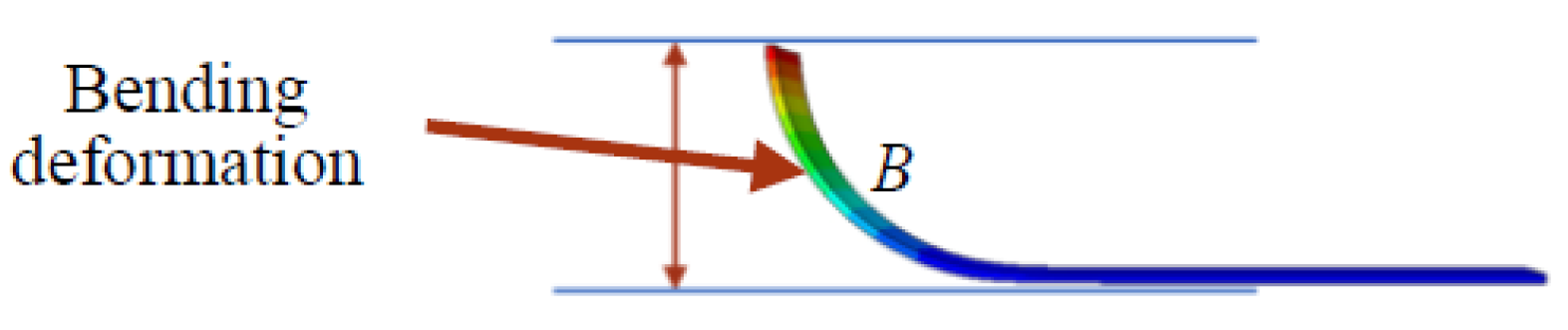
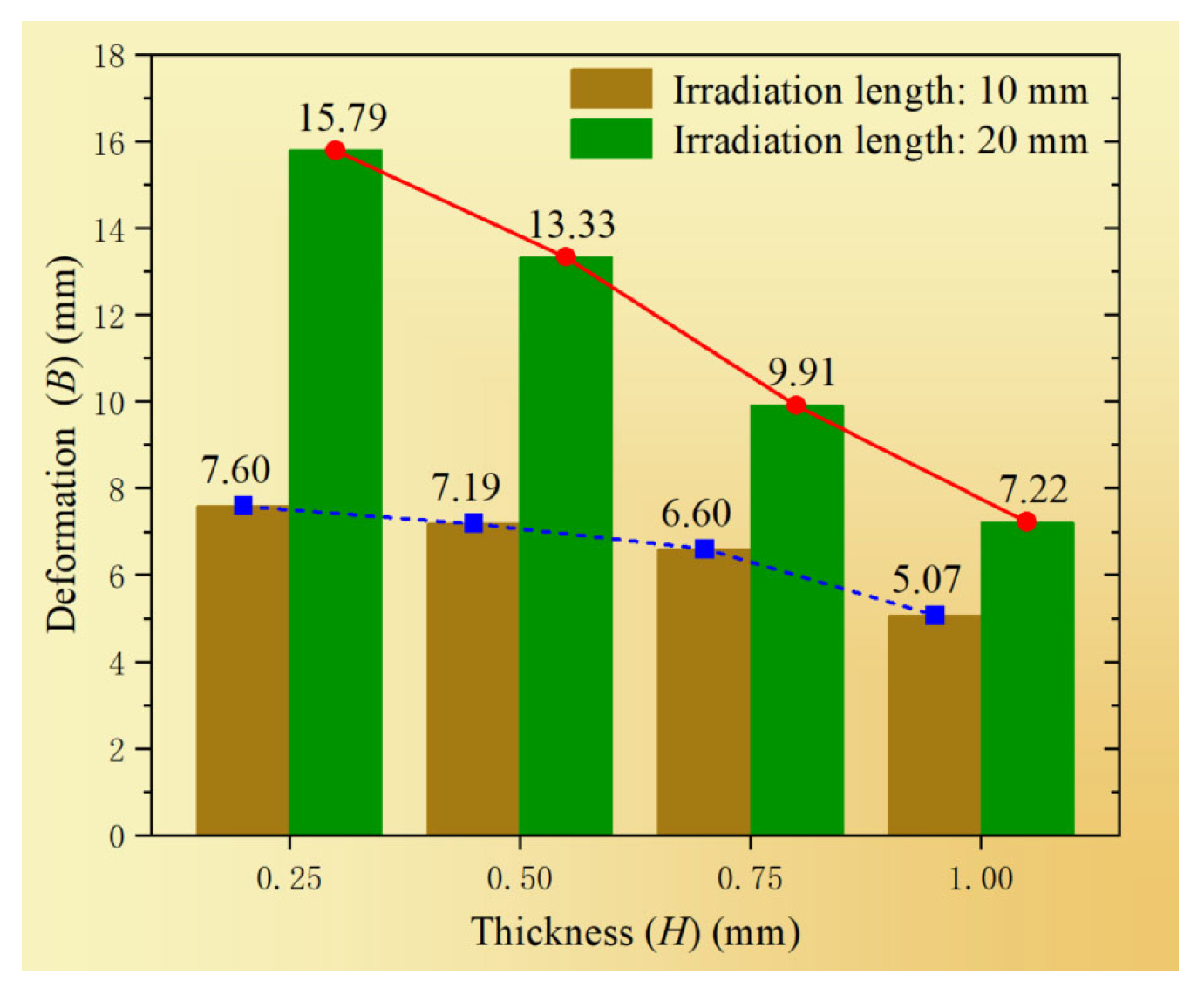
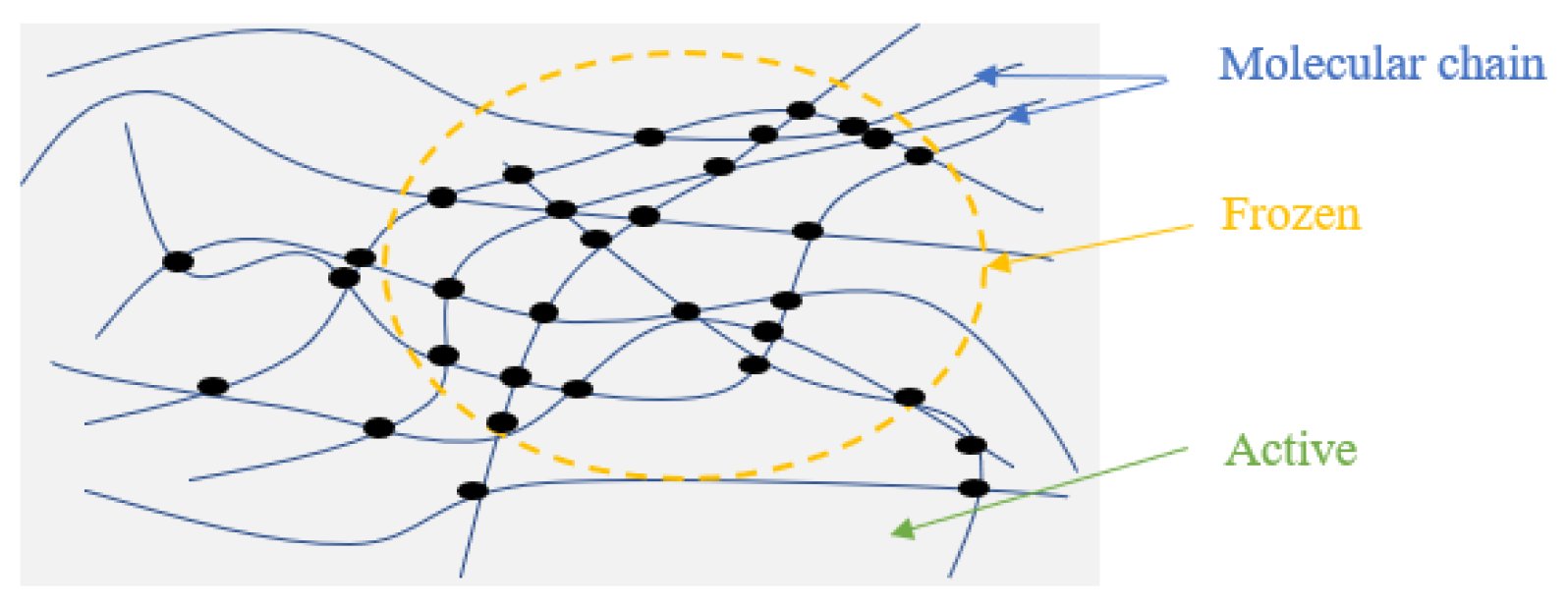
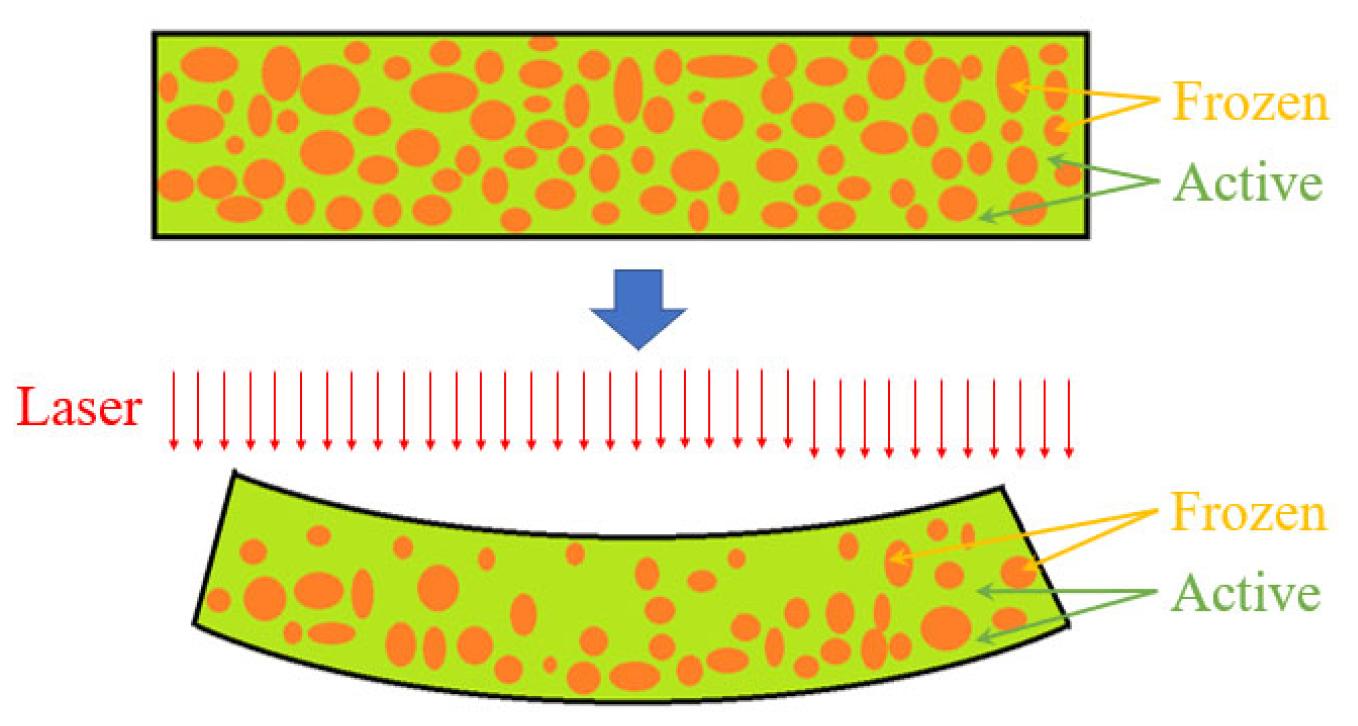
4.1. Analysis of Bending Deformation Mechanism
4.2. N–B Law Mechanism Analysis
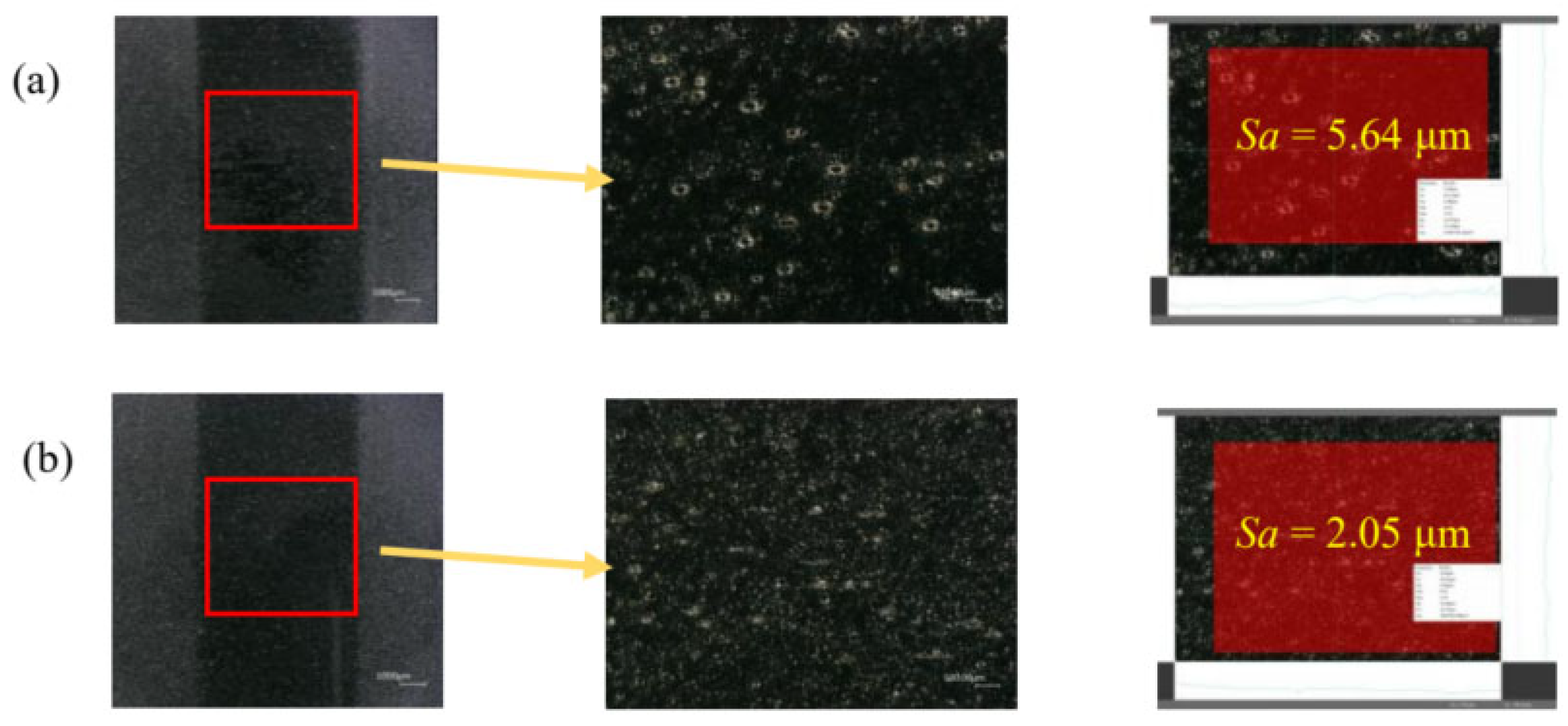
4.3. Surface Morphology Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, L.; Pei, Y.S.; Liu, Z.; Gao, C.; Xie, P.F.; Xu, C.C.; Li, L.X. Manufacturing of curved profiles using an extrusion-bending continuous forming process. Thin Wall. Struct. 2024, 199, 111831. [Google Scholar] [CrossRef]
- Elyasi, M.; Talebi-Ghadikolaee, H.; Zeinolabedin-Beygi, A.; Modanloo, V.; Khatir, F.A. The effect of aging heat treatment on the formability and microstructure of the AA6063 tube in the rotary draw bending process. J. Eng. Res. 2023, 13, 283–293. [Google Scholar] [CrossRef]
- Hu, S.H.; Cheng, C.; El-Aty, A.A.; Zheng, S.; Wu, C.; Luo, H.R.; Guo, X.Z.; Tao, J. Forming characteristics of thin-walled tubes manufactured by free bending process-based nontangential rotation bending die. Thin Wall. Struct. 2024, 194, 111313. [Google Scholar] [CrossRef]
- Wang, M.Y.; Yan, M.; Yang, C.Y.; Liu, Y.; Huang, H.G. A study on the evolution mechanism of small diameter thin-walled stainless steel bellows during a bending process. Eng. Fail. Anal. 2023, 152, 107462. [Google Scholar] [CrossRef]
- Malekipour, E.; Sharifi, E. Effect of high-power ultrasonic vibration on the flexible bending process of thin-walled circular tubes: Numerical and experimental research. Ultrasonics 2023, 134, 107059. [Google Scholar] [CrossRef]
- Mendes-Fonseca, N.; Diab, M.; Kang, J.D.; Wilkinson, D.S. A comparative study on the bendability of a Dual Phase steel: Three-point bend versus V-die test. J. Mater. Res. Technol. 2025, 36, 7603–7614. [Google Scholar] [CrossRef]
- Safari, M.; Babaei, A.M.; Zamzami, B.; Sousa, R.A. Experimental investigation, statistical modeling and optimization of laser bending process of perforated sheets. Opt. Laser. Technol. 2024, 175, 110810. [Google Scholar] [CrossRef]
- Cheng, Z.H.; El-Aty, A.A.; Zhang, R.; Cheng, C.; Guo, X.Z.; Tao, J. Finite element modeling and experimental investigation on manufacturing TA18 alloy pipes via hot free bending forming technology: Forming characteristics and process optimization. J. Mater. Res. Technol. 2024, 29, 5225–5240. [Google Scholar] [CrossRef]
- Zhang, Z.C.; Furushima, T.; Manabe, K. Microstructure and mechanical properties evolution of 65Cu-35Zn brass tube during cyclic rotating-bending process. Trans. Nonferr. Metal. Soc. 2022, 32, 3610–3622. [Google Scholar] [CrossRef]
- Sharma, Y.P.; Kant, R.; Sidhu, B.S.; Yadav, R. Mechanical behaviour of mild steel during multi-scan laser bending with forced cooling. Opt. Laser. Technol. 2024, 171, 110417. [Google Scholar] [CrossRef]
- Khandai, B.K.; Shukla, S.; Muvvala, G. Real-time monitoring of temperature gradients and bending mechanism in multi-scan laser forming process. J. Manuf. Process. 2024, 119, 975–986. [Google Scholar] [CrossRef]
- Sala, S.T.; Keller, S.; Chupakhin, S.; Poltl, D.; Klusemann, B.; Kashaev, N. Effect of laser peen forming process parameters on bending and surface quality of Ti-6Al-4V sheets. J. Mater. Process. Technol. 2022, 305, 117578. [Google Scholar] [CrossRef]
- Baig, A.; Barse, R.; Paryekar, A.; Jagtap, V. Evolution of pharmaceuticals using 3D and 4D printing. Intell. Pharm. 2024, 2, 804–813. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Bayati, A.; Khajepour, M.; Mirasadi, K.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; Baghani, M. Poly(ethylene terephthalate) glycol/carbon black composites for 4D printing, Materials Chemistry and Physics. Mater. Chem. Phys. 2024, 325, 129737. [Google Scholar] [CrossRef]
- Im, S.H.; Jung, Y.; Kim, S.H. Current status and future direction of biodegradable metallic and polymeric vascular scaffolds for next-generation stents. Acta. Biomater. 2017, 60, 3–22. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Khajepour, M.; Bayati, A.; Mirasadi, K.; Yousefi, M.A.; Shegeft, A.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; et al. Advancing sustainable shape memory polymers through 4D printing of polylactic acid-polybutylene adipate terephthalate blends. Eur. Polym. J. 2024, 216, 113289. [Google Scholar] [CrossRef]
- Bukala, J.; Buszman, P.P.; Małachowski, J.; Mazurkiewicz, L.; Sybilski, K. Experimental tests, FEM constitutive modeling and validation of PLGA bioresorbable polymer for stent applications. Materials 2020, 13, 2003. [Google Scholar] [CrossRef]
- Liu, T.Z.; Liu, L.W.; Yu, M.; Li, Q.F.; Zeng, C.J.; Lan, X.; Liu, Y.J.; Leng, J.S. Integrative hinge based on shape memory polymer composites: Material, design, properties and application. Compos. Struct. 2018, 206, 164–176. [Google Scholar] [CrossRef]
- Kajia, M.; Bita, H.; Taifi, N.; Malaoui, A. Analytical and numerical study of rectangular reinforced concrete beam using robot structural analysis software. Mater. Today Proc. 2023; in press. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Yang, D.Z.; Yan, P.N.; Zhou, P.W.; Zou, J.; Gu, G.Y. Inchworm inspired multimodal soft robots with crawling, climbing, and transitioning locomotion. IEEE. Trans. Robot. 2022, 38, 1806–1819. [Google Scholar] [CrossRef]
- Ullah, H.; Khan, R.U.; Silberschmidt, V.V. Assessing pseudo-ductile behavior of woven thermoplastic composites under tension and bending. Compos. Sci. Technol. 2024, 248, 110465. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, J.; Su, C.; Hua, H.L. Finite element simulation of the removal mechanism and ablation morphology of HA bio-coating by nanosecond laser ablation. Opt. Laser. Technol. 2025, 180, 111448. [Google Scholar] [CrossRef]
- Leng, J.S.; Lan, X.; Liu, Y.J.; Du, S.Y. Shape-memory polymers and their composites: Stimulus methods and applications. Prog. Mater. Sci. 2011, 56, 1077–1135. [Google Scholar] [CrossRef]
- Bhattacharyya, A. Isothermal mechanical response of shape memory polymer (SMP)-based hybrid models and SMP-composites. J. Mech. Behav. Mater. 2004, 15, 1–2. [Google Scholar] [CrossRef]
- Reun, A.L.; Louët, V.L.; Corre, S.L.; Sobotka, V. Numerical simulation at the micro-scale for the heat transfer modelling in the thermoplastic composites laser-assisted AFP process. Compos. Part A—Appl. Sci. Manuf. 2024, 179, 108010. [Google Scholar] [CrossRef]
- Ran, W.G.; Zhang, Z.C.; Ma, X.L.; Sun, G.S.; Yan, T.J. A novel optical temperature sensor based on Boltzmann function in BiZn2PO6 phosphor. J. Lumin. 2023, 255, 119562. [Google Scholar] [CrossRef]
- Flayyih, A.H.; Al-Khursan, A.H. Theory of four-wave mixing in quantum dot semiconductor optical amplifiers. J. Phys. D Appl. Phys. 2013, 46, 445102. [Google Scholar] [CrossRef]
- Obilor, A.F.; Pacella, M.; Wilson, A.; Silberschmidt, V.V. Micro-texturing of polymer surfaces using lasers: A review. Int. J. Adv. Manuf. Technol. 2022, 120, 103–135. [Google Scholar] [CrossRef]







| Rated power | 20 W | Pulse energy | 0.4 mJ |
| Pulse width | 50 ns | Peak power | 7.5 kW |
| Wavelength | 475 nm | Peak intensity | 7.8 × 108 W/cm2 |
| Frequency range | 20~50 kHz | Laser flux | 41.6 J/cm2 |
| Spot diameter | 50 μm |
| Parameters | Application Distance D | Scanning Path Spacing d | Sheet Width w | Illumination Length l | Scanning Speed v |
|---|---|---|---|---|---|
| Value | 35 mm | 0.25 mm | 5 mm | 10 mm and 20 mm | 2000 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kan, F.; Xu, H.; Zhou, Y.; Li, K.; Hu, J. Research on Multi-Orbital Scanning Laser Bending Process of Polyvinyl Chloride Sheets. Coatings 2025, 15, 609. https://doi.org/10.3390/coatings15050609
Kan F, Xu H, Zhou Y, Li K, Hu J. Research on Multi-Orbital Scanning Laser Bending Process of Polyvinyl Chloride Sheets. Coatings. 2025; 15(5):609. https://doi.org/10.3390/coatings15050609
Chicago/Turabian StyleKan, Fuchao, Haojie Xu, You Zhou, Kangmei Li, and Jun Hu. 2025. "Research on Multi-Orbital Scanning Laser Bending Process of Polyvinyl Chloride Sheets" Coatings 15, no. 5: 609. https://doi.org/10.3390/coatings15050609
APA StyleKan, F., Xu, H., Zhou, Y., Li, K., & Hu, J. (2025). Research on Multi-Orbital Scanning Laser Bending Process of Polyvinyl Chloride Sheets. Coatings, 15(5), 609. https://doi.org/10.3390/coatings15050609






