Investigation on the Viscosity–Temperature Properties for Various EPDM Solutions Based on Three-Dimensional Solubility Parameters and Flory–Huggins Interaction Parameters
Abstract
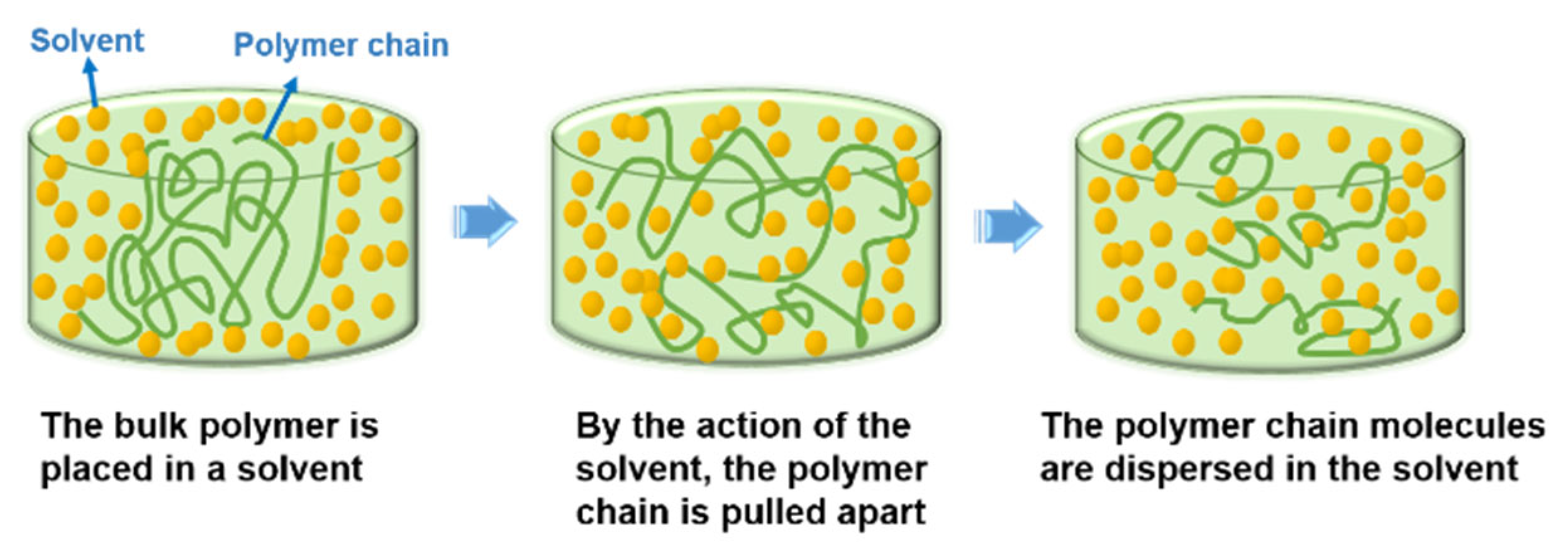
1. Introduction
2. Experimental Section
2.1. Materials
2.2. Viscosity Test of EPDM Solutions
3. Results and Discussion
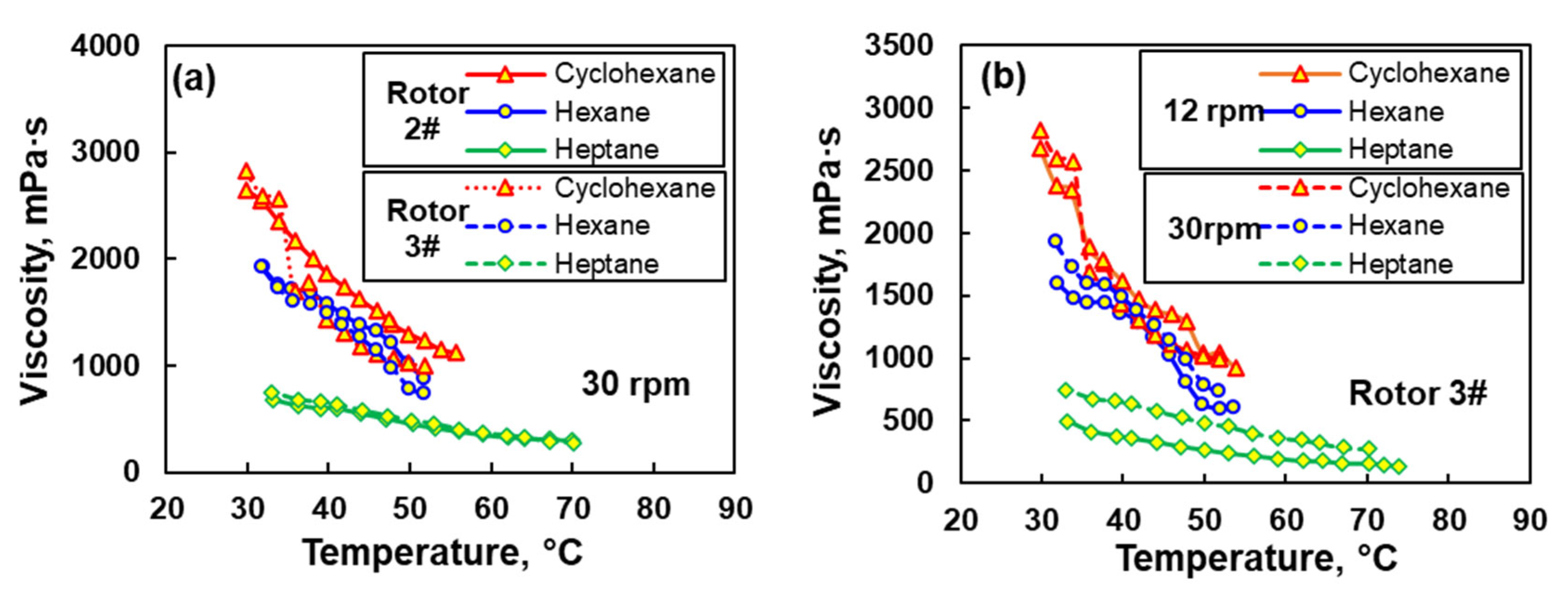
3.1. Effects of Rotor Type and Speed on the Viscosity of EPDM Solution
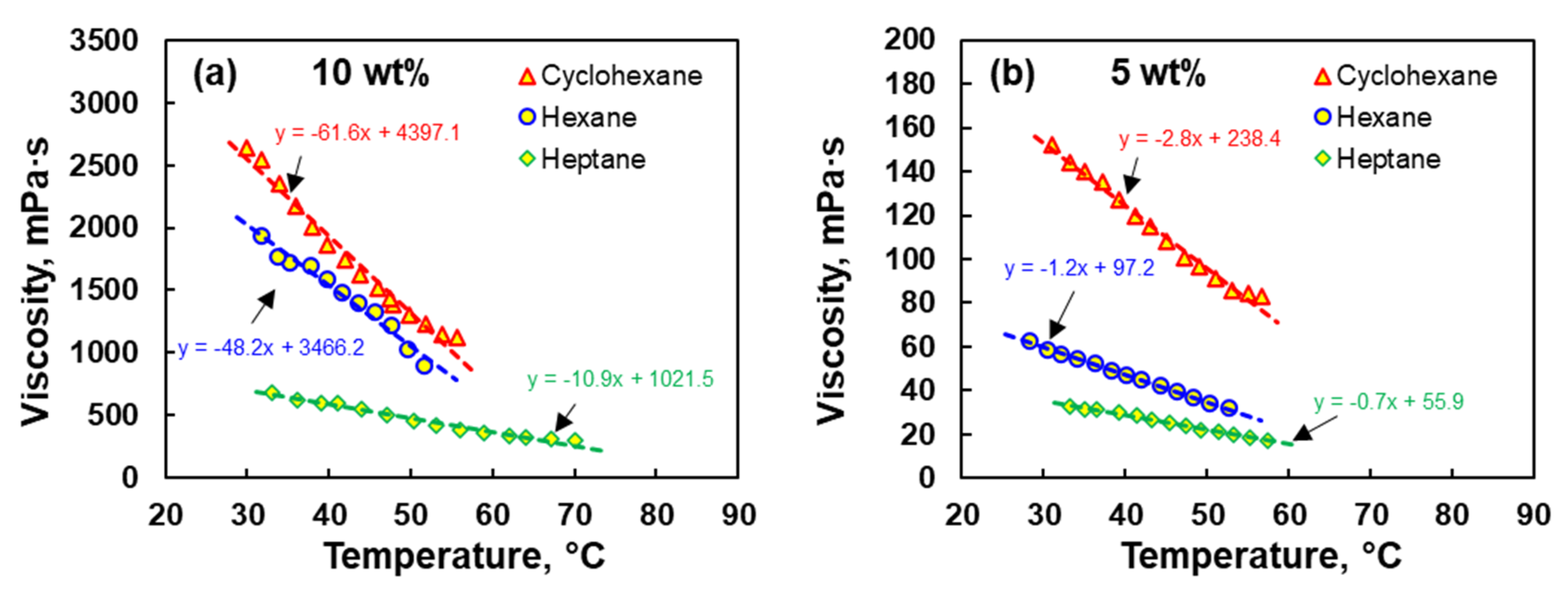
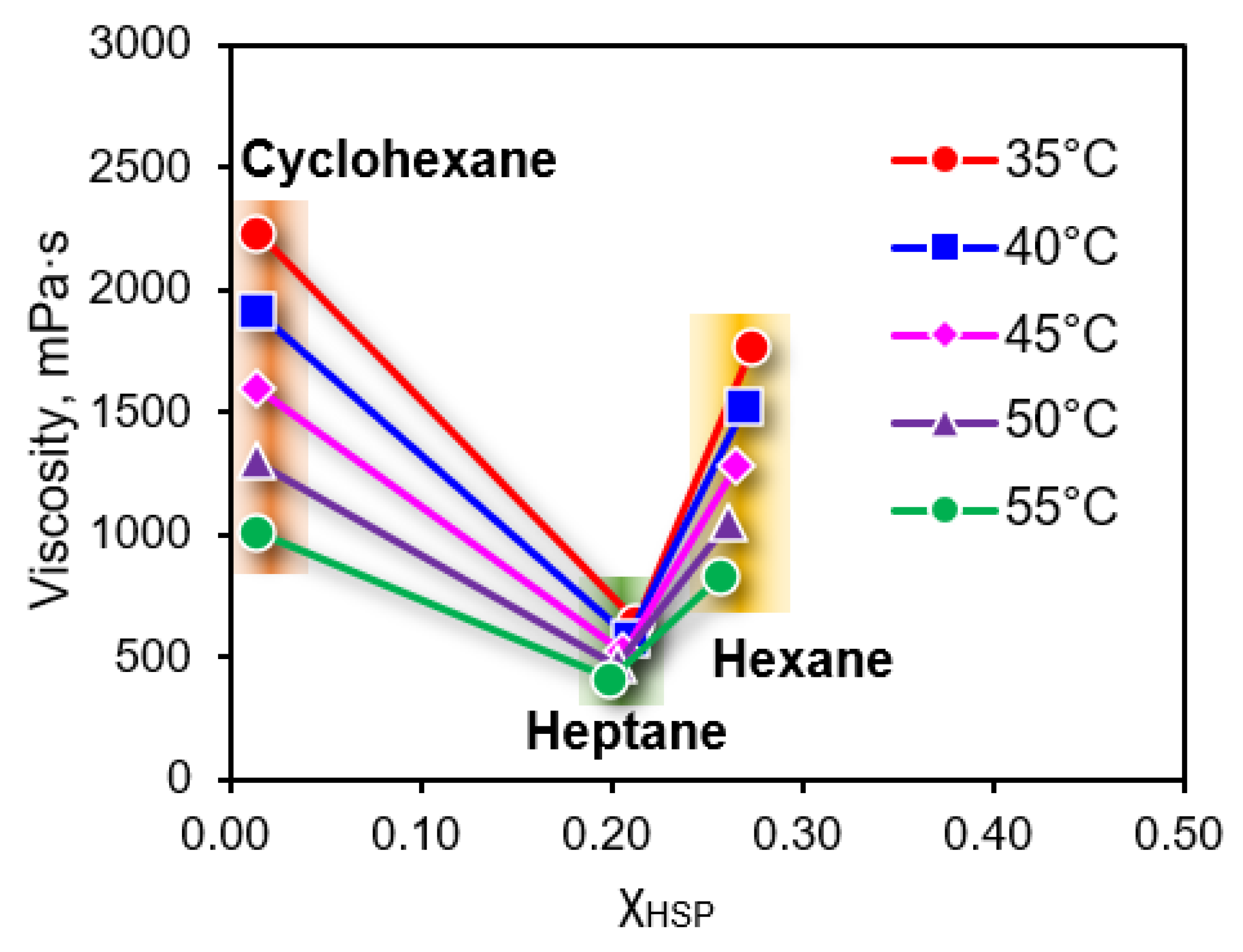
3.2. Effect of Temperature on the Viscosity of EPDM Solution
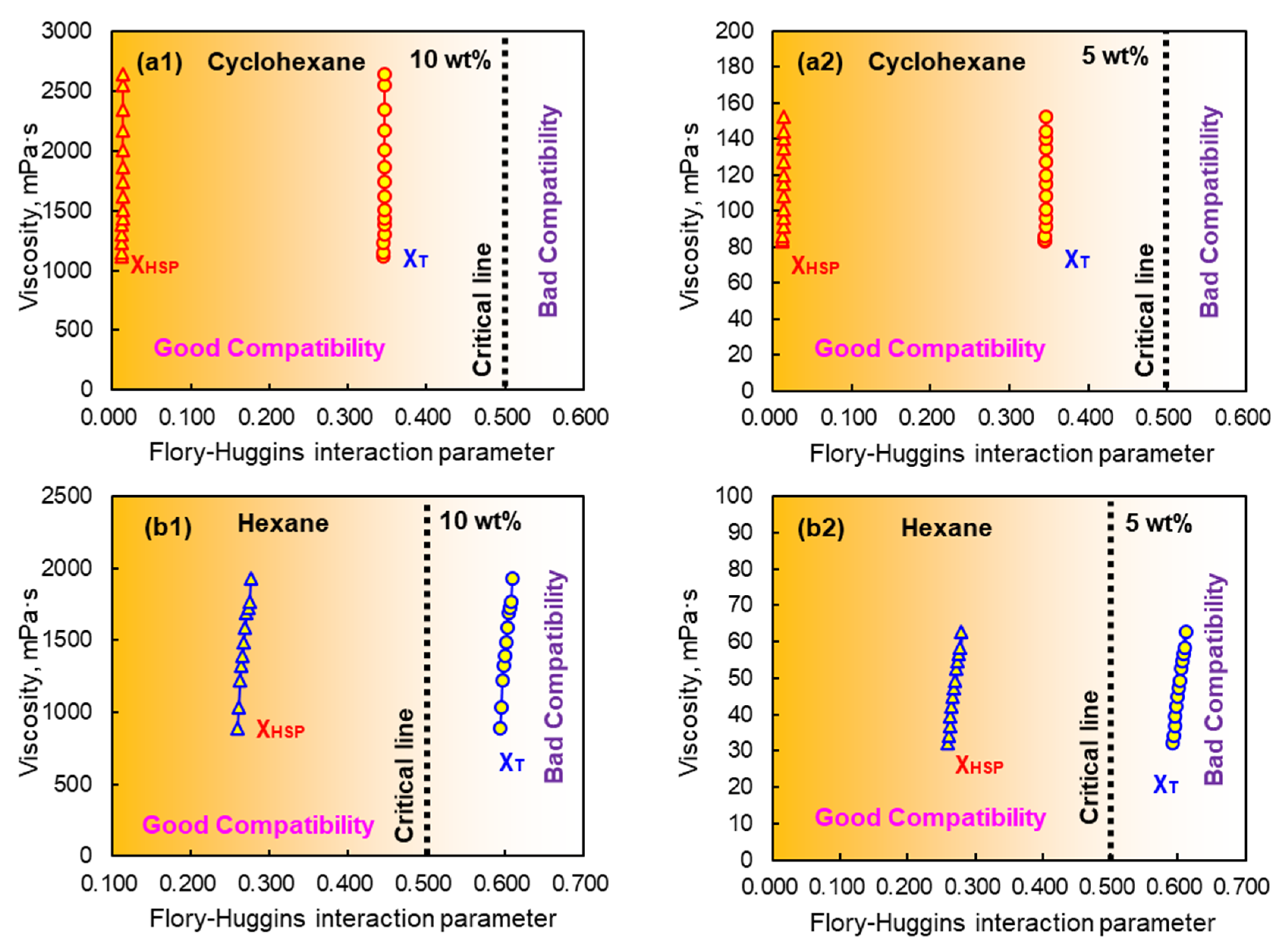
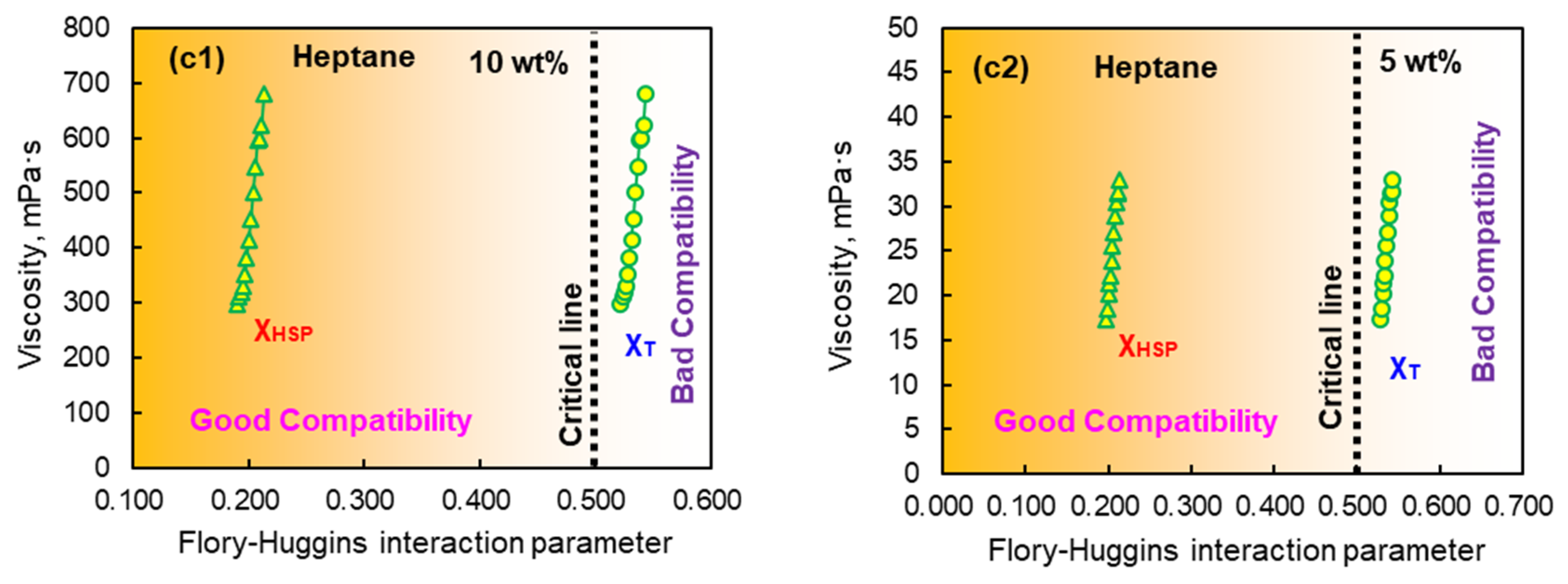
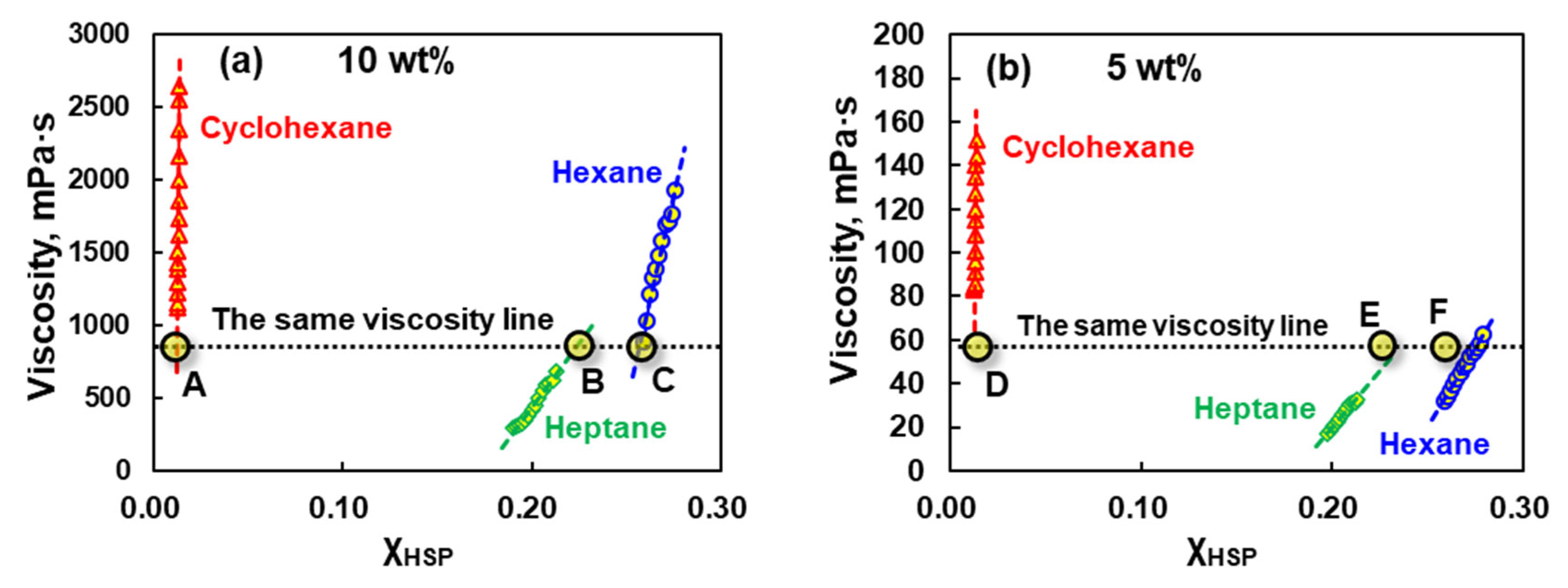
3.3. Relationship Between Viscosity and Compatibility of EPDM Solution
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, X.; Ji, T.; Zhang, J.; Shen, S.; Wang, S.; Wang, J.; Hou, X.; Yang, S.; Ma, X. A double-decker silsesquioxane of norbornene and performance of crosslinking reactive modified EPDM ablation resistance composites. Compos. Part A Appl. Sci. Manuf. 2023, 165, 107370. [Google Scholar] [CrossRef]
- Jovanović, V.; Samaržija-Jovanović, S.; Budinski-Simendić, J.; Marković, G.; Marinović-Cincović, M. Composites based on carbon black reinforced NBR/EPDM rubber blends. Compos. Part B Eng. 2013, 45, 333–340. [Google Scholar] [CrossRef]
- Li, C.; Ding, Y.; Yang, Z.; Yuan, Z.; Ye, L. Compressive stress-thermo oxidative ageing behaviour and mechanism of EPDM rubber gaskets for sealing resilience assessment. Polym. Test. 2020, 84, 106366. [Google Scholar] [CrossRef]
- Li, C.; Wang, Y.; Yuan, Z.; Ye, L. Construction of sacrificial bonds and hybrid networks in EPDM rubber towards mechanical performance enhancement. Appl. Surf. Sci. 2019, 484, 616–627. [Google Scholar] [CrossRef]
- Mishra, V. Effect of carbon black and graphene on the performance of EPDM rubber composites: A short review. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1116, 012004. [Google Scholar] [CrossRef]
- Chen, G.; Gupta, A.; Mekonnen, T.H. Silane-modified wood fiber filled EPDM bio-composites with improved thermomechanical properties. Compos. Part A Appl. Sci. Manuf. 2022, 159, 107029. [Google Scholar] [CrossRef]
- OuYang, B.; Liu, Z.; Wang, X.; Zhang, T.; Zhang, C.; Chi, Q. Investigation of electrical properties of ZnO@Ag/EPDM composites. AIP Adv. 2020, 10, 095108. [Google Scholar] [CrossRef]
- Cazan, C. Advances in Sustainable Polymeric Materials. Polymers 2022, 14, 4972. [Google Scholar] [CrossRef]
- Miller-Chou, B.A.; Koenig, J.L. A review of polymer dissolution. Prog. Polym. Sci. 2003, 28, 1223–1270. [Google Scholar] [CrossRef]
- Narasimhan, B. Mathematical models describing polymer dissolution: Consequences for drug delivery. Adv. Drug Deliv. Rev. 2001, 48, 195–210. [Google Scholar] [CrossRef]
- Kaunisto, E.; Marucci, M.; Borgquist, P.; Axelsson, A. Mechanistic modelling of drug release from polymer-coated and swelling and dissolving polymer matrix systems. Int. J. Pharm. 2011, 418, 54–77. [Google Scholar] [CrossRef]
- Alfrey, T.; Bartovics, A.; Mark, H. The Effect of Temperature and Solvent Type on the Intrinsic Viscosity of High Polymer Solutions. J. Am. Chem. Soc. 1942, 64, 1557–1560. [Google Scholar] [CrossRef]
- Fischer, C.; Luttge, A. Pulsating dissolution of crystalline matter. Proc. Natl. Acad. Sci. USA 2018, 115, 897–902. [Google Scholar] [CrossRef] [PubMed]
- Gordon, M. Modern theory of polymer solutions. H. Yamakawa. Harper & Row, London. 1971. pp. 419. Price £9.35. Polym. Int. 2010, 4, 541–542. [Google Scholar] [CrossRef]
- Marani, D.; Gadea, C.; Hjelm, J.; Hjalmarsson, P.; Wandel, M.; Kiebach, R. Influence of hydroxyl content of binders on rheological properties of cerium–gadolinium oxide (CGO) screen printing inks. J. Eur. Ceram. Soc. 2015, 35, 1495–1504. [Google Scholar] [CrossRef]
- Cooper, W. Properties of polymers: Correlations with chemical structures. Polymer 1973, 14, 40. [Google Scholar] [CrossRef]
- El Aferni, A.; Guettari, M.; Kamli, M.; Tajouri, T.; Ponton, A. A structural study of a polymer-surfactant system in dilute and entangled regime: Effect of high concentrations of surfactant and polymer molecular weight. J. Mol. Struct. 2020, 1199, 127052. [Google Scholar] [CrossRef]
- Agasty, A.; Wisniewska, A.; Kalwarczyk, T.; Koynov, K.; Holyst, R. Scaling equation for viscosity of polydimethylsiloxane in ethyl acetate: From dilute to concentrated solutions. Polymer 2020, 203, 122779. [Google Scholar] [CrossRef]
- Germann, N. Shear banding in semidilute entangled polymer solutions. Curr. Opin. Colloid Interface Sci. 2019, 39, 1–10. [Google Scholar] [CrossRef]
- Yan, Z.-C.; Wang, W. Dynamics of polymers in concentrated solutions: A weaker self-concentration effect. Polymer 2018, 153, 33–42. [Google Scholar] [CrossRef]
- Flory; Paul, J. Thermodynamics of High Polymer Solutions. J. Chem. Phys. 1941, 9, 660. [Google Scholar] [CrossRef]
- Huang, B.; Li, X.; Fu, C.; Wang, Y.; Cheng, H. Study Rheological Behavior of Polymer Solution in Different-Medium-Injection-Tools. Polymers 2019, 11, 319. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, F.C. The Solubility of Nonelectrolytes (Hildebrand, Joel H.). J. Chem. Educ. 1952, 29, 51. [Google Scholar] [CrossRef][Green Version]
- Jiang, X.; Yuan, X.; Guo, X.; Zeng, F.; Liu, G. Determination of three-dimensional solubility parameters of HNBR/EPDM blends and the transport behaviors in ester solvents. J. Appl. Polym. Sci. 2022, 139, e52881. [Google Scholar] [CrossRef]
- Jing, Y.; Cui, Z.; Zou, H.; Tu, J.; Jiang, X.; Shi, X.; Yong, Z.; Liu, S.; Liu, G. Three-dimensional solubility parameters of natural rubber and its predictive power in diffusion coefficients. J. Appl. Polym. Sci. 2022, 139, 51473. [Google Scholar] [CrossRef]
- Seymour, R.B.; Sosa, J.M. Estimation of solubility parameters of nonelectrolytes. Nature 1974, 248, 759–761. [Google Scholar] [CrossRef]
- Nielsen, T.B.; Hansen, C.M. Elastomer swelling and Hansen solubility parameters. Polym. Test. 2005, 24, 1054–1061. [Google Scholar] [CrossRef]
- Murase, M.; Ohta, R.; Iseki, T. Liquid-Repellent Films Comprising Octamethylsilsesquioxane Selected Based on Three-Dimensional Solubility Parameters. Langmuir 2020, 36, 2247–2254. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Bi, L.Y.; Zhang, H.J.; Zhu, X.T.; Liu, G.Y.; Qiu, G.X.; Liu, S.S. Predictive power in oil resistance of fluororubber and fluorosilicone rubbers based on three-dimensional solubility parameter theory. Polym. Test. 2019, 75, 380–386. [Google Scholar] [CrossRef]
- Liu, G.; Hoch, M.; Liu, S.; Kulbaba, K.; Qiu, G. Quantitative exploration of the swelling response for carbon black filled hydrogenated nitrile rubber with three-dimensional solubility parameters. Polym. Bull. 2015, 72, 1961–1974. [Google Scholar] [CrossRef]
- Wiśniewski, R.; Śmieszek, E.; Kamińska, E. Three-dimensional solubility parameters: Simple and effective determination of compatibility regions. Prog. Org. Coat. 1995, 26, 265–274. [Google Scholar] [CrossRef]
- Huang, J.-C.; Lin, K.-T.; Deanin, R.D. Three-dimensional solubility parameters of poly(ε-caprolactone). J. Appl. Polym. Sci. 2006, 100, 2002–2009. [Google Scholar] [CrossRef]
- Pospiech, D.; Gottwald, A.; Jehnichen, D.; Friedel, P.; John, A.; Harnisch, C.; Voigt, D.; Khimich, G.; Bilibin, A. Determination of interaction parameters of block copolymers containing aromatic polyesters from solubility parameters obtained from solution viscosities. Colloid Polym. Sci. 2002, 280, 1027–1037. [Google Scholar] [CrossRef]
- Han, K.H.; Jeon, G.S.; Hong, I.K.; Lee, S.B. Prediction of solubility parameter from intrinsic viscosity. J. Ind. Eng. Chem. 2013, 19, 1130–1136. [Google Scholar] [CrossRef]
- Gillespie, T. The viscosity of concentrated polymer solutions. J. Polym. Sci. 1960, 46, 383–393. [Google Scholar] [CrossRef]
- Peleg, M. Temperature–viscosity models reassessed. Crit. Rev. Food Sci. Nutr. 2018, 58, 2663–2672. [Google Scholar] [CrossRef]
- Agasty, A.; Wisniewska, A.; Kalwarczyk, T.; Koynov, K.; Holyst, R. Macroscopic Viscosity of Polymer Solutions from the Nanoscale Analysis. ACS Appl. Polym. Mater. 2021, 3, 2813–2822. [Google Scholar] [CrossRef]
- Yan, Y.; Guo, R.; Cheng, C.; Fu, C.; Yang, Y. Viscosity prediction model of natural rubber-modified asphalt at high temperatures. Polym. Test. 2022, 113, 107666. [Google Scholar] [CrossRef]
- Kol, R.; Nachtergaele, P.; De Somer, T.; D’hooge, D.R.; Achilias, D.S.; De Meester, S. Toward More Universal Prediction of Polymer Solution Viscosity for Solvent-Based Recycling. Ind. Eng. Chem. Res. 2022, 61, 10999–11011. [Google Scholar] [CrossRef]
- Rotational Viscometer. Science 1975, 189, 1110. [CrossRef]
- Liu, S.; Jing, Y.; Tu, J.; Zou, H.; Yong, Z.; Gao, Y.; Tang, Z.; Liu, G. New Flory-Huggins interaction parameter between SBR and p-phenylenediamine antioxidants and the predictive power in molecular structure and rubber formula design. J. Appl. Polym. Sci. 2022, 139, 51840. [Google Scholar] [CrossRef]
- Huang, J. Probe dependency of flory–huggins interaction parameters between solvents: Cases of hydrocarbons and isosteric derivatives. J. Appl. Polym. Sci. 2013, 127, 5000–5006. [Google Scholar] [CrossRef]
- Jiang, X.; Yuan, X.; Guo, X.; Zeng, F.; Wang, H.; Liu, G. Study on the application of Flory–Huggins interaction parameters in swelling behavior and crosslink density of HNBR/EPDM blend. Fluid Phase Equilibria 2023, 563, 113589. [Google Scholar] [CrossRef]


| Solvent | Molecular Structural | Molecular Formula | δd, MPa1/2 | δp, MPa1/2 | δh, MPa1/2 | δt, MPa1/2 | Vmol, (cm3/mol) |
|---|---|---|---|---|---|---|---|
| Cyclohexane |  | C6H12 | 16.8 | 0 | 0.2 | 16.8 | 108.7 |
| Heptane |  | C7H16 | 15.2 | 0 | 0 | 15.3 | 147 |
| Hexane |  | C6H14 | 15.0 | 0 | 0 | 14.9 | 131.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Jing, Y.; Liu, G. Investigation on the Viscosity–Temperature Properties for Various EPDM Solutions Based on Three-Dimensional Solubility Parameters and Flory–Huggins Interaction Parameters. Coatings 2025, 15, 582. https://doi.org/10.3390/coatings15050582
Yang Y, Jing Y, Liu G. Investigation on the Viscosity–Temperature Properties for Various EPDM Solutions Based on Three-Dimensional Solubility Parameters and Flory–Huggins Interaction Parameters. Coatings. 2025; 15(5):582. https://doi.org/10.3390/coatings15050582
Chicago/Turabian StyleYang, Yuqing, Yiran Jing, and Guangyong Liu. 2025. "Investigation on the Viscosity–Temperature Properties for Various EPDM Solutions Based on Three-Dimensional Solubility Parameters and Flory–Huggins Interaction Parameters" Coatings 15, no. 5: 582. https://doi.org/10.3390/coatings15050582
APA StyleYang, Y., Jing, Y., & Liu, G. (2025). Investigation on the Viscosity–Temperature Properties for Various EPDM Solutions Based on Three-Dimensional Solubility Parameters and Flory–Huggins Interaction Parameters. Coatings, 15(5), 582. https://doi.org/10.3390/coatings15050582






