First-Principles Analysis of Phase Stability and Transformation Suppression for Hydrogen-Doped Alumina
Abstract
1. Introduction
2. Materials and Methods of Research
3. Results and Discussion
3.1. Mechanical Property Validation
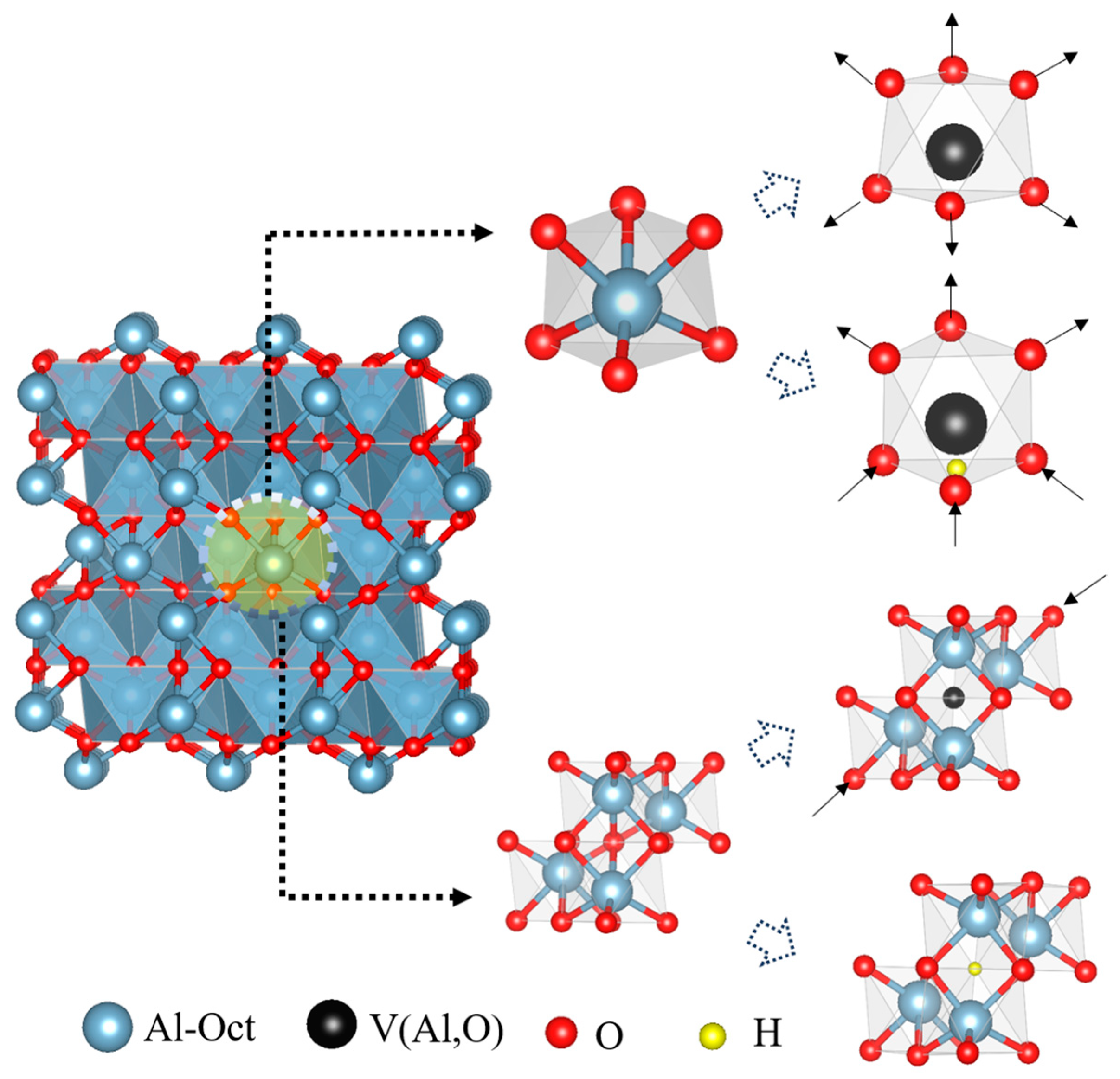
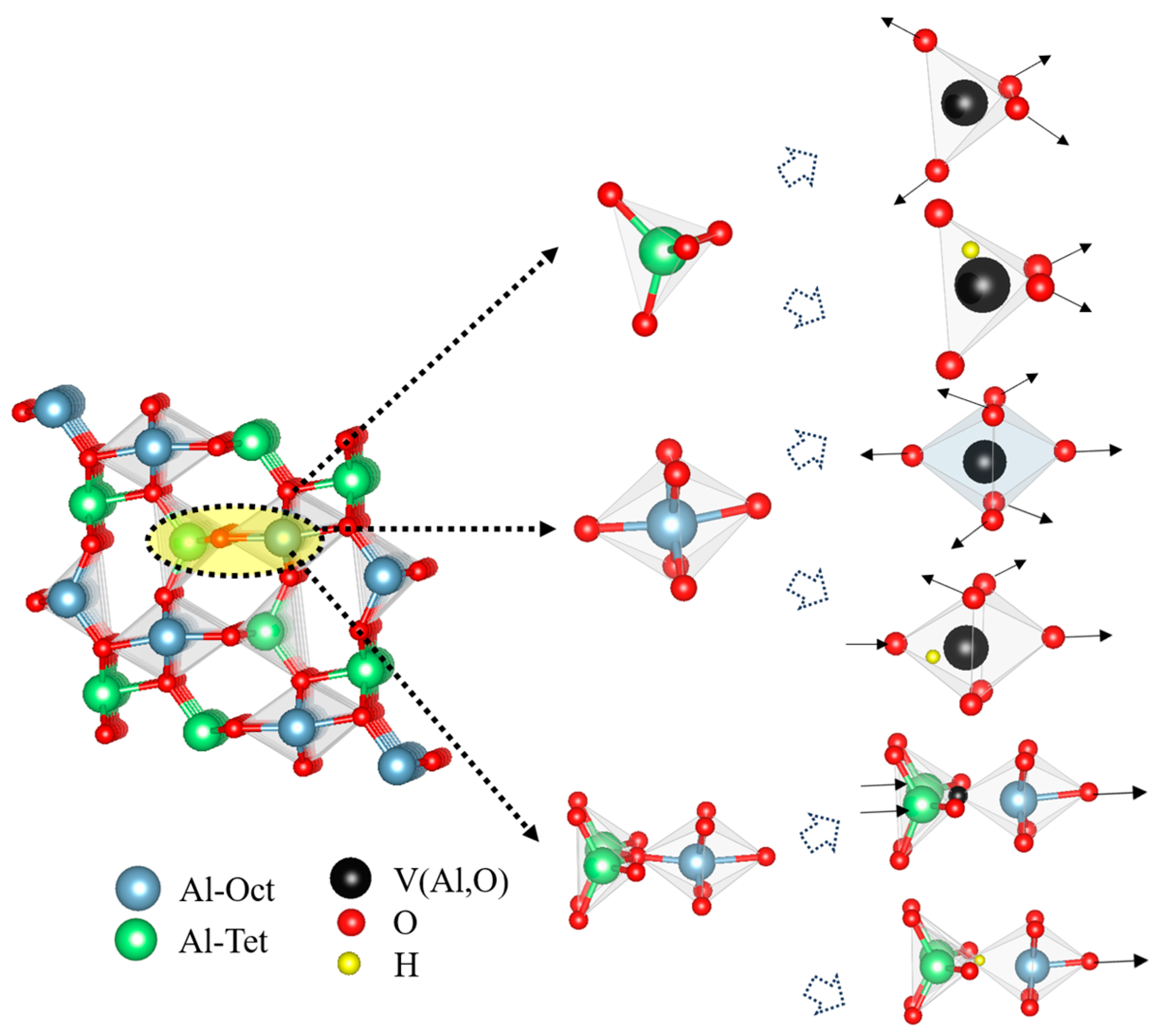
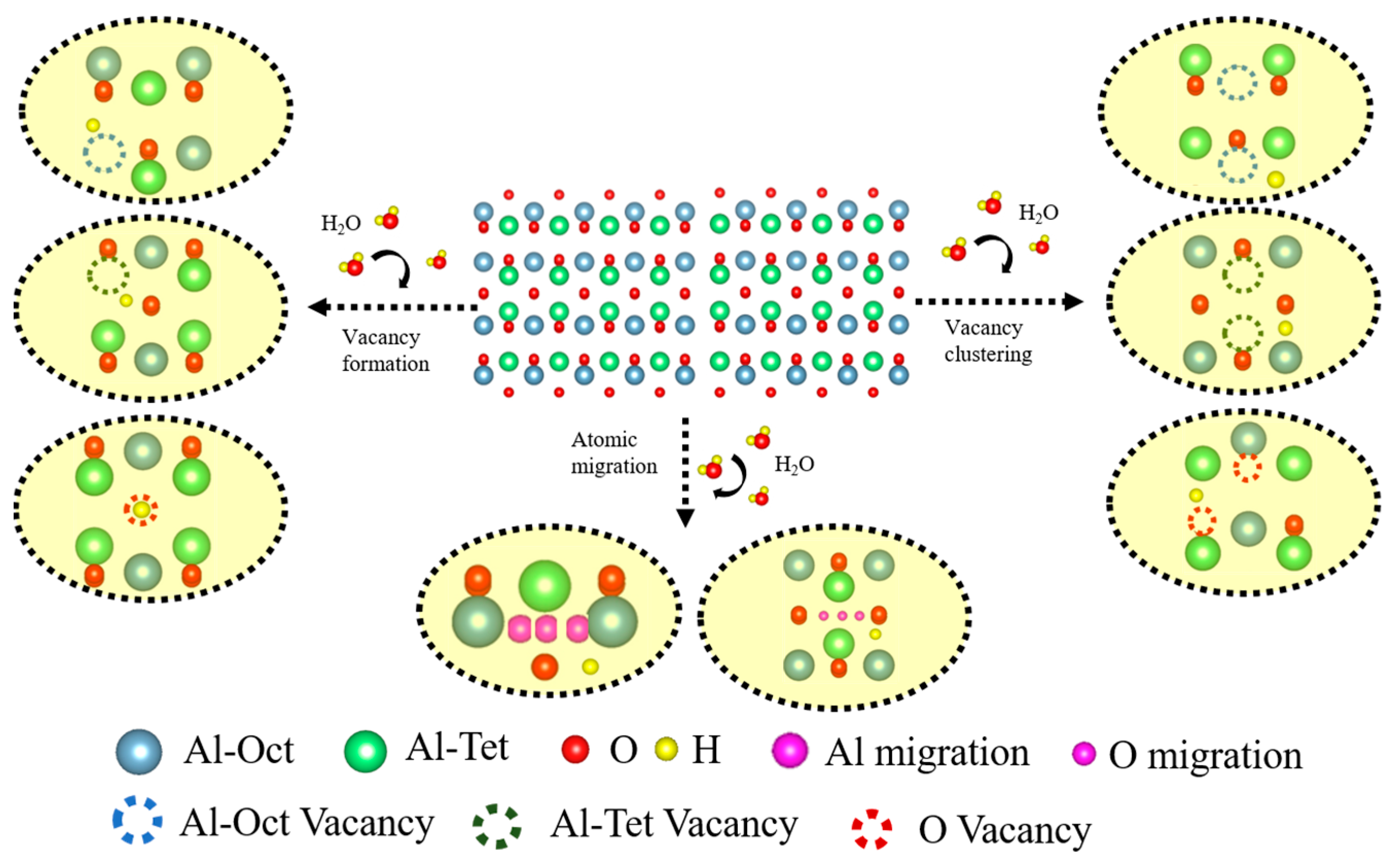
3.2. Vacancy Formation and Lattice Distortion
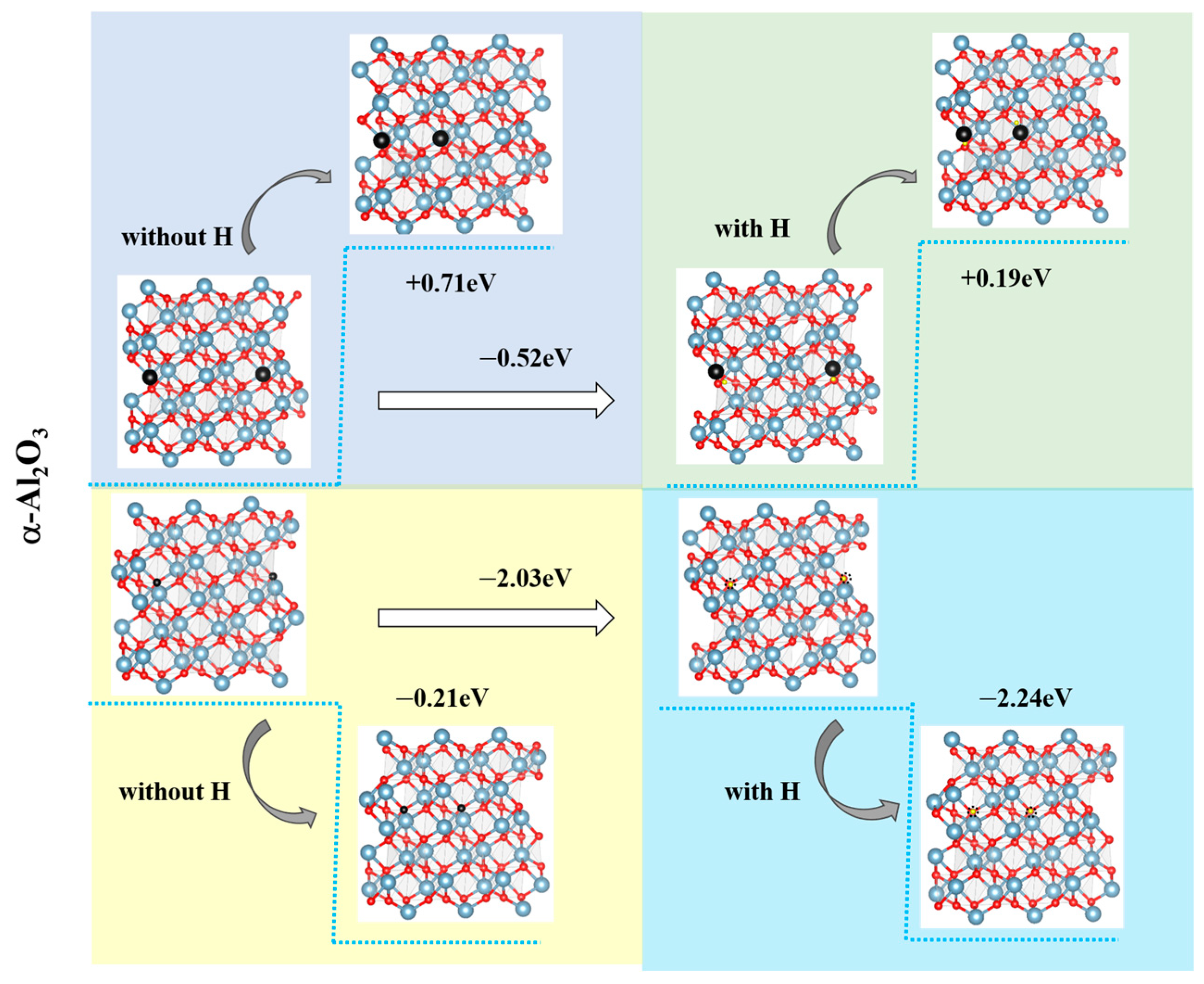
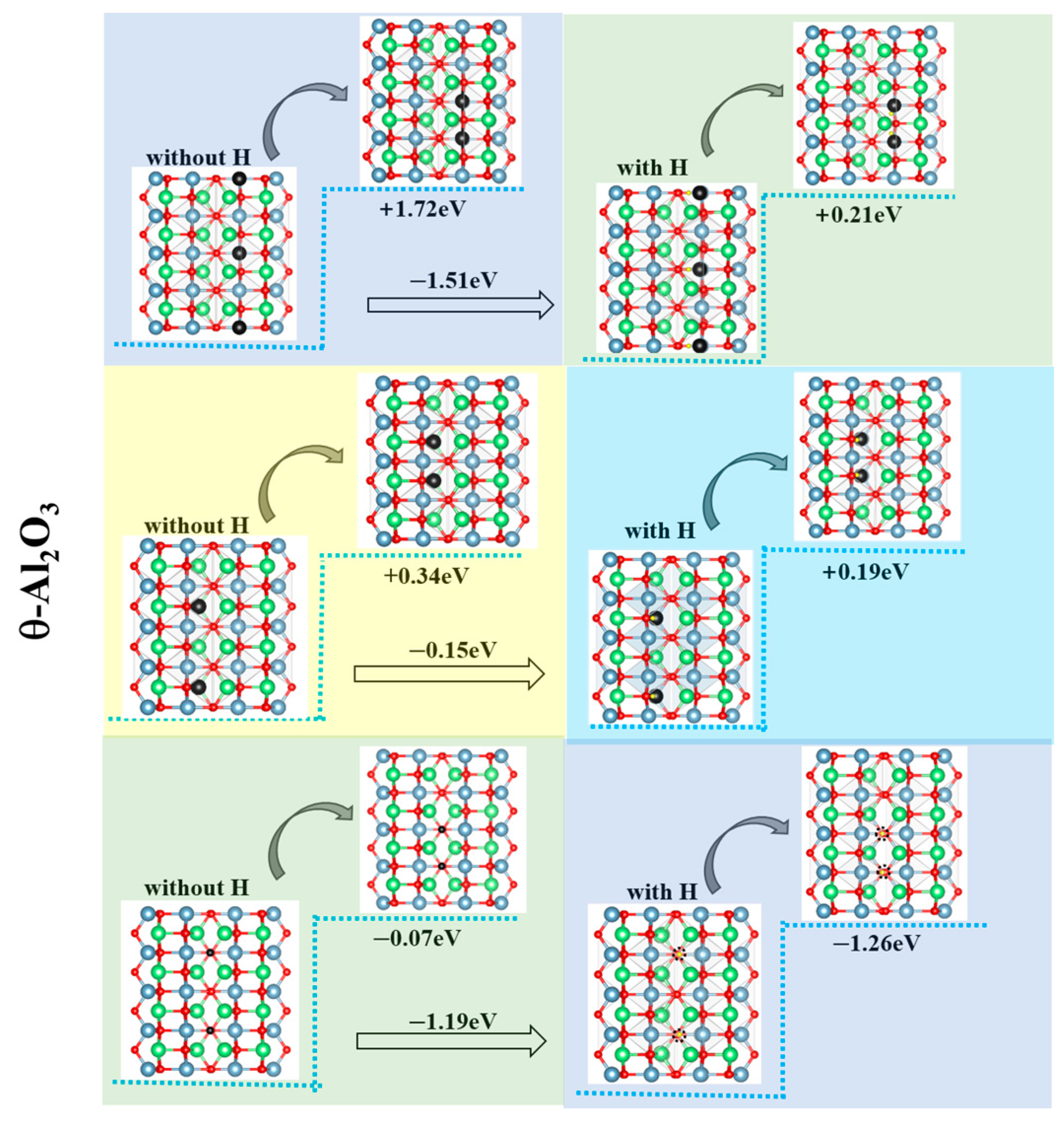
3.3. Vacancy Aggregation Behavior
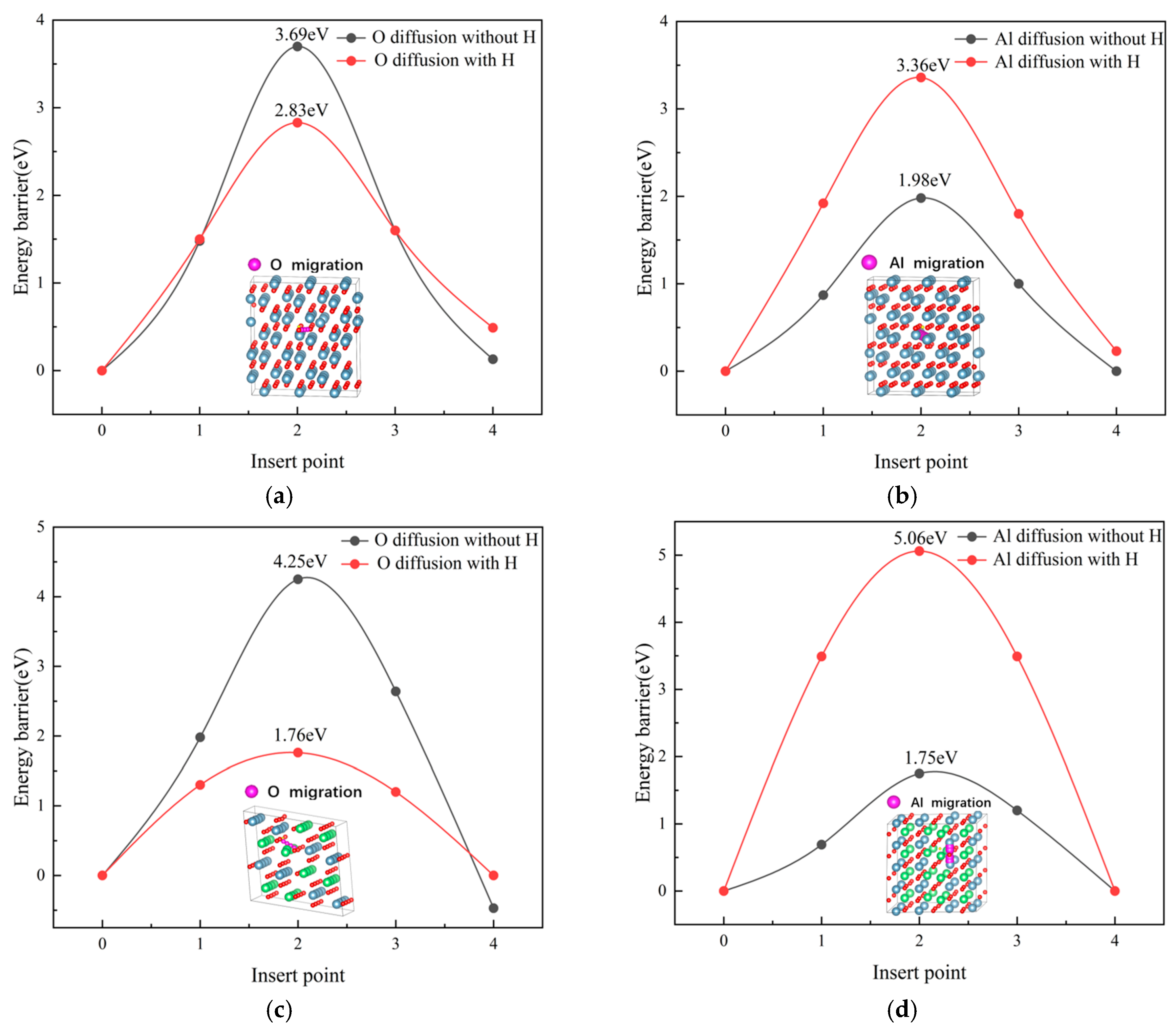
3.4. Atomic Migration in Alumina Phases
3.5. Alumina Growth with H Proton Incorporation
4. Concluding Remarks
- Hydrogen protons significantly reduce the formation energies of aluminum (Al) and oxygen (O) vacancies in both α-Al2O3 and θ-Al2O3. This promotes the generation of tetrahedral Al vacancies (VAl-tet), octahedral Al vacancies (VAl-oct), and O vacancies (VO). The resulting local lattice disordering stabilizes metastable alumina phases by mimicking their defect-rich structures, enabling the transient growth of metastable θ-Al2O3 under operational conditions.
- Hydrogen preferentially occupies O vacancy sites in both α-Al2O3 and θ-Al2O3, while stabilizing near Al vacancies at low-energy configurations. High H concentrations hinder O migration by saturating VO sites, disrupting the oxygen sublattice shear that is required for the θ- to α-Al2O3 transition. This inhibits the structural reorganization from a metastable face-centered cubic oxygen arrangement to the thermodynamically stable hexagonal close-packed α-Al2O3 structure.
- Hydrogen enhances the clustering of O vacancies while suppressing repulsion between Al vacancies. Aggregated O vacancies redistribute to form migration pathways for Al and O atoms, sustaining metastable phase growth by expanding oxygen sublattice disorder and defect-mediated Al mobility.
- Hydrogen suppresses Al migration but accelerates O diffusion in both phases. While enhanced O mobility facilitates metastable phase growth through defect propagation, the inhibition of Al migration prevents structural relaxation into the steady-state α-Al2O3 configuration. This kinetic imbalance perpetuates a disordered alumina matrix, favoring prolonged metastability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clarke, D.R.; Oechsner, M.; Padture, N.P. Thermal-Barrier Coatings for More Efficient Gas-Turbine Engines. MRS Bull. 2012, 37, 891–898. [Google Scholar] [CrossRef]
- Boissonnet, G.; Grégoire, B.; Bonnet, G.; Pedraza, F. Development of Thermal Barrier Coating Systems from Al Microparticles. Part I: Influence of Processing Conditions on the Mechanisms of Formation. Surf. Coat. Technol. 2019, 380, 125085. [Google Scholar] [CrossRef]
- Bo, C.; Jianjun, L.; Guosheng, A.; Wensheng, L.; Xinjiang, Z. Durable Columnar Structure Design for Thermal Barrier Coatings. Rare Met. Mater. Eng. 2022, 51, 1660–1666. [Google Scholar]
- Stefan, E.; Talic, B.; Larring, Y.; Gruber, A.; Peters, T.A. Materials Challenges in Hydrogen-Fuelled Gas Turbines. Int. Mater. Rev. 2022, 67, 461–486. [Google Scholar] [CrossRef]
- Cong, D.; Li, Z.; He, Q.; Chen, H.; Zhao, Z.; Zhang, L.; Wu, H. Wear Behavior of Corroded Al-Al2O3 Composite Coatings Prepared by Cold Spray. Surf. Coat. Technol. 2017, 326, 247–254. [Google Scholar] [CrossRef]
- Qiannan, T.A.O.; Yanrong, W.; Dasheng, W.E.I.; Shun, Y. Thermal Oxidation Description Methodology of Thermal Barrier Coatings on Gas Turbine Blades Considering Service Characteristics. Chin. J. Aeronaut. 2024, 37, 410–424. [Google Scholar]
- Mora-García, A.G.; Ruiz-Luna, H.; Alvarado-Orozco, J.M.; Mondragón-Rodríguez, G.C.; Schulz, U.; Muñoz-Saldaña, J. Microstructural Analysis after Furnace Cyclic Testing of Pre-Oxidized ReneN5/(Ni, Pt) Al/7YSZ Thermal Barrier Coatings. Surf. Coat. Technol. 2020, 403, 126376. [Google Scholar] [CrossRef]
- Zhao, W.; Gleeson, B. Assessment of the Detrimental Effects of Steam on Al2O3-Scale Establishment. Oxid. Met. 2015, 83, 607–627. [Google Scholar] [CrossRef]
- Jang, S.; Gun Oh, D.; Kim, H.; Hyun Kim, K.; Khivantsev, K.; Kovarik, L.; Hun Kwak, J. Controlling the Phase Transformation of Alumina for Enhanced Stability and Catalytic Properties. Angew. Chem. 2024, 136, e202400270. [Google Scholar] [CrossRef]
- Götlind, H.; Liu, F.; Svensson, J.-E.; Halvarsson, M.; Johansson, L.-G. The Effect of Water Vapor on the Initial Stages of Oxidation of the FeCrAl Alloy Kanthal AF at 900 C. Oxid. Met. 2007, 67, 251–266. [Google Scholar] [CrossRef]
- Rudolph, M.; Salomon, A.; Schmidt, A.; Motylenko, M.; Zienert, T.; Stöcker, H.; Himcinschi, C.; Amirkhanyan, L.; Kortus, J.; Aneziris, C.G. Thermally Induced Formation of Transition Aluminas from Boehmite. Adv. Eng. Mater. 2017, 19, 1700141. [Google Scholar] [CrossRef]
- Busca, G. The Surface of Transitional Aluminas: A Critical Review. Catal. Today 2014, 226, 2–13. [Google Scholar] [CrossRef]
- Kovarik, L.; Bowden, M.; Szanyi, J. High Temperature Transition Aluminas in δ-Al2O3/θ-Al2O3 Stability Range. J. Catal. 2021, 393, 357–368. [Google Scholar] [CrossRef]
- Kang, S.; Zhao, X.; Guo, J.; Liang, J.; Sun, J.; Yang, Y.; Yang, L.; Liao, R.; Randall, C.A. Thermal-Assisted Cold Sintering Study of Al2O3 Ceramics: Enabled with a Soluble γ-Al2O3 Intermediate Phase. J. Eur. Ceram. Soc. 2023, 43, 478–485. [Google Scholar] [CrossRef]
- Brumm, M.W.; Grabke, H.J. The Oxidation Behaviour of NiAl-I. Phase Transformations in the Alumina Scale during Oxidation of NiAl and NiAl-Cr Alloys. Corros. Sci. 1992, 33, 1677–1690. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, H.; Zhao, K.; Jia, W.; Fang, L. Influence of Inhomogeneous Thermally Grown Oxide Thickness on Residual Stress Distribution in Thermal Barrier Coating System. Ceram. Int. 2018, 44, 16937–16946. [Google Scholar] [CrossRef]
- Lee, K.N.; Garg, A.; Jennings, W.D. Effects of the Chemistry of Coating and Substrate on the Steam Oxidation Kinetics of Environmental Barrier Coatings for Ceramic Matrix Composites. J. Eur. Ceram. Soc. 2021, 41, 5675–5685. [Google Scholar] [CrossRef]
- Tolpygo, V.K.; Clarke, D.R. Microstructural Study of the Theta-Alpha Transformation in Alumina Scales Formed on Nickel-Aluminides. Mater. High Temp. 2000, 17, 59–70. [Google Scholar] [CrossRef]
- Zhang, X.; Ji, Y.; Chen, L.-Q.; Wang, Y. First-Principles Calculations of γ-Al2O3/Al Interfaces. Acta Mater. 2023, 252, 118786. [Google Scholar] [CrossRef]
- Sakakibara, M.; Hanaya, M.; Nakamuro, T.; Nakamura, E. Nondeterministic Dynamics in the η-to-θ Phase Transition of Alumina Nanoparticles. Science 2025, 387, 522–527. [Google Scholar] [CrossRef]
- Alnaeli, M.; Alnajideen, M.; Navaratne, R.; Shi, H.; Czyzewski, P.; Wang, P.; Eckart, S.; Alsaegh, A.; Alnasif, A.; Mashruk, S. High-Temperature Materials for Complex Components in Ammonia/Hydrogen Gas Turbines: A Critical Review. Energies 2023, 16, 6973. [Google Scholar] [CrossRef]
- Chen, K.; Seo, D.; Canteenwalla, P. The Effect of High-Temperature Water Vapour on Degradation and Failure of Hot Section Components of Gas Turbine Engines. Coatings 2021, 11, 1061. [Google Scholar] [CrossRef]
- Brossard, M.; Bouchaud, B.; Pedraza, F. Influence of Water Vapour on the Oxidation Behaviour of a Conventional Aluminide and a New Thermal Barrier Coating System Sintered from a Slurry. Mater. Corros. 2014, 65, 161–168. [Google Scholar] [CrossRef]
- Allo, J.; Jouen, S.; Roussel, M.; Gibouin, D.; Sauvage, X. Influence of Sulfur and Water Vapor on High-Temperature Oxidation Resistance of an Alumina-Forming Austenitic Alloy. Oxid. Met. 2021, 95, 359–376. [Google Scholar] [CrossRef]
- Yan, K.; Guo, H.; Gong, S. High-Temperature Oxidation Behavior of Minor Hf Doped NiAl Alloy in Dry and Humid Atmospheres. Corros. Sci. 2013, 75, 337–344. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, X.; Zhao, J.; Lu, J.; Zhou, Y.; Cai, C.; Huang, J.; Zhou, G. Effect of Water Vapor on High-Temperature Oxidation of NiAl Alloy. Corros. Sci. 2020, 177, 108963. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, C.; Yuan, X.; Huang, T.; Song, P. The Role of High-Temperature Water Vapor on Oxidation Behavior for CoNiCrAlHf Alloys at 1100 °C. Mater. Charact. 2024, 210, 113829. [Google Scholar] [CrossRef]
- Bagwell, R.B.; Messing, G.L.; Howell, P.R. The Formation of α-Al2O3 from θ-Al2O3: The Relevance of a “Critical Size” and: Diffusional Nucleation or “Synchro-Shear”? J. Mater. Sci. 2001, 36, 1833–1841. [Google Scholar] [CrossRef]
- Huang, Y.; Peng, X.; Chen, X.-Q. The Mechanism of θ-to α-Al2O3 Phase Transformation. J. Alloys Compd. 2021, 863, 158666. [Google Scholar] [CrossRef]
- Ru, Q.; Qiu, X.L. The Electronic Structure and Mechanical Property of Alpha Al2O3 by First Principles Calculation. Mater Res Appl. 2009, 3, 162–167. [Google Scholar]
- Wang, X.-L.; Hubbard, C.R.; Alexander, K.B.; Becher, P.F.; Fernandez-Baca, J.A.; Spooner, S. Neutron Diffraction Measurements of the Residual Stresses in Al2O3-ZrO2 (CeO2) Ceramic Composites. J. Am. Ceram. Soc. 1994, 77, 1569–1575. [Google Scholar] [CrossRef]
- Ishizawa, N.; Miyata, T.; Minato, I.; Marumo, F.; Iwai, S. A Structural Investigation of α-Al2O3 at 2170 K. Struct. Sci. 1980, 36, 228–230. [Google Scholar] [CrossRef]
- Husson, E.; Repelin, Y. Structural Studies of Transition Aluminas. Theta Alumina. Eur. J. Solid State Inorg. Chem. 1996, 33, 1223–1231. [Google Scholar]
- Zhang, G.; Xiang, X.; Yang, F.; Peng, X.; Tang, T.; Shi, Y.; Wang, X. Helium Stability and Its Interaction with H in α-Al2O3: A First-Principles Study. Phys. Chem. Chem. Phys. 2016, 18, 1649–1656. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Lu, Y.; Wang, X. Hydrogen Interactions with Intrinsic Point Defects in Hydrogen Permeation Barrier of α-Al2O3: A First-Principles Study. Phys. Chem. Chem. Phys. 2014, 16, 17523–17530. [Google Scholar] [CrossRef]
- Zhou, H.; Ji, Y.; Wang, Y.; Feng, K.; Luan, B.; Zhang, X.; Chen, L.-Q. First-Principles Lattice Dynamics and Thermodynamic Properties of α-, θ-, κ-and γ-Al2O3 and Solid State Temperature-Pressure Phase Diagram. Acta Mater. 2024, 263, 119513. [Google Scholar] [CrossRef]
- Lei, Y.; Gong, Y.; Duan, Z.; Wang, G. Density Functional Calculation of Activation Energies for Lattice and Grain Boundary Diffusion in Alumina. Phys. Rev. B—Condens. Matter Mater. Phys. 2013, 87, 214105. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, G. Linking Diffusion Kinetics to Defect Electronic Structure in Metal Oxides: Charge-Dependent Vacancy Diffusion in Alumina. Scr. Mater. 2015, 101, 20–23. [Google Scholar] [CrossRef]
- Hinuma, Y.; Kamachi, T.; Hamamoto, N.; Takao, M.; Toyao, T.; Shimizu, K. Surface Oxygen Vacancy Formation Energy Calculations in 34 Orientations of β-Ga2O3 and θ-Al2O3. J. Phys. Chem. C 2020, 124, 10509–10522. [Google Scholar] [CrossRef]
- He, Q.; Liu, D.; Zhou, Y.; Sun, T.-Y.; Huang, L.-F. Nitride Coatings for Environmental Barriers: The Key Microscopic Mechanisms and Momentous Applications of First-Principles Calculations. Surf. Sci. Technol. 2024, 2, 24. [Google Scholar] [CrossRef]
- Henderson, M.A. The Interaction of Water with Solid Surfaces: Fundamental Aspects Revisited. Surf. Sci. Rep. 2002, 46, 1–308. [Google Scholar] [CrossRef]
- Salmeron, M.; Bluhm, H.; Tatarkhanov, M.; Ketteler, G.; Shimizu, T.K.; Mugarza, A.; Deng, X.; Herranz, T.; Yamamoto, S.; Nilsson, A. Water Growth on Metals and Oxides: Binding, Dissociation and Role of Hydroxyl Groups. Faraday Discuss. 2009, 141, 221–229. [Google Scholar] [CrossRef]
- Chen, X.; Shan, W.; Wu, D.; Patel, S.B.; Cai, N.; Li, C.; Ye, S.; Liu, Z.; Hwang, S.; Zakharov, D.N. Atomistic Mechanisms of Water Vapor–Induced Surface Passivation. Sci. Adv. 2023, 9, eadh5565. [Google Scholar] [CrossRef] [PubMed]
- Xiang, X.; Yang, F.; Hu, L.; Zhang, G.; Chen, C. The Role of Carbon in the Formation of Intrinsic Point Defects and Hydrogen Migration in α-Al2O3-Based Tritium Permeation Barriers. Phys. Status Solidi B 2022, 259, 2200284. [Google Scholar] [CrossRef]
- Li, H.; Zhao, X.; Zhang, H.; Li, J.; Li, D. High-Temperature Oxidation of 60Si2Mn Spring Steel in Dry Air and Wet Air: Insights from an Experimental and First-Principles Study. Steel Res. Int. 2023, 94, 2200691. [Google Scholar] [CrossRef]
- Luo, L.; Su, M.; Yan, P.; Zou, L.; Schreiber, D.K.; Baer, D.R.; Zhu, Z.; Zhou, G.; Wang, Y.; Bruemmer, S.M. Atomic Origins of Water-Vapour-Promoted Alloy Oxidation. Nat. Mater. 2018, 17, 514–518. [Google Scholar] [CrossRef]
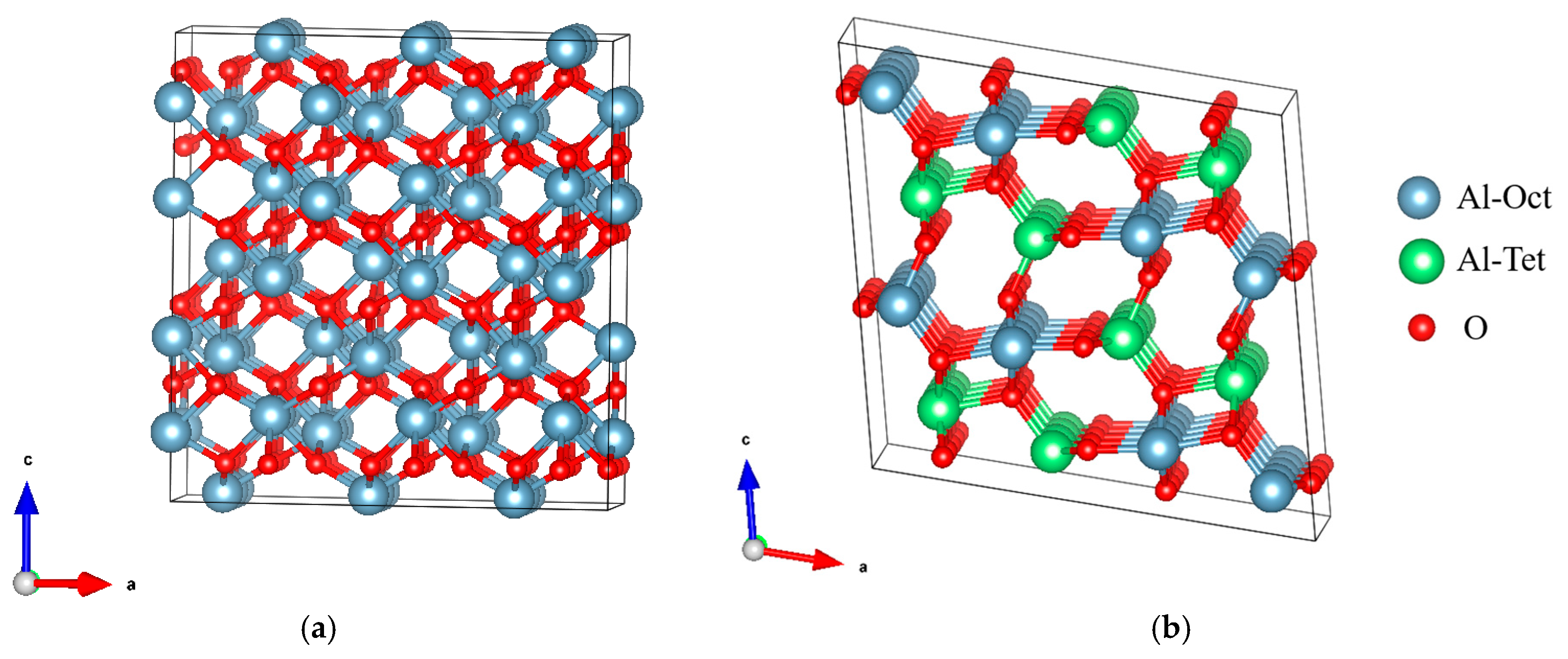
| Phase | Bulk Modulus (GPa) | Shear Modulus (GPa) | Young’s Modulus (GPa) | |
|---|---|---|---|---|
| α-Al2O3 | Present model | 223.26 | 165.75 | 399.56 |
| Reference | 220.63 [36] | 162.28 [36] | 390.98 [36] | |
| θ-Al2O3 | Present model | 201.74 | 142.67 | 343.35 |
| Reference | 199.04 [36] | 143.65 [36] | 347.38 [36] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, K.; Sun, S.; Yuan, B.; Guo, X.; Song, W.; Boiko, A.A. First-Principles Analysis of Phase Stability and Transformation Suppression for Hydrogen-Doped Alumina. Coatings 2025, 15, 545. https://doi.org/10.3390/coatings15050545
Lv K, Sun S, Yuan B, Guo X, Song W, Boiko AA. First-Principles Analysis of Phase Stability and Transformation Suppression for Hydrogen-Doped Alumina. Coatings. 2025; 15(5):545. https://doi.org/10.3390/coatings15050545
Chicago/Turabian StyleLv, Kun, Shiyang Sun, Bo Yuan, Xiaofeng Guo, Weiao Song, and Andrei A. Boiko. 2025. "First-Principles Analysis of Phase Stability and Transformation Suppression for Hydrogen-Doped Alumina" Coatings 15, no. 5: 545. https://doi.org/10.3390/coatings15050545
APA StyleLv, K., Sun, S., Yuan, B., Guo, X., Song, W., & Boiko, A. A. (2025). First-Principles Analysis of Phase Stability and Transformation Suppression for Hydrogen-Doped Alumina. Coatings, 15(5), 545. https://doi.org/10.3390/coatings15050545








