A Resource Composition Optimization Algorithm Based on Improved Polar Bear Optimization Algorithm for Manufacturing Wallboard for Coating Machine
Abstract
1. Introduction
- The results of the evaluation of wallboard manufacturing resources are subjective and inadequately supported by data.
- There is a lack of models and efficient solution algorithms related to the actual production of wallboards.
- Based on the actual production research, the processing technology of the wallboard is analyzed, and the task decomposition of wallboard manufacturing process level is realized.
- A manufacturing resource composition evaluation indicator system for wallboards is proposed, and a non-cooperative game decision is used to construct a wallboard manufacturing resource composition optimization model.
- The PBO algorithm is improved from two perspectives: adaptive horizon and mutation strategy, and the IPBO algorithm is applied to solve the model.
2. Materials and Methods
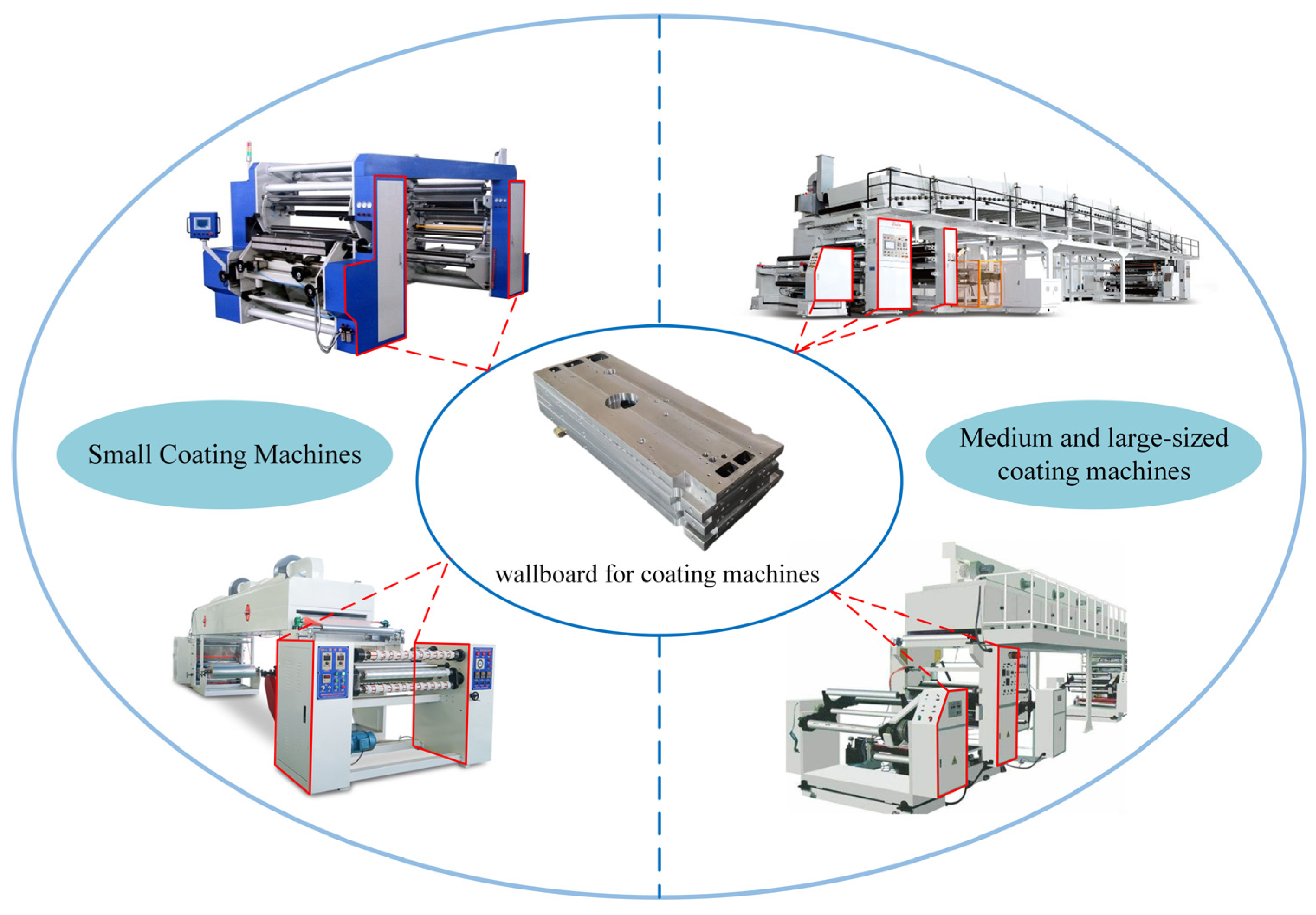
2.1. Materials
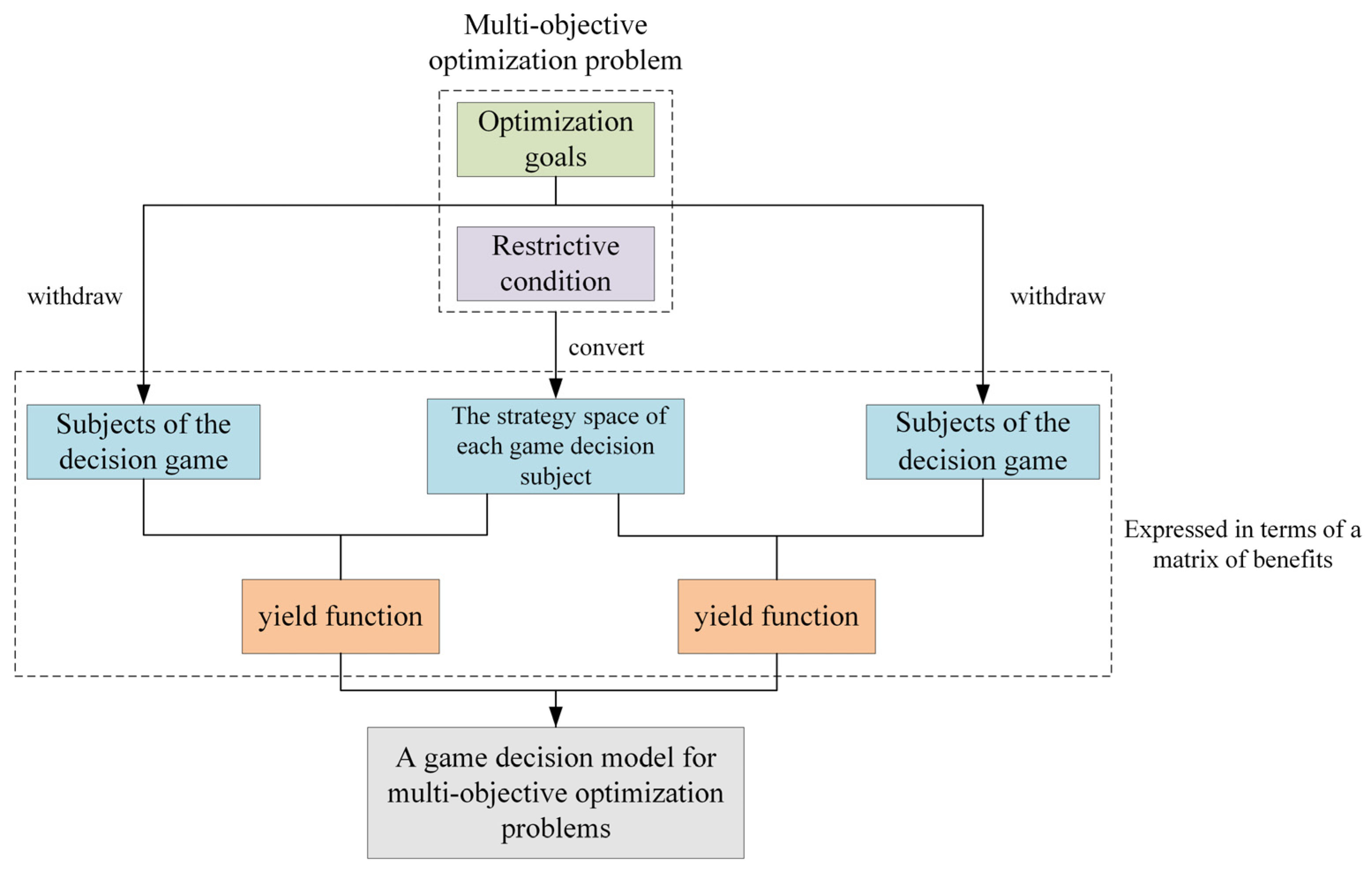
2.2. Analysis of Wallboard Resource Composition Optimization Issues
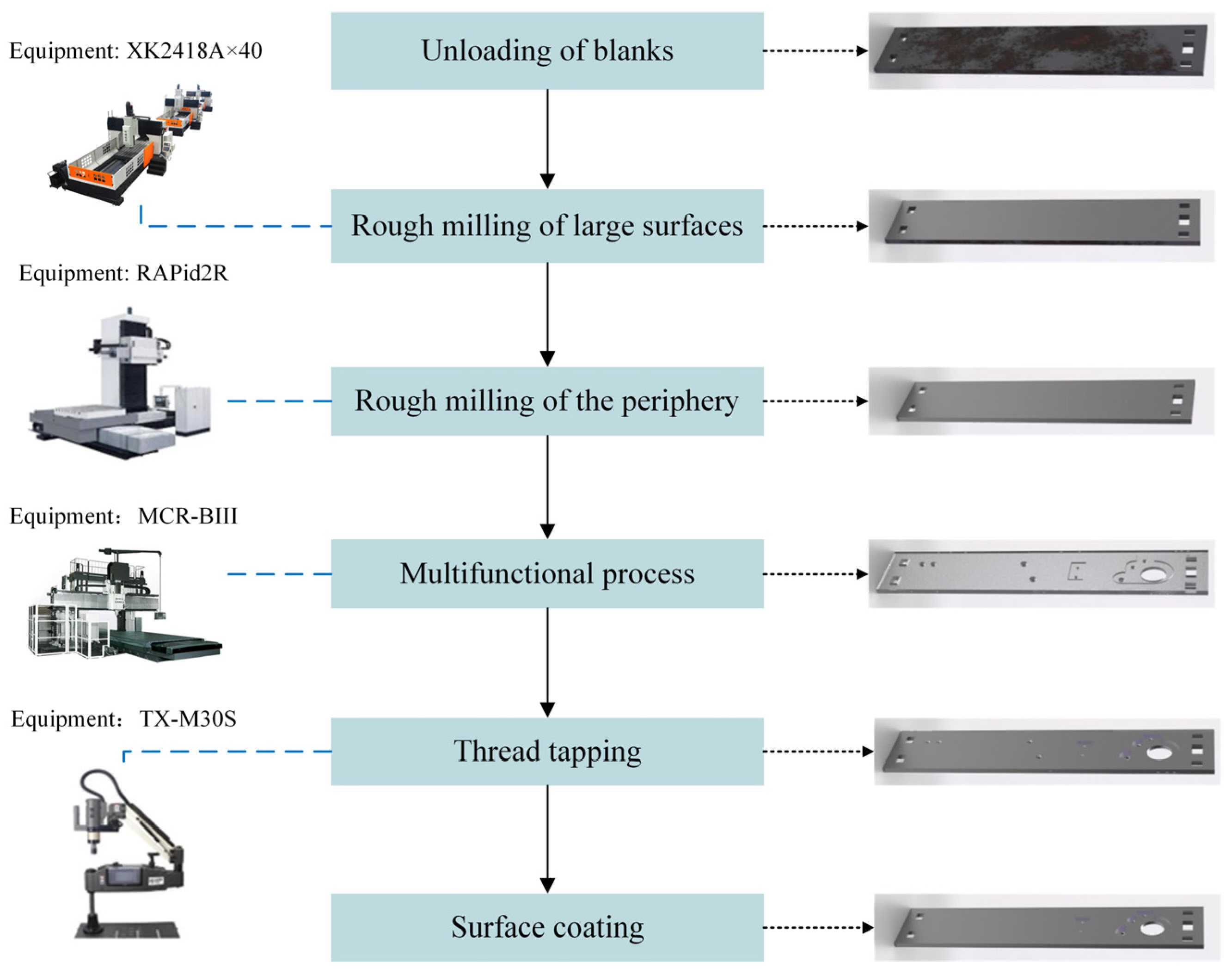
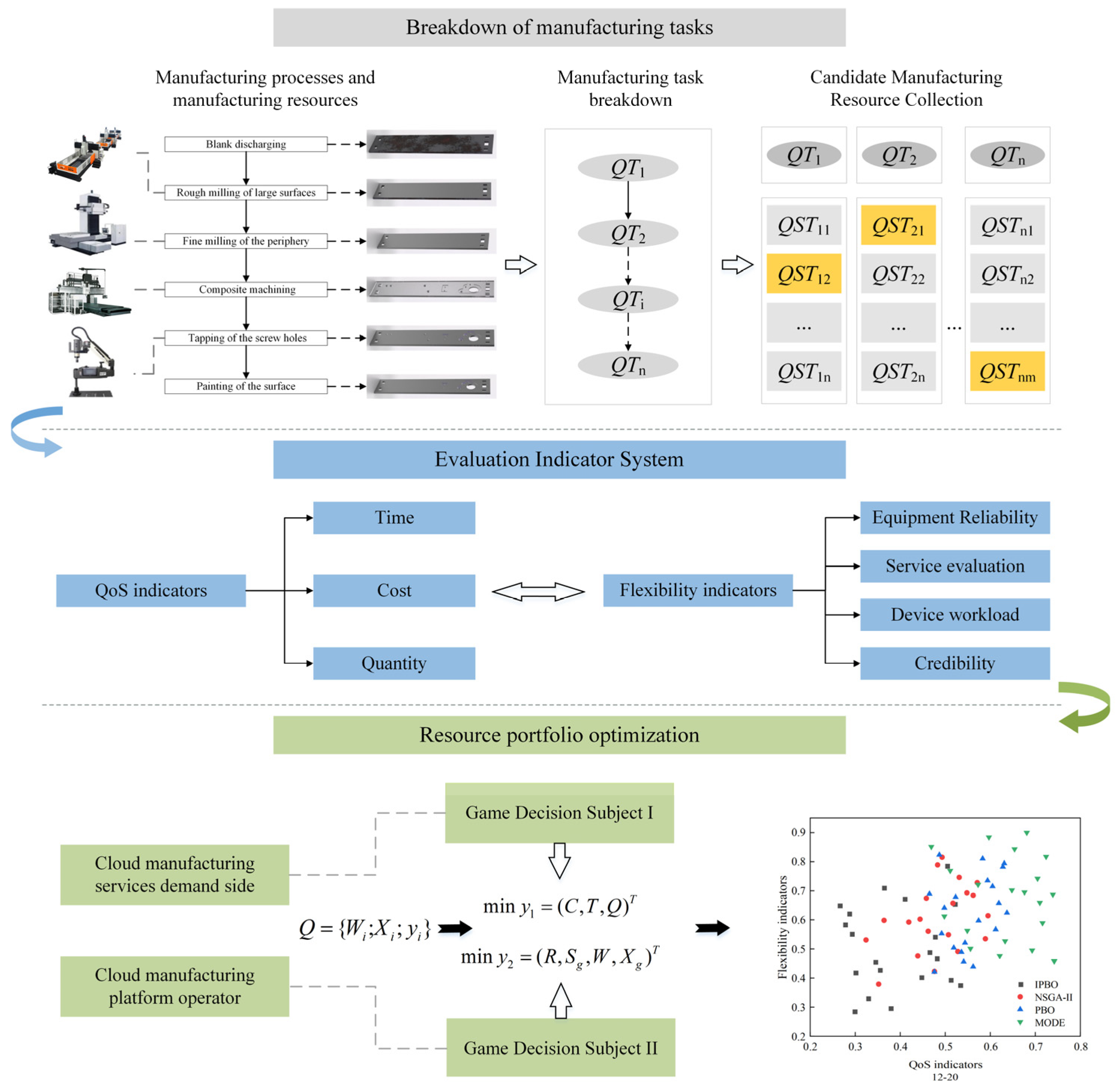
- Manufacturing resource analysis and task decomposition: Based on the wallboard manufacturing requirements put forward by the user, the cloud platform first disassembles the overall manufacturing task into multiple process manufacturing sub-tasks, and then carries out the subsequent processing based on the functional and non-functional attributes of these process manufacturing sub-tasks. Match the manufacturing resources that satisfy the wallboard processing requirements and form the set of candidate manufacturing resources QTi, QTi = {QSTi,1, QSTi,2, QSTi,3, …, QSTi,n}, where QTi denotes the set of wallboard manufacturing resources corresponding to the ith wallboard manufacturing process sub-task, and QSTi,j denotes the ith candidate wallboard manufacturing resource and the jth wallboard manufacturing resource in the set.
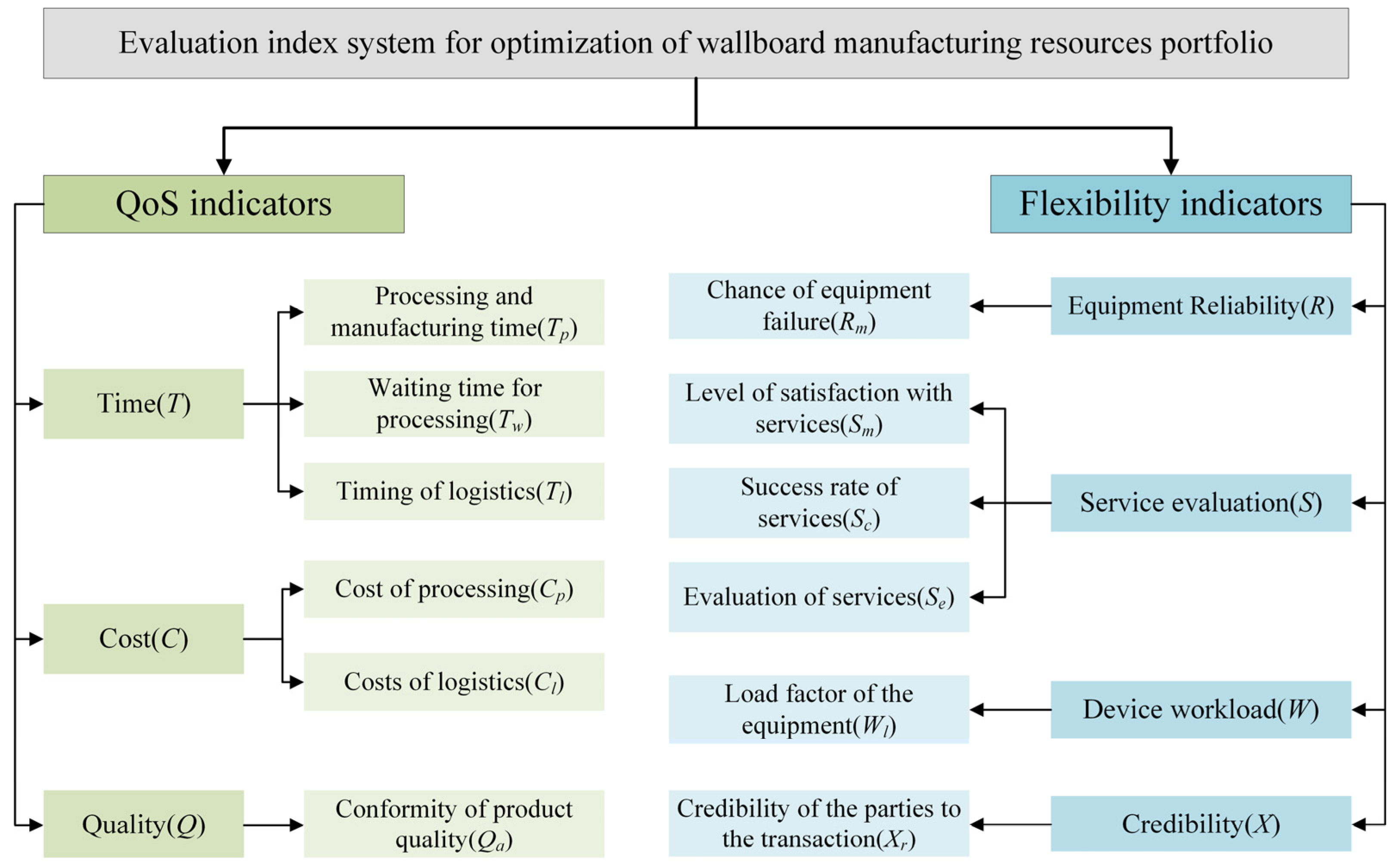
- Construct a manufacturing resource composition optimization indicator system: Constructing a reasonable indicator system can help organizations and individuals optimize resource allocation more effectively and promote continuous improvement. From the aspects of QoS indicators and flexibility indicators, consider the common interests of the demand side and the operation side, and construct a portfolio optimization assessment indicator system.
- Manufacturing resource composition optimization method: In order to meet the demand of manufacturing tasks, these manufacturing resources are combined to complete the manufacturing tasks together. The non-cooperative game idea is used to construct the manufacturing resource composition optimization model, and the IPBO algorithm is used to solve the problem of composition optimization of manufacturing resources.
2.3. Wallboard Manufacturing Resource Composition Optimization Evaluation Indicator System
2.4. A Resource Composition Optimization Model for Cloud Manufacturing of Wallboards Based on Non-Cooperative Game
- A single game decision subject model for QoS indicators:
- 2.
- A single game decision subject model with flexible indicators:
- 3.
- A resource composition optimization model for cloud manufacturing of wallboards:
2.5. PBO Algorithm
2.5.1. Global Search
2.5.2. Local Search
2.5.3. Reproduction and Death
2.6. Composition Optimization Method Based on IPBO Algorithm
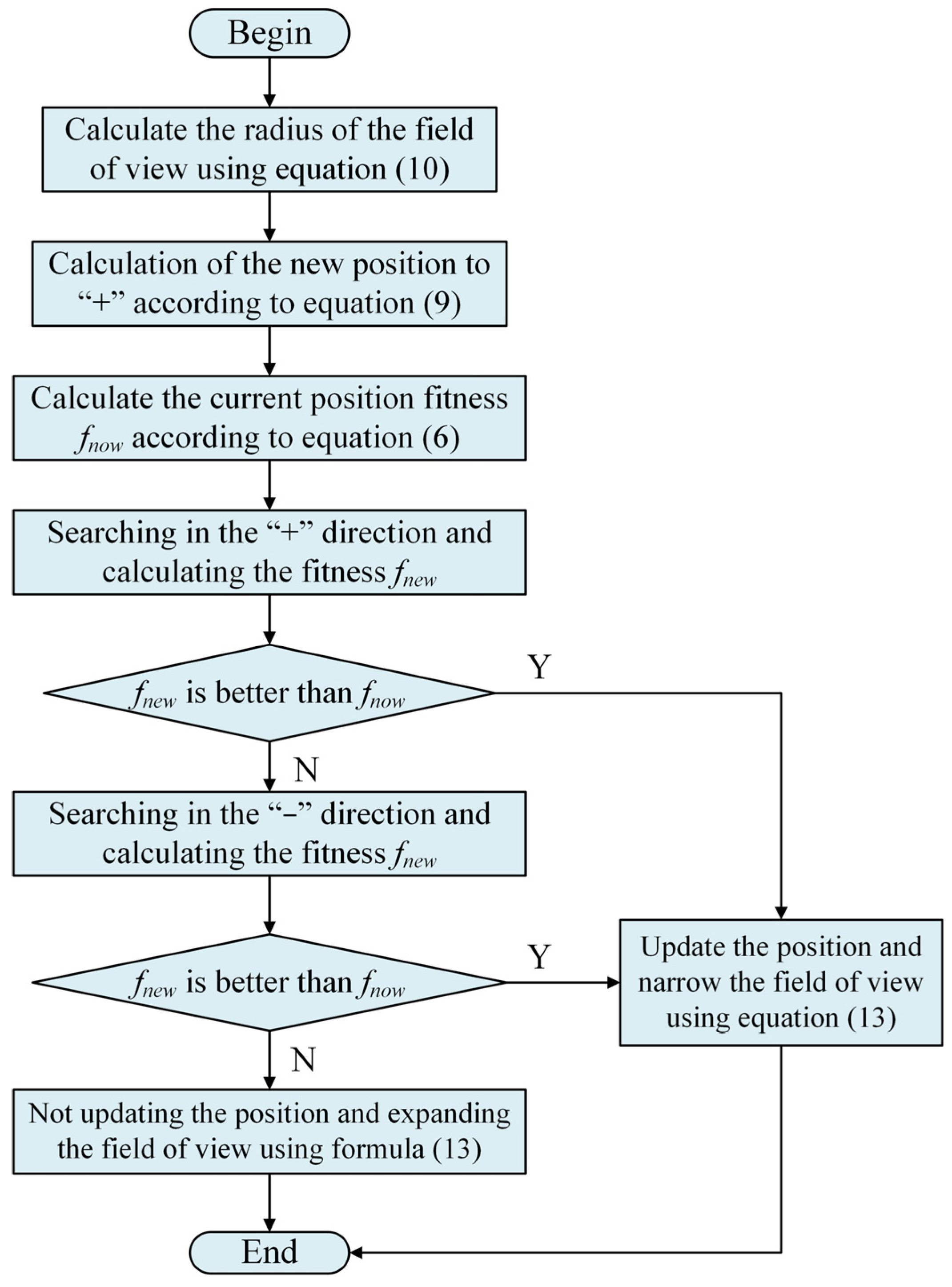
2.6.1. Adaptive Field of View
2.6.2. Strategy of Variation
2.6.3. IPBO Algorithm
3. Results
3.1. Algorithm Performance Comparison
- The hypervolume indicator, HV [31], measures the volume of the target space constituted between the non-dominated solution set and a reference point, and a larger value of HV indicates better convergence and diversity of the solution set, i.e., better overall performance of the algorithm. The specific expression is shown in Equation (14), where is the Lebesgue used to measure the volume, S denotes the set of non-dominated solutions, |S| denotes the number of non-dominated solutions, and vi denotes the hypervolume formed by the reference point and the ith solution in the solution set.
- Generation distance GD is an indicator used to evaluate the convergence of multi-objective optimization algorithms [32]. The smaller the value of GD—indicating that the solution is closer to the real Pareto solution set—the better the convergence performance. The specific expression is shown in Equation (15), where P is the set of non-dominated solutions on the frontier derived by the algorithm, P* denotes the solutions distributed on the optimal Pareto frontier, d(a, b) denotes the minimum Euclidean distance between the two decision-making subjects of the game, and P is the total number of solutions on the Pareto frontier obtained.
- Inverse generation distance (IGD) calculates the average value of the distance between each solution in the solution set and the true preamble [33]. The distribution of the solution set is also taken into account, and the smaller value of IGD reflects the better overall performance of the algorithm in terms of convergence and diversity, as shown in the expression in Equation (16).
3.2. Arithmetic Analysis
3.3. Examples of Scaling up
4. Discussion
5. Conclusions
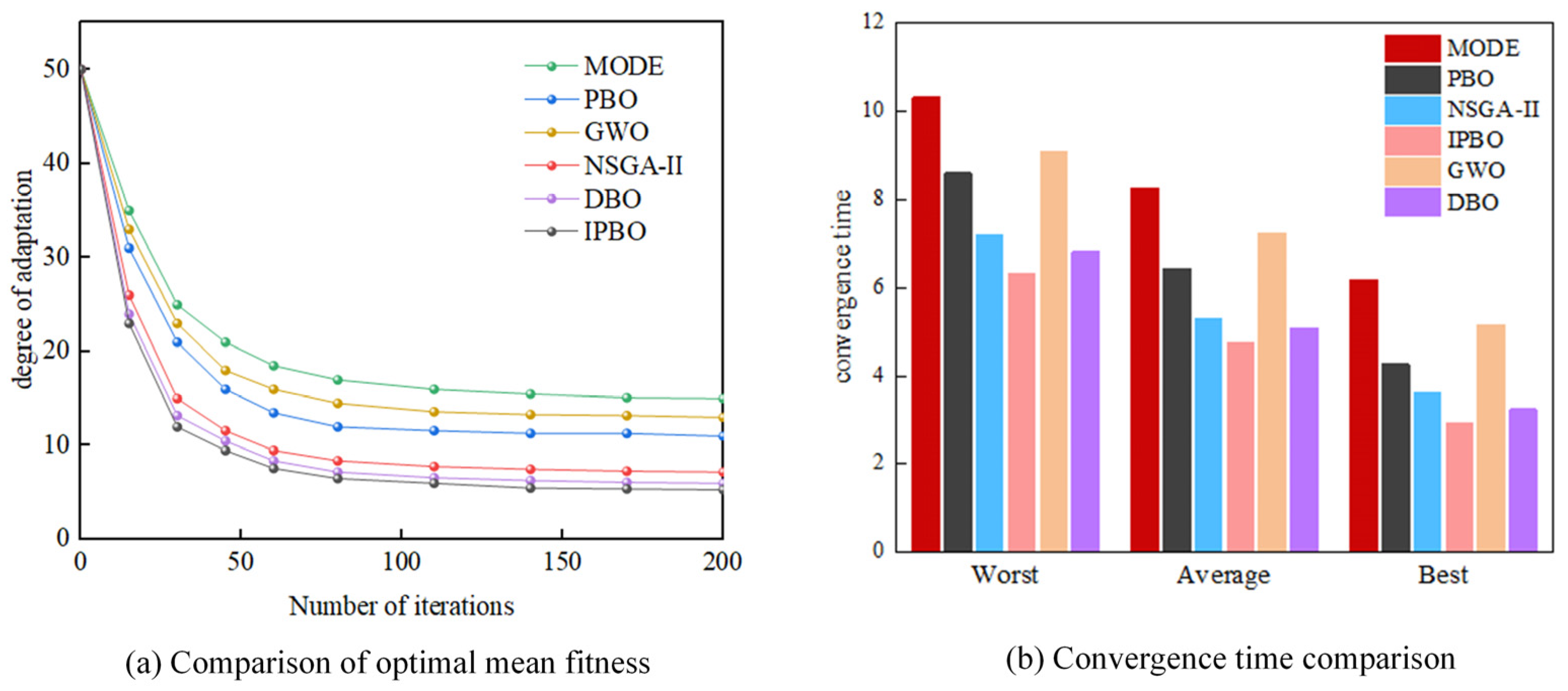
- With the same number of iterations and population size of the test function, compared to the NSGA-II algorithm, PBO algorithm, DBO algorithm, GWO algorithm, and MODE algorithm, the IPBO algorithm has a lower GD value under six conditions, with a minimum of 2.96 × 10−3 under the DTLZ1 function; a lower IGD value under seven conditions, with a minimum of 3.06 × 10−3 under the C-DTLZ1 function of 3.06 × 10−3; and high HV values under six conditions, with a maximum value of 9.24 × 10−1 under the DTLZ1 function. This further illustrates the effectiveness of the IPBO algorithm in solving such problems.
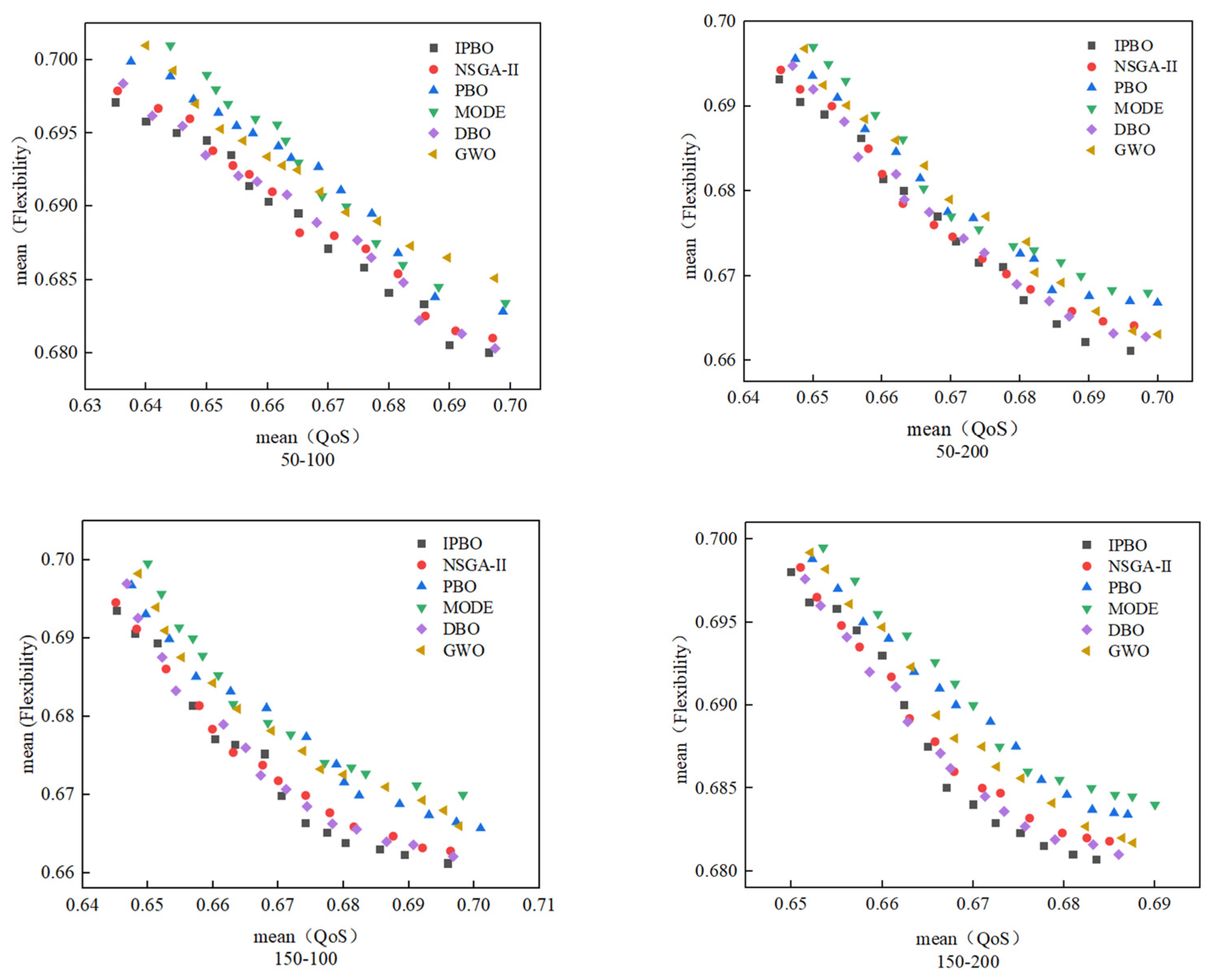
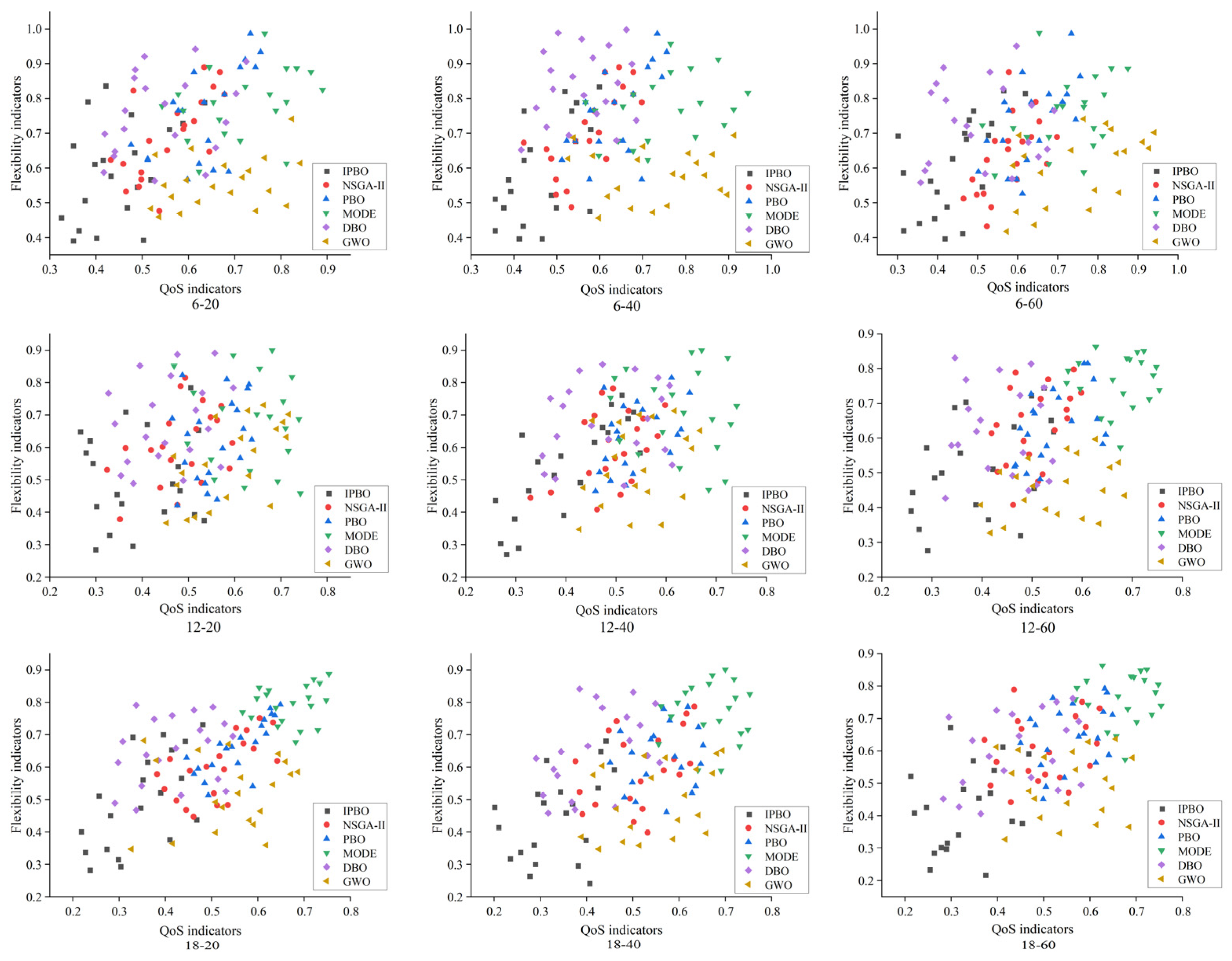
- The IPBO algorithm has lower fitness under specific iteration and population size conditions, with the fitness function leveling off as the number of iterations approaches 70. It also has faster convergence, with an optimal convergence time of only 2.94 s, which is a 9.26% reduction in the optimal convergence time compared to the suboptimal DBO algorithm. The average convergence time is reduced by 6.51%. Moreover, for the conditions set in Conclusion I, the Pareto frontier distribution of the IPBO algorithm for most of the test points is more in line with the preference criteria in the modeling, with smaller flexibility indicator values for smaller QoS indicator values.
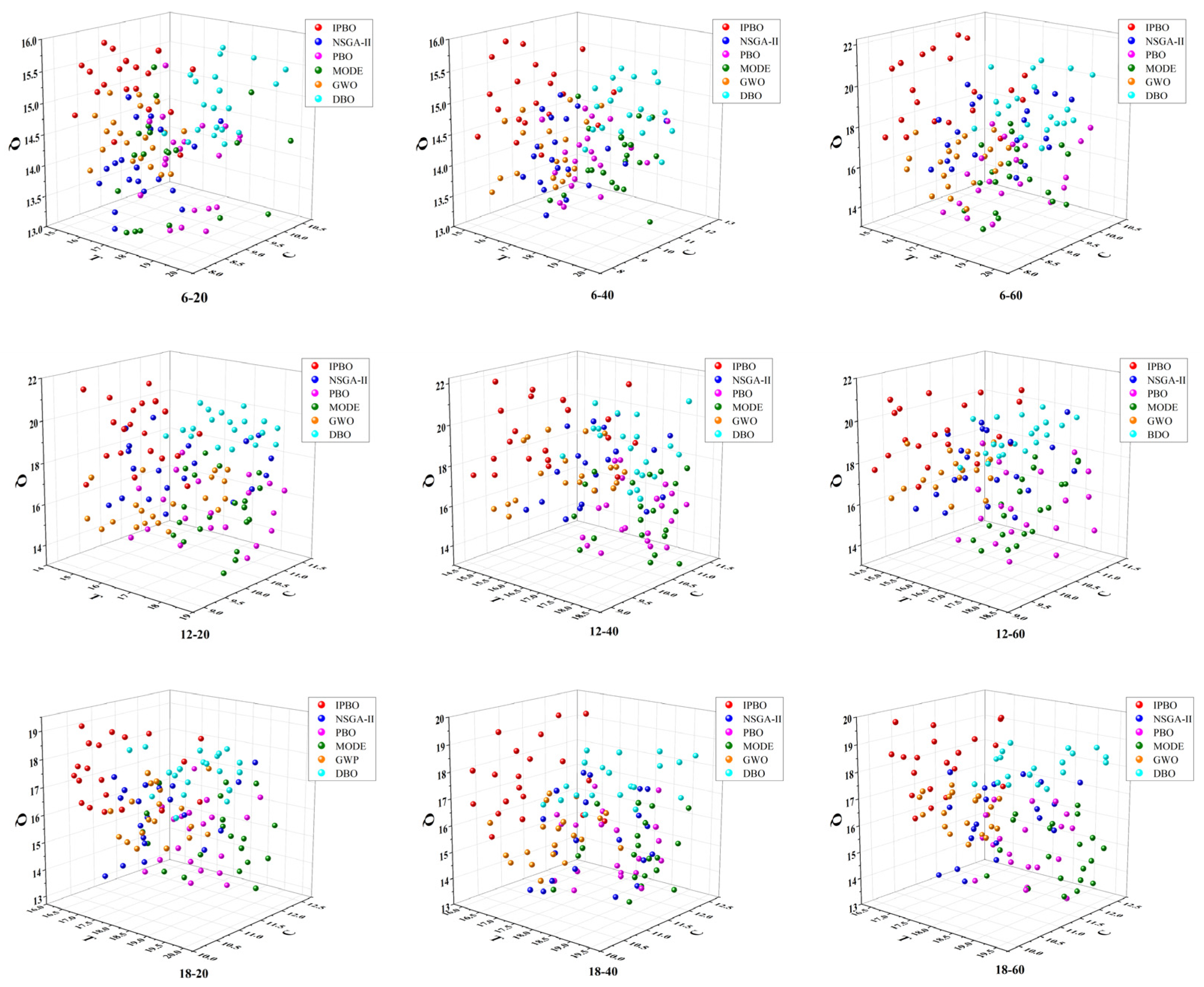
- Expanding the problem to the manufacturing of wallboards for nine different sizes of coating machines, the QoS values of the four algorithms were compared, which can positively reflect the benefit of the demand side of the service. On the basis of six processes, twelve processes, and eighteen processes, the time indicators of the IPBO algorithms are all concentrated in (14–17) h, (15–18) h, and (17–19) h; the cost indicators are all concentrated in (8–9), (9–10.5), and (10–12); and the quality indicators are all concentrated in (14–16), (17–22), and (16–20). At the same time, through normalization, the IPBO algorithm obtains smaller values for the flexibility indicator, concentrated between (0.25–0.75).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, X. Optimized Configuration of Manufacturing Resources for Middle and Lower Batch Customization Enterprises in Cloud Manufacturing Environment. Complexity 2020, 2020, 5619758. [Google Scholar]
- Mou, J. Multi-Objective Optimization for Resource Allocation in Intelligent Manufacturing. Int. J. Simul. Model. 2024, 23, 359–370. [Google Scholar]
- Song, C.; Zheng, H.; Han, G. Cloud edge collaborative service composition optimization for intelligent manufacturing. IEEE Trans. Ind. Inform. 2022, 19, 6849–6858. [Google Scholar]
- Tong, H.; Zhu, J. New peer effect-based approach for service matching in cloud manufacturing under uncertain preferences. Appl. Soft Comput. 2020, 94, 106444. [Google Scholar]
- Li, X.; Fang, Z.; Yin, C. A machine tool matching method in cloud manufacturing using Markov Decision Process and cross-entropy. Robot. Comput. Integr. Manuf. 2020, 65, 101968. [Google Scholar]
- Bouzary, H.; Chen, F.F. A classification-based approach for integrated service matching and composition in cloud manufacturing. Robot. Comput. Integr. Manuf. 2020, 66, 101989. [Google Scholar]
- Xiao, Y.; Li, C.; Song, L.; Yang, J.; Su, J. A multidimensional information fusion-based matching decision method for manufacturing service resource. IEEE Access 2021, 9, 39839–39851. [Google Scholar]
- Liu, S.; Zhang, Z.; Jiang, X. An Optimal Selection Method of Cloud Manufacturing Resource for Guide Roller based on Combination Algorithm. J. Imaging Sci. Technol. 2024, 68, 1–10. [Google Scholar]
- Shi, K.; Liu, S.; Zhang, Z.; Qian, S.; Zhu, L.; Zhang, H. optimization Method of Sewing Machine Case Manufacturing Resources Sets. In Proceedings of the 2023 IEEE 3rd International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Chongqing, China, 26–28 May 2023; Volume 3, pp. 1530–1534. [Google Scholar]
- Rodriguez-Mier, P.; Mucientes, M.; Lama, M. Hybrid optimization algorithm for large-scale QoS-aware service composition. IEEE Trans. Serv. Comput. 2015, 10, 547–559. [Google Scholar]
- Du, Z.; Miao, H. Research on edge service composition method based on BAS algorithm. Comput. Intell. Neurosci. 2021, 2021, 9931689. [Google Scholar]
- Li, T.; Zhang, Y.; Li, K.; Li, Y.; Ma, X. A multi-objective optimization algorithm based on subgroup stratified coarse-grained model and its application. Comput. Electr. Eng. 2021, 92, 107180. [Google Scholar]
- Meng, Y.; Sun, X.; Dong, S.; Wang, Y.; Liu, X. Cutting energy consumption modelling of end milling cutter coated with AlTiCrN. Coatings 2023, 13, 679. [Google Scholar] [CrossRef]
- Zhe, Z.; Chen, Y.; Lyu, S. Virtualization of Manufacturing Resources in Cloud Manufacturing Environment. In Proceedings of the 2019 International Conference on Robotics, Intelligent Control and Artificial Intelligence, Shanghai, China, 20–22 September 2019; pp. 83–88. [Google Scholar]
- Liu, X.; Luo, J. A dynamic multi-objective optimization model with interactivity and uncertainty for real-time reservoir flood control operation. Appl. Math. Model. 2019, 74, 606–620. [Google Scholar]
- Rahmani, S.; Amjady, N. Enhanced goal attainment method for solving multi-objective security-constrained optimal power flow considering dynamic thermal rating of lines. Appl. Soft Comput. 2019, 77, 41–49. [Google Scholar]
- Liang, H.; Wen, X.; Liu, Y.; Zhang, H.; Zhang, L.; Wang, L. Logistics-involved QoS-aware service composition in cloud manufacturing with deep reinforcement learning. Robot. Comput. Integr. Manuf. 2021, 67, 101991. [Google Scholar]
- Zhou, L.; Zhang, L.; Horn, B.K.P. Collaborative optimization for logistics and processing services in cloud manufacturing. Robot. Comput. Integr. Manuf. 2021, 68, 102094. [Google Scholar]
- Zhao, C.; Ma, C.; Zhang, H.; Ma, Z.; Yang, J.; Li, M.; Wang, X.; Lv, Q. Modeling manufacturing resources based on manufacturability features. Sci. Rep. 2022, 12, 10775. [Google Scholar]
- Verma, S.; Pant, M.; Snasel, V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar]
- Geng, Z.; Kong, W.; Wang, X. Adaptive search based Grey Wolf optimization algorithm for multi-objective optimization of ethylene cracking furnace. Swarm Evol. Comput. 2025, 92, 101810. [Google Scholar]
- Kaya, E.; Gorkemli, B.; Akay, B.; Karaboga, D. A review on the studies employing artificial bee colony algorithm to solve combinatorial optimization problems. Eng. Appl. Artif. Intell. 2022, 115, 105311. [Google Scholar]
- Polap, D.; Wozniak, M. Polar bear optimization algorithm: Meta-heuristic with fast population movement and dynamic birth and death mechanism. Symmetry 2017, 9, 203. [Google Scholar] [CrossRef]
- Iqbal, M.M.; Zia, M.F.; Beddiar, K.; Benbouzid, M. Optimal scheduling of grid transactive home demand responsive appliances using polar bear optimization algorithm. IEEE Access 2020, 8, 222285–222296. [Google Scholar]
- Fayyaz, S.; Sattar, M.K.; Waseem, M.; Ashraf, M.U.; Ahmad, A.; Hussain, H.A.; Alsubhi, K. Solution of combined economic emission dispatch problem using improved and chaotic population-based polar bear optimization algorithm. IEEE Access 2021, 9, 56152–56167. [Google Scholar]
- Nasr, M.A.; Zangian, M.; Abbasi, M.; Zolfaghari, A. Neutronic and thermal-hydraulic aspects of loading pattern optimization during the first cycle of VVER-1000 reactor using Polar Bear Optimization method. Ann. Nucl. Energy 2019, 133, 538–548. [Google Scholar]
- Tian, Y.; Liu, X.; Zhang, L.; Luo, Q.; Xu, Q.; Yao, H.; Yang, F.; Wang, J.; Dang, C.; Xuan, Y. Prediction of thermophysical properties of chlorine eutectic salts via artificial neural network combined with polar bear optimization. J. Energy Storage 2022, 55, 105658. [Google Scholar]
- Yu, J.; Zhang, Y.; Sun, C. Balance of exploration and exploitation, Non-cooperative game-driven evolutionary reinforcement learning. Swarm Evol. Comput. 2024, 91, 101759. [Google Scholar]
- Deb, K.; Thiele, L.; Laumanns, M.; Zitzler, E. Scalable test problems for evolutionary multiobjective optimization. In Evolutionary Multiobjective Optimization: Theoretical Advances and Applications; Springer: London, UK, 2005; pp. 105–145. [Google Scholar]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar]
- Xu, B.; Lv, J.; Liu, J. Manufacturing Cloud Service Composition Optimization Based on Usability Analysis. Ind. Eng. Manag. 2024, 29, 1–11. [Google Scholar]
- Schutze, O.; Esquivel, X.; Lara, A.; Coello, C.A.C. Using the averaged Hausdorff distance as a performance measure in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2012, 16, 504–522. [Google Scholar]
- Coello, C.A.C.; Cortés, N.C. Solving multiobjective optimization problems using an artificial immune system. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar]
- Babu, B.; Anbarasu, B. Multi-objective differential evolution (MODE): An evolutionary algorithm for multi-objective optimization problems (MOOPs). In Proceedings of the International Symposium and 58th Annual Session of IIChE, Delhi, India, 14–17 December 2005. [Google Scholar]
- Zhu, F.; Li, G.; Tang, H.; Li, Y.; Lv, X.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert. Syst. Appl. 2024, 236, 121219. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, B.; Wang, S.; Zhang, Z.; Tang, X. Bi-objective service composition and optimal selection for cloud manufacturing with QoS and robustness criteria. Appl. Soft Comput. 2022, 128, 109530. [Google Scholar] [CrossRef]



| Arithmetic | Parameters |
|---|---|
| MODE | Maximum number of iterations: 100/200 Population size: 50/150, external archive size: 50, scaling factor: 0.5, crossover prob ability: 0.2 |
| PBO | Maximum number of iterations: 100/200, Population size: 50/150, Search space dimension: 6, Search range: [−10, 10], Local search step: 0.1, Variation rate: 0.02, Number of elite reservations: 2 |
| NSGA-II | Maximum number of iterations: 100/200, Population size: 50/150, External archive size: 50, Crossover ratio: 0.6, Variation ratio: 0.3, Variation rate: 0.02 |
| IPBO | Maximum number of iterations: 100/200, Population size: 50/150, Search space dimension: 6, Search range: [−10, 10], Local search step:0.1, Variation rate: 0.02, Number of elite reservations: 2, Initial field of view adjustment factor: 0.25, Variation ratio: 0.4 |
| DBO | Maximum number of iterations: 100/200, Population size: 50/150, Number of variable dimensions: 2, Penalty factor C: 0.3, Learning factor: 0.5, inertia weight: 0.9, randomization factor: 0.1 |
| GWO | Maximum number of iterations: 100/200, Population size: 50/150, Convergence factor: linearly decreasing from 2.0 to 0, Search space range: [−10, 10] |
| Test Function | GWO | DBO | MODE | PBO | IPBO | NSGA-II |
|---|---|---|---|---|---|---|
| DTLZ1 | 4.88 × 10−2 | 3.73 × 10−2 | 5.69 × 10−2 | 4.39 × 10−1 | 3.62 × 10−2 | 3.88 × 10−2 |
| DTLZ2 | 2.03 × 10−1 | 3.52 × 10−2 | 5.32 × 10−2 | 4.78 × 10−2 | 2.68 × 10−1 | 8.75 × 10−3 |
| C-DTLZ1 | 4.48 × 10−2 | 3.23 × 10−2 | 3.96 × 10−2 | 5.19 × 10−2 | 2.86 × 10−2 | 3.86 × 10−2 |
| C-DTLZ2 | 4.57 × 10−2 | 4.07 × 10−2 | 3.54 × 10−2 | 4.39 × 10−2 | 3.28 × 10−2 | 4.21 × 10−2 |
| DTLZ1 | 7.26 × 10−3 | 4.63 × 10−3 | 8.14 × 10−3 | 6.33 × 10−3 | 2.96 × 10−3 | 5.39 × 10−3 |
| DTLZ2 | 6.85 × 10−1 | 2.96 × 10−2 | 7.32 × 10−1 | 3.94 × 10−1 | 3.56 × 10−2 | 4.22 × 10−2 |
| C-DTLZ1 | 6.06 × 10−2 | 5.03 × 10−2 | 7.91 × 10−2 | 5.97 × 10−2 | 1.68 × 10−2 | 2.58 × 10−2 |
| C-DTLZ2 | 5.31 × 10−2 | 3.92 × 10−2 | 6.36 × 10−2 | 6.27 × 10−2 | 2.86 × 10−2 | 3.73 × 10−2 |
| Test Function | GWO | DBO | MODE | PBO | IPBO | NSGA-II |
|---|---|---|---|---|---|---|
| DTLZ1 | 1.96 × 10−1 | 2.28 × 10−2 | 7.36 × 10−2 | 2.84 × 10−1 | 1.33 × 10−2 | 2.94 × 10−1 |
| DTLZ2 | 6.91 × 10−2 | 9.83 × 10−3 | 5.49 × 10−2 | 7.62 × 10−2 | 7.59 × 10−3 | 2.64 × 10−2 |
| C-DTLZ1 | 5.36 × 10−2 | 4.47 × 10−2 | 5.28 × 10−2 | 4.52 × 10−2 | 3.94 × 10−2 | 6.84 × 10−2 |
| C-DTLZ2 | 7.16 × 10−2 | 5.11 × 10−2 | 6.28 × 10−2 | 8.29 × 10−1 | 4.29 × 10−2 | 6.92 × 10−3 |
| DTLZ1 | 5.33 × 10−2 | 8.36 × 10−3 | 1.68 × 10−2 | 3.28 × 10−2 | 1.98 × 10−2 | 4.38 × 10−2 |
| DTLZ2 | 1.76 × 10−1 | 7.28 × 10−2 | 3.81 × 10−1 | 8.76 × 10−2 | 5.81 × 10−2 | 6.13 × 10−2 |
| C-DTLZ1 | 4.83 × 10−3 | 5.06 × 10−3 | 4.29 × 10−3 | 4.19 × 10−3 | 3.06 × 10−3 | 7.39 × 10−3 |
| C-DTLZ2 | 5.94 × 10−2 | 3.13 × 10−2 | 4.06 × 10−6 | 4.29 × 10−2 | 9.28 × 10−3 | 5.29 × 10−2 |
| Test Function | GWO | DBO | MODE | PBO | IPBO | NSGA-II |
|---|---|---|---|---|---|---|
| DTLZ1 | 8.66 × 10−1 | 8.73 × 10−1 | 8.54 × 10−1 | 8.91 × 10−1 | 9.24 × 10−1 | 9.06 × 10−1 |
| DTLZ2 | 7.38 × 10−1 | 7.59 × 10−1 | 7.64 × 10−1 | 7.23 × 10−1 | 8.29 × 10−1 | 7.76 × 10−1 |
| C-DTLZ1 | 4.92 × 10−1 | 5.22 × 10−1 | 5.12 × 10−1 | 4.88 × 10−1 | 5.09 × 10−1 | 5.47 × 10−1 |
| C-DTLZ2 | 7.25 × 10−1 | 7.69 × 10−1 | 7.43 × 10−1 | 7.18 × 10−1 | 8.06 × 10−1 | 7.94 × 10−1 |
| DTLZ1 | 6.54 × 10−1 | 8.86 × 10−1 | 6.68 × 10−1 | 6.34 × 10−1 | 9.15 × 10−1 | 8.28 × 10−1 |
| DTLZ2 | 4.97 × 10−1 | 5.37 × 10−1 | 4.77 × 10−1 | 5.16 × 10−1 | 6.27 × 10−1 | 5.93 × 10−1 |
| C-DTLZ1 | 8.17 × 10−1 | 9.76 × 10−1 | 9.64 × 10−1 | 7.61 × 10−1 | 8.26 × 10−1 | 8.86 × 10−1 |
| C-DTLZ2 | 6.53 × 10−1 | 7.64 × 10−1 | 7.19 × 10−1 | 6.27 × 10−1 | 8.32 × 10−1 | 5.29 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Liu, S.; Qian, S.; Zhu, L.; Shi, G.; Zhao, J. A Resource Composition Optimization Algorithm Based on Improved Polar Bear Optimization Algorithm for Manufacturing Wallboard for Coating Machine. Coatings 2025, 15, 418. https://doi.org/10.3390/coatings15040418
Gao Z, Liu S, Qian S, Zhu L, Shi G, Zhao J. A Resource Composition Optimization Algorithm Based on Improved Polar Bear Optimization Algorithm for Manufacturing Wallboard for Coating Machine. Coatings. 2025; 15(4):418. https://doi.org/10.3390/coatings15040418
Chicago/Turabian StyleGao, Zhenjie, Shanhui Liu, Song Qian, Langze Zhu, Gan Shi, and Jiawen Zhao. 2025. "A Resource Composition Optimization Algorithm Based on Improved Polar Bear Optimization Algorithm for Manufacturing Wallboard for Coating Machine" Coatings 15, no. 4: 418. https://doi.org/10.3390/coatings15040418
APA StyleGao, Z., Liu, S., Qian, S., Zhu, L., Shi, G., & Zhao, J. (2025). A Resource Composition Optimization Algorithm Based on Improved Polar Bear Optimization Algorithm for Manufacturing Wallboard for Coating Machine. Coatings, 15(4), 418. https://doi.org/10.3390/coatings15040418






