Calibration and Verification of Coated Caragana korshinskii Seeds Based on Discrete Element Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Determination of Basic Physical Parameters of Coated Caragana korshinskii Seeds
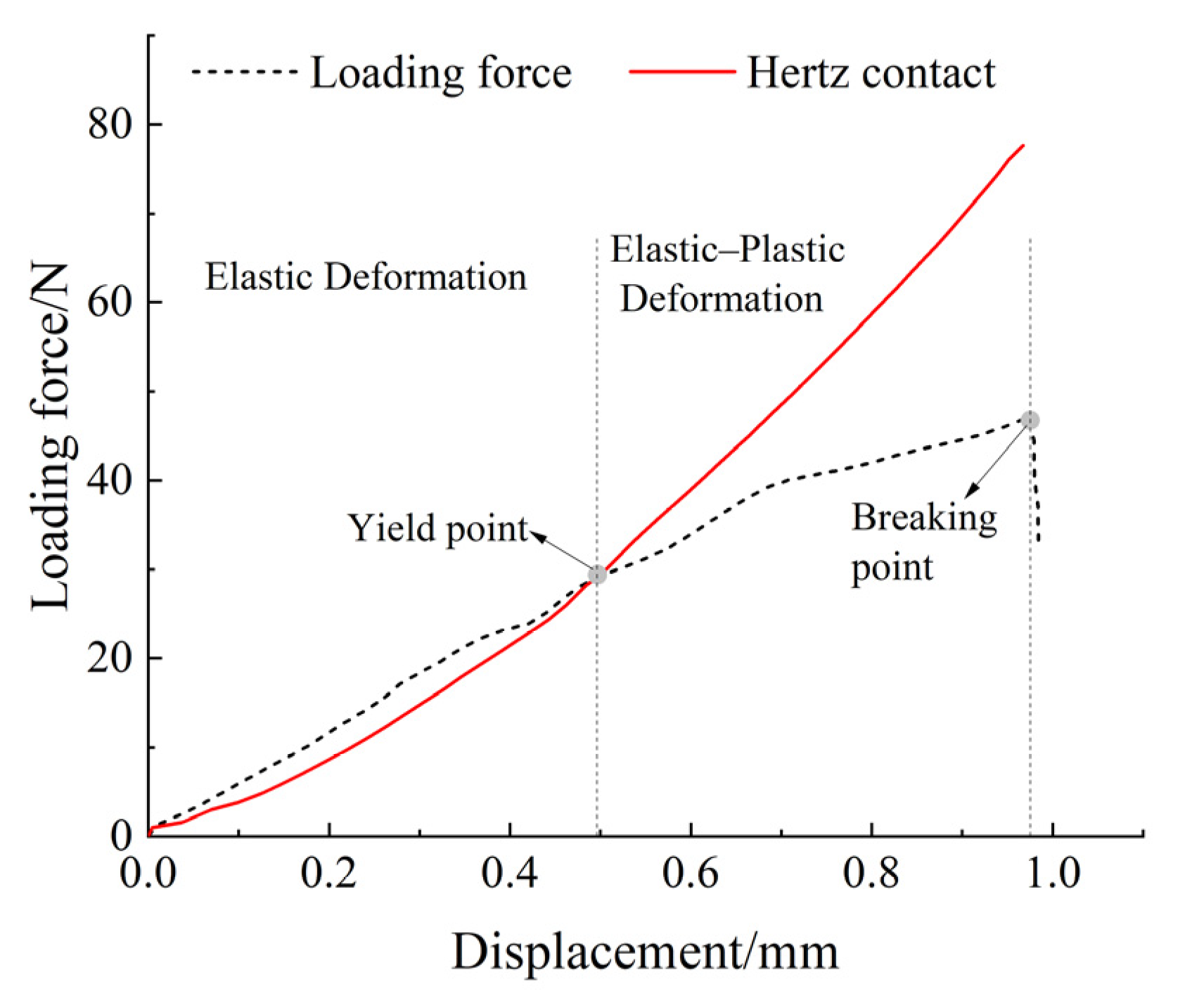
2.2. Determination of Shear Modulus for Coated Caragana korshinskii Seeds
2.3. Determination of Contact Parameters for Coated Caragana korshinskii Seeds
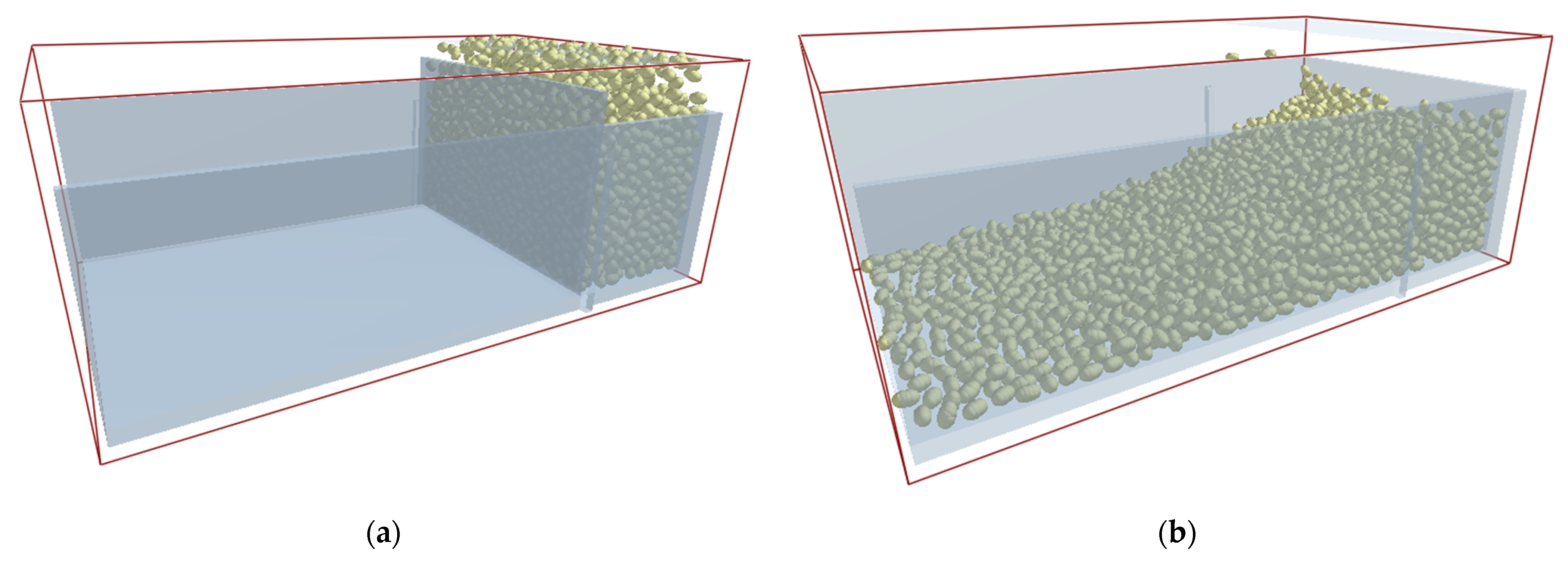
2.4. Determination of Angle of Repose for Coated Caragana korshinskii Seeds
2.5. Simulation Parameter Settings
2.6. Testing Methodology
2.7. Seed Metering Verification Experiments
3. Results
3.1. Calibration Test Results
3.2. Seeding Performance Tests
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Deaker, R.; Roughley, R.J.; Kennedy, I.R. Legume Seed Inoculation Technology—A Review. Soil Biol. Biochem. 2004, 36, 1275–1288. [Google Scholar] [CrossRef]
- Taylor, A.G.; Allen, P.S.; Bennett, M.A.; Bradford, K.J.; Burris, J.S.; Misra, M.K. Seed Enhancements. Seed Sci. Res. 1998, 8, 245–256. [Google Scholar] [CrossRef]
- Li, C.; Tang, Y.; McHugh, A.D.; Wu, X.; Liu, M.; Li, M.; Xiong, T.; Ling, D.; Tang, Q.; Liao, M.; et al. Development and Performance Evaluation of a Wet-Resistant Strip-till Seeder for Sowing Wheat Following Rice. Biosyst. Eng. 2022, 220, 146–158. [Google Scholar] [CrossRef]
- Zhou, H.; Dai, F.; Shi, R.; Zhao, C.; Deng, H.; Pan, H.; Zhao, Q. Simulation and Optimization of a Pendulum-Lever-Type Hole-Seeding Device. Agriculture 2024, 14, 750. [Google Scholar] [CrossRef]
- Yu, D.; Peng, F.; Zeng, Z.; Zhang, M.; Yang, W.; Zang, Y.; He, J.; Huang, Y.; Wu, Y.; Zhong, W.; et al. Vibrational Dynamics of Rice Precision Hole Seeders and Their Impact on Seed Dispensation Efficacy. Agriculture 2024, 14, 324. [Google Scholar] [CrossRef]
- Wei, L.; Wang, Q.; Niu, K.; Bai, S.; Wei, L.; Qiu, C.; Han, N. Design and Test of Seed–Fertilizer Replenishment Device for Wheat Seeder. Agriculture 2024, 14, 374. [Google Scholar] [CrossRef]
- Ma, X.; Liu, M.; Hou, Z.; Gao, X.; Bai, Y.; Guo, M. Numerical Simulation and Experimental Study of Pelletized Coating of Small Grain Forage Seeds. Trans. Chin. Soc. Agric. Eng. 2023, 39, 43–52. [Google Scholar]
- Zeng, F.; Cui, J.; Li, X.; Bai, H. Establishment of the Interaction Simulation Model between Plug Seedlings and Soil. Agronomy 2023, 14, 4. [Google Scholar] [CrossRef]
- Bai, H.; Wu, Y.; Ma, Y.; Xuan, D.; Du, W.; Liu, F.; Zhao, X. Discrete Element Model Construction and Dehulling Simulation Verification Based on Harvested Quinoa Grains. J. Food Sci. 2024, 89, 9336–9353. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Zhao, L.; Zhang, H.; Shi, F. Research on the Calibration Method of the Bonding Parameters of the EDEM Simulation Model for Asphalt Mixtures. Coatings 2024, 14, 1553. [Google Scholar] [CrossRef]
- Bembenek, M.; Buczak, M.; Baiul, K. Modelling of the Fine-Grained Materials Briquetting Process in a Roller Press with the Discrete Element Method. Materials 2022, 15, 4901. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Hou, Z.; Ma, X.; Zhang, X.; Dai, N. Determination and Testing of Pelletized Coated Particles. INMATEH-Agric. Eng. 2022, 66, 247–256. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, Z.; Zhang, D.; Cui, T.; Shi, S.; Li, K.; Yang, L. Calibration Method of Contact Characteristic Parameters for Corn Seeds Based on EDEM. Trans. Chin. Soc. Agric. Eng. 2016, 32, 36–42. [Google Scholar] [CrossRef]
- Adilet, S.; Zhao, J.; Sayakhat, N.; Chen, J.; Nikolay, Z.; Bu, L.; Sugirbayeva, Z.; Hu, G.; Marat, M.; Wang, Z. Calibration Strategy to Determine the Interaction Properties of Fertilizer Particles Using Two Laboratory Tests and DEM. Agriculture 2021, 11, 592. [Google Scholar] [CrossRef]
- Su, Q.; Zhang, J.; Liu, W.; Ma, X.; Yu, Z.; Liu, Z. Fracture Failure Model of Caragana Korshinskii Kom. Branches Constructed Using ABAQUS/Explicit. Forests 2025, 16, 90. [Google Scholar] [CrossRef]
- Hanley, K.J.; O’Sullivan, C.; Oliveira, J.C.; Cronin, K.; Byrne, E.P. Application of Taguchi Methods to DEM Calibration of Bonded Agglomerates. Powder Technol. 2011, 210, 230–240. [Google Scholar] [CrossRef]
- Xiao, L.; Sha, W.; Tao, C.; Hou, C.; Xiao, G.; Ren, J. Effect on Purine Releasement of Lentinus Edodes by Different Food Processing Techniques. Food Chem. X 2022, 13, 100260. [Google Scholar] [CrossRef]
- Xu, T.; Fu, H.; Liu, M.; Feng, W.; Zhang, R.; Wang, Y.; Wang, J. Ellipsoidal Seed Modeling and Simulation Parameter Selection Based on the Discrete Element Method. Mater. Today Commun. 2023, 37, 106923. [Google Scholar] [CrossRef]
- Shi, L.; Zhao, W.; Sun, B.; Sun, W.; Zhou, G. Determination and Analysis of Basic Physical and Contact Mechanics Parameters of Quinoa Seeds by DEM. Int. J. Agric. Biol. Eng. 2023, 16, 35–43. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Bai, J.; Fang, W.; Hong, T.; Zang, N.; Wang, G. Virtual Parameter Calibration of Pod Pepper Seeds Based on Discrete Element Simulation. Heliyon 2024, 10, e31686. [Google Scholar] [CrossRef]
- Walunj, A.; Chen, Y.; Tian, Y.; Zeng, Z. Modeling Soil–Plant–Machine Dynamics Using Discrete Element Method: A Review. Agronomy 2023, 13, 1260. [Google Scholar] [CrossRef]
- Hasseldine, B.P.J.; Gao, C.; Collins, J.M.; Jung, H.-D.; Jang, T.-S.; Song, J.; Li, Y. Mechanical Response of Common Millet (Panicum miliaceum) Seeds under Quasi-Static Compression: Experiments and Modeling. J. Mech. Behav. Biomed. Mater. 2017, 73, 102–113. [Google Scholar] [CrossRef]
- Du, C.; Han, D.; Song, Z.; Chen, Y.; Chen, X.; Wang, X. Calibration of Contact Parameters for Complex Shaped Fruits Based on Discrete Element Method: The Case of Pod Pepper (Capsicum annuum). Biosyst. Eng. 2023, 226, 43–54. [Google Scholar] [CrossRef]
- Ma, X.; Yu, Z.; Liu, M.; Wang, J.; Su, Q.; Zhang, J.; Xie, J.; Wang, T. Mechanical Properties and Critical State Characteristics of Maize Root-Soil Composites at Different Soil Depths. Biosyst. Eng. 2025, 250, 163–173. [Google Scholar] [CrossRef]
- Portnikov, D.; Kalman, H. Determination of Elastic Properties of Particles Using Single Particle Compression Test. Powder Technol. 2014, 268, 244–252. [Google Scholar] [CrossRef]
- Ma, X.; Guo, M.; Tong, X.; Hou, Z.; Liu, H.; Ren, H. Calibration of Small-Grain Seed Parameters Based on a BP Neural Network: A Case Study with Red Clover Seeds. Agronomy 2023, 13, 2670. [Google Scholar] [CrossRef]
- Hou, Z.; Dai, N.; Chen, Z.; Qiu, Y.; Zhang, X. Measurement and Calibration of Physical Property Parameters for Agropyron Seeds in a Discrete Element Simulation. Trans. Chin. Soc. Agric. Eng. 2020, 36, 46–54. [Google Scholar] [CrossRef]
- Rundlöf, M.; Andersson, G.K.S.; Bommarco, R.; Fries, I.; Hederström, V.; Herbertsson, L.; Jonsson, O.; Klatt, B.K.; Pedersen, T.R.; Yourstone, J.; et al. Seed Coating with a Neonicotinoid Insecticide Negatively Affects Wild Bees. Nature 2015, 521, 77–80. [Google Scholar] [CrossRef]










| Physical Parameters | Value | |
|---|---|---|
| Particle density | kg·m−3 | 1060.3 ± 0.21 |
| Thousand-grain weight | g | 76.4 ± 0.53 |
| Moisture content | % | 8.35 ± 0.06 |
| Overall dimensions (L × W × H) | mm × mm × mm | 6.832 ± 0.48 × 4.818 ± 0.19 × 4.542 ± 0.68 |
| Factors | Code |
|---|---|
| Poisson’s ratio of coated Caragana korshinskii seeds | A |
| Shear modulus of coated Caragana korshinskii seeds/Mpa | B |
| Coefficient of restitution between coated Caragana korshinskii seeds | C |
| Static friction coefficient between coated Caragana korshinskii seeds | D |
| Rolling friction coefficient between coated Caragana korshinskii seeds | E |
| Coefficient of restitution between coated Caragana korshinskii seeds and aluminum plate | F |
| Static friction coefficient between coated Caragana korshinskii seeds and aluminum plate | G |
| Rolling friction coefficient between coated Caragana korshinskii seeds and aluminum plate | H |
| NO. | A | B | C | D | E | F | G | H | Angle of Repose θ (°) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5 | 20 | 0.235 | 0.166 | 0.585 | 0.482 | 0.147 | 0.171 | 37.76 |
| 2 | 0.3 | 20 | 0.235 | 0.426 | 0.585 | 0.482 | 0.077 | 0.257 | 42.25 |
| 3 | 0.3 | 5 | 0.235 | 0.166 | 0.749 | 0.634 | 0.077 | 0.257 | 17.99 |
| 4 | 0.5 | 20 | 0.205 | 0.426 | 0.749 | 0.634 | 0.077 | 0.171 | 39.17 |
| 5 | 0.5 | 5 | 0.205 | 0.166 | 0.749 | 0.482 | 0.147 | 0.257 | 34.56 |
| 6 | 0.5 | 5 | 0.235 | 0.426 | 0.749 | 0.482 | 0.077 | 0.171 | 45.45 |
| 7 | 0.3 | 20 | 0.235 | 0.166 | 0.749 | 0.634 | 0.147 | 0.171 | 33.83 |
| 8 | 0.5 | 5 | 0.235 | 0.426 | 0.585 | 0.634 | 0.147 | 0.257 | 64.39 |
| 9 | 0.3 | 20 | 0.205 | 0.426 | 0.749 | 0.482 | 0.147 | 0.257 | 45.67 |
| 10 | 0.5 | 20 | 0.205 | 0.166 | 0.585 | 0.634 | 0.077 | 0.257 | 15.59 |
| 11 | 0.3 | 5 | 0.205 | 0.426 | 0.585 | 0.634 | 0.147 | 0.171 | 48.33 |
| NO. | C | D | G | Relative Error/% |
|---|---|---|---|---|
| 1 | 0.205 | 0.166 | 0.077 | 75.11 |
| 2 | 0.211 | 0.218 | 0.091 | 46.93 |
| 3 | 0.217 | 0.270 | 0.105 | 29.39 |
| 4 | 0.223 | 0.322 | 0.119 | 19.94 |
| 5 | 0.229 | 0.374 | 0.133 | 27.18 |
| 6 | 0.235 | 0.426 | 0.147 | 31.13 |
| Level | C | D | G |
|---|---|---|---|
| −1 | 0.217 | 0.270 | 0.105 |
| 0 | 0.223 | 0.322 | 0.119 |
| +1 | 0.229 | 0.374 | 0.133 |
| NO. | C | D | G | Angle of Repose θ (°) |
|---|---|---|---|---|
| 1 | −1 | −1 | 0 | 29.22 |
| 2 | 1 | −1 | 0 | 27.88 |
| 3 | −1 | 1 | 0 | 34.94 |
| 4 | 1 | 1 | 0 | 38.85 |
| 5 | −1 | 0 | −1 | 29.15 |
| 6 | 1 | 0 | −1 | 34.26 |
| 7 | −1 | 0 | 1 | 33.30 |
| 8 | 1 | 0 | 1 | 36.87 |
| 9 | 0 | −1 | −1 | 28.20 |
| 10 | 0 | 1 | −1 | 35.24 |
| 11 | 0 | −1 | 1 | 29.71 |
| 12 | 0 | 1 | 1 | 40.53 |
| 13 | 0 | 0 | 0 | 39.64 |
| 14 | 0 | 0 | 0 | 39.95 |
| 15 | 0 | 0 | 0 | 41.77 |
| 16 | 0 | 0 | 0 | 41.10 |
| 17 | 0 | 0 | 0 | 39.82 |
| Source | Sum of Squares | df | F-Value | p-Value |
|---|---|---|---|---|
| Model | 395.18 | 9 | 36.3 | <0.0001 |
| C | 16.16 | 1 | 13.36 | 0.0081 |
| D | 152.25 | 1 | 125.88 | <0.0001 |
| G | 23.5 | 1 | 19.43 | 0.0031 |
| CD | 7.02 | 1 | 5.81 | 0.0468 |
| CG | 0.6006 | 1 | 0.4966 | 0.5038 |
| DG | 3.65 | 1 | 3.02 | 0.126 |
| C2 | 64.69 | 1 | 53.49 | 0.0002 |
| D2 | 63.79 | 1 | 52.74 | 0.0002 |
| G2 | 43.51 | 1 | 35.98 | 0.0005 |
| Residual | 8.47 | 7 | ||
| Lack of Fit | 4.93 | 3 | 1.86 | 0.2768 |
| Pure Error | 3.53 | 4 | ||
| Cor Total | 403.65 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tai, Z.; Tong, X.; Xu, H.; Hu, H.; Bao, P.; Jia, B. Calibration and Verification of Coated Caragana korshinskii Seeds Based on Discrete Element Method. Coatings 2025, 15, 387. https://doi.org/10.3390/coatings15040387
Tai Z, Tong X, Xu H, Hu H, Bao P, Jia B. Calibration and Verification of Coated Caragana korshinskii Seeds Based on Discrete Element Method. Coatings. 2025; 15(4):387. https://doi.org/10.3390/coatings15040387
Chicago/Turabian StyleTai, Zhongkai, Xin Tong, Hongli Xu, Haoran Hu, Pengyu Bao, and Bing Jia. 2025. "Calibration and Verification of Coated Caragana korshinskii Seeds Based on Discrete Element Method" Coatings 15, no. 4: 387. https://doi.org/10.3390/coatings15040387
APA StyleTai, Z., Tong, X., Xu, H., Hu, H., Bao, P., & Jia, B. (2025). Calibration and Verification of Coated Caragana korshinskii Seeds Based on Discrete Element Method. Coatings, 15(4), 387. https://doi.org/10.3390/coatings15040387






