Abstract
The use of bound states in the continuum (BICs) has emerged as an effective tool to trap light at the nanoscale and has many potential applications in photonics. Breaking the structural symmetry is regarded as an effective way to excite quasi-BICs (QBICs) and generate high-Q resonances. However, this approach may impact the resonance polarization sensitivity, consequently limiting its practicality in multi-wavelength polarization-dependent applications. Furthermore, the introduction of different types of structural perturbations into the design to form BICs has yet to be explored in depth. In this study, we present an optical sensor consisting of an L-shaped metasurface that supports three quasi-BIC modes in the terahertz band, where specific displacements, collective perturbations, or both occur. Furthermore, we analyze the field distributions in detail and combine them with multipolar decomposition to reveal the underlying mechanisms of the different resonant modes. Multiple asymmetric perturbations are found to affect the sensitivity of the metasurface in refractive index sensing, thus allowing for a comparison of different resonant modes. The quasi-BIC mode can attain a Q-factor of 1067.6, a sensitivity (S) of 300 GHz/RIU, and a figure of merit (FOM) of 5367.8 RIU−1 for vertical light incidence. These three quasi-BIC modes are polarization-independent, and their properties are maintained even for circularly polarized light. The results reveal a novel design strategy for metasurface-based sensors with promising application potential in biosensing, filtering, and lasers.
1. Introduction
In recent years, bound states in the continuum (BICs) have shown significant potential in applications such as the detection of trace substances in micro- and nanostructures. By varying the structural parameters, the structures can be operated in the wavelength range spanning from visible to microwave. Recent research has underscored the versatility of metasurfaces across various wavelength bands and sensing applications. Wang et al. have crafted a terahertz metasurface, featuring periodically arranged split-ring resonators integrated with functional colloidal gold nanoparticles (AuNPs) [1]. In the mid-infrared region, a dual-band refractive index (RI) sensor has been ingeniously constructed by using an all-dielectric metasurface, comprising silicon elliptical and circular nanodisks on a BaF2 substrate [2]. Theoretical explorations have given rise to an innovative metallic toroidal dipole (TD) metasurface, propelled by Friedrich–Wintgen bound states in the continuum (FW-BICs), showcasing potential for advanced sensing mechanisms [3]. Hollow gap nanocubes have been strategically designed for metasurface operations near 785 nm in the visible light spectrum [4]. Algorri et al. have conducted a comprehensive theoretical and experimental study on a metasurface that supports a silicon-slot quasi-bound state in the continuum (QBIC) mode, resonating in the near-infrared spectrum. This metasurface is meticulously engineered with circular slots etched in a silicon layer atop a sapphire substrate [5]. Furthermore, the sensing capabilities of an all-dielectric metasurface consisting of periodic amorphous silicon (a-Si) nanobar pairs on a glass substrate have been both theoretically modeled and experimentally confirmed, reinforcing the practicality of metasurfaces in sensing technologies [6]. These advancements collectively illustrate the burgeoning potential of metasurfaces in optical engineering and sensor development. The terahertz band (0.1 to 10 THz) between infrared and microwave is useful for sensing applications due to low energy, small damage, and strong penetrability [7,8,9]. Biosensing technology requires micro- and nanostructures with a large quality factor (Q-factor), high absorbance (scattering rate), large specific surface area, and tailored optical properties and biocompatibility.
Conventional optical nanostructures typically have insufficient transmission capacity because of the single-resonant-mode response, which compromises the sensitivity. The introduction of bound states in the continuum (BICs) with extremely narrow linewidths and ultrahigh quality factors into periodically arranged three-dimensional structures with special electromagnetic properties, known as optical metasurfaces, opens up new opportunities for the development of high-performance sensors in the terahertz band. Previous studies have investigated metasurfaces utilizing quasi-BICs to excite Fano resonances in all-dielectric materials, including dual-nanorod metasurface structures in asymmetrical silicon [10], semi-elliptical disks with asymmetrical radii [11], double-open resonance rings [12], and optics with high field enhancement factors [13]. However, the formation of quasi-bound states in most of these structures relies on a single excitation condition; it is, therefore, particularly important to study in depth the conditions for quasi-bound state formation (e.g., structural symmetry breaking, specific displacements, and collective perturbations) while introducing two or more perturbations.
Generating quasi-BIC resonances usually requires that the structural symmetry is broken, and metasurface structures designed to support SP-BICs (symmetry-protected BICs) can be easily converted into quasi-BICs, but they are usually polarization-sensitive, for example, tilted silicon rod pairs [14], split rings [12,15], asymmetric nanorods [16], eccentric cavities [17], and tetrameric cluster of nanodisks of varying height [18]. These structures are only compatible with specific polarization states, thereby restricting flexibility and versatility in practical applications. Hence, it is important to design metasurfaces that can operate efficiently in a range of polarization states and excite multi-wavelength resonances. Introducing collective perturbations and specific displacements into the BIC metasurface can show unique optical properties and potential applications. It has been demonstrated that the introduction of minor collective perturbations, encompassing alterations in arrangement, size, and material properties of the constituent units, can effectively induce novel resonance modes in metasurfaces comprising multiple identical or analogous structures. This, in turn, exerts a profound influence on the optical properties, as evidenced in previous studies [19,20,21]. Furthermore, precise control of the reflection, transmission and absorption properties of light has been achieved by tuning specific displacements (spacing and angle) in nanobeams in metasurfaces composed of silicon nanobeams [22]. The combination of collective perturbations and specific displacements is anticipated to enhance the precision of tuning (resonance frequency, quality factor, etc.), facilitate the integration of multiple optical functions (e.g., polarization, sensing, etc.), and strengthen the coupling between photons and matter to form hybrid photon–polariton states [23,24,25]. A comprehensive investigation of these two areas will facilitate the advancement of nanophotonics and optoelectronics while also establishing the groundwork for future technological innovations.
In this work, we mainly focus on the influence of multiple perturbation methods on the formation of quasi-BICs, with particular attention to the currently less studied multiple resonance modes and their polarization-independent properties. For this reason, we theoretically demonstrate an optical sensor composed of an L-shaped metasurface, which is based on three quasi-BIC modes excited under normal incidence in the terahertz band after specific displacement, collective perturbation, or both of the constituent particles. The proposed metasurface consists of silicon tetramer and quartz substrate, which is characterized by a simple structure and easy fabrication. It is not confined to a single function but rather capable of achieving multiple-frequency polarization independence and sensing simultaneously. This metasurface demonstrates the ability to induce quasi-BICs at 0.781 THz, 0.828 THz, and 0.989 THz. The study of the Q-factor and light-field distribution properties of these three modes reveals that each mode is predominantly excited by specific displacements and collective perturbations to break the structural symmetry. The L-shaped metasurface sensor exhibits three narrow resonances dominated by the toroidal dipole (TD), electric quadrupole (EQ), and toroidal dipole (TD), respectively, with a high Q-factor of 1067.6. Potential applications to terahertz biosensing and polarization correlations are studied. The introduction of multiple asymmetric perturbations affects metasurface sensitivity in refractive index sensing and allows for the comparison of the performance of different resonant modes. The quasi-BIC mode shows a maximum sensitivity (S) of 300 GHz/RIU and a figure of merit (FOM) of 5367.8 RIU−1, and it can realize accurate detection under small changes, which is potentially valuable in biomedical and environmental monitoring. The results reveal a general and simple structural design strategy for multi-band polarization-independent quasi-BIC high-quality resonances for metasurface sensitivity measurements and demonstrate promising applications in biosensing, filtering, and lasers.
2. Model and Method
The all-dielectric L-shaped metasurface with high sensitivity and polarization independence based on specific displacements and collective perturbations is depicted in Figure 1. The metasurface structure is formed by a periodic array of silicon (Si) L-type strips with a thickness of H2 = 30 μm on a quartz substrate with a thickness of H1 = 133 μm. The period of the unit cell P is 300 μm along the x- and y-directions. The lengths of the arms are s = 80 μm, a = 55 μm, and b = s − a = 25 μm, and the separation between neighboring L-type structures is G = 33 μm. The refractive indexes, n, of Si and quartz are 3.45 and 1.45, respectively [26,27]. The semiconductor material silicon has moderate electrical conductivity and excellent optical properties, and its low-loss characteristics make it excellent in the optical frequency range [28,29]. The combination of silicon and quartz can form a stable interface with efficient electromagnetic wave manipulation, which can achieve polarization control, Q-factor enhancement, and excellent performance in sensing applications [30,31,32]. In the simulation, the wave optical module in COMSOL 6.1 Multiphysics (COMSOL, Burlington, MA, USA) was used, and the electromagnetic frequency domain (ewfd) interface was selected. The full three-dimensional finite element method (FEM) was used to simulate the transmission mission spectrum at 0.7–1.1 THz and thus derive the optical properties. The geometry was modeled by using an adaptive tetrahedral mesh with periodic boundary conditions applied along the x- and y-directions and perfectly matched layer conditions along the z-direction [33]. After setting up the model and mesh, the solver was run to obtain the number of degrees of freedom, which is affected by a number of factors, such as the complexity of the geometry, meshing, the frequency range, and so on. The terahertz (THz) wave impacts the metasurface along the negative direction of the z-axis, with the polarization state controlled arbitrarily. Moreover, convergence tests were carried out by optimizing the mesh size and PML thickness to produce more accurate results. The metasurface can be produced by depositing a silicon film on the quartz substrate by magnetron sputtering, followed by the patterning of the Si layer by laser etching [34].
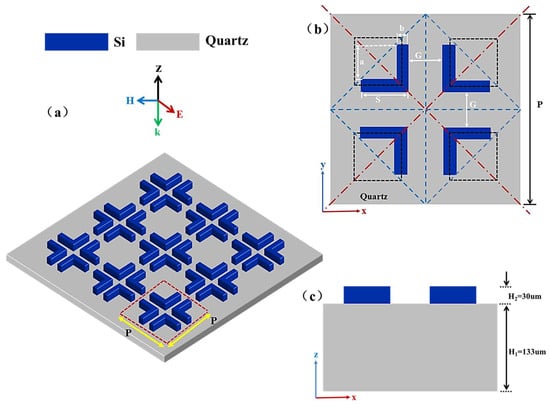
Figure 1.
(a) Metasurface. (b) Top view of a polymeric structural unit, where the lengths of the arms are s, a, and b = s − a and the spacing between L-shaped structures is G. (c) Side view of the tetrameric structural unit, where H1 is the thickness of the substrate and H2 is the height of the L-type tetramer. The black dotted line represents the location of the initial structure.
The radiation channel between quasi-BICs and THz waves, manifesting as a narrow dip in the transmission spectrum, is established by the slight tuning of the structural parameters [35]. In order to highlight the distinct advantages of photomodulation by the metasurface structures, the formation of tri-band quasi-BICs on the metasurface (including particular displacements, collective perturbations, and a combination of the above) is investigated, as shown in Figure 2. The metasurface of the tetrameric cluster with the C4v symmetry is first studied, followed by the step-by-step transformation of the SP-BICs into tri-band quasi-BICs after particular displacements or collective perturbations. Finally, the positive effect of the combination of these two approaches on the generation of multi-wavelength quasi-BICs is explored. Special note: The thickness of the blue material in Figure 2c,d is for illustrative purposes only and does not represent the actual variation in material thickness.
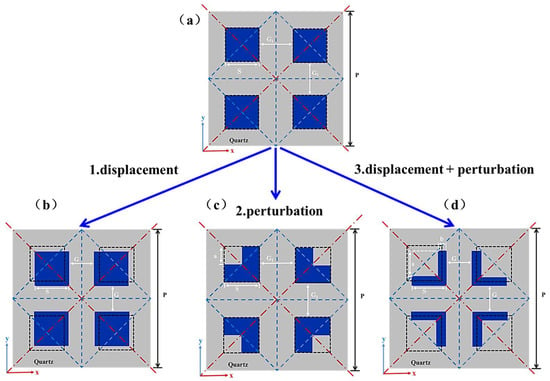
Figure 2.
Tetrameric cluster structures: (a) Initial tetrameric cluster. (b) Particular displacement. (c) Collective perturbation. (d) Combination of particular displacement and collective perturbation. The black dashed cubes represent the position of the initial tetrameric cluster before operation, where the spacing is G1, the side length is s, and the spacing after a specific displacement becomes G. The side length of the block cut by collective perturbation is a, and a < s.
3. Results and Discussion
3.1. The Generation of Tri-Band Quasi-BICs
3.1.1. Characteristics of the Shift from BICs to Tri-Band Quasi-BICs Produced by Particular Displacements
Figure 3a,b show the unit cells of metasurface structures; specifically, these structures are periodic repeating basic units. The transmission mode in Figure 3c is achieved by periodically repeating four structures. Figure 3a shows the symmetric metasurface consisting of four Si cubes (with a side length of s = 80 μm and a gap between cubes of G1 = 70 μm) on the quartz substrate. This is the most common structure to excite BICs and serves as the starting nanostructure. The specific displacements are moved as shown in Figure 3b, where four Si cubes are moved toward the center along two diagonal lines. The spacing of neighboring cubes after the move is defined as G. The black dashed cubes represent the position of the initial tetrameric cluster before operation. Figure 3c shows that the metasurface has the C4v symmetry with four silicon cubes located at the diagonal center (G1 = 70 µm). At this point, the linewidth at the BICs approaches infinity; therefore, the Q-factor also approaches infinity, making it indistinguishable in the transmission spectrum. The results illustrate the physical nature of BICs, which are waves that remain localized. Bound states that manifest in the background of a continuous spectrum cannot be observed in the far field [36,37,38]. There are three resonance depressions in the frequency range of 0.75 THz–1 THz when G is varied from 37 μm to 28 μm, manifesting as quasi-BICs. In addition, the resonance peaks show a slight redshift as G becomes smaller.
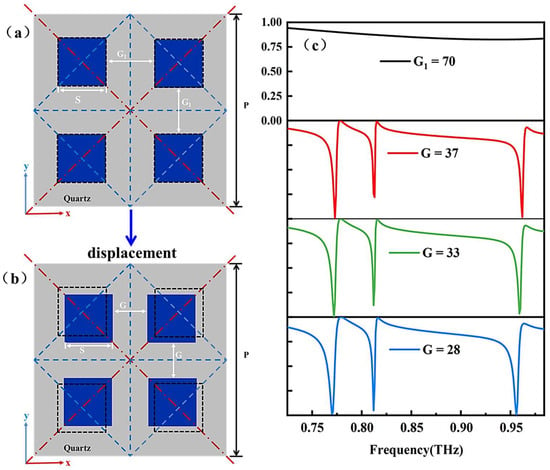
Figure 3.
Tetrameric cluster structures: (a) Initial tetrameric cluster. (b) Particular displacement. (c) Transmission spectra for different spacings G. The black dashed cubes represent the position of the initial tetrameric cluster before operation, where the spacing is G1, the side length is s, and the spacing after a specific displacement becomes G.
3.1.2. Characteristics of Transformation from BICs to Tri-Band Quasi-BICs Caused by Collective Perturbation
The tri-band quasi-BICs generated by the collective perturbation of equidistant particles are studied. The perturbation is the formation of the L-shaped structure by cutting off a small cubic notch at one corner of each cubic block in the initial tetrameric cluster (Figure 4a,b). The edge length, a, of the small cubic notch is defined as the perturbation quantity. Following collective perturbation, each cubic block undergoes the L-type transformation that breaks its own symmetry, enabling a weak coupling between the incident wave and the metasurface. In other words, the cubic block tetramer turns into an L-type tetramer forming a channel radiating outward, and the initial bound state keeps leaking energy outward to convert the original BICs into quasi-BICs.
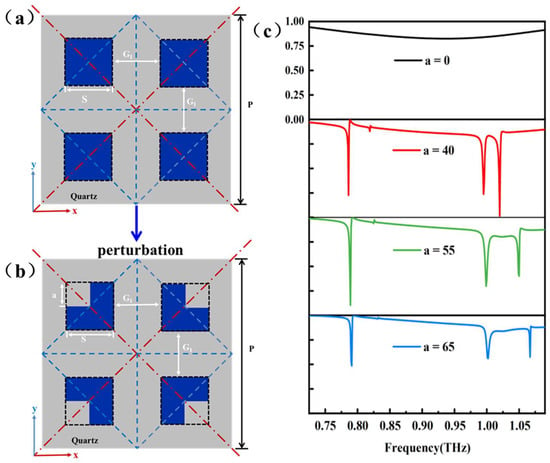
Figure 4.
Tetrameric cluster structures: (a) Initial tetrameric cluster. (b) Collective perturbation. (c) Transmission spectra for different lengths when G1 = 70 μm. The black dashed cubes represent the position of the initial tetrameric cluster before operation, where the spacing is G1, the side length is s, and the spacing after a specific displacement becomes G. The side length of the block cut by collective perturbation is a, and a < s.
The simulated transmission spectra for different perturbations are plotted in Figure 4c. The transmission spectra are characterized by infinite linewidths and infinite Q-factors when a = 0, which corresponds to the BIC. After introducing the perturbation (a = 40 μm), three distinct resonances are observed from the spectrum. Model A exhibits the narrowest linewidth, Model B has the widest linewidth, and Model C shows the transmission value closest to 0. This implies that BICs are converted into triple-band quasi-BICs. The three modes change as a increases, but in general, the modes are not effective enough, i.e., the linewidths are wide and the depth of transmission is shallow.
3.1.3. Tri-Band Quasi-BICs Generated by the Combination of Particular Displacement and Collective Perturbation
In the previous sections, particular displacement and collective perturbation are applied to the metasurface and discussed. Both of them can realize the transition from BICs to tri-band quasi-BICs. Therefore, we attempt to combine particular displacement and collective perturbation of the metasurface at the same time to explore the formation mechanism of QBICs, as shown in Figure 5a,b. In order to control the variables while maintaining favorable tri-band resonance, a = 55 μm, and the particles are shifted. When a = 55 μm, the transmission spectra corresponding to different spacings G are shown in Figure 5c. When G = 33 μm, the transmission spectrum shows three resonance modes at 0.781 THz, 0.828 THz, and 0.989 THz. When G decreases or increases, there is no obvious redshift or blueshift. However, at G = 33 μm, the three mode transmission values reach 0 and have the narrowest linewidths, implying a high Q-factor and resonance capability. The mechanism of the formation of triple resonances will be described in Section 3.2.
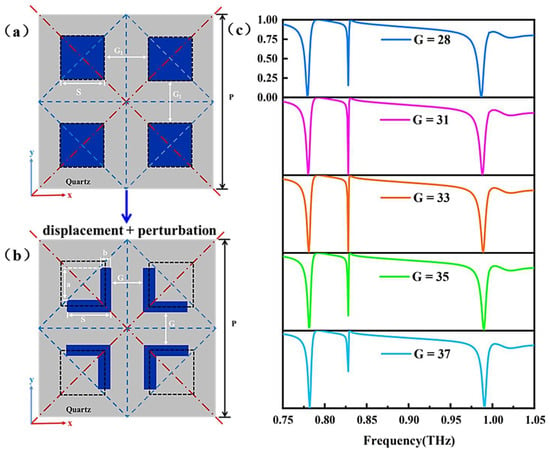
Figure 5.
Tetrameric cluster structures: (a) Initial tetrameric cluster. (b) Combination of particular displacement and collective perturbation. (c) Transmission spectra for different spacings G when a = 55 μm. The black dashed cubes represent the position of the initial tetrameric cluster before operation, where the spacing is G1, the side length is s, and the spacing after a specific displacement becomes G. The side length of the block cut by collective perturbation is a, a < s, and b = s − a.
To further elucidate the impact of different structural evolutions on the final performance, we compared and analyzed the transmission spectra obtained by the three methods (Figure 3c, Figure 4c and Figure 5c). Through comparison, we found that the commonality among these three methods is that each method successfully excited quasi-BICs resonance in three frequency bands. However, the difference lies in the fact that the excitation effect of quasi-BICs can be significantly improved by combining specific displacement and collective perturbation methods (as shown in Figure 5c). Specifically, as shown in Figure 5c, compared with Figure 3c and Figure 4c, the linewidths of these three resonances are narrower, and the transmission values are closer to 0. This indicates that the combination of specific displacement and collective perturbation can effectively excite better quasi-BICs, thereby significantly improving the performance of the sensor. In addition, after further careful comparison, we also noticed that the three resonances in Figure 5c showed a significant redshift compared with the resonances in Figure 3c and Figure 4c.
3.2. Mechanisms: Near-Field Properties and Effects of Structural Parameters
To investigate the resonance characteristics of the three modes, the scattering powers of different multipoles, including the electric dipole (ED), magnetic dipole (MD), toroidal dipole (TD), electric quadrupole (EQ), and magnetic quadrupole (MQ), are derived, as shown in Figure 6a,c,e [39,40,41,42]. In Model A, the contribution of the TD is dominant, indicating that Model A is mainly influenced by the TD, as shown in Figure 6a. The MQ also contributes, but it is smaller than the TD, and the ED and MD intersect at 0.781 THz. In Model B, the EQ is predominant, with smaller contributions from the MD and MQ, as shown in Figure 6c. In Model C, the contribution from the TD is the largest, while the ED provides minor contributions, as shown in Figure 6e. The linearity of Fano resonance is formed by the coupling of a discrete Lorentz line shape (representing resonant states) with a continuous background scattering state (representing non-resonant states), commonly referred to as the interaction between “bright modes” and “dark modes”. Specifically, Figure 6a,c,e employ the multipolar decomposition method to investigate in depth the formation mechanism of three resonances and reveal the dominant mode of each Fano resonance. The curves of Model A, Model B, and Model C when G = 33 μm with the classical Fano formula are fitted and presented in Figure 6b,d,f. Model A, Model B, and Model C when G = 33 μm can be evaluated with Q = ω0/τ and derived from QA = 158.9, QB = 1067.6, and QC = 145.1. The results show that the prediction of the Fano model for the three modes agrees well with the simulation results around the resonance dips, indicating the essence of Fano resonance.
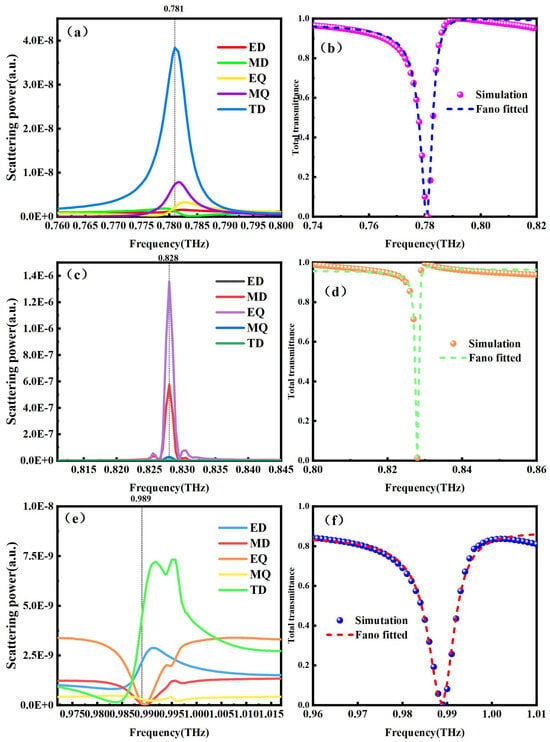
Figure 6.
Multipolar decompositions of (a) Model A, (c) Model B, and (e) Model C. (b) Resonances of QBIC A, (d) QBIC B, and (f) QBIC C when G = 33 μm and the fitted results obtained by the Fano model.
Metasurfaces with high-order multipoles have been extensively documented [43,44]. To examine the confined optical modes at the resonant frequency of BICs, field analysis is conducted for the three modes. The arrows indicate the direction of the electric and magnetic field vectors, and the color scale corresponds to the field strength. Figure 6a shows that the contribution of the TD dominates the Model A resonance. To obtain a better understanding of Model A, the displacement current distribution is shown in Figure 7a. Four toroidal currents are generated at the metasurface, where each of the two toroids reverses in the y-direction and generates four longitudinal magnetic moments oriented along the z-axis. Figure 7b,c show the distributions of the magnetic field vectors in the y–z section of Model A (corresponding to S1 and S2, respectively). The counterclockwise and clockwise closed displacement current loops are obtained in the x–y cross-section, respectively, indicating that the opposite phases of the magnetic dipole (MD) are produced in the z-direction. The magnetic field vortices in opposite rotational directions between neighboring L-structures indicate the presence of the TD. The directional arrows of the magnetic field head-to-head form a loop and circulate clockwise between the y-directions, which is a characteristic of the TD [45]. The field distribution of Model B is also plotted. The charge distribution of Model B in Figure 7d shows that two pairs of positive and negative charges are formed at every two L-type structures in the y-direction, which suggests the presence of EQ modes. Combined with the opposite magnetic field vectors along the z-axis in S3 and S4 in Figure 7e,f, the existence of the MD mode is demonstrated. The near-field electromagnetic field distributions of Model A and Model B are consistent with the multipolar decomposition results in Figure 6a,c, respectively.
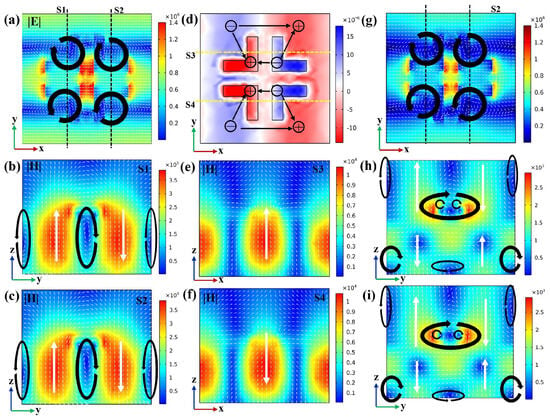
Figure 7.
(a) Electric field distribution of Model A on the x–y plane. (b,c) Magnetic field distribution on the y–z plane corresponding to cross-sections S1 and S2, respectively. (d) Charge distribution of Model B on the x–y plane. (e,f) Magnetic field distribution on the x–z plane corresponding to cross-sections S3 and S4, respectively. (g) Electric field distribution of Model C on the x–y plane. (h,i) Magnetic field distribution on the y–z plane corresponding to cross-sections S1 and S2, respectively. Additional information: S1 uses the y–z plane with x = 50 µm, S2 uses the y–z plane with x = −50 µm, S3 uses the x–z plane with y = −50 µm, and S4 uses the x–z plane with y = 50 µm.
The primary radiation source is determined by calculating the electromagnetic field distribution at the corresponding location in the near field of the metasurface [10]. Although toroidal dipole (TD) resonances are highly localized with large quality (Q) factors, TD resonances are weaker than electric or magnetic dipole resonances for most structures [46]. Coincidentally, Model C remains TD-dominant in the metasurface. The x–y cross-section in Figure 7g shows two pairs of circular displacement currents in opposite directions, proving the presence of TD. This has a similar electric field distribution as Model A, thus verifying that the dominant mode is the TD (Figure 6e). Taking two y–z cross-sections (S1 and S2) to analyze the magnetic field distribution characteristics, multiple loop currents are observed in Figure 7h,i, indicating that this mode is subject to the co-coupling effect of multiple polaritons. This is consistent with the multipole results calculated by simulation in Figure 6e.
Since different sizes of the metasurface structure affect the properties, the linewidths, resonant frequencies, and transmission depths of the three modes can be varied individually by adjusting geometrical parameters such as H1, a, s, H2, and so on. In order to analyze the dependence of the resonance properties on the geometrical parameters, the variation in the transmission profile of the metasurface was derived when the thickness of the substrate H1, the side length a of the small cubic notch, the side length s of the initial cubic block, and the thickness of the structure H2 were varied. As shown in Figure 8, the resonant wavelength redshifts all four cases. Specifically, Figure 8b–d show that the variations in a, s, and H2 have a remarkable effect on Model B and impact the depth of the notch, while Model A and Model C are not affected significantly. After comprehensive consideration, the parameters of the final L-shaped metasurface are s = 80 µm, H2 = 30 µm, H1 = 133 µm, a = 55 µm, and particle spacing G = 33 µm.
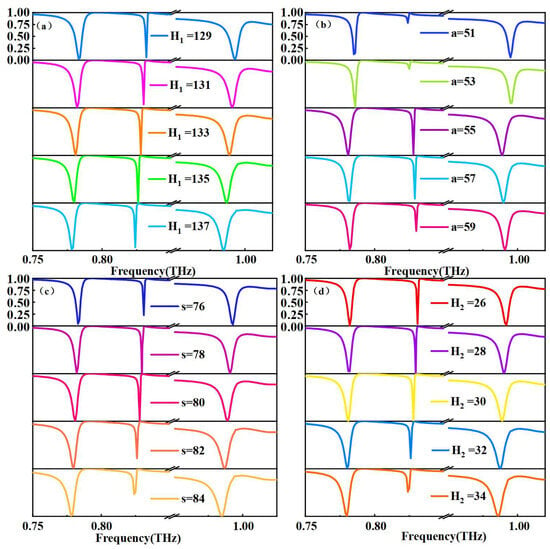
Figure 8.
Effects of metasurface unit structural parameters on transmission spectra: (a) Thickness of substrate H1. (b) Length of the side of the small cubic notch a. (c) Length of the side of the initial cubic block s. (d) Thickness of the structure H2.
3.3. Application of L-Type Metasurface
3.3.1. Tri-Band Quasi-BICs in Terahertz Biosensing
In order to investigate the sensing properties of the metasurface and take into account the refractive index of water (which is 1.33), we gradually increase the background refractive index n from 1.3 to 1.4 [47,48], as shown in Figure 9a. As the refractive index increases, Model A exhibits redshifting, and the corresponding frequency shift versus refractive index n is presented in Figure 9b. Model A in water exhibited a significant redshift compared with the case where the initial refractive index was set to 1.0, indicating that the presence of water affects the resonance characteristics of the metasurface. The sensitivity of the refractive index sensor can be described by S = Δλ/Δn, where Δλ is the wavelength shift of the transmission drop caused by the refractive index change [49]. The value of S for the resonance depression of Model A is 280 GHz/RIU, as determined by linear fitting.
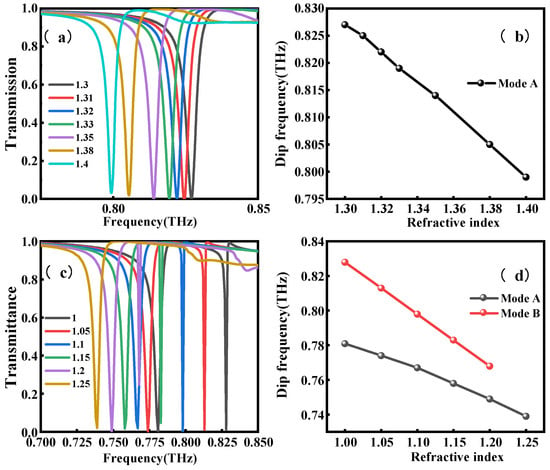
Figure 9.
Simulation of metasurface biosensing characteristics: (a) Transmission spectrum of mode A when the background refractive index n is changed from 1.3 to 1.4. (b) Effect of n on the resonance depression position and linear fitting results. (c) Transmission spectrum of mode B when the background refractive index n is changed from 1 to 1.25. (d) Effects of n on the resonance depression position and linear fitting results.
The figure of merit (FOM), an important parameter for the sensing performance, is defined as FOM = S/FWHM [50]. The FOM is 64.1 RIU−1 for Model A, and Model A and Model B also have good sensing characteristics for the refractive index range from 1 to 1.25. As shown in Figure 9c, Model B has a larger redshift frequency and a narrower FWHM than Model A. The S values are 164 GHz/RIU and 300 GHz/RIU, and the FOMs are 30.1 RIU−1 and 5367.8 RIU−1 for Model A and Model B, respectively, demonstrating that the metasurface has promising applications in narrowband biosensing.
In recent years, a variety of terahertz metasurface sensors have been proposed, especially for biochemical sensing and environmental monitoring. The sensitivity and the FOM of our designed sensors are compared as shown in Table 1.

Table 1.
The list for the performance metrics of various terahertz metasensors, including the resonance type, the sensitivity, and the FOM.
3.3.2. Polarization Characteristics of Tri-Band Quasi-BICs
As the value of G changes from 28 to 37 um, the transmission spectra of the metasurface under normal incidence of an x-polarized terahertz wave are presented in Figure 10a. There are three quasi-BICs corresponding to three narrowband resonance dips in the transmittance spectra: Model A = 0.781 THz, Model B = 0.828 THz, and Model C = 0.989 THz.
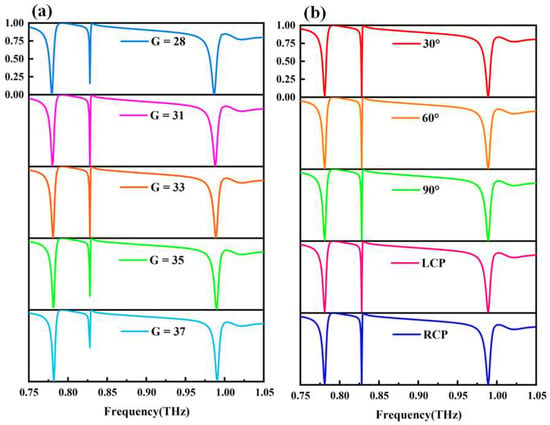
Figure 10.
(a) Transmission spectra of the metasurfaces with different asymmetry parameters. (b) Transmission spectra for five polarization states (specifically, 30°polarization, 60° polarization, y polarization, and left-handed and right-handed circular polarization) when G = 33 μm.
To demonstrate the polarization independence of the metasurface, the transmittance spectra for five other polarization states (specifically, 30° polarization, 60° polarization, y-polarization, and left-handed and right-handed circular polarization) are shown in Figure 10b. Most previously reported metasurfaces with protected BICs are polarization-correlated and require special polarization waves to excite sharp quasi-BICs [58,59,60]. In other words, the optical response of polarization-correlated metasurfaces changes with polarization. Since the tetrameric cluster always maintains C4v symmetry and mirror symmetry throughout the operation processes, all the resultant quasi-BICs are polarization-independent. Surprisingly, three resonance peaks consistently maintain a high magnitude for different polarization directions, which clearly implies that the three transmittance spectra are independent of polarization. Since the metasurface is insensitive to the polarization state of the incident light, it has wide application prospects and important research significance in the fields of imaging and sensing [61,62,63], communication and radar [64], security detection and imaging [65,66], photonics devices [67], and material characterization and detection [68].
4. Conclusions
In summary, a new design scheme for polarization-independent quasi-BIC resonance is achieved by applying a combination of specific displacement and collective disturbance on a metasurface composed of four silicon L-shaped structures and a quartz substrate. Through the analysis of far-field scattering and near-field electromagnetic distribution, it was revealed that the polarization-independence of quasi-BICs is due to the C4v symmetry maintained by the tetrameric cluster throughout the entire operation process. Moreover, different combinations of asymmetry and structural parameters were studied, and the results showed that this method can stably excite the three-band quasi-BICs. In addition, we will demonstrate the potential applications of metasurfaces in terahertz biosensing by measuring different refractive indices. Our findings provide a universal and simple structural design strategy for designing polarization-independent devices with multi-band polarization and quasi-BICs high-quality resonance and promote potential applications in biosensing [69], filtering [70], and lasers [71].
Author Contributions
Conceptualization, Y.R. and D.W.; methodology, Y.R.; software, Y.R.; validation, R.L., L.L. and X.L.; formal analysis, Y.R.; investigation, J.W.; resources, W.L.; data curation, J.L.; writing—original draft preparation, Y.R.; writing—review and editing, J.L.; visualization, D.W.; supervision, Q.L.; project administration, C.L.; funding acquisition, J.L. and P.K.C. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China [12304480]; Heilongjiang Provincial Natural Science Foundation of China [JQ2023F001]; Local Universities Reformation and Development Personnel Training Supporting Project from Central Authorities; Natural Science Foundation of Heilongjiang Province [LH2021F007]; China Postdoctoral Science Foundation funded project [2020M670881]; Study Abroad returnees merit based Aid Foundation in Heilongjiang Province (070-719900103); City University of Hong Kong Strategic Research Grant (SRG) [7005505]; City University of Hong Kong Donation Research Grants [DON-RMG 9229021 and 9220061].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The authors declare that this research study was conducted in the absence of any commercial or financial relationships that could be construed as potential conflicts of interest.
References
- Wang, R.; Xu, L.; Huang, L.; Zhang, X.; Ruan, H.; Yang, X.; Lou, J.; Chang, C.; Du, X. Ultrasensitive Terahertz Biodetection Enabled by Quasi-BIC-Based Metasensors. Small 2023, 19, 2301165. [Google Scholar]
- Sun, W.; Liang, Z.; Shi, X.; Yang, F.; Dong, Y.; Dai, R.; Jia, Y.; Xin, W.; Hou, E.; Wu, Z. Potential of high Q dual band Mid-Infrared metasurfaces with Quasi-BIC for refractive index sensing. Opt. Laser Technol. 2024, 174, 110631. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W.; Jiang, X.; Yan, H. High-Q toroidal dipole metasurfaces driven by bound states in the continuum for ultra-sensitive terahertz sensing. J. Light. Technol. 2021, 40, 2181–2190. [Google Scholar] [CrossRef]
- Algorri, J.; Dmitriev, V.; Hernández-Figueroa, H.; Rodríguez-Cobo, L.; Dell’olio, F.; Cusano, A.; López-Higuera, J.; Zografopoulos, D. Polarization-independent hollow nanocuboid metasurfaces with robust quasi-bound states in the continuum. Opt. Mater. 2023, 147, 114631. [Google Scholar] [CrossRef]
- Algorri, J.; Dell’olio, F.; Ding, Y.; Labbé, F.; Dmitriev, V.; López-Higuera, J.; Sánchez-Pena, J.; Andreani, L.; Galli, M.; Zografopoulos, D. Experimental demonstration of a silicon-slot quasi-bound state in the continuum in near-infrared all-dielectric metasurfaces. Opt. Laser Technol. 2023, 161, 109199. [Google Scholar] [CrossRef]
- Hsiao, H.H.; Hsu, Y.C.; Liu, A.Y.; Hsieh, J.C.; Lin, Y.H. Ultrasensitive refractive index sensing based on the quasi-bound states in the con-tinuum of all-dielectric metasurfaces. Adv. Opt. Mater 2022, 10, 2200812. [Google Scholar]
- Srivastava, Y.K.; Ako, R.T.; Gupta, M.; Bhaskaran, M.; Sriram, S.; Singh, R. Terahertz sensing of 7 nm dielectric film with bound states in the continuum metasurfaces. Appl. Phys. Lett. 2019, 115, 151105. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W.-H.; Yan, H. Toroidal dipole bound states in the continuum metasurfaces for terahertz nanofilm sensing. Opt. Express 2020, 28, 17102–17112. [Google Scholar] [CrossRef]
- Ouimet, M.; Cortés, J. Collective estimation of ocean nonlinear internal waves using robotic underwater drifters. IEEE Access 2013, 1, 418–427. [Google Scholar] [CrossRef]
- Wang, T.; Liu, S.; Zhang, J.; Xu, L.; Yang, M.; Ma, D.; Jiang, S.; Jiao, Q.; Tan, X. Dual high-Q Fano resonances metasurfaces excited by asymmetric dielectric rods for refractive index sensing. Nanophotonics 2024, 13, 463–475. [Google Scholar] [CrossRef]
- Lin, H.; Ye, X.; Chen, X.; Zhou, Z.; Yi, Z.; Niu, G.; Yi, Y.; Hua, Y.; Hua, J.; Xiao, S. Plasmonic absorption enhancement in graphene circular and elliptical disk arrays. Mater. Res. Express 2019, 6, 045807. [Google Scholar] [CrossRef]
- Cong, L.; Singh, R. Symmetry-protected dual bound states in the continuum in metamaterials. Adv. Opt. Mater. 2019, 7, 1900383. [Google Scholar] [CrossRef]
- Wu, C.; Arju, N.; Kelp, G.; Fan, J.A.; Dominguez, J.; Gonzales, E.; Tutuc, E.; Brener, I.; Shvets, G. Spectrally selective chiral silicon metasurfaces based on infrared Fano resonances. Nat. Commun. 2014, 5, 3892. [Google Scholar] [CrossRef] [PubMed]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Wang, M.; Li, B.; Wang, W. Symmetry-protected dual quasi-bound states in the continuum with high tunability in metasur-face. J. Opt. 2020, 22, 125102. [Google Scholar] [CrossRef]
- Kupriianov, A.S.; Xu, Y.; Sayanskiy, A.; Dmitriev, V.; Kivshar, Y.S.; Tuz, V.R. Metasurface engineering through bound states in the continuum. Phys. Rev. Appl. 2019, 12, 014024. [Google Scholar] [CrossRef]
- Zhou, C.; Pu, T.; Huang, J.; Fan, M.; Huang, L. Manipulating optical scattering of quasi-bic in dielectric metasurface with off-center hole. Nanomaterials 2021, 12, 54. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W. Ultrahigh-Q toroidal dipole resonance in all-dielectric metamaterials for terahertz sensing. Opt. Lett. 2019, 44, 5876–5879. [Google Scholar] [CrossRef]
- Meng, B.; Wang, J.; Zhou, C.; Huang, L. Bound states in the continuum supported by silicon oligomer metasurfaces. Opt. Lett. 2022, 47, 1549–1552. [Google Scholar] [CrossRef]
- Chen, Y.; Li, M.; Zhao, M.; Wang, J. Multiple quasibound states in the continuum of permittivity-asymmetric all-dielectric metasurface: Group-theoretical description. Opt. Mater. 2023, 138, 113693. [Google Scholar] [CrossRef]
- Kühne, J.; Wang, J.; Weber, T.; Kühner, L.; Maier, S.A.; Tittl, A. Fabrication robustness in BIC metasurfaces. Nanophotonics 2021, 10, 4305–4312. [Google Scholar] [CrossRef]
- Shi, T.; Deng, Z.-L.; Tu, Q.-A.; Cao, Y.; Li, X. Displacement-mediated bound states in the continuum in all-dielectric superlattice metasurfaces. PhotoniX 2021, 2, 7. [Google Scholar] [CrossRef]
- van Hoof, N.J.; Abujetas, D.R.; ter Huurne, S.E.; Verdelli, F.; Timmermans, G.C.; Sánchez-Gil, J.A.; Rivas, J.G. Unveiling the symmetry protection of bound states in the continuum with terahertz near-field imaging. ACS Photonics 2021, 8, 3010–3016. [Google Scholar] [CrossRef] [PubMed]
- Biswas, S.K.; Adi, W.; Beisenova, A.; Rosas, S.; Arvelo, E.R.; Yesilkoy, F. From weak to strong coupling: Quasi-BIC metasurfaces for mid-infrared light–matter interactions. Nanophotonics 2024, 13, 2937–2949. [Google Scholar] [CrossRef]
- Liu, Q.K.; Luo, X.Q.; Xu, X.; Li, Y.; Zhu, W.; Chen, Z.; Liu, W.M.; Wang, X.L. Interplay of bound states in the continuum empowers spectral-lineshape manipulation in all-dielectric metasurfaces. Phys. Rev. B 2023, 107, 205422. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, X.; Zhao, R.; Lu, G. Dual resonance based on quasi-bound states in continuum in the all-dielectric terahertz metasurface and its application in sensing. Results Phys. 2023, 49, 106518. [Google Scholar] [CrossRef]
- Labbé-Lavigne, S.; Barret, S.; Garet, F.; Duvillaret, L.; Coutaz, J.-L. Far-infrared dielectric constant of porous silicon layers measured by terahertz time-domain spectroscopy. J. Appl. Phys. 1998, 83, 6007–6010. [Google Scholar] [CrossRef]
- Hsiao, H.; Chu, C.H.; Tsai, D.P. Fundamentals and Applications of Metasurfaces. Small Methods 2017, 1, 1600064. [Google Scholar] [CrossRef]
- Hsu, W.L.; Chen, Y.C.; Yeh, S.P.; Zeng, Q.C.; Huang, Y.W.; Wang, C.M. Review of metasurfaces and metadevices: Advantages of different materials and fab-rications. Nanomaterials 2022, 12, 1973. [Google Scholar] [CrossRef]
- Shanei, M.M.; Fathi, D.; Ghasemifard, F.; Quevedo-Teruel, O. All-silicon reconfigurable metasurfaces for multifunction and tunable performance at optical frequencies based on glide symmetry. Sci. Rep. 2019, 9, 13641. [Google Scholar] [CrossRef]
- Han, S.; Cong, L.; Srivastava, Y.K.; Qiang, B.; Rybin, M.V.; Kumar, A.; Jain, R.; Lim, W.X.; Achanta, V.G.; Prabhu, S.S.; et al. All-Dielectric active terahertz photonics driven by bound states in the continuum. Adv. Mater. 2019, 31, e1901921. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, N.; Kim, I.; Mehmood, M.Q.; Jeong, H.; Akbar, A.; Lee, D.; Saleem, M.; Zubair, M.; Anwar, M.S.; Tahir, F.A.; et al. Polarisation insensitive multifunctional metasurfaces based on all-dielectric nanowaveguides. Nanoscale 2018, 10, 18323–18330. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J.; Liu, X.; Liang, Z.; Zhu, J. Ultra-wideband perfect reflection and tunneling by all-dielectric metamaterials. Opt. Lett. 2021, 46, 849–852. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Zeng, B.; Wang, C.; Gao, P.; Liu, K.; Pu, M.; Jin, J.; Zhao, Z.; Li, X.; Yu, H.; et al. Fabrication of anisotropically arrayed nano-slots metasurfaces using reflective plasmonic lithography. Nanoscale 2015, 7, 18805–18812. [Google Scholar] [CrossRef]
- Saadabad, R.M.; Huang, L.; Miroshnichenko, A.E. Polarization-independent perfect absorber enabled by quasi-bound states in the continuum. Phys. Rev. B 2021, 104, 235405. [Google Scholar]
- Azzam, S.I.; Kildishev, A.V. Photonic bound states in the continuum: From basics to applications. Adv. Opt. Mater. 2020, 9. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Rybin, M.V.; Koshelev, K.L.; Sadrieva, Z.F.; Samusev, K.B.; Bogdanov, A.A.; Limonov, M.F.; Kivshar, Y.S. High-Q supercavity modes in subwavelength dielectric resonators. Phys. Rev. Lett. 2017, 119, 243901. [Google Scholar]
- Tang, C.; Yan, B.; Wang, Q.; Chen, J.; Yan, Z.; Liu, F.; Chen, N.; Sui, C. Toroidal dipolar excitation in metamaterials consisting of metal nanodisks and a dielectrc spacer on metal substrate. Sci. Rep. 2017, 7, 582. [Google Scholar] [CrossRef]
- Yang, B.; Liu, W.; Li, Z.; Cheng, H.; Choi, D.-Y.; Chen, S.; Tian, J. Ultrahighly saturated structural colors enhanced by multipolar-modulated metasurfaces. Nano Lett. 2019, 19, 4221–4228. [Google Scholar] [CrossRef]
- Prokhorov, A.V.; Gubin, M.Y.; Shesterikov, A.V.; Arsenin, A.V.; Volkov, V.S.; Evlyukhin, A.B. Lasing Effect in Symmetrical van der Waals Heterostructured Metasurfaces Due to Lattice-Induced Multipole Coupling. Nano Lett. 2023, 23, 11105–11111. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Huang, L.; Jin, R.; Xu, L.; Li, G.; Rahmani, M.; Chen, X.; Lu, W.; Miroshnichenko, A.E. Bound states in the continuum in asymmetric dielectric metasurfaces. Laser Photonics Rev. 2022, 17, 2200564. [Google Scholar] [CrossRef]
- Terekhov, P.D.; Babicheva, V.E.; Baryshnikova, K.V.; Shalin, A.S.; Karabchevsky, A.; Evlyukhin, A.B. Multipole analysis of dielectric metasurfaces composed of non-spherical nanoparticles and lattice invisibility effect. Phys. Rev. B 2019, 99, 045424. [Google Scholar]
- Evlyukhin, A.B.; Reinhardt, C.; Seidel, A.; Luk’yanchuk, B.S.; Chichkov, B.N. Optical response features of Si-nanoparticle arrays. Phys. Rev. B 2010, 82, 045404. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Y.; Zhu, Y.; Cui, Z.; Sun, G.; Zhang, X.; Yao, Z.; Zhang, X.; Zhang, K. Ultra-high Q resonances governed by quasi-bound states in the continuum in all-dielectric THz metamaterials. Opt. Commun. 2022, 520, 128555. [Google Scholar] [CrossRef]
- Wu, J.; Jiang, H.T.; Guo, Z.; Sun, Y.; Li, Y.; Chen, H. Giant optical chirality in dielectric metasurfaces induced by toroidal dipole resonances. Opt. Lett. 2023, 48, 916–919. [Google Scholar] [CrossRef]
- Maleki, J.; Fathi, D. Refractive index sensor based on fano-magnetic toroidal quadrupole resonance enabled by bound state in the continuum in all-dielectric metasurface. Sci. Rep. 2024, 14, 4110. [Google Scholar] [CrossRef]
- Wang, T.; Liu, S.; Zhang, J.; Xu, L.; Yang, M.; Han, B.; Ma, D.; Jiang, S.; Jiao, Q.; Tan, X. Highly sensitive polarization-tunable Fano resonant metasurface excited by BICs for re-fractive index detection. Results Phys. 2024, 58, 107451. [Google Scholar]
- Yanik, A.A.; Cetin, A.E.; Huang, M.; Artar, A.; Mousavi, S.H.; Khanikaev, A.; Connor, J.H.; Shvets, G.; Altug, H. Seeing protein monolayers with naked eye through plasmonic Fano resonances. Proc. Natl. Acad. Sci. USA 2011, 108, 11784–11789. [Google Scholar] [CrossRef]
- Sherry, L.J.; Chang, S.-H.; Schatz, G.C.; Van Duyne, R.P.; Wiley, B.J.; Xia, Y. Localized surface plasmon resonance spectroscopy of single silver nanocubes. Nano Lett. 2005, 5, 2034–2038. [Google Scholar] [CrossRef]
- Pan, W.; Yan, Y.; Ma, Y.; Shen, D. A terahertz metamaterial based on electromagnetically induced transparency effect and its sensing performance. Opt. Commun. 2019, 431, 115–119. [Google Scholar] [CrossRef]
- Yahiaoui, R.; Tan, S.; Cong, L.; Singh, R.; Yan, F.; Zhang, W. Multispectral terahertz sensing with highly flexible ultrathin metamaterial absorber. J. Appl. Phys. 2015, 118, 083103. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, H.; Yan, X.; Liang, L.; Wei, D.; Wang, M.; Yang, Q.; Yao, J. Sensitive detection of cancer cell apoptosis based on the non-bianisotropic metamaterials biosensors in terahertz frequency. Opt. Mater. Express 2018, 8, 659–667. [Google Scholar] [CrossRef]
- Gupta, M.; Srivastava, Y.K.; Manjappa, M.; Singh, R. Sensing with toroidal metamaterial. Appl. Phys. Lett. 2017, 110, 121108. [Google Scholar] [CrossRef]
- Ma, S.; Li, F.; Su, Y.; Chen, L.; Song, Y.; Ye, J. Detection of benzoic acid additive based on a terahertz metasurface sensor. Photonics 2023, 10, 663. [Google Scholar] [CrossRef]
- Kameshkov, O.; Gerasimov, V.; Kuznetsov, S. Sensing performance analysis of spiral metasurface utilizing phase spectra measurement technique. Photonics 2023, 10, 243. [Google Scholar] [CrossRef]
- Janneh, M.; De Marcellis, A.; Palange, E.; Tenggara, A.T.; Byun, D. Design of a metasurface-based dual-band Terahertz perfect absorber with very high Q-factors for sensing applications. Opt. Commun. 2018, 416, 152–159. [Google Scholar]
- Wang, X.; Li, S.; Zhou, C. Polarization-independent toroidal dipole resonances driven by symmetry-protected BIC in ultra-violet region. Opt. Express 2020, 28, 11983–11989. [Google Scholar]
- Ding, J.; Huang, L.; Luo, Y.; Wang, T.; Hu, J.; Li, R.; Xiao, S. Multi-Band Polarization-Independent Quasi-Bound States in the Continuum Based on Te-tramer-Based Metasurfaces and Their Potential Application in Terahertz Microfluidic Biosensing. Adv. Opt. Mater. 2023, 11, 2300685. [Google Scholar]
- Liu, D.; Yu, X.; Wu, F.; Xiao, S.; Itoigawa, F.; Ono, S. Terahertz high-Q quasi-bound states in the continuum in laser-fabricated metallic double-slit arrays. Opt. Express 2021, 29, 24779–24791. [Google Scholar] [CrossRef]
- Zheng, Z.; Rocco, D.; Ren, H.; Sergaeva, O.; Zhang, Y.; Whaley, K.B.; Ying, C.; de Ceglia, D.; De-Angelis, C.; Rahmani, M.; et al. Advances in nonlinear metasurfaces for imaging, quantum, and sensing applications. Nanophotonics 2023, 12, 4255–4281. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; Lin, R.; Fu, Y.; Gong, G.; Zhou, X.; Wang, S.; Zhu, S.; Wang, Z. Advanced optical imaging based on metasurfaces. Adv. Opt. Mater. 2023, 12, 2203149. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, J.; Yang, X. Chiral grayscale imaging with plasmonic metasurfaces of stepped nanoapertures. Adv. Opt. Mater. 2019, 7, 201801467. [Google Scholar] [CrossRef]
- Mishra, K.V.; Hodge, J.A.; Zaghloul, A.I. Reconfigurable metasurfaces for radar and communications systems. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; pp. 1–4. [Google Scholar]
- Zeng, B.; Huang, Z.; Singh, A.; Yao, Y.; Azad, A.K.; Mohite, A.D.; Taylor, A.J.; Smith, D.R.; Chen, H.T. Hybrid graphene metasurfaces for high-speed mid-infrared light modulation and sin-gle-pixel imaging. Light Sci. Appl. 2018, 7, 51. [Google Scholar] [CrossRef]
- Keren-Zur, S.; Tal, M.; Fleischer, S.; Mittleman, D.M.; Ellenbogen, T. Generation of spatiotemporally tailored terahertz wavepackets by nonlinear metasurfaces. Nat. Commun. 2019, 10, 1–6. [Google Scholar] [CrossRef]
- Ahmed, H.; Kim, H.; Zhang, Y.; Intaravanne, Y.; Jang, J.; Rho, J.; Chen, S.; Chen, X. Optical metasurfaces for generating and manipulating optical vortex beams. Nanophotonics 2022, 11, 941–956. [Google Scholar] [CrossRef]
- Huang, Y.-W.; Lee, H.W.H.; Sokhoyan, R.; Pala, R.A.; Thyagarajan, K.; Han, S.; Tsai, D.P.; Atwater, H.A. Gate-tunable conducting oxide metasurfaces. Nano Lett. 2016, 16, 5319–5325. [Google Scholar] [CrossRef]
- Gladyshev, S.; Karamanos, T.D.; Kuhn, L.; Beutel, D.; Weiss, T.; Rockstuhl, C.; Bogdanov, A. Inverse design of all-dielectric metasurfaces with accidental bound states in the continuum. Nanophotonics 2023, 12, 3767–3779. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Xing, X.; Zou, D.; Mao, B.; Yao, J.-Q.; Ouyang, C.; Wang, Z.; Wu, L. Terahertz narrowband filter metasurfaces based on bound states in the continuum. Opt. Express 2023, 31, 35272–35281. [Google Scholar] [CrossRef]
- Yang, J.; Huang, Z.; Maksimov, D.N.; Pankin, P.S.; Timofeev, I.V.; Hong, K.; Li, H.; Chen, J.; Hsu, C.; Liu, Y.; et al. Low-threshold bound state in the continuum lasers in hybrid lattice resonance metasurfaces. Laser Photonics Rev. 2021, 15, 2100118. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).