Effects of Adding Al/Fe Content on the Wear Properties in CoCrNi Medium-Entropy Alloy Coatings Deposited by Laser Cladding

Abstract

CoCrNi medium-entropy alloy (MEA) coatings prepared using laser cladding (LC) with unique properties have aroused great interest in recent years and have been widely studied. However, limited studies have been conducted on the effect of adding Al/Fe on the wear properties of CoCrNi MEA coatings prepared on the surface of stainless steel. In this study, AlCoCrFeNi, CoCrFeNi, and CoCrNi MEA LC coatings were prepared on a stainless steel substrate. The grain structures and microscopic morphologies of coatings were characterized, and the wear mechanisms were analyzed using the nano-indentation and wear tests. The hardness-strengthening mechanism was theoretically investigated using phase diagrams and molecular dynamics (MD). The phase diagram results show that the addition of Al lowered the nucleation initiation temperature, thereby increasing the nucleation rate and forming more grains. Moreover, according to the Voronoi volumes and mean–square atomic displacements (MASD) results using MD, the addition of Al makes the appearance of severe localized lattice distortions, while the addition of Fe tends to form short-range ordered structures. In summary, fine-grain strengthening and the hardness strengthening caused by local lattice distortion were the main strengthening mechanisms of AlCoCrFeNi. These findings are highly significant for expanding the application potential and provide profound insights into the wear properties of the CoCrNi MEA coatings.

1. Introduction

The quest for novel materials with superior mechanical properties in the surface engineering field has driven technological advancements. Medium-entropy alloys (MEAs) have emerged as promising materials with excellent mechanical strength and chemical stability owing to their unique composition and microstructure [1,2,3]. Among the various HEAs, the CoCrNi-based [4,5,6,7,8] MEAs have gained significant attention due to their remarkable combination of mechanical properties, making them a potential candidate for a wide range of surface engineering applications.

Laser cladding (LC) is a widely used material surface modification technique that improves surface properties by cladding certain materials onto the surface using a laser beam. At the same time, laser cladding has unique properties, such as low processing cost, fast cooling speed, and convenient operation. Many CoCrNi-based coatings with excellent performance are prepared using LC [9,10,11].

In the preparation of high-hardness coatings, K. Xiang et al. [12] successfully prepared CoCrNiTi coatings by adding Ti to the CoCrNi system to strengthen the solid solution. Due to the slow diffusion of Ti in MEA, the solution strengthening effect was increased, which greatly improved the hardness and wear resistance of the coating. X. Liu et al. [13] investigated adding Ti/Al to analyze the wear properties of the CrCoNi-(Ti, Al) coatings using LC. The wear performance of CrCoNiTi and CrCoNiAl coatings was enhanced by the combined effects of solid-solution and second-phase strengthening after adding Ti and Al. The above studies successfully demonstrated that the high-entropy effect [14,15,16] and sluggish diffusion effect [17,18], which were core effects [19,20] of MEAs, played a vital role in the mechanical properties of CoCrNi-based MEAs. Obviously, the different elemental compositions have a crucial influence on the quality of the CoCrNi-based cladding coatings. Lee et al. [21] studied the performance changes of Al_7.5CoCrNi by adding Al. They found that the addition of Al resulted in the formation of a precipitate phase containing NiAl, which refined the grain size and improved the plastic deformation properties. Additionally, the incorporation of Fe can also enhance the wettability between the coating and the substrate (stainless steel). At present, limited research on the strengthening mechanism of CoCrNi-based LC coatings by adding Al/ Fe has been reported.

In this paper, AlCoCrFeNi, CoCrFeNi, and CoCrNi coatings prepared using laser cladding were chosen to investigate. The effects of adding Al/Fe on the grain structure, microstructure, and wear properties of the three coatings were evaluated through experiments. In addition, molecular dynamics studies were carried out to reveal the strengthening mechanism of the MEA coatings due to local lattice distortion. The investigation of CoCrNi MEA coatings shall achieve a better understanding of their industrial application.

2. Experimental Procedures

2.1. Preparation of Laser Cladding Coatings

Commercial stainless steel (P550) with a thickness of 10 mm was used as the substrate. The experimental equipment utilized a semiconductor laser (LDM1050, Zhongke Yuchen Laser Intelligent Technology Co., Ltd, Nanjing, China). Commercial AlCoCrFeNi, CoCrFeNi, and CoCrNi powders (prepared using vacuum air atomization) were chosen as the laser cladding (LC) materials. Figure 1a shows the atomic size and element mixed enthalpy of binary pairs (ΔH). It is worth noting that the ΔH between these introduced elements, Fe, Ni, and Co, is close to 0, indicating that they have remarkably high mutual solubility. The parameters in the LC preparation process are listed in

Table 1. The set parameters in the LC process.

Laser Power	Spot Diameter	Feeding Speed	Scanning Speed
1200 W	5 mm	10 g·min−1	20 mm·s−1

. Figure 1b shows the schematic diagram of the LC preparation process.

After the LC preparation, the coatings were cut into specimens with 10 mm × 10 mm × 10 mm by wire electrical discharge cutting and polished for the following characterization. The AlCoCrFeNi, CoCrFeNi, and CoCrNi coatings are designated as M1, M2, and M3, respectively, for ease of description.

2.2. Characterization Methods

The microstructures and worn tracks of obtained M1, M2, and M3 coatings were characterized using electron scanning microscopy (SEM, LYRA3 GMU, TESCAN CHINA, Ltd., Shanghai, China), with elemental distribution (EDS). The crystalline structure of the coated specimens was characterized using an X-ray diffractometer (XRD, Empyrean, Malvern Panalytical Ltd., Malvern, UK) with Cu Kα radiation (λ = 1.54 Å) operating at 45 kV voltage and 40 mA over a scanning range from 10° to 90°. The grain structures were further analyzed using electron backscatter diffraction (EBSD, JEOL JSM-7900F, JEOL Japan Electronics Co., Ltd., Tokyo, Japan). The nano-indentation test was carried out on a tester (U9820A G200, Agilent Co., Ltd., Santa Clara, CA, USA). EBSD data were processed subsequently using Channel 5 software, and the external load of Schmid factor maps is on the Z-axis, consistent with the direction of nano-indentation.

2.3. CALPHAD Simulation and MD Simulation Analysis

The Calculation of Phase Diagram (CALPHAD) simulations of AlCoCrFeNi, CoCrFeNi, and CoCrNi MEAs were established on the CALPHAD software Pandat (CompuTherm Co., Ltd., database2023, Middleton, WI, USA).

Molecular dynamics (MD) simulations were carried out with LAMMPS [22] code. AlCoCrFeNi, CoCrFeNi, and CoCrNi systems were set up using embedded atom method (EAM) potential merged with the optimized Lennard-Jones (LJ) coefficients (see Figure 2). The optimized LJ parameters are listed in

Table 2. LJ potential parameters AlCoCrFeNi, CoCrFeNi, and CoCrNi systems.

	Al	Co	Cr	Fe	Ni
σ (ev)	0.392	0.004	0.502	0.526	0.520
$\epsilon$ (Å)	2.620	2.584	2.336	2.321	2.282

.

2.4. Wear Properties Test

The wear properties of obtained M1, M2, and M3 coatings were performed using a material friction machine (HT-1000, Lanzhou, China) at 25 °C. The test parameters were set as follows: load 9.5 N, grinding ball Φ5 mm Si₃N₄ ceramic ball, test time 30 min.

3. Results and Discussion

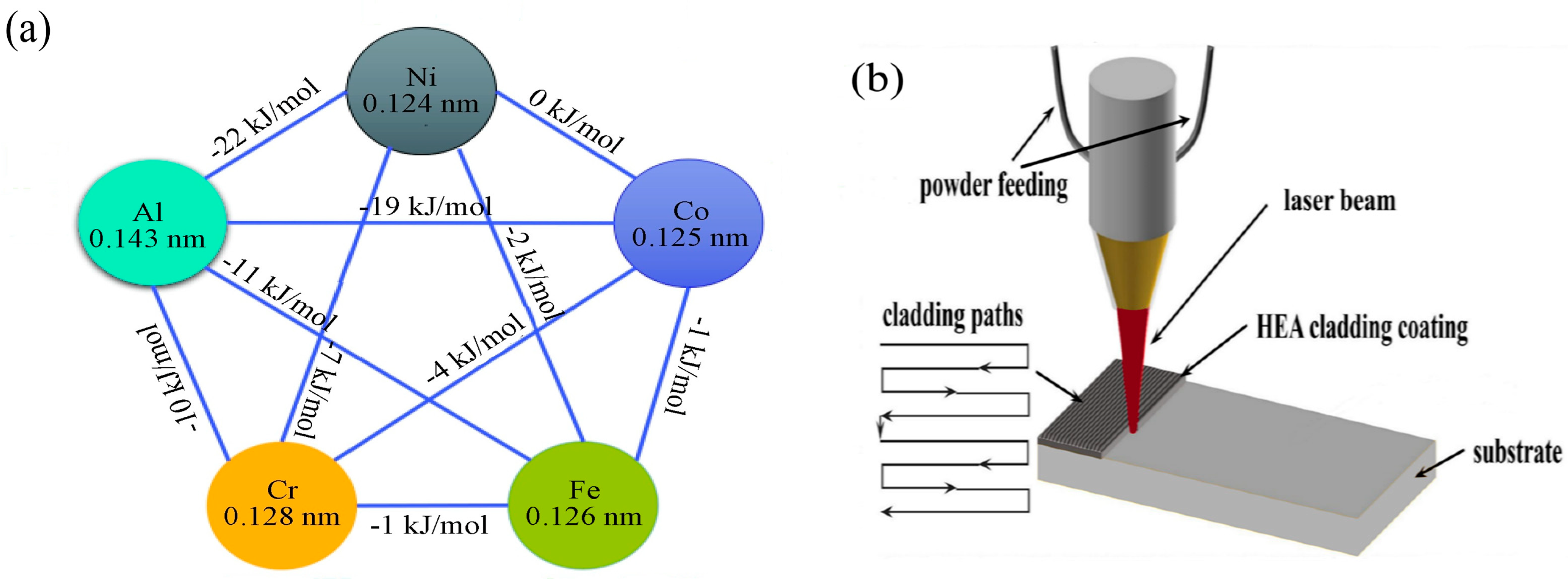
3.1. Cross-Section of Obtained Coatings Analysis

Figure 3 shows the cross-section maps of M1, M2, and M3 coatings using SEM. The three coatings exhibit different morphology appearances, with obvious elongated columnar crystals observed in M2 and M3 but not in M1. However, approximately the same coating thickness is observed, around 440 μm. According to the extensively used classical heat input equation [23], Equation (1), for LC, the generated heat input K in the melt pool is considered the same when under the same process parameters. Berger and Uporov’s studies [24,25] have shown that there is no significant statistical difference in the thermophysical properties of the three alloys, such as thermal conductivity and coefficient of thermal expansion.

$$\mathrm{K}={\displaystyle \frac{\mathrm{W}}{v\cdot d}}$$

(1)

where W is the laser power (w), v is the scanning speed (mm·s⁻¹), and d is the laser spot diameter (mm).

In addition, Zhou’s [26] study reveals that coatings prepared with the same process have the same thickness. Thus, these factors contribute to the approximately identical thickness of coatings M1, M2, and M3.

An element line scan was further used to understand the dissolution of the coating elements. The element line scan results are also attached in Figure 3. The content of the Fe element shows a significant decreasing trend due to the high proportion of Fe in the substrate (about 64%) and the lower proportion in the coating. For coating M1, the Al, Co, and Ni elements show an upward trend. In addition, the elements in the coating are not completely equal to the nominal due to the dilution of the Cr element in the substrate into the coating, while some of the other elements are burned off during the fusion cladding process. This dilution makes coatings form a good metallurgical bond with the substrate, which does not easily fall off and protects the substrate well.

Based on the empirical parameters of the medium-entropy alloys, it is predictable whether a solid solution can be formed, as well as the type of structure of the solid solution. The calculated results of M1, M2, and M3 MEAs are listed in

Table 3. Empirical parameters of the MEAs.

	ΔSmix (Mixing Entropy)	ΔHmix (Mixing Enthalpy)	δ (%)	VEC
M1	1.34R	−5.11	3.33	7.77
M2	1.39R	−3.75	1.20	8.25
M3	1.10R	−4.89	0.16	8.16

, based on Equations (2)–(6) below:

$$\delta =100\sqrt{{\displaystyle {\sum }_{i=1}^n{c}_i{\left(1-r_i/\overline{r}\right)}^2}}$$

(2)

$$\overline{r}={\displaystyle {\sum }_{i=1}^n{c}_i{r}_i}$$

(3)

$$\Delta S_{mix}=-R{\displaystyle {\sum }_{i=1}^n{c}_i\ln c_i}$$

(4)

$$\Delta H_{mix}={\displaystyle {\sum }_{i=1,i\ne j}^{n}4\Delta H_{ij}^{mix}{c}_i{c}_j}$$

(5)

$$\mathit{VEC}=c_i{\displaystyle \sum VE{C}_i}$$

(6)

where $c_i$ is the atomic fraction (at.), $r_i$ is the atomic radius, $VE{C}_i$ is the valence electrons, $\overline{r}$ is the average radius, δ is atomic radius discrepancy, ΔS_mix is mixing entropy, and $\Delta H_{ij}^{mix}$ is the mixing enthalpy.

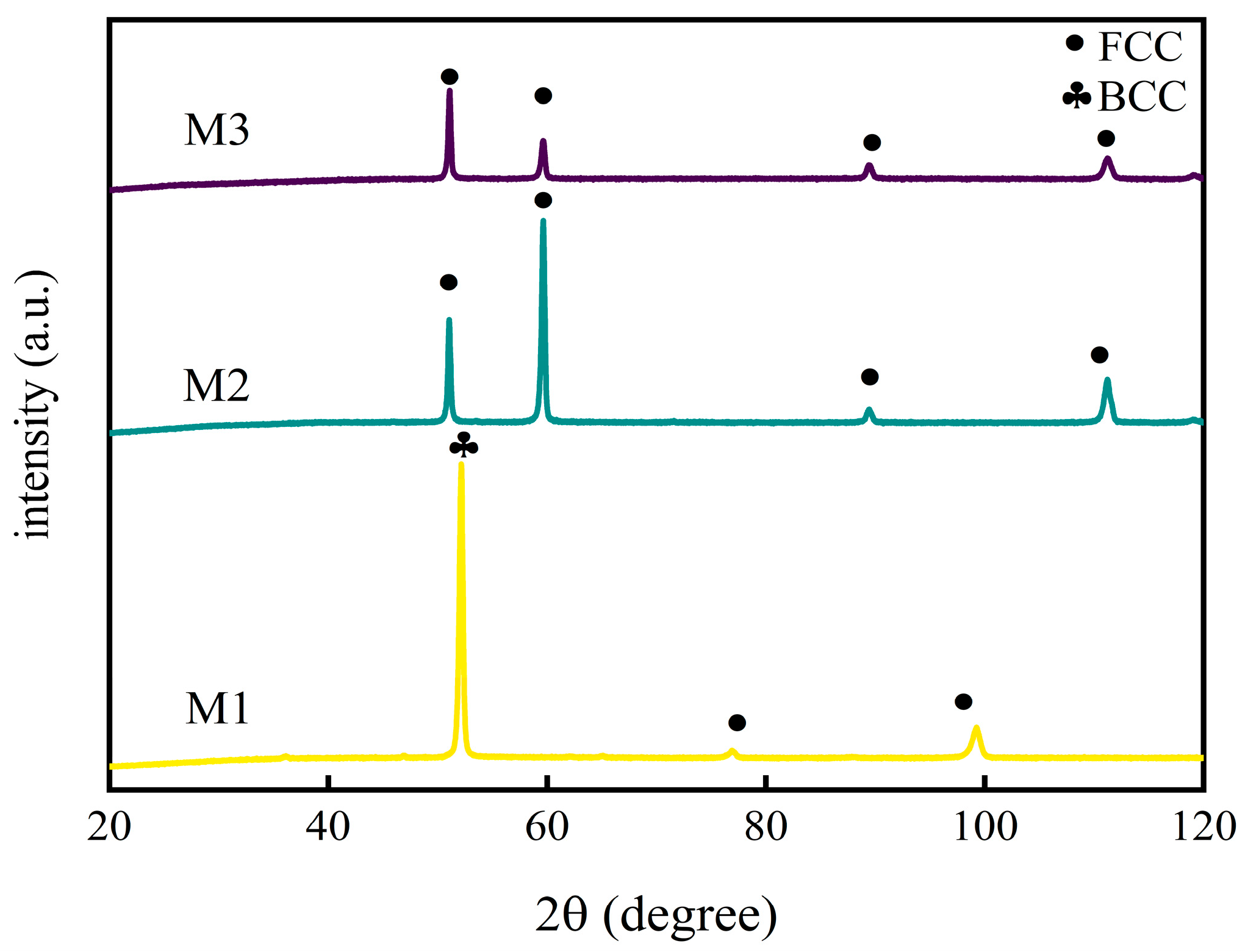
Based on the calculation results and comparison with empirical parameters [27], M2 and M3 MEAs can form a single solid solution in a typical non-equilibrium state, while M1 does not satisfy this condition. Figure 4 shows the XRD curves of M1, M2, and M3 coatings. The M2 and M3 coatings show approximately the same characteristic peaks of the FCC structure, while M1 shows an FCC structure with some BCC structures, which is consistent with the previous parameter calculations. In addition, the fast cooling rate of the coating surface during LC makes the martensitic transformation easy to realize and promotes the precipitation of the BCC phase structure [28]. In M1, the BCC phase is an (α-Fe, AlNi)-based solid solution, while the FCC phase is an FeNi-based solid solution. In M2, the coating consists of a single FCC (PDF#47–1417) phase. In M3, the XRD peak is assigned as the (111) peak of FCC CoCrNi (with reference to ICDD 00-033-0945). Lou and Liu et al. [29] found that when solute atoms of a larger radius entered the solid solution structure, it led to lattice distortion in the solid solution, which would show up as shifted peaks on the XRD peak spectra.

Table 4. Atomic radius (Å).

Al	Co	Cr	Fe	Ni
1.82	1.67	1.85	1.72	1.62

shows the atomic radii. Shifts observed in Figure 4 of the M2 and M3 coatings are inferred to be lattice distortion caused by the dissolution of Fe into the CoCrNi solid solution, and the specific mechanism of the effect will be described below. For M1, new phases are created, which will be discussed later.

3.2. Grain Structure Analysis

To further study the grain structure of coatings M1, M2, and M3 and its effect on the mechanical properties of coatings, the micrograins were characterized using EBSD. Figure 5 shows the pictures of coatings M1, M2, and M3 using EBSD characterization. Different grain structures are observed, as shown in the inverse pole figures (IPFs). For M1, the grains do not exhibit significant orientation characteristics. However, for coatings M2 and M3, elongated columnar grains are observed, distinct from the fine equiaxed grains in M1. Moreover, M2 and M3 show a strong orientation in the [001] direction. The grain structures of coatings M2 and M3 are approximately the same, showing a typical FCC structure. This can be explained by the non-equilibrium nucleation density equation [30] shown in Equation (7) for both coatings. M2 and M3 were fabricated at the same laser power, which means the same heat input and ΔT, so their nucleation densities were the same. For M1, the grains are different, which will be discussed in the following part.

$$\epsilon (\Delta T)={\displaystyle \underset{0}{\overset{\Delta T}{\int }}\frac{dn}{d(\Delta T)}}d(\Delta T)={\displaystyle \frac{{\epsilon }_{\max }}{\Delta T_0}}{\displaystyle \underset{0}{\overset{\Delta T}{\int }}\exp }\left[{\displaystyle \frac{{(\Delta T-\Delta T_{\sigma })}^2}{2\Delta T_{\sigma }}}\right]d(\Delta T)$$

(7)

where ε_max is the nucleation density, ΔT_σ is the temperature change standard deviation, and ΔTε is the subcooling.

EBSD was used to characterize the grain boundary misorientations, displacement density, and Smith factor of coatings M1, M2, and M3. Low-angle grain boundaries (LAGBs) represent large lattice distortions [31] (the green lines in the map). M1 has the highest LAGBs, almost two times more than M3, as seen in the data attached in Figure 5. On the basis of the characterization results, the dislocation strength was calculated using Equation (8). The dislocation density of the characterized region (ρ) of coatings M1, M2, and M3 are 0.92 × 10¹⁴, 0.40 × 10¹⁴, and 0.39 × 10¹⁴ m⁻², respectively.

$$\rho ={\displaystyle \frac{2{\rho }_{\mathrm{ave}}}{\overrightarrow{\mathrm{v}}\times \mathrm{u}}}$$

(8)

where ρ_ave is the core average misorientation of the characterized region (°), $\overrightarrow{\mathrm{v}}$ refers to the Burgers vector (nm), and u represents the step size (nm).

Yield strength represents the plastic deformation ability of the materials. The relationship between the critical shear stress τ and yield strength θ as well as the Schmid factor can be expressed in Equation (9).

$$\tau =\theta (SF)\cdot \cos \phi (SF)\cdot \cos \gamma$$

(9)

where SF refers to the value of the Schmid factor coefficient.

Since τ remains constant in certain metals, the smaller the Schmid factor coefficient values, the larger θ, in which case plastic deformation is less likely to occur. As a result, coating M1 is more resistant to plastic deformation compared to the other two coatings. There is also a part of the study wherein Schmid factors represent the percentage of soft particles on the surface of the material. From this aspect, it can also be concluded that coating M1 has lower soft particles and higher hardness compared to the other two coatings.

3.3. Nano-Indentation Test Analysis

The mechanical properties of coatings M1, M2, and M3 were measured using nano-indentation. The hardness (H) and elastic modulus (E) are usually applied to evaluate the plastic deformability of the material under test [32]. Specifically, the magnitude of a material’s modulus of elasticity relates to the ease with which the material undergoes elastic deformation.

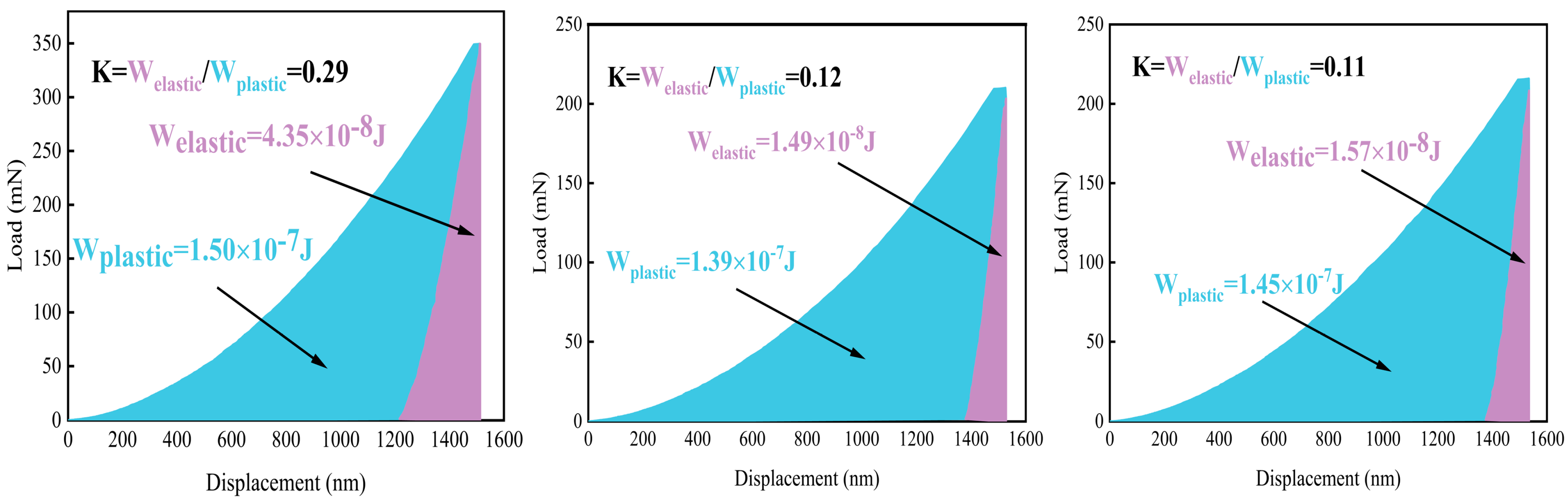
Figure 6 shows the data curves using Oliver and Pharr’s method [33]. The integral area between the loading curve and the x-axis is the total work (W_total), and the integral area of the unloading curve and the x-axis is the elastic deformation work (W_elastic). Consequently, the integral area between the loading and unloading curves is the plastic deformation work (W_plastic). The formulas for all three are listed as Equations (10)–(12):

$${\mathrm{W}}_{\mathrm{total}}={\displaystyle \underset{0}{\overset{i_{\max }}{\int }}{F}_a}dh$$

(10)

$${\mathrm{W}}_{\mathrm{elastic}}={\displaystyle \underset{{\mathrm{r}}_{\max }}{\overset{i_{\max }}{\int }}{F}_u}dh$$

(11)

$${\mathrm{W}}_{\mathrm{plastic}}{=\mathrm{W}}_{\mathrm{total}}-{\mathrm{W}}_{\mathrm{elastic}}$$

(12)

where i is the indentation depth (nm), F_a is the load force (N), r is the residual indentation depth (nm), and F_u is the unloading force (N). The ratio of W_elastic and W_plastic, called the K value, represents the capacity when subject to certain loads.

Based on the values recorded in real-time from the tests, calculations were performed to study the three coatings’ H/E* and H³/E*², as listed in

Table 5. The calculated data (GPa).

	H	E*	H/E*	H3/E*2
M1	8.37 ± 0.1	341.60	0.0245	0.0050
M2	7.68 ± 0.4	329.94	0.0232	0.0041
M3	7.52 ± 0.2	325.01	0.0231	0.0040

, where H is the ratio of nano-hardness, E*is the effective modulus of elasticity, the value of H/E* indicates wear resistance, and H³/E*² is the deformation resistance. It is clear from the data that coating M1 has higher values than coatings M2 and M3, indicating that it has optimal wear and plastic deformation resistance, which further supports the results of the analysis on the Smith factor coefficient. In addition, it can be intuitively seen that the addition of Al increases the H and E*values, but the addition of Fe is less pronounced than Al.

3.4. CALPHAD and MD Simulation Analysis

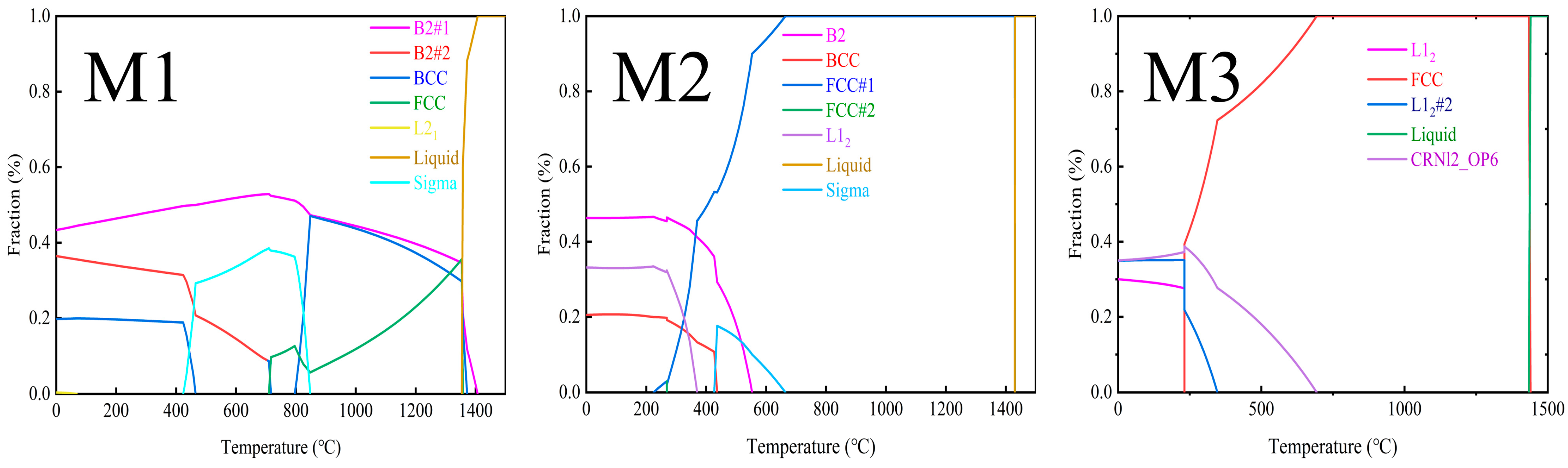
The CALPHAD helps understand alloys’ compositional changes as a temperature function [34,35,36]. To understand the phase composition of the MEAs in-depth, especially the variation of their phase compositions with temperature, the CALPHAD phase diagrams of M1, M2, and M3 MEAs are carried out, as shown in Figure 7. Both M1 and M2 are close in melting points (about 1400 °C). The B2 phase (40%) is the major phase at the range of 0–20 °C. However, in the XRD results, B2 phases (ordered body-centered cubic structure) are not detected due to the Fe element in the substrate entering the coating. For M3, L1₂ phases (ordered face-centered cubic structure) are the main phase, consistent with the XRD results in Figure 4.

In conjunction with the CALPHAD, we further modeled the melt temperatures as well as the supercooling of CoCrFeNi and AlCoCrFeNi systems at approximate equilibrium solidification conditions. It is thus derived that the T_N of CoCrFeNi and AlCoCrFeNi is 62.1 and 9.1 °C, using Equations (13) and (14):

$$\Delta {\mathrm{T}}_N=T_{EQ}-T_N$$

(13)

$$\Delta {\mathrm{T}}_{MAX}=T_{EQ}-T_{RE}$$

(14)

where ΔT_N is the nucleation supercooling, ΔT_MAX is the max nucleation supercooling, T_EQ is the liquid-phase line temperature, T_N is the nucleation start temperature, and T_RE is the re-glow start temperature. Zhang et al. [37] concluded that alloys with higher alloy-growth limiting factors (Q) could form a larger compositional supercooling region at a faster rate at the solid/liquid (S/L) interface front, thereby refining the solidification organization.

The T_N of AlCoCrFeNi MEA is smaller, so the energy required for nucleation is lower, the nucleation rate increases, and more nuclei can be formed; therefore, the grain size is the smallest. This is in agreement with the EBSD results.

MD simulations give a good insight into the microscopic mechanisms of the atomic composition of medium-entropy alloys. Xu et al. [38] investigated the microstructure of high-entropy alloys at different temperatures using molecular dynamics methods to determine their effect on atomic size differences. Thus, the AlCoCrFeNi and CoCrFeNi MEA systems were built, in which the lattice parameters and atomic-force model are in reference to Mayahi’s [39] and Deluigi’s [40] simulations, respectively.

Table 6. Voronoi volumes (ų).

Alloy	Al	Co	Cr	Fe	Ni
AlCoCrFeNi	13.49	13.42	13.47	13.45	13.41
CoCrFeNi	-	11.72	11.91	11.78	11.77

shows the Voronoi volumes of AlCoCrFeNi and CoCrFeNi MEAs at 298 K. The Voronoi volume is the nearest neighborhood space of atoms, which incorporates the effects of interatomic forces, and it is used to represent differences in the size of atoms, which is more accurate than a direct comparison of the size of atomic radii [41]. Liu et al. [42] concluded in their simulation results of the CoCrFeMnNi system that the Mn element has a larger Voronoi volume, which leads to more severe local lattice distortion than other elements, resulting in the maximum local stress around the Mn element. In AlCoCrFeNi MEA, Al and Cr have the largest Voronoi volumes, while in CoCrFeNi MEA, they are Cr and Fe.

To understand the lattice distortion in more detail, we introduce the method of mean–square atomic displacements (MASD), i.e., the ideal atomic arrangement of a medium-entropy alloy is obtained after multiple relaxations (pressure 0 Mpa, temperature 0 k) and compared with the positions of the atom in the undisturbed lattice to derive their mean–square atomic displacements (MASD). The calculation method is shown in Equation (15):

$$\mathrm{D}={\displaystyle \frac{1}{N}}{{\displaystyle \sum _i‖{\overrightarrow{A}}_i-{\overrightarrow{A}}_{i,0}‖}}^2$$

(15)

where N is the total number of certain atoms in the system, and ${\overrightarrow{A}}_i$ and ${\overrightarrow{A}}_{i,0}$ are the relaxed and ideal atomic coordinates of the ith atom, respectively.

Table 7. MASD data of M1, M2, and M3 MEAs (pm²).

	Al	Co	Cr	Fe	Ni	Ave.
M1	60.1	15.0	51.8	25.0	7.1	31.8
M2	-	14.0	50.9	21.0	9.1	23.7
M3	-	18.4	50.8	-	9.6	26.2

shows the results. Comparing Co, Cr, and Ni, it can be deduced that the values of MASD are not necessarily related to the radius of the atom but rather to the structure in which the atom is located. δ is usually considered to be the elemental average lattice distortion, but the MASD values for M2 and M3 are not at all consistent with the δ, as shown in Table 3. Y. Tong et al. [42] in their study using synchrotron radiation, tested the localized lattice distortions of CoCrNi and CoCrFeNi attributed to their formation of short-range ordered structures rather than to atomic size differences. In addition, the MSAD value can predict the changing trend of yield strength of the medium entropy alloy, which will be the basis for further research in the future.

3.5. Wear Properties Analysis

Figure 8 shows the worn tracks of coatings M1, M2, and M3 after the wear tests. Specifically, a small number of adhesive marks on coating M1 indicate that slight adhesive and abrasive wear are dominant on the surface, while severe grooves detected in the worn surface of coating M2 suggest that the wear mechanism is peeling and abrasive wear. However, more severe spalling tracks are obviously found on the surface of coating M3, indicating that the wear mechanism is peeling and experiencing abrasive wear. Based on Equation (16), the wear rate R of coatings M1, M2, and M3 are calculated to evaluate the wear properties of the coatings. The corresponding results of coatings M1, M2, and M3 are 0.35, 0.89, and 1.68 μm³·N⁻¹·m⁻¹, respectively.

$$\mathrm{R}={\displaystyle \frac{\mathrm{S}}{F\cdot l}}$$

(16)

where S is the wear volume (μm³), F is the load (N), and l is the width of the wear tracks (m).

4. Discussion

4.1. Wear Behaviors of the MEAs Coatings

According to the coatings’ wear track characteristics, all coating surfaces show plow marks under cyclic loading. M1 coating with high hardness could carry the friction ball well and effectively resist the micro-cutting of the friction partner. On the other hand, the M2 and M3 coatings show severe plastic deformation and peeling under cyclic cutting, which accelerates wear. The M1 coating has the best wear performance, which is also reflected by comparing the wear rate values of the three coatings. M1 exhibits excellent tribological properties, which is the result of the combined effect of fine grain strengthening as well as dislocations. For M2 and M3, we speculate that Fe₃O₄ was formed, which plays a role in reducing wear.

From a microscopic point of view, the addition of Al and Fe increases the local lattice distortion in the solid solution, increases the dislocation density, and enhances the hardness. The resistance to plastic deformation is also improved. For the CoCrFeNi system, the effect of Fe addition is not as significant as that of Al addition. Therefore, for subsequent studies, the addition of other types of elements, such as Mn, to the CoCrFe system, or the addition of Ti to form a short-range ordered structure, could be considered. In the preparation process, the mechanism of strengthening the fine-grain reinforcement can be considered.

4.2. Perspectives of the Application of Medium-Entropy Alloys

The addition of different elements can be considered to strengthen the lattice distortion to obtain alloy materials with excellent properties. By combining CALPHAD and molecular dynamics, the properties of the new generation of medium-entropy alloys can be simulated and predicted to expand the application of medium-entropy alloys.

5. Conclusions

The AlCoCrFeNi, CoCrFeNi, and CoCrNi medium-entropy alloy (MEA) coatings were prepared using laser cladding. The effects of Al and Fe on the wear properties of coatings have been systematically investigated in combination with experimental characterization and simulation.

Thus, the following conclusions were drawn:

(1) Laser cladding can prepare medium-entropy alloy coatings with good morphology, and its rapid melting and cooling also help to form solid solutions.

(2) The addition of Al and Fe enhances the hardness of the coatings. By adjusting the constituent elements, localized lattice distortion and fine-grain strengthening mechanisms can be introduced to obtain medium entropy alloy coatings with excellent mechanical properties.

(3) The combination of CALPHAD and MD offers a unique perspective on the strengthening mechanism of different MEAs.