Damage Detection of Beam Structures Using Displacement Differences and an Artificial Neural Network
Abstract
1. Introduction
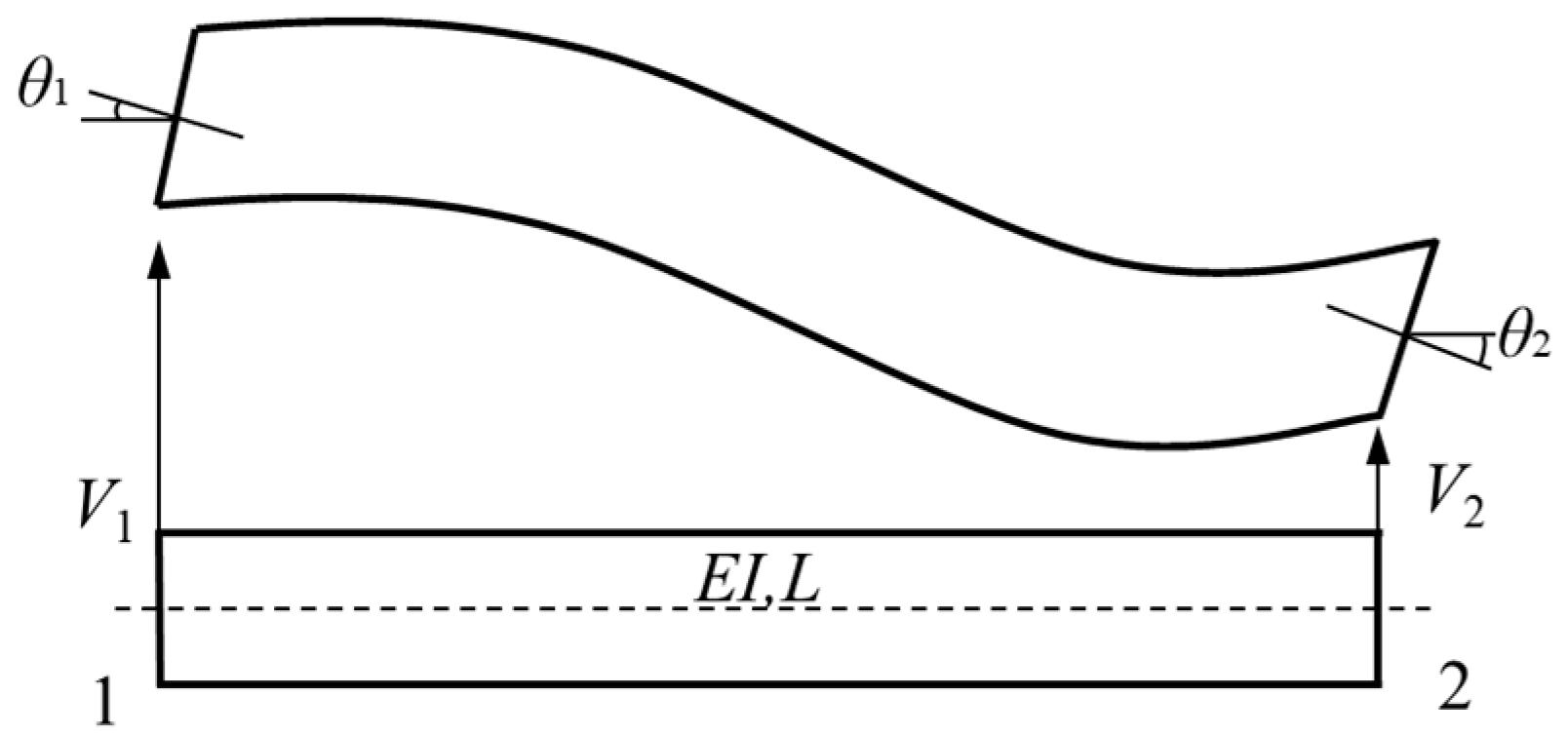
2. Theoretical Development
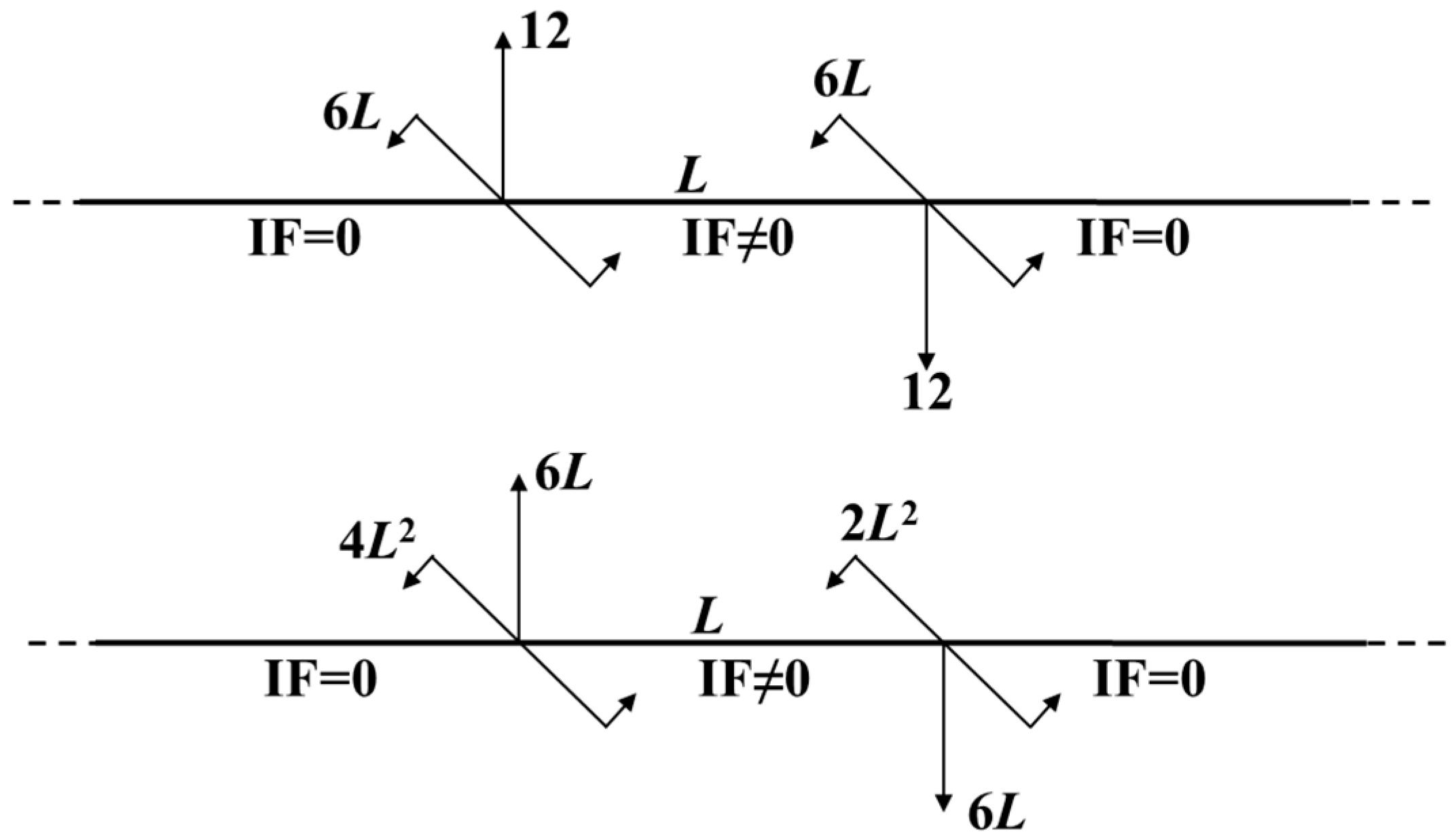
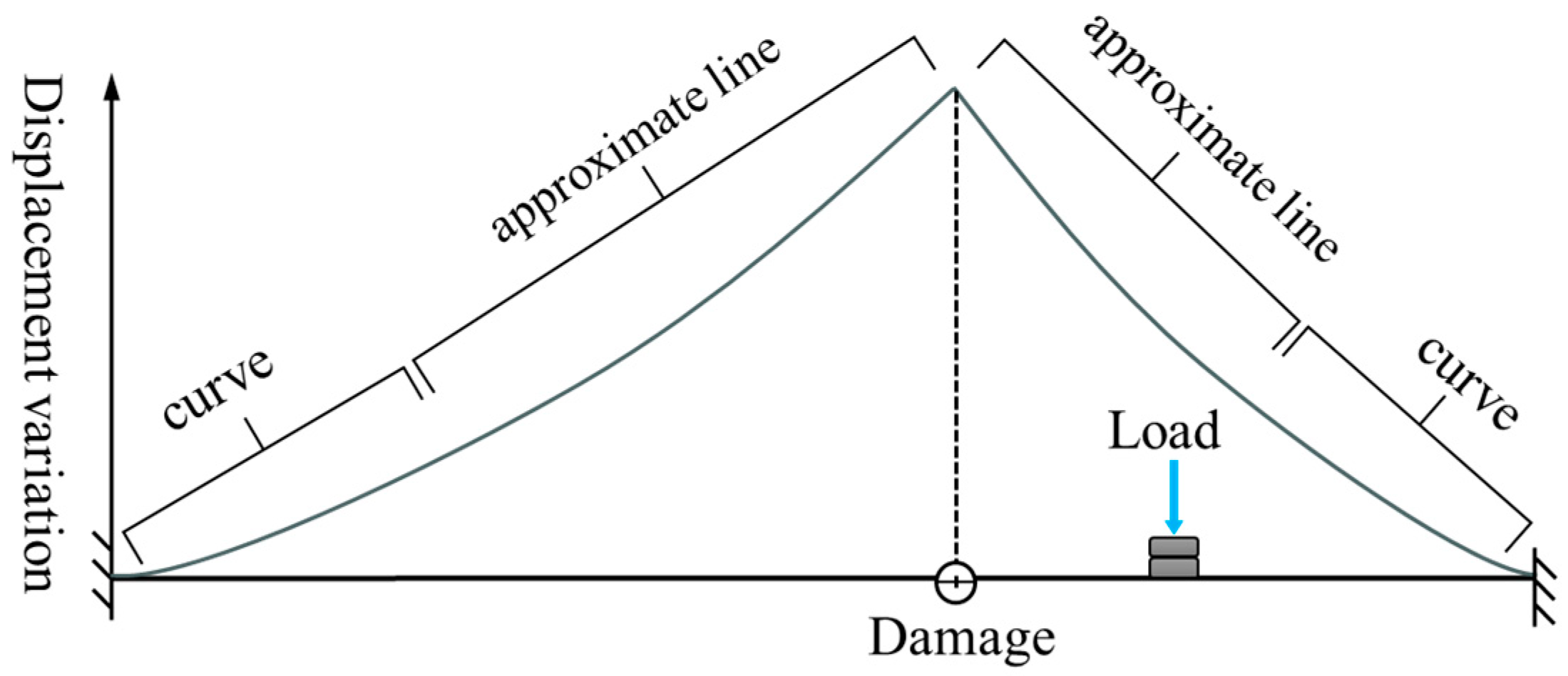
2.1. Damage Localization
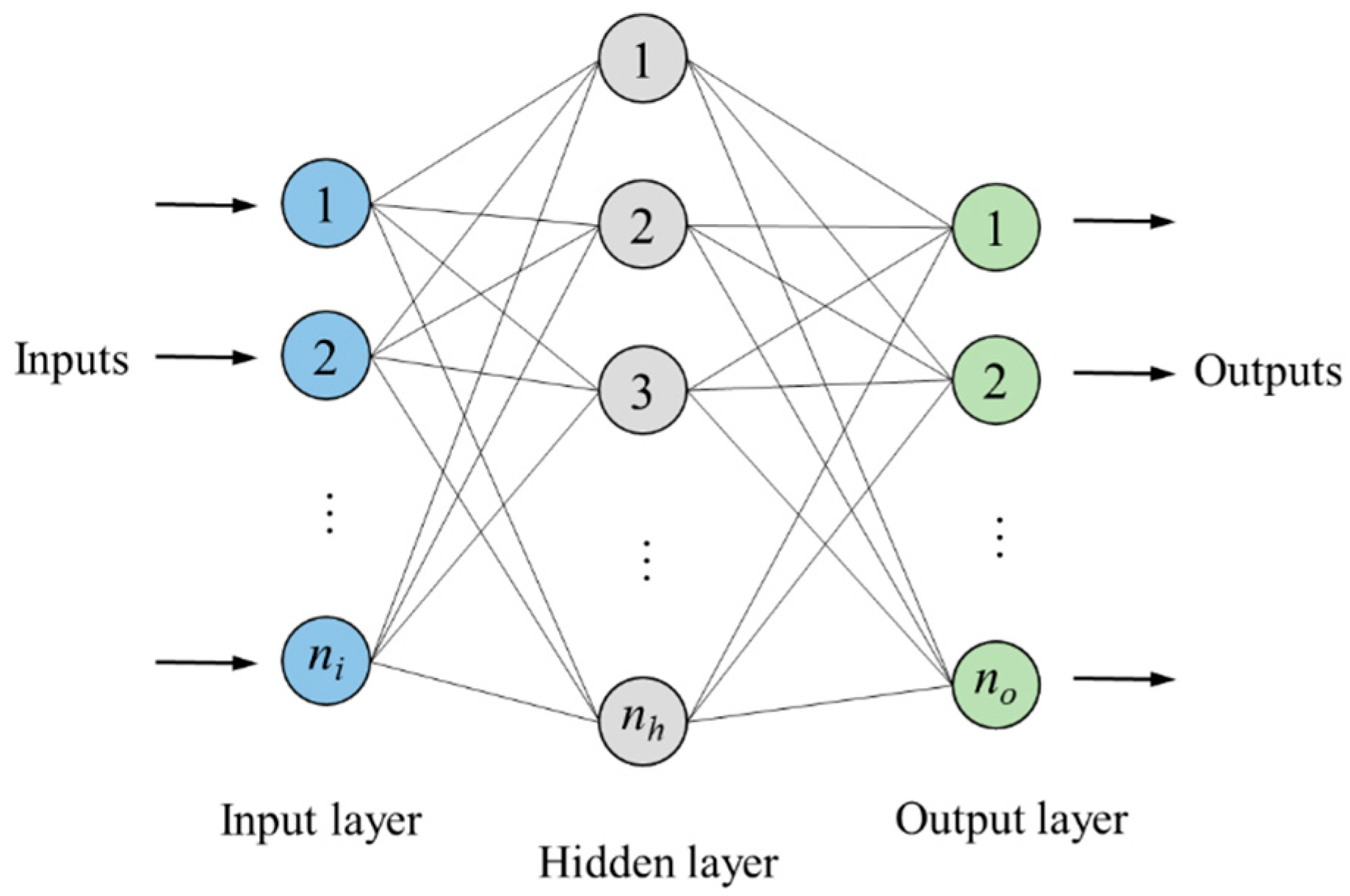
2.2. Damage Quantification
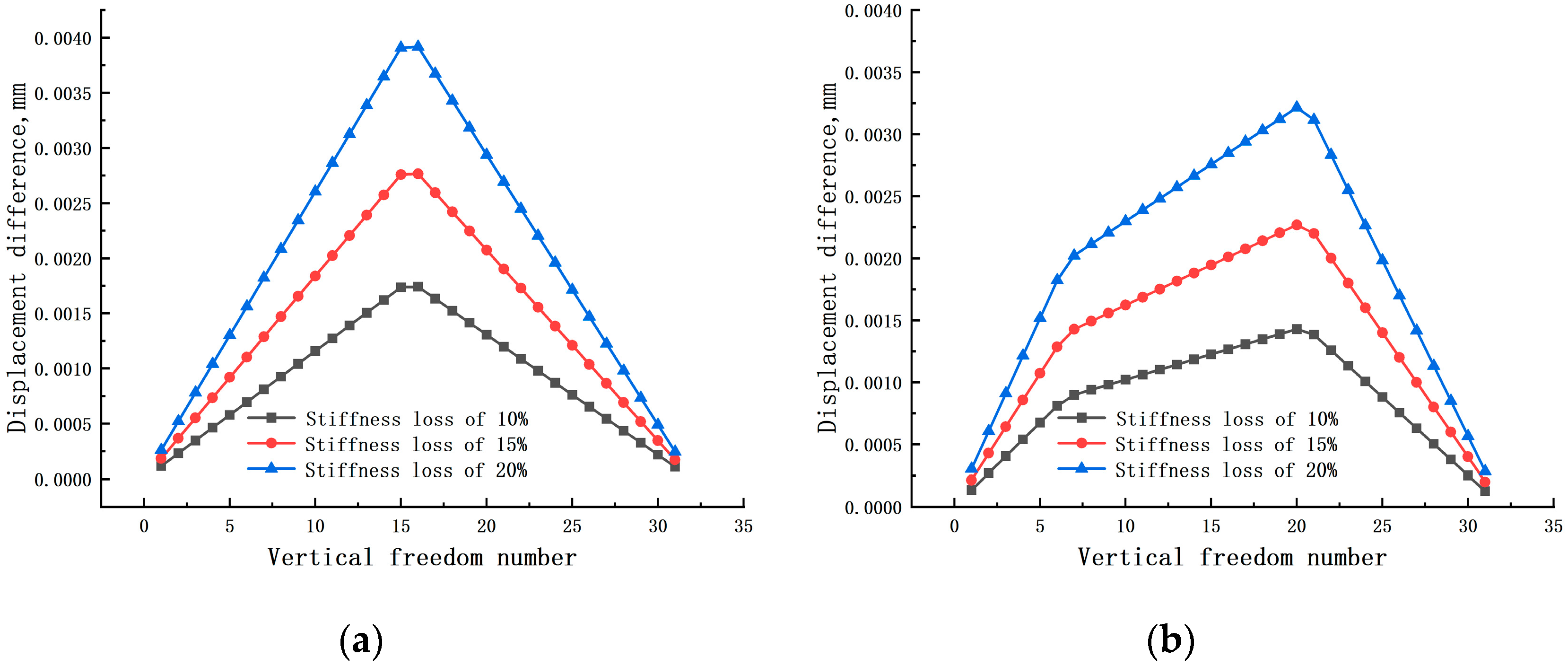
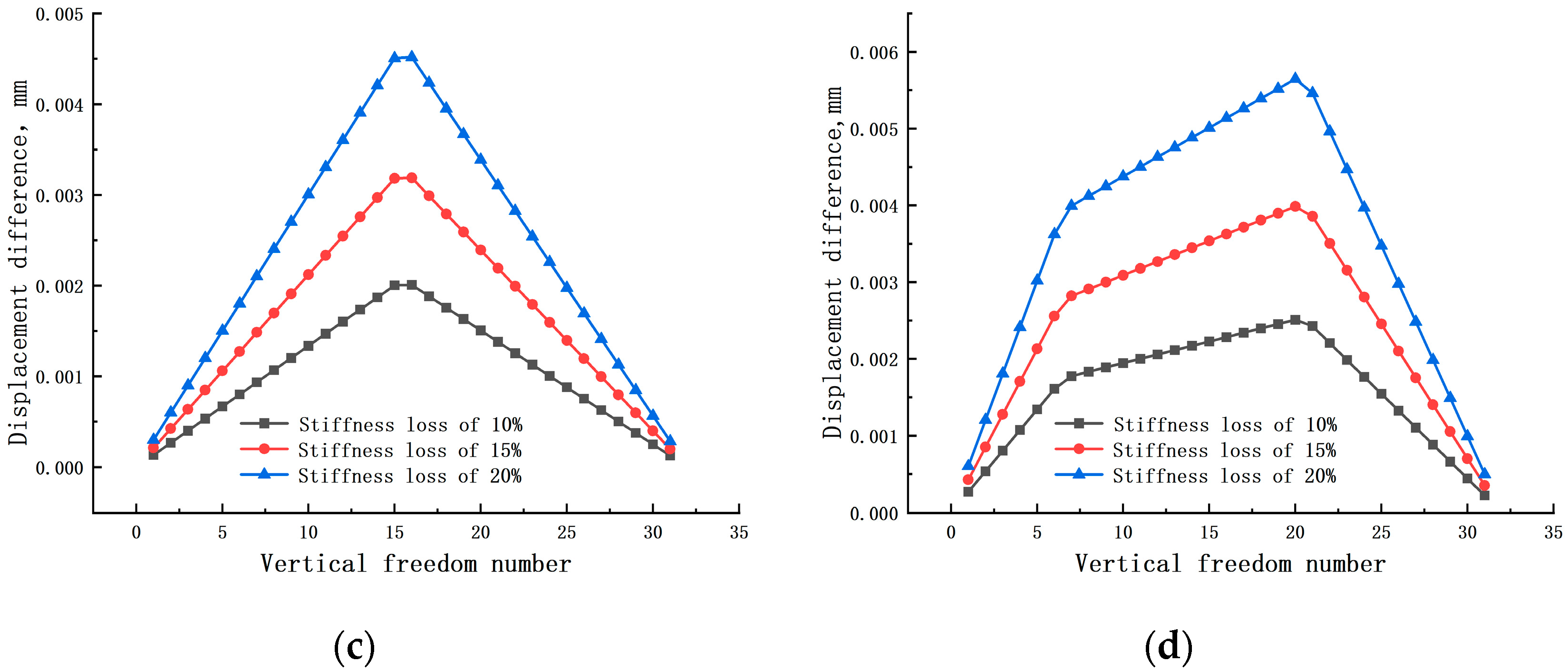
3. Numerical Example
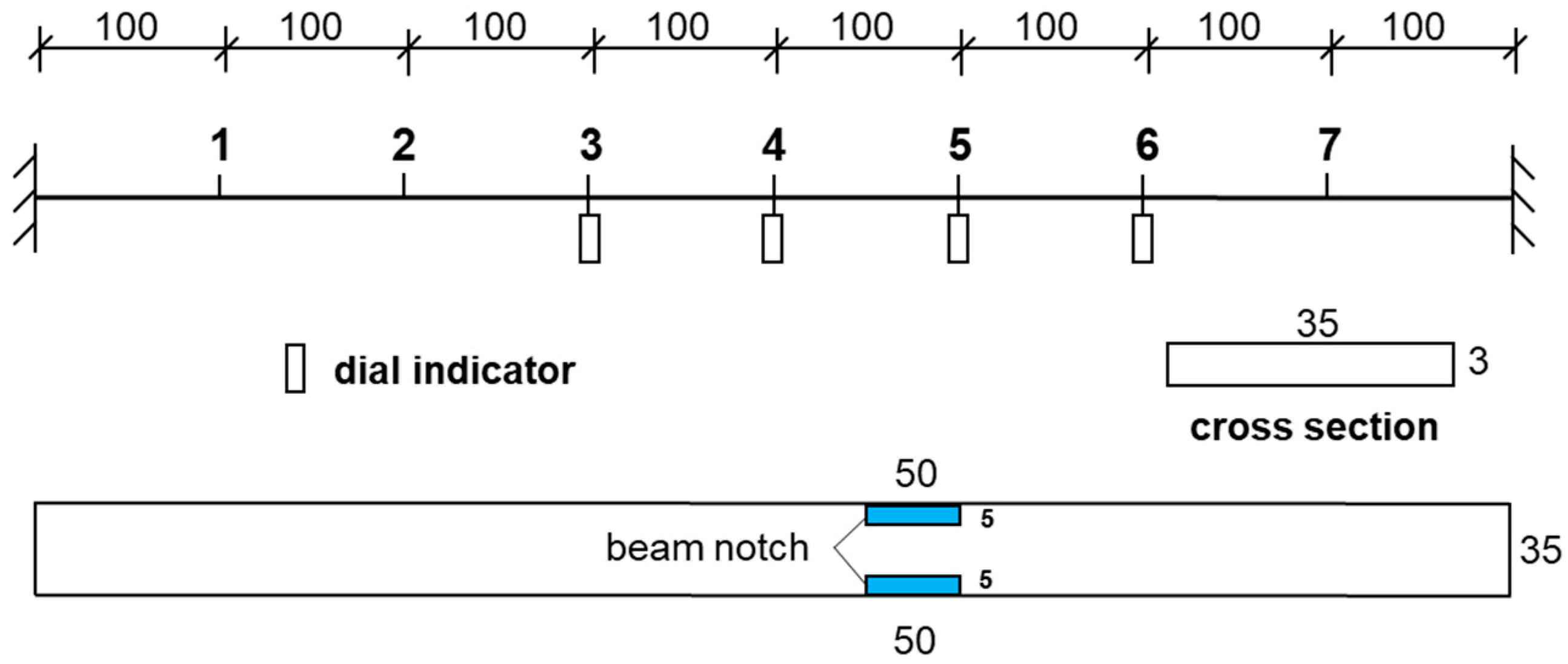
4. Experimental Verification
4.1. Rectangular Section Beam
4.2. Slotted Section Beam
5. Conclusions
- When there is a single damage in the beam structure, the displacement difference curve will exhibit one inflection point. When multiple damages exist in the beam structure, the displacement difference curve will show multiple inflection points;
- On the basis of the damage location already being determined, further adoption of a trained ANN can more accurately calculate the severity of structural damage. Pre-locating the damage can significantly reduce the number of samples required for training the ANN model, as well as decrease the number of neurons in the ANN model.
- For experiment example 1, under three loading modes, the identified damage positions from the left support were 465.17 mm, 463.64 mm, and 484.09 mm, respectively. They all fell within the range of the actual damage location, which was between 450 mm and 500 mm. The trained neural network accurately calculated the severity of the damage, with errors of 3.40%, 1.78%, and 6.16% for the three loading modes, respectively.
- For experiment example 2, the actual damage was simulated by cutting a portion of the steel beam at a distance of 1175 mm from the left support. The identified damage location was 1158.3 mm away from the left support. The distance error between the identified damage location and the actual damage location was 1.4%. The calculated severity of the damage (42.67%) was also very close to the actual degree of damage (41.51%), with an error of 2.8%.
- The implementation of this two-phase damage detection approach is highly convenient, as it facilitates precise identification of damage in beam structures with minimal displacement data, offering a straightforward and immensely practical means for defect detection in such structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| SSB | Single slotted beam system |
| DSB | Double slotted beam system |
| DC | Deflection change |
| BP | Backpropagation |
| ANN | Artificial neural network |
| IF | Internal force |
| diff. | Difference |
| MW | Megawatts |
| CFD | Computational fluid dynamics |
| DFBI | Dynamic fluid body interaction |
| VOF | Volume of fluid |
| LC | Load condition |
| Displacement before and after damage | |
| Stiffness matrix before damage | |
| Displacement before damage | |
| Stiffness matrix after damage | |
| Displacement after damage | |
| Load vector | |
| The change in the stiffness matrix caused by damage | |
| The damage extent of the -th element | |
| The -th elemental stiffness matrix | |
| The | |
| Characteristic displacement vector | |
| The characteristic force vector | |
| The stiffness matrix of a single beam element | |
| Input layer’s neuron count | |
| Output layer’s neuron count | |
| Hidden layer’s neuron count | |
| Young’s modulus | |
| Density | |
| Moment of inertia | |
| Cross-sectional area |
References
- He, W.Y.; Ren, W.X.; Zhu, S. Baseline-free damage localization method for statically determinate beam structures using dual-type response induced by quasi-static moving load. J. Sound Vib. 2017, 400, 58–70. [Google Scholar] [CrossRef]
- He, W.Y.; Ren, W.X.; Zhu, S. Damage detection of beam structures using quasi-static moving load induced displacement response. Eng. Struct. 2017, 145, 70–82. [Google Scholar] [CrossRef]
- Greco, A.; Pluchino, A.; Cannizzaro, F. Closed-form solution based genetic algorithm software: Application to multiple cracks detection on beam structures by static tests. Appl. Soft Comput. 2018, 64, 35–48. [Google Scholar] [CrossRef]
- Oudah, F.; El-Hacha, R. Damage and deformation assessment of earthquake-resistant RC slotted beam-column connections using digital image correlation technique. Eng. Struct. 2020, 215, 110442. [Google Scholar] [CrossRef]
- Ma, Q.; Solís, M.; Galvín, P. Wavelet analysis of static deflections for multiple damage identification in beams. Mech. Syst. Signal Process. 2021, 147, 107103. [Google Scholar] [CrossRef]
- Jahangir, H.; Hasani, H.; Esfahani, M.R. Wavelet-based damage localization and severity estimation of experimental RC beams subjected to gradual static bending tests. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 34, pp. 3055–3069. [Google Scholar]
- Wu, N.; Wang, Q. Experimental studies on damage detection of beam structures with wavelet transform. Int. J. Eng. Sci. 2011, 49, 253–261. [Google Scholar] [CrossRef]
- Pooya, S.M.H.; Massumi, A. A novel damage detection method in beam-like structures based on the relation between modal kinetic energy and modal strain energy and using only damaged structure data. J. Sound Vib. 2022, 530, 116943. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, J.; Sun, B. Damage localization for beam structure by moving load. Adv. Mech. Eng. 2017, 9, 91–105. [Google Scholar] [CrossRef]
- Omid, Y.; Ali, R.I.; Mehdi, D. Static data based damage localization of beam-column structures considering axial load. Mech. Adv. Mater. Struct. 2020, 27, 1433–1450. [Google Scholar]
- Shi, Q.; Hu, K.; Wang, L.; Wang, X. Uncertain identification method of structural damage for beam-like structures based on strain modes with noises. Appl. Math. Comput. 2021, 390, 125682. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Q.W. Damage detection in beam-like structures using static shear energy redistribution. Front. Struct. Civ. Eng. 2023, 16, 1552–1564. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Izadifard, R.A.; Yazdanpanah, O. Experimental static data-based damage localization of beam-like structures considering axial load. Inverse Probl. Sci. Eng. 2021, 29, 1729–1745. [Google Scholar] [CrossRef]
- Ma, Q.Y.; Mario, S. Damage localization and quantification in beams from slope discontinuities in static deflections. Smart Struct. Syst. 2018, 22, 291–302. [Google Scholar]
- Le, T.N.; Nguyen, A.; Thambiratnam, P.D.; Chan, T.H.T.; Khuc, T. Locating and Quantifying Damage in Beam-like Structures Using Modal Flexibility-based Deflection Changes. Int. J. Struct. Stab. Dyn. 2020, 20, 20. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, Y. Damage Detection in Beam Bridges Using Quasi-static Displacement Influence Lines. Appl. Sci. 2019, 9, 1805. [Google Scholar] [CrossRef]
- Yang, J.; Li, P.; Yang, Y.; Xu, D. An improved EMD method for modal identification and a combined static-dynamic method for damage detection. J. Sound Vib. 2018, 420, 242–260. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, R.; Zheng, S. Identification and Diagnosis of Bridge Structural Damage Based on Static Test Data. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 48, 2981–2996. [Google Scholar] [CrossRef]
- Wang, Z.F.; Huang, B.; Tee, K.F.; Zhang, W.D. A Novel Stochastic Approach for Static Damage Identification of Beam Structures Using Homotopy Analysis Algorithm. Sensors 2021, 21, 2366. [Google Scholar] [CrossRef]
- Shen, J.B.; Li, Z.K.; Luo, S.; Wang, W. A Structural Damage Identification Method Based on Arrangement of the Static Force Residual Vector. Front. Mater. 2022, 9, 918069. [Google Scholar] [CrossRef]
- Alkhabbaz, A.; Hamza, H.; Daabo, M.A.; Yang, H.S.; Yoon, M.; Koprulu, A.; Lee, Y.H. The aero-hydrodynamic interference impact on the NREL 5-MW floating wind turbine experiencing surge motion. Ocean Eng. 2024, 295, 116970. [Google Scholar] [CrossRef]
- Yang, S.H.; Alkhabbaz, A.; Tongphong, W.; Lee, H.Y. Cross-comparison analysis of environmental load components in extreme conditions for pontoon-connected semi-submersible FOWT using CFD and potential-based tools. Ocean Eng. 2024, 304, 117248. [Google Scholar] [CrossRef]
- Daabo, M.A.; Alkhabbaz, A.; Ibrahim, S.S.; Hamzah, H.; Hassan, H.; Basem, A.; Easa, H.; Pavlovic, S. Thirteen vital factors for micro-scale radial turbine vane’s design of geo-solar-powered Brayton cycle applications. Energy Convers. Manag. 2024, 315, 118774. [Google Scholar] [CrossRef]
- Yang, Q.W.; Du, S.G.; Liang, C.F.; Yang, L.J. A Universal Model-Independent Algorithm for Structural Damage Localization. CMES Comput. Model. Eng. Sci. 2014, 100, 223–248. [Google Scholar]
- Le, N.T.; Thambiratnam, D.P.; Nguyen, A.; Chan, T.H.T. A new method for locating and quantifying damage in beams from static deflection changes. Eng. Struct. 2019, 180, 779–792. [Google Scholar] [CrossRef]



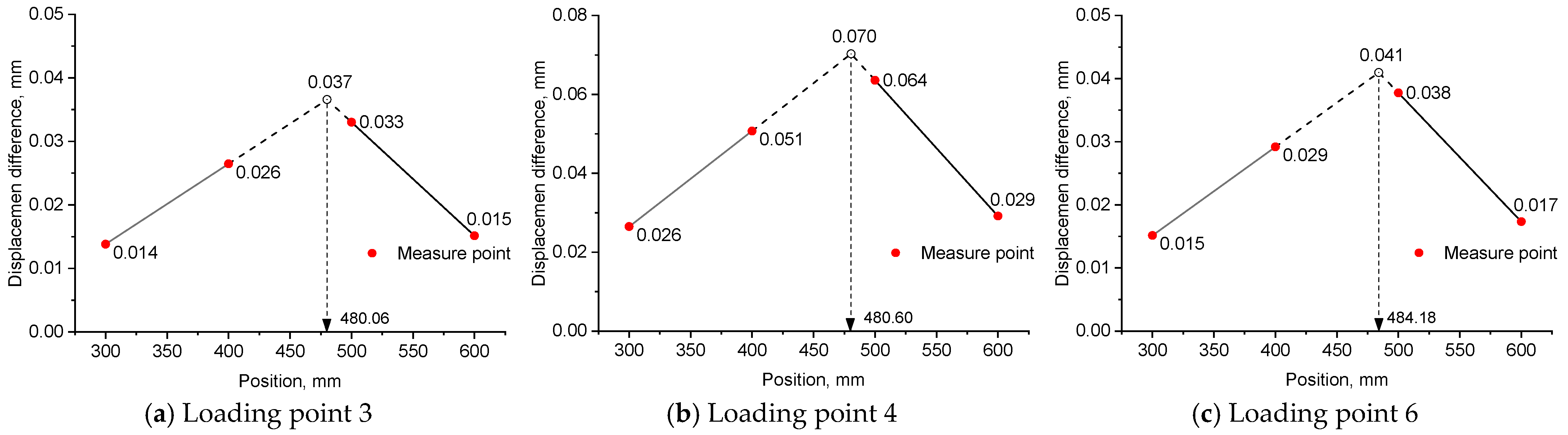
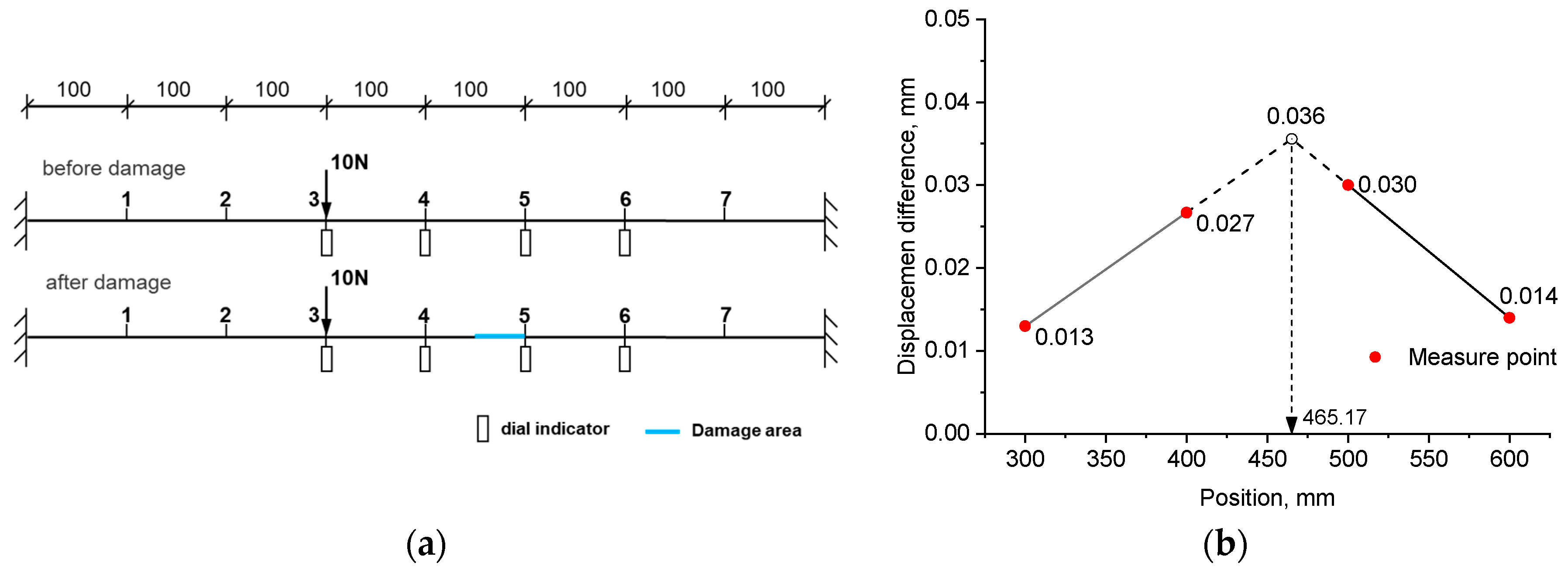
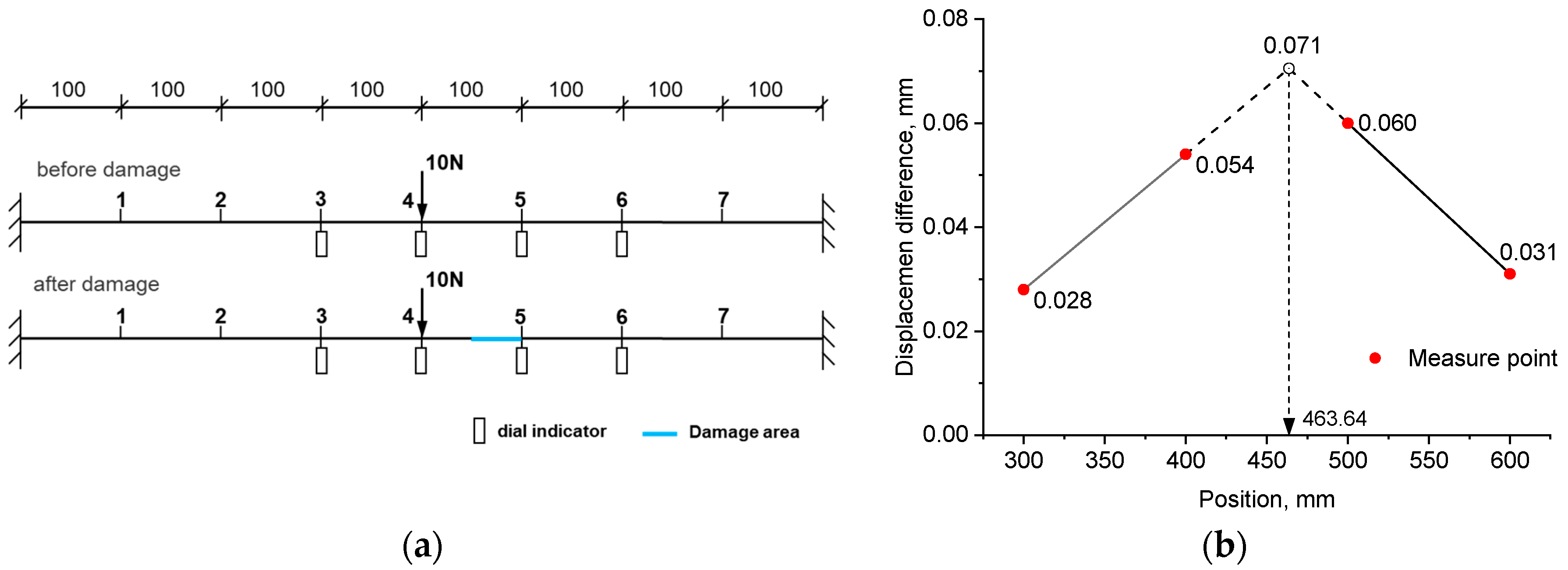
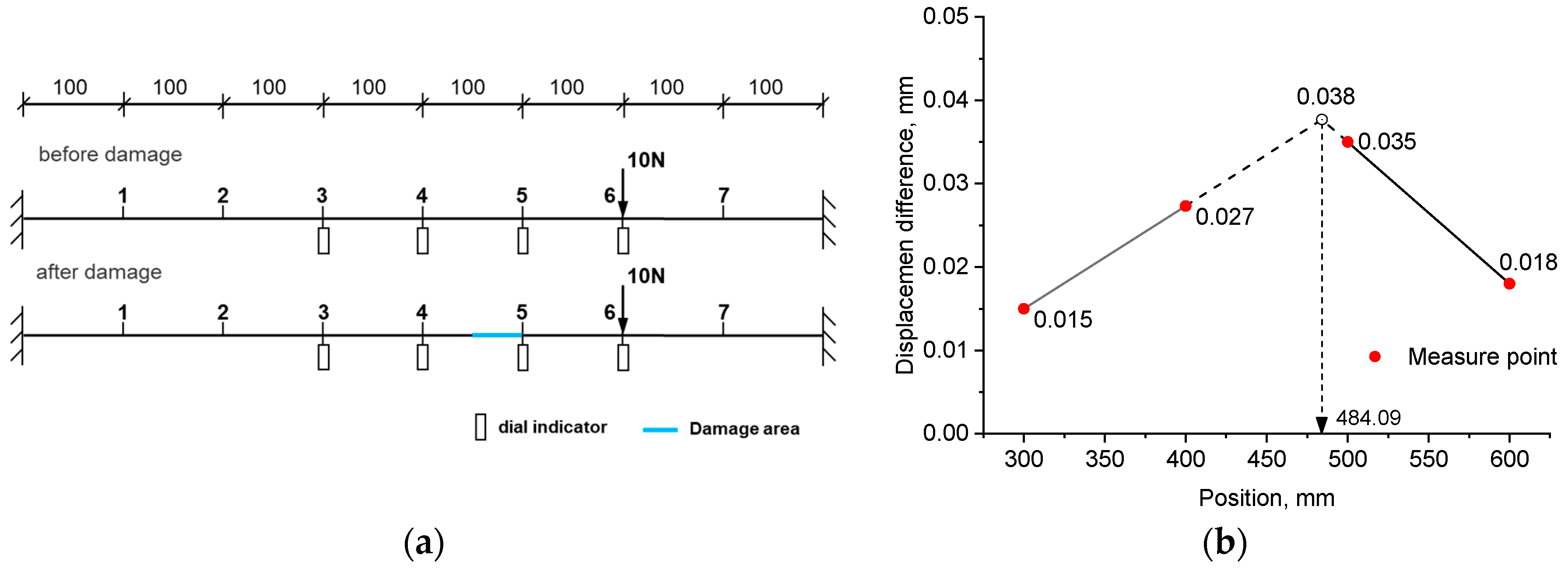

| Measure point | 3 | 4 | 5 | 6 |
| Mean value | 0.013 | 0.027 | 0.030 | 0.014 |
| Standard deviation | 0.0020 | 0.0012 | 0.0020 | 0.0010 |
| Measure point | 3 | 4 | 5 | 6 |
| Mean value | 0.028 | 0.054 | 0.060 | 0.031 |
| Standard deviation | 0.0020 | 0.0026 | 0.0053 | 0.0026 |
| Measure point | 3 | 4 | 5 | 6 |
| Mean value | 0.015 | 0.027 | 0.035 | 0.018 |
| Standard deviation | 0.0044 | 0.0006 | 0.0026 | 0.0095 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Peng, X.; Qin, F.; Yang, Q.; Xu, B. Damage Detection of Beam Structures Using Displacement Differences and an Artificial Neural Network. Coatings 2025, 15, 289. https://doi.org/10.3390/coatings15030289
Huang X, Peng X, Qin F, Yang Q, Xu B. Damage Detection of Beam Structures Using Displacement Differences and an Artificial Neural Network. Coatings. 2025; 15(3):289. https://doi.org/10.3390/coatings15030289
Chicago/Turabian StyleHuang, Xudi, Xi Peng, Fengjiang Qin, Qiuwei Yang, and Bin Xu. 2025. "Damage Detection of Beam Structures Using Displacement Differences and an Artificial Neural Network" Coatings 15, no. 3: 289. https://doi.org/10.3390/coatings15030289
APA StyleHuang, X., Peng, X., Qin, F., Yang, Q., & Xu, B. (2025). Damage Detection of Beam Structures Using Displacement Differences and an Artificial Neural Network. Coatings, 15(3), 289. https://doi.org/10.3390/coatings15030289









