Abstract
The evolution of the microstructure of TA18 titanium alloy tube during the differential heating push-bending forming process has a significant impact on its macroscopic mechanical properties. This paper obtained the experimental stress–strain data of TA18 titanium alloy through high-temperature tensile tests, solved the key parameters of the cellular automata (CA) model through fitting calculation, established a finite-element model of differential heating push-bending of TA18 titanium alloy tube using DEFORM-3D, and simulated the evolution of the microstructure during the bending process of the tube based on the CA method. The study investigated the influence of heating temperature, internal pressure, and feed speed of the pusher on the average grain size of the material on the outer side of the bent tube. Experiments were conducted, and the key areas of the manufactured tube were analyzed through metallographic observation. The research indicated that the average grain size of the material on the outer side of the bent tube increases slightly and then decreases with the rise in heating temperature and decreases continuously with the increase of internal pressure or feed speed of the pusher. This study provides theoretical support for optimizing the differential heating push-bending forming of TA18 titanium alloy tube at a microscopic level.
1. Introduction
TA18 titanium alloy (nominal composition Ti–3Al–2.5V) is a near-α titanium alloy known for its high strength, corrosion resistance, light weight, high-temperature stability, and good weldability. Considering the aforementioned advantages, TA18 titanium alloy tubes are widely used in aerospace, shipbuilding, desalination, and gas turbine applications [1,2,3]. In the study of tube bending, common bending methods include push-bending, roll-bending, draw-bending, rotary-bending, etc., of which push-bending is often used for manufacturing thin-walled tubes with a small bending radius (bending radius ≤ 1D, where D is the outer diameter of the tube). For tube materials such as titanium alloys, which are difficult to manufacture at room temperature, the application of differential heating push-bending can effectively address the challenge of manufacturing small-bending-radius tubes made of titanium alloy [4]. During the differential heating push-bending process of tubes, not only do the macroscopic shape and sizes change, but a series of changes also occur in the microstructure. The evolution of the microstructure of metallic materials has a significant impact on the result of plastic deformation, which can determine the quality and performance of the manufactured parts [5]. Therefore, investigating the microstructure evolution of TA18 titanium alloy tube with a small bending radius during the differential heating push-bending forming process has important practical significance.
Currently, researchers in the field of tube bending mainly focus on the study of the impact and optimization of process parameters at the macroscopic level. Fang et al. [6] established a three-dimensional elastic–plastic finite-element model for the numerical control bending forming process of high-strength TA18 titanium tube and verified the accuracy of the model. They simulated and analyzed the effects of different geometric parameters, including bending angle, relative bending radius, and tube size on the forming quality, and found that a qualified bent tube part could be obtained when the relative bending radius is larger than 2. This research provides an important theoretical basis for the optimization of geometric parameters in tube bending. Tao et al. [7] approached the subject from the perspective of process improvement. They used differential lubrication to control the angular velocity of material flow on the inner and outer sides of the bent tube during the push-bending forming process, effectively avoiding the cracking defect at the front end of the inner side of the tube. By combining finite-element simulation analysis with experimental verification, they successfully manufactured a thin-walled aluminum alloy tube with a bending radius of 0.9D. Huang et al. [8] studied the optimization of technological parameters and the numerical simulation of the hot pushing pipe bending process to reveal the pipe forming mechanism. Through theoretical analysis and orthogonal experiments, they found that controlling the axial compression and circumferential expansion in proportion is key to achieving a constant wall thickness. Using a horn mandrel with a variable curvature axis benefits the uniformity of metal flow from the concave side to the convex side, avoiding the increase of inner wall thickness and the decrease of outer wall thickness during pipe bending. Cheng et al. [9] investigated the manufacturing of complex-shaped TA18 alloy pipes through hot free bending forming (FBF) technology. They combined finite-element modeling, experimental validation, and theoretical analysis to optimize the bending process parameters. The research employed a Johnson–Cook constitutive model to accurately simulate the hot FBF process. It was concluded that the hot FBF process enhances the forming quality of TA18 pipes by reducing wall thickening and cross-sectional distortion. However, despite significant progress at the macroscopic level, existing studies still have some limitations. Most studies related to tube bending focus on the direct impact of process parameters on forming quality, with less attention paid to the evolution of microstructure and its potential impact on macroscopic properties.
With the rapid development of computer technology, mesoscale simulation methods are increasingly being applied to the study of the microstructure of metallic materials. Among these methods, the CA method has gradually become one of the important methods for simulating the evolution of material microstructures [10,11]. Scholars have also begun to apply it to the study of plastic forming in metallic materials, achieving positive results. In addition, the widespread application of the CA method has also achieved significant progress in the fields of dynamic recrystallization and static recrystallization. For example, Ji et al. [12] studied the dynamic recrystallization behavior of TC4 titanium alloy based on the CA method, established relevant models for that method, analyzed the effects of temperature, strain, and strain rate on the volume fraction of dynamic recrystallization during hot working, and verified the accuracy of the CA model by comparing it with EBSD test results. Li et al. [13] investigated the thermomechanical behavior and microstructural evolution of Ti–6Al–4V alloy sheets during the heat-assisted incremental sheet forming (SPIF) process. The research established multi-scale models, including a crystal plasticity finite-element model, representative volume element, and cellular automata, which can predict the initiation and development of dynamic recrystallization during the SPIF process. CA analysis of the dynamic recrystallization progress in the upper, center, and lower regions of the deformed workpiece revealed that the increase of the strain rate has significant effects on the dislocation density, which is proportional to the dynamic recrystallization percentage. Asgharzadeh et al. [14] studied the kinetics of static recrystallization in steel tubes subjected to post-hydroforming annealing treatment. Utilizing digital image correlation measurement technology and analytical solution calculations for stress to calculate storage energy, along with EBSD for acquiring grain topology and crystallographic orientation, they integrated these data into a CA model to predict the static recrystallization kinetics. It was observed that significant grain coarsening occurred during the static recrystallization process, which is due to the dynamics of grain growth being much faster than the nucleation dynamics. Yu et al. [15] studied the evolution of microstructure during the cross-wedge rolling process of aluminum alloy hollow shafts, combined finite-element simulation with the CA method to analyze the effects of different process parameters on the average grain size of the workpiece, and found that large sectional shrinkage, a small spreading angle, and low initial rolling temperature can effectively refine the grains. Majta et al. [16] presented a comprehensive study on modeling grain refinement inhomogeneity during a combined metal forming process using the finite-element method and cellular automata techniques. Through CA simulation, detailed information on microstructural evolution under severe plastic deformation conditions was obtained, including changes in the shape and size of the modeled representative volume, changes in the number of grains, subgrains, and dislocation cells, development of grain boundary angle distribution, and changes in pole figures. Based on the CA method, Yao [17] simulated the hot shearing bending forming process of TA18 titanium alloy rectangular tubes, analyzed microstructure evolution in typical areas of the tube under different temperatures, strain rates, and internal pressures, and found that the grains in the straight-wall lateral area of the formed part were significantly refined. These research results indicate that the CA method can effectively simulate the microstructure evolution and provide a theoretical basis for optimizing process parameters. However, in spite of the success of the CA method in these studies, most existing research focuses on the forming processes of sheets or simple geometric shapes, and its application in the field of tube bending forming is still relatively limited, especially in the study of push-bending forming of tubes with a small bending radius.
The above findings are mainly related to the optimization design of process parameters in tube bending and the study of microstructure evolution using the CA method, which has certain reference value for this paper’s study of microstructure evolution during the differential heating push-bending forming process of TA18 titanium alloy tubes with a small bending radius. The microstructure of metallic materials is closely related to their macroscopic mechanical properties. In summary, in the field of tube push-bending forming, based on the results of previous studies, in addition to optimizing process parameters to improve the forming quality of tubes, it is also necessary to fully utilize mesoscale simulation methods to actively explore the microstructure evolution during the differential heating push-bending forming process of tubes.
This paper primarily investigates the evolution of microstructure in the differential heating push-bending forming process of TA18 titanium alloy tubes with a small bending radius. Through high-temperature tensile tests, the experimental stress–strain curves of the material were obtained. A finite-element model of the differential heating push-bending of TA18 titanium alloy tubes with a small bending radius was established using DEFORM-3D to provide the necessary conditions for subsequent microstructure evolution simulation research. Based on the CA method, the evolution of microstructure in key areas of the tube during the differential heating push-bending forming process under different temperatures, internal pressures, and feed speeds of the pusher was studied and analyzed. It was found that increasing the heating temperature and the internal pressure and accelerating the feed speed of the pusher can achieve a better grain refinement effect. By combining experiments with simulations, samples were taken from the inner and outer bending areas of the manufactured tube, processed, and subjected to metallographic tests, which showed small deviation when compared with the simulation results. The work of this paper fills a gap in the study of microstructure evolution in the tube push-bending forming field and provides guidance for engineers to regulate the mechanical properties of push-bending parts from a microscopic level. The research findings not only contribute significantly to the scientific understanding of titanium alloy processing but also have potential positive impacts on industrial practice and environmental sustainability. By optimizing the heating temperature, internal pressure, and feed speed in the differential heating push-bending process, the production efficiency and product quality of TA18 titanium alloy tubes can be improved. This may reduce material waste, energy consumption, and waste generation in the production process, thereby lowering costs and the environmental impact of titanium alloy processing, and enhancing industrial competitiveness.
2. Test Schemes
2.1. Materials
The experimental material is high-strength TA18 titanium alloy tube, with the chemical composition shown in Table 1. Samples were cut along the rolling direction of the tube using a wire-cutting machine and then ground and cleaned. High-temperature uniaxial tensile mechanical property tests were conducted according to the international standard ISO 6892-2:2011 [18]. The tests were carried out under isothermal and constant strain rate conditions using an automatic control system. Before each test, a high-temperature lubricant, boron nitride, was evenly applied to the surface of the samples to reduce the impact of oxidation during the tensile test. After reaching the set temperature, the samples were held for 5 min to ensure uniform temperature distribution throughout the sample. The temperature range was set to 400 °C, 450 °C, and 500 °C, and the tensile rate range was set to 0.001 s−1, 0.01 s−1, and 0.1 s−1, after which the high-temperature tensile test data of the TA18 titanium alloy were obtained. The selection of these above parameters is based on the material properties of TA18 titanium alloy, the requirements of the differential heating push-bending forming experimental design, and the experience from our research group’s previous studies. The experimental stress–strain curves were obtained after processing the data with Origin 2021 software, as shown in Figure 1. Samples taken from the original tube blank were embedded, ground, polished, and etched using Kroll etchant (HF:HNO3:H2O = 1.5:3:45.5) for 10–20 s, and the microstructure was observed using the IM300 metallurgical microscope (manufactured by Nanjing Jueyu Precision Instrument Co., Ltd., Nanjing, China). Figure 2 shows the original microstructure of the TA18 titanium alloy; the average grain size of the original microstructure in the metallographic images was measured three times using the Image-Pro Plus v6.0 image processing software, and the average value was taken to be approximately 11.46 μm, with a standard deviation of 0.58.

Table 1.
Chemical composition of TA18 titanium alloy (mass fraction%) [19].
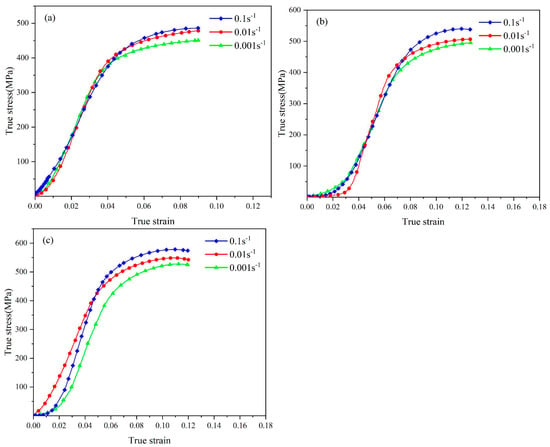
Figure 1.
Experimental stress–strain curves of TA18 titanium alloy at different temperatures: (a) T = 500 °C; (b) T = 450 °C; (c) T = 400 °C.

Figure 2.
Original microstructure of TA18 titanium alloy.
2.2. Differential Heating Push-Bending Method
The schematic diagram of differential heating push-bending is shown in Figure 3. Compared to traditional cold push-bending, differential heating push-bending includes a heating stage before the forming stage. After the tube blank is placed in the initial position and the dies are closed, the heating process begins. A thermocouple is inserted into the reserved hole to measure the temperature on the inner and outer sides of the bend. Heating stops when the temperature reaches the target value and stabilizes, and then the forming stage begins. As the pusher gradually advances, the tube blank undergoes plastic deformation from the straight section to the bending section in the die cavity. When it reaches the end position, the pusher stops advancing, completing the differential heating push-bending process. During this process, the tube blank is subjected to the combined effects of the push force F1 from the pusher, the counter-push force F2 from the flexible rod, the support force provided by the radial expansion of the elastic rubber block on the inner wall of the tube blank, friction between the die cavity and the outer wall of the tube blank, friction between the inner wall of the tube blank and the segmented filler rubber, and the constraint of the die. The differential heating push-bending method effectively addresses the difficulty of manufacturing small-bending-radius tubes from titanium alloys. By heating the outer side of the bend, it reduces the deformation resistance of the material on the outer side of the bend, enhances the material’s plastic deformation ability, and mitigates the risk of thinning on the outer side of the bent tube. Meanwhile, cooling with water in the inner side of the bend reduces the temperature, thereby weakening the fluidity of the material, which prevents material accumulation, indentation, and wrinkling defects on the inner side of the bent tube.
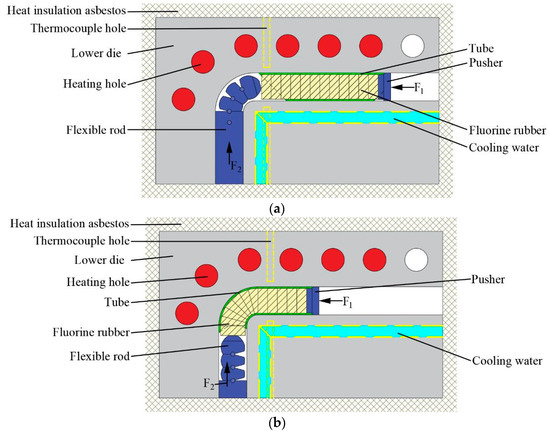
Figure 3.
Schematic diagram of differential heating push-bending forming. (a) Initial position; (b) end position.
3. Model Construction
3.1. Finite Element Model
We imported the 3D models of the die and the tube blank into the finite-element simulation software DEFORM v10.2, as shown in Figure 4. The finite element model consists of the lower die, the pusher, and the tube blank. Due to the horizontal symmetry of the die structure, half of the model can be taken to improve computational efficiency. In actual experiments, a flexible rod provides a counter-push force that causes the rubber block to expand radially and support the inner wall of the tube. In numerical simulation, this condition is simplified by assuming that the internal pressure provided by the radial expansion of the elastic filler rubber block is constant and uniform, and the pressure applied to the inner surface of the tube is used as a substitute.
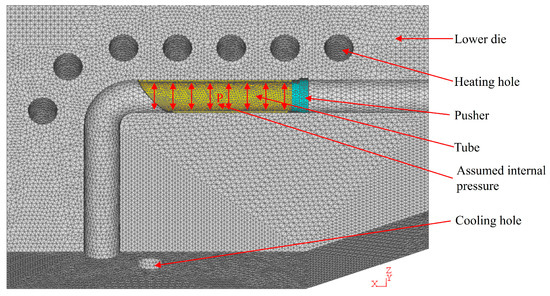
Figure 4.
Finite element model.
The finite-element simulation process for differential heating push-bending of small-bending-radius tubes is coupled with heat transfer and thermal forming processes; relevant parameter settings for simulation are shown in Table 2. The first step involves simulating the temperature field of the model. Taking into account the heat transfer within the die, the heating hole positions in three temperature groups are set at 530 °C, 480 °C, and 430 °C, to ensure that the temperature on the outer side of the bent tube matches that of the experiment.

Table 2.
Main parameter settings for simulation.
3.2. Cellular Automata Model
Cellular automata is a vital method for simulating the evolution of microstructures in materials and is extensively used to simulate the recrystallization and grain growth processes in metallic materials with great reliability [20,21,22]. A CA model typically consists of four components: cells, cell space, cell neighbors, and cell rules. Cells are the fundamental units of the CA, and the orderly arrangement of all cell units forms the cell space. Common types of neighbors in two-dimensional cell space include the von Neumann and Moore types. Cell rules describe the mutual influence between a cell unit and its surrounding neighbors, which is the core content of the CA model. The recrystallization process of metallic materials is actually influenced by many factors. To simplify the CA model for analysis, this paper establishes a CA model for the microstructure evolution during the differential heating push-bending process of TA18 titanium alloy tubes based on the following assumptions: (1) The initial dislocation density of the material is uniform and consistent, and as the plastic deformation of the material intensifies, the dislocation density gradually increases, reaching a critical value at which recrystallization nucleation occurs with a certain probability. (2) The nucleation of recrystallized grains only occurs at grain boundaries, where new grains grow and gradually consume the original grains, and the dislocation density of the material changes based on the Laasraoui–Jonas model.
The microstructure functional module of the finite-element simulation software DEFORM is capable of simulating material microstructure. It embeds various mesoscale simulation methods within its program, such as the cellular automata method, monte carlo method, and phase field method, providing users with the convenience to establish models. As shown in Figure 5, based on the finite element simulation, after entering the microstructure functional module and selecting the CA method, one simply needs to input the corresponding model parameters in the user interface and set different options according to the program steps to begin the calculation and result analysis of microstructure evolution. The derivation and calculation of the key parameters of the CA model are as follows. The L–J model is used to describe the variation of material dislocation density:
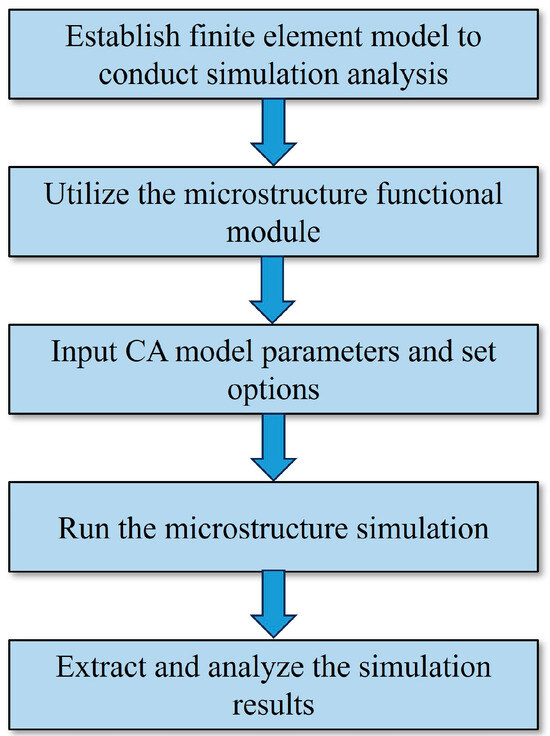
Figure 5.
Flowchart of microstructure simulation process.
In Equations (1)–(3), represents the dislocation density; represents the strain; is the work hardening coefficient; is the recovery softening coefficient; is the volume swept by grain boundary migration; is the recovery constant; is the hardening constant; is the strain rate; is the reference strain rate, = 1 s−1; is the strain-rate sensitivity coefficient; is the self-diffusion activation energy, J/mol; is the gas constant, = 8.314 J/mol·K; and is the absolute temperature, K. Below are the derivation and calculation of key parameters in the model.
Equation (1) includes a term that describes the influence of grain boundary migration on dislocation density. Considering the low correlation between the two, this term can be neglected, and the equation can be simplified to:
Solving the aforementioned first-order differential equation and transforming it yields the expression for dislocation density:
is the integration constant. By introducing the initial condition: , where is the initial dislocation density, then . Substituting into Equation (5) gives:
Based on the research by Kocks and Mecking [23], it is believed that the flow stress of the material is related to its dislocation density as follows:
In the formula, represents the shear modulus, = 47 Gpa; represents the burgers vector, = 3.7 × 10−10 m.
When the strain is sufficiently large, then , and at this point, the saturation stress is approximately equal to the flow stress, so Equation (7) can be written as:
Solving the system of Equations (6)–(8) allows the flow stress to be expressed as:
Taking the derivative of Equation (9) with respect to and simplifying yields:
The definition of the work hardening rate is . By solving Equations (9) and (10) and rearranging, the following is obtained:
From the above formula, it can be seen that is linearly related to . As shown in Figure 6, by performing a linear regression on and finding the slope, which is , the recovery factor can be determined. The slope of the black dashed line in Figure 5 is , and the fitting range is determined by the experimental data before the critical strain. In Figure 6a,b, the linear relationship is evident and the fitting is good. However, in Figure 6c, the strain rate is higher and the material does not have sufficient time for dynamic recovery, resulting in a narrower fitting range.
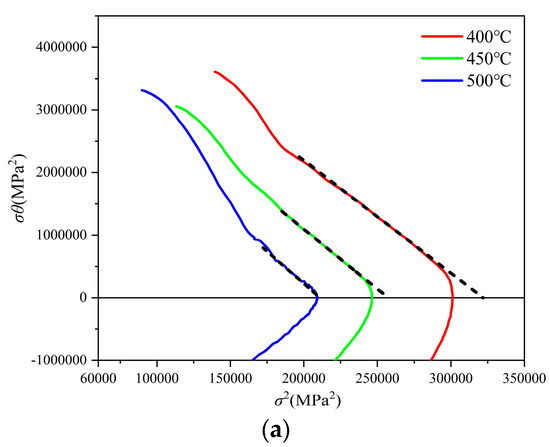
Figure 6.
. (a) 0.001 s−1; (b) 0.01 s−1; (c) 0.1 s−1.
Taking the logarithm of both sides of Equation (2) yields:
From the above formula, it can be deduced that is linearly related to . By performing a linear regression on and determining the slope, which is , we obtain the strain-rate sensitivity coefficient = 0.01735 on average. The intercept is , as shown in Figure 7. The fitting is very good in the figure, and it can be found that increases with the rise in temperature.
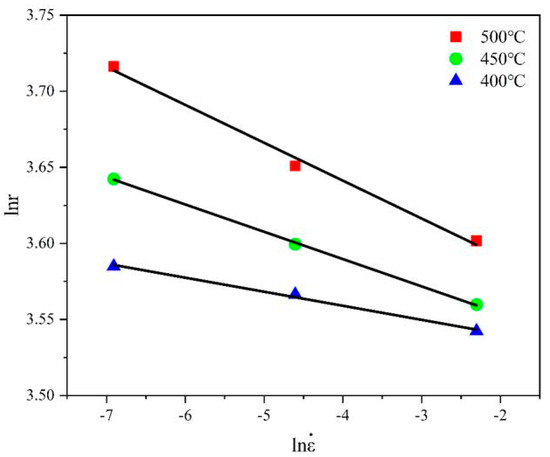
Figure 7.
.
Transforming Equation (11) yields:
When the strain rate is determined, is linearly related to . As shown in Figure 8, by performing a linear regression on and finding the slope, which is , we can then calculate the average self-diffusion activation energy as = 227,132 J/mol. The figure shows that the value of increases as the strain rate decreases.
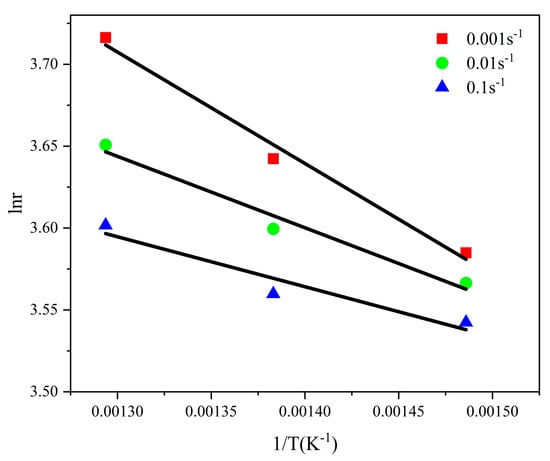
Figure 8.
.
Substituting and into the intercept expression allows us to calculate the average recovery constant = 66.2889.
From Equation (8), the following can be deduced:
Referring to the method of He et al. [24], the saturation stress in the above equation can be determined by plotting. Substituting the saturation stress and the other parameters allows us to obtain the hardening coefficient .
Taking the logarithm of both sides of Equation (3) yields:
Using the same method, when the temperature is fixed, fitting gives the intercept of the straight line. Substituting the parameters allows us to calculate the average hardening constant = 0.07412. Finally, we input the obtained relevant parameters into the software for microstructure simulation analysis. The main parameters set for the CA model are as shown in Table 3.

Table 3.
Parameters of CA model.
4. Results and Discussion
Forming experiments on TA18 titanium alloy tube with a small bending radius were conducted using the differential heating push-bending method. The tube blank had an outer diameter of 20 mm, a wall thickness of 1 mm, and an overall length of 90 mm. The bending angle is 90°, and the bending radius is 0.9D. Bevels were cut on both ends of the tube blank to obtain the appropriate shape for deformation. The experimental dies are shown in Figure 9. Multiple heating resistors are used to heat the outer side of the bend. The external temperature control device is connected to the heating resistors. A thermocouple is inserted into the reserved hole on the side of the lower die to measure the internal temperature. When the temperature reaches the set values, the device cuts off the power supply, and the heating resistors stop working, thus controlling the temperature. High-temperature-resistant grease was used for lubrication between the die cavity and the tube blank. As shown in Figure 10, the forming experiment was conducted on a four-column servo internal high-pressure forming equipment. Its PLC control system can set the thrust, stroke, and feed speed of each hydraulic cylinder on the operating console and provide real-time data feedback on the console screen to control the experimental conditions. The manufactured tube that met the requirements is shown in Figure 11, where the red arrow indicates the location of the tracking points selected based on the CA method, which is near the inner and outer regions at the symmetric plane of a 45° bending angle. Samples were also cut from the aforementioned areas for metallographic observation tests. The sample size is 7 mm × 6 mm (length × width). During the differential heating push-bending process, the material on the outer side of the tube is subjected to tangential tensile stress, while the inner side material is subjected to tangential compressive stress. The resulting thinning on the outer side of the bent tube and the wrinkling defects on the inner side become important criteria for evaluating the quality of the push-bending process. Moreover, such macroscopic plastic deformation leads to changes in the microstructure of the material, which in turn affect its overall mechanical properties.

Figure 9.
Experimental dies for differential heating push-bending.

Figure 10.
Experiment equipment.

Figure 11.
Manufactured tube with bending radius of 0.9D.
4.1. Microstructure Evolution in the Critical Areas During Differential Heating Push-Bending
As mentioned before, during the bending process of the tube, the materials on both sides of the bend are subjected to tangential stresses in different directions. Whether it is tensile or compressive stress, it will lead to an increase in dislocation density within the material and distortion of the lattice, which is an important prerequisite for the occurrence of dynamic recrystallization. When the material is heated to a sufficiently high temperature and meets the critical strain required for dynamic recrystallization, the dynamic recrystallization process will initiate.
Figure 12 presents the simulation results of the microstructure evolution of tracking point 1 using the CA method when the temperature of the outer side of the bent tube is 500 °C, as well as the strain contour maps. Figure 12a shows the initial microstructure, where grains are marked in different and random colors for distinction and grain boundaries are represented by black lines. Figure 12b depicts the situation in which the shear strain on the zx plane reaches 0.08 (the negative sign indicates direction); as the tube blank enters the bending section of the die cavity (92 represents the analysis steps), the degree of plastic deformation of the material is low, and initial dynamic recrystallization occurs, with a small number of recrystallized grains nucleating at the original grain boundaries. Figure 12c shows that when the shear strain increases to 0.13, while new recrystallized grains grow, more small-sized grains nucleate. Figure 12d illustrates that as the shear strain continues to increase to 0.18, the tube bends more, the growth of recrystallized grains is evident, and the original grains are gradually consumed by the recrystallized grains, yet some original grains are still preserved. Figure 12e shows that as the shear strain reaches 0.20 finally, the strain in the inner region of the bend is greater than the strain in the outer region of the bend. The tube has fully entered the bending section of the die cavity, the bending angle reaches 90°, and the tube blank has completed the differential heating push-bending forming process. The material on the outer side of the bend has undergone a complete dynamic recrystallization process, with a large number of dynamic recrystallized grains appearing. Due to the temperature of the material on the outer side of the bend not being high enough and the strain not being large enough, the dynamic recrystallization of the material is incomplete; thus, after deformation, some original large grains can still be observed. Figure 13 shows the change in the average grain size of the tracking point 1. As the shear strain increases, meaning that the degree of tube bending deformation increases, the average grain size of the material on the outer side of the bend gradually decreases, indicating significant grain refinement and an improvement in the mechanical properties of the material [25].
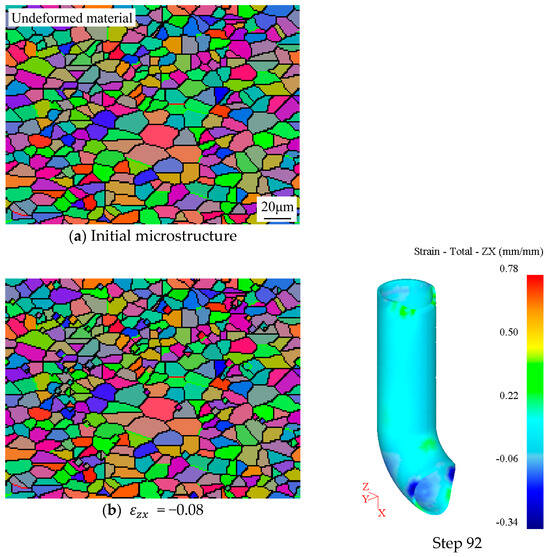
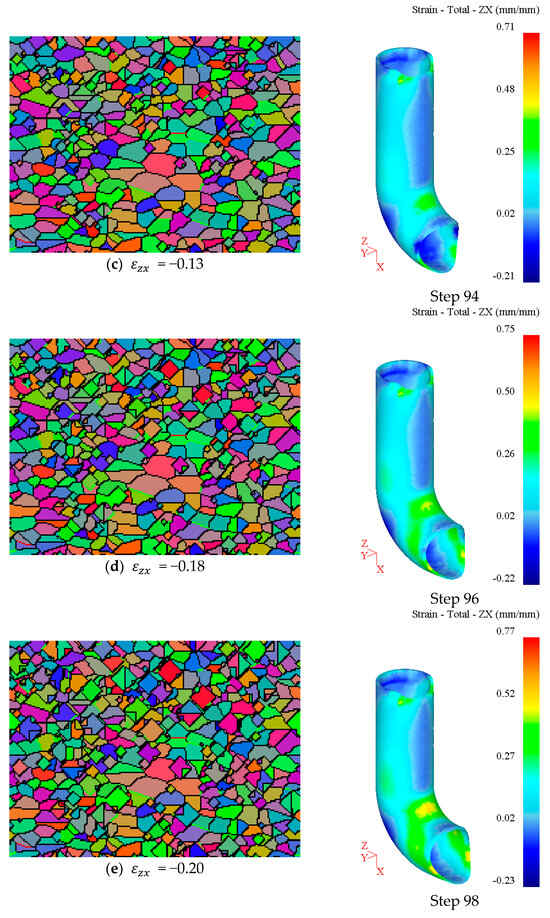
Figure 12.
Simulation results of the CA method of tracking point 1 and strain contour maps.
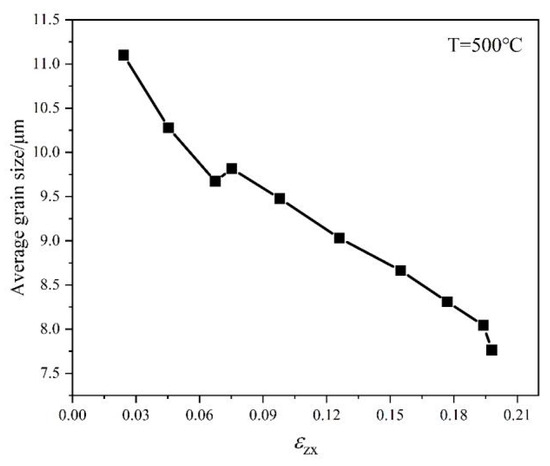
Figure 13.
Relationship between strain and average grain size.
In addition to temperature factors, the stress state also plays a key role in the microstructure evolution of material. Figure 14 shows the microstructure evolution results of the CA method at tracking point 2 when the temperature of the outer side of the bent tube is 500 °C, and it can be observed that the simulation results of tracking point 2 do not exhibit dynamic recrystallization. As previously mentioned, the strain contour map on the zx plane corresponding to Figure 12e shows that at the end of the push-bending forming process, the strain on the inner side of the bend is greater than that on the outer side, implying that the tangential compressive stress of the inner material is greater than the tangential tensile stress on the outer side. Dynamic recrystallization nucleation typically occurs in areas with higher dislocation density, but the increased dislocation density on the inner side due to the larger tangential compressive stress did not lead to the occurrence of dynamic recrystallization. This phenomenon indicates that in the differential heating push-bending forming process, temperature has a stronger influence on dynamic recrystallization than stress, playing a dominant role. Tracking point 2 is located on the inner side of the bent tube and is affected by the water cooling treatment in the inner area of the bend. Thus, the dominant factor of temperature is lower on the inner side of the bent tube. Although the inner side material has higher dislocation density and stores more energy of distortion in deformation, the lower temperature on the inner side cannot provide sufficient energy to drive the occurrence of dynamic recrystallization compared to the outer area of the bend with higher temperature.
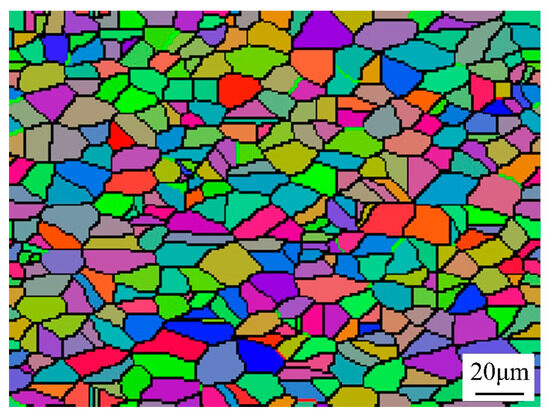
Figure 14.
Simulation results of the CA method of tracking point 2.
4.2. The Effect of Heating Temperature on the Evolution of Microstructure
Based on the previous analysis, during the differential heating push-bending process, the inner side of the bent tube does not undergo dynamic recrystallization due to the lower temperature. Therefore, the discussion mainly focuses on the microstructure evolution of the material on the outer side of the bend. Figure 15 shows the final results of the microstructure simulation of the CA method and the grain size distribution histogram for the tracking point 1 with the outer side of the bend at temperatures of 400 °C, 450 °C, and 500 °C. The CA simulation results indicate an increasing trend of dynamic recrystallization with rising temperature, as higher temperatures provide a greater driving force for recrystallization, leading to more dynamic recrystallization in the material. The grain size distribution histogram shows that as the temperature on the outer side of the bend increases, the average grain size first slightly increases and then decreases. This trend can be attributed to the competition between grain growth and recrystallization nucleation during deformation. At lower temperature, the driving force for dynamic recrystallization is insufficient, and the continuous growth of existing small grains is slightly more dominant than the nucleation of new grains. This results in a subtle increase in average grain size. As the temperature continues to rise, the driving force for dynamic recrystallization increases significantly, as exactly shown in Figure 16, which illustrates the relationship between the proportion of small grains (<5 μm) and temperature. It can be observed that the change in the slope of the line is very significant. When the temperature increases from 450 °C to 500 °C, the proportion of small grains increases extremely rapidly compared to before, as higher temperature provides sufficient energy to facilitate the nucleation and growth of new recrystallized grains, both of which contribute to the formation of a greater number of fine grains, and the microstructure is effectively refined. Consequently, the average grain size decreases due to the increased presence of fine recrystallized grains. Therefore, in the differential heating push-bending process, the temperature on the outer side of the bend can be increased to achieve a better grain refinement effect.
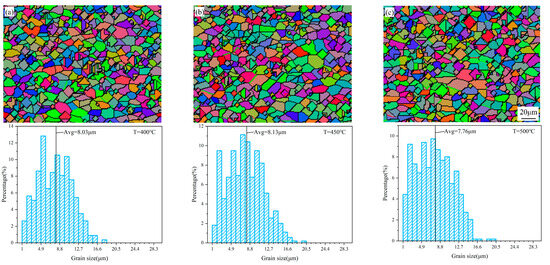
Figure 15.
CA simulation results and grain size distribution histogram at different temperatures: (a) T = 400 °C; (b) T = 450 °C; (c) T = 500 °C.
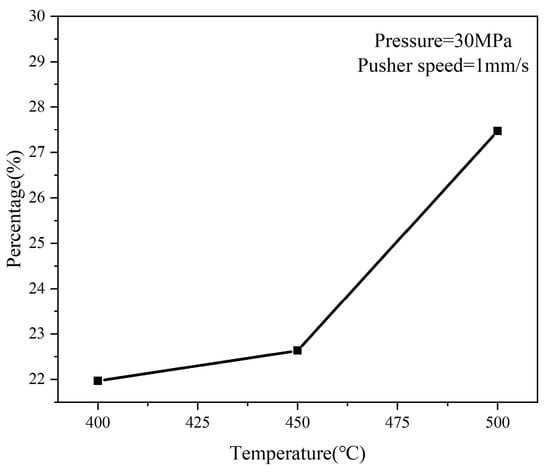
Figure 16.
The relationship between the proportion of small grains and temperature.
The metallographic observation results of the samples taken from the material on the outer side of the bent tube at different temperatures are shown in Figure 17a–c. The average grain size of the microstructure in the metallographic images was measured using the Image-Pro Plus software, as shown in Table 4. It can be observed that as the temperature on the outer side of the bend increases, the actual average grain size gradually decreases. This trend is similar to the variation observed in the microstructure simulation results of the CA method, indicating that an increase in temperature leads to an increase in the proportion of small grains. Moreover, the deviation between the simulated and actual average grain sizes is within 6%, which demonstrates that the CA method provides a good simulation of the microstructure.

Figure 17.
Metallographic images of the inner and outer sides of the bent tube: (a,d) T = 400 °C; (b,e) T = 450 °C; (c,f) T = 500 °C.

Table 4.
Comparison of simulated and actual average grain sizes.
However, within the temperature range from 400 °C to 450 °C, the CA model predicts an increase in average grain size, while the experimental results show a decrease in average grain size. This inconsistency indicates that the established CA model cannot accurately predict subtle physical effects within this temperature range. Such inconsistency may be due to the simplification of model assumptions. The CA model is based on a series of assumptions, such as the uniformity of initial dislocation density and the singularity of recrystallization nucleation. These assumptions may be overly simplified in some cases and fail to fully reflect the complexity of the actual physical process, and this is one of the reasons that lead to the deviation between the simulation and the experiment. The variation in dislocation density of the material may be influenced by other microstructural features such as grain boundary migration and subgrain formation, which are not fully considered in the model, causing the simulated results to deviate from the actual ones. Additionally, the material’s sensitivity to temperature and the presence of measurement errors in the experiment can also affect the comparison of results, leading to differences. In future research, the model assumptions can be further refined to consider more microstructural features, thereby more accurately reflecting the actual physical process and improving the applicability of the model. Additionally, more accurate and efficient microstructure characterization methods such as the EBSD technology and SEM can be employed to study and analyze the microstructure evolution behavior of material from a more comprehensive perspective, and to conduct data measurement and collection in a more scientific manner.
Figure 17d–f show the microstructure metallographic images of the samples taken from the material on the inner side of the bent tube at different temperatures. Due to the lower temperature on the inner side of the bent tube, the thermal energy provided by the outside did not reach the material’s thermal activation energy, and no dynamic recrystallization occurred on the material of the inner side of the bend. Simultaneously, it can be observed from the figures that the morphology of the α phase has undergone significant deformation, which is due to the larger compressive force experienced by the material on the inner side of the bend. The degree of deformation is greater, and the strain is larger.
4.3. The Effect of Internal Pressure on the Evolution of Microstructure
Figure 18 presents the CA simulation results and the corresponding grain size distribution histograms for the microstructure at tracking point 1 under different internal pressure conditions. In the CA simulation results, nucleated small grains at the grain boundaries, recrystallized grains of different sizes that are growing, and some original large grains that have not been consumed can be observed separately, forming a relatively complete process of dynamic recrystallization. The presence of some unchanged original grains also indicates the incompleteness of dynamic recrystallization. The grain size distribution histograms indicate that as the internal pressure increases, the average grain size of the material on the outer side of the bend gradually decreases. This is because the increasing internal pressure leads to a greater tangential tensile stress on the material on the outer side of the bend, causing the tube wall to fit more closely to the die cavity, and increasing the radial deformation of the material on the outer side of the bend. Microscopically, this results in an increase in dislocation density and a higher degree of dynamic recrystallization, with the emergence of more newly nucleated small grains, leading to a reduction in average grain size. Figure 19 shows the relationship between the proportion of small grains and the internal pressure. It can be observed that as the internal pressure increases, the proportion of small grains gradually increases, indicating that a higher internal pressure is beneficial for achieving better grain refinement in the material on the outer side of the bend. Therefore, in the differential heating push-bending process, increasing the counter-push force can be used to obtain a higher internal pressure, which in turn enhances the comprehensive mechanical properties of the material on the outer side of the bent tube.
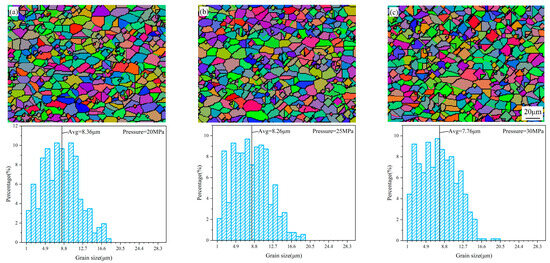
Figure 18.
CA simulation results and grain size distribution histograms under different internal pressures: (a) internal pressure = 20 MPa; (b) internal pressure = 25 MPa; (c) internal pressure = 30 MPa.
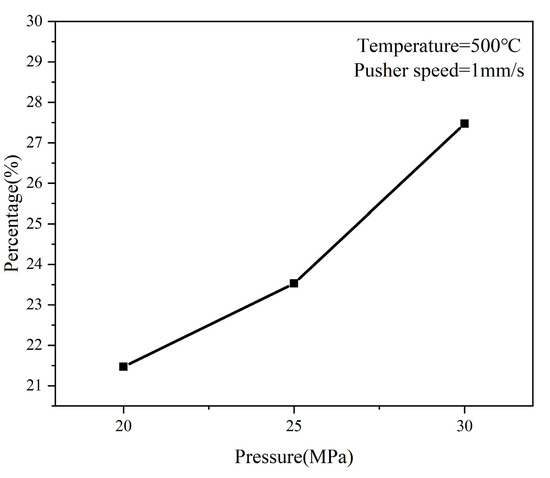
Figure 19.
The relationship between the proportion of small grains and internal pressure.
4.4. The Effect of Feed Speed on the Evolution of Microstructure
Figure 20 illustrates the CA simulation results and the corresponding grain size distribution histograms for the microstructure at tracking point 1 under different feed speeds of the pusher. Similar to the previous results, the CA simulation results also demonstrate the main process of dynamic recrystallization, with grains undergoing different stages from nucleation at the grain boundaries to growing and consuming the original grains. It can be observed from the grain size distribution histograms that as the feed speed of the pusher increases, the average grain size gradually decreases. This is because the increased feed speed causes the metal material to undergo a large deformation in a shorter period of time, leading to changes in the stress field. This rapidly increasing stress field promotes the movement of dislocations within the grains, which helps to release stress and promote grain refinement, resulting in a reduction in the average grain size of the material on the outer side of the bend. Figure 21 shows the relationship between the proportion of small grains and the feed speed of the pusher. It is found that as the feed speed of the pusher increases, the proportion of small grains is greater, indicating that a higher feed speed is conducive to the nucleation of recrystallizing grains in the material on the outer side of the bend. Therefore, in the differential heating push-bending process, a higher feed speed of the pusher can be used to achieve better grain refinement effects.
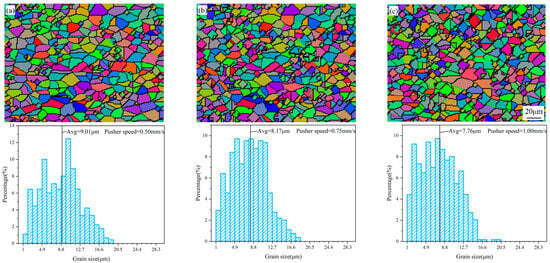
Figure 20.
CA simulation results and grain size distribution histograms at different feed speeds of the pusher: (a) pusher speed = 0.50 mm/s; (b) pusher speed = 0.75 mm/s; (c) pusher speed = 1.00 mm/s.
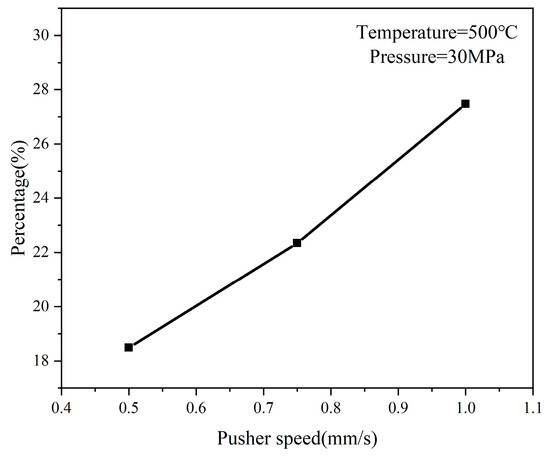
Figure 21.
The relationship between the proportion of small grains and the feed speed of the pusher.
5. Conclusions
Based on the experiment of differential heating push-bending of TA18 titanium alloy tubes with a small bending radius, the influence of different process parameters on the evolution of microstructure had been obtained through the simulation of the CA method and the experimental results. These findings not only contribute to the optimization of the forming process and the enhancement of mechanical properties but also have significant implications for improving industrial efficiency, reducing environmental impact and guiding future research directions by identifying current limitations and potential areas for further exploration. The conclusions are as follows:
- (1)
- Integrating the mesoscale simulation method into the study of the microstructure evolution of TA18 titanium alloy tubes in the differential heating push-bending forming process, key parameters of the CA model were determined based on a high-temperature tensile test as follows: self-diffusion activation energy = 227,132 J·mol−1, hardening constant = 0.07412, recovery constant = 66.2889, and strain-rate sensitivity coefficient = 0.01735.
- (2)
- Combining simulation with experimentation, a finite element model for differential heating push-bending of TA18 titanium alloy tubes was established, and microstructure simulation based on the CA method was conducted. Concurrently, experiments yielded qualified tubes with a small bending radius of 0.9D, and the average grain size of the microstructure in key areas of the formed tubes was measured. The deviation between these measurements and the CA simulation results was within 6%.
- (3)
- During the differential heating push-bending process of TA18 titanium alloy tubes, the average grain size on the outer side of the bend gradually decreases with the increase of plastic deformation, indicating dynamic recrystallization. On the inner side of the bend, no recrystallization phenomenon occurs due to the lower temperature. Different process parameters have a significant impact on the microstructure on the outer side of the bend. Fine grain strengthening effects, which are beneficial for enhancing the comprehensive mechanical properties of the material on the outer side of the bend, can be achieved under the conditions of a heating temperature of 500 °C, internal pressure of 30 MPa, and pusher feed speed of 1 mm/s.
Author Contributions
Conceptualization, Y.L. and X.X.; methodology, Y.L. and X.X.; software, L.W.; validation, L.W., Y.F., S.L., and J.X.; formal analysis, S.L. and J.X.; investigation, Y.L. and X.Z.; resources, X.X. and Y.F.; writing—original draft preparation, Y.L. and S.L.; writing—review and editing, X.Z.; visualization, J.X.; supervision, L.W.; funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (Grant No. 52265052), National Major Science and Technology Projects of China (No. J2019-VII-0014-0154), Natural Science Foundation of Jiangxi, China (No. 20224BAB214050), and National Natural Science Foundation of China (No. 52365050).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be provided when required.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Yang, Z.; Wu, J.; Wang, M.; Zhang, Z.; Yan, J.; Wu, W.; Liu, L.; Wang, H.; Wang, W. Tensile deformation behavior of high-strength TA18 titanium alloy tube under warm forming conditions and constitutive model based on dislocation density. Mater. Today Commun. 2023, 37, 107336. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, J.; Huang, W.; Ma, J.; Li, H. Uncertainty analysis and robust design optimization for the heat-assisted bending of high-strength titanium tube. Sci. China Technol. Sci. 2021, 64, 2174–2185. [Google Scholar] [CrossRef]
- Li, Z.; Zhan, M.; Guo, K.; Huang, T. Texture development of Ti-3Al-2.5V titanium alloy tubes. Rare Mat. Mat. Eng. 2017, 46, 3169–3175. [Google Scholar] [CrossRef]
- Yang, H.; Li, H.; Ma, J.; Li, G.; Huang, D. Breaking bending limit of difficult-to-form titanium tubes by differential heating-based reconstruction of neutral layer shifting. Int. J. Mach. Tool. Manu. 2021, 166, 103742. [Google Scholar] [CrossRef]
- Han, D.; Zhao, Y.; Zeng, W.; Li, L.; Zhang, Y. Cellular automata based microstructure prediction in accumulative roll-bonding of TA15 sheets. Rare Metal. Mat. Eng. 2021, 50, 3437–3445. [Google Scholar] [CrossRef]
- Fang, J.; Liang, C.; Lu, S.; Wang, K. Effect of geometrical parameters on forming quality of high-strength TA18 titanium alloy tube in numerical control bending. Trans. Nonferrous Met. Soc. China 2018, 28, 309–318. [Google Scholar] [CrossRef]
- Tao, R.; Xu, X.; Fan, Y.; Xiao, J.; Wang, Y.; Wei, L. Differential flow velocities control method for push-bending of the thin-walled tube with a 0.9D bending radius by differential lubrication. Int. J. Adv. Manuf. Technol. 2023, 124, 3359–3369. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, X.; Lu, X.; Zhong, Q. Technological parameters optimization and numerical simulation of hot pushing pipe bending process. Int. J. Adv. Manuf. Technol. 2023, 126, 4439–4451. [Google Scholar] [CrossRef]
- Cheng, Z.; Abd El-Aty, A.; Zhang, R.; Cheng, C.; Guo, X.; Tao, J. Finite element modeling and experimental investigation on manufacturing TA18 alloy pipes via hot free bending forming technology: Forming characteristics and process optimization. J. Mater. Res. Technol. 2024, 29, 5225–5240. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, J.; Gong, H.; Wu, Y.; Hao, T.; He, X. Microstructure simulation of AA2219 alloy in hot/warm forming and heat treatment using cellular automata methods. J. Mater. Sci. 2023, 58, 7968–7985. [Google Scholar] [CrossRef]
- Cao, Z.; Sun, Y.; Zhou, C.; Wan, Z.; Yang, W.; Ren, L.; Hu, L. Cellular automaton simulation of dynamic recrystallization behavior in V-10Cr-5Ti alloy under hot deformation conditions. Trans. Nonferrous Met. Soc. China 2019, 29, 98–111. [Google Scholar] [CrossRef]
- Ji, H.; Peng, Z.; Huang, X.; Wang, B.; Xiao, W.; Wang, S. Dynamic recrystallization of Ti-6Al-4V titanium alloy based on cellular automata. Proc. Inst. Mech. Eng. Part E 2023, 237, 1442–1459. [Google Scholar] [CrossRef]
- Li, W.; Li, S.; Li, X.; Xu, D.; Shao, Y.; Attallah, M.M.; Essa, K. Crystal plasticity model of induction heating-assisted incremental sheet forming with recrystallisation simulation in cellular automata. Int. J. Adv. Manuf. Technol. 2022, 123, 903–925. [Google Scholar] [CrossRef]
- Asgharzadeh, A.; Nazari Tiji, S.; Park, T.; Kim, J.; Pourboghrat, F. Cellular automata modeling of the kinetics of static recrystallization during the post-hydroforming annealing of steel tube. J. Mater. Sci. 2020, 55, 7938–7957. [Google Scholar] [CrossRef]
- Yu, Z.; Peng, W.; Zhang, X.; Oleksandr, M.; Titov, V. Evolution of microstructure of aluminum alloy hollow shaft in cross wedge rolling without mandrel. J. Cent. South Univ. 2022, 29, 807–820. [Google Scholar] [CrossRef]
- Majta, J.; Madej, L.; Svyetlichnyy, D.; Perzynski, K.; Kwiecien, M.; Muszka, K. Modeling of the inhomogeneity of grain refinement during combined metal forming process by finite element and cellular automata methods. Mat. Sci. Eng. A 2016, 671, 204–213. [Google Scholar] [CrossRef]
- Yao, Y. Research on Microstructure Evolution Law of TA18 Titanium Alloy During Isothermal Hot Shear Bending Deformation. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2020. (In Chinese). [Google Scholar]
- ISO 6892-2:2011; Metallic Materials—Tensile Testing—Part 2: Method of Test at Elevated Temperature. International Organization for Standardization: Geneva, Switzerland, 2011.
- Wei, L. Study on Necking and Thickening Process of TA18 Titanium Alloy Thin-Walled Tube. Master’s Thesis, Nanchang Hangkong University, Nanchang, China, 2022. (In Chinese). [Google Scholar]
- Li, H.; Sun, X.; Yang, H. A three-dimensional cellular automata-crystal plasticity finite element model for predicting the multiscale interaction among heterogeneous deformation, DRX microstructural evolution and mechanical responses in titanium alloys. Int. J. Plast. 2016, 87, 154–180. [Google Scholar] [CrossRef]
- Zhang, Y.; Quan, G.; Lei, S.; Zhao, J.; Xiong, W. Description of dynamic recrystallization behaviors and grain evolution mechanisms during the hot forming process for SAE 5137H steel. Materials 2022, 15, 5593. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Y.; Ahmad, A. A novel simulation of continuous dynamic recrystallization process for 2219 aluminium alloy using cellular automata technique. Mater. Sci. Eng. A 2021, 815, 141256. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- He, Y.; Pan, Q.; Qin, Y.; Liu, X.; Li, W.; Chiu, Y.; Chen, J. Dynamic recrystallization kinetics of ZK60 magnesium alloy during hot deformation. Chin. J. Nonferrous Met. 2011, 21, 205–1213. [Google Scholar] [CrossRef]
- Cui, C.; He, J.; Wang, W.; Chen, W.; Zhang, W. Microstructure, texture and mechanical properties of extruded AZ31 Mg alloy during small strain multi-directional forging with gradient cooling. J. Alloys Compd. 2022, 909, 164795. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).