Thermo-Chemo-Mechanical Coupling in TGO Growth and Interfacial Stress Evolution of Coated Dual-Pipe System

Abstract

Improving the energy efficiency of advanced ultra-supercritical (USC) power plants by increasing steam operating temperature up to 700 °C can be achieved, at reduced cost, by using novel engineering design concepts, such as coated steam pipe systems manufactured from high temperature materials commonly used in current operational power plants. The durability of thermal barrier coatings (TBC) in advanced USC coal power systems is critically influenced by thermally grown oxide (TGO) evolution and interfacial stress under thermo-chemo-mechanical coupling. This study investigates a novel dual-pipe coating system comprising an inner P91 steel pipe with dual coatings and external cooling, designed to mitigate thermal mismatch stresses while operating at 700 °C. A finite element framework integrating thermo-chemo-mechanical coupling theory is developed to analyze TGO growth kinetics, oxygen diffusion, and interfacial stress evolution. Results reveal significant thermal gradients across the coating, reducing the inner pipe surface temperature to 560 °C under steady-state conditions. Oxygen diffusion and interfacial curvature drive non-uniform TGO thickening, with peak regions exhibiting 23% greater thickness than troughs after 500 h of oxidation. Stress analysis identifies axial stress dominance at top coat/TGO and TGO/bond coat interfaces, increasing from 570 MPa to 850 MPa due to constrained volumetric changes and incompatible growth strains. The parabolic TGO growth kinetics and stress redistribution mechanisms underscore the critical role of thermo-chemo-mechanical interactions in interfacial degradation. These research findings will facilitate the optimization of coating architectures and the enhancement of structural integrity in high-temperature energy systems. Meanwhile, clarifying the stress evolution within the coating can improve the ability to predict failures in USC coal power technology.

1. Introduction

Advanced ultra-supercritical (USC) coal power technology operating at 630–700 °C is globally recognized as a key approach for enhancing energy efficiency and achieving cleaner, more secure energy systems. However, the primary challenge in developing 630–700 °C USC coal power plants lies in the need for heat-resistant materials capable of withstanding extreme thermo-mechanical loads in structural components. To address the limitations of conventional heat-resistant materials, a novel dual-pipe system has been designed, as illustrated in Figure 1 [1]. The system consists of an inner P91 steel pipe coated with yttria-stabilized zirconia (YSZ) thermal barrier coatings (TBC), combined with external cooling steam pipes to optimize thermo-mechanical performance. The TBC system comprises four key layers: the topcoat (TC), bond coat (BC), P91 steel substrate, and alumina-dominated thermally grown oxides (TGO) that form between the TC and BC. Operating with internal steam at 700 °C and external cooling at 450 °C, this configuration reduces surface temperatures of heat-resistant steel pipes, thereby enabling the use of 700 °C USC main steam pipelines without requiring nickel-based alloys.

Unlike conventional main steam pipelines, which maintain near-isothermal wall conditions, the ceramic-steel multilayer heterostructure in the coated dual-pipe system induces thermal gradients and mismatch stresses due to differences in thermomechanical properties. These stresses critically impact structural integrity. High-temperature oxygen and BC elements diffuse to the interface, forming TGO through a temperature-dependent process influenced by thermomechanical stress, with stress accelerating diffusion [2,3]. TGO grows via ionic diffusion, resulting in non-uniform oxide thickening. The deformation compatibility between the layers of the TBC during growth generates localized stresses, which depend on the thickness and morphology of TGO, altering the overall stress distribution in the TBC. Consequently, TGO evolution at TBC interfaces represents a thermo-chemo-mechanical coupling process, where thickness and morphology are governed by temperature, stress, and elemental diffusion gradients, which, in turn, influence the system’s stress field [4]. Combined thermal mismatch and constrained TGO growth contribute to elevated interfacial stress, increasing TGO layer stress by one to two orders of magnitude relative to adjacent layers, ultimately leading to crack initiation, propagation, and TBC spallation.

TGO growth and stress evolution during high-temperature operation are key factors in TBC interface spallation. Accurate modeling of TGO morphology and stress states is essential for understanding and mitigating such failures. Over the past two decades, significant research has focused on modeling TGO thermal growth due to TBC interface oxidation, establishing essential simulation frameworks for thermomechanical analysis. Freborg et al. [5] applied the finite element method to model TGO growth, capturing material property transitions but neglecting oxidation-induced growth stresses. Karlsson et al. [6,7] simulated TGO thermal growth by implementing stress-free strain through the UEXPAN subroutine, allowing for thickness expansion in the BC-adjacent TGO layer while considering lateral growth strain. Although widely adopted, this method exhibits limitations in simulating substantial TGO thickening, as excessive expansion strain in single-layer elements compromises finite element accuracy. He et al. [8,9] addressed this issue by employing material parameter conversion and a volumetric strain analogy. Hille et al. [10] introduced a volume fraction variable into diffusion-reaction equations based on TBC interface oxidation kinetics, enabling more accurate TGO growth analysis. However, these methods fail to fully capture the thermo-chemo-mechanical coupling mechanisms governing TBC interface oxidation, providing only phenomenological descriptions of TGO thermal growth.

Recent advancements in thermo-chemo-mechanical coupling theory have facilitated more comprehensive studies of TGO thermal growth by integrating multi-field interactions. Loeffel et al. [11,12] pioneered a large-deformation-based thermo-chemo-mechanical constitutive model for TGO growth at TBC interfaces. Hu et al. [13] proposed a fully coupled thermo-chemo-mechanical model based on variational principles, emphasizing phase transformations within a continuum mechanics framework. Xu et al. [14] investigated thermo-chemo-mechanical coupling mechanisms in TBC interfaces under molten deposit conditions using finite element modeling. Zhang et al. [15] developed a thermodynamically consistent continuum framework that unifies mass diffusion, heat transfer, and chemical reactions, enabling the prediction of transient chemo-mechanical coupling in swelling solids. Qin et al. [16] extended this theory to finite strain plasticity by incorporating strain-dependent exponential kinetics, allowing precise modeling of far-from-equilibrium chemical processes. Zhou et al. [17] formulated a continuum model for high-temperature interfacial oxidation in deformed superalloys, validated through experimental data, confirming significant Al₂O₃ growth acceleration under tensile loading.

This study applies thermo-chemo-mechanical coupled theory to investigate TGO growth and interfacial stress evolution in a novel dual-pipe coating system. The remainder of the paper is structured as follows: Section 2 establishes the theoretical framework, integrating conservation laws, constitutive equations, and an oxygen diffusion model. Section 3 details the finite element methodology, including geometric and boundary-condition specifications, material parameters for each constituent layer, and meshing strategies. Results and discussions are presented in Section 4, with a focus on steady-state heat transfer analysis, oxygen diffusion characteristics, nonlinear TGO growth driven by thermo-chemo-mechanical coupling, and stress evolution at critical interfaces. Concluding remarks summarize the key findings and their implications for coating system durability are given at the end of the work. These research findings will facilitate the optimization of coating architectures and the enhancement of structural integrity in high-temperature energy systems. Meanwhile, clarifying the stress evolution within the coating can improve the ability to predict failures in USC coal power technology.

2. Theoretical Framework

2.1. Conservation Laws in TBCs

To establish a thermo-chemo-mechanical coupled model for nonlinear TGO growth at coating interfaces, small-strain elastic deformation is assumed for the TBC. Inertial effects are neglected due to the significantly slower chemical reaction process compared to mechanical deformation. The stress equilibrium equation is given by

$$\nabla ·\mathsf{\sigma }+\mathit{f}=0,$$

(1)

where $\mathsf{\sigma }$ is the Cauchy stress tensor (MPa) and $\mathit{f}$ the body force tensor (N/m³).

The diffusion–oxidation mechanism at TBC interfaces follows Fick’s Second Law:

$$\dot{c}=-\nabla ·\mathit{J}+\dot{r},$$

(2)

where $c$ and $\mathit{J}$ are the oxygen concentration (mol/m³) and diffusion flux (mol·m⁻²·s⁻¹), respectively. The oxide formation/oxygen consumption rate per unit volume $\dot{r}$ is defined (mol·m⁻³·s⁻¹) as

$$\dot{r}=-M\dot{n},$$

(3)

where $M$ is the ratio of confined oxygen atoms to formed TGO volume (m³·mol⁻¹·s⁻¹), which is equal to the molarity of oxygen in alumina, $n$ the TGO volume fraction, and $1-n$ the BC volume fraction. This study assumes TGO comprises solely of Al₂O₃, with Al diffusion neglected due to the significantly higher diffusion rate of oxygen [10].

The TBC system functions as an open thermodynamic system [18], we can obtain the equation for internal energy equilibrium from the first law of thermodynamics:

$${\displaystyle {\int }_{\mathsf{\Omega }}\dot{e}\mathrm{d}\mathsf{\Omega }}={\displaystyle {\int }_{\mathsf{\Gamma }}\left(\mathsf{\sigma }·\mathit{n}\right)·\mathit{v}\mathrm{d}\mathsf{\Gamma }}+{\displaystyle {\int }_{\mathsf{\Omega }}\mathit{f}·\mathit{v}\mathrm{d}\mathsf{\Omega }}+{\displaystyle {\int }_{\mathsf{\Omega }}{r}_{\mathrm{q}}\mathrm{d}\mathsf{\Omega }}-{\displaystyle {\int }_{\mathsf{\Gamma }}\mathit{q}·\mathit{n}\mathrm{d}\mathsf{\Gamma }}-{\displaystyle {\int }_{\mathsf{\Gamma }}\mu \mathit{J}·\mathit{n}\mathrm{d}\mathsf{\Gamma }},$$

(4)

where $\mathsf{\Omega }$ represents the volume domain of TBC, $\mathsf{\Gamma }$ the surface area, $e$ the volumetric internal energy density (J/m³), $\mathit{v}$ the velocity (m/s), $\mathit{n}$ the outward normal direction, $r_{\mathrm{q}}$ the volumetric heat source (W/m³), $\mathit{q}$ the heat flux (W/m²), and $\mu$ the chemical potential (J/mol). The first and second terms on the right correspond to surface and body force power, the third and fourth terms represent internal energy changes due to heat sources and heat flux, and the last term accounts for internal energy variations from external mass diffusion. Applying the divergence theorem, Equation (4) is rewritten in local form:

$$\dot{e}=\left(\nabla ·\mathsf{\sigma }\right)·\mathit{v}+\mathsf{\sigma }:\nabla \mathit{v}+\mathit{f}·\mathit{v}-\nabla ·\mathit{q}+r_{\mathrm{q}}-\nabla \mu ·\mathit{J}-\mu \nabla ·\mathit{J},$$

(5)

Combining Equation (1) with Equation (2) and substituting into Equation (5) gives

$$\dot{e}=\mathsf{\sigma }: \dot{\mathsf{\epsilon }}-\nabla ·\mathit{q}+r_{\mathrm{q}}-\nabla \mu ·\mathit{J}+\mu \dot{c}-\mu \dot{r}.$$

(6)

2.2. Constitutive Equations

During interfacial oxidation in coatings, entropy must not decrease over time, invoking the second law of thermodynamics in local form:

$$\dot{s}\ge -\nabla ·\left({\displaystyle \frac{\mathit{q}}{T}}\right)+{\displaystyle \frac{r_{\mathrm{q}}}{T}},$$

(7)

where $s$ denotes entropy per unit volume (J·m⁻³·K⁻¹) and $T$ is absolute temperature (K). The right-hand terms represent entropy change rates from heat flux and thermal sources. Substituting Equation (6) yields

$$T\dot{s}-{\displaystyle \frac{\mathit{q}·\nabla T}{T}}-\dot{e}+\mathsf{\sigma }: \dot{\mathsf{\epsilon }}+\mu \dot{c}-\mu \dot{r}-\nabla \mu ·\mathit{J}\ge 0.$$

(8)

Since the system is open, requiring a state function that governs spontaneous evolution, the volumetric Helmholtz free energy $\psi$ (J/m³) is introduced

$$\psi =e-Ts.$$

(9)

Replacing internal energy with Helmholtz free energy in Equation (8) gives

$$-{\displaystyle \frac{\mathit{q}·\nabla T}{T}}-\dot{\psi }-\dot{T}s+\mathsf{\sigma }: \dot{\mathsf{\epsilon }}+\mu \dot{c}-\mu \dot{r}-\nabla \mu ·\mathit{J}\ge 0.$$

(10)

The Helmholtz free energy $\psi =\stackrel{⌢}{\psi }\left(c,n,T,\mathsf{\epsilon }\right)$ is defined as a function of concentration $c$, TGO volume fraction $n$, temperature $T$, and strain $\mathsf{\epsilon }$. Its time derivative is

$$\dot{\psi }={\displaystyle \frac{\partial \psi }{\partial c}}\dot{c}+{\displaystyle \frac{\partial \psi }{\partial n}}\dot{n}+{\displaystyle \frac{\partial \psi }{\partial T}}\dot{T}+{\displaystyle \frac{\partial \psi }{\partial \mathsf{\epsilon }}}: \dot{\mathsf{\epsilon }}.$$

(11)

Strain during interfacial oxidation is expressed as [19]

$$\mathsf{\epsilon }={\mathsf{\epsilon }}^{\mathrm{e}}+{\mathsf{\epsilon }}^{\mathrm{th}}+{\mathsf{\epsilon }}^{\mathrm{d}}+{\mathsf{\epsilon }}^{\mathrm{c}},$$

(12)

where ${\mathsf{\epsilon }}^{\mathrm{e}}$ is the elastic strain, ${\mathsf{\epsilon }}^{\mathrm{th}}$ the thermal expansion strain, ${\mathsf{\epsilon }}^{\mathrm{d}}$ the material diffusion-induced strain, and ${\mathsf{\epsilon }}^{\mathrm{c}}$ the chemical expansion strain. Substituting Equations (11), (12), and (3) into (10) yields

$$\left(-{\displaystyle \frac{\partial \psi }{\partial \mathsf{\epsilon }}}+\mathsf{\sigma }\right): \dot{\mathsf{\epsilon }}+\left(-{\displaystyle \frac{\partial \psi }{\partial T}}-s\right)\dot{T}+\left(-{\displaystyle \frac{\partial \psi }{\partial c}}+\mu \right)\dot{c}+\left(-{\displaystyle \frac{\partial \psi }{\partial n}}+\mathrm{M}\mu \right)\dot{n}-{\displaystyle \frac{\mathit{q}·\nabla T}{T}}-\nabla \mu ·\mathit{J}\ge 0,$$

(13)

As $c$, $T$ and $\mathsf{\epsilon }$ are arbitrary, coefficients of $\dot{c}$, $\dot{T}$ and $\dot{\mathsf{\epsilon }}$ vanish, yielding constitutive equations for stress, entropy, and chemical potential under TBC interfacial oxidation:

$$\left.\begin{array}{l}\mathsf{\sigma }={\displaystyle \frac{\partial \psi }{\partial \mathsf{\epsilon }}}\hfill \\ s=-{\displaystyle \frac{\partial \psi }{\partial T}}\hfill \\ \mu ={\displaystyle \frac{\partial \psi }{\partial c}}\hfill \end{array}\right\}.$$

(14)

Expanding the Helmholtz free energy as a second-order series with respect to $c$, $n$, $T$, $\mathsf{\epsilon }$ yields its explicit form [18]:

$$\begin{array}{cc}\hfill \psi & ={\psi }_0+{\mathsf{\sigma }}_0:\mathsf{\epsilon }-s_{0}T+{\mu }_{0}c-A_{0}n+{\displaystyle \frac{1}{2}}\lambda {\epsilon }_{\mathrm{kk}}^2+{\epsilon }_{\mathrm{kk}}{R}^{\mathsf{\alpha }}\left(c-c_0\right)\hfill \\ & -3\alpha K{\epsilon }_{\mathrm{kk}}\left(T-T_0\right)-3\beta K{\epsilon }_{\mathrm{kk}}\left(n-n_0\right)+G\Lambda +{\displaystyle \frac{1}{2}}{N}^{\mathsf{\alpha }}{\left(c-c_0\right)}^2\hfill \\ & +\left(T-T_0\right)L\left(c-c_0\right)-\zeta \left(c-c_0\right)\left(n-n_0\right)-{\displaystyle \frac{1}{2}}{C}_{\mathrm{v}}{\displaystyle \frac{{\left(T-T_0\right)}^2}{T_0}}\hfill \\ & -{\displaystyle \frac{T-T_0}{T_0}}P\left(n-n_0\right)-{\displaystyle \frac{1}{2}}{\alpha }_{\mathrm{n}}{\left(n-n_0\right)}^2\hfill \end{array},$$

(15)

Subscript “0” denotes initial values. And $K$ is bulk modulus (GPa), $G$ is shear modulus (GPa), $\lambda$ is Lamé coefficient (GPa), ${\epsilon }_{\mathrm{kk}}$ is volumetric strain, $\Lambda =\mathsf{\epsilon }:\mathsf{\epsilon }$ is the double-point product of the strain, $A$ is chemical affinity (GPa), $\alpha$ is thermal expansion coefficient (1/K), $\beta$ is chemical expansion coefficient, $R^{\mathsf{\alpha }}=-K{V}_{\mathrm{m}}$ is stress-chemical coefficient (concentration-stress coupling), which measures the influence of concentration change on stress. $V_{\mathrm{m}}$ is partial molar volume (m³/mol), $N^{\mathsf{\alpha }}$ is chemical potential constant (J·m³·mol⁻²), $L=9K{V}_{\mathrm{m}}\alpha$ is thermo-chemical potential coefficient (temperature-chemical potential coupling), which characterizes the influence of temperature changes on the chemical potential. $\zeta$ is reaction-dependent chemical potential constant (concentration-reaction coupling) (J/m³), which characterizes the influence of concentration changes on chemical affinity. $C_{\mathrm{v}}=\rho C$ is volumetric heat capacity, $\rho$ is material density (kg/m³), $C$ is specific heat capacity (J·kg⁻¹·K⁻¹), $P$ is reaction latent heat (J·m⁻³·K⁻¹), ${\alpha }_{\mathrm{n}}$ is the decrease in chemical affinity per unit change in reaction extent (J/m³). Substituting Equation (15) into Equation (14) yields the explicit constitutive relations for interfacial oxidation in coatings:

$$\left.\begin{array}{l}\mathsf{\sigma }={\displaystyle \frac{\partial \psi }{\partial \mathsf{\epsilon }}}={\mathsf{\sigma }}_0+\lambda {\epsilon }_{\mathrm{kk}}\mathit{I}+2G\mathsf{\epsilon }+R^{\mathsf{\alpha }}\left(c-c_0\right)\mathit{I}-3\alpha K\left(T-T_0\right)\mathit{I}-3\beta K\left(n-n_0\right)\mathit{I}\hfill \\ s=-{\displaystyle \frac{\partial \psi }{\partial T}}=s_0+3\alpha K{\epsilon }_{\mathrm{kk}}-L\left(c-c_0\right)+C_{\mathrm{v}}{\displaystyle \frac{T-T_0}{T_0}}+{\displaystyle \frac{1}{T_0}}P\left(n-n_0\right)\hfill \\ \mu ={\displaystyle \frac{\partial \psi }{\partial c}}={\mu }_0+R^{\mathsf{\alpha }}{\epsilon }_{\mathrm{kk}}+N^{\mathsf{\alpha }}\left(c-c_0\right)+L\left(T-T_0\right)-\zeta \left(n-n_0\right)\hfill \end{array}\right\}.$$

(16)

Neglecting diffusion-induced strain and chemical thermal variations, under small deformation assumption, the equation simplifies to

$$\left.\begin{array}{l}\mathsf{\sigma }={\mathsf{\sigma }}_0+\lambda {\epsilon }_{\mathrm{kk}}\mathit{I}+2G\mathsf{\epsilon }-K{V}_{\mathrm{m}}\left(c-c_0\right)\mathit{I}-3\alpha K\left(T-T_0\right)\mathit{I}-3\beta K\left(n-n_0\right)\mathit{I}\hfill \\ s=s_0+3\alpha K{\epsilon }_{\mathrm{kk}}+C_{\mathrm{v}}{\displaystyle \frac{T-T_0}{T_0}}\hfill \\ \mu ={\mu }_0+N^{\mathsf{\alpha }}\left(c-c_0\right)+V_{\mathrm{m}}{\sigma }_{\mathrm{m}}+9K{V}_{\mathrm{m}}\alpha \left(T-T_0\right)\hfill \end{array}\right\},$$

(17)

where ${\sigma }_{\mathrm{m}}=-K{\epsilon }_{\mathrm{kk}}$ is hydrostatic pressure.

2.3. Oxygen Diffusion Model

Applying Fourier’s heat conduction law, $\nabla ·\mathit{q}=\nabla ·\left(\nabla k_{\mathrm{c}}T\right)$ where $k_{\mathrm{c}}$ represents thermal conductivity coefficients (W·m⁻¹·K⁻¹), retaining solely the heat flux term yields the temperature governing equation:

$$\rho C\dot{T}=\nabla ·\left(k_{\mathrm{c}}\nabla T\right).$$

(18)

The oxygen diffusion flux relates to the chemical potential, that is,

$$\mathit{J}=-m\nabla \mu ,$$

(19)

where $m$ is oxygen mobility (mol²·J⁻¹·m⁻¹·s⁻¹). Substituting Equation (17) into Equation (19) yields:

$$\mathit{J}=-m\nabla \left[N^{\mathsf{\alpha }}\left(c-c_0\right)-V_{\mathrm{m}}{\sigma }_{\mathrm{m}}\right].$$

(20)

For oxygen diffusion, $m=cD/RT$ and $N^{\mathsf{\alpha }}=D/m$ (where $R$ is ideal gas constant (J·mol⁻¹·K⁻¹), and $D$ the diffusion coefficient (m²/s)); therefore, Equation (2) becomes

$$\dot{c}=\nabla ·\left[D\nabla \left(c-{\displaystyle \frac{V_{\mathrm{m}}c}{RT}}{\sigma }_m\right)\right]-M\dot{n}.$$

(21)

The diffusion coefficient $D$ is stress- and temperature-dependent [20]:

$$D=D_0·e^{{\displaystyle \frac{\gamma V_{\mathrm{m}}{\sigma }_m}{RT}}},$$

(22)

where $D_0$ is the stress-free diffusion coefficient (m²/s), $\gamma$ the positive dimensionless coefficient. The diffusion coefficient coupling term $D({\sigma }_{\mathrm{m}})$ represents stress-dependent oxygen diffusion.

Assuming TGO formation is proportional to oxygen and Al concentrations, with Al concentration equivalent to the BC layer’s volume fraction, the TGO reaction rate is expressed as

$$\dot{n}=Qc\left(1-n\right),$$

(23)

where $Q$ denotes the reaction rate (m³·mol⁻¹·s⁻¹).

Within the framework of linear elasticity and small deformation, governing Equations (1), (18), (21), and constitutive Equation (17) for thermo-chemo-mechanical coupling in novel dual-pipe coating systems are derived based on thermodynamic consistency principles, with a nonlinear stress-dependent diffusion coefficient established.

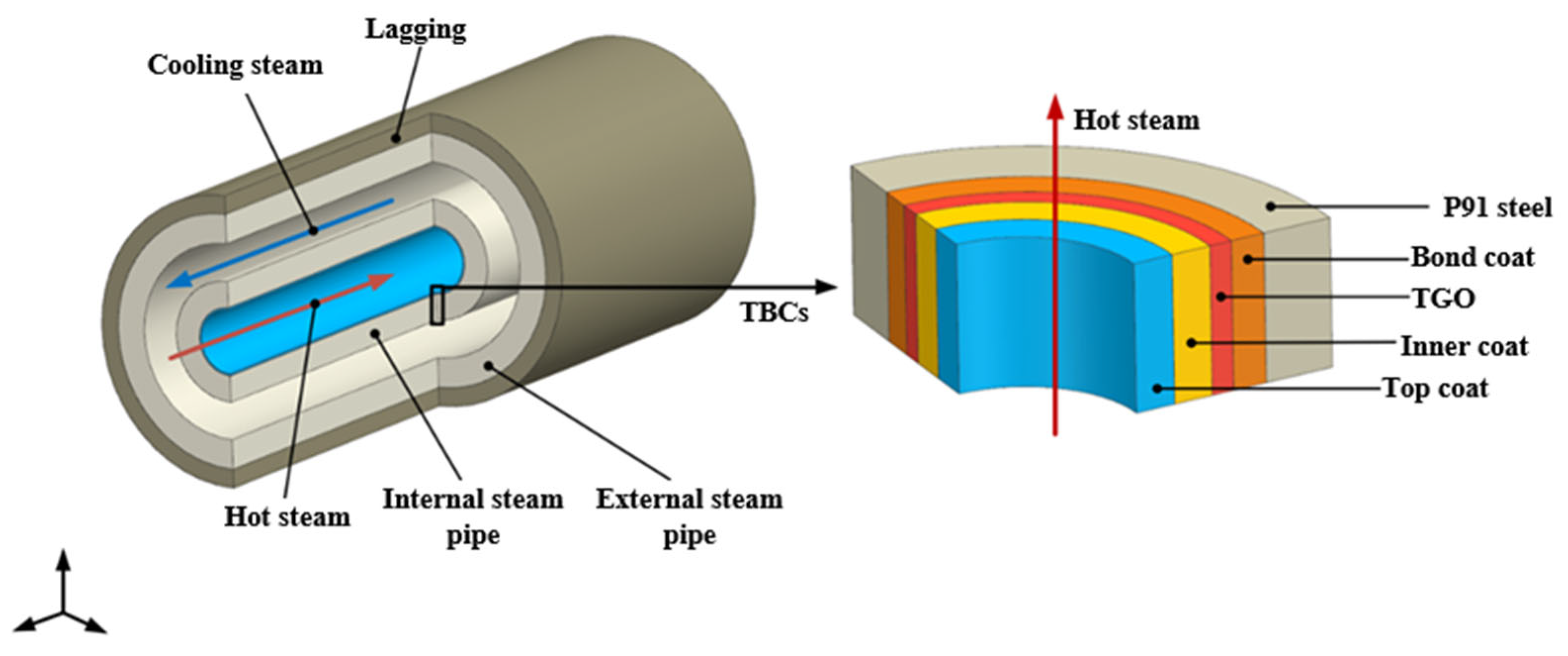
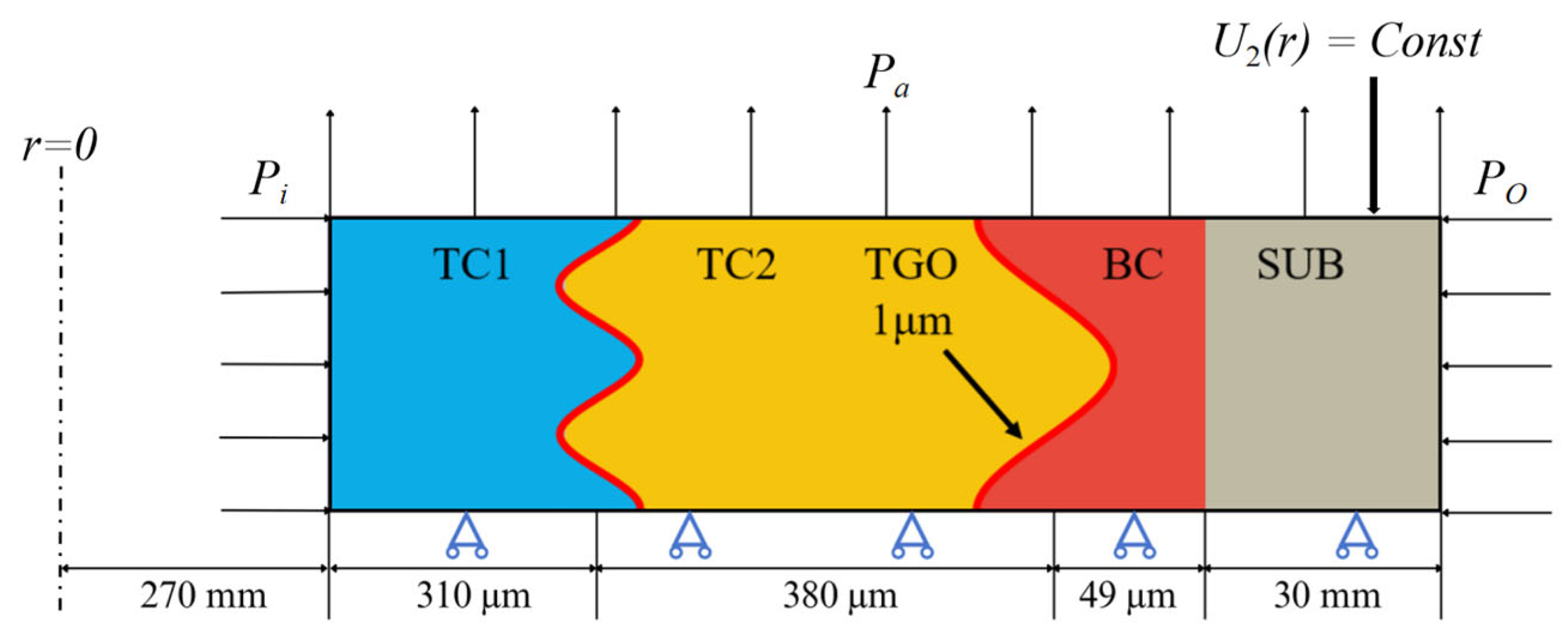
3. Finite Element Model of Dual-Pipe Coating System

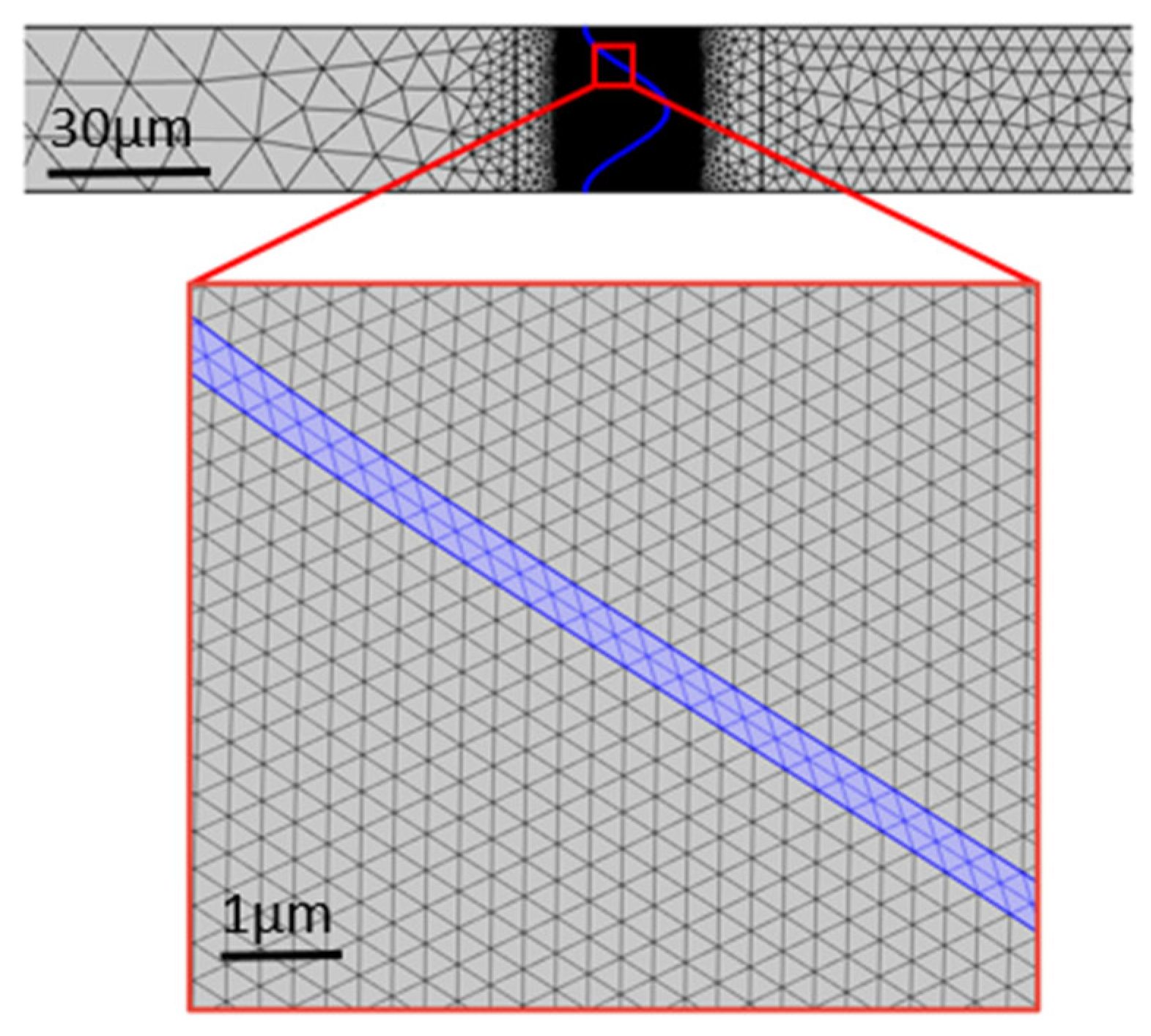
3.1. Geometric Model and Mesh Generation

Figure 2 shows a schematic diagram of a two-dimensional axisymmetric finite element model of a novel dual-pipe system. The components of the system are as follows: TC1 is composed of LZO, TC2 is made of 8YSZ, the component of TGO is α-Al₂O₃, BC is composed of NiCoCrAlY, and the substrate is P91 steel [21]. Moreover, based on the literature [21], we determined the dimensions of the dual-pipe system. The total thickness of the system is 30.74 mm, of which the thickness of the outer topcoat (TC1) is 0.31 mm, the thickness of the inner topcoat (TC2) is 0.38 mm, and the thickness of the BC is 0.049 mm. To improve coating life, the coating is usually pre-treated to produce a prefabricated TGO with a thickness of 0.001 mm. The outer diameter of the main steam pipeline is 270 mm, and the wall thickness is 30 mm. In addition, the model width is 0.06 mm. Considering that the basal layer has little influence on TGO growth, the basal part is ignored in finite element modeling. Due to the uneven porosity of the material caused by the manufacturing process, the interface of each layer is usually rough, and the cosine curve is used to roughly describe the interface morphology of TC1/TC2 and TC2/BC, and the morphology curve function is

$$y_1=A_{\mathrm{z}}\cos (2\mathsf{\pi }/0.03),$$

(24)

and

$$y_2=A_{\mathrm{z}}\cos (2\mathsf{\pi }/0.06),$$

(25)

Amplitude $A_{\mathrm{z}}$ is set to 0.008 mm [21].

Finite element analysis in this model was performed using COMSOL Multiphysics 6.3. Assuming perfect bonding between adjacent layers. The model geometry is appropriately partitioned prior to meshing. The triangular quadratic Lagrange elements under the plane strain assumption is used. Local mesh refinement was implemented near the TC1/TC2, TC2/TGO, and TGO/BC interfaces, initial TGO, and TGO growth zones, shown in Figure 3. Meshing strategy sensitivity analysis detected element mixing and size-related issues. In local regions as shown in Figure 3, thermo-mechanical response (temperature and stress) remains stable at a minimum element size of 0.017 μm. Sensitivity analysis detected no element mixing at boundaries. This finite element model consists of 50,465 elements and 25,589 nodes. An iterative solver is adopted for computation to balance efficiency and resource consumption. For the time-dependent analysis, the initial time step is set to 1 × 10⁻⁸ and the maximum time step to 1 h, with the convergence criterion specified as a relative residual less than 0.001. This setup not only ensures the calculation accuracy of the physical field response but also controls the overall computational cost through time step constraints and the iterative algorithm, achieving a balance between precision and efficiency.

3.2. Material Parameters and Boundary Conditions

Model boundary conditions are shown in Figure 2: axial displacement at the bottom edge is constrained to zero and uniform displacement is enforced at the top edge. COMSOL lacks native multi-point constraint support (MPC). This study implements MPC boundary conditions via displacement averaging across the entire edge. Initial TGO $n=1$, BC $n=0$. Oxygen concentration details: TGO upper surface uses 1.55 mol/m³ [10], BC/SUB with 0, others are 0. Thermal boundaries: TC1 left 700 °C, SUB right 403 °C, initial temperature 25 °C. Material parameters (coefficient of thermal expansion, thermal conductivity, density, specific heat) for each layer in the dual-pipe coating system align with prior studies, detailed in

Table 1. Material parameters of each layer in the coated dual-pipe system [21].

	T (°C)	E (GPa)	v	ρ (kg/m3)	α (10−6/°C)	kc (W/(m·°C))	C (J/(kg·°C))
TC1	-	63	0.25	6300	9.1	0.87	460
TC2	20 800	204 179	0.1 0.11	6037	9.68 9.88	1.2	500
TGO	20 1000	400 325	0.23 0.25	3984	8 9.3	10 4	755
BC	20 800	200 145	0.3 0.32	7711	12.5 14.3	5.8 14.5	628
SUB	20 100 200 300 400 450 500 550 600 650	218 213 207 199 190 186 181 175 168 162	0.3	488 461 441 427 396 - 360 331 285 206	- 10.9 11.3 11.7 12.1 12.1 12.3 12.4 12.6 12.7	26 27 28 28 29 29 30 30 30 30	440 480 510 550 630 630 660 710 770 860

[21]. Oxidation kinetics parameters are listed in

Table 2. TGO oxidation kinetics parameters.

	BC	TGO	Reference
D0 (m2/s)	8 × 10−13	8 × 10−13	[23]
M (m3/(mol·s))	-	1.11 × 105	[22]
Q (mol/m3)	-	1 × 10−4	[22]

[22,23].

Interfacial oxidation in TBCs involves BC-to-TGO material evolution, necessitating prescribed:

$$\chi =n·{\chi }_{TGO}+\left(1-n\right)·{\chi }_{BC},$$

(26)

where $\chi$, ${\chi }_{TGO}$ and ${\chi }_{BC}$ represent the material parameters of the reaction process, TGO, and BC layer, respectively.

4. Results and Discussion

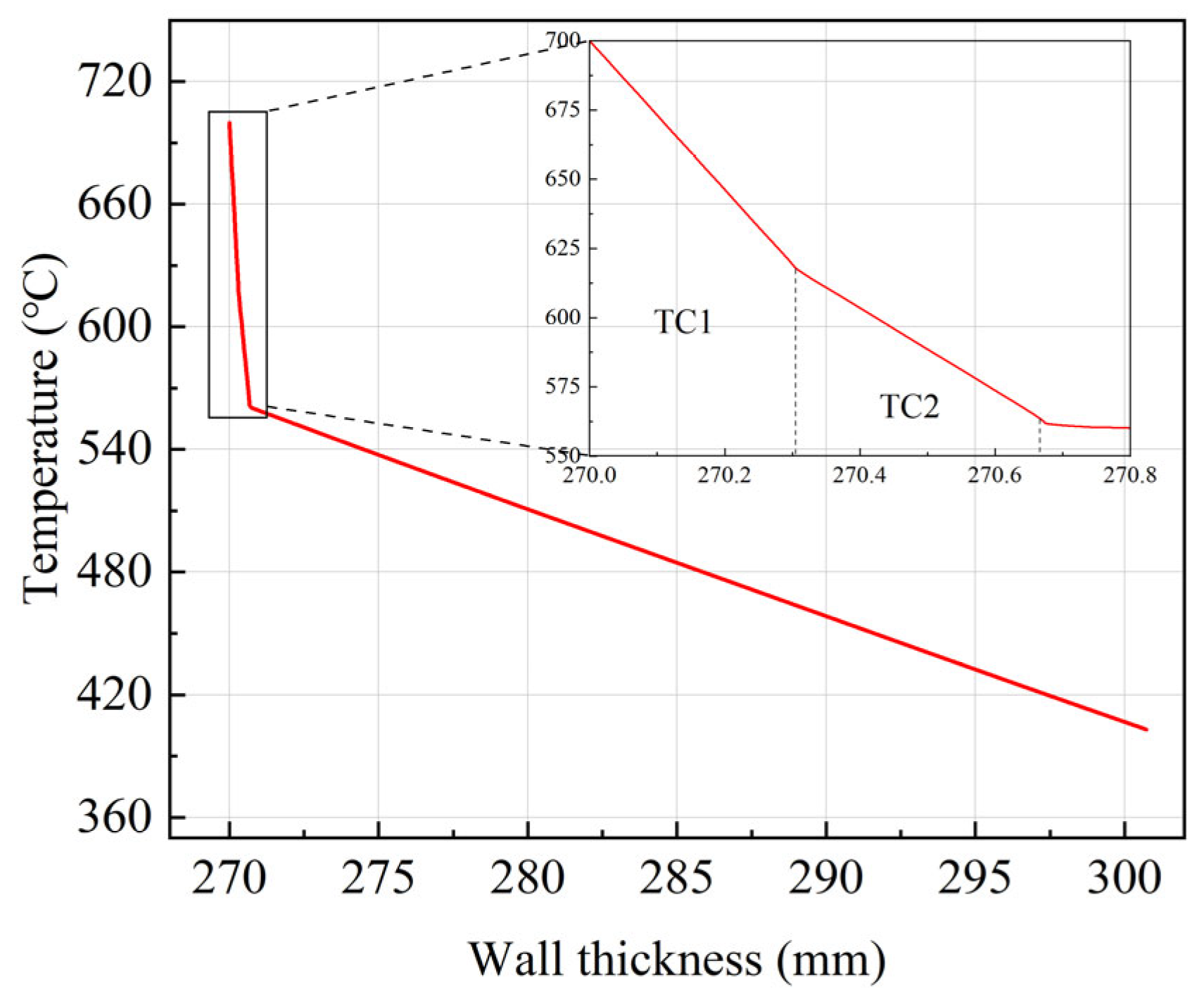
4.1. Steady-State Heat Transfer Analysis of Dual-Pipe Coating System

Figure 4 depicts the temperature distribution along the coating thickness of the novel dual-pipe coating system. The temperature field monotonically decreases with nonuniform characteristics under steady-state operation. The coating inner surface is subjected to 700 °C; the outer surface maintains a 403 °C boundary condition due to cooling steam. Low thermal conductivity of dual-layer TBCs induces a significant thermal gradient, inner wall 700 °C, main steam pipeline inner wall 560 °C. The TBC thus provides sufficient thermal insulation for the main steam pipeline.

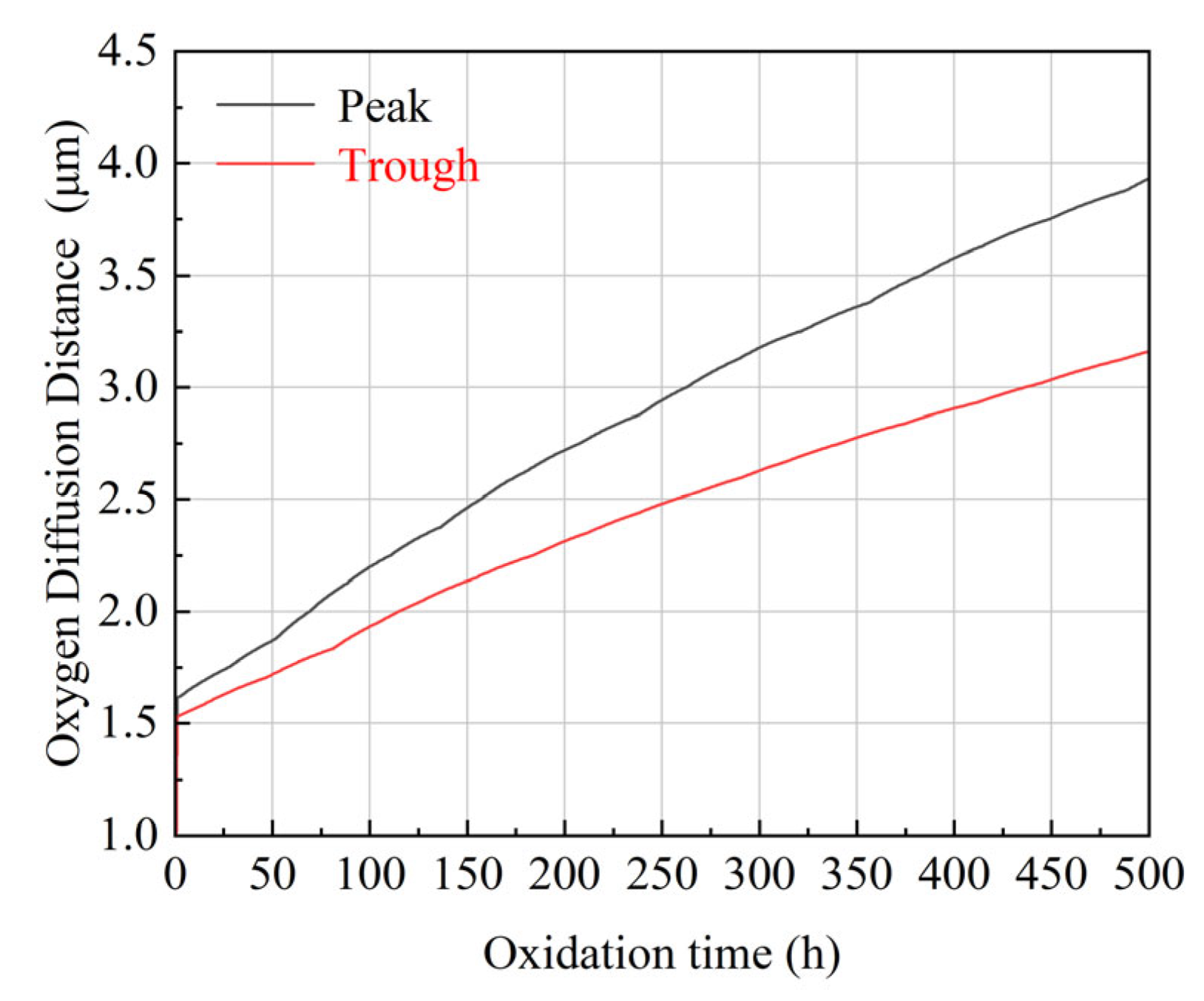
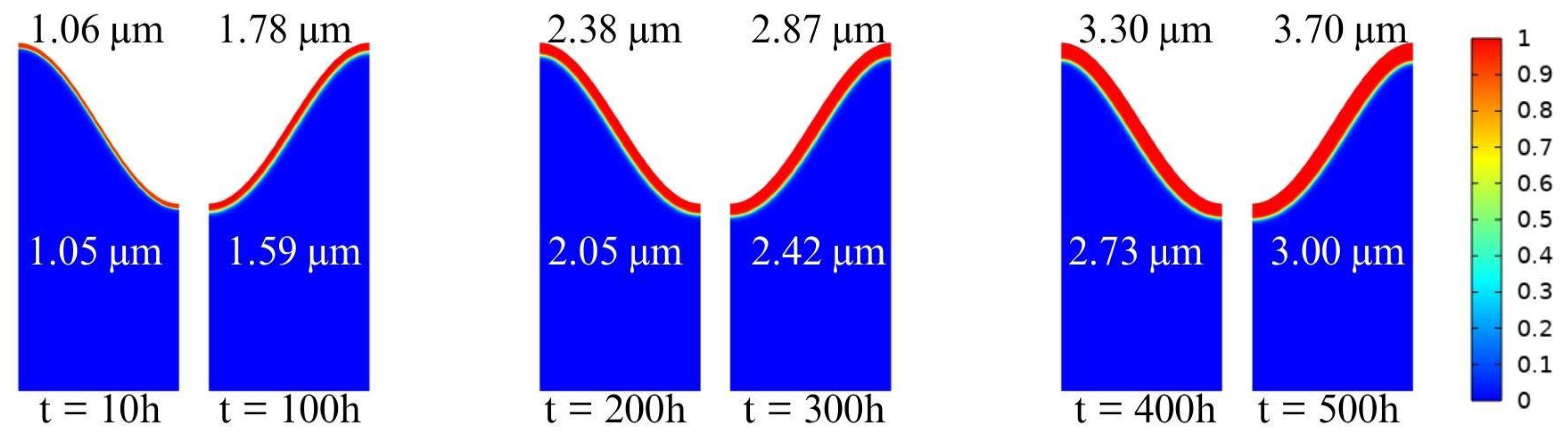
4.2. Oxygen Diffusion Characteristics

Figure 5 shows oxygen concentration contour maps at varying oxidation times. The maximum concentration 1.55 mol/m³ corresponds to yellow regions; purple indicates zero concentration. Per Fick’s law, oxygen diffuses along the TGO interface normal direction. Geometric curvature variations induce oxygen accumulation at peaks and lateral dispersion at troughs. Moreover, local oxygen concentration exhibits significant spatial heterogeneity along the TGO interface with increasing oxidation time, as shown in Figure 6. After 500 h oxidation, oxygen diffusion distances at peaks and troughs are 3.93 μm and 3.16 μm, respectively. The parabolic diffusion distance trend, as shown in Figure 6, demonstrates that progressive TGO formation effectively impedes further oxygen transport. This conclusion is consistent with the results of our previous study [24].

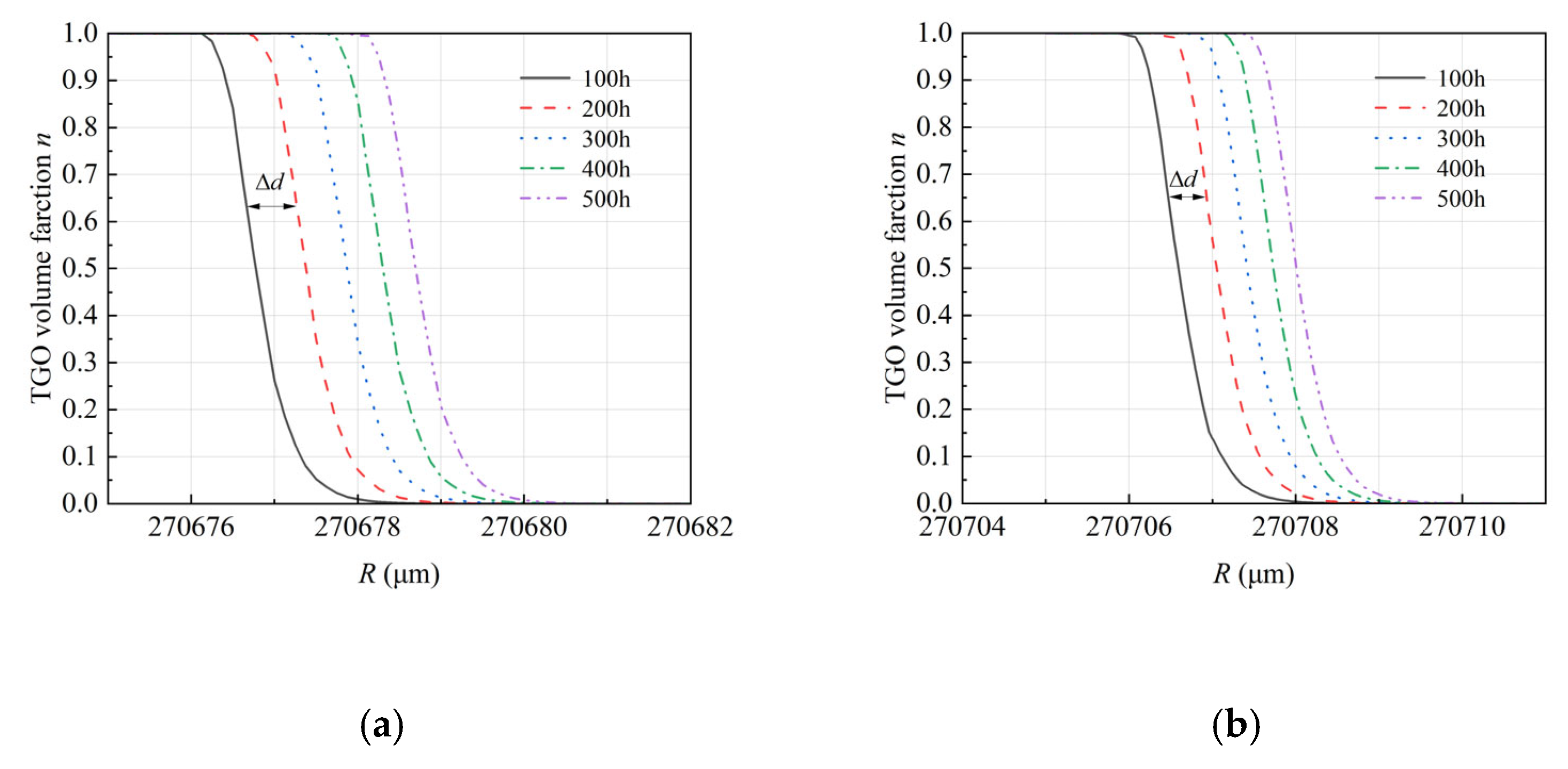
4.3. Thermo-Chemo-Mechanical Coupling Growth of TGO

Figure 7 illustrates TGO thickness evolution contours at varying oxidation times, where red ( $n=1$) represents the TGO layer and blue ( $n=0$) the BC layer. TGO thickness exhibits continuous non-uniform growth along the BC interface with increasing oxidation time, being significantly greater at peaks than troughs. After 500 h oxidation, peak and trough thicknesses reach 3.70 μm and 3.00 μm, respectively. This TGO growth heterogeneity arises from oxygen diffusion disparities at cosine interface features during high-temperature oxidation. The interfacial oxidation rate is governed by the diffusion rate of reactive species through the oxide scale and local oxidation kinetics. Geometric curvature variations, particularly between peaks and trough, induce distinct oxygen concentration gradients, directly driving non-uniform TGO growth across the interface.

To further analyze TGO growth patterns at distinct interfacial positions during oxidation, Figure 8 shows TGO thickness profiles and oxidation kinetics curves at peaks and troughs after 500 h oxidation at 700 °C. Both peak and trough TGO growth follow a parabolic law: rapid reaction rates during initial oxidation gradually stabilize, aligning with findings by Shen and Zhou [25,26]. This behavior stems from dense TGO formation at early stages, which increasingly impedes oxygen diffusion as the TGO thickens, thereby decelerating growth rates.

Figure 9 illustrates the temporal evolution of TGO volume fraction at peaks and trough, reflecting dynamic evolution of the BC/TGO interface and mixed zone. The spacing between curves during initial oxidation exceeds later stages, indicating faster interfacial oxidation rates at early times, consistent with the parabolic TGO growth trend in Figure 8. Furthermore, peak volume fractions surpass trough values over identical intervals, confirming higher TGO growth rates in BC/TGO mixed zones at peaks versus troughs.

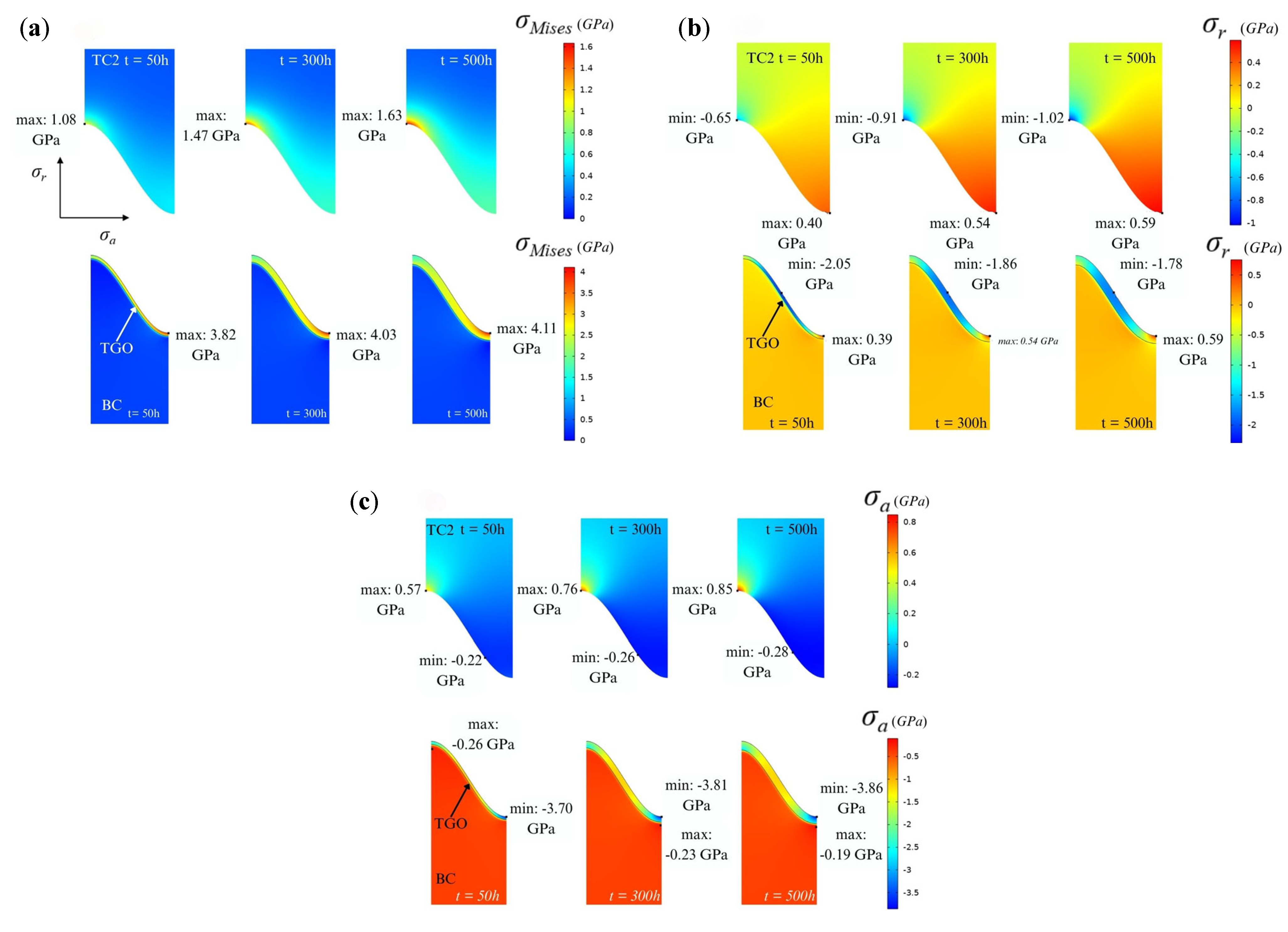
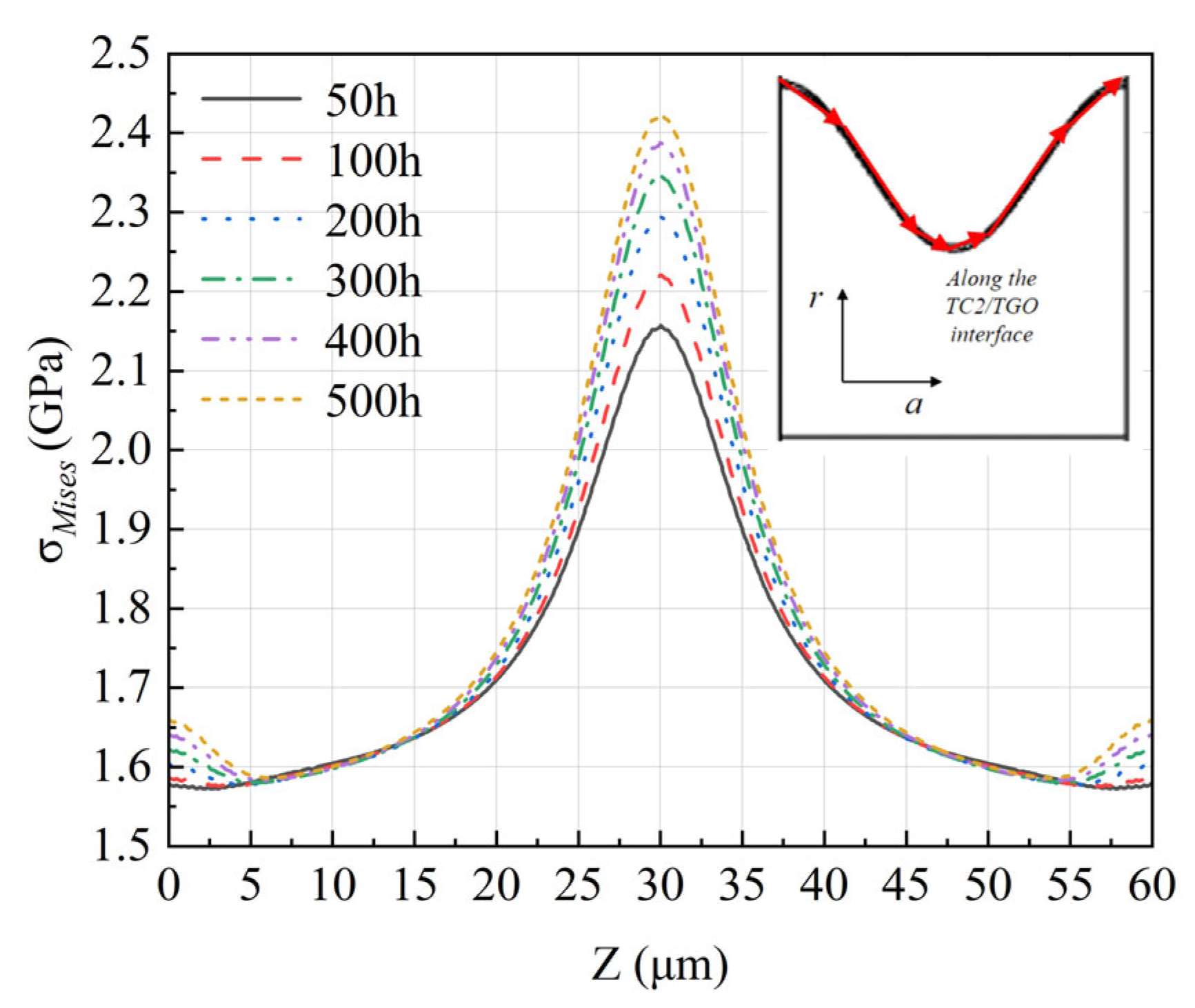
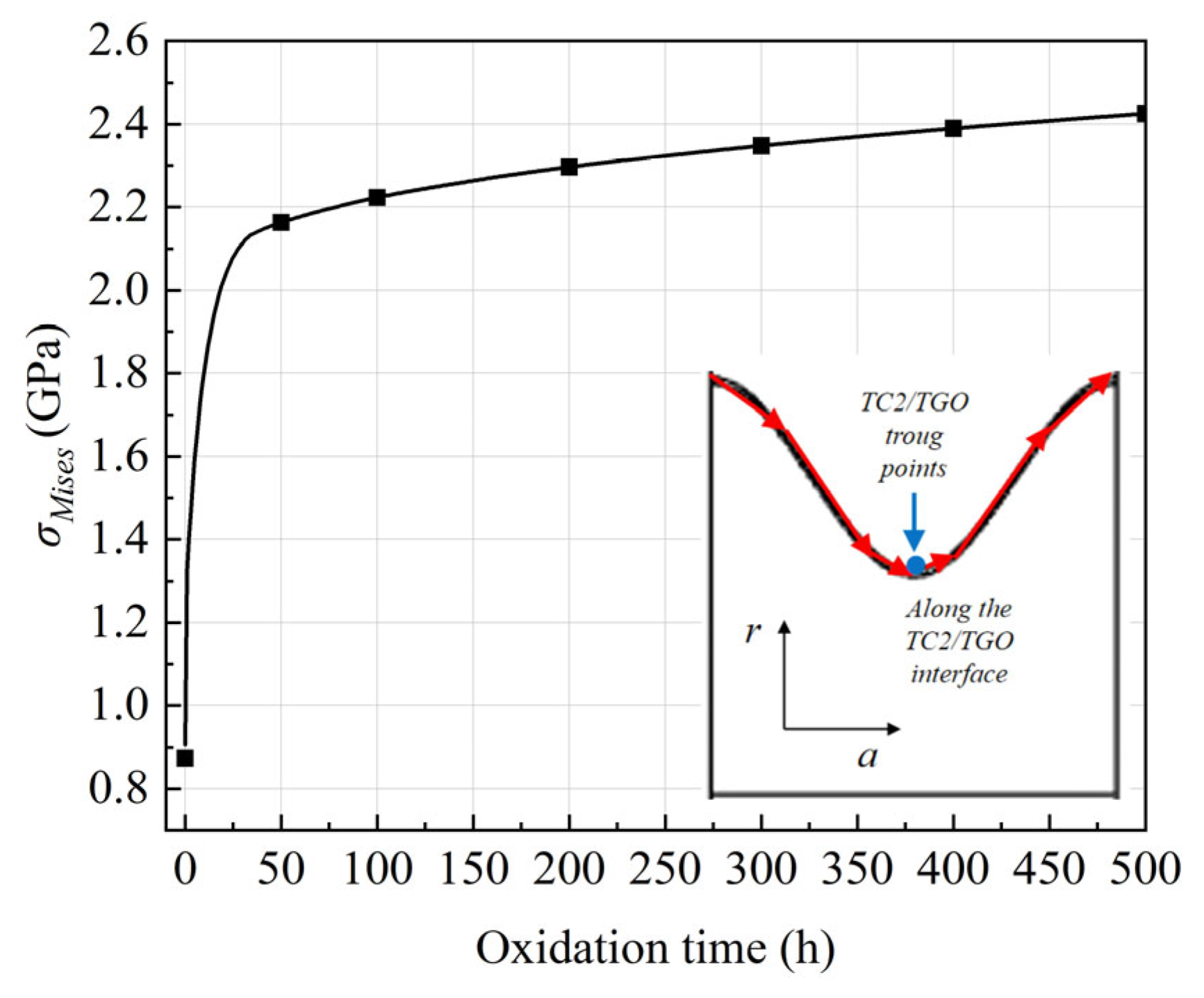
4.4. Stress Distribution and Evolution at Interfaces

Numerous studies indicate that during thermo-chemo-mechanical coupled nonlinear TGO growth, volumetric changes are constrained by coating/substrate materials or self-incompatible growth deformation [12,22,26]. Combined with alumina’s high elastic modulus, localized stress concentration in TGO often occurs, potentially inducing interfacial cracking, propagation, and delamination. This study focuses on stress distribution and evolution at the TC2/TGO and TGO/BC interfaces.

Figure 10 illustrates stress distribution and evolution at the TC2/TGO and TGO/BC interfaces of the dual-pipe coating system under varying oxidation times. Figure 10a reveals significant stress heterogeneity near the TGO due to its thermo-chemo-mechanical coupled growth under thermo-mechanical loading, driven by substantial coefficient of thermal expansion mismatch among layers. Maximum Mises stress under steady-state operation occurs at the TC2/TGO interface near TGO trough, identifying TGO as the critical factor in interfacial degradation, consistent with Evans et al. [27]. The current dual-pipe coating system experiences combined mechanical, thermal, and growth stresses, inducing dynamic stress redistribution at the TC2/TGO and TGO/BC interfacial regions during thermo-chemo-mechanical coupled TGO growth. As shown in Figure 10a, under constant thermo-mechanical loading, maximum Mises stress increases from 3.82 GPa at 50 h to 4.11 GPa after 500 h oxidation, demonstrating stress reconfiguration in TC2/TGO and TGO/BC zones. This stress evolution primarily stems from growth stresses generated by constrained volumetric changes and incompatible deformation during TGO non-uniform thickening, intensified by TC2 and BC layer restrictions. Previous studies revealed that the heterogeneous architecture of the dual-pipe coating system renders thermal gradients and thermal mismatch stresses along the wall thickness direction the primary determinant of structural integrity under steady-state operating conditions [28]. Compared to thermal stresses, growth stresses generated during TBC interfacial oxidation exhibit limited influence on overall coating stress distribution.

Figure 10b,c demonstrate that axial stresses at TC2/TGO and TGO/BC interfaces under steady-state operating conditions significantly exceed radial stresses, with peak axial stress occurring at TGO peaks near the TC2/TGO interface. As oxidation time increases from 50 h to 500 h, maximum axial stress rises continuously from 570 MPa to 850 MPa. This progression indicates that continuous TGO growth elevates localized growth stresses, altering initial interfacial stresses (primarily governed by coating thermal stresses) and generating a reorganized stress field. In the research on coating failure mechanisms elaborated by Padture et al. [29], it is also confirmed that the axial stress at the coating interface is significantly higher than the radial stress; as the service duration increases, the TGO thickens, and the axial tensile stress in the wave peak region of the interface shows an increasing trend, which eventually induces cracking behavior at the wave peak position.

Figure 11 displays Mises stress distribution curves at the TC2/TGO interface under varying oxidation times, analyzing thermo-chemo-mechanical coupled non-uniform TGO growth effects on interfacial stresses. The Mises stress at TC2/TGO trough exhibits a continuous monotonic increase with prolonged oxidation. Figure 12 quantifies this trend: Mises stress at trough rises from 2.16 GPa at 50 h to 2.43 GPa at 500 h, representing a 12.5% increase. Concurrently, the maximum incremental stress growth rate progressively diminishes over time. This conclusion is consistent with the research findings of Min et al. [30].

5. Concluding Remarks

This study developed a framework integrating thermo-chemo-mechanical coupling to investigate the growth kinetics of TGO and the evolution of interfacial stress within a novel dual-pipe coating system. By quantifying the interactions between oxygen diffusion, geometric curvature, and mechanical constraints under USC conditions (700 °C), the following conclusions are drawn:

• The dual-pipe architecture effectively mitigates thermal loads through a significant thermal gradient. Under steady-state conditions with internal steam at 700 °C, the surface temperature of the inner P91 steel pipe is reduced to 560 °C. This thermal reduction confirms the system’s capability to utilize ferritic steels in advanced USC environments without requiring nickel-based alloy upgrades.
• The growth of TGO follows the parabolic growth kinetics but exhibits significant spatial heterogeneity driven by geometric curvature. The simulation reveals that oxygen diffusion flux is concentrated at interfacial peaks, resulting in a 23% thicker TGO at the peaks than at the troughs after 500 h. This confirms that interface morphology is a governing factor in local oxidation kinetics.
• The evolution of interfacial stress is dominated by the synergism between thermal mismatch and constrained volumetric expansion. This study identifies that axial stress significantly exceeds radial stress, with a 49% increase in axial stress at the TGO peaks over 500 h. This stress escalation is attributed to the incompatible growth strains within the TGO layer, which are constrained by the adjacent TC and BC.
• TGO evolution is a fully coupled thermo-chemo-mechanical process where growth stresses eventually surpass initial thermal mismatch stresses. The stress concentration identified at the wave peaks suggests these regions are the primary initiation sites for vertical cracking and subsequent spallation. These findings provide a theoretical basis for optimizing coating surface textures to enhance the structural integrity of high-temperature energy systems.