An Artificial Intelligence for the Analysis of a DC Magnetron Sputtering System Combined with a Particle-in-Cell Simulation
Abstract
1. Introduction
2. Methodology
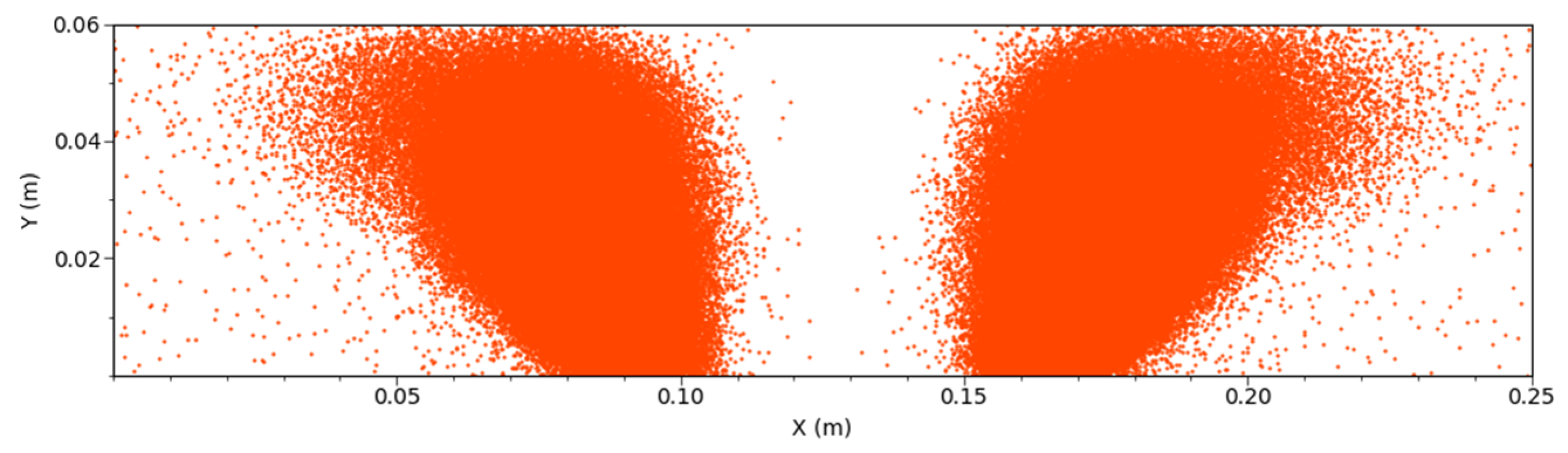
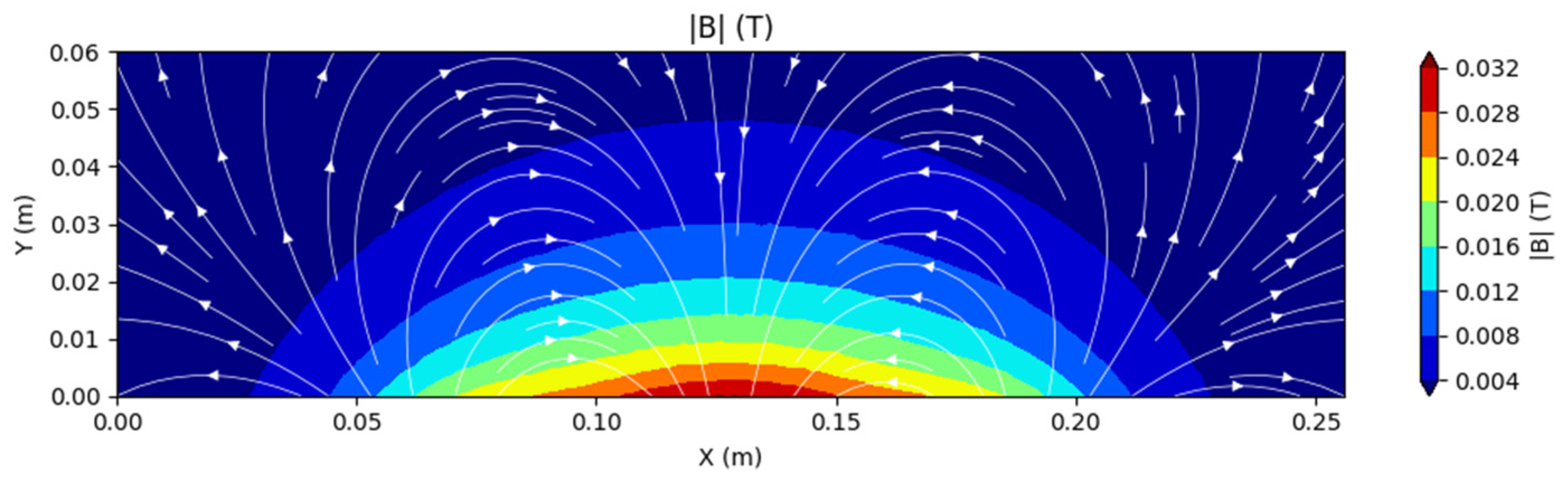
2.1. Two-Dimensional PIC Model for DC Magnetron Sputtering
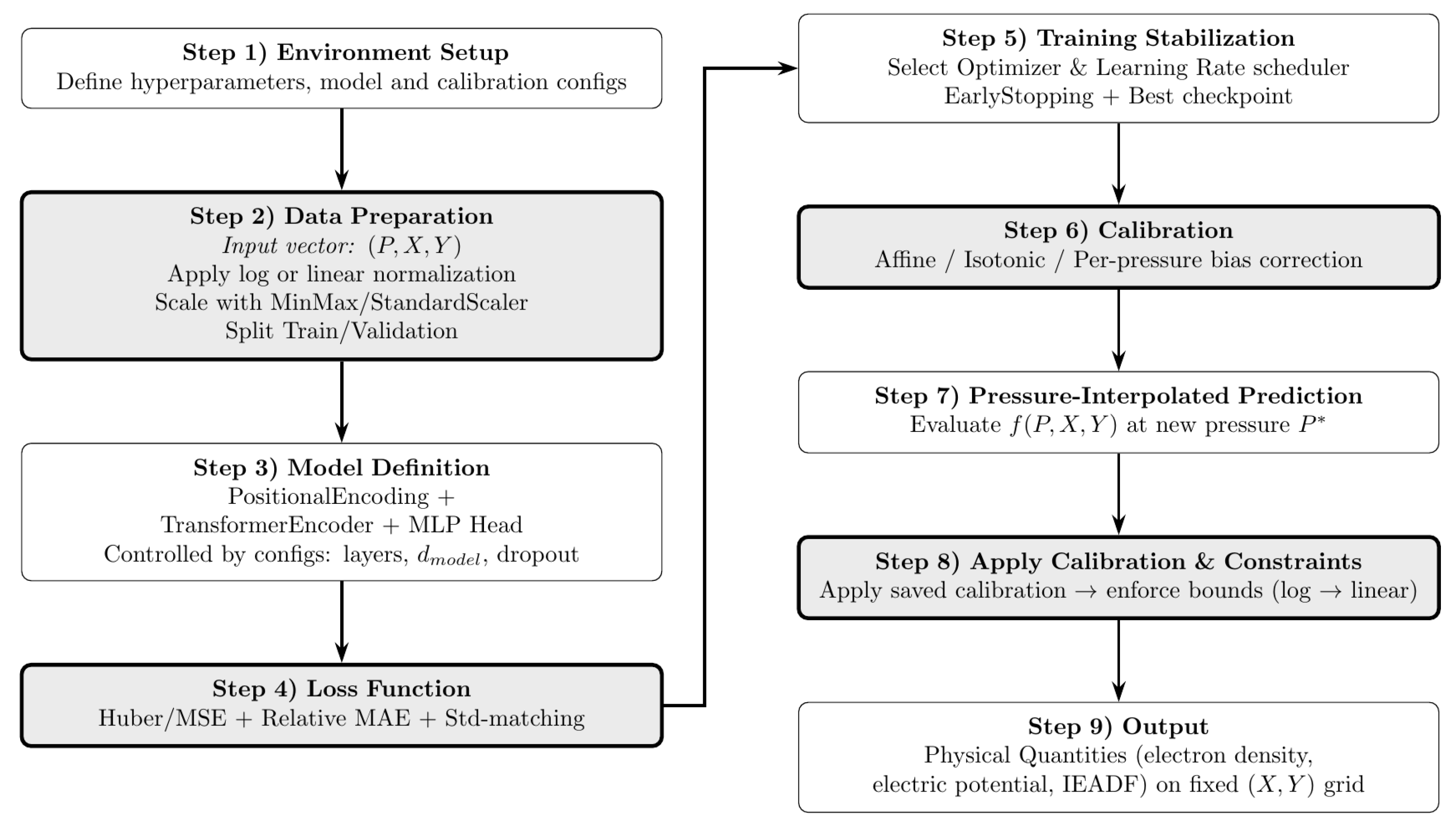
2.2. Transformer-Based Regression Framework
2.3. Data Transformation and Loss Design for Wide-Dynamic-Range Regression
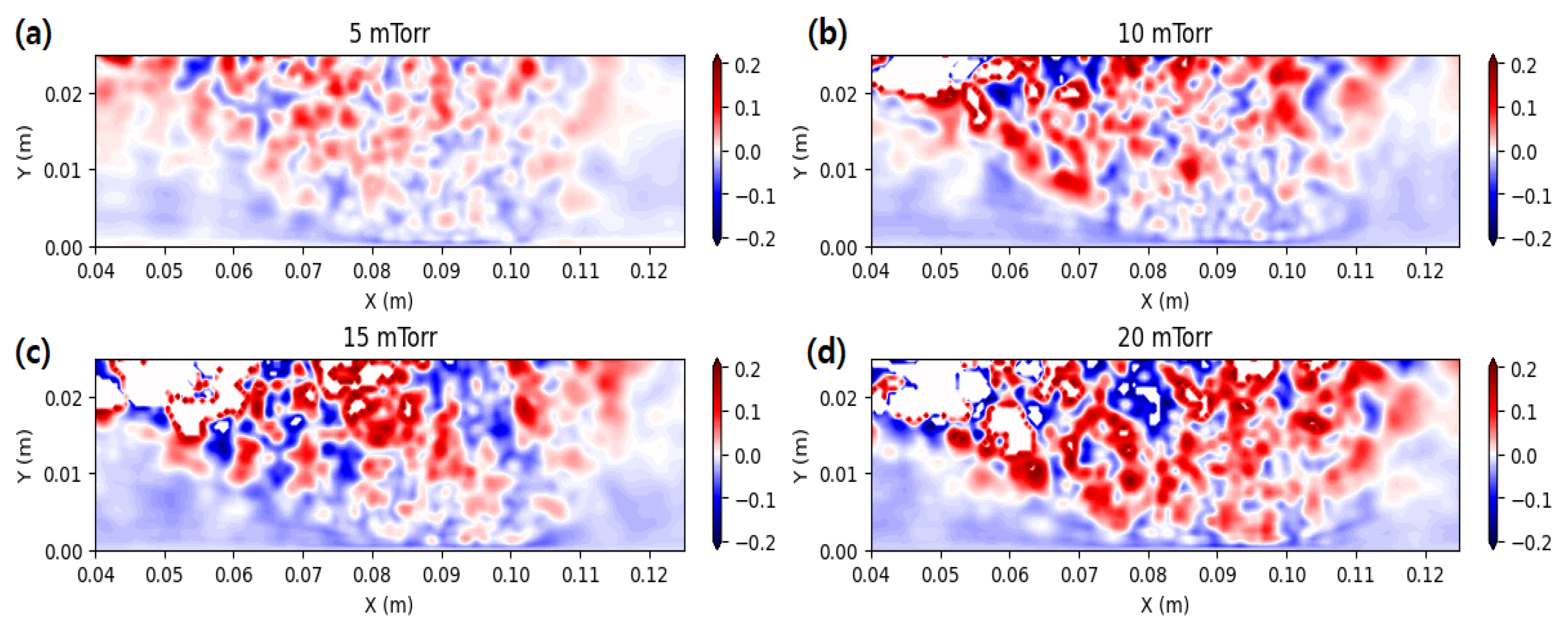
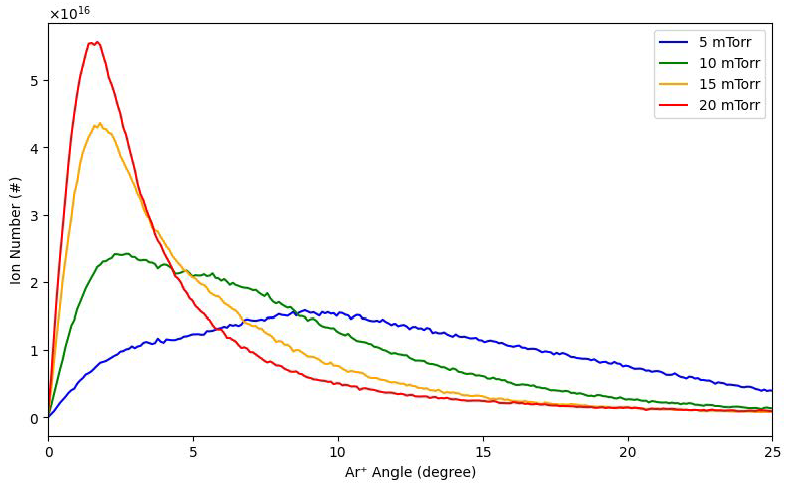
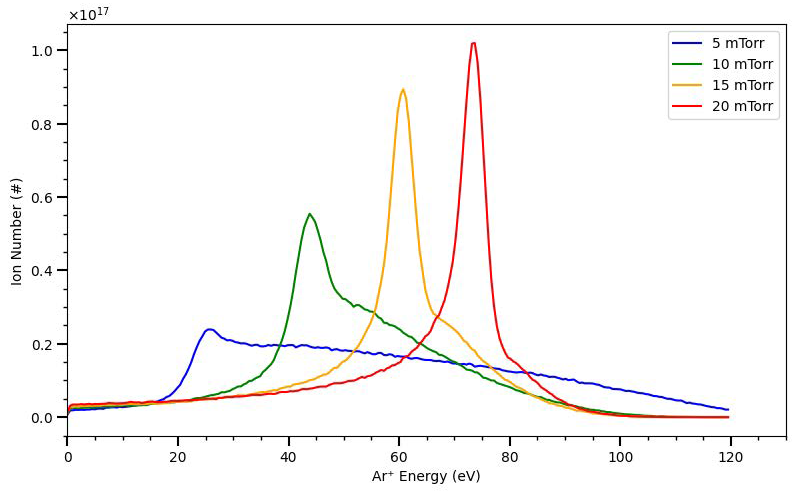
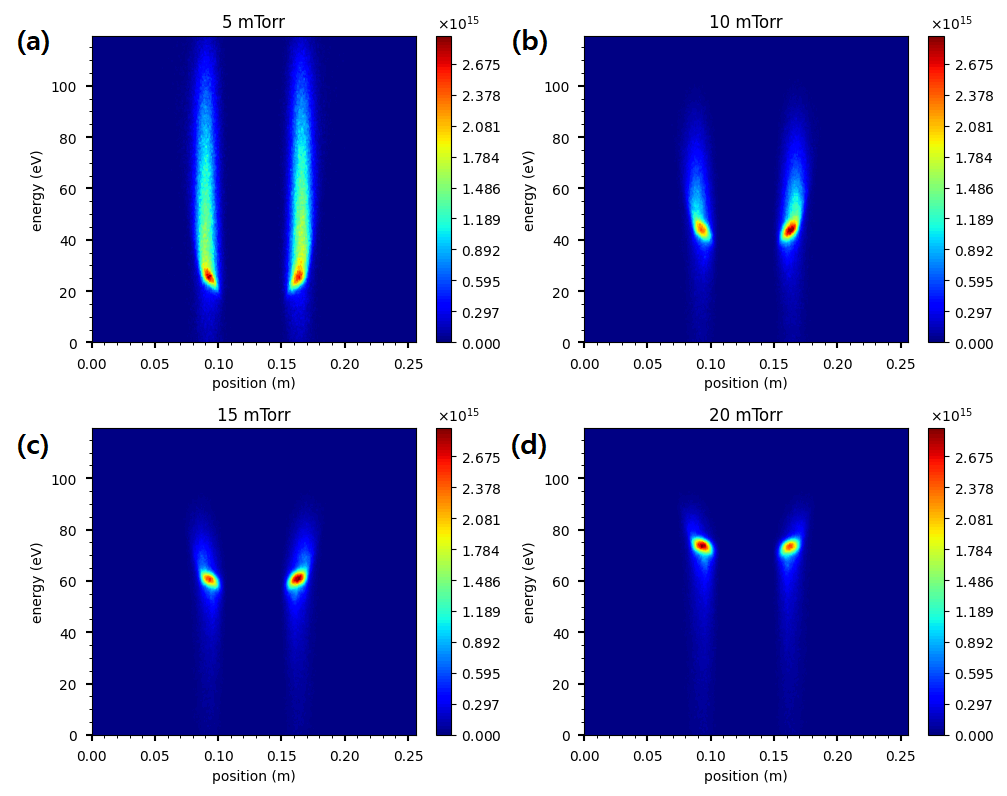
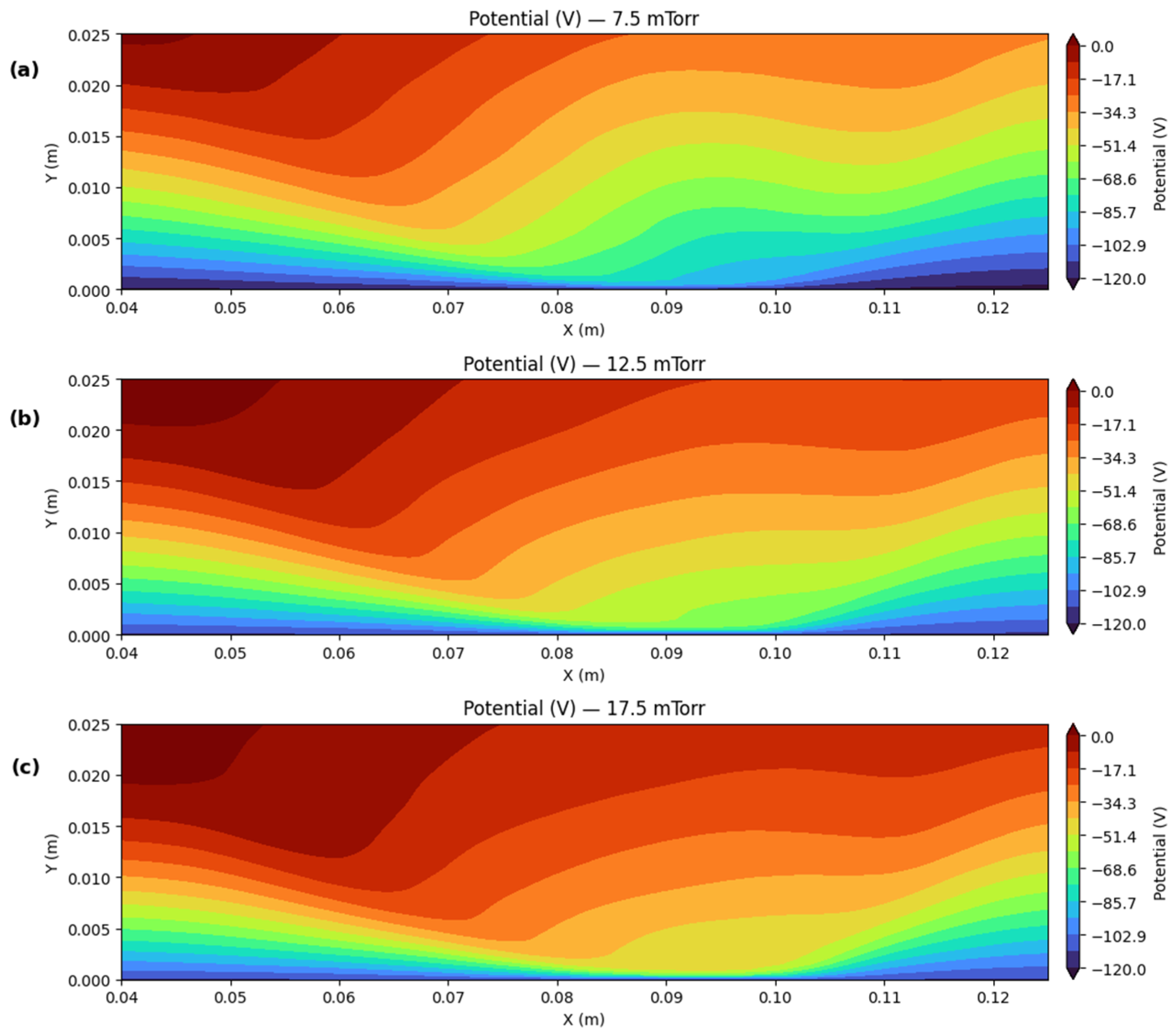
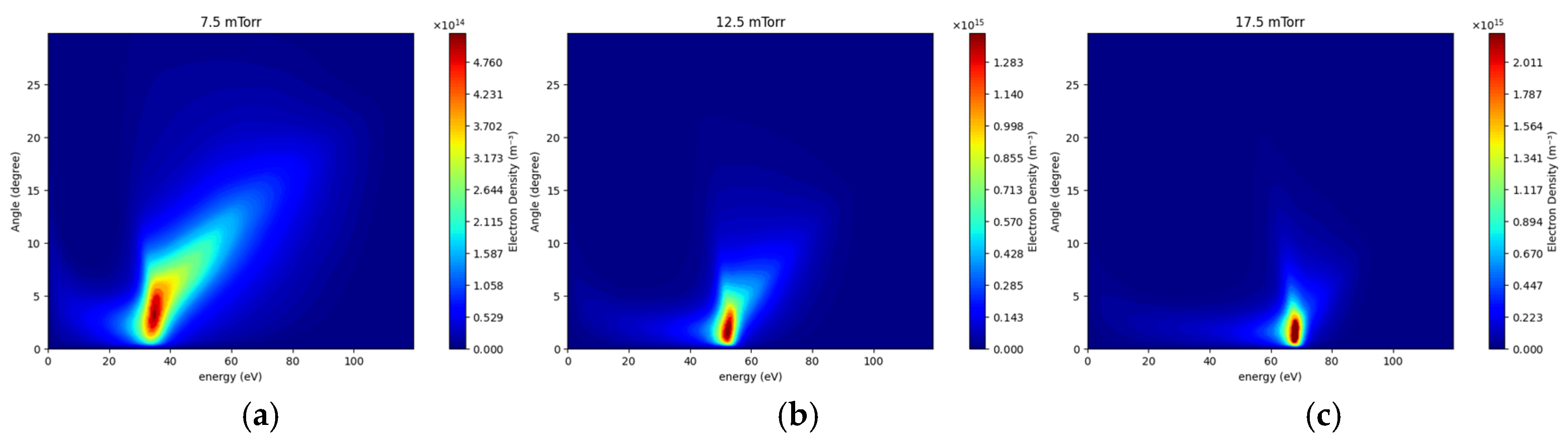
3. Results and Discussion
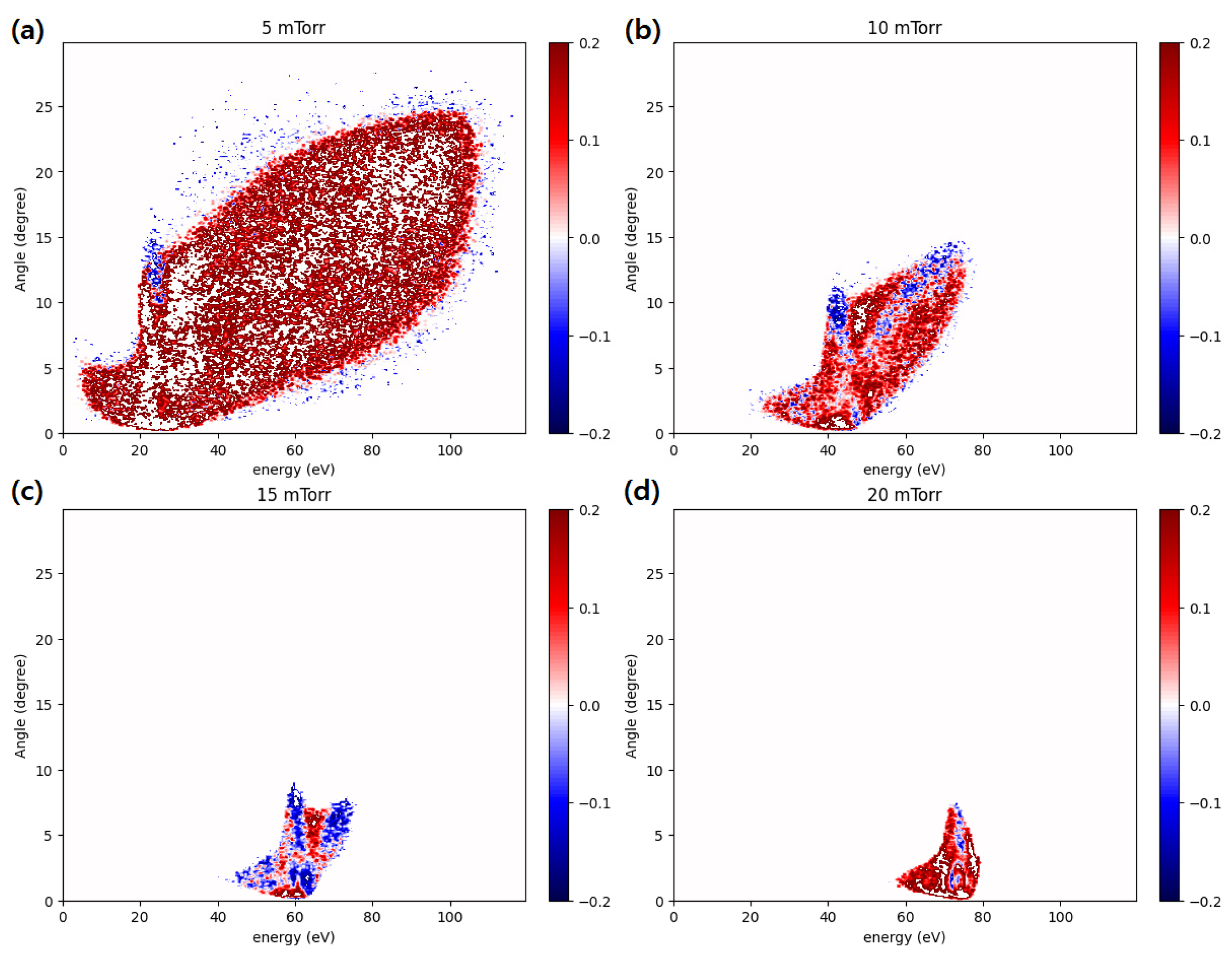
4. New Prediction Capability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kelly, P.J.; Arnell, R.D. Magnetron sputtering: A review of recent developments and applications. Vacuum 2000, 56, 159–172. [Google Scholar] [CrossRef]
- Safi, I. Recent aspects concerning DC reactive magnetron sputtering of thin films: A review. Surf. Coat. Technol. 2000, 127, 203–219. [Google Scholar] [CrossRef]
- Alami, J.; Gudmundsson, J.T.; Bohlmark, J.; Birch, J.; Helmersson, U. Plasma dynamics in a highly ionized pulsed magnetron discharge. Plasma Sources Sci. Technol. 2005, 14, 525–531. [Google Scholar] [CrossRef]
- Ellmer, K.; Welzel, T. Reactive magnetron sputtering of transparent conductive oxide thin films: Role of energetic particle bombardment. J. Mater. Res. 2012, 27, 765–779. [Google Scholar] [CrossRef]
- Sarakinos, K.; Alami, J.; Konstantinidis, S. High power pulsed magnetron sputtering: A review on scientific and engineering state of the art. Surf. Coat. Technol. 2010, 204, 1661–1684. [Google Scholar] [CrossRef]
- Gudmundsson, J. Physics and technology of magnetron sputtering discharges. Plasma Sources Sci. Technol. 2020, 29, 113001. [Google Scholar] [CrossRef]
- Berg, S.; Nyberg, T. Fundamental understanding and modeling of reactive sputtering processes. Thin Solid Films 2005, 476, 215–230. [Google Scholar] [CrossRef]
- Birdsall, C.K.; Langdon, A.B. Plasma Physics via Computer Simulation; Taylor & Francis Group: New York, NY, USA, 2005. [Google Scholar]
- Vahedi, V.; Surendra, M. A Monte Carlo collision model for the particle-in-cell method. Comput. Phys. Commun. 1995, 87, 179–198. [Google Scholar] [CrossRef]
- Verboncoeur, J.P. Particle simulation of plasmas: Review and advances. Plasma Phys. Control. Fusion 2005, 47, A231. [Google Scholar] [CrossRef]
- Nanbu, K.; Kondo, S. Analysis of Three-Dimensional DC Magnetron Discharge by the Particle-in-Cell/Monte Carlo Method. Jpn. J. Appl. Phys. 1997, 36, 4808–4814. [Google Scholar] [CrossRef]
- Ryabinkin, A.N.; Serov, A.O.; Pal, A.F.; Mankelevich, Y.A.; Rakhimov, A.T.; Rakhimova, T.V. Structure of DC magnetron sputtering discharge at various gas pressures: A two-dimensional particle-in-cell Monte Carlo collision study. Plasma Sources Sci. Technol. 2021, 30, 055009. [Google Scholar] [CrossRef]
- Zheng, B.; Fu, Y.; Wang, K.; Tran, T.; Schuelke, T.; Fan, Q.H. Comparison of 1D and 2D particle-in-cell simulations for DC magnetron sputtering discharges. Phys. Plasmas 2021, 28, 014504. [Google Scholar] [CrossRef]
- Hur, M.Y.; Kim, J.S.; Lee, H.J. The effect of negative ions from the target on thin film deposition in a direct current magnetron sputtering system. Thin Solid Films 2015, 587, 3. [Google Scholar] [CrossRef]
- Jo, Y.H.; Park, H.; Hur, M.Y.; Lee, H.J. Curved-boundary particle-in-cell simulation for the investigation of the target erosion effect of DC magnetron sputtering system. AIP Adv. 2020, 10, 125224. [Google Scholar] [CrossRef]
- Jo, Y.H.; Cheon, C.; Park, H.; Lee, H.J. Particle-in-Cell Simulations for the Improvement of the Target Erosion Uniformity by the Permanent Magnet Configuration of DC Magnetron Sputtering Systems. Coatings 2023, 13, 749. [Google Scholar] [CrossRef]
- Cheon, C.; Hur, M.Y.; Kim, H.J.; Lee, H.J. Multi-Step Simulations of Ionized Metal Physical Vapor Deposition to Enhance the Plasma Formation Uniformity. Coatings 2025, 15, 11. [Google Scholar] [CrossRef]
- Sigmund, P. Theory of sputtering. I. Sputtering yield of amorphous and polycrystalline targets. Phys. Rev. 1969, 184, 383–416. [Google Scholar] [CrossRef]
- Seah, M.P.; Nunney, T.S. Quantitative AES and XPS: The strength of evidence. J. Phys. D Appl. Phys. 2010, 43, 253001. [Google Scholar] [CrossRef]
- Behrisch, R.; Eckstein, W. Sputtering by Particle Bombardment; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Vahedi, V.; DiPeso, G. Simultaneous Potential and Circuit Solution for Two-Dimensional Bounded Plasma Simulation Codes. J. Comput. Phys. 1997, 131, 149–163. [Google Scholar] [CrossRef]
- Kim, H.H.; Shin, J.H.; Lee, H.J. Control of the ion flux and energy distribution of dual-frequency capacitive RF plasmas by the variation of the driving voltages. J. Vac. Sci. Technol. A 2023, 41, 023004. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Estimation of a Location Parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Yamamura, Y.; Tawara, H. Energy dependence of ion-induced sputtering yields from monatomic solids. At. Data Nucl. Data Tables 1996, 62, 149–253. [Google Scholar] [CrossRef]





| Component | Value/Description |
|---|---|
| 64 | |
| 4 | |
| 7 | |
| Feed-forward dim. | 512 |
| Dropout rate | 0.1 |
| Optimizer | AdamW (, weight decay ) |
| Learning schedule | Warm-up (5 epochs)→ReduceLROnPlateau |
| Batch size | 8192 |
| Epochs/Early stopping | 1200/120 patience |
| Validation split | 10% of the total dataset |
| Working gas | Ar |
| Target material | Cu |
| Domain size | 256 mm × 70 mm |
| Number of cells (grid size) | 512 × 140 (∆x = ∆y = 0.5 mm) |
| Number ratio of real particles to a super-particle | 5 × 107 |
| ∆t | 1.0 × 10−11 s |
| Discharge current | 0.5 A |
| Magnetic field | 250 Gauss (on target) |
| Gas pressure | 5, 10, 15, 20 mTorr |
| Boundary conditions for the field | Dirichlet on the top and the bottom boundaries Neumann on the left and the right boundaries |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.J.; Lee, H.J. An Artificial Intelligence for the Analysis of a DC Magnetron Sputtering System Combined with a Particle-in-Cell Simulation. Coatings 2025, 15, 1248. https://doi.org/10.3390/coatings15111248
Kim YJ, Lee HJ. An Artificial Intelligence for the Analysis of a DC Magnetron Sputtering System Combined with a Particle-in-Cell Simulation. Coatings. 2025; 15(11):1248. https://doi.org/10.3390/coatings15111248
Chicago/Turabian StyleKim, Yeun Jung, and Hae June Lee. 2025. "An Artificial Intelligence for the Analysis of a DC Magnetron Sputtering System Combined with a Particle-in-Cell Simulation" Coatings 15, no. 11: 1248. https://doi.org/10.3390/coatings15111248
APA StyleKim, Y. J., & Lee, H. J. (2025). An Artificial Intelligence for the Analysis of a DC Magnetron Sputtering System Combined with a Particle-in-Cell Simulation. Coatings, 15(11), 1248. https://doi.org/10.3390/coatings15111248






