Microfluidic Edible Coatings: Multiphase VOF Modeling, Physicochemical Properties, Image Analysis, and Applications in Fried Foods
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents and Supplies
2.2. Microfluidic Coating System
2.3. Microfluidic Device and Spray Setup
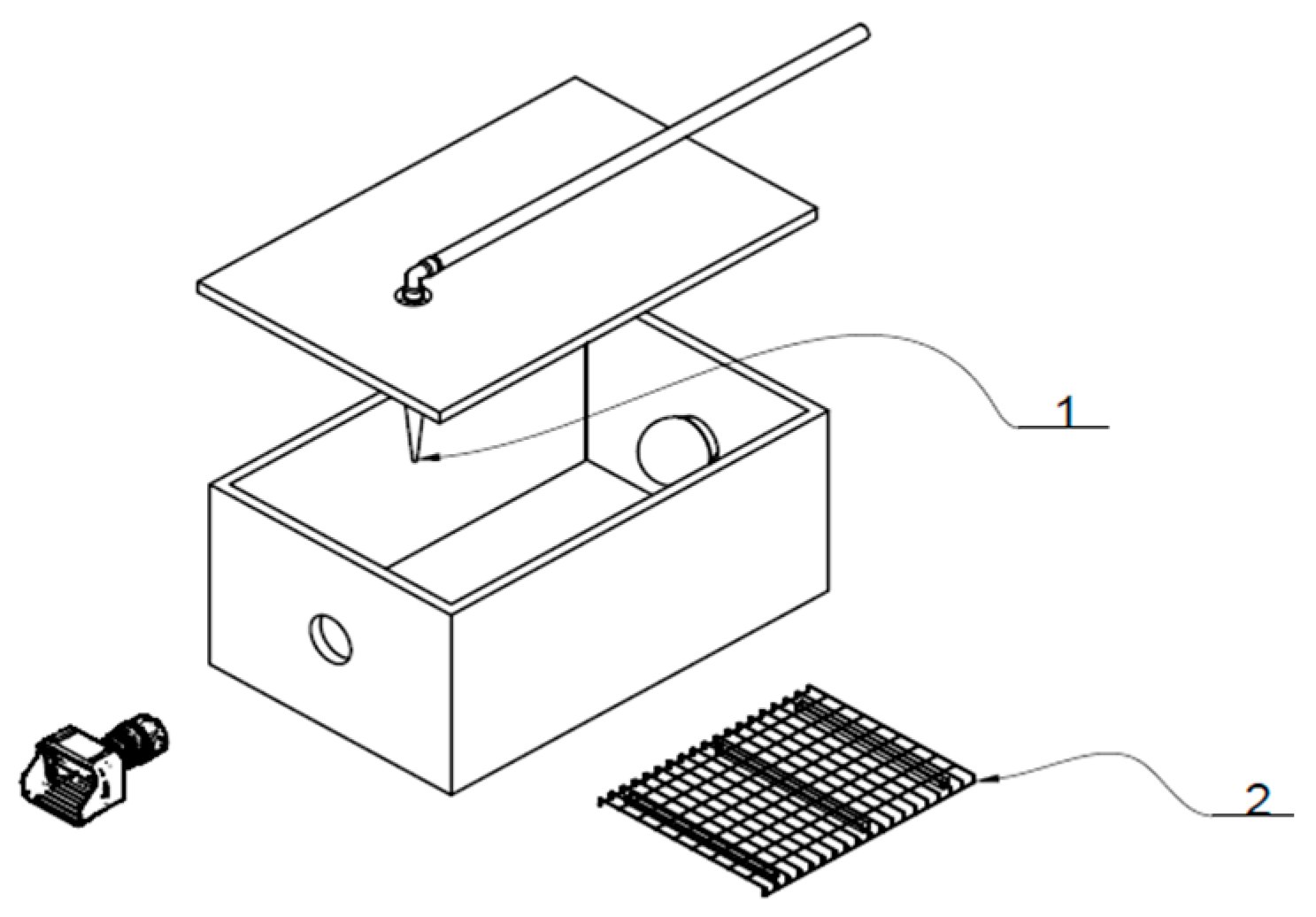
2.4. Closed Deposition Chamber
2.5. Sample Preparation
2.6. Coating Formulation (WPI)
2.7. Conventional Coating Application (WPI-Conv)
2.8. Microfluidic Coating Application (WPI-McF)
2.9. Frying Process
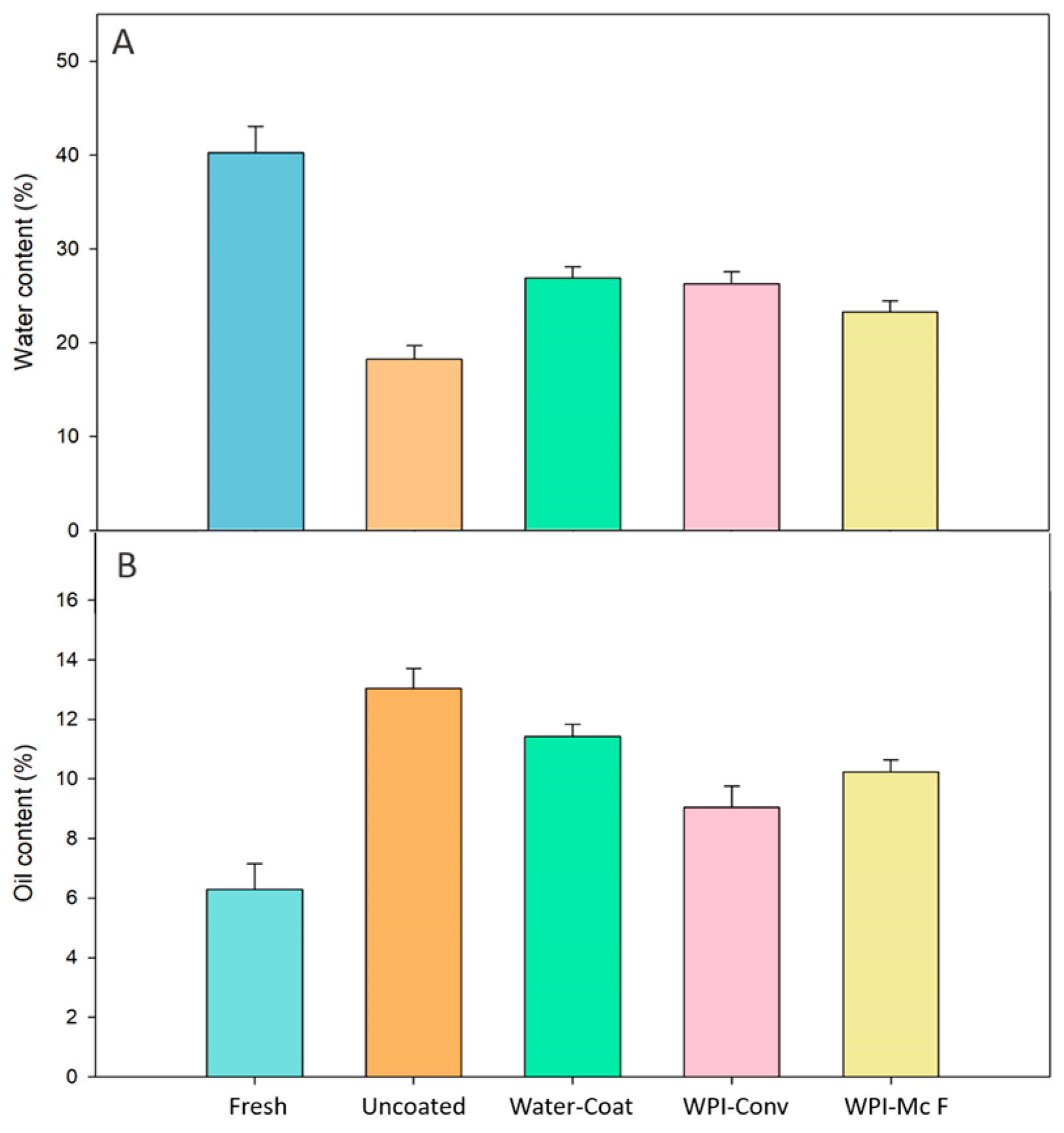
2.10. Water Content and Oil Content Determination
2.11. Determination of the Minimum Required Volume of Coating Solution
2.11.1. Conventional Coating Application (WPI-Conv)
2.11.2. Microfluidic Coating Application (WPI-McF)
2.12. Image Preprocessing and Droplet Analysis
2.12.1. Image Acquisition for Droplet Characterization
2.12.2. Image Preprocessing
Image Capture and Grayscale Conversion
Image Preprocessing and Segmentation Process
Droplet Detection and Analysis
Statistical Analysis
2.13. Contact Angle Measurement
2.14. Multiphase Modeling and Volume of Fluid (VOF)
2.14.1. Geometry and Mesh Generation
2.14.2. Governing Equations and Physical Models
2.14.3. Boundary and Initial Conditions
2.14.4. Numerical Setup
2.14.5. Parallelisation and Computational Resources
2.14.6. Post-Processing and Data Availability
2.15. General Statistical Analysis
3. Results and Discussion
3.1. Water Content and Fat Uptake
3.2. Determination of the Minimum Required Volume of Coating Solution
3.3. Image Processing and Droplet Segmentation
3.3.1. Out-of-Focus Particle Removal
3.3.2. Droplet Segmentation and Contrast Enhancement
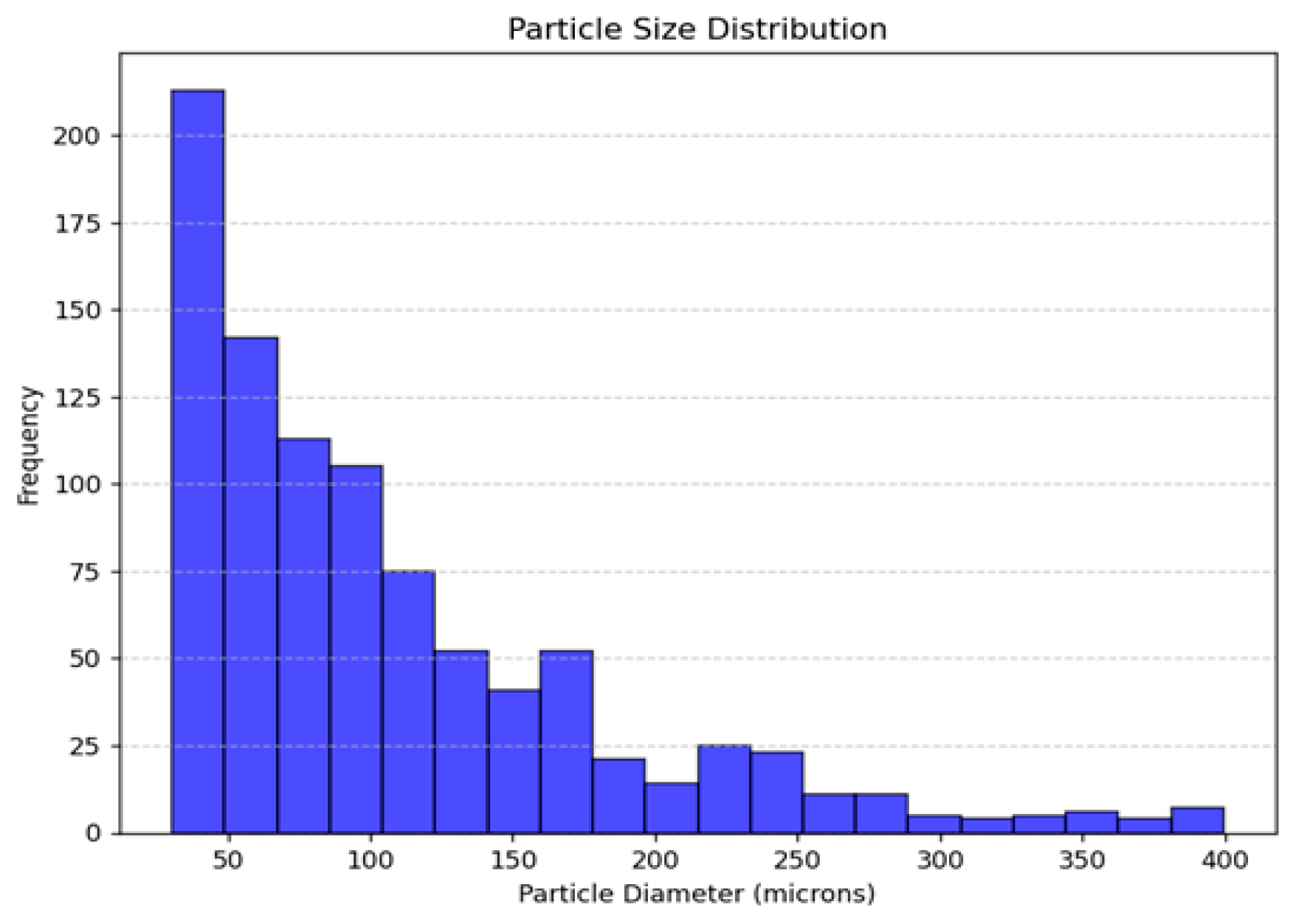
3.4. Statistical Analysis of Droplet Diameters
3.5. Contact Angle
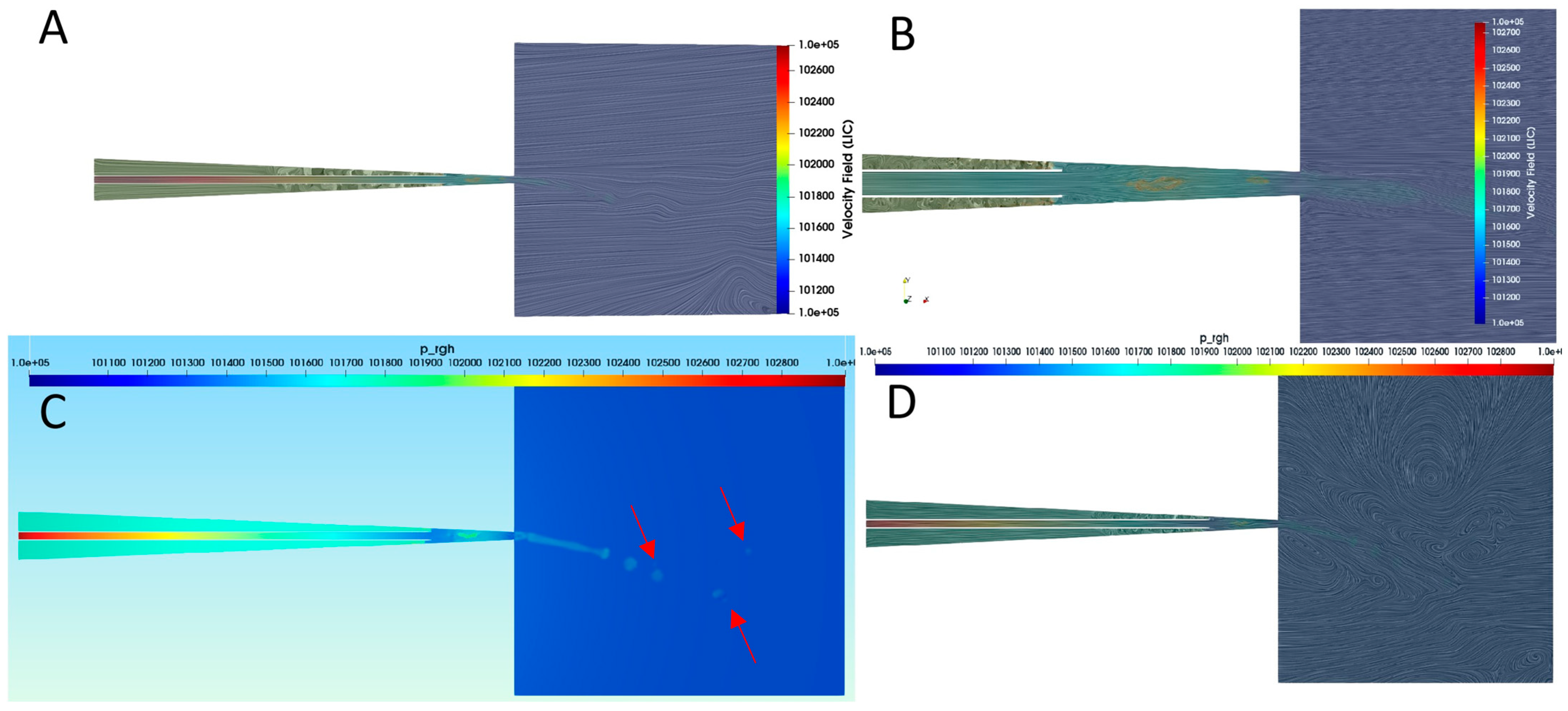
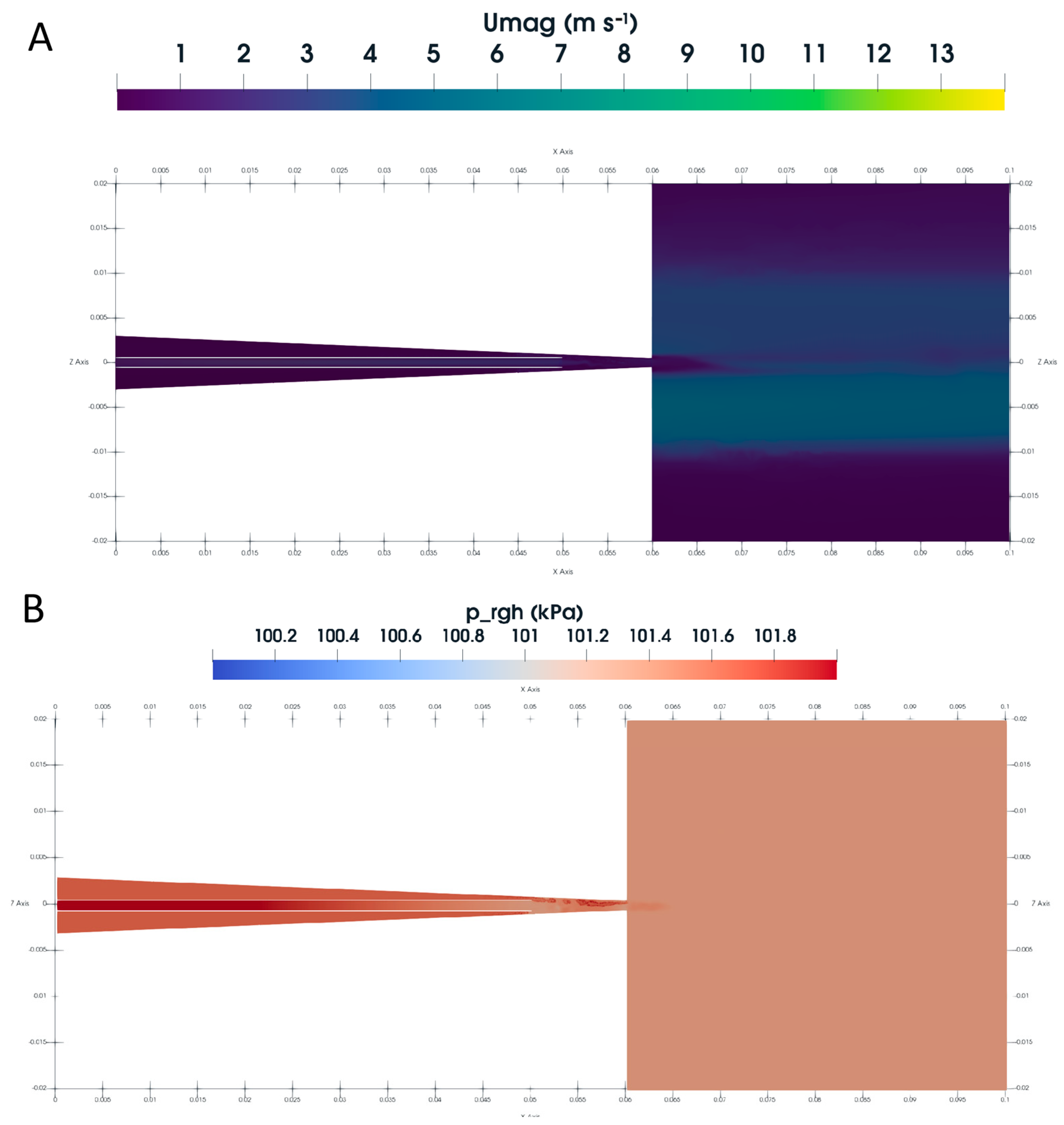
3.6. CFD Using VOF Method
3.7. Jet Break-Up Dynamics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol (Unity) | Description |
|---|---|
| ρ (kg·m−3) | Density |
| u (m·s−1) | Velocity vector |
| ϕ | Conserved scalar (e.g., concentration, temperature, or phase fraction) |
| Γϕ (m2·s−1) | Effective diffusivity of ϕ |
| Sϕ (unid. de ϕ·s−1) | Source/sink of ϕ |
| p (Pa) | Pressure |
| μ (Pa·s) | Dynamic viscosity |
| g (m·s−2) | Gravity |
| fσ (N·m−3) | Surface tension force |
References
- Rossi-Márquez, G.; Dávalos-Saucedo, C.A.; Di Pierro, P. Edible Films and Coatings Applied in the Food Industry. Coatings 2023, 13, 670. [Google Scholar] [CrossRef]
- Dhall, R.K. Advances in Edible Coatings for Fresh Fruits and Vegetables: A Review. Crit. Rev. Food Sci. Nutr. 2013, 53, 435–450. [Google Scholar] [CrossRef]
- Blumenthal, M.M.; Stier, R.F. Optimization of Deep-Fat Frying Operations. Trends Food Sci. Technol. 1991, 2, 144–148. [Google Scholar] [CrossRef]
- Mehta, U.; Swinburn, B. A Review of Factors Affecting Fat Absorption in Hot Chips. Crit. Rev. Food Sci. Nutr. 2001, 41, 133–154. [Google Scholar] [CrossRef]
- Saguy, I.-S. Oil Uptake during Deep-Fat Frying: Factors and Mechanism. Food Technol. 1995, 49, 142–145. [Google Scholar]
- Falguera, V.; Quintero, J.P.; Jiménez, A.; Muñoz, J.A.; Ibarz, A. Edible Films and Coatings: Structures, Active Functions and Trends in Their Use. Trends Food Sci. Technol. 2011, 22, 292–303. [Google Scholar] [CrossRef]
- Talens, P.; Pérez-Masia, R.; Jiménez, A.; Fabra, M.J.; Chiralt, A. Use of Edible Films to Control Moisture Migration in Multicomponent Food Systems. In Proceedings of the International Conference of Food Innovation (FoodInnova 2010), Valencia, Spain, 25–29 October 2010. [Google Scholar]
- Rossi Marquez, G.; Di Pierro, P.; Esposito, M.; Mariniello, L.; Porta, R. Application of Transglutaminase-Crosslinked Whey Protein/Pectin Films as Water Barrier Coatings in Fried and Baked Foods. Food Bioproc. Tech. 2014, 7, 447–455. [Google Scholar] [CrossRef]
- Gañán-Calvo, A.M.; Montanero, J.M.; Martín-Banderas, L.; Flores-Mosquera, M. Functional Materials for Health Care and Pharmacy from Microfluidic Principles and Flow Focusing. Adv. Drug Deliv. Rev. 2013, 65, 1447–1469. [Google Scholar] [CrossRef] [PubMed]
- Maan, A.A.; Nazir, A.; Khan, M.K.I.; Boom, R.; Schroën, K. Microfluidic Emulsification in Food Processing. J. Food Eng. 2015, 147, 1–7. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.-W. Computational Fluid Dynamics (CFD)—An Effective and Efficient Design and Analysis Tool for the Food Industry: A Review. Trends Food Sci. Technol. 2006, 17, 600–620. [Google Scholar] [CrossRef]
- Tavares, M.; Josserand, C.; Limare, A.; Lopez-Herrera, J.M.; Popinet, S. A Coupled VOF/Embedded Boundary Method to Model Two-Phase Flows on Arbitrary Solid Surfaces. Comput. Fluids 2024, 278, 106317. [Google Scholar] [CrossRef]
- Skurtys, O.; Aguilera, J.M. Applications of Microfluidic Devices in Food Engineering. Food Biophys. 2008, 3, 1–15. [Google Scholar] [CrossRef]
- Association of Official Analytical Chemists. AOAC Method 950.46. In Official Methods of Analysis; AOAC International: Rockville, MD, USA, 1990. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 Years of Image Analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Stalder, A.F.; Kulik, G.; Sage, D.; Barbieri, L.; Hoffmann, P. A Snake-Based Approach to Accurate Determination of Both Contact Points and Contact Angles. Colloids Surf. A Physicochem. Eng. Asp. 2006, 286, 92–103. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, J.; Feng, M.; Yang, B.; Cai, X. Study on Imaging Method for Measuring Droplet Size in Large Sprays. Particuology 2015, 22, 100–106. [Google Scholar] [CrossRef]
- Zhou, H.; Shu, D.; Wu, C.; Wang, Q.; Wang, Q. Image Illumination Adaptive Correction Algorithm Based on a Combined Model of Bottom-Hat and Improved Gamma Transformation. Arab. J. Sci. Eng. 2023, 48, 3947–3960. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man. Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Ng, H.-F. Automatic Thresholding for Defect Detection. Pattern Recognit. Lett. 2006, 27, 1644–1649. [Google Scholar] [CrossRef]
- Roerdink, J.B.T.M. Group Morphology. Pattern Recognit. 2000, 33, 877–895. [Google Scholar] [CrossRef]
- Basu, M. Gaussian-Based Edge-Detection Methods-a Survey. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2002, 32, 252–260. [Google Scholar] [CrossRef]
- Dhar, R.; Gupta, R.; Baishnab, K.L. An Analysis of CANNY and LAPLACIAN of GAUSSIAN Image Filters in Regard to Evaluating Retinal Image. In Proceedings of the 2014 International Conference on Green Computing Communication and Electrical Engineering (ICGCCEE), Coimbatore, India, 6–8 March 2014; pp. 1–6. [Google Scholar]
- Kato, S.; Carlson, D.W.; Shen, A.Q.; Guo, Y. Twisted Fiber Microfluidics: A Cutting-Edge Approach to 3D Spiral Devices. Microsyst. Nanoeng. 2024, 10, 14. [Google Scholar] [CrossRef]
- Azzini, F.; Pulvirenti, B.; Rossi, M.; Morini, G.L. Squeezing Droplet Formation in a Flow-Focusing Micro Cross-Junction. Micromachines 2024, 15, 339. [Google Scholar] [CrossRef] [PubMed]
- Maurya, T.C.K.; Dutta, S. Pinch-off Dynamics of Droplet Formation in Microchannel Flow. Chem. Eng. Sci. 2023, 282, 119296. [Google Scholar] [CrossRef]
- Okagaki, Y.; Yonomoto, T.; Ishigaki, M.; Hirose, Y. Numerical Study on an Interface Compression Method for the Volume of Fluid Approach. Fluids 2021, 6, 80. [Google Scholar] [CrossRef]
- Ananth, M.; Trujillo, M.F. Breakup of Planar Liquid Sheets Injected at High Speed in a Quiescent Gas Environment. J. Fluid. Mech. 2023, 975, A38. [Google Scholar] [CrossRef]
- Zhao, C.; Maarek, J.; Taleghani, S.M.; Zaleski, S. A Hybrid Continuum Surface Tension Force for the Three-Phase VOF Method. J. Comput. Phys. 2024, 504, 112872. [Google Scholar] [CrossRef]
- Cimarelli, A.; Romoli, F.; Stalio, E. On Wind–Wave Interaction Phenomena at Low Reynolds Numbers. J. Fluid. Mech. 2023, 956, A13. [Google Scholar] [CrossRef]
- Wagner, W.; Pruß, A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Huber, M.L.; Perkins, R.A.; Laesecke, A.; Friend, D.G.; Sengers, J.V.; Assael, M.J.; Metaxa, I.N.; Vogel, E.; Mareš, R.; Miyagawa, K. New International Formulation for the Viscosity of H2O. J. Phys. Chem. Ref. Data 2009, 38, 101–125. [Google Scholar] [CrossRef]
- Petrova, T.; Dooley, R.B. Revised Release on Surface Tension of Ordinary Water Substance. In Proceedings of the International Association for the Properties of Water and Steam, Moscow, Russia, 22–27 June 2014; Volume 63, pp. 23–27. [Google Scholar]
- Nath, A.J.; Deka, D.K.; Pati, S. Numerical Investigation of Droplet Generation Within a Microfluidic T-Junction With Semicylindrical Obstacle. J. Fluids Eng. 2023, 145, 011202. [Google Scholar] [CrossRef]
- Ierardi, C.; Torre, A.D.; Montenegro, G.; Onorati, A.; Radaelli, F.; Visconti, L.; Miarelli, M. Modeling of Two-Phase Flows at Low Capillary Number with VoF Method. Comput. Fluids 2023, 252, 105772. [Google Scholar] [CrossRef]
- Laín, S.; Lozano-Parada, J.H.; Guzmán, J. Computational Characterization of Turbulent Flow in a Microfluidic Actuator. Appl. Sci. 2022, 12, 3589. [Google Scholar] [CrossRef]
- Brogi, F.; Bnà, S.; Boga, G.; Amati, G.; Esposti Ongaro, T.; Cerminara, M. On Floating Point Precision in Computational Fluid Dynamics Using OpenFOAM. Future Gener. Comput. Syst. 2024, 152, 1–16. [Google Scholar] [CrossRef]
- Olenik, G.; Koch, M.; Boutanios, Z.; Anzt, H. Towards a Platform-Portable Linear Algebra Backend for OpenFOAM. Meccanica 2025, 60, 1659–1672. [Google Scholar] [CrossRef]
- Piscaglia, F.; Ghioldi, F. GPU Acceleration of CFD Simulations in OpenFOAM. Aerospace 2023, 10, 792. [Google Scholar] [CrossRef]
- Nivedita, V.; Srisowmeya, G.; Chakravarthy, M.; Antony, U.; Nandhini Devi, G. Effects of Microbial Polysaccharides on the Oil Absorption and Quality Characteristics of a Deep-Fried Snack Namkeen. Eur. J. Lipid Sci. Technol. 2022, 124, 2000404. [Google Scholar] [CrossRef]
- Muthukrishnan, R.; Radha, M. Edge Detection Techniques For Image Segmentation. Int. J. Comput. Sci. Inf. Technol. 2011, 3, 259–267. [Google Scholar] [CrossRef]
- Machado, D.A.; de Souza Costa, F.; de Andrade, J.C.; Dias, G.S.; Fischer, G.A.A. Schlieren Image Velocimetry of Swirl Sprays. Flow. Turbul. Combust. 2023, 110, 489–513. [Google Scholar] [CrossRef]
- Athanasopoulou, E.; Bigi, F.; Maurizzi, E.; Karellou, E.I.E.; Pappas, C.S.; Quartieri, A.; Tsironi, T. Synthesis and Characterization of Polysaccharide- and Protein-Based Edible Films and Application as Packaging Materials for Fresh Fish Fillets. Sci. Rep. 2024, 14, 517. [Google Scholar] [CrossRef]
- Yashwant, A.S.; Kashyap, P.; Goksen, G. Recent Advances in the Improvement of Protein-Based Edible Films through Non-Thermal and Thermal Techniques. Food Biosci. 2023, 55, 103032. [Google Scholar] [CrossRef]
- Dutra, G.; Canning, J.; Padden, W.; Martelli, C.; Dligatch, S. Large Area Optical Mapping of Surface Contact Angle. Opt. Express 2017, 25, 21127. [Google Scholar] [CrossRef] [PubMed]
- Lößlein, S.M.; Merz, R.; Müller, D.W.; Kopnarski, M.; Mücklich, F. An In-Depth Evaluation of Sample and Measurement Induced Influences on Static Contact Angle Measurements. Sci. Rep. 2022, 12, 19389. [Google Scholar] [CrossRef] [PubMed]
- Ponomar, M.; Krasnyuk, E.; Butylskii, D.; Nikonenko, V.; Wang, Y.; Jiang, C.; Xu, T.; Pismenskaya, N. Sessile Drop Method: Critical Analysis and Optimization for Measuring the Contact Angle of an Ion-Exchange Membrane Surface. Membranes 2022, 12, 765. [Google Scholar] [CrossRef]
- Der, O.; Bertola, V. An Experimental Investigation of Oil-Water Flow in a Serpentine Channel. Int. J. Multiph. Flow. 2020, 129, 103327. [Google Scholar] [CrossRef]
- Akbari, R.; Antonini, C. Contact Angle Measurements: From Existing Methods to an Open-Source Tool. Adv. Colloid. Interface Sci. 2021, 294, 102470. [Google Scholar] [CrossRef] [PubMed]
- Vu, L.; Machicoane, N.; Li, D.; Morgan, T.B.; Heindel, T.J.; Aliseda, A.; Desjardins, O. A Computational Study of a Two-Fluid Atomizing Coaxial Jet: Validation against Experimental Back-Lit Imaging and Radiography and the Influence of Gas Velocity and Contact Line Model. Int. J. Multiph. Flow. 2023, 167, 104520. [Google Scholar] [CrossRef]
- Carmona, J.; Odier, N.; Desjardins, O.; Cuenot, B.; Misdariis, A.; Cayre, A. A comparative study of direct numerical simulation and experimental results on a prefilming airblast atomization configuration. At. Sprays 2021, 31, 9–32. [Google Scholar] [CrossRef]
- Oshima, I.; Sou, A. Air-Blast Atomization of a Liquid Film. J. Fluid. Mech. 2024, 985, A36. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Y.; Wu, Z.; Fang, G.; Chen, Y.; Duan, J. Near-Nozzle Atomization Characteristics in Air-Assisted Spraying: Integrated VOF-DPM Modeling and Experimental Validation. Coatings 2025, 15, 939. [Google Scholar] [CrossRef]
- Payri, R.; Salvador, F.J.; Carreres, M.; Moreno-Montagud, C. A Computational Methodology to Account for the Liquid Film Thickness Evolution in Direct Numerical Simulation of Prefilming Airblast Atomization. Int. J. Multiph. Flow. 2023, 161, 104403. [Google Scholar] [CrossRef]
- Wu, W.; Wang, D.; Zhang, Y.; Yu, L.; Han, W. Numerical Analysis of the Airflow Field and Experiments of Fiber Motion for Solution Blowing. ACS Omega 2024, 9, 26941–26950. [Google Scholar] [CrossRef] [PubMed]
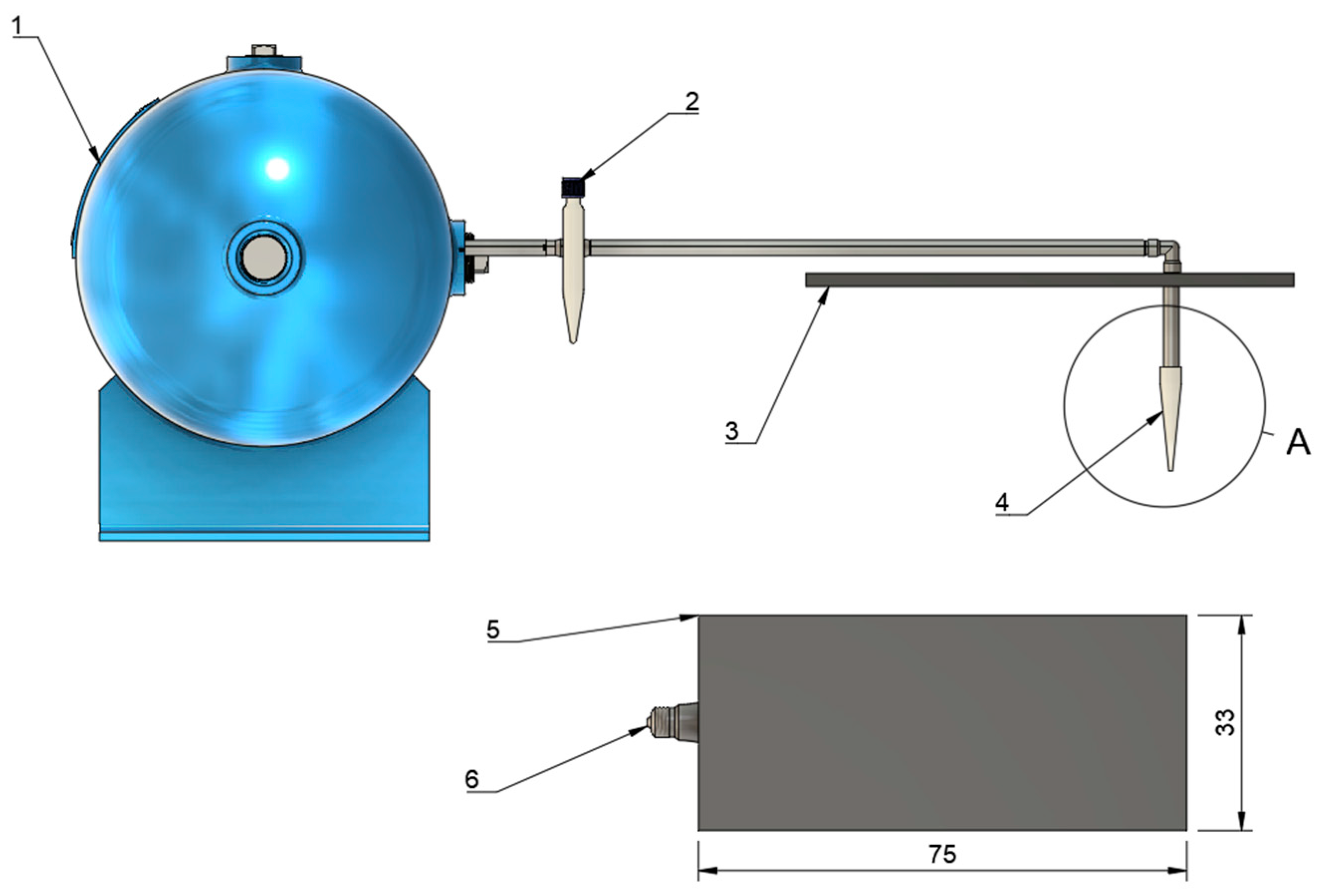
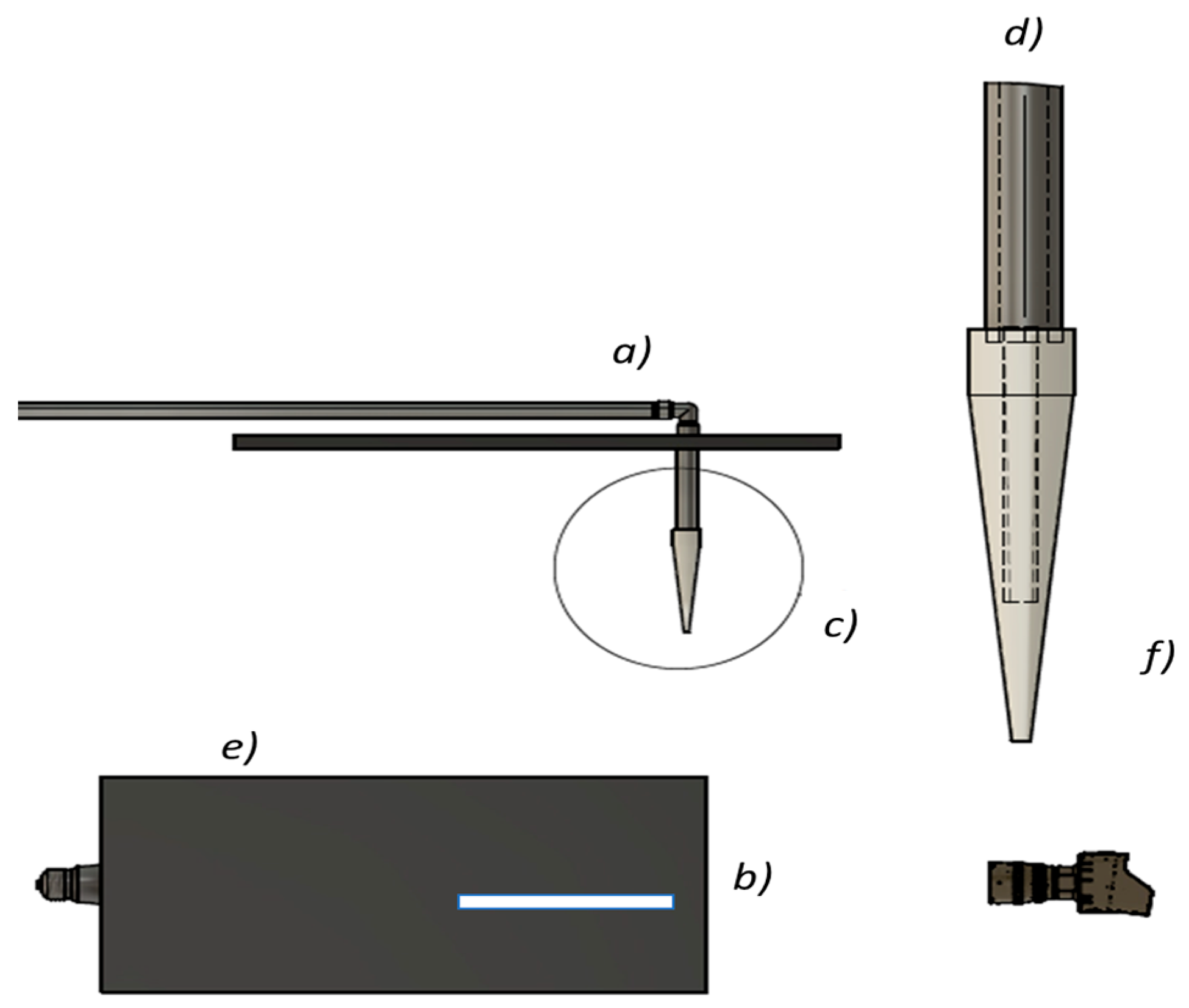
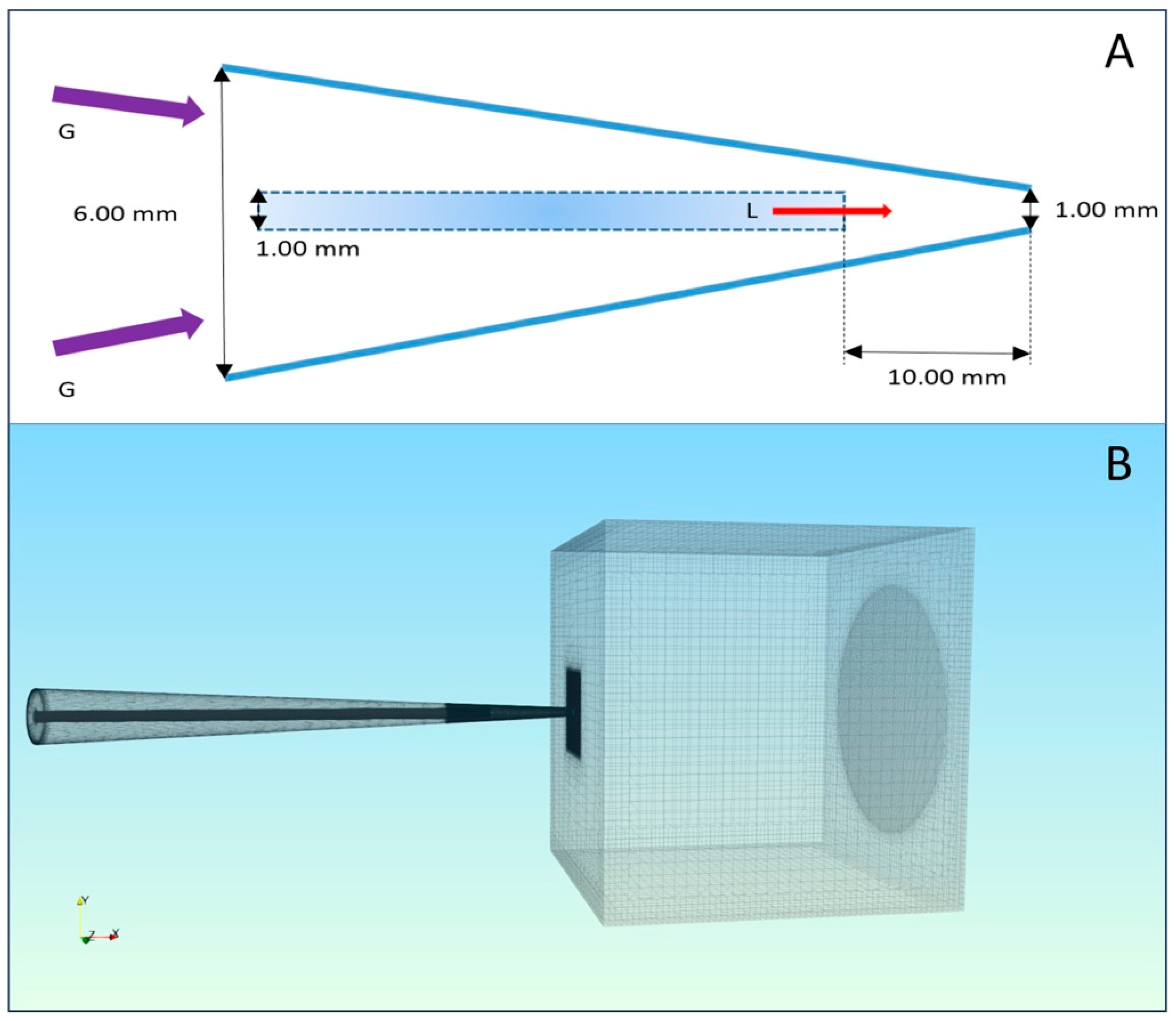





| Component | Dimension | Function |
|---|---|---|
| Inner capillary | 1.0 mm ID, 1.5 mm OD (borosilicate glass capillary) | Delivers the protein coating solution |
| Outer air capillary | Internal diameter tapers from 6 mm (inlet) to 1.0 mm (exit) over 60 mm axial length | Generates a converging annular air sheath for flow-blurring atomization |
| Liquid-tip recess | 10 mm upstream of the cone exit | Stabilizes the liquid jet and prevents wall impingement |
| Phase | Density ρ (kg m−3) | Kinematic Viscosity ν (m2 s−1) | Surface Tension σ (N m−1) |
|---|---|---|---|
| Air (24 °C) | 1.188 | 1.48 × 10−5 | — |
| Coating (24 °C) | 997.3 | 9.14 × 10−7 | 0.0721 |
| Method | V Used (mL) | V Sample (mL) |
|---|---|---|
| Conventional coating application (WPI-Conv) | 15.0 | 1.5 |
| Microfluidic coating application (WPI-McF) | 8.0 | 0.8 |
| Parameter | Value (µm) |
|---|---|
| Mean (μm) | 106.99 |
| Standard deviation (σ) | 55.88 |
| Minimum (Dmin) | 30.45 |
| Percentile 25 (P25) | 51.49 |
| Median (D50) | 83.69 |
| Percentile 75 (P75) | 137.15 |
| Maximum (Dmax) | 399.49 |
| Image | Substrate | θL (°) | θR (°) | (°) | ∆θ (°) | Classification |
|---|---|---|---|---|---|---|
| a | Coating/Glass | 97.34 | 95.43 | 96.38 | 0.96 | Hydrophobic |
| b | Water/Plastic | 84.34 | 83.32 | 83.83 | 0.51 | Intermedium |
| c | Coating/Plastic | 50.38 | 50.02 | 50.20 | 0.18 | Hydrophilic |
| d | Coating/Sausage | N.D. | N.D. | N.D. | N.D. | N.D. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dávalos-Saucedo, C.A.; Rossi-Márquez, G.; Rodríguez-Miranda, S.; Castañeda, C.E. Microfluidic Edible Coatings: Multiphase VOF Modeling, Physicochemical Properties, Image Analysis, and Applications in Fried Foods. Coatings 2025, 15, 1245. https://doi.org/10.3390/coatings15111245
Dávalos-Saucedo CA, Rossi-Márquez G, Rodríguez-Miranda S, Castañeda CE. Microfluidic Edible Coatings: Multiphase VOF Modeling, Physicochemical Properties, Image Analysis, and Applications in Fried Foods. Coatings. 2025; 15(11):1245. https://doi.org/10.3390/coatings15111245
Chicago/Turabian StyleDávalos-Saucedo, Cristian Aarón, Giovanna Rossi-Márquez, Sergio Rodríguez-Miranda, and Carlos E. Castañeda. 2025. "Microfluidic Edible Coatings: Multiphase VOF Modeling, Physicochemical Properties, Image Analysis, and Applications in Fried Foods" Coatings 15, no. 11: 1245. https://doi.org/10.3390/coatings15111245
APA StyleDávalos-Saucedo, C. A., Rossi-Márquez, G., Rodríguez-Miranda, S., & Castañeda, C. E. (2025). Microfluidic Edible Coatings: Multiphase VOF Modeling, Physicochemical Properties, Image Analysis, and Applications in Fried Foods. Coatings, 15(11), 1245. https://doi.org/10.3390/coatings15111245








