Enhanced Piezoelectric and Ferroelectric Properties in the Lead-Free [(BiFeO3)m/(SrTiO3)n]p Multilayers by Varying the Thickness Ratio r = n/m and Periodicity p
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.1.1. Indium Tin Oxide Bottom Electrode
2.1.2. Preparation of Multilayer Systems
2.2. Characterization of Structure, Composition, and Ferroelectric Response
3. Results and Discussion
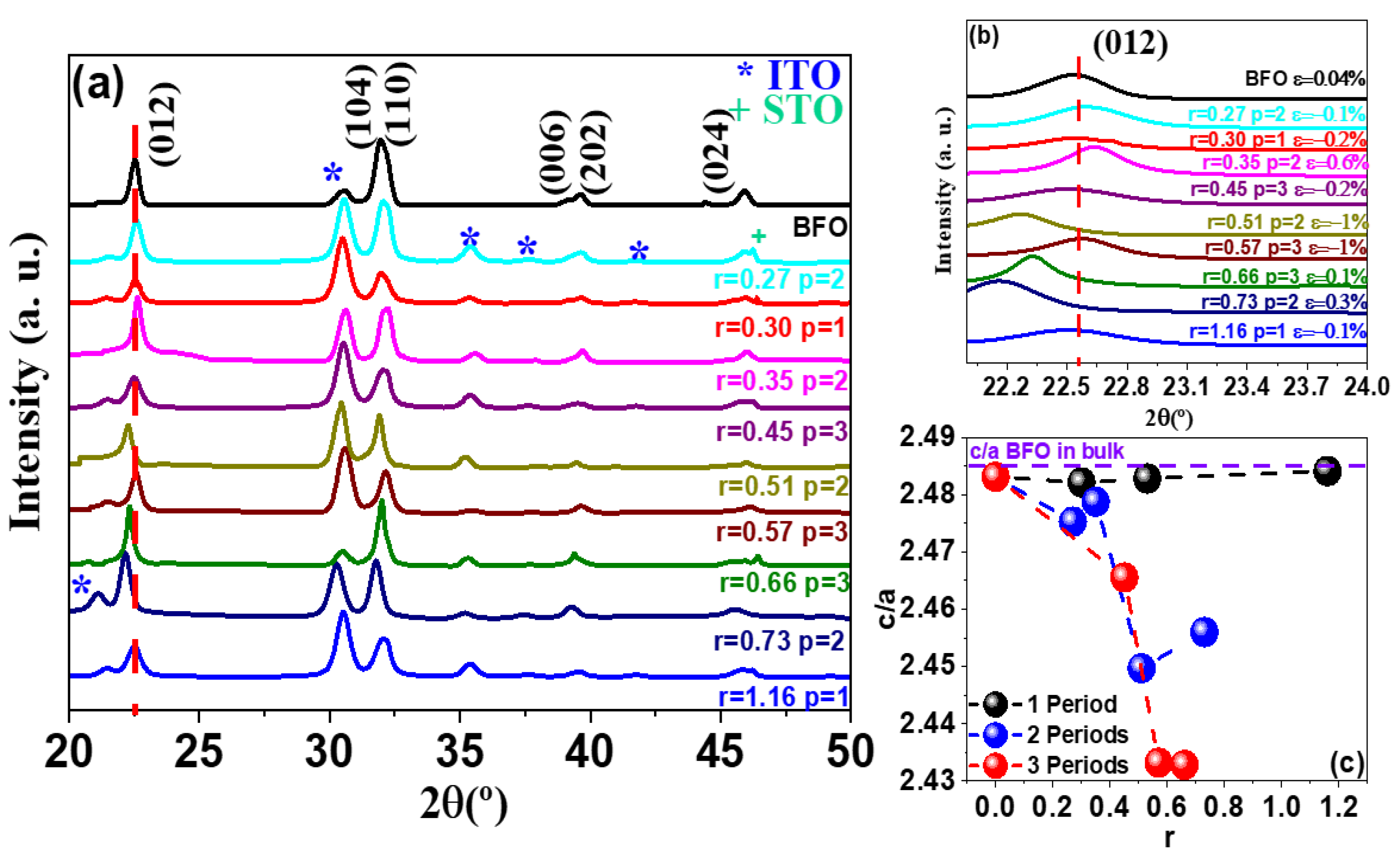
3.1. Microstructure
3.1.1. Rietveld Refinement
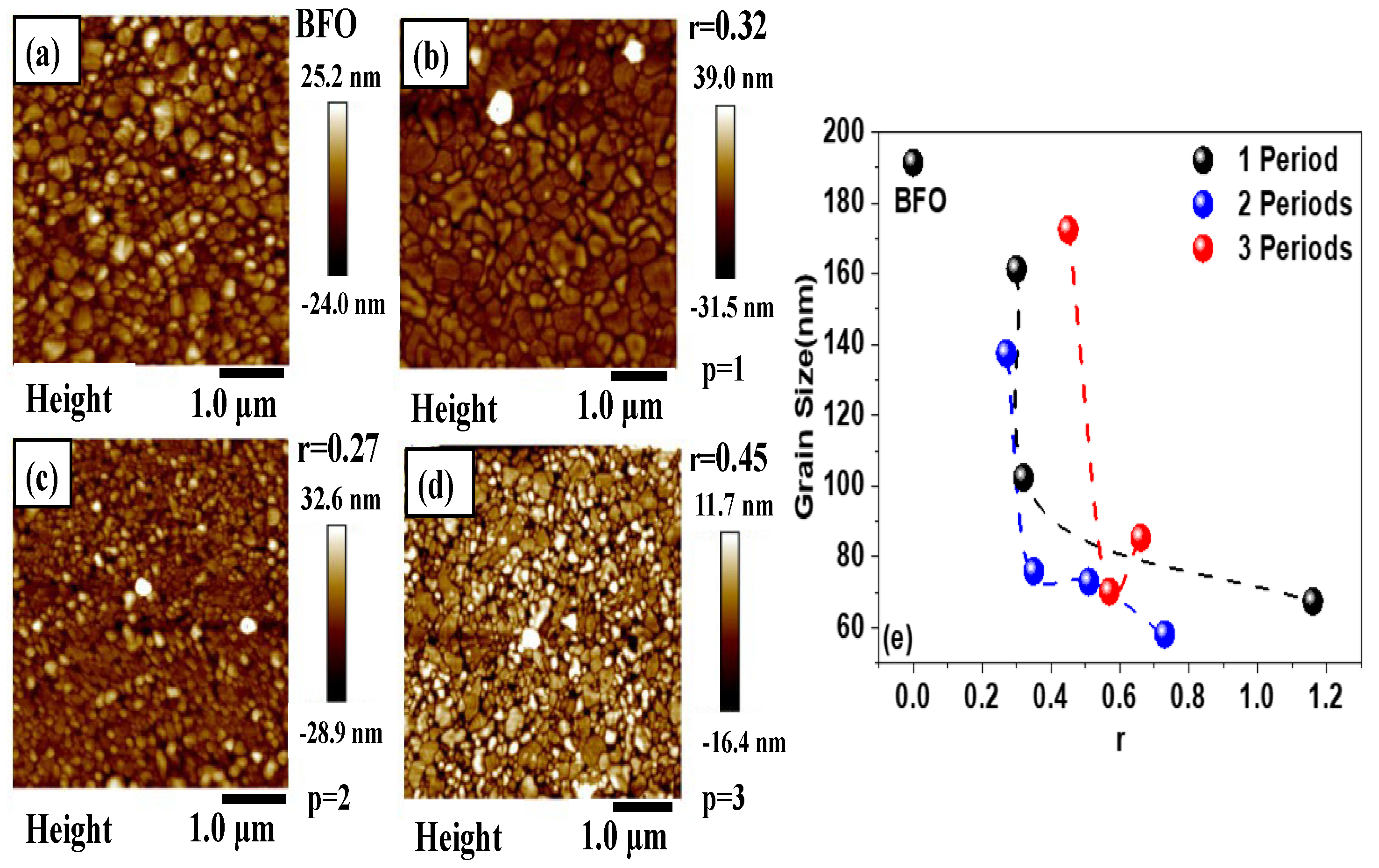
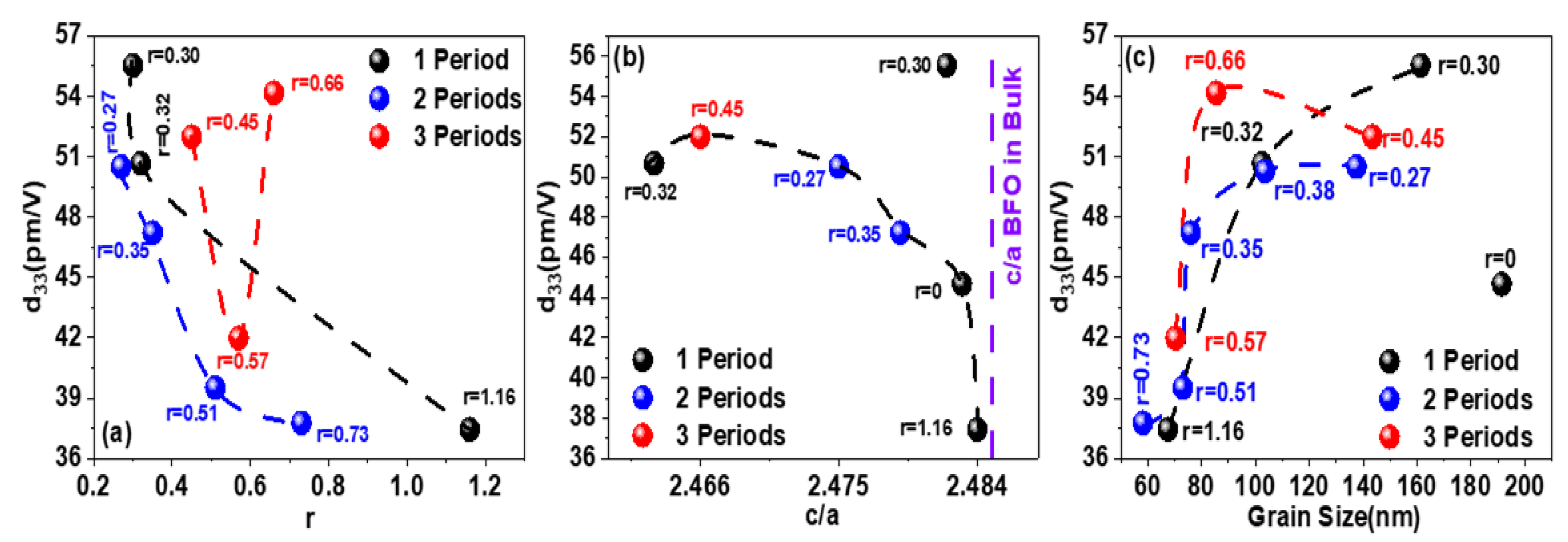
3.1.2. Grain Size Measurements
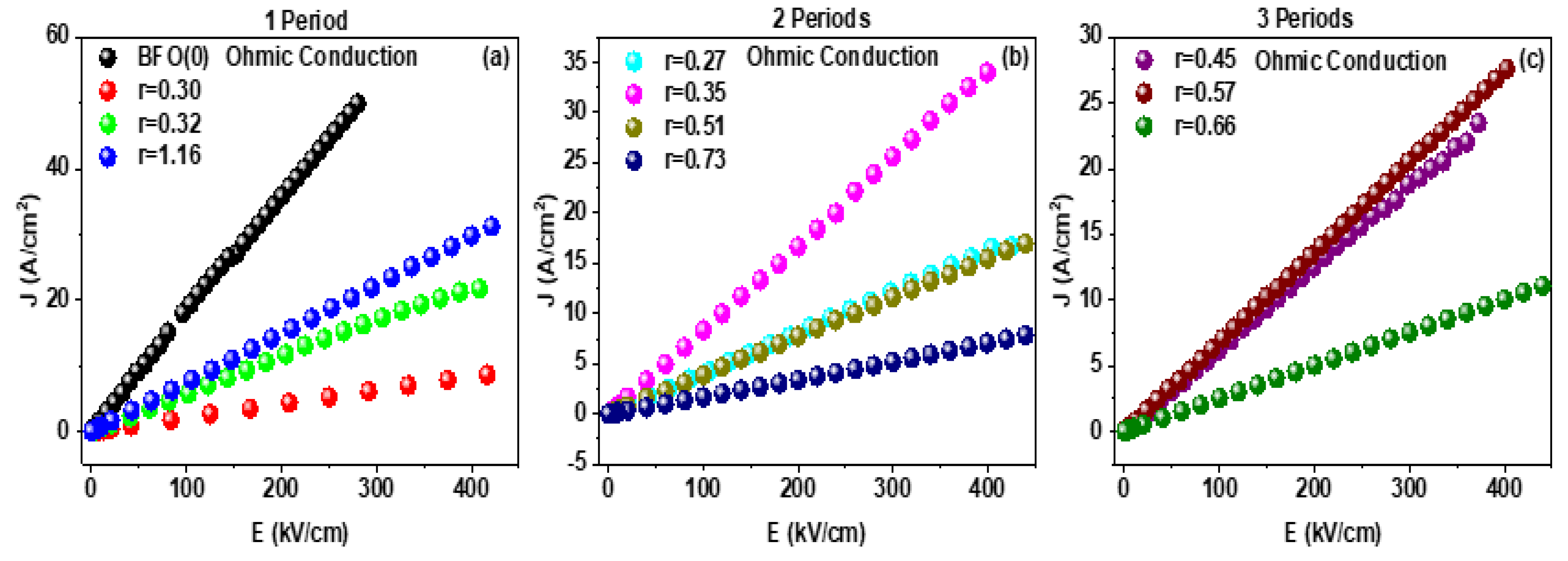
3.2. Leakage Current Density Analysis
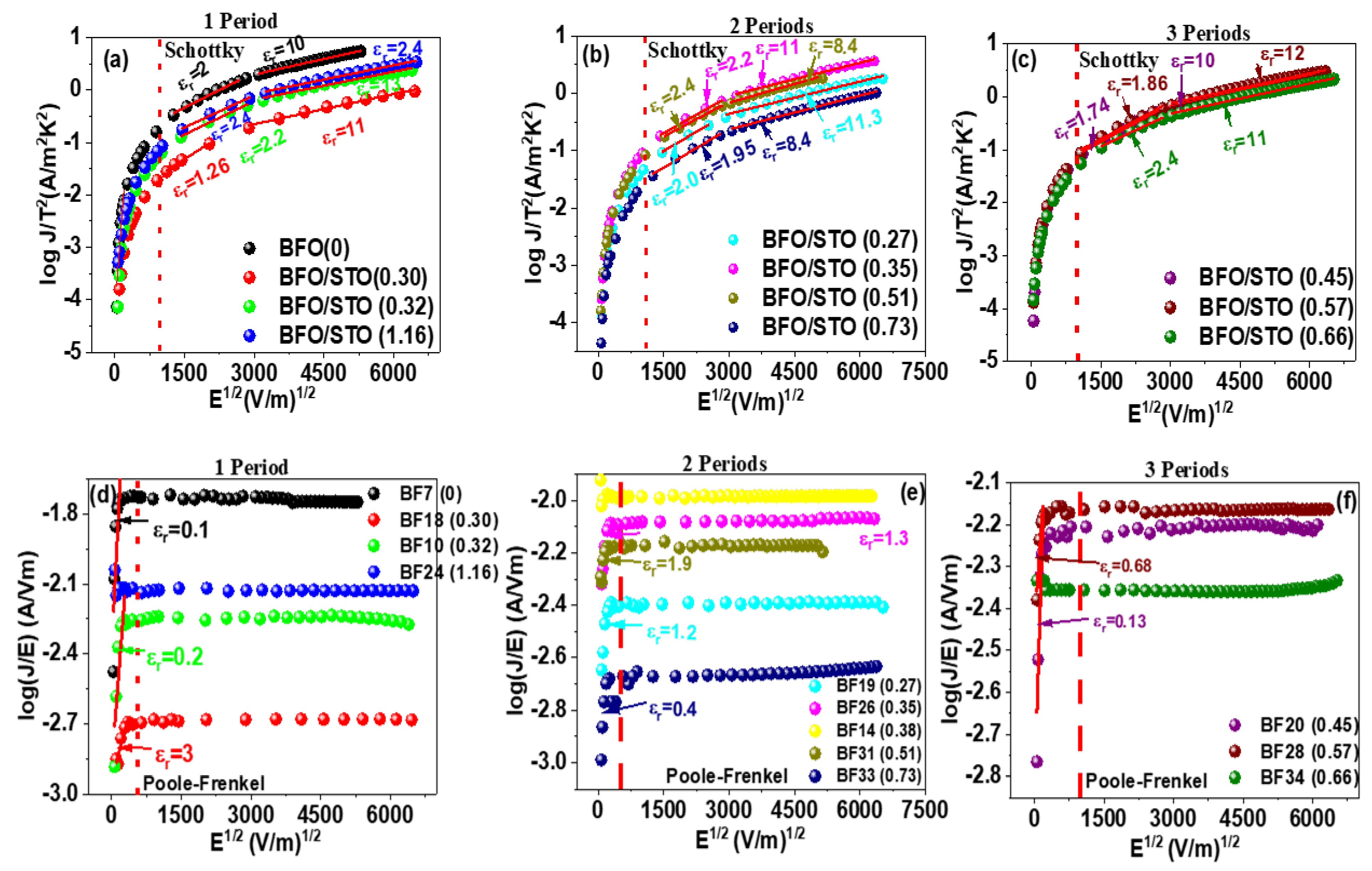
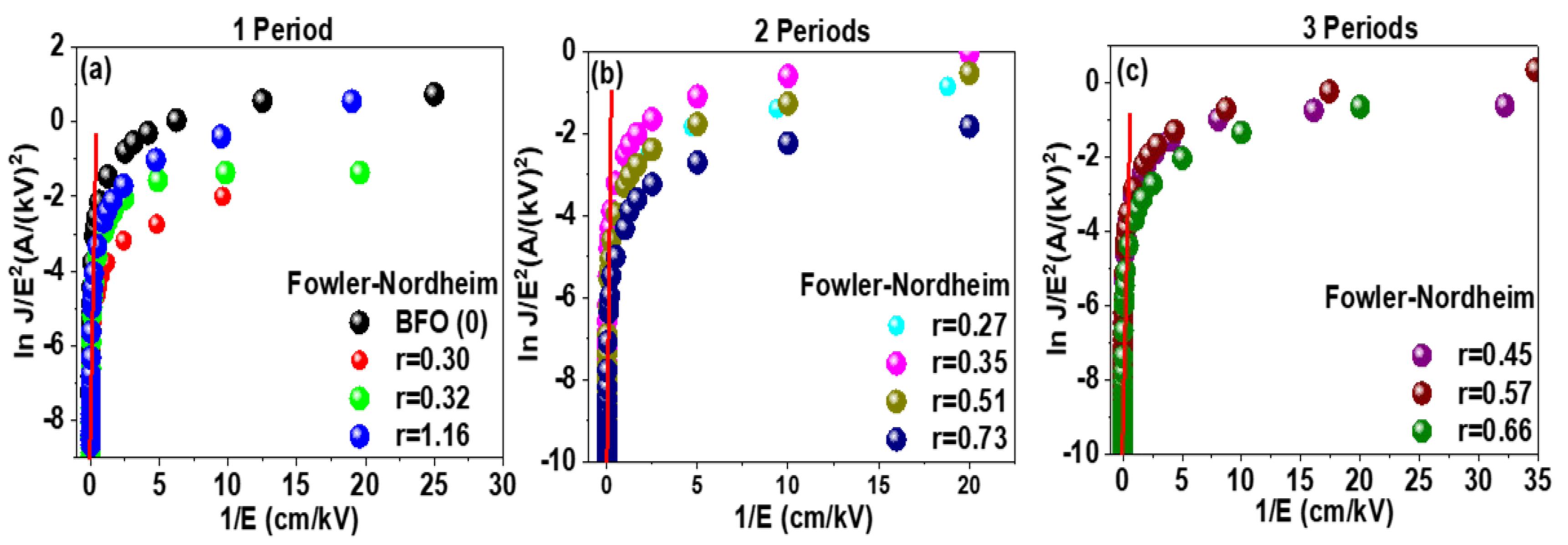
3.3. Conduction Mechanisms
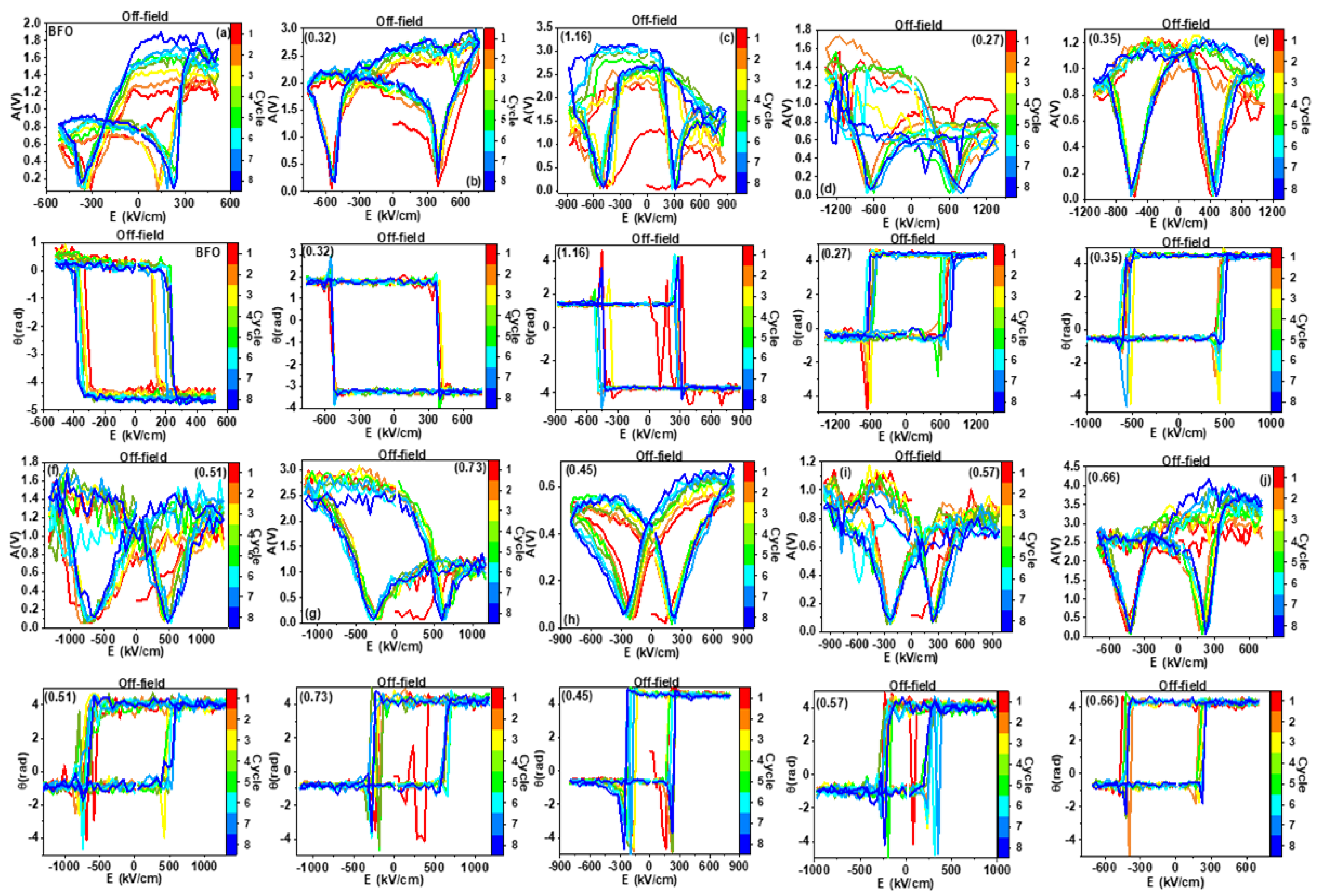
3.4. Ferroelectric Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liang, X.; Chen, H.; Sun, N. Magnetoelectric materials and devices. APL Mater. 2021, 9, 041114. [Google Scholar] [CrossRef]
- Khomskii, D.I. Multiferroics: Different ways to combine magnetism and ferroelectricity. J. Magn. Magn. Mater. 2006, 306, 1–8. [Google Scholar] [CrossRef]
- Fiebig, M. Revival of the magnetoelectric effect. J. Phys. D Appl. Phys. 2005, 38, R123–R152. [Google Scholar] [CrossRef]
- Bersuker, I.B. Origin of Perovskite Multiferroicity and Magnetoelectric-Multiferroic Effects—The Role of Electronic Spin in Spontaneous Polarization of Crystals. Magnetochemistry 2022, 8, 9. [Google Scholar] [CrossRef]
- Deng, X.; Zeng, Z.; Xu, R.; Qin, X.; Li, X.; Wang, Y.; Gao, R.; Wang, Z.; Chen, G.; Cai, W.; et al. Effect of annealing atmosphere on structural and multiferroic properties of BiFeO3 thin film prepared by RF magnetron sputtering. J. Mater. Sci. Mater. Electron. 2019, 30, 16502–16509. [Google Scholar] [CrossRef]
- Michel, C.; Moreau, J.M.; Achenbach, G.D.; Gerson, R.; James, W.J. The atomic structure of BiFeO3. Solid State Commun. 1969, 7, 701–704. [Google Scholar] [CrossRef]
- Nan, C.W.; Bichurin, M.I.; Dong, S.; Viehland, D.; Srinivasan, G. Multiferroic magnetoelectric composites: Historical perspective, status, and future directions. J. Appl. Phys. 2008, 103, 031101. [Google Scholar] [CrossRef]
- Wang, J.; Neaton, J.B.; Zheng, H.; Nagarajan, V.; Ogale, S.B.; Liu, B.; Viehland, D.; Vaithyanathan, V.; Schlom, D.G.; Waghmare, U.V.; et al. Epitaxial BiFeO3 multiferroic thin film heterostructures. Science 2008, 299, 1719–1722. [Google Scholar] [CrossRef]
- Lebeugle, D.; Colson, D.; Forget, A.; Viret, M. Very large spontaneous electric polarization in BiFeO3 single crystals at room temperature and its evolution under cycling fields. Appl. Phys. Lett. 2007, 91, 022907. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X. Large electric polarization in BiFeO3 film prepared via a simple sol-gel process. J. Sol-Gel Sci. Technol. 2008, 47, 154–157. [Google Scholar] [CrossRef]
- Reddy, V.A.; Dabra, N.; Hundal, J.S.; Pathak, N.P.; Nath, R. Structural and multiferroic characteristics of nanocomposite Ba0.5Sr0.5TiO3-Bi0.9La0.1Fe0.9Mn0.1O3 thin film heterostructures. Sci. Adv. Mater. 2014, 6, 1043–1051. [Google Scholar] [CrossRef]
- Martin, L.W.; Crane, S.P.; Chu, Y.H.; Holcomb, M.B.; Gajek, M.; Huijben, M.; Yang, C.H.; Balke, N.; Ramesh, R. Multiferroics and magnetoelectrics: Thin films and nanostructures. J. Phys. Condens. Matter 2008, 20, 434220. [Google Scholar] [CrossRef]
- Catalan, G.; Scott, J.F. Physics and applications of bismuth ferrite. Adv. Mater. 2009, 21, 2463–2485. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, H.Y.; Pan, X.; Wang, L.X.; Feng, Z.; Guo, X.; Shen, P.; Ma, Z.; Zhang, F.; Tian, Q.; et al. Effect of the thickness of Sr2Bi4Ti5O18 transition layer on the properties of BiFeO3/Sr2Bi4Ti5O18 bilayer composite thin films. Ceram. Int. 2020, 46, 10536–10544. [Google Scholar] [CrossRef]
- Qi, X.; Dho, J.; Tomov, R.; Blamire, M.G.; MacManus-Driscoll, J.L. Greatly reduced leakage current and conduction mechanism in aliovalent-ion-doped BiFeO3. Appl. Phys. Lett. 2005, 86, 062903. [Google Scholar] [CrossRef]
- Wang, Y.P.; Zhou, L.; Zhang, M.F.; Chen, X.Y.; Liu, J.M.; Liu, Z.G. Room-temperature saturated ferroelectric polarization in BiFeO3 ceramics synthesized by rapid liquid phase sintering. Appl. Phys. Lett. 2004, 84, 1731–1733. [Google Scholar] [CrossRef]
- Clark, S.J.; Robertson, J. Band gap and Schottky barrier heights of multiferroic BiFeO3. Appl. Phys. Lett. 2007, 90, 10–13. [Google Scholar] [CrossRef]
- Singh, S.K.; Ishiwara, H.; Maruyama, K. Room temperature ferroelectric properties of Mn-substituted BiFeO3 thin films deposited on Pt electrodes using chemical solution deposition. Appl. Phys. Lett. 2006, 88, 262908. [Google Scholar] [CrossRef]
- Yun, K.Y.; Ricinschi, D.; Kanashima, T.; Okuyama, M. Enhancement of electrical properties in polycrystalline BiFeO3 thin films. Appl. Phys. Lett. 2006, 89, 192902. [Google Scholar] [CrossRef]
- Ranjith, R.; Prellier, W.; Cheah, J.W.; Wang, J.; Wu, T. dc leakage behavior and conduction mechanism in (BiFeO3)m(SrTiO3)m superlattices. Appl. Phys. Lett. 2008, 92, 232905. [Google Scholar] [CrossRef]
- Khan, M.A.; Comyn, T.P.; Bell, A.J. Leakage mechanisms in bismuth ferrite-lead titanate thin films on PtSi substrates. Appl. Phys. Lett. 2008, 92, 072908. [Google Scholar] [CrossRef]
- Ranjith, R.; Kundys, B.; Prellier, W. Periodicity dependence of the ferroelectric properties in BiFeO3 SrTiO3 multiferroic superlattices. Appl. Phys. Lett. 2007, 91, 222904. [Google Scholar] [CrossRef]
- Zhou, N.; Zhao, K.; Liu, H.; Lu, H.B.; He, M.; Zhao, S.; Leng, W.; Wang, A.; Huang, Y.; Jin, K.J.; et al. Enhanced photovoltage in perovskite-type artificial superlattices on Si substrates. J. Phys. D Appl. Phys. 2008, 41, 155414. [Google Scholar] [CrossRef][Green Version]
- Zheng, R.Y.; Gao, X.S.; Zhou, Z.H.; Wang, J. Multiferroic BiFeO3 thin films deposited on SrRuO3 buffer layer by rf sputtering. J. Appl. Phys. 2007, 101, 054104. [Google Scholar] [CrossRef]
- Chung, C.F.; Lin, J.P.; Wu, J.M. Influence of Mn and Nb dopants on electric properties of chemical-solution-deposited BiFeO3 films. Appl. Phys. Lett. 2006, 88, 242909. [Google Scholar] [CrossRef]
- Lee, Y.H.; Wu, J.M.; Lai, C.H. Influence of La doping in multiferroic properties of BiFeO3 thin films. Appl. Phys. Lett. 2006, 88, 042903. [Google Scholar] [CrossRef]
- Yasui, S.; Uchida, H.; Nakaki, H.; Nishida, K.; Funakubo, H.; Koda, S. Analysis for crystal structure of Bi(Fe,Sc)O3 thin films and their electrical properties. Appl. Phys. Lett. 2007, 91, 022906. [Google Scholar] [CrossRef]
- Palkar, V.R.; Kundaliya, D.C.; Malik, S.K. Effect of Mn substitution on magnetoelectric properties of bismuth ferrite system. J. Appl. Phys. 2003, 93, 4337–4339. [Google Scholar] [CrossRef]
- Kim, J.K.; Kim, S.S.; Kim, W.J.; Bhalla, A.S.; Guo, R. Enhanced ferroelectric properties of Cr-doped BiFeO3 thin films grown by chemical solution deposition. Appl. Phys. Lett. 2006, 88, 132901. [Google Scholar] [CrossRef]
- Pabst, G.W.; Martin, L.W.; Chu, Y.H.; Ramesh, R. Leakage mechanisms in BiFeO3 thin films. Appl. Phys. Lett. 2007, 90, 072902. [Google Scholar] [CrossRef]
- Shin, J.; Goyal, A.; Jesse, S.; Heatherly, L. Polarization manipulation via orientation control in polycrystalline BiFeO3 thin films on biaxially textured, flexible metallic tapes. Appl. Phys. Express 2011, 4, 021501. [Google Scholar] [CrossRef]
- Jiang, Q.; Lee, H.J.; Kim, G.H.; Hwang, C.S. The inlaid AI2O3 tunnel switch for ultrathin ferroelectric films. Adv. Mater. 2009, 21, 2870–2875. [Google Scholar] [CrossRef]
- Lee, H.J.; Park, M.H.; Kim, Y.J.; Hwang, C.S.; Kim, J.H.; Funakubo, H.; Ishiwara, H. Improved ferroelectric property of very thin Mn-doped BiFeO3 films by an inlaid Al2O3 tunnel switch. J. Appl. Phys. 2011, 110, 074111. [Google Scholar] [CrossRef]
- Lee, G.; Fuentes-Fernandez, E.M.A.; Lian, G.; Katiyar, R.S.; Auciello, O. Hetero-epitaxial BiFeO3/SrTiO3 nanolaminates with higher piezoresponse performance over stoichiometric BiFeO3 films. Appl. Phys. Lett. 2015, 106, 022905. [Google Scholar] [CrossRef]
- Garduño-Medina, A.; Flores-Ruiz, F.J.; Camps, E.; García-Zaldívar, O.; Pérez-Rodríguez, F. Coercive field modified via partial ion substitution, mechanical load and charge injection in (Ba, Ta, Cr) doped BiFeO3 films. Ceram. Int. 2023, 49, 31046–31056. [Google Scholar] [CrossRef]
- Tiron, V.; Jijie, R.; Dumitru, I.; Cimpoesu, N.; Burducea, I.; Iancu, D.; Borhan, A.; Gurlui, S.; Bulai, G. Piezo-ferroelectric response of bismuth ferrite based thin films and their related photo/piezocatalytic performance. Ceram. Int. 2023, 49, 20304–20314. [Google Scholar] [CrossRef]
- Dai, Y.Q.; Dai, J.M.; Tang, X.W.; Zhang, K.J.; Zhu, X.B.; Yang, J.; Sun, Y.P. Thickness effect on the properties of BaTiO3-CoFe2O4 multilayer thin films prepared by chemical solution deposition. J. Alloys Compd. 2014, 587, 681–687. [Google Scholar] [CrossRef]
- Arulraj, A. Enhanced photoconductive response of ZnO thin films with the impact of annealing temperatures on structural and optical properties. Sci. Rep. 2025, 15, 28851. [Google Scholar] [CrossRef]
- Gupta, S.; Tomar, M.; James, A.R.; Gupta, V. Ce-doped bismuth ferrite thin films with improved electrical and functional properties. J. Mater. Sci. 2014, 49, 5355–5364. [Google Scholar] [CrossRef]
- Singh, V.R.; Dixit, A.; Garg, A.; Agrawal, D.C. Effect of heat treatment on the structure and properties of chemical solution processed multiferroic BiFeO3 thin films. Appl. Phys. A Mater. Sci. Process. 2008, 90, 197–202. [Google Scholar] [CrossRef]
- Simões, A.Z.; Riccardi, C.S.; Santos, M.L.D.; Garcia, F.G.; Longo, E.; Varela, J.A. Effect of annealing atmosphere on phase formation and electrical characteristics of bismuth ferrite thin films. Mater. Res. Bull. 2009, 44, 1747–1752. [Google Scholar] [CrossRef]
- Cole, M.W.; Ngo, E.; Hubbard, C.; Hirsch, S.G.; Ivill, M.; Sarney, W.L.; Zhang, J.; Alpay, S.P. Enhanced dielectric properties from barium strontium titanate films with strontium titanate buffer layers. J. Appl. Phys. 2013, 114, 164107. [Google Scholar] [CrossRef]
- Bersuker, G.; Yum, J.; Vandelli, L.; Padovani, A.; Larcher, L.; Iglesias, V.; Porti, M.; Nafría, M.; McKenna, K.; Shluger, A.; et al. Grain boundary-driven leakage path formation in HfO2 dielectrics. Solid-State Electron. 2011, 65–66, 146–150. [Google Scholar] [CrossRef]
- Mudinepalli, V.R.; Feng, L.; Lin, W.C.; Murty, B.S. Effect of grain size on dielectric and ferroelectric properties of nanostructured Ba0.8Sr0.2TiO3 ceramics. J. Adv. Ceram. 2015, 4, 46–53. [Google Scholar] [CrossRef]
- Lee, S.Y.; Tseng, T.Y. Electrical and dielectric behavior of MgO doped Ba0.7Sr0.3TiO3 thin films on Al2O3 substrate. Appl. Phys. Lett. 2002, 80, 1797–1799. [Google Scholar] [CrossRef]
- Li, J.; Sha, N.; Zhao, Z. Effect of annealing atmosphere on the ferroelectric properties of inkjet printed BiFeO3 thin films. Appl. Surf. Sci. 2018, 454, 233–238. [Google Scholar] [CrossRef]
- Yousfi, S.; El Marssi, M.; Bouyanfif, H. Impedance spectroscopy and conduction mechanism of a BiFe0.95Mn0.05O3 thin film. Thin Solid Film. 2021, 724, 138616. [Google Scholar] [CrossRef]
- Tsurumaki, A.; Yamada, H.; Sawa, A. Impact of Bi deficiencies on ferroelectric resistive switching characteristics observed at p-type schottky-like Pt/Bi1-δFeO3 interfaces. Adv. Funct. Mater. 2012, 22, 1040–1047. [Google Scholar] [CrossRef]
- Qiao, H.; Kwon, O.; Kim, Y. Electrostatic effect on off-field ferroelectric hysteresis loop in piezoresponse force microscopy. Appl. Phys. Lett. 2020, 116, 172901. [Google Scholar] [CrossRef]
- Jiang, J.; Bitla, Y.; Huang, C.W.; Do, T.H.; Liu, H.J.; Hsieh, Y.H.; Ma, C.H.; Jang, C.Y.; Lai, Y.H.; Chiu, P.W.; et al. Flexible ferroelectric element based on van der Waals heteroepitaxy. Sci. Adv. 2017, 3, e1700121. [Google Scholar] [CrossRef]
- Fujino, S.; Murakami, M.; Anbusathaiah, V.; Lim, S.-H.; Nagarajan, V.; Fennie, C.J.; Wuttig, M.; Salamanca-Riba, L.; Takeuchi, I. Giant Ferroelectric Polarization and Piezoelectricity in Sm-Doped Epitaxial BiFeO3 Thin Films. Appl. Phys. Lett. 2008, 92, 202904. [Google Scholar] [CrossRef]
- Chen, J.; Tang, Z.; Zhao, S. Giant Magnetoelectric Coupling Effect in Lead-Free Perovskite BiFeO3/Na0.5Bi4.5Ti4O15 Composite Films. J. Alloys Compd. 2017, 712, 256–262. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Chen, Y.; Zhang, Z.; Tang, Y.-L.; Smith, M.; Lindley, M.; Cao, X.; Hopkinson, D.G.; Bell, A.J.; et al. Bulk Ferroelectric Heterostructures for High Temperature Lead-Free Piezoelectrics. arXiv 2023, arXiv:2307.09673. [Google Scholar]
- Tuluk, A.; van der Zwaag, S. Exploring the BiFeO3-PbTiO3-SrTiO3 Ternary System to Obtain Good Piezoelectrical Properties at Low and High Temperatures. Materials 2023, 16, 6840. [Google Scholar] [CrossRef]





| 1 Period | ||||||||||
| Sample | Total Thickness (nm) ± 2.59 nm | Individual (m/n) nm ± 2.59 nm | Crystallite Size (nm) ± 0.02 | a = b (Å) | c (Å) | c/a | V (A3) | Bi-O Bond (Å) | O-Fe-O Angle (°) | Ec (kV/cm) |
| BFO (0) | 250 | 250 | 53.78 | 5.573 | 13.838 | 2.483 | 369.86 | 1.00 | 101.00 | 295 |
| BFO/STO (0.30) | 48 | 37 nm/11 nm | 5.556 | 13.791 | 2.482 | 368.68 | 2.63 | 88.29 | 870 | |
| BFO/STO (0.32) | 98 | 73 nm/25 nm | 44.11 | 5.561 | 13.699 | 2.463 | 365.46 | 2.00 | 138.00 | 446 |
| BFO/STO (1.16) | 95 | 44 nm/51 nm | 5.569 | 13.834 | 2.484 | 371.46 | 2.25 | 90.02 | 405 | |
| 2 Periods | ||||||||||
| Sample | Total thickness(nm) ± 2.59 nm | Individual (m/n) nm ± 2.59 nm | Crystallite size (nm) ± 0.02 | a = b (Å) | c (Å) | c/a | V (A3) | Bi-O bond (Å) | O-Fe-O angle (°) | Ec (kV/cm) |
| BFO/STO (0.27) | 94 | 37 nm/10 nm | 5.586 | 13.827 | 2.475 | 373.73 | 2.54 | 89.44 | 666 | |
| BFO/STO (0.35) | 100 | 37 nm/13 nm | 5.575 | 13.819 | 2.479 | 371.96 | 2.27 | 89.38 | 458 | |
| 3 Periods | ||||||||||
| Sample | Total thickness(nm) ± 2.59 nm | Individual (m/n) nm ± 2.59 nm | Crystallite size (nm) ± 0.02 | a = b (Å) | c (Å) | c/a | V (A3) | Bi-O bond (Å) | O-Fe-O angle (°) | Ec (kV/cm) |
| BFO/STO (0.45) | 161 | 37 nm/17 nm | 5.572 | 13.738 | 2.466 | 369.44 | 1.68 | 118.50 | 238 | |
| 1 Period | |||||
| r | J (A/cm2) (−100 kV/cm) | J (A/cm2) (−400 kV/cm) | Grain size (nm) | Surface Roughness (nm) | d33 (pm/V) |
| 0 | 15.07 | 58.27 | 191.40 | 6.7 | |
| 0.30 | 1.73 | 8.64 | 161.30 | 2.7 | 55.55 ± 1.49 |
| 0.32 | 5.73 | 21.74 | 102.40 | 7.3 | 50.67 ± 0.86 |
| 1.16 | 7.87 | 29.74 | 67.47 | 5.7 | 37.45 ± 0.37 |
| 2 Periods | |||||
| r | J (A/cm2) (−100 kV/cm) | J (A/cm2) (−400 kV/cm) | Grain size (nm) | Surface Roughness (nm) | d33 (pm/V) |
| 0.27 | 4.27 | 16.53 | 137.50 | 6.4 | 50.51 ± 0.49 |
| 0.35 | 8.33 | 34.00 | 75.97 | 2.8 | 47.23 ± 0.57 |
| 0.38 | 10.13 | 40.67 | 103.50 | 50.30 ± 0.39 | |
| 0.51 | 4.67 | 16.80 | 76.58 | 4.1 | 39.52 ± 0.51 |
| 0.73 | 2.03 | 9.44 | 58.21 | 45.29 ± 0.69 | |
| 3 Periods | |||||
| r | J (A/cm2) (−100 kV/cm) | J (A/cm2) (−400 kV/cm) | Grain size (nm) | Surface Roughness (nm) | d33 (pm/V) |
| 0.45 | 6.13 | 23.47 | 143.4 | 5.4 | 52.00 ± 1.21 |
| 0.57 | 7.07 | 27.60 | 78.96 | 2.5 | 41.98 ± 0.47 |
| 0.66 | 4.53 | 19.74 | 85.42 | 2.8 | 54.18 ± 0.40 |
| System/Composition | Type of Material | Measurement Method | Reported d33 | Reference |
|---|---|---|---|---|
| [(BiFeO3)m/(SrTiO3)n]p multilayers (this work) | Multilayer thin film | PFM (local d33,eff) | 30–56 pm/V (max 55.55 pm/V) | This study |
| Stoichiometric BiFeO3 films | Thin film | PFM (d33,eff) | ~70 pm/V; 68.9 pm/V | [8] |
| Sm-doped BiFeO3 films | Epitaxial thin film | PFM | ~110 pm/V | [51] |
| BFO/STO/BFO nanolaminates | Nanolaminate heterostructure | PFM | ~331 pm/V | [34] |
| BiFeO3/Na0.5Bi4.5Ti4O15 composites | Composite thin film | PFM | ~285 pm/V | [52] |
| BiFeO3–BaTiO3 ceramics | Bulk ceramic | Berlincourt (macroscopic) | ~115 pm/V | [53] |
| BiFeO3–PbTiO3–SrTiO3 ceramics | Bulk ceramic (ternary system) | Berlincourt (macroscopic) | Up to 250 pm/V | [54] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vera Montes, J.; Flores-Ruiz, F.J.; Hernández-Gutiérrez, C.A.; Camps, E.; Campos-González, E.; Viramontes Gamboa, G.; Ramírez-Zavaleta, F.; Cardona Ramírez, D. Enhanced Piezoelectric and Ferroelectric Properties in the Lead-Free [(BiFeO3)m/(SrTiO3)n]p Multilayers by Varying the Thickness Ratio r = n/m and Periodicity p. Coatings 2025, 15, 1170. https://doi.org/10.3390/coatings15101170
Vera Montes J, Flores-Ruiz FJ, Hernández-Gutiérrez CA, Camps E, Campos-González E, Viramontes Gamboa G, Ramírez-Zavaleta F, Cardona Ramírez D. Enhanced Piezoelectric and Ferroelectric Properties in the Lead-Free [(BiFeO3)m/(SrTiO3)n]p Multilayers by Varying the Thickness Ratio r = n/m and Periodicity p. Coatings. 2025; 15(10):1170. https://doi.org/10.3390/coatings15101170
Chicago/Turabian StyleVera Montes, Jonathan, Francisco J. Flores-Ruiz, Carlos A. Hernández-Gutiérrez, Enrique Camps, Enrique Campos-González, Gonzalo Viramontes Gamboa, Fernando Ramírez-Zavaleta, and Dagoberto Cardona Ramírez. 2025. "Enhanced Piezoelectric and Ferroelectric Properties in the Lead-Free [(BiFeO3)m/(SrTiO3)n]p Multilayers by Varying the Thickness Ratio r = n/m and Periodicity p" Coatings 15, no. 10: 1170. https://doi.org/10.3390/coatings15101170
APA StyleVera Montes, J., Flores-Ruiz, F. J., Hernández-Gutiérrez, C. A., Camps, E., Campos-González, E., Viramontes Gamboa, G., Ramírez-Zavaleta, F., & Cardona Ramírez, D. (2025). Enhanced Piezoelectric and Ferroelectric Properties in the Lead-Free [(BiFeO3)m/(SrTiO3)n]p Multilayers by Varying the Thickness Ratio r = n/m and Periodicity p. Coatings, 15(10), 1170. https://doi.org/10.3390/coatings15101170







