Optimizing FDM Printing Parameters via Orthogonal Experiments and Neural Networks for Enhanced Dimensional Accuracy and Efficiency
Abstract
1. Introduction
2. Experimental Principles and Methods
2.1. Model Forming Principle
2.2. Experimental Methods and Procedures
2.3. Analysis of the Impact of Printing Process Parameters on the Quality of Printed Models
2.3.1. Orthogonal Experimental Design
2.3.2. Determining Optimal Printing Process Parameters Using the Extreme Difference Method
3. Analysis of Factors Affecting Printed Model Quality and Physical Comparison of Different Parameters
3.1. Building a BP Neural Network
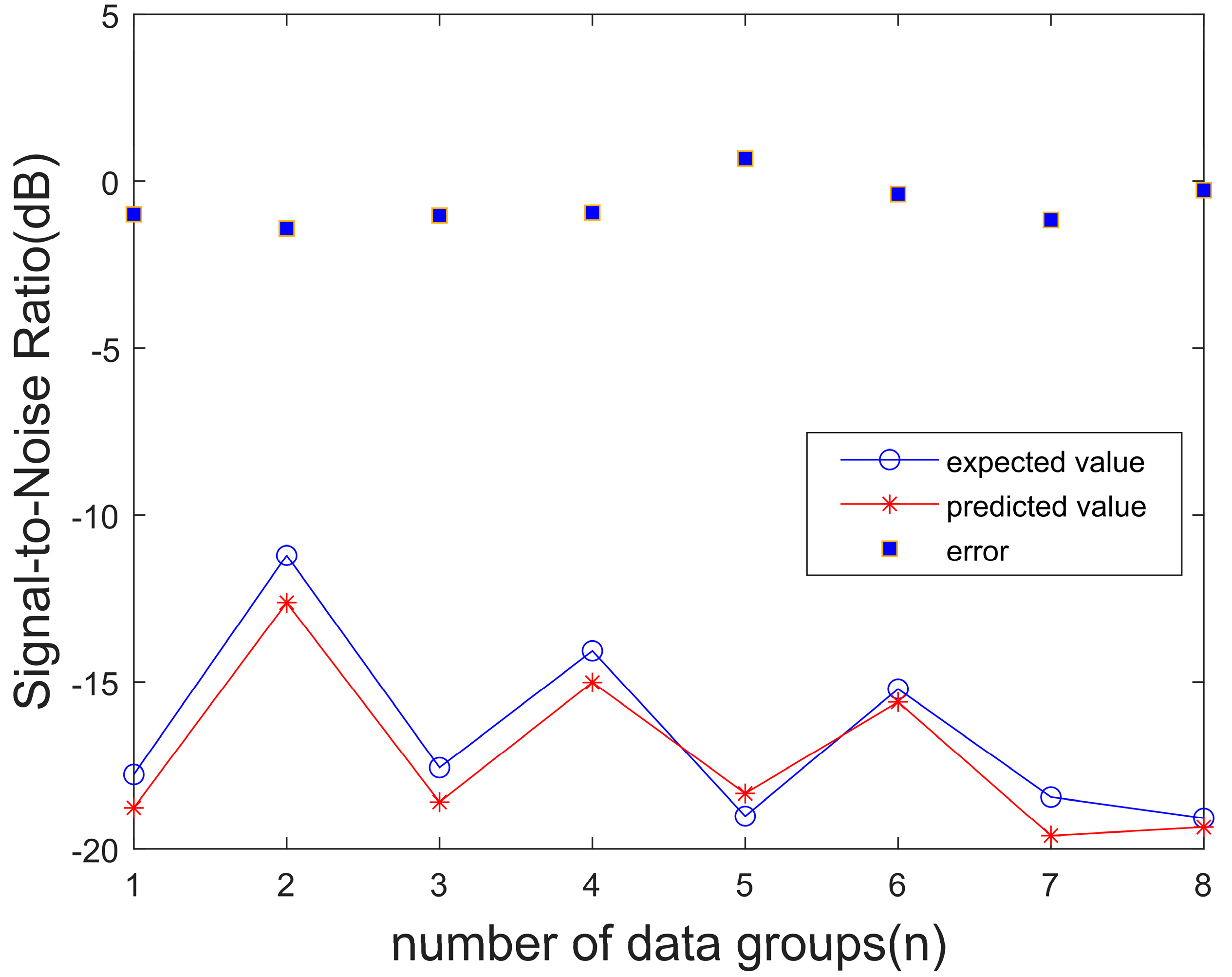
3.2. BP Neural Network Prediction Verification
3.3. Physical Comparison of Different Parameters
4. Results and Discussion
5. Conclusions
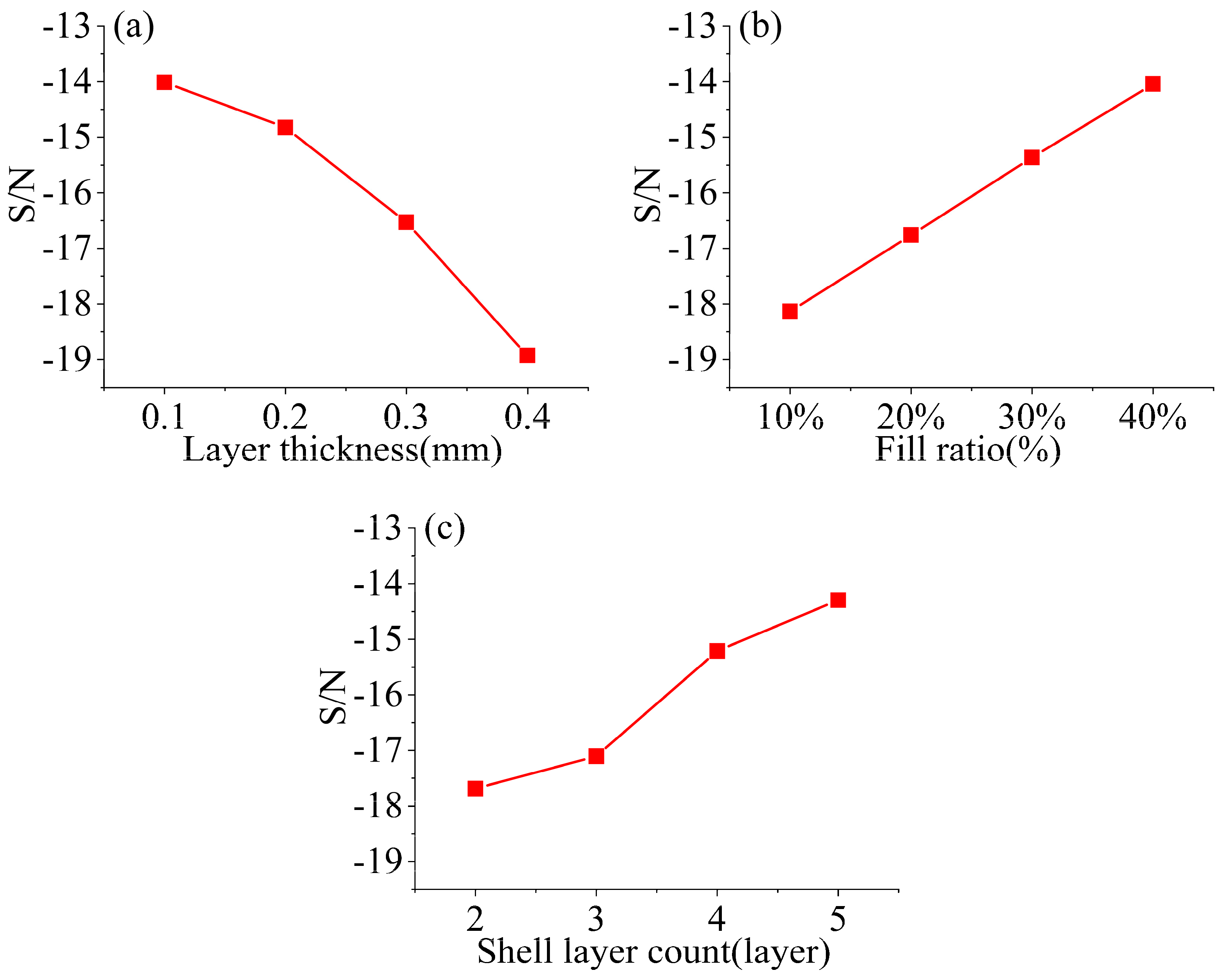
- Layer thickness exerts the most significant impact on printing time, followed by infill density and shell layers. Testing revealed that a 0.1 mm layer thickness combined with 40% infill density and a 5-layer shell structure effectively reduces volumetric error while enhancing surface quality, constituting the optimal parameter combination for achieving the best printing results.
- Under optimized parameters, both volumetric error rate and signal-to-noise ratio were significantly reduced, thereby improving the geometric accuracy and structural consistency of printed parts.
- The BP neural network-based prediction model demonstrated high accuracy, with mean absolute percentage errors for volume error and signal-to-noise ratio below 5.41% and 5.58%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Silveira, Z.D.C.; Freitas, M.S.; Inforçatti Neto, P.; Noritomi, P.Y.; da Silva, J.V.L. Design development and functional validation of an interchangeable head based on mini screw extrusion applied in an experimental desktop 3-D printer. Int. J. Rapid Manuf. 2014, 4, 49–65. [Google Scholar] [CrossRef]
- Zhou, H.M.; Wang, Z.Y. Distance-Field-Based Layered Manufacturing of FGM Objects. In Proceedings of the 2nd Annual International Conference on Advanced Material Engineering (AME 2016), Wuhan, China, 15–17 April 2016; Volume 52, pp. 694–699. [Google Scholar]
- Xiao, X.; Joshi, S. Automatic toolpath generation for heterogeneous objects manufactured by directed energy deposition additive manufacturing process. J. Manuf. Sci. Eng. 2018, 140, 071005. [Google Scholar] [CrossRef]
- Mei, S.M.; Zhang, M.Y.; Li, Z.W.; He, B.G.; Song, J.Q. Forming quality evaluation of 3D printed lines and layers with cement-based materials under different process parameters. Rapid Prototyp. J. 2025, 31, 1567–1580. [Google Scholar] [CrossRef]
- Lu, S.W.; Zhang, B.N.; Wang, Y.Z.; Bai, J.C.; Yang, C.C.; Sun, C.N.; Li, D.C. Sensitivity analysis of process parameters on the properties of carbon fiber reinforced polyether-ether-ketone composites in screw extrusion 3D printing. Polym. Test. 2025, 150, 108884. [Google Scholar] [CrossRef]
- Jiang, T.; Zhao, Y.; Yu, Y.; Gao, S.; Guo, B.; Wu, X.; Doumbia, B.S. Optimization Study of Digital Light Processing 3D Printing Process Parameters by Surface Response Approach. J. Mater. Eng. Perform. 2025, 1–12. [Google Scholar] [CrossRef]
- Kechagias, J.; Zaoutsos, S. Effects of 3D-printing processing parameters on FFF parts’ porosity: Outlook and trends. Mater. Manuf. Process. 2024, 39, 804–814. [Google Scholar] [CrossRef]
- Dwivedi, K.; Joshi, S.; Nair, R.; Sapre, M.S.; Jatti, V. Optimizing 3D printed diamond lattice structure and investigating the influence of process parameters on their mechanical integrity using nature-inspired machine learning algorithms. Mater. Today Commun. 2024, 38, 108233. [Google Scholar] [CrossRef]
- Ye, W.; Dou, H.; Zhang, D.; Yang, F.; Cheng, Y.; Cai, W. Effects of process parameters on mechanical properties and interface of 3D printed bamboo-inspired CCFR-PLA/TPU composites. Polym. Compos. 2024, 45, 227–242. [Google Scholar] [CrossRef]
- Mishra, A.; Kumar, R.; Sharma, A.K.; Gupta, N.K.; Somani, N. A statistical analysis on effect of process parameters on tensile, flexural, and hardness characteristics of wood–polylactic acid composites using FDM 3D printing. Int. J. Interact. Des. Manuf. 2024, 18, 1303–1315. [Google Scholar] [CrossRef]
- Kechagias, J.D.; Vidakis, N.; Petousis, M.; Mountakis, N. A multi-parametric process evaluation of the mechanical response of PLA in FFF 3D printing. Mater. Manuf. Process. 2023, 38, 941–953. [Google Scholar] [CrossRef]
- Sherif, M.; Mekhiel, S.; Elmesalamy, A.S.; Mahmoud, H. Investigation of FDM Process Parameters and their Interactions on Surface Roughness of PLA 3D Printed Parts. J. Phys. Conf. Ser. 2025, 3058, 012017. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Long, Y.; Ran, X.; Guo, Y.; Li, Y. Enhanced Mechanical Properties of Continuous Carbon Fiber-Reinforced PEEK Composites via Process Parameters Optimization and Assisted Infrared Irradiation Heating. Compos. Commun. 2025, 58, 102531. [Google Scholar] [CrossRef]
- Gupta, A.; Meshram, J.R.; Singh, M.; Francis, V.; Saini, J.S. Experimental and numerical studies on the contributions of the different geometric and process parameters on 3D printed PLA pin joints. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 379. [Google Scholar] [CrossRef]
- Hartomacıoğlu, S.; Oksuz, M.; Ekinci, A.; Ates, M. Optimization of Produced Parameters for PA6/PA6GF30 Composite Produced by 3D Printing with Novel Knitting Method. Polymers 2025, 17, 1590. [Google Scholar] [CrossRef]
- Haque, M.M.M.; Dhrubo, S.R.; Pranto, A.F.Z.; Ahmed, A.; Arefin, M.M.; Arifuzzaman, M.; Islam, M.S. Impact of Process Parameters and Material Selection on the Mechanical Performance of FDM 3D-Printed Components. Hybrid Adv. 2025, 10, 100502. [Google Scholar] [CrossRef]
- Towaiq, A.; Obaidat, S.; Mumani, A.; Ziout, A. An application of the preference selection index decision making method for parameters selection of FDM printing process. J. Eng. Res. 2025, 13, 636–642. [Google Scholar] [CrossRef]
- Tran, N.H.; Phan, N.D.M. Analyzing the impact of process parameters on surface roughness and mechanical properties in FDM 3D printing using machine learning. Int. J. Interact. Des. Manuf. 2025, 1–20. [Google Scholar] [CrossRef]
- Özdoğan, S.; Meram, A.; Çetin, M.E. Manufacturing parameters’ effects on the flexural properties of 3D-printed PLA. Mater. Test. 2025, 67, 811–820. [Google Scholar] [CrossRef]
- Vemuri, V.P.B.; Basavaraja, V.K.G.; Chinthalapudi, R.; Pappula, B. Advanced process parameter optimization for dimensional accuracy in SS 316L 3D printing using response surface methodology. Mater. Res. Express 2025, 12, 056510. [Google Scholar] [CrossRef]
- Ashok, S.; Kaji, S.G.; Sabit, A. Effect of FDM process parameters on mechanical properties of 3D-printed fabrics and yarns from polyethylene terephthalate glycol, nylon and thermoplastic polyurethane. Rapid Prototyp. J. 2025, 31, 934–949. [Google Scholar] [CrossRef]
- Kidie, F.M.; Ayaliew, T.G.; Mekonone, S.T. Optimizing 3D printing process parameters to improve surface quality and investigate the microstructural characteristics of PLA material. Int. J. Adv. Manuf. Technol. 2025, 138, 457–470. [Google Scholar] [CrossRef]
- Medibew, T.M.; Ali, A.N. Analysis and optimization of FFF process parameters to enhance the mechanical properties of 3D printed PLA products. Int. Polym. Process. 2023, 38, 61–76. [Google Scholar] [CrossRef]
- Nyiranzeyimana, G.; Mutua, J.M.; Ochuku Mbuya, T.; Mose, B.R.; Bisengimana, E. Fused deposition modelling (FDM) process parameter optimization to minimize residual stresses of 3 d printed carbon fiber nylon 12 hip joint implant. Mater. Und Werkst. 2022, 53, 1184–1199. [Google Scholar] [CrossRef]
- Olam, M. Determining of process parameters of the PLA/titanium dioxide/hydroxyapatite filament. Adv. Mater. Process. Technol. 2022, 8, 4776–4787. [Google Scholar] [CrossRef]
- Monticeli, F.M.; Neves, R.M.; Ornaghi Jr, H.L.; Almeida Jr, J.H.S. Prediction of bending properties for 3D-printed carbon fibre/epoxy composites with several processing parameters using ANN and statistical methods. Polymers 2022, 14, 3668. [Google Scholar] [CrossRef]
- Abas, M.; Habib, T.; Noor, S.; Salah, B.; Zimon, D. Parametric investigation and optimization to study the effect of process parameters on the dimensional deviation of fused deposition modeling of 3D printed parts. Polymers 2022, 14, 3667. [Google Scholar] [CrossRef]
- Morvayová, A.; Contuzzi, N.; Fabbiano, L. Multi-Attribute Decision Making: Parametric Optimization and Modeling of the FDM Manufacturing Process Using PLA/Wood Biocomposites. Materials 2024, 17, 924. [Google Scholar] [CrossRef]
- Ge, G.; Fan, X.; Jiang, X. Parametric Optimization of FDM Process for Improving Mechanical Strengths Using Taguchi Method and Response Surface Method: A Comparative Investigation. Machines 2022, 10, 750. [Google Scholar] [CrossRef]
- Lv, N.; Ouyang, X.; Qiao, Y. Adaptive layering algorithm for FDM-3D printing based on optimal volume error. Micromachines 2022, 13, 836. [Google Scholar] [CrossRef]
- Wang, B.; Yang, R.; Li, P.; Li, Q.; Yu, H.; Li, Z. Design of Quality Gain-Loss Function with the Cubic Term Consideration for Larger-the-Better Characteristic and Smaller-the-Better Characteristic. Mathematics 2025, 13, 777. [Google Scholar] [CrossRef]
- Mohammadiun, H.; Mohammadiun, M.; Parvaneh, V. Investigation of the inverse problem in inclined lid-driven cavity with non-uniform heating on both side walls using the Levenberg-Marquardt algorithm. Case Stud. Therm. Eng. 2025, 69, 106051. [Google Scholar]
- Cicek, U.I.; Johnson, A.A. Multi-objective optimization of FDM process parameters for 3D-printed polycarbonate using Taguchi-based Gray Relational Analysis. Int. J. Adv. Manuf. Technol. 2025, 137, 3709–3725. [Google Scholar] [CrossRef]
- Liu, C.H.; Li, H.; Yu, C.L.; Liao, X.R.; Liu, X.J.; Sun, J.Z.; Yu, M. Balanced optimization of dimensional accuracy and printing efficiency in FDM based on data-driven modeling. Addit. Manuf. Front. 2025, 4, 200220. [Google Scholar] [CrossRef]


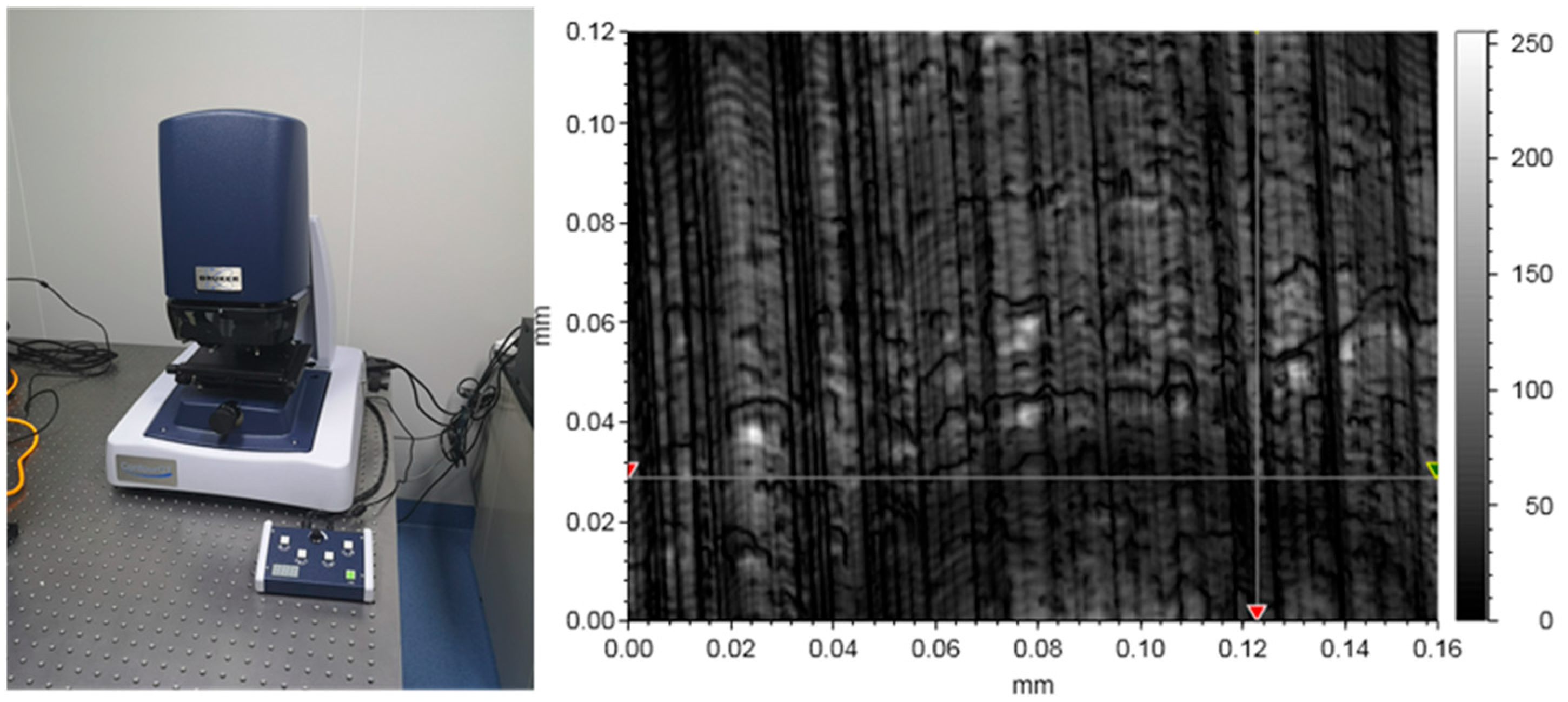




| PARAMETER NAME | LEVEL |
|---|---|
| LAYER THICKNES (MM) | 0.1, 0.2, 0.3, 0.4 |
| FILLING RATIO (%) | 10%, 20%, 30%, 40% |
| SHELL LAYERS (LAYER) | 2, 3, 4, 5 |
| Serial Number | Layer Thickness (mm) | Filling Ratio (%) | Shell Layers (Layer) |
|---|---|---|---|
| 1 | 0.1 | 10% | 2 |
| 2 | 0.2 | 20% | 3 |
| 3 | 0.3 | 30% | 4 |
| 4 | 0.4 | 40% | 5 |
| Serial Number | Layer Thickness (MM) | Filling Ratio (%) | Shell Layers | Number of Measurements (n) | Volumetric Error Rate (%) | S/N |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 6 | 7.896 ± 0.336 | −17.949 ± 0.275 |
| 2 | 1 | 2 | 2 | 6 | 6.471 ± 0.341 | −16.219 ± 0.226 |
| 3 | 1 | 3 | 3 | 6 | 4.062 ± 0.329 | −12.195 ± 0.244 |
| 4 | 1 | 4 | 4 | 6 | 3.062 ± 0.321 | −9.719 ± 0.242 |
| 5 | 2 | 1 | 2 | 6 | 7.843 ± 0.326 | −17.889 ± 0.343 |
| 6 | 2 | 2 | 1 | 6 | 6.613 ± 0.341 | −16.408 ± 0.234 |
| 7 | 2 | 3 | 4 | 6 | 4.929 ± 0.328 | −13.855 ± 0.366 |
| 8 | 2 | 4 | 3 | 6 | 3.609 ± 0.320 | −11.148 ± 0.391 |
| 9 | 3 | 1 | 3 | 6 | 7.843 ± 0.306 | −17.889 ± 0.327 |
| 10 | 3 | 2 | 4 | 6 | 5.492 ± 0.329 | −14.795 ± 0.347 |
| 11 | 3 | 3 | 1 | 6 | 7.272 ± 0.312 | −17.259 ± 0.298 |
| 12 | 3 | 4 | 2 | 6 | 6.432 ± 0.320 | −16.167 ± 0.394 |
| 13 | 4 | 1 | 4 | 6 | 8.716 ± 0.320 | −18.806 ± 0.394 |
| 14 | 4 | 2 | 3 | 6 | 9.572 ± 0.300 | −19.620 ± 0.302 |
| 15 | 4 | 3 | 2 | 6 | 8.079 ± 0.291 | −18.147 ± 0.275 |
| 16 | 4 | 4 | 1 | 6 | 9.057 ± 0.311 | −19.139 ± 0.356 |
| Level Printing Process Parameters | Layer Thickness (MM) | Filling Ratio (%) | Shell Layers |
|---|---|---|---|
| K1 | −56.082 | −72.533 | −70.755 |
| K2 | −59.30 | −67.042 | −68.422 |
| K3 | −66.11 | −61.456 | −60.852 |
| K4 | −75.712 | −56.173 | −57.175 |
| K1 | −14.021 | −18.133 | −17.689 |
| K2 | −14.825 | −16.761 | −17.106 |
| K3 | −16.528 | −15.364 | −15.213 |
| K4 | −18.928 | −14.043 | −14.293 |
| R | 4.907 | 4.09 | 3.396 |
| Impact ranking | 1 | 2 | 3 |
| Serial Number | Layer Thickness (MM) | Filling Ratio (%) | Shell Layers | Volumetric Error Rate (%) | S/N |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 7.064 | −16.741 |
| 2 | 1 | 3 | 4 | 3.528 | −10.532 |
| 3 | 2 | 1 | 1 | 6.178 | −15.429 |
| 4 | 2 | 3 | 3 | 3.694 | −11.072 |
| 5 | 3 | 1 | 4 | 8.809 | −19.024 |
| 6 | 3 | 3 | 2 | 5.601 | −15.213 |
| 7 | 4 | 1 | 3 | 8.526 | −18.449 |
| 8 | 4 | 3 | 1 | 8.900 | −19.082 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Zhang, Y.; Hu, W.; Wu, C.; Yang, Z.; Duan, G. Optimizing FDM Printing Parameters via Orthogonal Experiments and Neural Networks for Enhanced Dimensional Accuracy and Efficiency. Coatings 2025, 15, 1117. https://doi.org/10.3390/coatings15101117
Wu J, Zhang Y, Hu W, Wu C, Yang Z, Duan G. Optimizing FDM Printing Parameters via Orthogonal Experiments and Neural Networks for Enhanced Dimensional Accuracy and Efficiency. Coatings. 2025; 15(10):1117. https://doi.org/10.3390/coatings15101117
Chicago/Turabian StyleWu, Jinxing, Yi Zhang, Wenhao Hu, Changcheng Wu, Zuode Yang, and Guangyi Duan. 2025. "Optimizing FDM Printing Parameters via Orthogonal Experiments and Neural Networks for Enhanced Dimensional Accuracy and Efficiency" Coatings 15, no. 10: 1117. https://doi.org/10.3390/coatings15101117
APA StyleWu, J., Zhang, Y., Hu, W., Wu, C., Yang, Z., & Duan, G. (2025). Optimizing FDM Printing Parameters via Orthogonal Experiments and Neural Networks for Enhanced Dimensional Accuracy and Efficiency. Coatings, 15(10), 1117. https://doi.org/10.3390/coatings15101117





