A New Method for Determining Necking of Sheet Metal Based on Main Strain Topography
Abstract
1. Introduction
- Time-based criteria are based on the characteristics of the change in a physical quantity over time to determine the necking of the sheet, such as strain rate criteria, strain path criteria, etc. These criteria are based on the selection of several stages in the sheet and the comparison of the changes in stress or strain at these stages. These methods are highly sensitive, but selecting a large number of stage points and processing the data for comparison are not only complex and time-consuming, but they also neglect the distance between points and cut the continuity of the sheet and data, which will cause certain errors.
- Position-based criteria are based on a physical quantity on the change in position characteristics to determine sheet necking, such as ISO, the flat valley method and surface curvature. In this type of criterion, the ISO criterion is used for fractures before the frame frequency part of the data for secondary fitting, taking the maximum value as the limit strain. This approach is very controversial because necking failure occurs prior to fracture, but there is no clear boundary between the two. Although fitting the value with the fracture frame frequency data ensures that the sheet does not fracture, it is not reasonable and is a questionable method to determine the necking failure of the sheet. With the exception of the ISO guidelines, the rest of the position-dependent guidelines are based on the occurrence of depressions on the surface form of the sheet to determine necking; these methods are physically meaningful, but are poorly sensitive and only applicable to softer materials where necking is evident.
- Time- and position-related methods: These methods are both time- and position-related and combine the advantages of both time and position judgment criteria, and the results are more reliable. The above three types of judgment criteria have their own advantages and disadvantages, but they have a single function, can only determine the forming limit of the sheet under specific circumstances, and cannot describe the strain distribution, strain change or sheet fracture location of a sheet during the experimental process.
2. Methods
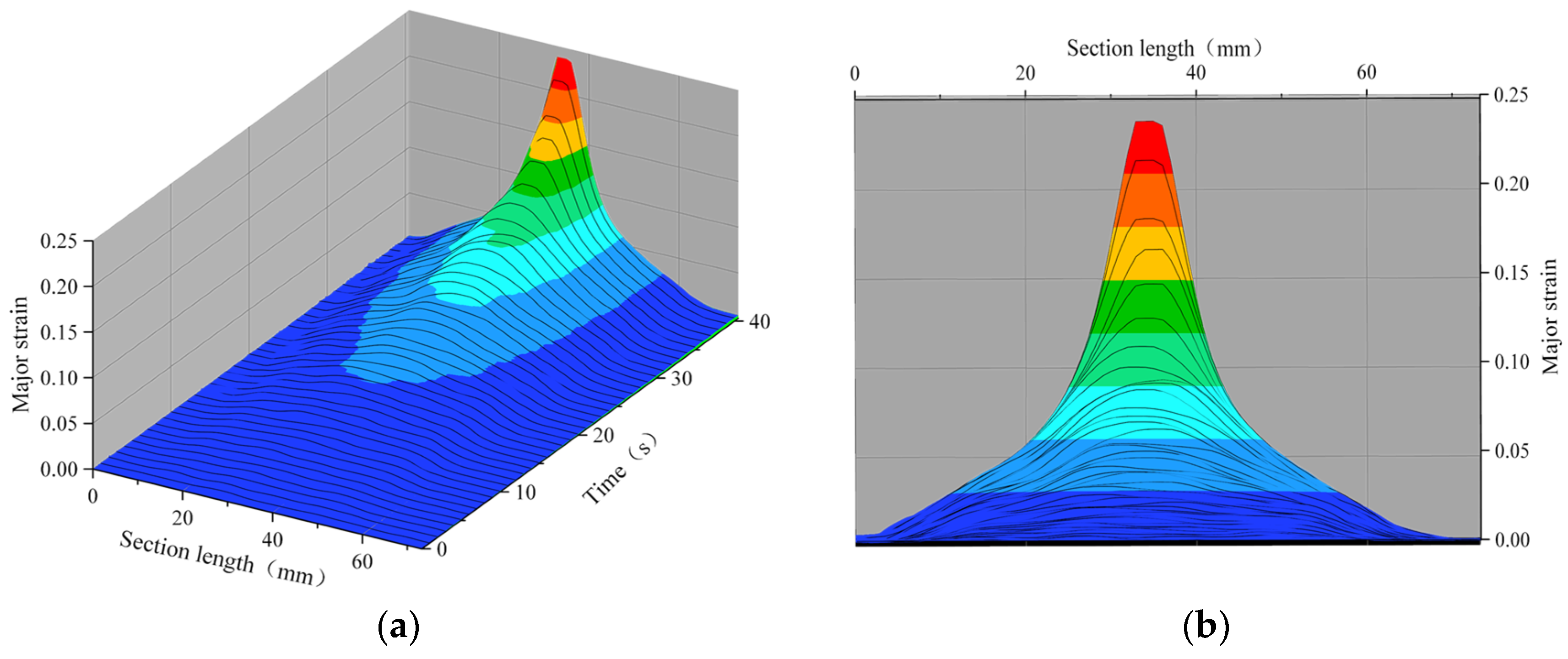
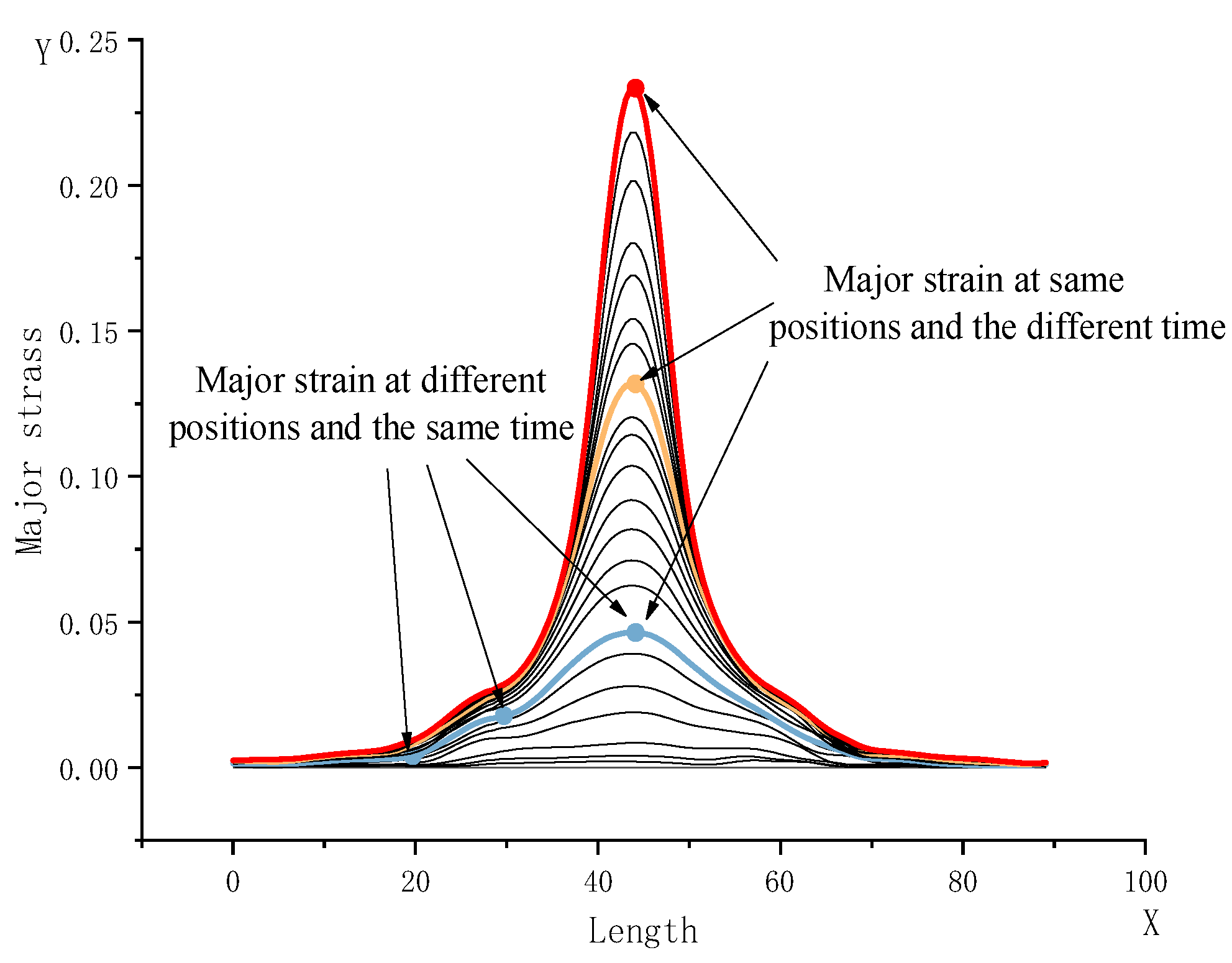
2.1. Basis of the Main-Strain-Based Shape Judgment
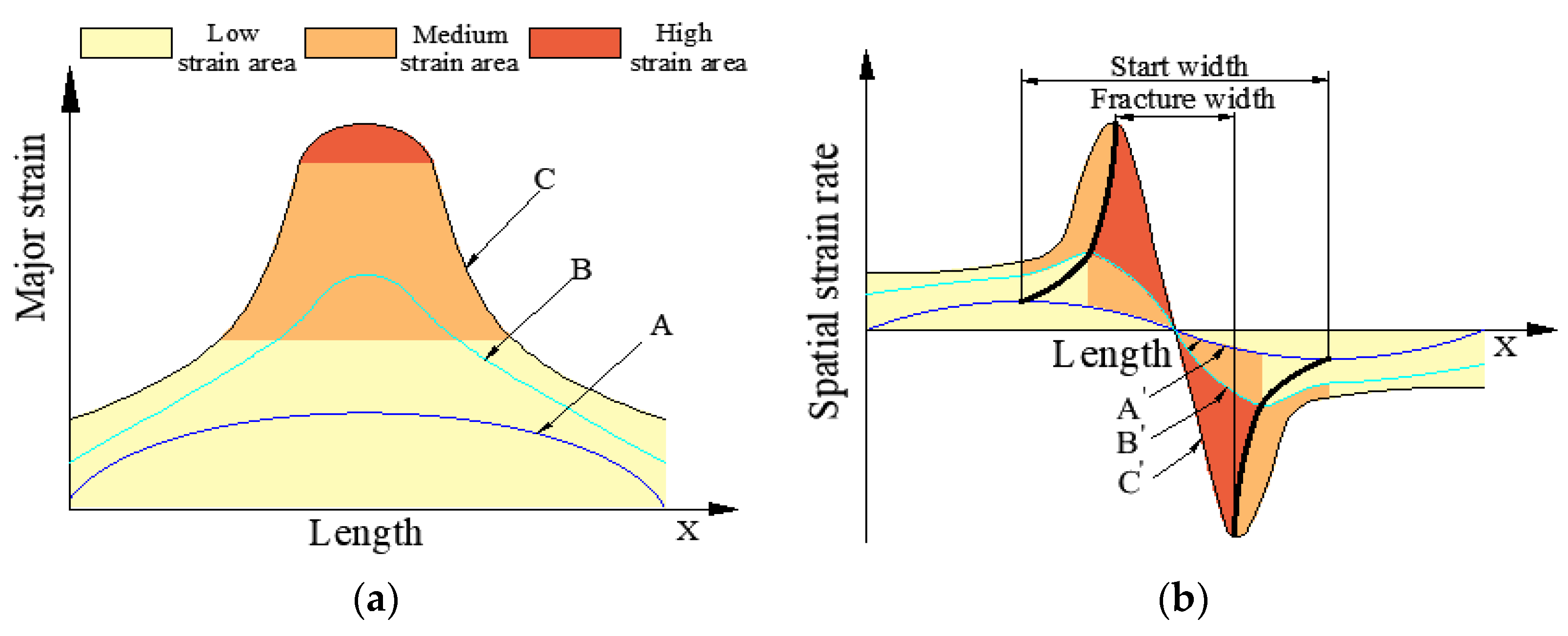
2.2. Spatial Strain Rate Judgment Criterion Based on the Main Strain Topography
- A low-strain region—all of this region is located within the dispersive instability region, where the overall degree of strain is small and the strain levels within the region are similar and less variable.
- The medium-strain region, which is partly located in the aggregated instability region and partly located in the non-aggregated instability region and has a medium overall strain level, but the strain level in this region exhibits large differences and large variations.
- High-strain region—all of this region is located within the aggregated instability region, where the degree of strain is greater overall, but the strain levels within the region are similar and less variable.
3. Experimental Procedure
3.1. Material and Method
3.2. Preparation of the Experimental Measurement System
3.3. Acquisition of Experimental Data
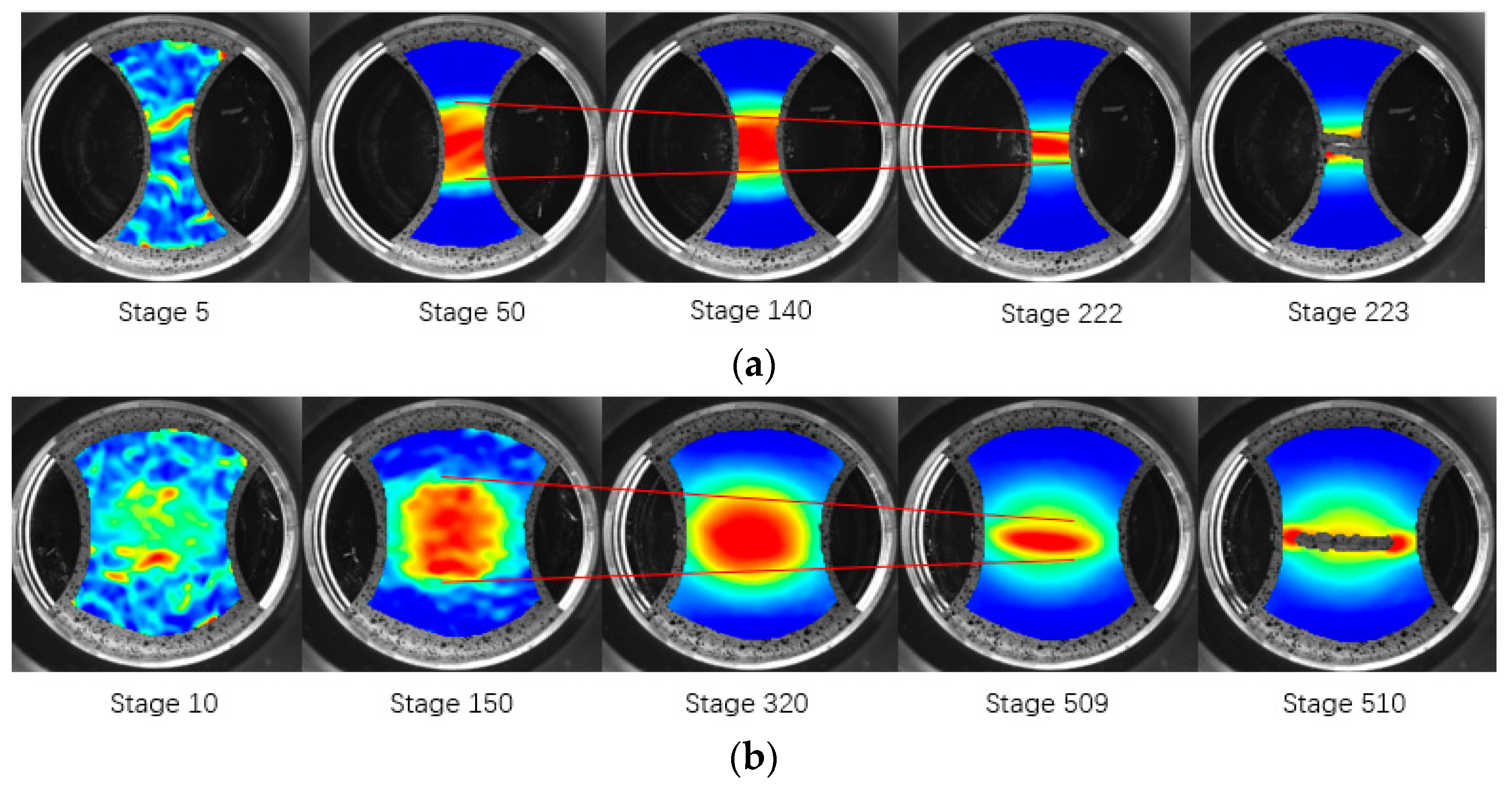
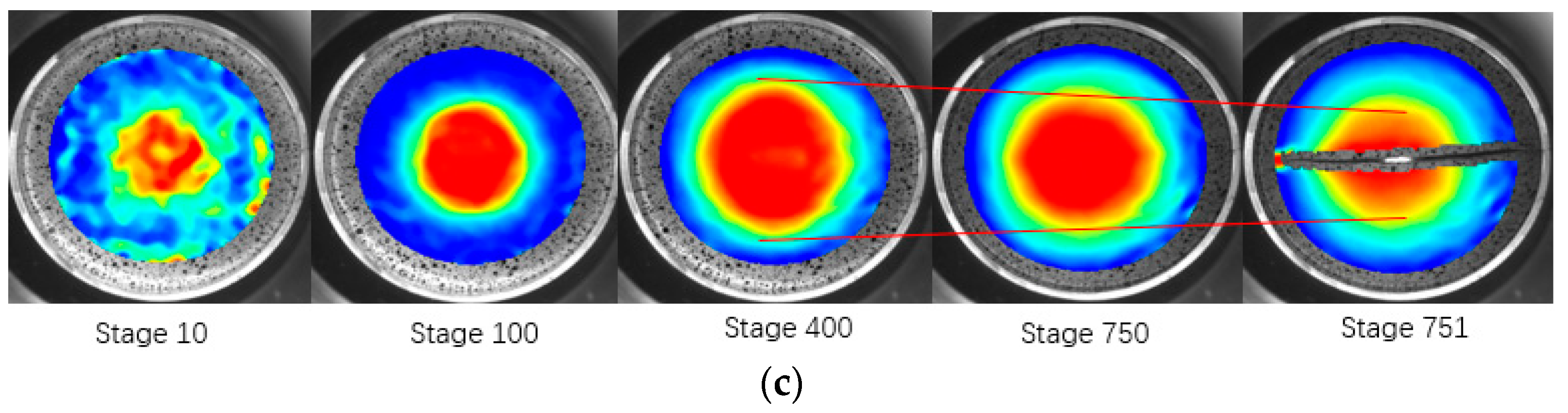
4. Results and Discussion
5. Conclusions
- (1)
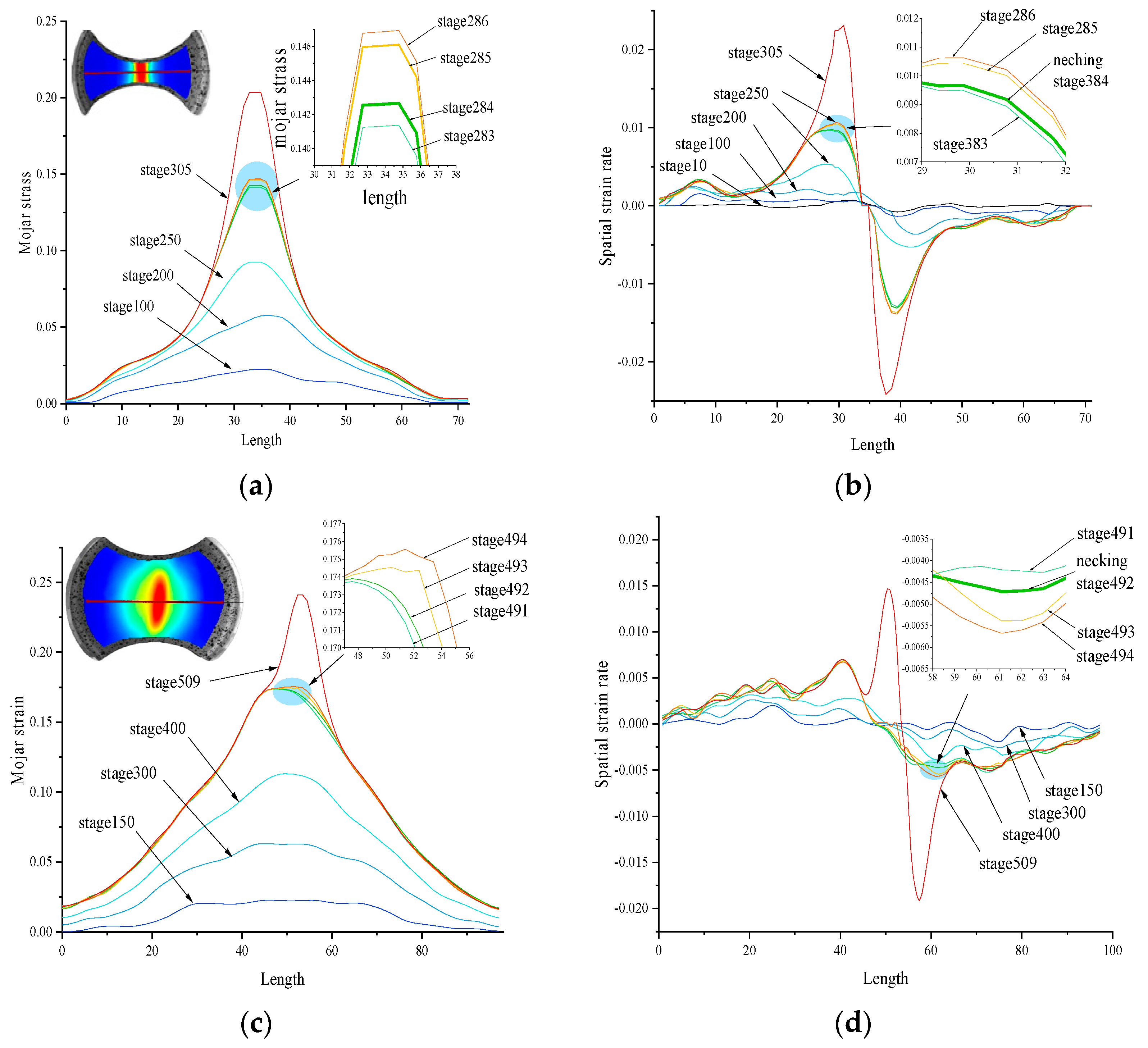
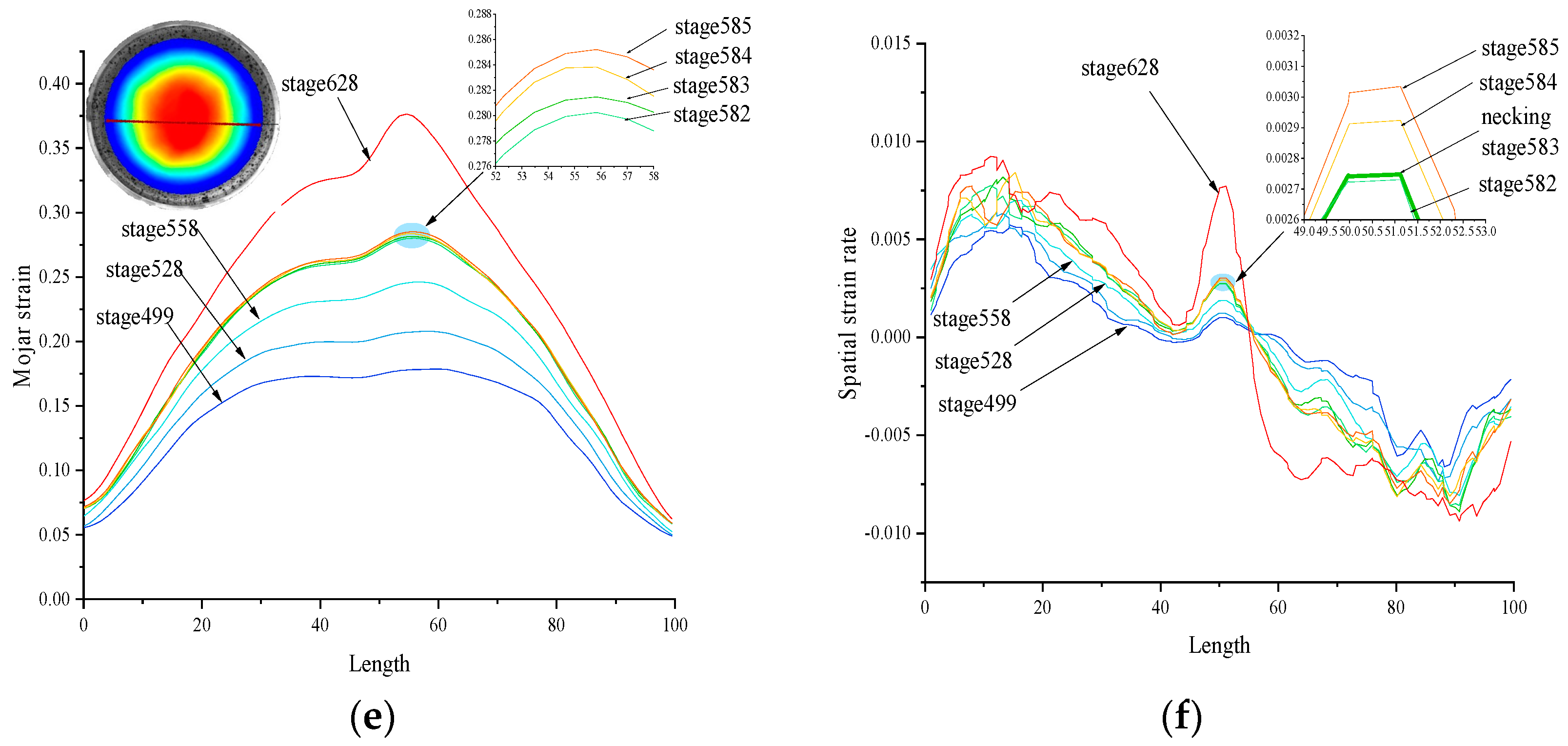
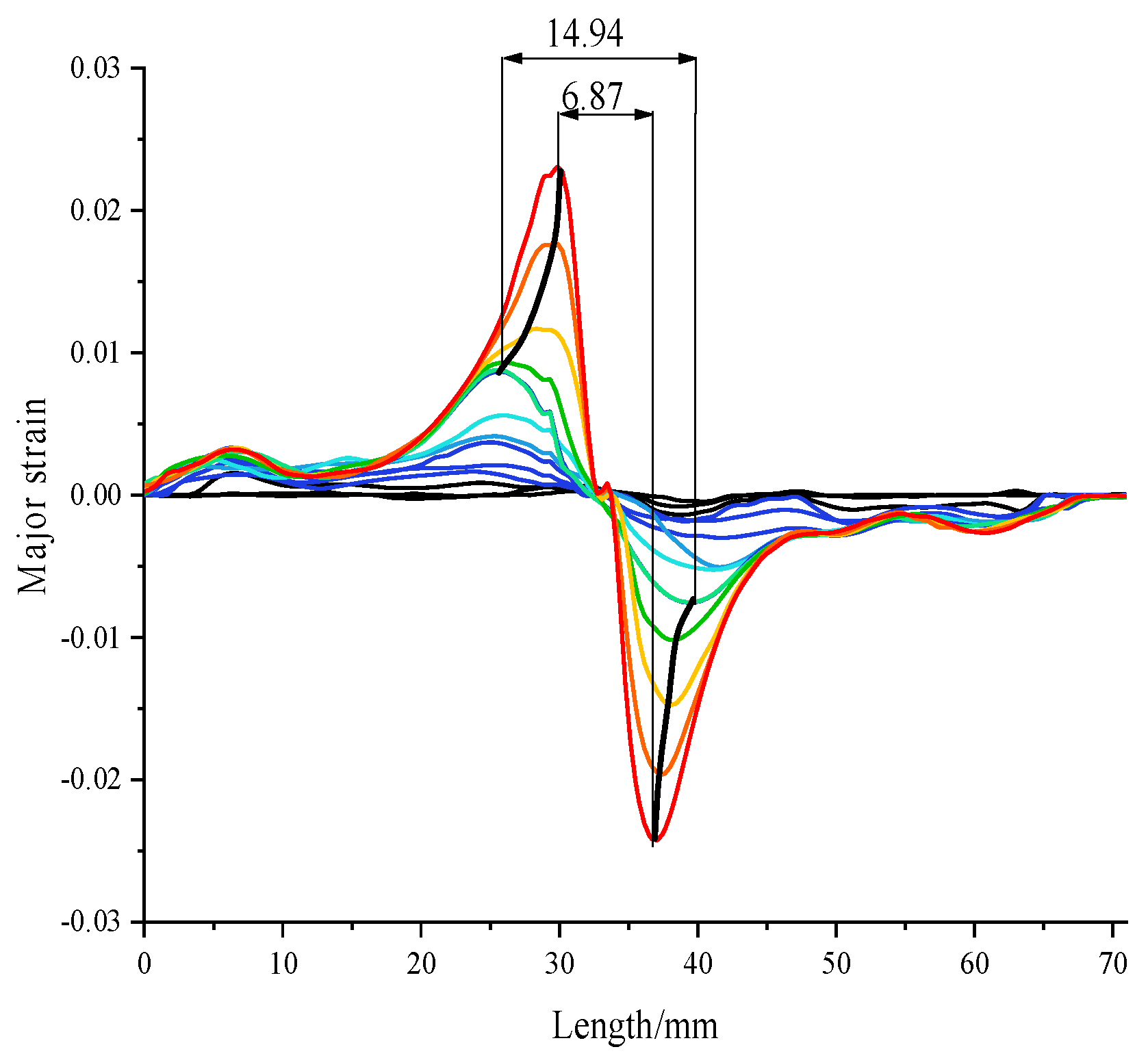
- The spatial strain rate is directly based on the strain, and can respond sensitively to the change in strain with position and time. When the spatial strain rate of the adjacent frame frequency suddenly increases, the sheet is judged to have entered the aggregated instability stage or necking area from the dispersed instability stage.
- (2)
- The sheet strain can be divided into low-, medium- and high-strain zones according to the change in spatial strain rate after the emergence of the aggregated instability region. In the low-strain zone, the strain is not only small but also increases weakly or even remains unchanged after entering the dispersive instability phase. The medium-strain zone is located between the high- and low-strain zones, and the strain increases monotonically and the strain difference between adjacent locations is large. The high-strain zone has the highest strain level and exhibits a monotonic increase, but the strain difference between adjacent locations is small.
- (3)
- The spatial strain rate method can depict the variation in the width of the aggregated instability region. This variation in width can be used to prove that aggregation instability is a gradual process and is not instantaneous. The width can not only depict the degree of aggregation instability but also determine the fracture location in the sheet.
- (4)
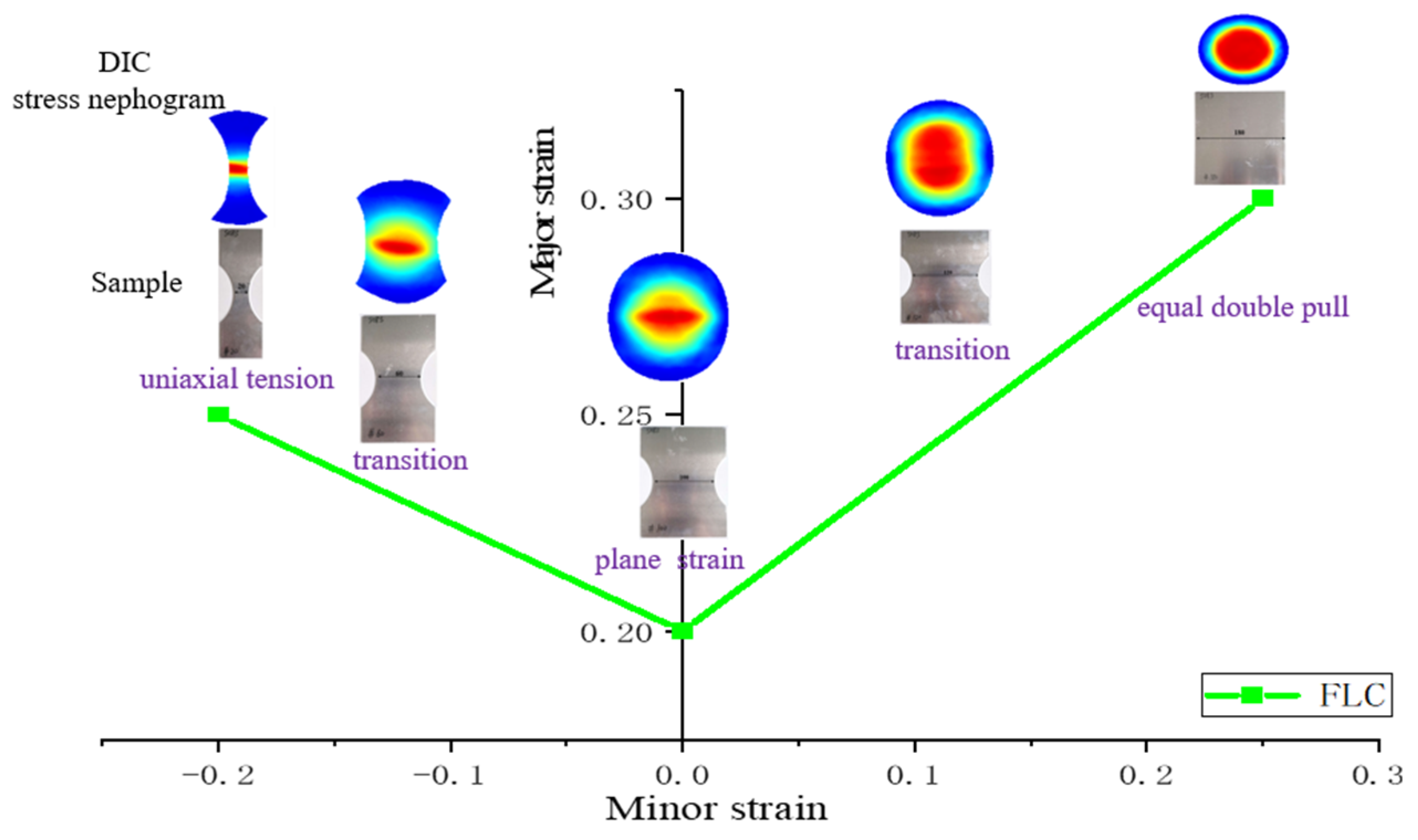
- The spatial strain rate method successfully predicted the forming limit of the sheet in the Nakazima experiment. This new method obtains results very similar to the results calculated by the T-D method and the flat valley method, and is an attractive alternative method for determining FLC.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuwabara, T.; Yoshida, K.; Narihara, K.; Takahashi, S. Anisotropic plastic deformation of extruded aluminum alloy tube under axial forces and internal pressure. Int. J. Plast. 2005, 21, 101–117. [Google Scholar] [CrossRef]
- Keeler, S.P.; Backofen, W.A. Plastic instability and fracture in sheets stretched over rigid punches. ASM Trans. Q. 1963, 56, 25–48. [Google Scholar]
- International Standard ISO 12004-2:2008; Metallic Materials Sheet and Strip Determination of Forming-Limit Curves, Part 2. Determination of Forming-Limit Curves in the Laboratory. International Organization for Standardization: Geneva, Switzerland, 2008.
- Eberle, B.; Volk, W.; Hora, P. Automatic approach in the evaluation of the experimental FLD with a full 2D approach based on a time depending method. In Numisheet 2008—Proceedings of the 7th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes; ETH: Zurich, Switzerland, 2008; pp. 279–284. Available online: https://www.researchcollection.ethz.ch/handle/20.500.11850/11331 (accessed on 1 September 2008).
- Hill, R. On discontinuous plastic states, with special reference to localized necking in thin sheets. Mech. Phys. Solids 1952, 1, 19–30. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczynski, K. Limit strains in processes of stretch-forming sheet metal. Int. Mech. Sci. 1967, 9, 609–612. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Neale, K.W. Sheet necking-II. Time-independent behaviour. In Mechanics of Sheet Metal Forming; Koistinen, D.P., Wang, N.M., Eds.; Plenum: New York, NY, USA, 1978; pp. 127–153. [Google Scholar] [CrossRef]
- Eyckens, P.; Van Bael, A.; Van Houtte, P. Marciniak-Kuczynski type modelling of the effect of through-thickness shear on the forming limits of sheet metal. Int. J. Plast. 2009, 25, 2249–2268. [Google Scholar] [CrossRef]
- Eyckens, P.; Van Bael, A.; Van Houtte, P. An extended Marciniak-Kuczynski model for anisotropic sheet subjected to monotonic strain paths with through thickness shear. Int. J. Plast. 2011, 27, 1577–1597. [Google Scholar] [CrossRef]
- Li, J.; Carsley, J.E.; Stoughton, T.B.; Hector, L.G., Jr.; Hu, S.J. Forming limit analysis for twostage forming of 5182-O aluminum sheet with intermediate annealing. Int. J. Plast. 2013, 45, 21–43. [Google Scholar] [CrossRef]
- Situ, Q.; Jain, M.; Bruhis, M. A suitable criterion for precise determination of incipient necking in sheet materials. Mater. Sci. Forum. 2006, 519–521, 111–116. [Google Scholar] [CrossRef]
- Martínez-Donaire, A.J.; Vallellano, C.; Morales, D.; García-Lomas, F.J. On the experimental detection of necking in stretch-bending tests. J. Am. Inst. Phys. Conf. Proc. 2009, 1181, 500–508. [Google Scholar] [CrossRef]
- Martínez-Donaire, A.J.; Vallellano, C.; Morales, D.; García-Lomas, F.J. Experimental detection of necking in stretch-bending conditions: A critical review and new methodology. Steel Res. Int. 2010, 81 (Suppl. S9), 785–788. Available online: https://www.researchgate.net/publication/290482917 (accessed on 2 June 2024).
- Martínez-Donaire, A.J.; García-Lomas, F.J.; Vallellano, C. New approaches to detect the onset of localised necking in sheets under through-thickness strain gradients. J. Mater. Des. 2014, 57, 135–145. [Google Scholar] [CrossRef]
- Lin, J.; Li, N.; Shao, Z.; Qian, B. Planar Test System. U.S. Patent US 20180238784 A1, 23 August 2018. Available online: https://www.freepatentsonline.com/20180238784 (accessed on 2 June 2024).
- Shao, Z. Development of a Novel Biaxial Testing System for Formability Evaluation of Sheet Metals under Hot Stamping Conditions; Imperial College London: London, UK, 2015. [Google Scholar] [CrossRef]
- Shao, Z.; Li, N.; Lin, J.; Dean, T. Formability evaluation for sheet metals under hot stamping conditions by a novel biaxial testing system and a new materials model. Int. J. Mech. Sci. 2017, 120, 149–158. [Google Scholar] [CrossRef]
- Zhang, R.; Shao, Z.; Lin, J.; Dean, T.A. Measurement and analysis of heterogeneous strain fields in uniaxial tensile tests for boron steel under hot stamping conditions. Exp. Mech. 2020, 60, 1289–1300. [Google Scholar] [CrossRef]
- Zhang, R.; Shao, Z.; Lin, J. Applications of the digital image correlation (DIC) technique for high-temperature strain measurement: A review. In Proceedings of the 4th International Conference on Advanced High Strength Steel and Press Hardening (ICHSU2018); World Scientific Publishing Co Pte Ltd.: Hefei, China, 2019; pp. 86–91. [Google Scholar] [CrossRef]
- Hotz, W.; Merklein, M.; Kuppert, A.; Friebe, H.; Klein, M. Time dependent FLC determination comparison of different algorithms to detect the onset of unstable necking before fracture. Key Eng. Mater. 2013, 549, 397–404. [Google Scholar] [CrossRef]
- Huang, L.; Shi, M. Determination of the forming limit curve using digital image correlation-comparison of different approaches to pinpoint the onset of localized necking. SAE Tech. Pap. 2017; 2017-01-0301. [Google Scholar] [CrossRef]
- Volk, W.; Hora, P. New algorithm for a robust user-independent evaluation of beginning instability for the experimental FLC determination. Int. J. Mater. Form. 2011, 4, 339–346. [Google Scholar] [CrossRef]
- Zhang, C.; Leotoing, L.; Zhao, G.; Guines, D.; Ragneau, E. A Comparative Study of Different Necking Criteria for Numerical and Experimental Prediction of FLCs. J. Mater. Eng. Perform. 2011, 20, 1036–1042. [Google Scholar] [CrossRef]
- Heidari, A.; Ghassemi, A.; Atrian, A. A Numerical and Experimental Investigation of Temperature Effects on the Formability of AA6063 Sheets Using Different Ductile Fracture Criteria. Int. J. Adv. Manuf. Technol. 2020, 106, 2595–2611. [Google Scholar] [CrossRef]
- Marrapu, B.; Barnwal, V.K.; Chakrabarty, S.; Tewari, A.; Mishra, S.K. Experimental and Numerical Analysis on Dual Phase Steel (DP780) Sheet Forming Limit and Effect of Microstructure Evolution on Formability. J. Mater. Eng. Perform. 2020, 29, 8247–8260. [Google Scholar] [CrossRef]
- Bhargava, M.; Tewari, A.; Mishra, S.K. Forming Limit Diagram of Advanced High Strength Steels (AHSS) Based on Strain-Path Diagram. Mater. Des. 2015, 85, 149–155. [Google Scholar] [CrossRef]
- Lumelskyj, D.; Lazarescu, L.; Banabic, D.; Rojek, J. Experimental and Numerical Investigations on Determination of Strain Localization in Sheet Forming. J. Phys. Conf. Ser. 2018, 1063, 012060. [Google Scholar] [CrossRef]
- Hora, P.; Berisha, B.; Gorji, M.; Manopulo, N. A Generalized Approach for the Prediction of Necking and Rupture Phenomena in the Sheet Metal Forming. IDDRG12. 2012. Available online: https://www.researchgate.net/publication/269709664 (accessed on 1 January 2012).
- Hou, Z.; Liu, Z.; Wan, M.; Wu, X.; Yang, B.; Lu, X. An Investigation on Anisotropy Behavior and Forming Limit of 5182-H111 Aluminum Alloy, ASM International. J. Mater. Eng. Perform. 2020, 11, 3745–3756. [Google Scholar] [CrossRef]
- Kong, X.; Chu, X.; Chen, C.; Wang, Y.; Liu, P.; Wang, Z. Comparative Investigation of the Experimental Determination of AA5086 FLCs under Different Necking Criteria. J. Mater. 2021, 14, 3685. [Google Scholar] [CrossRef] [PubMed]
- Fei, H.; Wan, M.; Wu, X.D. Progress of theoretical and experimental research on the limit of plate forming. J. Plast. Eng. 2006, 13, 7. [Google Scholar]
- Min, J.; Stoughton, T.B.; Carsley, J.E.; Lin, J. Compensation for process-dependent effects in the determination of localized necking limits. Int. J. Mech. Sci. 2016, 117, 115–134. [Google Scholar] [CrossRef]
- Min, J.; Stoughton, T.B.; Carsley, J.E.; Lin, J. A Method of Detecting the Onset of Localized Necking Based on Surface Geometry Measurements. Exp. Mech. 2017, 57, 521–535. [Google Scholar] [CrossRef]
- Yu, K.; Li, Q.; Wu, Y.; Guo, M.; Li, D.; Liu, C.; Zhuang, L.; Wu, P. An improved Marciniak-Kuczynski approach for predicting sheet metal formability. Int. J. Mech. Sci. 2022, 221, 107200. [Google Scholar] [CrossRef]
- Wang, Z.; Guines, D.; Chu, X.; Leotoing, L. Prediction and characterization of forming limits at necking from shear to equi-biaxial loading using the biaxial tensile testing method: Feasibility study and application to AA6061-T4. Mech. Mater. 2023, 179, 104598. [Google Scholar] [CrossRef]
- Zhang, R.; Shi, Z.; Shao, Z.; Dean, T.A.; Lin, J. A novel spatiotemporal method for determining necking and fracture strains of sheet metals. Int. J. Mech. Sci. 2020, 7, 105977. [Google Scholar] [CrossRef]
- Nakazima, K.; Kikuma, T.; Hasuka, K. Study on the formability of steel sheets. Yawata Tech. Rep. 1968, 264, 8517–8530. [Google Scholar]





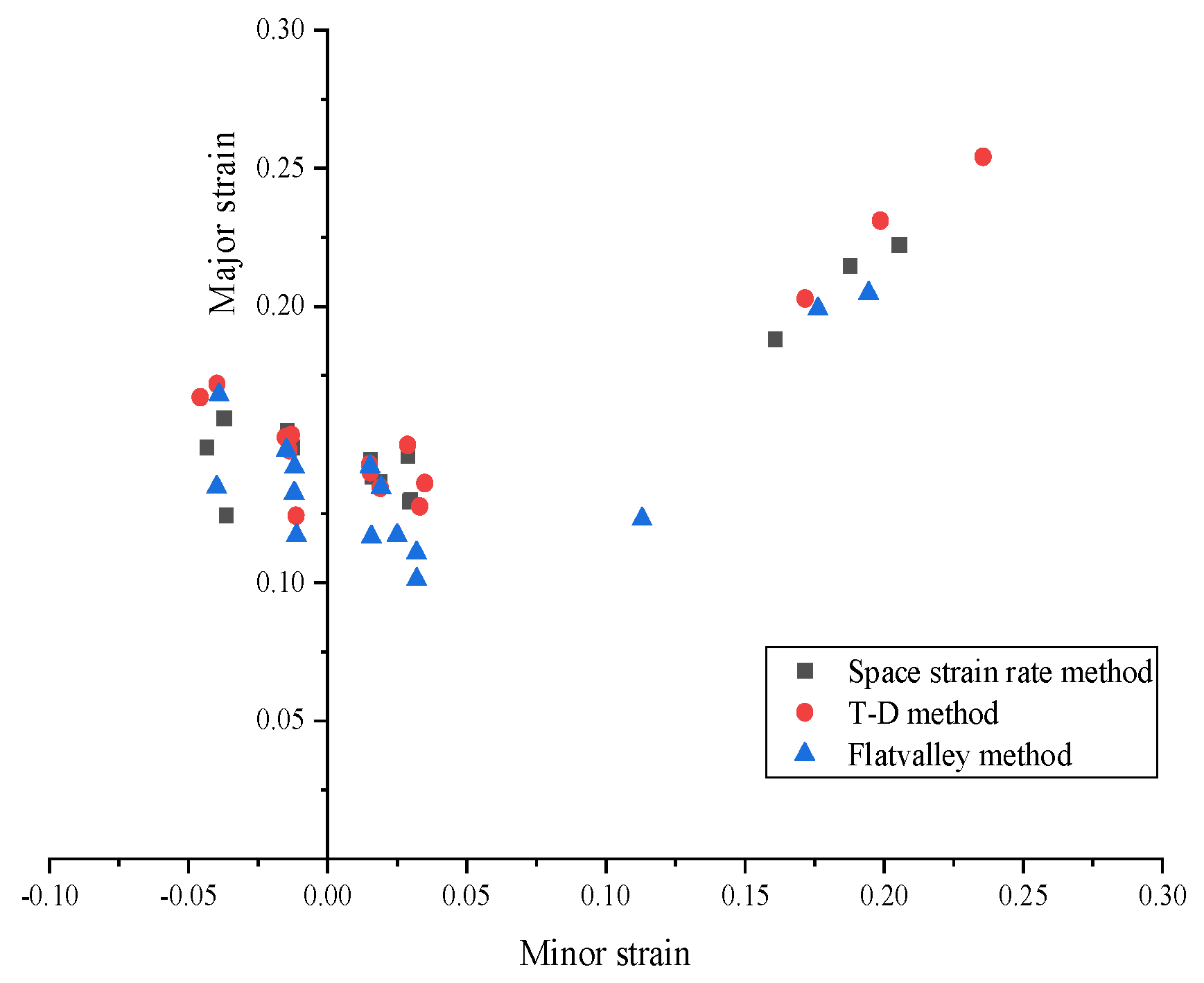
| Method | Space Strain Rate Method | T-D Method | Flat Valley Method | ||||
|---|---|---|---|---|---|---|---|
| Sheet Width | Number of Experiments | Minor Strain | Major Strain | Minor Strain | Major Strain | Minor Strain | Major Strain |
| wide20 | 1 | 0.036476539 | 0.124505529 | −0.011369701 | 0.12424656 | 0.011201164 | 0.1171638 |
| 2 | −0.04345199 | 0.149014732 | −0.045819861 | 0.167106059 | 0.039860501 | 0.134659137 | |
| 3 | −0.03737116 | 0.159841732 | −0.03979905 | 0.171893834 | −0.03905048 | 0.168062695 | |
| average | 0.039099896 | 0.144453997 | −0.032329537 | 0.154415484 | 0.030037382 | 0.139961878 | |
| wide60 | 1 | −0.01434684 | 0.153256637 | −0.015213876 | 0.152603543 | −0.01483906 | 0.148081124 |
| 2 | 0.014767866 | 0.154879479 | −0.013910533 | 0.14799986 | 0.012004909 | 0.132480289 | |
| 3 | 0.012868338 | 0.149245275 | −0.01301867 | 0.153391101 | 0.011847663 | 0.141863957 | |
| average | 0.013994348 | 0.152460463 | −0.014047693 | 0.151331501 | 0.012897211 | 0.140808457 | |
| wide100 | 1 | 0.015135523 | 0.144302924 | 0.015028344 | 0.142782338 | 0.015228287 | 0.142116574 |
| 2 | 0.015835353 | 0.138690188 | 0.015312571 | 0.139975283 | 0.015674182 | 0.116654937 | |
| 3 | 0.018578544 | 0.136522113 | 0.01895961 | 0.134384487 | 0.019170094 | 0.134453057 | |
| average | 0.016516473 | 0.139838408 | 0.016433508 | 0.139047369 | 0.016690854 | 0.131074856 | |
| wide120 | 1 | 0.029633455 | 0.129931186 | 0.033115859 | 0.127610476 | 0.031916686 | 0.110900275 |
| 2 | 0.029549416 | 0.1294918 | 0.034916783 | 0.13608088 | 0.032045297 | 0.101176126 | |
| 3 | 0.028705891 | 0.146314005 | 0.028729853 | 0.149846722 | 0.02495014 | 0.117210857 | |
| average | 0.029296254 | 0.135245664 | 0.032254165 | 0.137846026 | 0.029637375 | 0.109762419 | |
| wide180 | 1 | 0.187692871 | 0.215057325 | 0.198686267 | 0.231029141 | 0.176226649 | 0.199157627 |
| 2 | 0.205491423 | 0.222483037 | 0.235601357 | 0.254189705 | 0.194409041 | 0.204843259 | |
| 3 | 0.160965112 | 0.188399407 | 0.17162379 | 0.202850342 | 0.113011632 | 0.123065819 | |
| average | 0.184716469 | 0.20864659 | 0.201970472 | 0.229356396 | 0.161215774 | 0.175688902 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, L.; Yang, Y.; Hou, B.; Gu, W.; Zhao, H.; Feng, Y.; Hang, Z. A New Method for Determining Necking of Sheet Metal Based on Main Strain Topography. Coatings 2024, 14, 765. https://doi.org/10.3390/coatings14060765
Shi L, Yang Y, Hou B, Gu W, Zhao H, Feng Y, Hang Z. A New Method for Determining Necking of Sheet Metal Based on Main Strain Topography. Coatings. 2024; 14(6):765. https://doi.org/10.3390/coatings14060765
Chicago/Turabian StyleShi, Liqiu, Yingjie Yang, Bo Hou, Weifang Gu, Haitao Zhao, Yan Feng, and Zhouming Hang. 2024. "A New Method for Determining Necking of Sheet Metal Based on Main Strain Topography" Coatings 14, no. 6: 765. https://doi.org/10.3390/coatings14060765
APA StyleShi, L., Yang, Y., Hou, B., Gu, W., Zhao, H., Feng, Y., & Hang, Z. (2024). A New Method for Determining Necking of Sheet Metal Based on Main Strain Topography. Coatings, 14(6), 765. https://doi.org/10.3390/coatings14060765









