An Image Classification Method of Unbalanced Ship Coating Defects Based on DCCVAE-ACWGAN-GP
Abstract
1. Introduction
- At present, the transformation and upgrading of the shipbuilding industry driven by intelligent manufacturing is in its infancy. Aimed at the problems of over-reliance on domain expert knowledge and low intelligence level in the current stage of ship coating defect recognition, this paper proposes an intelligent coating defect recognition algorithm. Based on the data enhancement network model, painting defect images are generated, and the “end-to-end” recognition model is trained.
- Traditional data augment methods cannot change the sample categories. To solve this problem, this paper first combines the ideas of DCCVAE and ACWGAN-GP at the data level, so that the network can generate high-quality, multi-category images of minor ship coating defects in accordance with the original data distribution in a more stable and controllable way.
- The standard DCCVAE encoding stage is not conducive to feature extraction by establishing a connection with class labels instead. To solve this problem, this paper only adds class labels in the decoding stage.
- To avoid the problems of gradient disappearance and model overfitting inherent in the deep generation model, this paper introduces the residual block with an attention mechanism to fully extract the important features. At the same time, the algorithm model loss function is improved from the algorithm level to prevent problems such as gradient disappearance and gradient explosion to some extent. Then, the balanced dataset is used as the input of DCNN deep neural network, and the parameters are globally tuned by “layer-by-layer pre-training + fine-tuning” to obtain the optimal DCNN model parameters. Finally, the trained DCNN neural network is used to classify the coating defects in the test set, and the final classification results are obtained.
2. Proposed Methodology
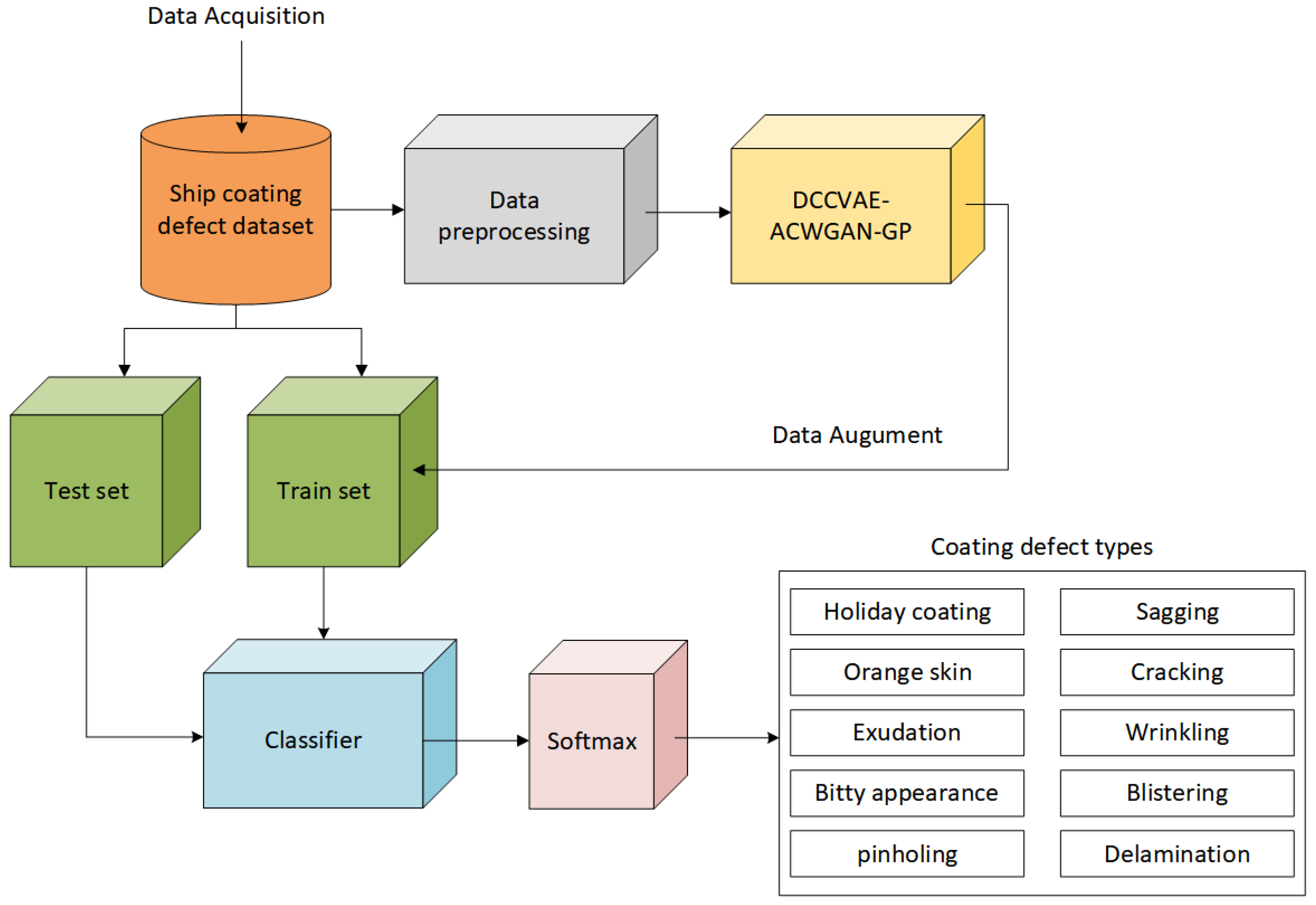
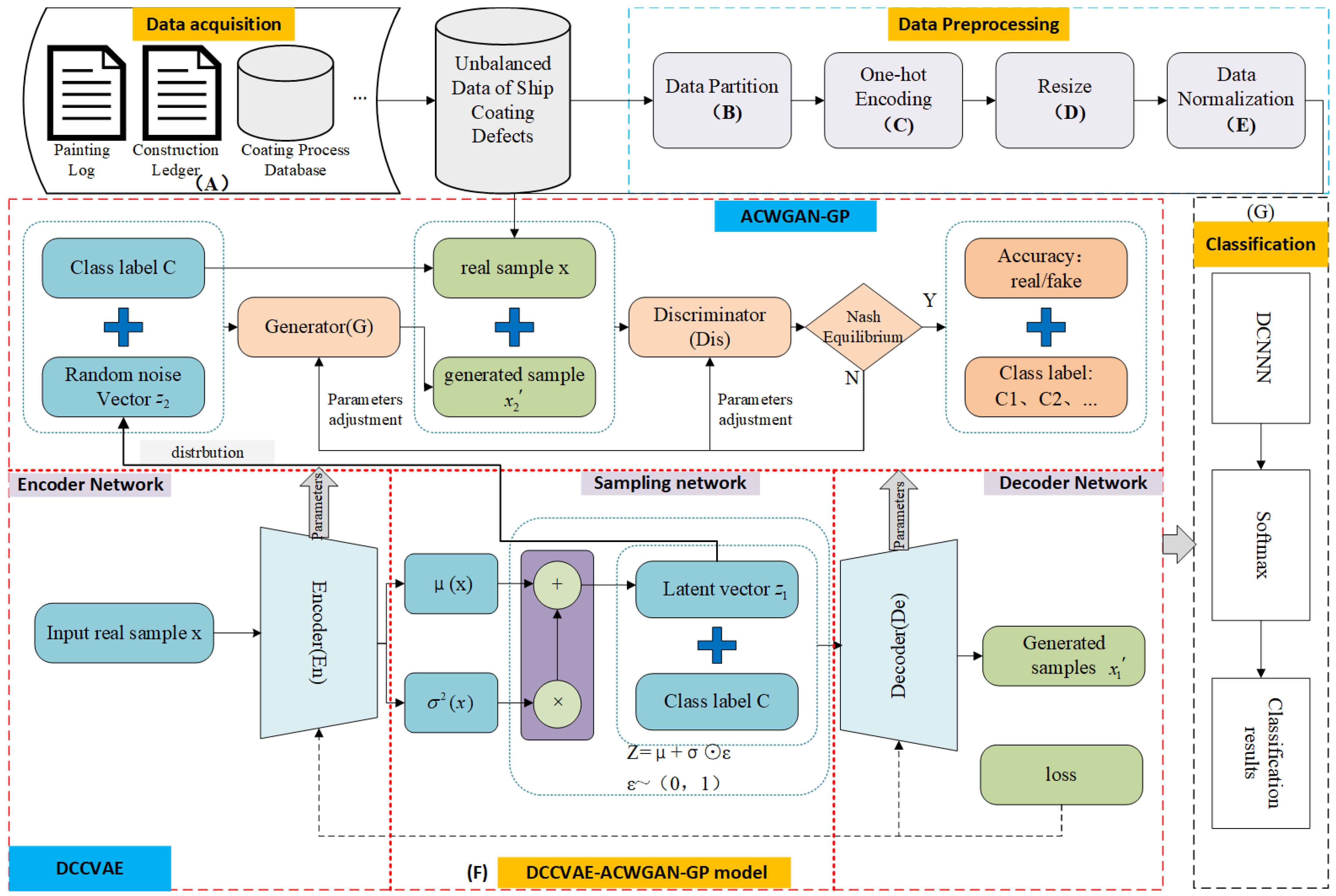
2.1. The Overall Framework of the Proposed Model
2.2. The Training Process and Total Loss Function of the Proposed Model
2.2.1. The Training Process of the Proposed Algorithm
| Algorithm 1: Training process of DCCVAE-ACWGAN-GP model |
| Input: batch size m, number of categories n, learning rate α, number of iteration k, spatial dimension of the noise z Output: Initialize network parameters of different networks While i < the maximum number of iterations or model parameters converges do 1: ← mini-batch sampling randomly from the real coating defect data set For each real minority sample do 2: Obtain the feature parameter vector µ, σ ← input x to the Encoder network 3: Obtain the potential representation ← re-parameterization trick () 4: Generate specific samples ← reconstruct by the Decoder network 5: Feed real samples and generated samples into discriminator network Dis to distinguish true from false 6: Feed real samples and generated samples into the Classification network C to ensure the recognition of coating defect categories and the final classification results are tested and verified in the original dataset. 7: Optimize the loss function of DCCVAE-ACWGAN-GP model: sampling from the initial distribution N(0,1) ← obtain ς by random sampling from a Gaussian distribution 8: Update network parameters: End For End While Print(New structure) End |
2.2.2. Loss Function
2.3. The Structure Design of the Proposed Model
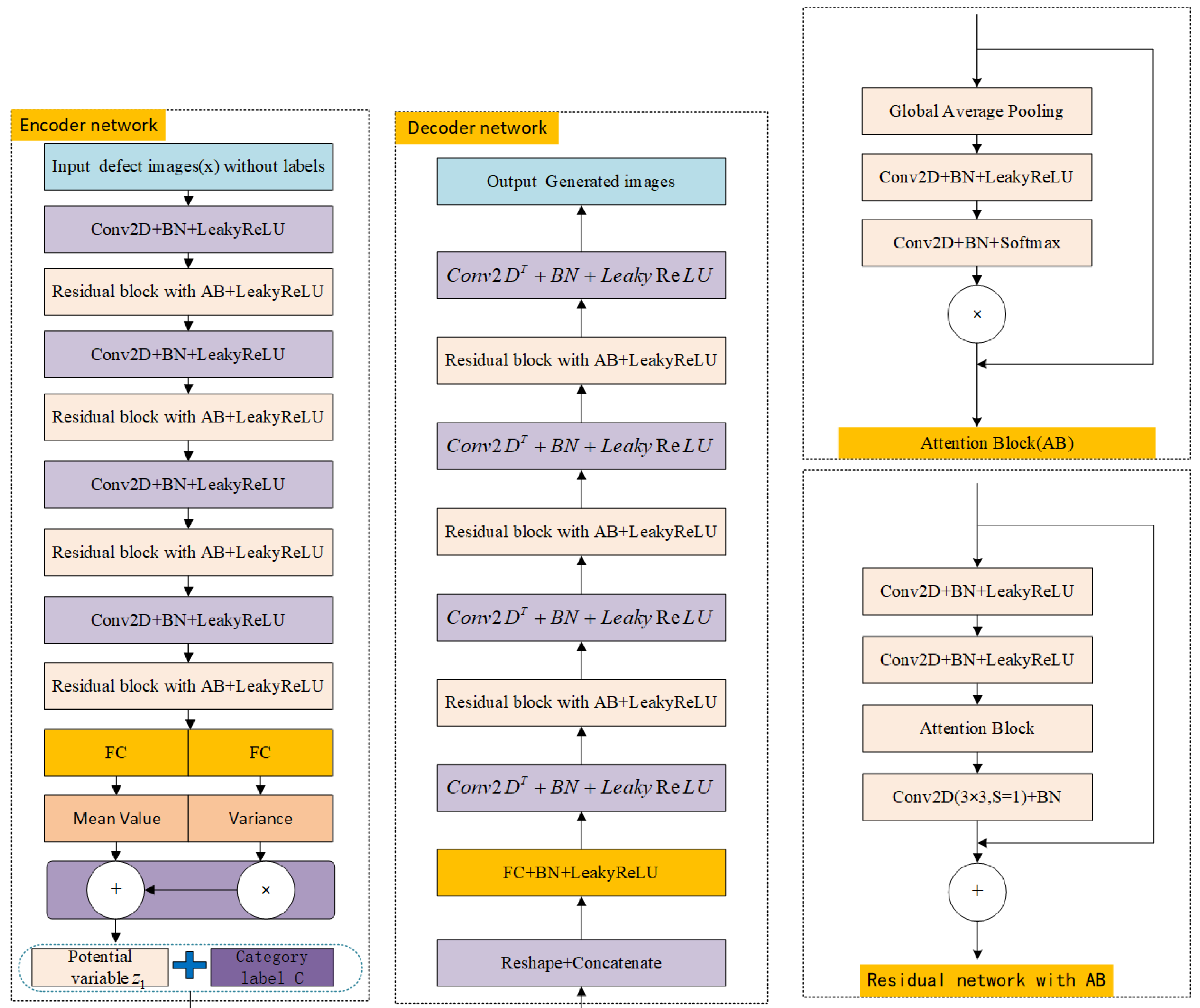
2.3.1. The Structure of the DCCVAE Network Model
- Encoder network
- 2.
- Decoder network
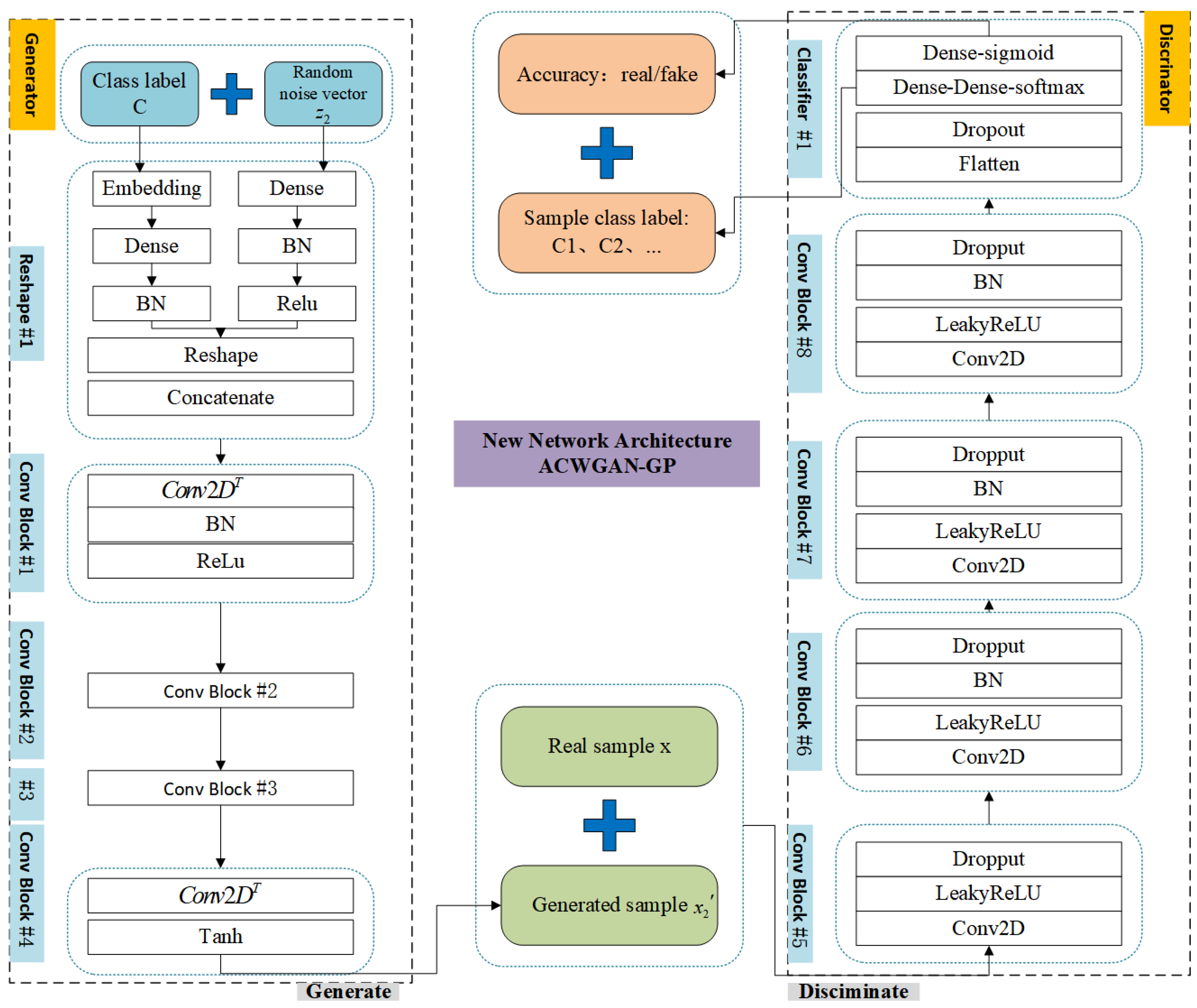
2.3.2. The Structure of the ACWGAN-GP Network Model
- Generator model
- 2.
- Discriminator network
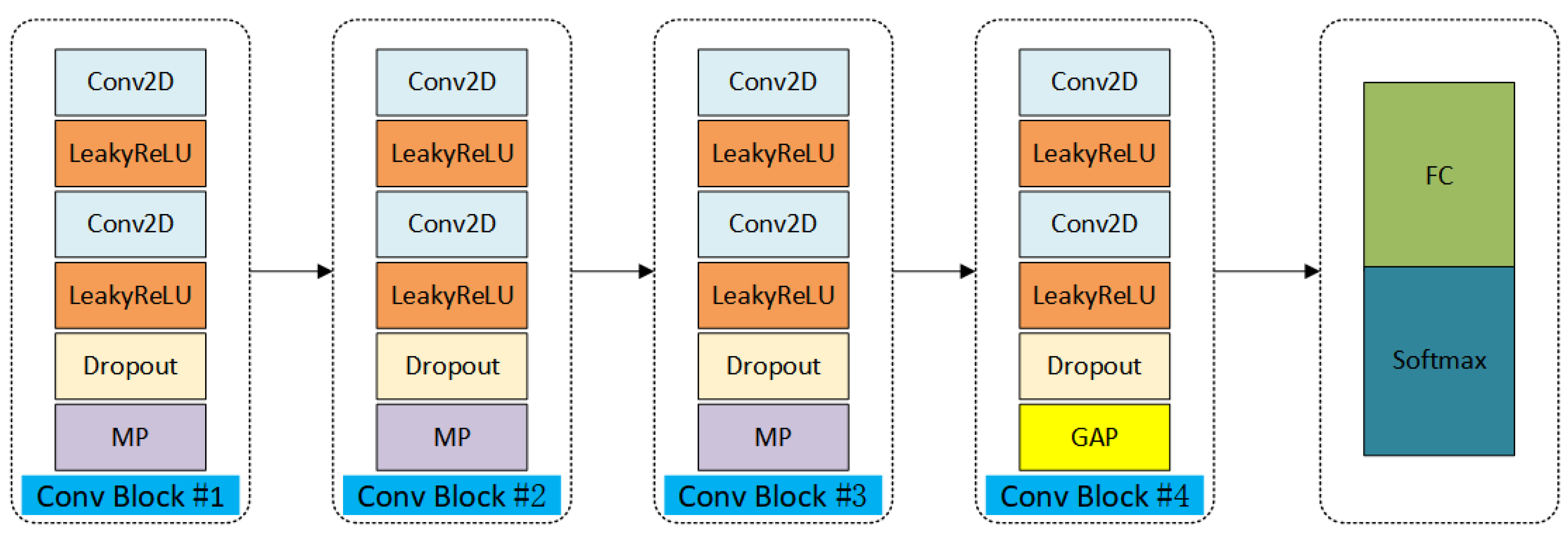
2.3.3. The Structure of the Classification Network Model
2.4. The Training Process Optimization Strategies and Implementation Details
3. Experiments Setup and Results
3.1. Dataset
3.2. Experimental Environment
3.3. Evaluation Metrics
3.4. Experimental Results and Analysis
3.4.1. Multi-Category Classification Results
3.4.2. AUC Performance Comparison of Different Data Enhancement Methods
3.4.3. The Effect of Removing Class Labels of the Encoder in the DCCVAE
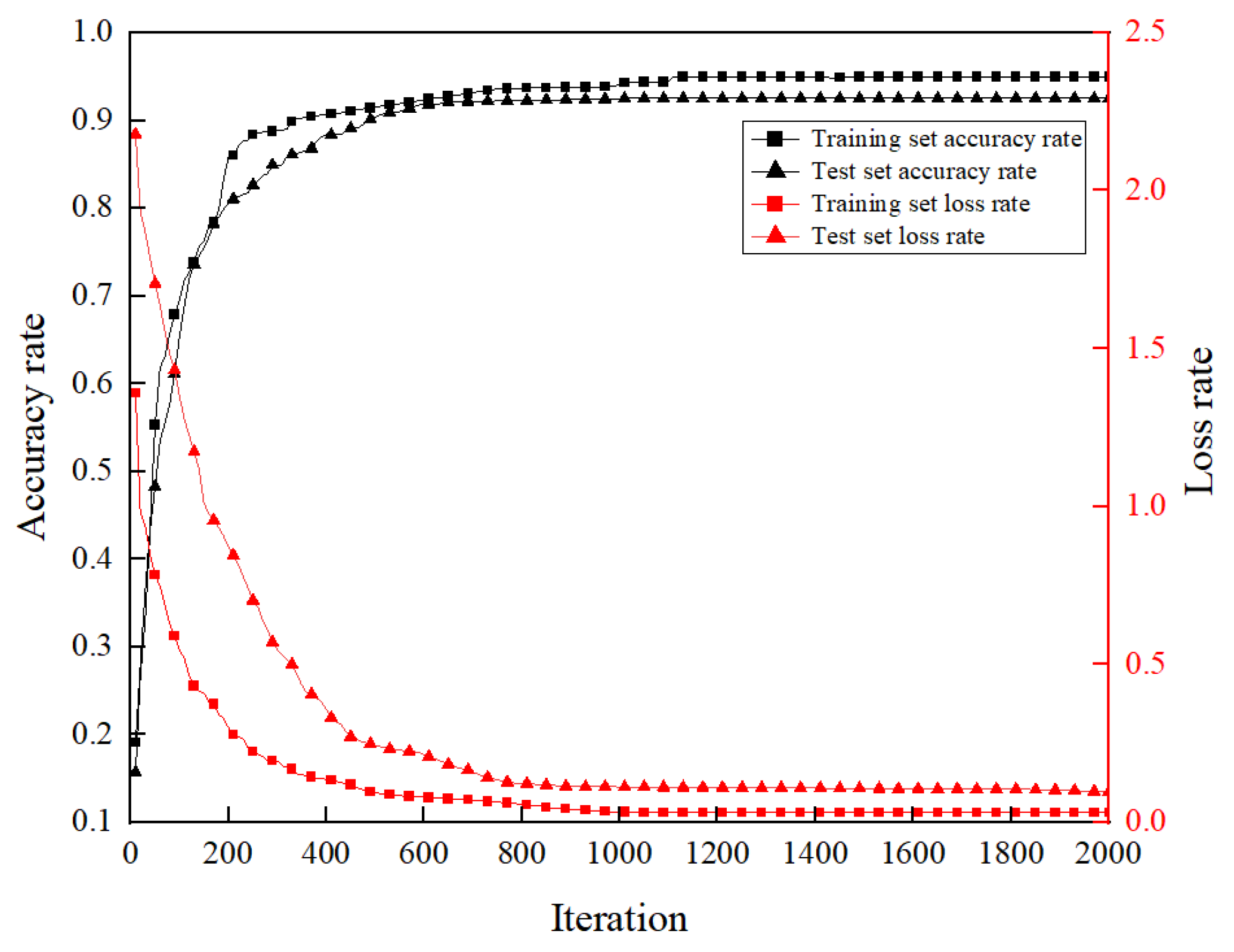
3.4.4. The Curves of Accuracy and Loss Function with Iteration Number
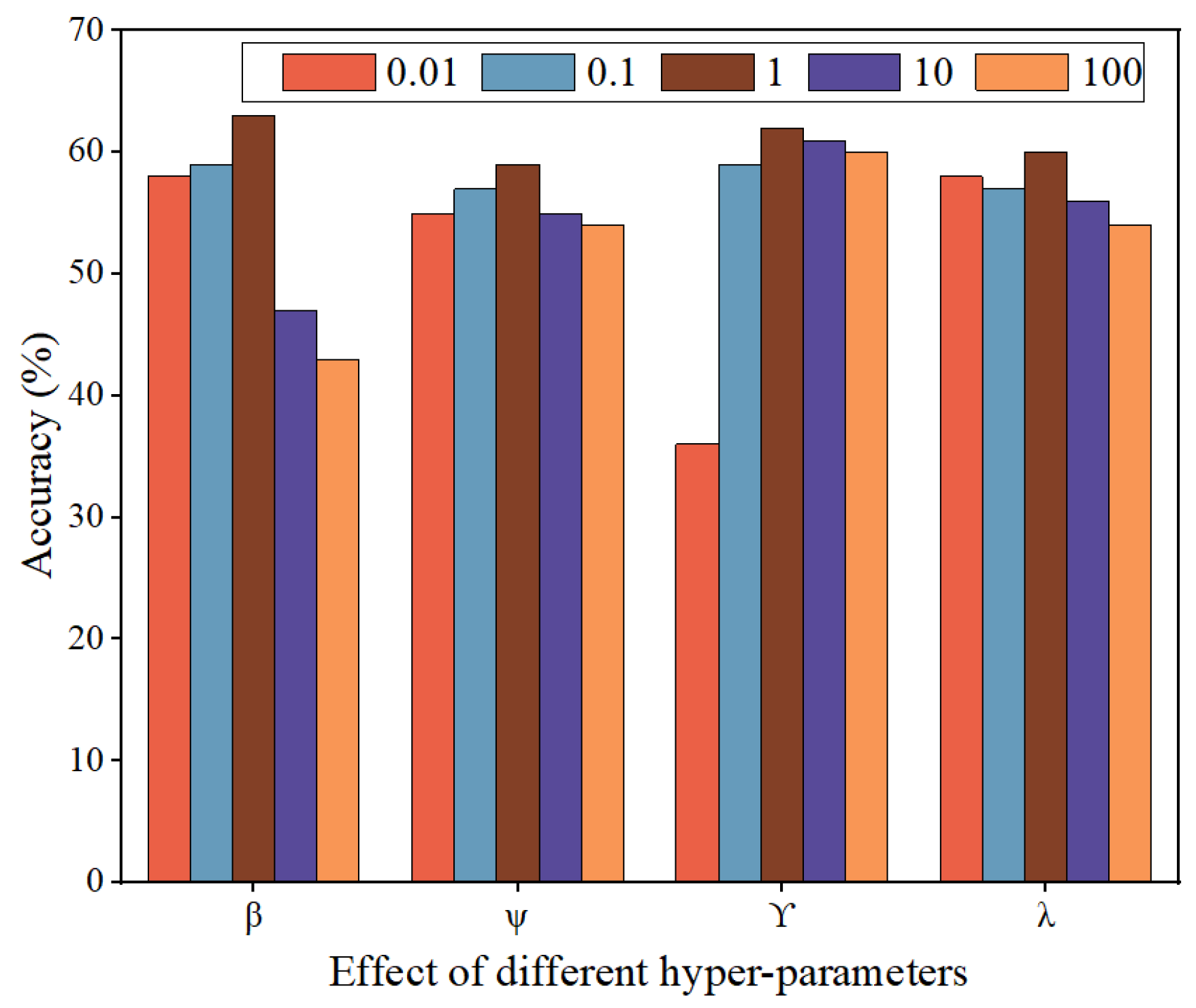
3.4.5. The Effect of Hyperparameter Settings on the Model Performance
3.4.6. Comparative Analysis of Classification Performance of Different Classifiers
3.4.7. Visual Analysis of Potential Spatial Feature Extraction Capability
4. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bu, H.; Yuan, X.; Niu, J.; Yu, W.; Ji, X.; Lyu, Y.; Zhou, H. Ship Painting Process Design Based on IDBSACN-RF. Coatings 2021, 11, 1458. [Google Scholar] [CrossRef]
- Bu, H.; Ji, X.; Yuan, X.; Han, Z.; Li, L.; Yan, Z. Calculation of coating consumption quota for ship painting: A CS-GBRT approach. J. Coat. Technol. Res. 2020, 376, 1. [Google Scholar] [CrossRef]
- Yuan, X.; Bu, H.; Niu, J.; Yu, W.; Zhou, H. Coating matching recommendation based on improved fuzzy comprehensive evaluation and collaborative filtering algorithm. Sci. Rep. 2021, 11, 14035. [Google Scholar] [CrossRef]
- Ma, H.; Lee, S. Smart System to Detect Painting Defects in Shipyards: Vision AI and a DeepLearning Approach. Appl. Sci. 2022, 12, 2412. [Google Scholar] [CrossRef]
- Bu, H.; Ji, X.; Zhang, J.; Lyu, Y.; Pang, B.; Zhou, H. A Knowledge Acquisition Method of Ship Coating Defects Based on IHQGA-RS. Coatings 2022, 12, 292. [Google Scholar] [CrossRef]
- Chris, A.K.; Fatemeh, A.; Hyeju, S.; Matthew, D.; Hall, P. Data-driven prediction of antiviral peptides based on periodicities of amino acid properties. Comput. Aided Chem. Eng. 2021, 50, 2019–2024. [Google Scholar] [CrossRef]
- Na, D.; Qiang, Y.; Meng, D.; Jian, F.; Xiao, M. A novel feature fusion based deep learning framework for white blood cell classification. J. Ambient. Intell. Humaniz. Comput. 2022, 14, 9839. [Google Scholar] [CrossRef]
- Ryan, M.C.; Mateen, R. Deep learning for image classification. In Proceedings of the 2020 2nd International Conference on Information Technology and Computer Application (ITCA), Guangzhou, China, 18–20 December 2020. [Google Scholar]
- Sadgrove, E.J.; Greg, F.; David, M.; David, W.L. The Segmented Colour Feature Extreme Learning Machine: Applications in Agricultural Robotics. Agronomy 2021, 11, 2290. [Google Scholar] [CrossRef]
- Maiti, A.; Chatterjee, B.; Santosh, C.K. Skin Cancer Classification Through Quantized Color Features and Generative Adversarial Network. Int. J. Ambient. Comput. Intell. 2021, 12, 75–97. [Google Scholar] [CrossRef]
- Yao, W.; Mishal, S. Design of Artistic Creation Style Extraction Model Based on Color Feature Data. Math. Probl. Eng. 2022, 481, 1191. [Google Scholar] [CrossRef]
- Rao, M.A.; Fahad, S.K.; Jorma, L. Compact Deep Color Features for Remote Sensing Scene Classification. Neural Process. Lett. 2021, 53, 1. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, J. An Improved Automatic Shape Feature Extraction Method Based on Template Matching. J. Phys. Conf. Ser. 2021, 2095, 012053. [Google Scholar] [CrossRef]
- Wang, F.; Xu, Z.C.; Shi, Q.S. Integrated Method for Road Extraction: Deep Convolutional Neural Network Based on Shape Features and Images. J. Nanoelectron. 2021, 16, 1011–1019. [Google Scholar] [CrossRef]
- Ravi, D.; Deboleena, S.; Ramakrishnan, S. Rotational moment shape feature extraction and decision tree based discrimination of mild cognitive impairment conditions using mr image processing. Biomed. Sci. Instrum. 2021, 57, 228–233. [Google Scholar] [CrossRef]
- Islam, S.M.; Pinki, F.T. Colour, Texture, and Shape Features based Object Recognition Using Distance Measures. Int. J. Eng. Manuf. 2021, 11, 42–50. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, M.; Zeng, M.; Wang, G. Intelligent Image Diagnosis of Pneumoconiosis Based on Wavelet Transform-Derived Texture Features. Comput. Math. Methods Med. 2022, 2022, 2037019. [Google Scholar] [CrossRef]
- Ong, K.; Young, D.M.; Sulaiman, S.; Shamsuddin, S.M.; Mohd Zain, R.M.; Hashim, H.; Yuen, K.; Sanders, S.J.; Yu, W.; Hang, S. Detection of subtle white matter lesions in MRI through texture feature extraction and boundary delineation using an embedded clustering strategy. Sci. Rep. 2022, 12, 4433. [Google Scholar] [CrossRef]
- Alireza, R.; Yasamin, J.; Ali, K. Explainable Ensemble Machine Learning for Breast Cancer Diagnosis Based on Ultrasound Image Texture Features. Forecasting 2022, 4, 262. [Google Scholar] [CrossRef]
- Jayesh, G.M.; Anto, S.D.; Binil, K.K.; KS, A. Breast cancer detection in mammogram: Combining modified CNN and texture feature based approach. J. Ambient. Intell. Humaniz. Comput. 2022, 14, 11397. [Google Scholar] [CrossRef]
- Kurniastuti, I.; Yuliati, E.N.I.; Yudianto, F.; Wulan, T.D. Determination of Hue Saturation Value (HSV) color feature in kidney histology image. J. Phys. Conf. Ser. 2022, 2157, 012020. [Google Scholar] [CrossRef]
- Panagiotis, K.; Gerasimos, T.; Boulougouris, E. Environmental-economic sustainability of hydrogen and ammonia fuels for short sea shipping operations. Int. J. Hydrogen Energy 2024, 57, 1070–1080. [Google Scholar] [CrossRef]
- Na, H.J.; Park, J.S. Accented Speech Recognition Based on End-to-End Domain Adversarial Training of Neural Networks. Appl. Sci. 2021, 11, 8412. [Google Scholar] [CrossRef]
- Siraj, K.; Muhammad, S.; Tanveer, H.; Amin, U.; Ali, S.I. A Review on Traditional Machine Learning and Deep Learning Models for WBCs Classification in Blood Smear Images. IEEE Access 2021, 9, 1065. [Google Scholar] [CrossRef]
- Ding, H.; Chen, H.; Dong, L.; Fu, Z.; Cui, X. Imbalanced data classification: A KNN and generative adversarial networks-based hybrid approach for intrusion detection. Future Gener. Comput. Syst. 2022, 131, 240–254. [Google Scholar] [CrossRef]
- Du, C.; Liu, P.; Zheng, M. Classification of Imbalanced Electrocardiosignal Data using Convolutional Neural Network. Comput. Methods Programs Biomed. 2022, 214, 106483. [Google Scholar] [CrossRef] [PubMed]
- Athanasios, A.; Nikolaos, D.; Anastasios, D.; Eftychios, P. Deep Learning for Computer Vision: A Brief Review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef]
- Young, T.; Hazarika, D.; Poria, S.; Cambria, E. Recent Trends in Deep Learning Based Natural Language Processing [Review Article]. IEEE. Comput. Intell. Mag. 2018, 13, 55. [Google Scholar] [CrossRef]
- Estiri, S.N.; Jalilvand, A.H.; Naderi, S.; Najafi, M.H.; Fazeli, M. A Low-Cost Stochastic Computing-based Fuzzy Filtering for Image Noise Reduction. In Proceedings of the IEEE 13th International Green and Sustainable Computing Conference (IGSC), Pittsburgh, PA, USA, 24–25 October 2022; pp. 1–6. [Google Scholar]
- Zhao, W.; Qin, W.; Li, M. An Optimized Model based on Metric-Learning for Few-Shot Classification. In Proceedings of the 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021; pp. 336–341. [Google Scholar]
- Park, S.; Zhong, R.R. Pattern Recognition of Travel Mobility in a City Destination: Application of Network Motif Analytics. J. Travel Res. 2022, 61, 1201. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Wu, S.; Shi, H.; Zhao, J.; Yao, D. An Investigation of a Multidimensional CNN Combined with an Attention Mechanism Model to Resolve Small-Sample Problems in Hyperspectral Image Classification. Remote Sens. 2022, 14, 785. [Google Scholar] [CrossRef]
- Dong, Y.; Li, Y.; Zheng, H.; Wang, R.; Xu, M. A new dynamic model and transfer learning based intelligent fault diagnosis framework for rolling element bearings race faults: Solving the small sample problem. ISA Trans. 2021, 121, 327. [Google Scholar] [CrossRef]
- Gao, H.; Yao, Y.; Li, C.; Zhang, X.; Zhao, J.; Yao, D. Convolutional neural network for spectral–spatial classification of hyperspectral images. Neural Comput. Appl. 2019, 31, 8997. [Google Scholar] [CrossRef]
- Sukarna, B.; Monirul, I.; Yao, X.; Kazuyuki, M. MWMOTE-Majority Weighted Minority Oversampling Technique for Imbalanced Data Set Learning. IEEE Trans. Knowl. Data Eng. 2014, 26, 405. [Google Scholar] [CrossRef]
- Ji, X.; Wang, J.; LI, Y.; Sun, Q.; Jin, S.; Tony, Q.S. Quek. Data-Limited Modulation Classification with a CVAE-Enhanced Learning Model. IEEE Commun. 2020, 24, 1. [Google Scholar] [CrossRef]
- Feng, X.; Shen, Y.; Wang, D. A Survey on the Development of Image Data Augmentation. Comput. Sci. Appl. 2021, 11, 370. [Google Scholar] [CrossRef]
- Waheed, A.; Goyal, M.; Gupta, D.; Khanna, A.; Turjman, F.A.; Pinheiro, P.R. CovidGAN: Data Augmentation Using Auxiliary Classifier GAN for Improved Covid-19 Detection. IEEE Access 2020, 8, 91916. [Google Scholar] [CrossRef]
- Jong, P.Y.; Woosang, C.S.; Gyogwon, K.; Kim, M.S.; Lee, C.; Lee, S.J. Automated defect inspection system for metal surfaces based on deep learning and data augmentation. J. Manuf Syst. 2020, 55, 324. [Google Scholar] [CrossRef]
- Aqib, H.A.M.; Nurlaila, I.; Ihsan, Y.; Mohd, N.T. VGG16 for Plant Image Classification with Transfer Learning and Data Augmentation. Int. J. Eng. Technol. 2018, 7, 4. [Google Scholar] [CrossRef]
- Sohn, Y.K.; Yan, X.; Lee, H. Learning structured output representation using deep conditional generative models. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Bali, Indonesia, 8–12 December 2021; pp. 3483–3491. [Google Scholar]
- Wu, X.; Feng, W.; Guo, Y.; Wang, Q. Feature Learning for SAR Target Recognition with Unknown Classes by Using CVAE-GAN. Remote Sens. 2021, 13, 3554. [Google Scholar] [CrossRef]
- Yang, H.; Lu, X.; Wang, S.; LU, Z.; Yao, J.; Jiang, Y.; Qian, J. Synthesizing Multi-Contrast MR Images Via Novel 3D Conditional Variational Auto-Encoding GAN. Mob. Netw. Appl. 2021, 26, 415–424. [Google Scholar] [CrossRef]
- Divya, S.; Tarun, T.; Cao, J.; Zhang, C. Multi-Constraint Adversarial Networks for Unsupervised Image-to-Image Translation. Conf. Inf. Process. 2022, 31, 1601. [Google Scholar] [CrossRef]
- Christian, L.; Lucas, T.; Ferencr, H.; Jose, C.; Andrew, P.; Alykhan, T.; Johannes, T.; Wang, Z.; Shi, W. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1063–6919. [Google Scholar]
- Zhou, Q.; Zhou, W.; Yang, B.; Jun, H. Deep cycle autoencoder for unsupervised domain adaptation with generative adversarial networks. IET Comput. Vis. 2019, 13, 659. [Google Scholar] [CrossRef]
- Khalil, M.A.; Sadeghiamirshahidi, M.; Joeckel, R.; Santos, F.M.; Riahi, A. Mapping a hazardous abandoned gypsum mine using self-potential, electrical resistivity tomography, and Frequency Domain Electromagnetic methods. J. Appl. Geophys. 2022, 205, 104771. [Google Scholar] [CrossRef]
- Ngoc, T.T.; Viet, H.T.; Ngoc, B.N.; Ngai, M.C. An Improved Selfsupervised GAN via Adversarial Training. In Proceedings of the Computer Vision and Pattern Recognition, Long Beach, CA, USA, 14 May 2019. [Google Scholar]
- Santiago, L.T.; Alice, C.; Rafael, M.; Aggelos, K.K. A single video superresolution GAN for multiple downsampling operators based on pseudo-inverse image formation models. Digit Signal Process. 2020, 104, 102801. [Google Scholar] [CrossRef]
- Jang, Y.; Sim, J.; Yang, J.; Kwon, N.K. Improving heart rate variability information consistency in Doppler cardiogram using signal reconstruction system with deep learning for Contact-free heartbeat monitoring. Biomed. Signal Process Control. 2022, 76, 103697. [Google Scholar] [CrossRef]
- Zou, L.; Zhang, H.; Wang, C.; Wu, F.; Gu, F. MW-ACGAN: Generating Multiscale High-Resolution SAR Images for Ship Detection. Sensors 2020, 20, 6673. [Google Scholar] [CrossRef]
- Ugo, F.; Alfredo, D.S.; Francesca, P.; Paolo, Z.; Francesco, P. Using generative adversarial networks for improving classification effectiveness in credit card fraud detection. Inf. Sci. 2017, 479, 448. [Google Scholar] [CrossRef]
- Augustus, O.; Christopher, O.; Jonathon, S. Conditional Image Synthesis With Auxiliary Classifier GANs. In Proceedings of the Computer Vision and Pattern Recognition, Honolulu, HI, USA, 20 July 2017. [Google Scholar]
- Pan, Z.; Yu, W.; Wang, B.; Xie, H.; Sheng, V.; Lei, J.; Kwong, S. Loss Functions of Generative Adversarial Networks (GANs): Opportunities and Challenges. IEEE Trans. Emerg. Topics Comput. 2020, 4, 500. [Google Scholar] [CrossRef]
- Demir, S.; Krystof, M.; Koen, K.; Nikolaos, G.P. Data augmentation for time series regression: Applying transformations, autoencoders and adversarial networks to electricity price forecasting. Appl. Energy 2021, 304, 117695. [Google Scholar] [CrossRef]






| Layers | Output Size | |
|---|---|---|
| Input layer (real sample x) | 3 × 128 × 128 | |
| Conv2D+BN+LeakyReLU | 128 × 64 × 64 | |
| Residual block with AB+LeakyReLU | 128 × 64 × 64 | |
| Conv2D+BN+LeakyReLU | 25 × 32 × 32 | |
| Residual block with AB+LeakyReLU | 256 × 32 × 32 | |
| Conv2D+BN+LeakyReLU | 512 × 16 × 16 | |
| Residual block with AB+LeakyReLU | 512 × 16 × 16 | |
| Conv2D+BN+LeakyReLU | 1024 × 8 × 8 | |
| Residual block with AB+LeakyReLU | 1024 × 8 × 8 | |
| FC | FC | 100 × 1 |
| Latent vector | 100 × 1 | |
| Input Layer | Output Size |
|---|---|
| Input layer (+class label C) | 100 × 1 |
| Reshape+Concatenate | - |
| FC+BN+LeakyReLU | 1024 × 8 × 8 |
| Conv2DT+BN+LeakyReLU | 512 × 16 × 16 |
| Residual block with AB+LeakyReLU | 512 × 16 × 16 |
| Conv2DT+BN+LeakyReLU | 256 × 32 × 32 |
| Residual block with AB+LeakyReLU | 256 × 32 × 32 |
| Conv2DT+BN+LeakyReLU | 128 × 64 × 64 |
| Residual block with AB+LeakyReLU | 128 × 64 × 64 |
| Conv2DT+BN+Sigmoid | 3 × 128 × 128 |
| Onput layer (generated samples ) | 3 × 128 × 128 |
| Layers | Output Size |
|---|---|
| Input layer (+class label C) | 110 × 1 |
| Reshape+Concatenate | - |
| FC+BN+LeakyReLU | 1024 × 8 × 8 |
| Conv2DT+BN+LeakyReLU | 512 × 16 × 16 |
| Conv2DT+BN+LeakyReLU | 256 × 32 × 32 |
| Conv2DT+BN+LeakyReLU | 128 × 64 × 64 |
| Conv2DT+Tanh | 3 × 128 × 128 |
| Ontput layer (generated samples ) | 3 × 128 × 128 |
| Layers | Output Size |
|---|---|
| Conv2D+LeakyReLU+Dropout | 128 × 64 × 64 |
| Conv2D+LeakyReLU+BN+Dropout | 256 × 32 × 32 |
| Conv2D+LeakyReLU+BN+Dropout | 512 × 16 × 16 |
| Conv2D+LeakyReLU+BN+Dropout | 1024 × 8 × 8 |
| Conv2D+LeakyReLU+BN+Dropout | 1 × 1 × 1 |
| Output layer | real/fake and sample class label C |
| Layers | Size | Stride |
|---|---|---|
| Conv+LeakyReLU | 3 × 3 | 1 |
| Conv+LeakyReLU+Dropout | 3 × 3 | 1 |
| Max-pooling | 2 × 2 | 2 |
| Conv+LeakyReLU | 3 × 3 | 1 |
| Conv+LeakyReLU+Dropout | 3 × 3 | 1 |
| Max-pooling | 2 × 2 | 2 |
| Conv+LeakyReLU | 3 × 3 | 1 |
| Conv+LeakyReLU+Dropout | 3 × 3 | 1 |
| Max-pooling | 2 × 2 | 2 |
| Conv+LeakyReLU | 3 × 3 | 1 |
| Conv+LeakyReLU+Dropout | 3 × 3 | 1 |
| GAP | — | |
| FC+Softmax | — |
| Parameters | Output Size |
|---|---|
| Number of iterations | 2000 |
| Number of mini-batch sizes | 64 |
| Optimizers and their learning rates | RMSProp (0.0002) |
| Degradation rate of the optimizer | 4 × 10−8 |
| Learning rate of generator | 0.0003 |
| Learning rate of discriminator | 0.0001 |
| Dropout | 0.5 |
| Slope of LeakyReLU | 0.2 |
| Defect Category | Sample Image | One-Hot Encoding | Number of Original Samples | Number of Samples after Data Augmentation |
|---|---|---|---|---|
| Holiday coating |  | [1,0,0,0,0,0,0,0,0,0] | 3 | 600 |
| Sagging |  | [0,1,0,0,0,0,0,0,0,0] | 86 | 860 |
| Orange skin |  | [0,0,1,0,0,0,0,0,0,0] | 759 | 759 |
| Cracking |  | [0,0,0,1,0,0,0,0,0,0] | 77 | 770 |
| Exudation |  | [0,0,0,0,1,0,0,0,0,0] | 71 | 710 |
| Wrinkling |  | [0,0,0,0,0,1,0,0,0,0] | 73 | 730 |
| Bitty appearance |  | [0,0,0,0,0,0,1,0,0,0] | 8 | 800 |
| Blistering |  | [0,0,0,0,0,0,0,1,0,0] | 108 | 756 |
| Pinholing |  | [0,0,0,0,0,0,0,0,1,0] | 26 | 780 |
| Delamination |  | [0,0,0,0,0,0,0,0,0,1] | 4 | 800 |
| Class | Predicted Positive Class | Predicted Negative Class |
|---|---|---|
| Actual positive class | TP | FN |
| Actual negative class | FP | TN |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bu, H.; Yang, T.; Hu, C.; Zhu, X.; Ge, Z.; Zhou, H. An Image Classification Method of Unbalanced Ship Coating Defects Based on DCCVAE-ACWGAN-GP. Coatings 2024, 14, 288. https://doi.org/10.3390/coatings14030288
Bu H, Yang T, Hu C, Zhu X, Ge Z, Zhou H. An Image Classification Method of Unbalanced Ship Coating Defects Based on DCCVAE-ACWGAN-GP. Coatings. 2024; 14(3):288. https://doi.org/10.3390/coatings14030288
Chicago/Turabian StyleBu, Henan, Teng Yang, Changzhou Hu, Xianpeng Zhu, Zikang Ge, and Honggen Zhou. 2024. "An Image Classification Method of Unbalanced Ship Coating Defects Based on DCCVAE-ACWGAN-GP" Coatings 14, no. 3: 288. https://doi.org/10.3390/coatings14030288
APA StyleBu, H., Yang, T., Hu, C., Zhu, X., Ge, Z., & Zhou, H. (2024). An Image Classification Method of Unbalanced Ship Coating Defects Based on DCCVAE-ACWGAN-GP. Coatings, 14(3), 288. https://doi.org/10.3390/coatings14030288





