Abstract
Hard–soft exchange coupling nanocomposites have critical applications in various important materials. The magnetic properties of nanocomposite permanent magnetic films improve with a higher nucleation field (Hns) of the soft magnetic phase. Hns is sensitive to the thickness (ds) of the soft magnetic layer. Understanding the dependence of Hns and irreversible field (Hirr) on ds, especially at the nanometric scale, is crucial for comprehending the magnetic mechanism and facilitating the design and preparation of high-performance nanocomposite permanent magnets. However, during the high-temperature deposition process, diffusion between hard and soft magnetic phases occurs, leading to the generation of other phases. This makes it challenging to accurately reflect the relationship between Hns and ds. To address this issue, we successfully fabricated high-quality SmCo5/Fe nanocomposite bilayer films with different soft magnetic thicknesses and high textures by controlling the preparation process. We conducted a quantitative analysis of the relationship between Hns and ds within the range of 2–40 nm. Based on the experimental results, we propose a new theoretical simulation formula that enhances the understanding of the characteristics at the interface between the soft magnetic and hard magnetic phases. The theoretical simulation results show that a thin softened hard layer of about 4–6 nm thickness exists at the interfacial region, which concurrently reverses with the soft magnetic phase during the demagnetization process. Our results offer the generality and critical basis for the further study of hard–soft nanocomposite magnetic materials.
1. Introduction
Hard and soft magnetic materials are two distinct yet crucial types of magnetic materials. Hard magnetic materials exhibit significant magnetic anisotropy, in contrast to soft magnetic materials, which possess lower anisotropy. When these two materials are combined to form nanocomposite magnetic materials, novel phenomena and properties emerge due to the magnetic exchange coupling effects between the phases [1,2,3,4,5,6,7]. Hard–soft systems have been extensively studied because of their important applications in permanent magnetic materials, high-density magnetic recording media, giant magnetostrictive materials, etc. [8,9,10,11,12,13,14,15,16,17]. For example, the anisotropic nanocomposite permanent magnetic material which contains the coupled and aligned hard and soft phases has the theoretically predicted giant maximum energy product (BH)max. It is expected to be a good candidate for the next generation of permanent magnetic materials. Isotropic nanocomposite magnets, containing randomly oriented hard magnetic grains, have been widely employed in magnetic devices due to their enhanced remanence. The hard–soft exchange coupled system has also been utilized in state-of-the-art high-density magnetic recording media to tune their coercive force Hc or irreversible field Hirr [10,11].
One key and basic feature in the hard–soft exchange coupling nanocomposite system is the significantly modified nucleation field (reversal field) of soft-phase Hns relative to that of the bulk single soft phase. Hns can be greatly enhanced by reducing ds, particularly in the nanometric scale. The value of Hns is influenced by both the size of the soft phase and the strength of the exchange coupling between the hard and soft phases [1,2]. quantitatively characterizing the dependence of Hns on ds forms a crucial basis for understanding the magnetic properties and reversal mechanisms in hard–soft magnetic materials. For instance, when designing a hard–soft nanocomposite permanent magnetic material with a specific coercive force or a single-phase hysteresis loop, the relationship between Hns and ds can essentially guide us in determining the appropriate size of the soft phase to ensure the desired properties.
Hns, as a function of ds, has been studied theoretically in hard–soft exchange coupled systems [2,18,19,20,21]. However, there is currently no unified theoretical formula that applies to a wide range of sizes of soft magnetic phases and different theoretical formulas are only applicable to specific size ranges.
The dependence of Hns on ds has been also experimentally studied. S.S. Yan et al. successfully fabricated well-textured SmFe/NiFe bilayer films and obtained the accurate value of Hns when ds varied from 34 to 170 nm [8]. To quantitatively describe the relationship between Hns and ds, a fitting formula, , was used to match the experimental data, yielding a satisfactory result [8]. S. Sawatzki et al. fabricated SmCo5/Fe/SmCo5 tri-layer films and determined the value of Hns for smaller ds but in a narrow range: ds = 6.3~12 nm [9]. Their tri-layer films, however, were fabricated at a high temperature. Diffusion between the Sm-Co and Fe layers was inevitable and an Fe-Co intermixed phase was introduced. So, the dependence of Hns on ds could not be determined strictly. Obtaining the precise value of Hns for small ds is typically difficult, as it requires achieving both a large coercive force and excellent texture for the hard phase. The quantitative relationship between Hns and ds in the sub-tens nanometer range remains significantly under-explored in experimental investigations.
A high-quality sample is a necessary prerequisite to determine accurately the quantitative dependence of Hns on ds. An ideal sample should have the following characteristics: (i) no diffusion between the hard and soft magnetic phases; (ii) the hard magnetic phase has a high coercive force considering that the value of Hns increases as the size of the soft phase decreases; (iii) the hard phase should be well textured.
To address these issues, high-quality nanostructured SmCo5/Fe double layers with different soft-phase sizes with large coercive forces and strong textures were successfully fabricated through strict control of the preparation process in the present work. We conducted a quantitative analysis of the relationship between Hns and ds within the range of 2–40 nm. Based on the experimental results, we propose a new theoretical simulation formula that enhances the understanding of the characteristics at the interface between the soft magnetic and hard magnetic phases. These results not only contribute to the understanding of the magnetic mechanism of nano-composite magnets but also provide important guidance for the design of high-performance nano-composite magnets.
2. Experimental Details
2.1. Materials
By adjusting the ratio of Sm and Co, a Sm-Co composite target was prepared. To compensate for the different yields of Sm and Co during the sputtering process of the Sm-Co composite target, we added an additional 38% of Sm in the composite target. The composition of the target, as measured by ICP, was 1:3.6. And the atomic ratio of Sm:Co of Sm-Co/Fe bilayer was 1:4.3, determined by EDX. Both Cr and Fe targets utilized commercially available pure metal targets with a purity higher than 99.999%.
2.2. Experimental Process
SmCo5(50 nm)/Fe (x nm) bi-layer film was fabricated on substrate MgO (110) by an ultra-high vacuum magnetron sputtering machine. Both Sm-Co and Fe targets mounted in the high vacuum chamber faced the substrate. The base pressure was better than 8 × 10−7 Pa. The size of soft layer Fe x was tuned from 0 to 40 nm. A thickness about 50 nm of Cr was used as a buffer layer. In an attempt to achieve a desirable texture and high coercive force in the Sm-Co hard-layer films, we experimented with various parameters. The optimal experimental conditions are as follows: the sputtering power for the Sm-Co composite target should be at least 150 W, and the sputtering temperature should be 600 °C. For more details please see the Supplementary Materials. To avoid the diffusion between the hard Sm-Co and soft Fe magnetic phases, the Sm-Co layer was first deposited at 600 °C to achieve a good texture and high coercive force and then cooled to room temperature to deposit the Fe soft layer. A thickness of about 50 nm of Cr was used as a capping layer to protect the film from oxidation.
2.3. Characterization Techniques
The surface morphologies of Sm-Co/Fe bilayer were characterized using atomic force microscopy and scanning electron microscopy. And the atomic ratio of Sm:Co was determined by EDX. The phase structure of the films was characterized by X-ray diffraction (XRD) patterns recorded at room temperature measured on a D8 Advance (Brüker, Billerica, MA, USA) diffractometer with a Cu Kα radiation with a wavelength about 1.5418 Å. The angle range spanned from 40 to 85, with a step of 0.02 and a scanning rate of 0.02° per second. The magnetic measurements were performed on SQUID-VSM designed by the Quantum Design (San Diego, CA, USA). The measurement temperature was room temperature, with a magnetic field range of 0–7 T, and both the ramp-up and ramp-down field rates were set at 200 Oe per second.
3. Results and Discussion
We tried many experimental parameters in an effort to achieve a good texture and high coercive force of the Sm-Co hard-layer films. We found that the high sputtering power and deposition temperature play important roles in developing the strong texture on the MgO (110)/Cr substrate, possibly due to the induced high kinetic energy of sputtered atoms conductive to make SmCo grow along the (110) as much as possible. Finally, the Sm-Co layer film with an excellent texture and high coercive force was achieved. Figure 1 shows the XRD patterns of the Cr (50 nm)/SmCo (50 nm)/Fe (x nm)/Cr (50 nm) films with x as 20 and 30 nm. Only (200) diffraction peak of SmCo5 was detected at 41.6030 and 41.6001 degrees and the full width at half maximum (FWHM) of the (200) diffraction peaks was 0.7049 and 0.7006 degrees for films with x as 20 and 30 nm, respectively. The grain size of SmCo was estimated to be around 2.6 nanometers based on the following Scherrer formula using the above data:
where K is the Scherrer factor, which is chosen as 0.89 here, λ is the wavelength of the incident light; β is the full width at half maximum (FWHM) of the diffraction peaks and θ is the diffraction angle. Specially, no (111) peaks exist, further demonstrating the excellent texture, which is much better than the Sm-Co film deposited on the SiO2/Cr substrate [14]. This indicates that the hard Sm-Co monolayer successfully achieves an excellent texture on the MgO (110) substrate via optimizing the sputtering fabrication parameters.
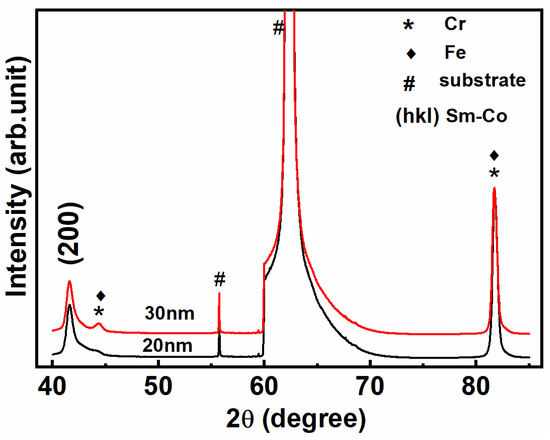
Figure 1.
X-ray diffraction patterns collected at room temperature of Cr (50 nm)/SmCo (50 nm)/Fe (x nm)/Cr (50 nm) films with x as 20 (black line) and 30 nm (red line).
The magnetic hysteresis loops of the Sm-Co monolayer measured at 300 and 25 K shown in Figure 2 exhibit a very good rectangular shape along the easy axis (MgO [0 0 1]) and extremely low remanence along the hard axis (MgO [1 −1 0]), further confirming the strongly textured Sm-Co phase. The coercive forces derived from the hysteresis loops measured at 300 and 25 K are 24.0 and 43.4 kOe, respectively. The increase in coercive force from 300 to 25 K should arise from the enhancement of Sm-Co magnetocrystalline anisotropy.
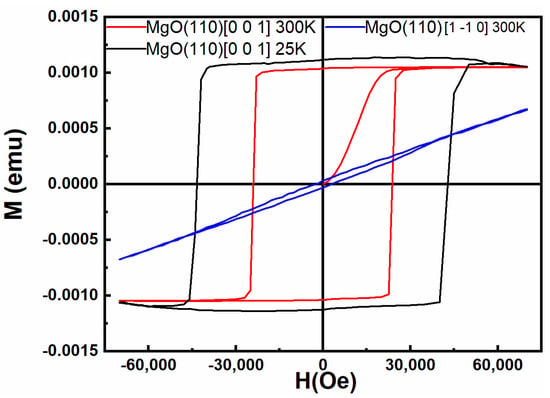
Figure 2.
The magnetic hysteresis loops of Sm-Co monolayer measured at 25 and 300 K.
Figure 3a,b present the magnetic hysteresis loops of SmCo/Fe bi-layer films with different thicknesses of soft phase ds from 2 to 40 nm measured at 25 and 300 K, respectively. For nanocomposite permanent magnetic materials, the exchange coupling between the hard and soft phase is dominated by the direct exchange coupling, a kind of short-range interaction effective within one atomic distance. During the demagnetization process, atom spins of the hard phase can have an influence on the rotation of those of the soft phase with a maximum distance of domain wall width through a cascade of interactions between neighbor atom spins. For the very large size of soft phase, e.g., 40 nm, the spins far from the hard phase very easily rotate, meaning that the Hns of the soft phase is very low. During the demagnetization process, that part of soft phase first rotates, while the direction of the hard-phase spins still persists until the applied magnetic field reaches the Hirr, where the hard phase starts to reverse. Therefore, a two-step demagnetization curve is observed. We can see that the Hirr of the hard phase in the hard–soft bi-layer film is much lower than the Hc (or Hirr) of the single hard-layer film, which should be attributed to the formation of a domain wall upon the rotation of the soft phase, prompting the rotation of the hard phase [22]. With the decrease in ds, the total soft-phase spins become closer to the hard phase and their rotations turn out to be harder; therefore, Hns increases. As ds further decreases, Hns becomes very large. At a critical size of soft phase dsc, Hns is identical to Hirr, i.e., the rotation of the soft phase immediately leads to the reverse of the hard phase, signifying that the hard and soft phases start to reverse together and a single-phase behavior in the demagnetization curve is observed.
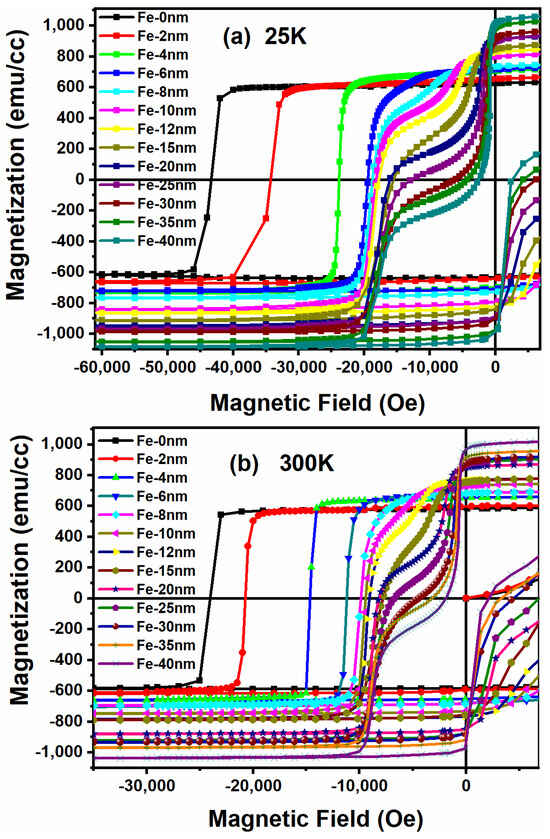
Figure 3.
The magnetic hysteresis loops of SmCo/Fe bi-layer films with different thickness of soft phase measured at 25 (a) and 300 K (b), respectively.
The critical size of soft phase dsc at which the demagnetization curve changes from the single-phase behavior to two-step behavior is about 6 nm at 25 K and 8 nm at 300 K (Figure 3). In the hard–soft nanocomposite system, dsc is usually calculated in terms of the theoretical model invoked by Kneller and Hawig: dsc = , where As is the exchange energy of the soft phase and Kk is the magnetocrystalline anisotropy constant of the hard phase [1]. dsc was calculated for the Sm-Co/Fe hard–soft system (As = 2.53 × 10−11 J/m and Kk = 1.71 × 107 J/m3) [23] using the above formula and the value of dsc was 2.7 nm, which is inconsistent with our experimental results. This inconsistency suggests that dsc is not determined only by As and Kk. Hirr or Hc of the initial single hard phase (Figure 3) may also have an influence on dsc. A higher Hirr or Hc will lead to a smaller dsc [23].
We can determine the reversal field (nucleation field) of the soft phase Hns, the irreversible field of the hard phase Hirr and the coercive force Hc for different ds based on the experimentally measured demagnetization curves (Figure 3), which are shown in Figure 4. It can be seen that Hns gradually increases with the decrease in ds for ds ≥ 20 nm. The increase in Hns becomes more rapid when ds ≤ 20 nm. It rises up sharply for ds ≤ 10 nm. The value of Hirr was fixed at 17.6 ± 0.1 kOe at 25 K and 9.0 ± 0.1 kOe at 300 K for a relatively large size ds (15 nm ≤ ds ≤ 40 nm). In this ds range, the Bloch domain wall could be formed in the demagnetization process due to the 180° rotation of the soft-phase spins far from the hard phase, which will exert equal force on the hard phase, giving rise to the identical Hirr. It is interesting to observe that Hirr starts to increase with the decrease in ds for ds ≥ 15 nm, which is highly likely attributed to the incomplete Bloch domain wall formed at the same magnetic field exerting the reduced force on the reverse of the hard phase. Anyhow, we strictly and accurately obtained the dependence of Hns and Hirr on ds in experiments (Figure 4). The results can serve as an important basis for research on understanding the mechanism and practical design of a hard–soft system for different applications. For example, the nanocomposite magnet usually needs high Hc and Hirr. In this case, the preferred size of soft phase ds should be lower than 10 nm. The hard–soft exchange coupling system utilized in high-density magnetic recording media, however, requires a lower Hirr. In this case, a designed ds larger than 10 nm is favored. In addition, for the nanocomposite magnet with high (BH)max, a hysteresis loop with characteristics of single-phase behavior is necessary, the determined relationship between Hns and ds can tell us how much size of soft phase can be adopted in order to obtain the desired coercive force.
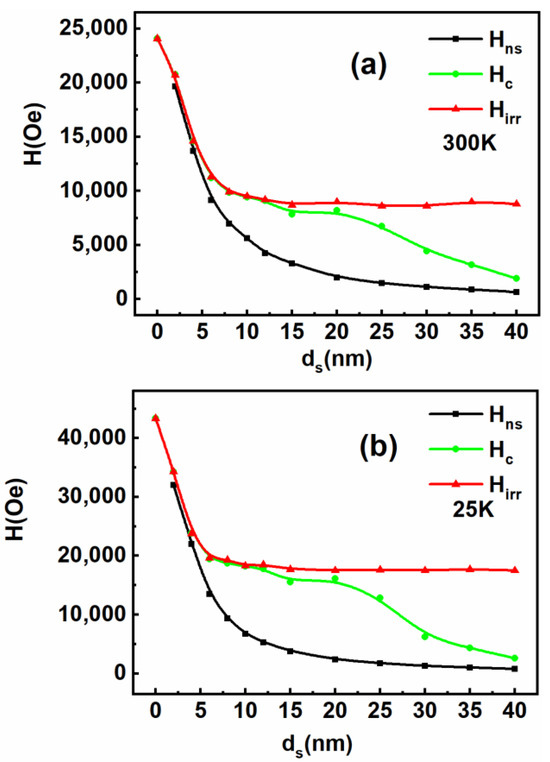
Figure 4.
The dependence of soft magnetic nucleation field (Hns), coercive force (Hc) and hard magnetic irreversible field (Hirr) on ds at 25 (a) and 300 K (b), respectively.
There have been some important theories and simulations on the relationship between Hns and ds. E. Goto et al. hypothesized an extremely hard magnetic layer and its magnetization during the demagnetization process was immobile before reaching its irreversible field in the hard and soft magnetic bi-layer film system [18]. Based on this model, an analytic solution was resolved as the following formula:
where A and Ms are the exchange coupling constant and saturation magnetization, respectively, and N is a constant and derived to be 2. T. Leineweber and H. Kronmüller analyzed the relationship between Hns and ds using the micromagnetic method [19]. They found that Hns was related to the width of the Bloch wall of the hard magnetic layer, and Hns~ds were divided into three regions:
where πδh is the width of the Bloch wall and h denotes the hard magnetic layer. It can be seen from Formula (3) that Hns keeps constant when 2ds is less than πδh and goes through a rapid descent process until 2ds reaches 8πδh. With further increasing ds, the relationship between Hns and ds is similar to Formula (1), with N chosen as 1.75.
When ds is large, Hns is small and relatively easy to determine experimentally. S.S Yan et al. experimentally measured Hns of SmFe/NiFe bi-layer films when ds was in a range of 34~170 nm [8]. Since ds is large, they used the formula in Formula (3) to fit the dependence of Hns on ds, and a good fitting was achieved for N = 1.73, which is close to the N value of Formula (3). Usually, it is difficult to obtain the accurate value of Hns for small ds in experiments because it needs a high-quality sample with good texture and high Hirr of the hard phase. We successfully determined the experimental value of Hns for very small ds = 2–40 nm. We used Formula (2) to fit the dependence of Hns on ds. However, no ideal result was achieved, as indicated in Figure 5a,b. Although the values of N obtained are 2.05 and 2.14 at 300 and 25 K, respectively, close to the values obtained by E. Goto et al. using Formula (1) [18], the fitting curves do not conform to the experimental data very well.
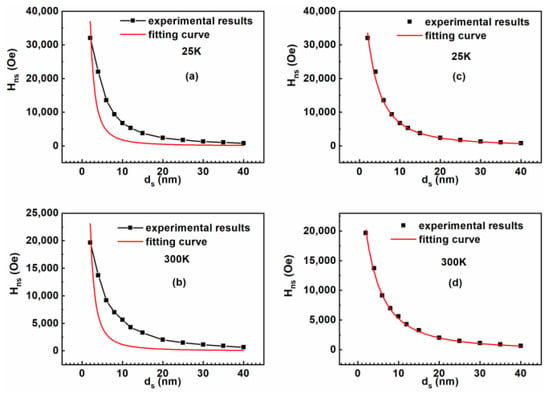
Figure 5.
The dependence of soft magnetic nucleation field (Hns) on ds at 25 (a) and 300 K (b) obtained from the experimental results and fitting curve using the formula . The dependence of soft magnetic nucleation field (Hns) on ds at 25 (c) and 300 K (d) obtained from the experimental results and fitting curve using the formula
In hard–soft nanocomposite magnetic systems, due to the strong exchange coupling between the hard and soft magnetic layers, the magnetic moment of the soft magnetic layer will not reverse during the demagnetization process until the external magnetic field increases to the nucleation field Hns of the soft phase. When the external magnetic field continues to increase and lies between the soft magnetic nucleation field Hns and the hard magnetic irreversible field Hirr, the magnetic moment of the soft magnetic layer reverses, while that of the hard magnetic layer is theoretically supposed to persist completely [18]. When the external magnetic field is larger than Hirr, the magnetic moment of the hard magnetic layer starts to rotate. The theoretical expectation that the hard magnetic layer is totally immobile during the reverse of the soft layer is just the ideal case. In real hard–soft systems, the magnetic anisotropy of the hard phase is not infinite. Moreover, an interfacial region between the hard and soft phases should exist, which would give rise to the softening of partial thickness of the hard layer close to the soft layer. This thin softened hard layer should also concurrently reverse during the soft magnetic layer reversal process, which means that a certain thin hard layer will become the soft layer, causing an increase in ds. Actually, a thin hard layer in the interfacial region rotating much easier concurrently with the reversal of the soft layer has been experimentally demonstrated [24,25,26]. Based on the analysis above, a modified formula is obtained:
where a is a parameter representing the extra soft magnetic layer from the softened thin hard layer in the interfacial region. The dependence of Hns on ds determined by our experimental SmCo/Fe nanocomposite bi-layer films is fitted by Formula (4). A perfect fitting is achieved, as indicated in Figure 5c,d. The values of N and parameter a produced from the fittings are shown in Table 1. The obtained N is very close to what has been achieved by E. Goto et al. using Formula (2) [16]. The values imply that 4.8 nm at 25 K and 6.6 nm at 300 K of the hard magnetic layer easily reverse, accompanying the reversal of the soft layer during the demagnetization process. The derived value of a at 25 K is smaller than that at 300 K, which is reasonable because the much-enhanced magnetocrystalline anisotropy of the hard layer at low temperatures makes its softening part become hard. Our results have important practical significance in designing a high-performance nanocomposite magnet at room temperature. In order to effectively pin the magnetic moment of the soft phase, the size of the hard phase should be larger than a certain thickness, e.g., about 6.6 nm in a Sm-Co/Fe bi-layer system, otherwise the total hard phase will reverse together with the soft phase, which will result in a very low coercive force of the whole nanocomposite magnet.

Table 1.
The values of N and parameter a produced from the fittings by formula .
4. Conclusions
In order to study the quantitative relationship between the nucleation field and soft magnetic size of hard–soft exchange coupling nanocomposites, high-quality SmCo-Fe bilayer films with high texture and coercivity were successfully obtained by strictly controlling the preparation conditions using magnetron sputtering. The coercive force derived from the hysteresis loops measured at 300 K can reach up to 24.0 kOe. The soft magnetic size of α-Fe varies between 0 and 40 nanometers. The results show that Hns gradually increases with the decrease in ds for ds ≥ 20 nm. The increase in Hns becomes more rapid when ds ≤ 20 nm. It rises sharply for ds ≤ 10 nm. Based on the existing general theoretical formula, we propose a new fitting formula that can fit the relationship between Hns and ds very well and provide a reasonable theoretical explanation for the new formula. The fitting results also essentially reveal that there is indeed a thin layer with a thickness of about 4–6 nm of softened hard magnetic phase at the interfacial region, which reverses simultaneously with the soft magnetic phase when the external magnetic field increases to the nucleation field of soft phase Hns. Our results clarify the fundamental mechanism underlying the reversal process of the hard–soft exchange coupling system and offer a basis for further critical study and design of hard–soft nanocomposite materials with desired properties.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/coatings14020219/s1, Figure S1: The hysteresis loops of Sm-Co films fabricated at different deposition temperatures. Figure S2: The hysteresis loops of Sm-Co films fabricated with different sputtering powers for TSm-Co = 500 °C. Figure S3: The hysteresis loops of Sm-Co films fabricated with different sputtering powers for TSm-Co = 600 °C. Figure S4: The hysteresis loops of Sm-Co films fabricated at higher deposition temperatures TSm-Co > 600 °C. Figure S5: The hysteresis loops of Sm-Co (50 nm)/Fe (x nm) on SiO2 and MgO substrates.
Author Contributions
Conceptualization, F.W.; Investigation, G.H. and Y.W.; Resources, P.Z.; Data curation, T.F. and R.S.; Writing—review & editing, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fund of Ningbo University of Technology, the National Natural Science Foundation of China No. 51971234; National Key Research and Development Program of China No. 2021YFB3500303; National Key Research and Development Program of China No. 2023YFB3507001.
Institutional Review Board Statement
Not applicable
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kneller, E.F.; Hawig, R. The exchange-spring magnet: A new material principle for permanent magnets. IEEE Trans. Magn. 1991, 27, 3560–3588. [Google Scholar] [CrossRef]
- Skomki, R.; Coey, J.M.D. Giant energy product in nanostructured two-phase magnets. Phys. Rev. B 1993, 48, 15812. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.B.; Takahashi, Y.K.; Hono, K. Nd2Fe14B/FeCo Anisotropic Nanocomposite Films with a Large Maximum Energy Product. Adv. Mater. 2012, 24, 6530. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Takahashi, Y.K.; Gopalan, R.; Hono, K. Sm (Co, Cu) 5/Fe exchange spring multilayer films with high energy product. Appl. Phys. Lett. 2005, 86, 122509. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.X.; Wang, F.; Shen, B.G.; Sun, J.R. Coercivity mechanism of nanocomposite Sm-Co/Fe multilayer films. J. Appl. Phys. 2010, 107, 043911. [Google Scholar] [CrossRef]
- Gong, Y.S.; Qiu, Z.G.; Liang, S.Z.; Zheng, X.R.; Meng, H.X.; Zheng, Z.G.; Chen, D.Y.; Yuan, S.F.; Xia, W.X.; Zeng, D.C.; et al. Strategy of preparing SmCo based films with high coercivity and remanence ratio achieved by temperature and chemical optimization. J. Rare Earths 2023, in press. [CrossRef]
- Dong, C.H.; Wu, H.C.; Liu, L.; Xu, D.S.; Zhou, B.; Sun, Y.L.; Ding, Y.; Liang, J.C.; Yan, A.R. Growth of defects around grain boundary and evolution of cellular structure during isothermal aging process in 2:17-type SmCo permanent magnets. J. Magn. Magn. Mater. 2024, 171823. [Google Scholar] [CrossRef]
- Yan, S.S.; Barnard, J.A.; Xu, F.T.; Weston, J.L.; Zang, G. Critical dimension of the transition from single switching to an exchange spring process in hard/soft exchange-coupled bilayers. Phys. Rev. B 2001, 64, 184403. [Google Scholar] [CrossRef]
- Sawatzki, S.; Heller, R.; Mickel, C.; Seifert, M.; Schultz, L.; Neu, V. Largely enhanced energy density in epitaxial SmCo5/Fe/SmCo5 exchange spring trilayers. J. Appl. Phys. 2011, 109, 123922. [Google Scholar] [CrossRef]
- Victora, R.H.; Shen, X. Exchange coupled composite media for perpendicular magnetic recording. IEEE Trans. Magn. 2005, 41, 2828–2833. [Google Scholar] [CrossRef]
- Wang, J.; Shen, P.; Bai, W.K.; Victora, J.M.; Judy, R.H.; Song, W.L. Composite media (dynamic tilted media) for magnetic recording. Appl. Phys. Lett. 2005, 86, 142504. [Google Scholar] [CrossRef]
- Vashisht, G.; Shashank, U.; Gupta, S.; Medwal, R.; Dong, C.L.; Chen, C.L.; Asokan, K.; Fukuma, Y.; Annapoorni, S. Pinning-assisted out-of-plane anisotropy in reverse stack FeCo/FePt intermetallic bilayers for controlled switching in spintronics. J. Alloys Compd. 2021, 877, 160249. [Google Scholar] [CrossRef]
- Li, H.L.; Li, X.H.; Guo, D.F.; Lou, L.; Li, W.; Zhang, X.Y. Three-Dimensional Self-Assembly of Core/Shell-Like Nanostructures for High-Performance Nanocomposite Permanent Magnets. Nano Lett. 2016, 16, 5631–5638. [Google Scholar] [CrossRef]
- Lou, L.; Li, Y.Q.; Li, X.H.; Li, H.L.; Li, W.; Hua, Y.X.; Xia, W.X.; Zhao, Z.H.; Zhang, H.T.; Yue, M.; et al. Directional Magnetization Reversal Enables Ultrahigh Energy Density in Gradient Nanostructures. Adv. Mater. 2021, 33, 2102800. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.D.; Zhang, Y.F.; Han, J.Z.; Yang, Y.C.; Han, L.; Yang, J.B. Synergetic crystallization in a Nd2Fe14B/α-Fe nanocomposite under electron beam exposure conditions. Nanoscale 2016, 8, 18221. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.W.; Li, X.H.; Lou, L.; Hua, Y.X.; Zhu, G.J.; Li, M.; Zhang, H.T.; Xiao, J.W.; Wen, B.; Yue, M.; et al. Engineering Bulk, Layered, Multicomponent Nanostructures with High Energy Density. Small 2018, 14, 1800619. [Google Scholar] [CrossRef] [PubMed]
- Li, X.H.; Lou, L.; Song, W.P.; Huang, G.W.; Hou, F.C.; Zhang, Q.; Zhang, H.T.; Xiao, J.W.; Wen, B.; Zhang, X.Y. Novel Bimorphological Anisotropic Bulk Nanocomposite Materials with High Energy Products. Adv. Mater. 2017, 29, 1606430. [Google Scholar] [CrossRef] [PubMed]
- Goto, E.; Hayashi, N.; Miyashita, T.; Nakagawa, K. Magnetization and Switching Characteristics of Composite Thin Magnetic Films. J. Appl. Phys. 1965, 36, 2951. [Google Scholar] [CrossRef]
- Leineweber, T.; Kronrniiller, H. Micromagnetic examination of exchange coupled ferromagnetic nanolayers. J. Magn. Magn. Mater. 1997, 176, 145. [Google Scholar] [CrossRef]
- Zhao, G.P.; Zhao, M.G.; Lim, H.S.; Feng, Y.P.; Ong, C.K. From nucleation to coercivity. Appl. Phys. Lett. 2005, 87, 162513. [Google Scholar] [CrossRef]
- Zhao, G.P.; Wang, X.L. Nucleation, pinning, and coercivity in magnetic nanosystems: An analytical micromagnetic approach. Phys. Rev. B 2006, 74, 012409. [Google Scholar] [CrossRef]
- Quesada, A.; Delgado, G.; Pascual, L.; Aragón, A.M.; Marín, P.; Granados-Miralles, C.; Foerster, M.; Aballe, L.; Prieto, J.E.; de la Figuera, J. Exchange-spring behavior below the ex.change length in hard-soft bilayers in multidomain confifigurations. Phys. Rev. B 2018, 98, 214435. [Google Scholar] [CrossRef]
- Asti, G.; Ghidini, M.; Pellicelli, R.; Pernechele, C.; Solzi, M.; Albertini, F.; Casoli, F.; Fabbrici, S.; Pareti, L. Magnetic phase diagram and demagnetization processes in perpendicular exchange-spring multilayers. Phys. Rev. B 2006, 73, 094406. [Google Scholar] [CrossRef]
- Schrefl, T.; Fischer, R.; Fidler, J.; Kronmüller, H. Two- and three-dimensional calculation of remanence enhancement of rare earth based composite magnets (invited). J. Appl. Phys. 1994, 76, 7053. [Google Scholar] [CrossRef]
- Röhlsberger, R.; Thomas, H.; Schlage, K.; Burke, E.; Leupold, O.; Rüffer, R. Imaging the Magnetic Spin Structure of Exchange-Coupled Thin Films. Phys. Rev. Lett. 2002, 89, 237201. [Google Scholar] [CrossRef]
- O’Donovan, K.V.; Borchers, J.A.; Majkrzak, C.F.; Hellwig, O.; Fullerton, E.E. Pinpointing Chiral Structures with Front-Back Polarized Neutron Reflectometry. Phys. Rev. Lett. 2002, 88, 067201. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).