Artificial Neural Network-Based Prediction and Morphological Evolution of Cu₂O Crystal Surface Energy

Abstract

In this study, we investigate the crystal structure, surface energy, and atomic arrangement of Cu₂O. Understanding these properties is crucial for exploring the potential applications and understanding the behavior of this material. We employ the Wulff construction method and an artificial neural network (ANN) model to analyze the relative surface energies of different crystal facets and predict the surface energy of Cu₂O. The ANN model exhibits excellent performance, demonstrating its effectiveness in predicting material properties and providing automated feature-learning and nonlinear-modeling capabilities. Moreover, we analyze the atomic arrangements on various crystal facets and observe the presence of oxygen atoms on the {100} facet, as well as exposed under-coordinated copper atoms on the {111} and {110} facets. High-index facets such as {211} exhibit a higher atomic step density and screw dislocation density. By precisely controlling the synthesis process, it is possible to manipulate the proportion of high-index facets. These findings highlight the significance of understanding the surface energy and atomic arrangement of Cu₂O crystals for comprehending their properties and surface reactions. In summary, this study provides valuable insights into the crystal structure, surface energy, and atomic arrangement of Cu₂O, offering inspiration for its properties and potential applications. The combination of the Wulff construction method and ANN modeling provides a comprehensive understanding of Cu₂O crystals and their surface behavior, contributing to the field of materials science and laying the foundation for various future applications utilizing the unique properties of Cu₂O.

1. Introduction

Cu₂O, also known as cuprous oxide, is a prominent semiconductor material with versatile applications that have gained significant attention in scientific research. Its promising characteristics have attracted attention with regard to its applications in solar cells, photocatalysis, and optoelectronic devices [1,2,3,4]. Among the notable features of Cu₂O, its low cost, abundant reserves, and environmental friendliness make it an ideal candidate for CO₂ reduction catalysts. Cu₂O nanostructures exhibit advantages such as enhanced surface area, interface charge separation and transfer, and quantum efficiency, holding the potential to promote the development of CO₂ reduction technologies [5]. However, interface conductivity is a key factor affecting device performance, and traditional metal contacts can result in inefficient charge transfer and high contact resistance. Therefore, nonmetallic materials for Cu₂O transparent contacts have been investigated. For example, first-principles calculations revealed that copper oxide–graphene composite materials could be used as transparent contacts for Cu₂O because of their interface electronic properties [6]. Additionally, Cu₂O can be electrochemically reduced to pure copper, which has excellent electrocatalytic performance in the CO₂ reduction reaction, potentially producing valuable multicarbon chemicals from CO₂ [7]. Cu₂O holds great promise in various technological fields, and its developments may contribute to renewable energy and environmental sustainability.

The research has indicated that the morphology of Cu₂O exerts a pronounced influence on its properties and performance, and the morphology of Cu₂O can be modulated through various synthesis methods and conditions, thereby affecting its crystal structure, surface energy level distribution, optical characteristics, and electronic transport properties [8]. In terms of optical properties, different morphologies exhibit significant variations in light absorption, transmission, and reflection. Comparisons of morphology-related absorption, transmission, and reflection for specific wavelength ranges are crucial [9]. Additionally, morphology modulation also affects the band structure and photoluminescence behavior of Cu₂O. Regarding electronic transport characteristics, morphology plays a pivotal role in regulating carrier transport, including carrier mobility, lifetime, and efficiency of electron transport pathways. In terms of electrochemical performance, morphology control can greatly enhance the catalytic activity, stability, and selectivity of Cu₂O as a catalyst or electrode material. Furthermore, morphology modulation can impact the electrocatalytic performance by altering the interface properties between Cu₂O and electrolyte/reactants. Cu₂O morphology influences its stability and reliability, whereby morphology design can improve the stability of the crystal structure, reduce surface defects, and optimize oxidation characteristics, thereby enhancing long-term performance and lifespan.

In crystallography, crystal surfaces are described by a set of indices (hkl) that represent the position and orientation of the surfaces within the crystal lattice. High-index facets refer to surfaces with larger surface indices. These high-index facets hold significant application value in the fields of materials science and catalysis due to their ability to provide an abundance of active surface sites, thereby facilitating alterations in material surface reactivity and catalytic activity [10]. The exploitation of high-index crystal surfaces offers promising prospects for improved material performance and enhanced catalytic efficiency, making them a subject of great interest in scientific research and exploration. High-index crystal surfaces of Cu₂O offer a greater number of surface atomic or molecular binding sites, thus exhibiting a higher density of active sites on the crystal surface compared to low-index crystal surfaces. These abundant active sites play a pivotal role in promoting chemical reactions and enhancing catalytic performance [11]. Consequently, high-index facets are extensively employed in interface catalysis and electrochemical devices such as photocatalysis, batteries, and sensors. Therefore, the presence of high-index crystal surfaces in Cu₂O holds significant implications in the fields of materials science, catalysis, and nanotechnology [1,2,5,11]. Their precise control and utilization contribute to diverse applications and pave the way for advancements in these areas.

Surface energy determines the stability and reactivity of crystal surfaces, influencing the development and evolution of crystal morphology [12,13,14,15]. Different crystal facets possess different surface energies, generally indicating that facets with a lower surface energy are more stable within the crystal structure. Surface energy governs the growth rate and evolution direction of crystal facets, driving the crystal to select facets with a lower surface energy in order to minimize the total surface energy. The Wulff construction method, based on the principle of energy minimization, utilizes the Wulff curve to display the relative stability of different crystal facets [15,16,17]. This polyhedral shape represents the most stable form that minimizes the total surface energy of the crystal. Hence, the Wulff construction offers a predictive approach for determining the crystal shape and growth direction. Density-functional theory (DFT) is currently the primary method for computing surface properties, based on electronic structure theory, which calculates the physical and chemical properties of materials [18]. However, these calculations often require high computational costs and significant computational resources. Additionally, the structure and energy of a crystal surface can vary under different experimental conditions, necessitating the consideration of various factors that influence the surface energy to accurately compute it.

In recent years, with the advancement of machine learning, it has become an important technology to accelerate materials research and development, optimize material performance, and drive the application of new materials [19,20,21,22]. Traditional materials research and development is a time-consuming and labor-intensive task, while machine learning can greatly reduce trial-and-error costs and time by analyzing large amounts of material data and experimental results, and establishing models to predict material properties and characteristics. This data-driven approach significantly improves the efficiency of materials research and development, playing a significant role in the study of Cu₂O. For instance, Werasak et al. [23] employed density-functional theory (DFT) and machine-learning models to investigate the binding energies between copper-containing metal-organic frameworks (MOFs) and Cu₂O nanoparticles (NPs). They applied supervised training algorithms to assess the relationship between tear creatinine levels and serum creatinine levels, providing potential technical support for the remote monitoring of kidney function. In another study, Zeng et al. [24] constructed branched nanostructures, employed spectral shifts and color changes, and implemented learning and training through a convolutional neural network (CNN). This approach enabled the color detection and analysis of Cu₂O. Moreover, machine-learning methods have been applied to extract structural information from experimental data, distinguishing different structural patterns of Cu oxide clusters (such as Cu₂O and CuO) and reliably evaluating average cluster sizes [25].

In this study, we conduct an analysis of the structural characteristics and surface energy of Cu₂O crystals and their influence on the control of crystal morphology. Furthermore, we have established a database comprising surface energy and Wulff shape data for different crystallographic surfaces of Cu₂O crystals, and diversified crystal morphologies are generated by adjusting the proportion of surface energies. Using the trained ANN model, the surface energy of a given crystal morphology is predicted, and the variation trend of the surface energies for different crystal facets is observed. The evolution process of crystal morphology from cubes to polyhedra composed of high-index crystal facets is predicted by the model, and the growth patterns and surface energy variations of different crystal facets are investigated. This study provides valuable insights into the crystal structure, surface energy, and atomic arrangements of Cu₂O, shedding light on its properties and potential applications. These findings contribute to the broader field of materials science and provide a foundation for future research aimed at harnessing the unique properties of Cu₂O for various applications.

2. Methods

2.1. Wulff Construction

Under thermodynamic equilibrium, the shape of crystals is determined by minimizing their total surface energy, which can be expressed as

$$∆G=\mathrm{m}\mathrm{i}\mathrm{n} \left\{{\sum }_{hkl}{A}_{hkl}{\gamma }_{hkl}\right\}$$

(1)

where $A_{hkl}$ is the area and ${\gamma }_{hkl}$ is the surface energy per unit area of the {hkl} surface. In 1901, mineralogist G. Wulff proposed a theory, called Wulff construction [16], stating that the equilibrium shape of a particle is dictated by minimizing the total surface free energy while preserving a constant volume. Additionally, he demonstrated that the optimal closed shape with minimum surface energy is characterized by the proportional relationship between the distance of each face from the center of the crystal, $d_{hkl}$, and the surface energy (${\gamma }_{hkl}$) of that particular face, expressed as

$$\frac{d_{hkl}}{{\gamma }_{hkl}}=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}$$

(2)

This mathematical expression signifies that the equilibrium shape of the material is influenced by the relative surface energies of its crystal facets. Facets with lower surface energy contribute more to the overall shape, while facets with higher surface energy have less influence or may even be absent. The concept of Wulff construction provides a geometric representation of this equilibrium shape based on the surface energy of the crystallographic surfaces, resulting in the formation of the Wulff polyhedron as an idealized equilibrium shape. The Wulff construction is a significant tool for predicting the morphology and preferential growth directions of crystals, thereby playing a crucial role in investigating the crystal growth mechanisms and properties of materials [12,15,17,26].

2.2. Artificial Neural Networks (ANNs)

With the rise of machine learning, significant breakthroughs have been achieved in various fields such as computer vision and natural language processing based on ANNs. ANNs consist of a large number of interconnected artificial neurons or nodes, which transmit and process information through weighted connections [27,28]. Each neuron receives inputs from other neurons, performs a weighted sum, applies a nonlinear activation function, and passes the result to the next layer of neurons. The training process of ANNs involves adjusting the weights and biases to enable the network to learn the complex mapping between inputs and outputs. ANNs find wide-ranging applications in materials science tasks like material exploration and discovery, prediction of material properties, optimization of material preparation and processing, correlation between material structure and properties, among others [21,22,29,30,31]. Their advantages include the ability to automatically learn feature representations, nonlinear-modeling capabilities, and a certain degree of robustness to noise.

The optimization and development of an ANN model using the MLPRegressor algorithm involve a systematic process. Firstly, we select the training dataset $T=\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_n,y_n\right)\}$, where $x_i=\left(A_{100}^i,A_{111}^i,\cdots ,A_{hkl}^i\right)$ represents the feature vector of the instance and $y_i=\left({\gamma }_{100}^i,{\gamma }_{111}^i,\cdots ,{\gamma }_{hkl}^i\right)$ denotes the instance class. Here, n represents the number of instances in the training dataset. Then, the architectural design of the ANN model is carefully considered to effectively capture the underlying patterns in the dataset. This involves determining the number of hidden layers, the number of neurons within each layer, and the activation function. To determine the optimal set of hyperparameters [32], we employ the grid search technique, ensuring a systematic and rigorous approach in optimizing and developing the model. Finally, to assess the performance of the ANN model, metrics of mean absolute error (MAE) and coefficient of determination (R²) are employed, defined as follows:

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n}\sum _{i=1}^n\left|{\gamma }_i-\widehat{\gamma }\right|$$

(3)

$$R^2=1-\frac{{\sum }_{i=1}^n{({\gamma }_i-\widehat{\gamma })}^2}{{\sum }_{i=1}^n{({\gamma }_i-{\overline{\gamma }}_i)}^2}$$

(4)

Here, n is the number of samples, ${\gamma }_i$ is the actual target value, $\widehat{\gamma }$ is the model’s predicted value, ${\overline{\gamma }}_i$ is the mean of the measured values. The MAE calculates the average absolute difference between the predicted and actual values, providing an indication of the ANN model’s average prediction error. The R² score quantifies the proportion of the variance in the dependent variable that is predictable from the independent variables, presenting a measure of how well the model fits the observed data.

3. Results

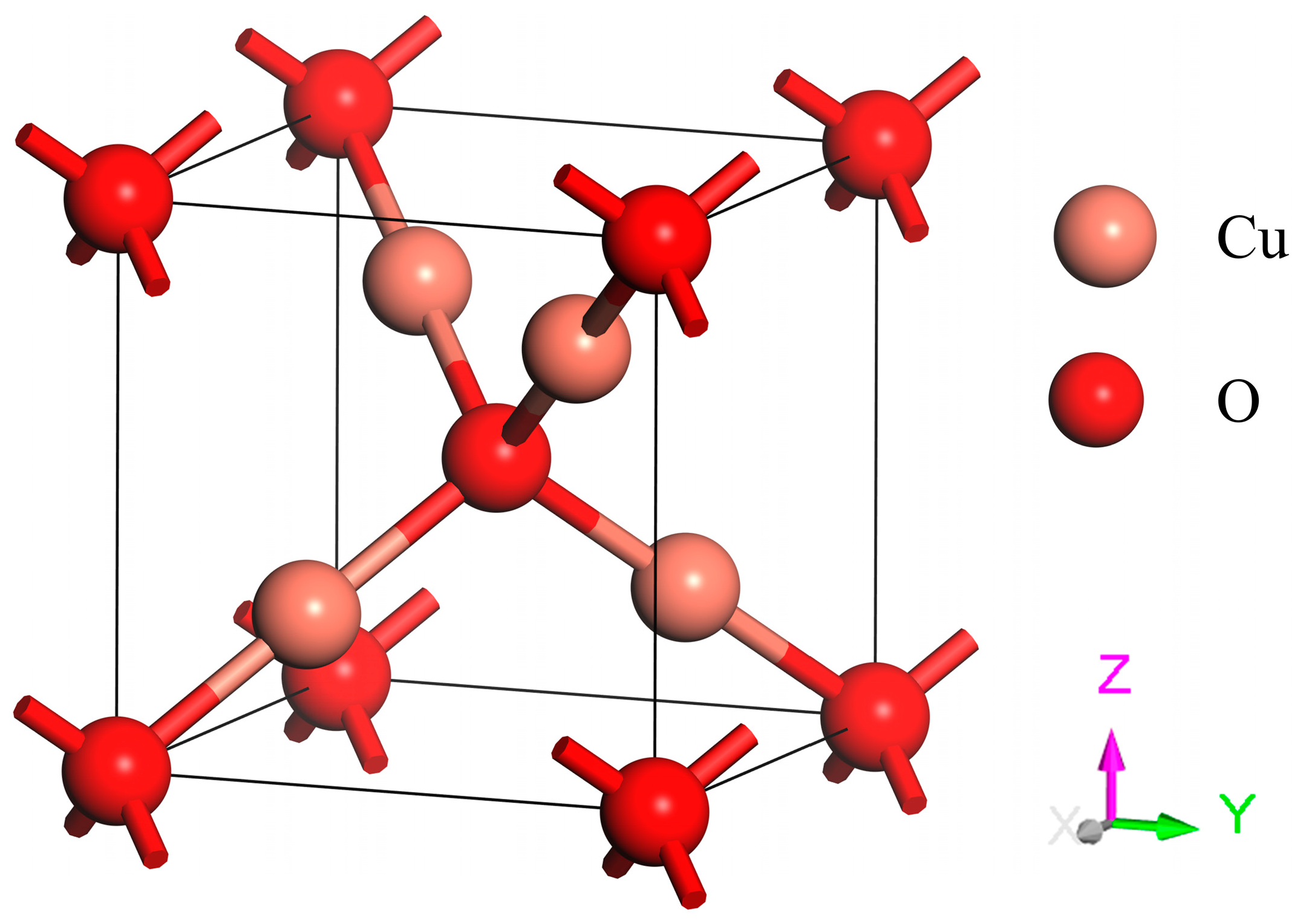
Cu₂O crystallizes in a cubic structure with lattice constants of a = b = c = 4.27 Å [33]. The copper atoms are arranged in a face-centered cubic (FCC) sublattice, while the oxygen atoms are located in a body-centered cubic (BCC) sublattice. One sublattice is shifted by a quarter of the body diagonal relative to the crystals. A unit cell scheme can be seen in Figure 1. The crystal belongs to the Pn$\overline{3}$m space group, which includes the point group with full octahedral symmetry.

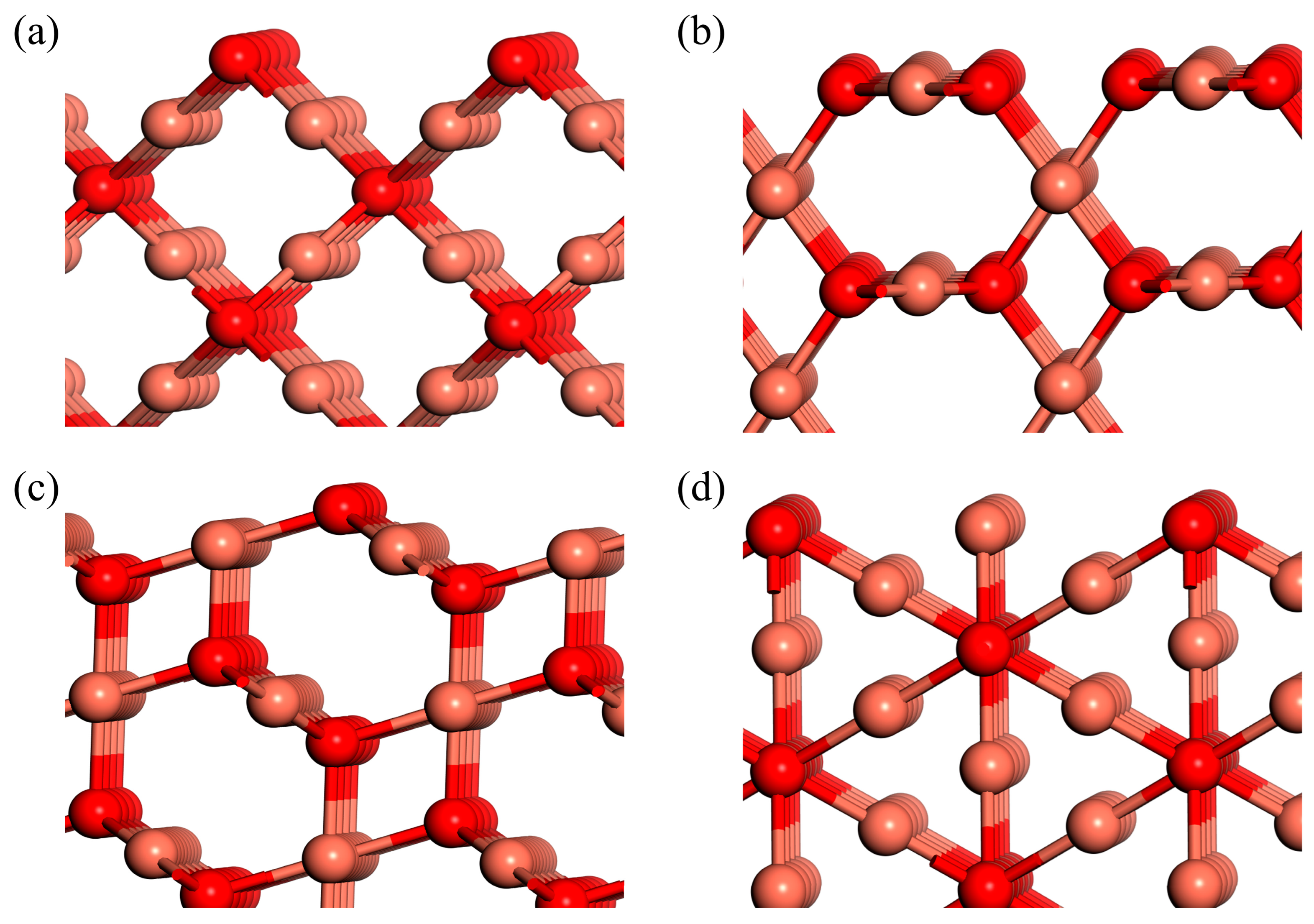
The arrangement of atoms on various crystallographic surfaces of Cu₂O is depicted in Figure 2. For the {100} facet, only O atoms are present on the surface, resulting in electrical neutrality. On the {111} facet, Cu atoms are under-coordinated. Each pair of Cu atoms possesses a dangling bond that extends perpendicularly to the {111} facet. These dangling bonds give rise to a positive charge on the {111} facet. Likewise, the {110} facet exhibits exposed Cu atoms with dangling bonds. The density of dangling Cu atoms on the {110} facet is approximately 1.5 times higher than that on the {111} facet [34]. As a consequence, the {110} facet has a higher positive charge density compared to the {111} facet. Therefore, the surface energies of Cu₂O follow the order: ${\gamma }_{100}<{\gamma }_{111}<{\gamma }_{110}$. High-index crystal facets of Cu₂O, such as {211}, {311}, {522}, and {744}, possess a higher density of atomic steps and kinks compared to low-index facets. Due to the fact that these high-index crystal facets are all expressed in the form of {hkk}, for the purpose of this study, we have chosen to exclusively focus on the classic {211} facets. The surface structure of the {211} facet is depicted in Figure 2d. The formation of high-index facets typically involves the combination of lower-index facets through steps and kinks configurations. The elevated surface energy stems from the augmented structural instability and atomic interactions resulting from the abundance of steps and kinks on high-index facets. Consequently, high-index facets tend to undergo surface reconstruction and exhibit enhanced catalytic activity. Their irregular structure renders them more reactive and susceptible to chemical reactions, such as adsorption and catalysis. This information about the surface energy and atomic arrangements on different facets of Cu₂O crystals is vital for understanding their properties and surface reactions.

Various well-defined morphologies of an enclosed Cu₂O polyhedron have been successfully synthesized in experiments, including cubes, octahedra, rhombic dodecahedra, 14-facet polyhedron (corner-truncated octahedra), 20-facet polyhedron (edge-truncated octahedra), as well as a polyhedron with 18, 26, 30, 50, and 74 facets [7,8,35,36,37]. The controlled synthesis techniques employed have achieved a diverse array of Cu₂O polyhedrons, showcasing their potential in catalysis, materials science, and related fields. During the synthesis of Cu₂O crystals, researchers aim to tailor their structures, specifically controlling the proportion of high-index crystal facets. High-index facets refer to crystal surfaces with a relatively high surface energy (${\gamma }_{H-index}$), while low-index facets have a lower surface energy (${\gamma }_{L-index}$). In Cu₂O crystals, the surface energies of different crystal surfaces follow a specific order: ${\gamma }_{L-index}<{\gamma }_{H-index}$ [1,11,38]. Research has shown that Cu₂O micro- and nanocrystals enveloped by high-index facets demonstrate superior performance in photocatalytic degradation and CO₂ reduction reaction performance [2,5]. This can be attributed to the presence of a greater number of active sites and increased surface reactivity offered by high-index facets, thereby enhancing the catalytic activity. Therefore, it is crucial to design and control the proportion of high-index facets when synthesizing Cu₂O crystals in order to enhance their catalytic performance and other relevant properties.

However, synthesizing Cu₂O crystals with high-index facets presents a significant challenge as the rate of crystal growth perpendicular to the high-index facets significantly surpasses that along the low-index facets. Consequently, the high-index facets tend to vanish rapidly during the crystal formation process. Current synthetic methods predominantly yield Cu₂O crystals dominated by low-index facets, which limits their catalytic activity. Even slight variations in these conditions can alter the crystal growth mechanism, leading to different morphologies. For example, with an increase in the NaOH concentration, the growth of high-index {522} facets becomes more prominent, leading to the formation of a polyhedron with 50 facets [35]. Hence, there is an urgent need to develop facile and controllable synthetic strategies to achieve Cu₂O nanostructures exclusively composed of high-index facets. Particularly, the synthesis of well-defined, sub-hundred-nanometer-sized polyhedral Cu₂O nanostructures is desirable as these morphologies are easier to manipulate and hold great potential for a superior catalytic and optoelectronic performance.

To accomplish this goal, an in-depth understanding of the surface energies of different crystal surfaces and their influence on catalytic activity and material properties is essential. Exploring synthetic approaches involving the modulation of experimental conditions and appropriate additives holds promise for achieving the selective growth of high-index facet-dominated Cu₂O crystals. Such synthetic methodologies will contribute to enhancing the catalytic performance of Cu₂O and drive advancements in related fields such as catalyst design and energy conversion. Sun et al. [39] successfully synthesized a Cu₂O crystal enclosed by 6 {100} facets, 8 {111} facets, 12 {110} facets, and 24 {211} facets, as shown in Figure 3a. The morphology of Cu₂O crystals is influenced significantly by the composition, concentration, and temperature of the solution [5,34,35,36]. Consequently, variations in the experimental conditions can lead to diverse morphologies of Cu₂O crystals enclosed by {100}, {111}, {110}, and {211} facets [37]. In the majority of experiments aiming to synthesize specific crystal morphologies, researchers manipulate the exposed facets of Cu₂O crystals by adjusting the surface energy through the application of suitable capping agents. By carefully selecting and controlling the concentrations and types of capping agents, researchers can direct the crystal growth toward the desired morphologies, allowing for the tailored synthesis of Cu₂O crystals with precise facet orientations [8]. Understanding and controlling these factors are of paramount importance for achieving the desired morphology control and harnessing the superior performance of Cu₂O with specific morphologies in catalysis, optoelectronics, and other applications [9]. Different crystal facets exhibit varying surface energies, and their relative stability and growth rates dictate the ultimate crystal morphology.

In this study, we have created an extensive database that encompasses the surface energies and corresponding Wulff shapes specifically for Cu₂O crystals. The {100} facets of Cu₂O crystals have the lowest surface energy among all the crystal facets studied in this study. To establish a baseline for comparison, we have selected the {100} facets and expressed the surface energies of the remaining facets as ratios relative to the {100} facets. By adjusting the ratios of the surface energies among the various crystal facets, we have successfully generated a diverse collection of 4423 potential morphologies, and the complete dataset is readily accessible through our website (https://github.com/F-M-Lai/Cu2O_Surface_energy_area, accessed on 4 September 2023). Figure 3b–d illustrate the relationship between the surface energy ratio and area fraction for each facet. It is worth noting that the surface area increases as the ratio of the surface energy decreases. This phenomenon can be attributed to the preferential growth exhibited by crystal facets with a higher surface energy, resulting in accelerated growth rates when compared to other facets.

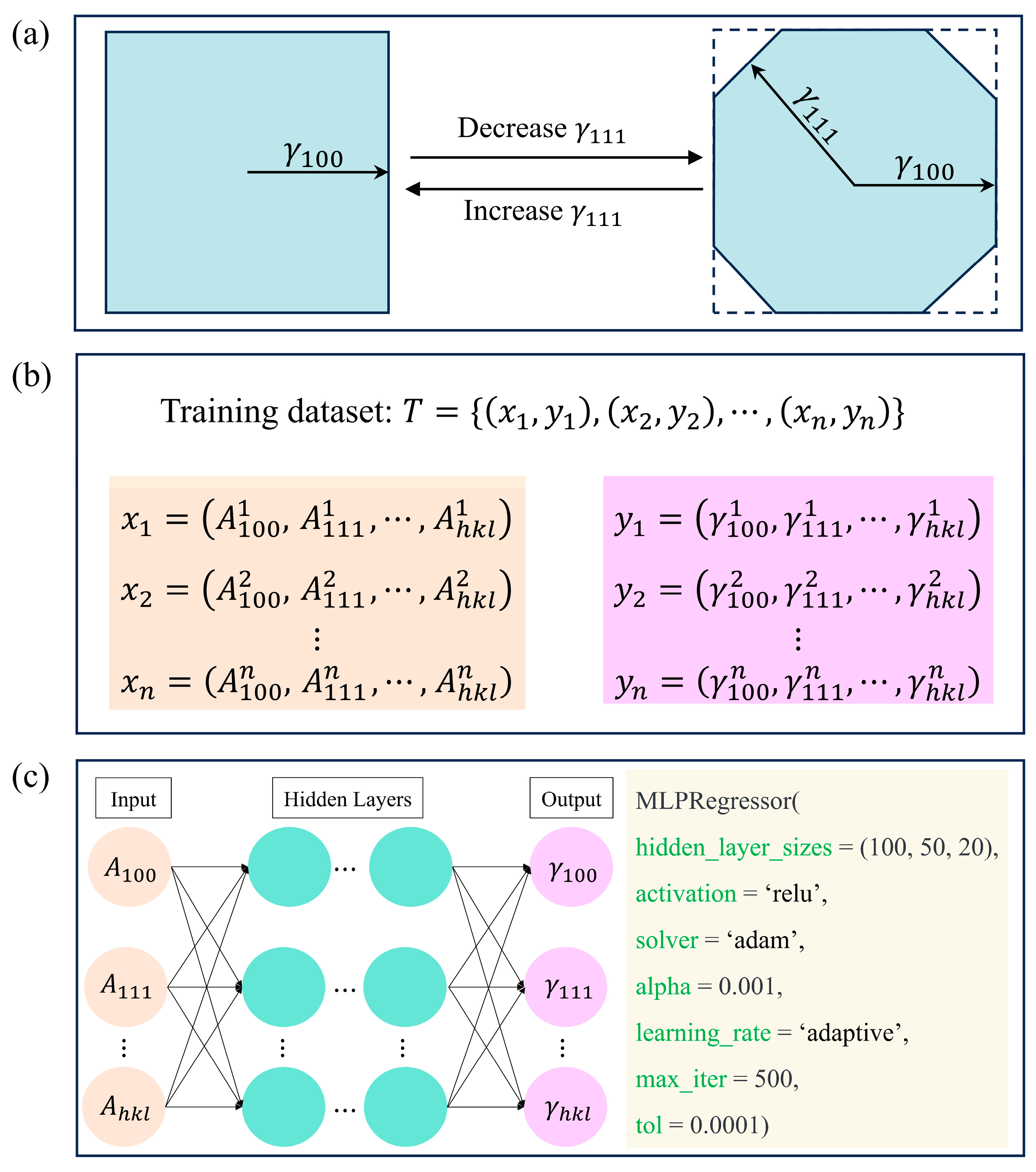
Figure 4a illustrates the use of the Wulff construction method with different surface energy values to generate a morphology dataset for Cu₂O, taking {100} and {111} facets as an example. By incorporating all crystallographic planes, we obtained the complete morphology dataset, as shown in Figure 4b. We used the open-source Python package scikit-learn to construct the regression model. The dataset is divided into a training set and a test set in an 8:2 ratio. To train the ANN model, we employed an algorithm and configured it with specific parameters (Figure 4c). The structure of an ANN model consists of input neurons, hidden layers, and an output layer. The input neurons in the input layer receive the surface area values, while the hidden layers process the data, and the output layer generates the result, which corresponds to the surface energy. Moreover, the hidden layers have dimensions of 50, 30, and 20, respectively. The ReLU activation function is employed for introducing nonlinearity. Training the model involves using the Adam optimization algorithm as the solver, with a maximum of 500 iterations and a tolerance level of 0.0001 to ensure convergence. Additionally, a regularization parameter of 0.001 is applied to control overfitting, while the adaptive learning rate scheme adapts the learning rate to the specific training progress. The loss function employed in this study is the mean squared error (MSE) loss function, which calculates the squared difference between each sample’s predicted value and the actual value, and then takes the average of the squared differences across all samples. The specific expression of MSE loss function is:

$$L\left({\gamma }_i,\widehat{\gamma }\right)=\frac{1}{n}{\sum }_{i=1}^n{\left({\gamma }_i-\widehat{\gamma }\right)}^2$$

(5)

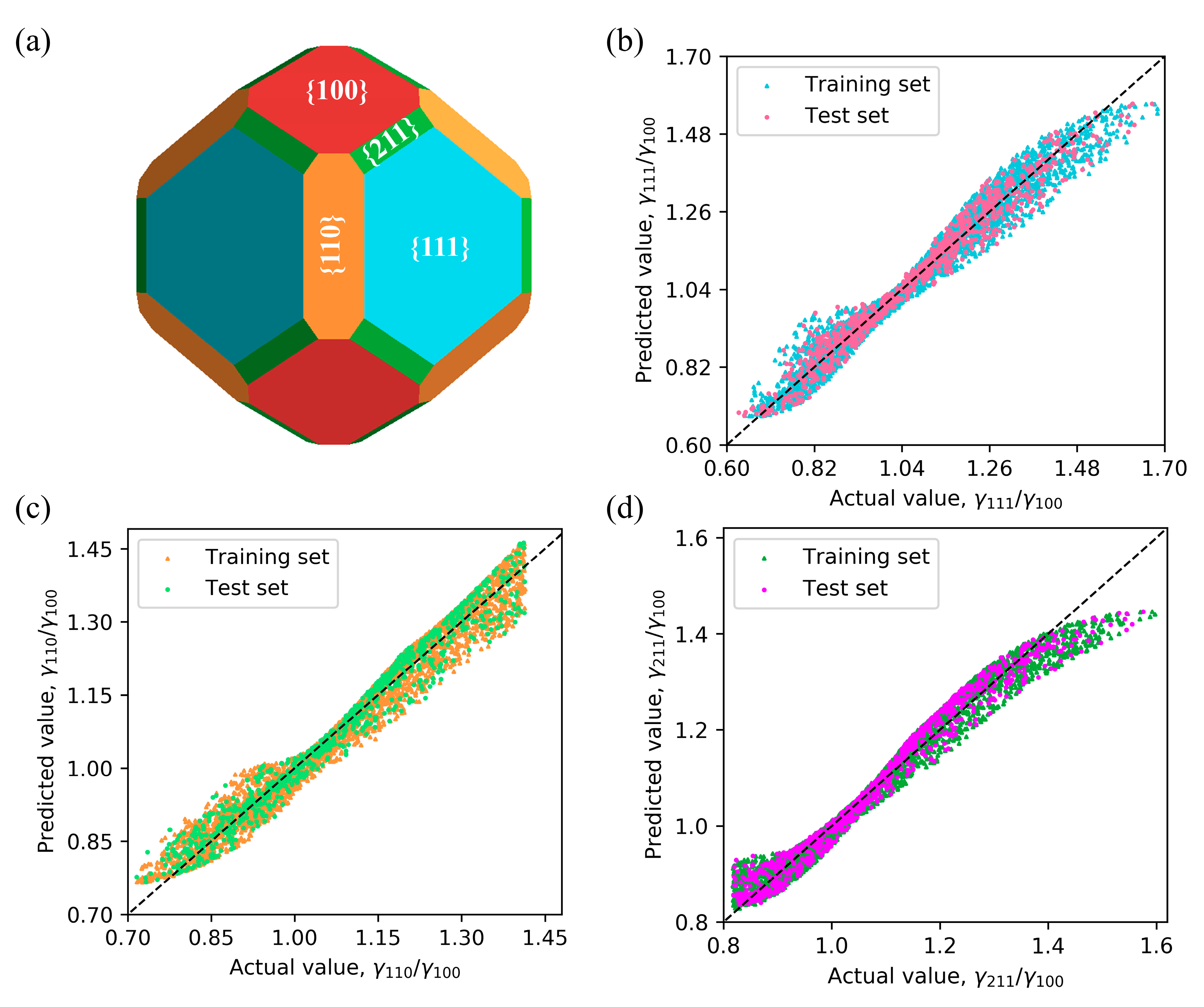
Based on the surface energies from our dataset, the morphology of Cu₂O can be predicted using our previously implemented Wulff construction algorithm [12,19]. Figure 5a presents the Cu₂O morphology obtained through the Wulff construction, which corresponds to the experimentally prepared morphology in Figure 3a. By employing the evaluation metrics and dividing the dataset into training and test sets, the effectiveness and generalization ability of the model can be assessed. The good performance of the ANN on the training set and test set are shown in Figure 5b–d.

The performance metrics of the ANN model on the training set are summarized in

Table 1. Performance metrics of the ANN model on training and test sets.

Surface Energy	Training Dataset		Test Dataset
	MAE	R2	MAE	R2
${\gamma }_{111}/{\gamma }_{100}$	0.03	0.97	0.03	0.97
${\gamma }_{110}/{\gamma }_{100}$	0.02	0.96	0.02	0.96
${\gamma }_{211}/{\gamma }_{100}$	0.02	0.98	0.02	0.98

. The MAE values for both the training and testing sets are similar, ranging from 0.2 to 0.3, indicating low levels of average absolute error. Additionally, the R² values for both sets ranged from 0.96 to 0.98, signifying a strong ability of the model to explain the variance in the target variable. Based on these outcomes, it can be concluded that the ANN model exhibits favorable performance characteristics, with consistent results on both the training and testing sets.

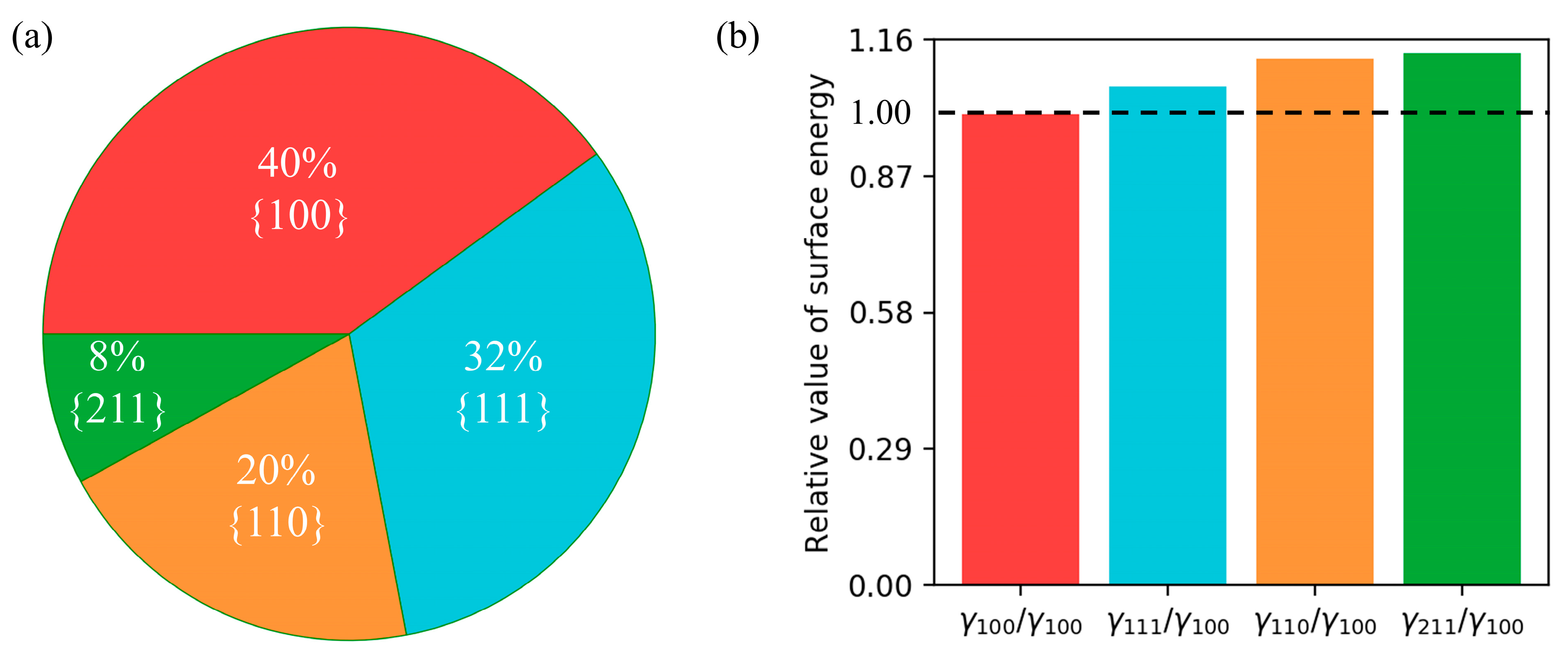
Based on the trained ANN model, the surface energy of a given crystal morphology can be predicted. From Figure 6a, it is observed that the {100} facets exhibit the largest surface area (40%), corresponding to the lowest surface energy value of 1.0 in Figure 6b. Conversely, the high-index facets {211} exhibit the smallest surface area (8%), corresponding to the highest surface energy value 1.13. These findings support the notion that the {111} facets are energetically more favorable, while the {211} facets are less favorable in terms of the surface energy.

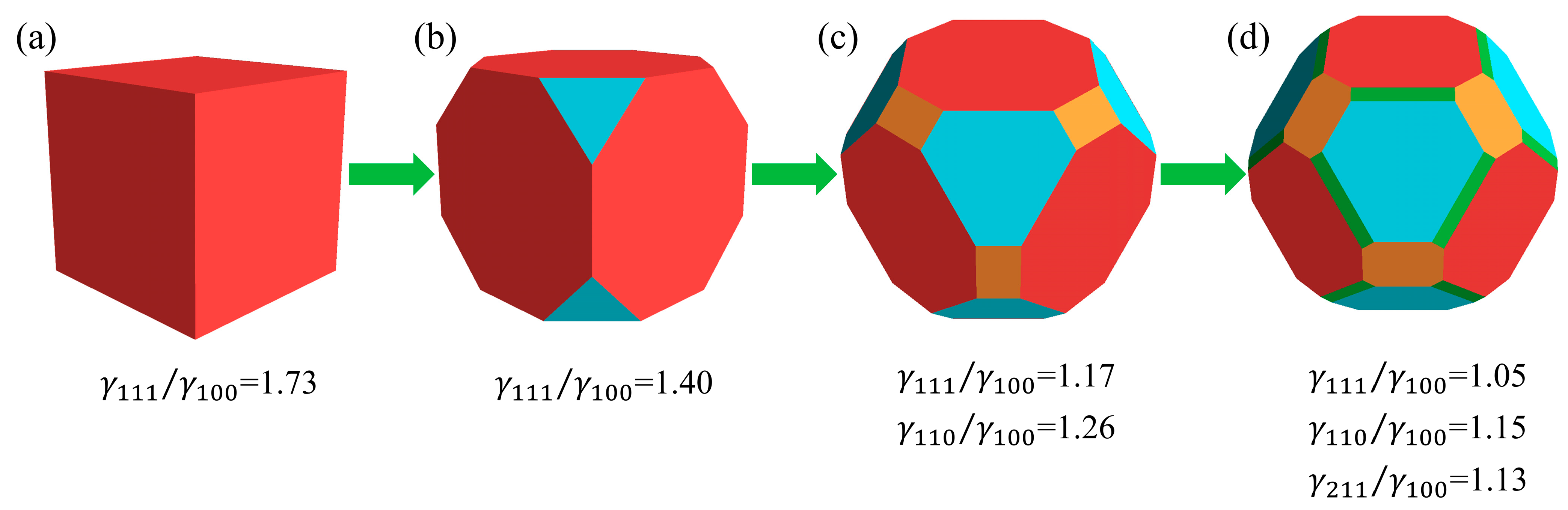
The morphology of Cu₂O crystals can provide crucial information about the growth mechanism and process. By studying the morphological evolution of crystals, a comprehensive understanding of the structural evolution during crystal growth can be achieved, unveiling the underlying growth mechanisms and principles in crystallography. Figure 7 illustrates the morphological evolution of a crystal from a cube to a polyhedron with fifty facets as the surface energy varies. The relative values of the surface energies are predicted using a well-trained ANN model. The crystal morphology transformation begins with a cube enclosed by {100} facets, which exhibit the lowest surface energy for Cu₂O, as shown in Figure 7a. As the surface energy of the {111} facets decreases, these facets initially emerge at the eight vertices of the cube, resulting in a truncated cube composed of six {1 0 0} facets and eight {1 1 1} facets (Figure 7b). Subsequently, {110} facets appear along the twelve edges of the truncated cube, generating twelve rectangular {1 1 0} facets and forming a geometric structure with twenty-six facets (Figure 7c). Finally, by further cutting the square, triangular, and rectangular facets along the edges of the cube, the highly symmetrical polyhedron with 50 facets is obtained (Figure 7d). This conclusion is consistent with the findings of Sun et al. [8].

The study of the morphological evolution in Cu₂O has profound implications in the fields of crystal growth and material optimization. By investigating the changes in crystal morphology, we can gain insights into the growth patterns of different crystal facets and the impact of the surface energy on crystal morphology. These results provide crucial guidance for controlling the Cu₂O crystal growth process and optimizing material properties, thereby offering significant contributions to the field.

4. Conclusions

In this study, we investigated the crystal structure and surface energy of Cu₂O using the Wulff construction and ANN model. The Wulff construction provided a geometric representation of the equilibrium shape of Cu₂O crystals based on the relative surface energies of different crystal facets. Additionally, the ANN model was employed to predict the surface energies of Cu₂O crystals. The model demonstrated good performance, as indicated by the low MAE and high R² values. The ANN approach showcased its effectiveness in predicting material properties, offering automated feature-learning and nonlinear-modeling capabilities. Moreover, the atomic arrangements on different crystal facets were analyzed, revealing the presence of oxygen atoms on the {100} facet and copper atoms with exposed unpaired bonds on the {111} and {110} facets. Higher-index crystal facets, such as {211}, are characterized by an increased atomic step density and spiral defect density. These findings indicated the importance of understanding the surface energy and atomic arrangements of Cu₂O crystals for comprehending their properties and surface reactions. Precise control over the synthesis process allowed for the manipulation of the proportions of high-index crystal facets. This successful synthesis showcased the significance of these Cu₂O polyhedra and opened up opportunities for further exploration and utilization in catalysis, materials science, and related fields.

Overall, this study provided valuable insights into the crystal structure, surface energy, and atomic arrangements of Cu₂O, shedding light on its properties and potential applications. The combination of the Wulff construction method and ANN modeling offered a comprehensive understanding of Cu₂O crystals and their surface behavior. These findings contribute to the broader field of materials science and provide a foundation for future research aimed at harnessing the unique properties of Cu₂O for various applications. The ANN model is a general machine-learning technique that can be extended to other crystals by collecting relevant data and adjusting the model parameters. However, this study did not conduct experiments under different conditions to validate the predictions of the model used in this study and investigate the stability and reactivity of Cu₂O crystals in various scenarios. Furthermore, the catalytic performance and material properties of Cu₂O crystals with different morphologies were not evaluated in this study. In future research, we will perform experiments to prepare Cu₂O crystals with diverse morphologies and conduct various tests such as photocatalytic degradation, CO₂ reduction, and optoelectronic measurements to demonstrate the advantages of Cu₂O crystals with high-index crystal facets.