Thermoelectric Performance of Ca2Si Synthesized by High-Temperature Melting
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Ca2Si
2.3. Characterization
3. Results and Discussion
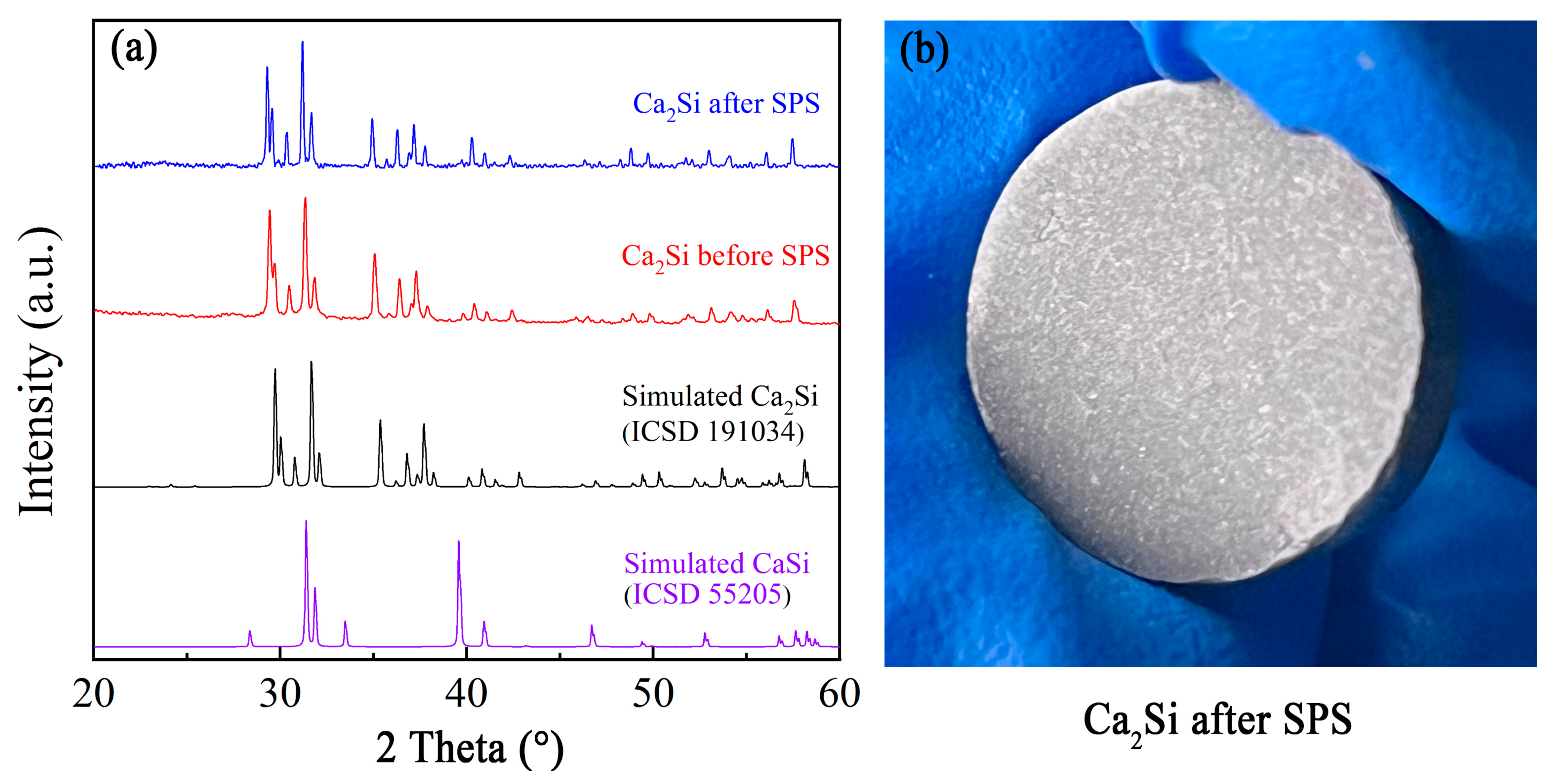
3.1. Preparation and Characterization of Ca2Si
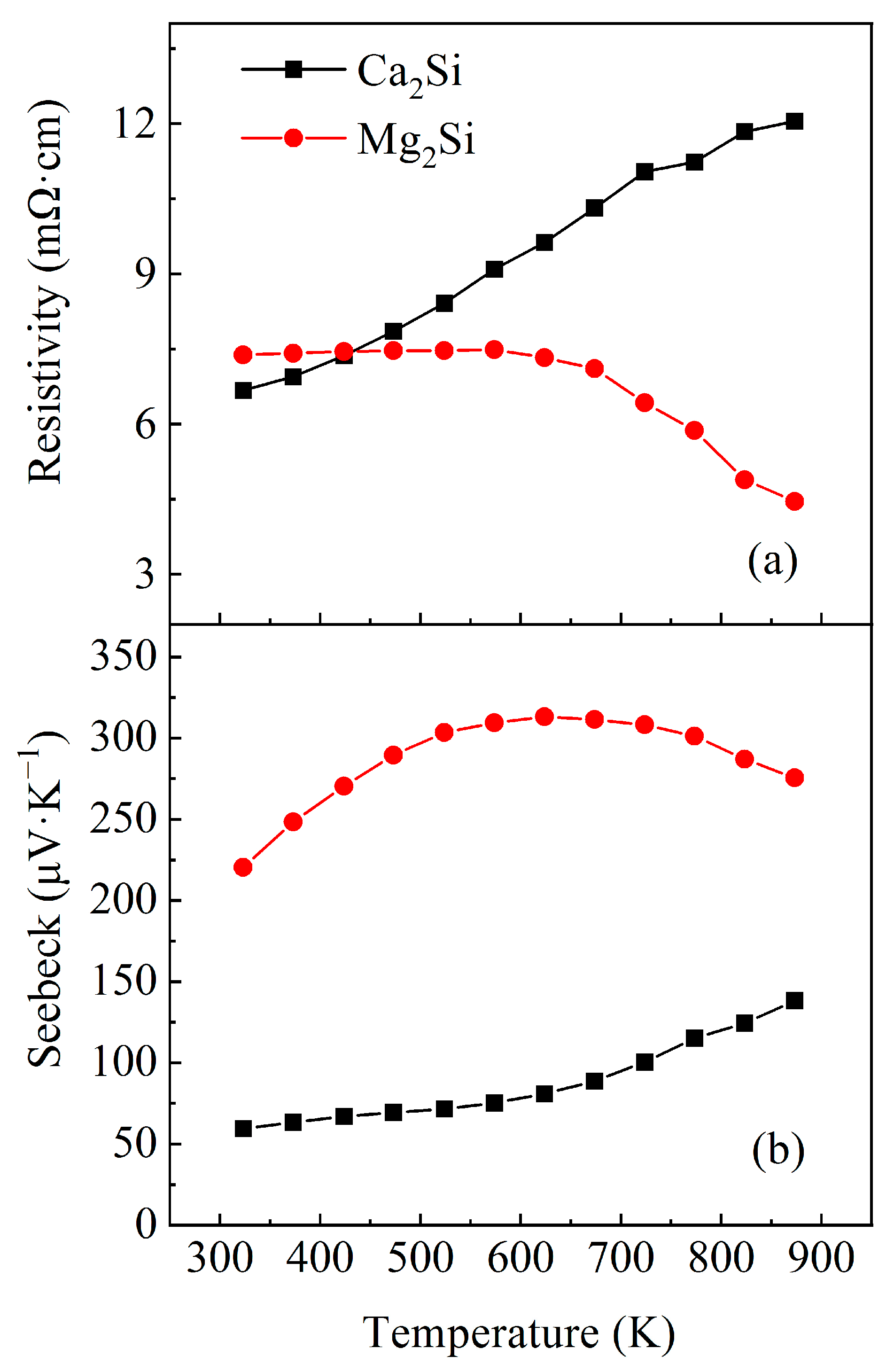
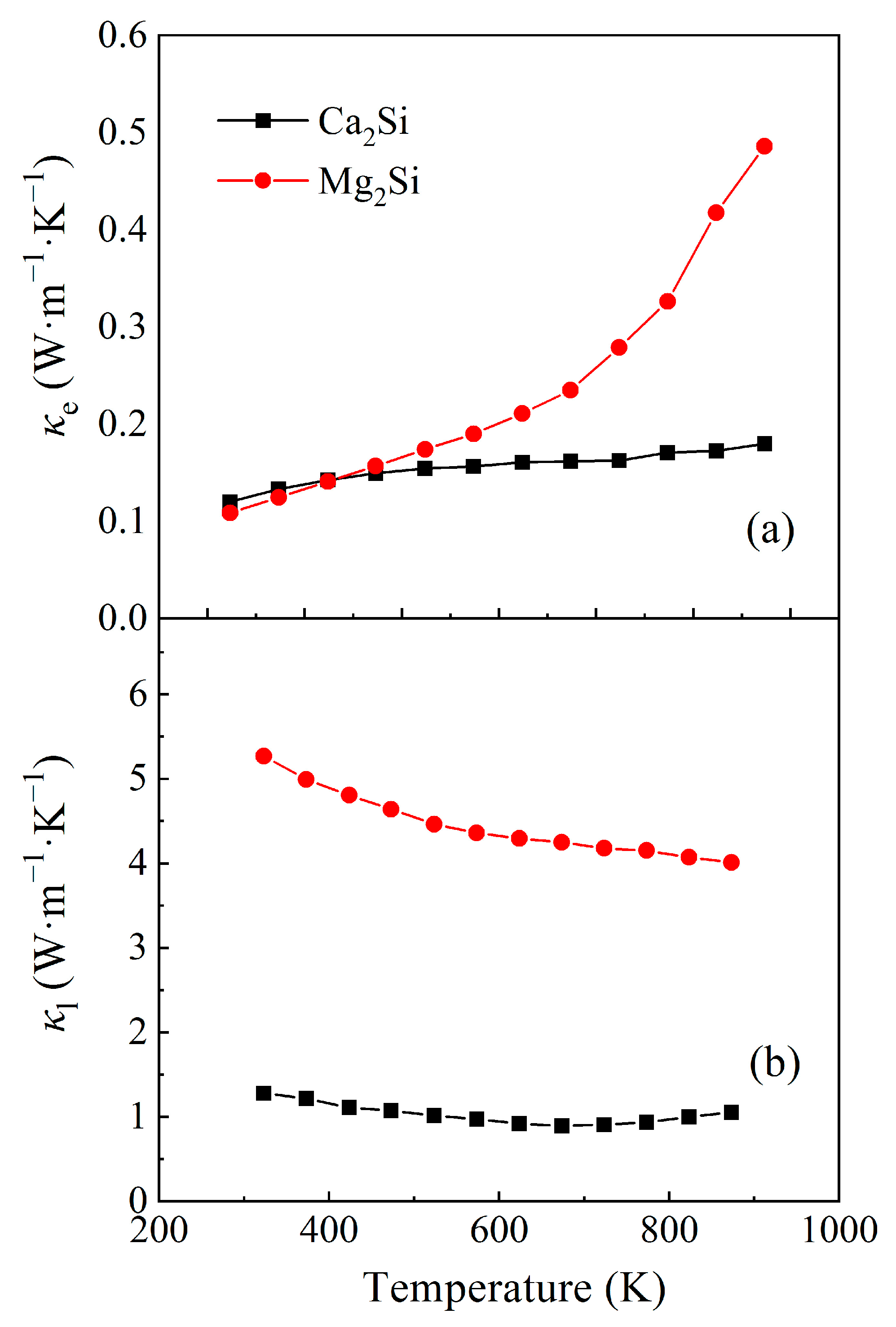
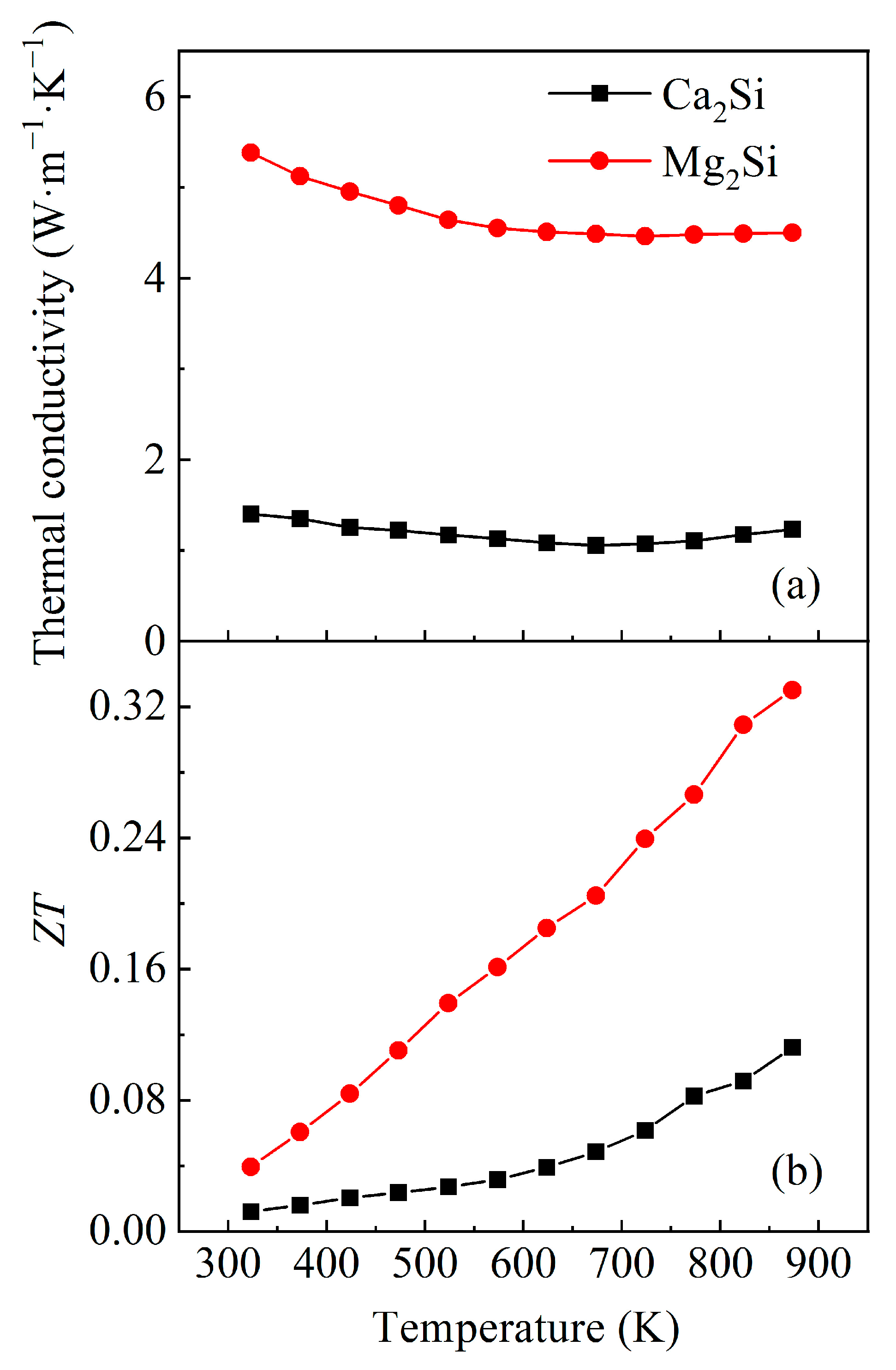
3.2. Thermoelectric Property
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.; Newbrook, D.W.; Dai, P.; de Groot, C.K.; Huang, R. Artificial neural network enabled accurate geometrical design and optimisation of thermoelectric generator. Adv. Energy Mater. 2022, 305, 117800. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, S.; Liu, Z.; Mu, E.; Hu, Z. Thermoelectric converter: Strategies from materials to device application. Nano Energy 2022, 91, 106692. [Google Scholar] [CrossRef]
- Min, G. New formulation of the theory of thermoelectric generators operating under constant heat flux. Energ. Environ. Sci. 2022, 15, 356–367. [Google Scholar] [CrossRef]
- Chen, W.-Y.; Shi, X.-L.; Zou, J.; Chen, Z.-G. Thermoelectric Coolers: Progress, Challenges, and Opportunities. Small Methods 2022, 6, 2101235. [Google Scholar] [CrossRef]
- Mamur, H.; Bhuiyan, M.R.A.; Korkmaz, F.; Nil, M. A review on bismuth telluride (Bi2Te3) nanostructure for thermoelectric applications. Renew. Sust. Energ. Rev. 2018, 82, 4159–4169. [Google Scholar] [CrossRef]
- Saberi, Y.; Sajjadi, S.A. A comprehensive review on the effects of doping process on the thermoelectric properties of Bi2Te3 based alloys. J. Alloy Compd. 2022, 904, 163918. [Google Scholar] [CrossRef]
- Zheng, Z.; Shi, X.; Ao, D.; Liu, W.; Li, M.; Kou, L.; Chen, Y.; Li, F.; Wei, M.; Liang, G.; et al. Harvesting waste heat with flexible Bi2Te3 thermoelectric thin film. Nat. Sustain. 2023, 6, 180–191. [Google Scholar] [CrossRef]
- Jia, B.; Huang, Y.; Wang, Y.; Zhou, Y.; Zhao, X.; Ning, S.; Xu, X.; Lin, P.; Chen, Z.; Jiang, B.; et al. Realizing high thermoelectric performance in non-nanostructured n-type PbTe. Energ. Environ. Sci. 2022, 15, 1920–1929. [Google Scholar] [CrossRef]
- Luo, Z.; Cai, S.; Hao, S.; Bailey, T.P.; Luo, Y.; Luo, W.; Yu, Y.; Uher, C.; Wolverton, C.; Dravid, V.P. Extraordinary role of Zn in enhancing thermoelectric performance of Ga-doped n-type PbTe. Energ. Environ. Sci. 2022, 15, 368–375. [Google Scholar] [CrossRef]
- Ciesielski, K.; Synoradzki, K.; Veremchuk, I.; Skokowski, P.; Szymański, D.; Grin, Y.; Kaczorowski, D. Thermoelectric Performance of the Half-Heusler Phases RNiSb (R = Sc, Dy, Er, Tm, Lu): High Mobility Ratio between Majority and Minority Charge Carriers. Phys. Rev. Appl. 2020, 14, 054046. [Google Scholar] [CrossRef]
- Jia, X.; Deng, Y.; Bao, X.; Yao, H.; Li, S.; Li, Z.; Chen, C.; Wang, X.; Mao, J.; Cao, F.; et al. Unsupervised machine learning for discovery of promising half-Heusler thermoelectric materials. npj Comput. Mater. 2022, 8, 34. [Google Scholar] [CrossRef]
- Satyam, J.K.; Saini, S.M. Role of R-f states on electronic structure and thermoelectric performance of RNiSb (R = Gd, Er and Lu) half Heusler compounds: Narrow gap thermoelectric materials. Appl. Phys. A 2021, 127, 828. [Google Scholar] [CrossRef]
- Musah, J.-D.; Ilyas, A.; Venkatesh, S.; Mensah, S.; Kwofie, S.; Roy, V.A.; Wu, C.-M.L. Isovalent substitution in metal chalcogenide materials for improving thermoelectric power generation–A critical review. Nano Res. Energy 2022, 1, 9120034. [Google Scholar] [CrossRef]
- Song, X.; Shai, X.; Deng, S.; Wang, J.; Li, J.; Ma, X.; Li, X.; Wei, T.; Ren, W.; Gao, L. Anisotropic Chalcogenide Perovskite CaZrS3: A Promising Thermoelectric Material. J. Phys. Chem. C 2022, 126, 11751–11760. [Google Scholar] [CrossRef]
- Ju, H.; Kim, J. Transparent and Hybrid Multilayer Films with Improved Thermoelectric Performance by Chalcogenide-Interlayer-Induced Transport Enhancement. ACS Appl. Mater. Inter. 2019, 11, 35354–35361. [Google Scholar] [CrossRef]
- Borgsmiller, L.; Li, Q.; Toriyama, M.Y.; Snyder, G.J. New Zintl Phase Yb10MgSb9 with High Thermoelectric Performance. Adv. Energy Mater. 2023, 13, 2300393. [Google Scholar] [CrossRef]
- Justl, A.P.; Ricci, F.; Pike, A.; Cerretti, G.; Bux, S.K.; Hautier, G.; Kauzlarich, S.M. Unlocking the thermoelectric potential of the Ca14AlSb11 structure type. Sci. Adv. 2022, 8, eabq3780. [Google Scholar] [CrossRef]
- Khireddine, A.; Bouhemadou, A.; Maabed, S.; Bin-Omran, S.; Khenata, R.; Al-Douri, Y. Elastic, electronic, optical and thermoelectric properties of the novel Zintl-phase Ba2ZnP2. Solid. State. Sci. 2022, 128, 106893. [Google Scholar] [CrossRef]
- Tani, J.I.; Kido, H. Thermoelectric properties of Bi-doped Mg2Si semiconductors. Phys. B 2005, 364, 218–224. [Google Scholar] [CrossRef]
- Zaitsev, V.K.; Fedorov, M.I.; Gurieva, E.A.; Eremin, I.S.; Konstantinov, P.P.; Samunin, A.Y.; Vedernikov, M.V. Highly effective Mg2Si1−xSnx thermoelectrics. Phys. Rev. B 2006, 74, 045207. [Google Scholar] [CrossRef]
- Akasaka, M.; Iida, T.; Nemoto, T.; Soga, J.; Sato, J.; Makino, K.; Fukano, M.; Takanashi, Y. Non-wetting crystal growth of Mg2Si by vertical Bridgman method and thermoelectric characteristics. J. Cryst. Growth. 2007, 304, 196–201. [Google Scholar] [CrossRef]
- Løvvik, O.M.; Flage-Larsen, E.; Skomedal, G. Screening of thermoelectric silicides with atomistic transport calculations. J. Appl. Phys. 2020, 128, 125105. [Google Scholar] [CrossRef]
- Nozariasbmarz, A.; Agarwal, A.; Coutant, Z.A.; Hall, M.J.; Liu, J.; Liu, R.; Malhotra, A.; Norouzzadeh, P.; Öztürk, M.C.; Ramesh, V.P.; et al. Thermoelectric silicides: A review. Jpn. J. Appl. Phys. 2017, 56, 05DA04. [Google Scholar] [CrossRef]
- Burkov, A.T. Silicide Thermoelectrics: Materials for Energy Harvesting. Phys. Status Solidi A 2018, 215, 1800105. [Google Scholar] [CrossRef]
- Tani, J.-i.; Kido, H. Thermoelectric properties of Sb-doped Mg2Si semiconductors. Intermetallics 2007, 15, 1202–1207. [Google Scholar] [CrossRef]
- Tani, J.-i.; Kido, H. Thermoelectric properties of Al-doped Mg2Si1−xSnx. J. Alloy Compd. 2008, 466, 335–340. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhao, X.; Yin, H.; Zhu, T. Effect of Sb-Doping on the Thermoelectric Properties of Mg2Si Based Compounds. Rare Met. Mater. Eng. 2009, 38, 165–168. [Google Scholar]
- Sakamoto, T.; Iida, T.; Matsumoto, A.; Honda, Y.; Nemoto, T.; Sato, J.; Nakajima, T.; Taguchi, H.; Takanashi, Y. Thermoelectric Characteristics of a Commercialized Mg2Si Source Doped with Al, Bi, Ag, and Cu. J. Electron. Mater. 2010, 39, 1708–1713. [Google Scholar] [CrossRef]
- Ihou-Mouko, H.; Mercier, C.; Tobola, J.; Pont, G.; Scherrer, H. Thermoelectric properties and electronic structure of p-type Mg2Si and Mg2Si0.6Ge0.4 compounds doped with Ga. J. Alloy Compd. 2011, 509, 6503–6508. [Google Scholar] [CrossRef]
- Liu, W.; Tan, X.; Yin, K.; Liu, H.; Tang, X.; Shi, J.; Zhang, Q.; Uher, C. Convergence of Conduction Bands as a Means of Enhancing Thermoelectric Performance of n-Type Mg2Si1-xSnx Solid Solutions. Phys. Rev. Lett. 2012, 108, 166601. [Google Scholar] [CrossRef] [PubMed]
- Wen, C.; Nonomura, T.; Warashina, Y.; Kubota, Y.; Nakamura, T.; Hayakawa, Y.; Tanaka, M.; Isobe, K.; Tatsuoka, H. Synthesis of single-phase polycrystalline Ca2Si powder and sintered compacts. Int. J. Mater. Res. 2011, 102, 401–405. [Google Scholar] [CrossRef]
- Xiong, R.; Sa, B.; Miao, N.; Li, Y.-L.; Zhou, J.; Pan, Y.; Wen, C.; Wu, B.; Sun, Z. Structural stability and thermoelectric property optimization of Ca2Si. RSC Adv. 2017, 7, 8936–8943. [Google Scholar] [CrossRef]
- Duan, X.; Hu, K.; Kuang, J.; Jiang, Y.; Yi, D. Effects of Ag-Doping on Thermoelectric Properties of Ca2−xAgxSi Alloys. J. Electron. Mater. 2016, 46, 2986–2989. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, W.; Yang, J.; Li, S. Recent Advances of Layered Thermoelectric Materials. Adv. Sustain. Syst. 2018, 2, 1800046. [Google Scholar] [CrossRef]
- Chuang, L.; Wang, D.Y.; Tan, T.T.; Assadi, M.H.N.; Li, S. Processing dependence of structural and physical properties of Mg2Ge thin films prepared by pulsed laser deposition. Thin Solid Film. 2012, 520, 6226–6229. [Google Scholar] [CrossRef]
- Galkin, N.G.; Galkin, K.N.; Tupkalo, A.V.; Subbotin, E.Y.; Chernev, I.M.; Shevlyagin, A.V.; Khovailo, V.V. Conduction Mechanisms and Thermoelectric Properties of Semimetallic CaSi and CaSi2 Films on Si100 and Si111 Substrates. Phys. Solid State 2023, 64, 616–623. [Google Scholar] [CrossRef]
- Galkin, N.G.; Galkin, K.N.; Chernev, I.M.; Goroshko, D.L.; Chusovitin, E.A.; Shevlyagin, A.V.; Usenko, A.A.; Khovaylo, V.V. Comparison of the Structural, Optical and Thermoelectrical Properties of Ca Silicide Films with Variable Composition on Si Substrates. Defect Diffus. Forum 2018, 386, 3–8. [Google Scholar] [CrossRef]
- Wen, C.; Nonomura, T.; Kato, A.; Kenichi, Y.; Udono, H.; Isobe, K.; Otake, M.; Kubota, Y.; Nakamura, T.; Hayakawa, Y.; et al. Electrical properties of Ca2Si sintered compact synthesized by spark plasma sintering. Phys. Procedia 2011, 11, 106–109. [Google Scholar] [CrossRef]
- Wen, C.; Xie, Q.; Xiong, R.; Sa, B.; Miao, N.; Zhou, J.; Wu, B.; Sun, Z. Computational mining of the pressure effect on thermodynamic and thermoelectric properties of cubic Ca2Si. Europhys. Lett. 2018, 123, 67003. [Google Scholar] [CrossRef]
- Sigmund, H. Solubilities of Magnesium and Calcium in Silicon. J. Electrochem. Soc. 1982, 129, 2809. [Google Scholar] [CrossRef]
| Hall Coefficient, RH/10−7 m3·C−1 | Carrier Concentration, p/1019 cm−1 | Mobility, μ/cm2·V−1·s−1 |
|---|---|---|
| 1.06 | 4.22 | 15.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, W.; Zhang, J.; Ma, F.; Jing, M.; Xing, N. Thermoelectric Performance of Ca2Si Synthesized by High-Temperature Melting. Coatings 2023, 13, 1426. https://doi.org/10.3390/coatings13081426
Tan W, Zhang J, Ma F, Jing M, Xing N. Thermoelectric Performance of Ca2Si Synthesized by High-Temperature Melting. Coatings. 2023; 13(8):1426. https://doi.org/10.3390/coatings13081426
Chicago/Turabian StyleTan, Wenjie, Jiarui Zhang, Fukun Ma, Min Jing, and Ningning Xing. 2023. "Thermoelectric Performance of Ca2Si Synthesized by High-Temperature Melting" Coatings 13, no. 8: 1426. https://doi.org/10.3390/coatings13081426
APA StyleTan, W., Zhang, J., Ma, F., Jing, M., & Xing, N. (2023). Thermoelectric Performance of Ca2Si Synthesized by High-Temperature Melting. Coatings, 13(8), 1426. https://doi.org/10.3390/coatings13081426





