Finite Element Analysis of Renewable Porous Bones and Optimization of Additive Manufacturing Processes
Abstract
1. Introduction
2. Porous Structure Model
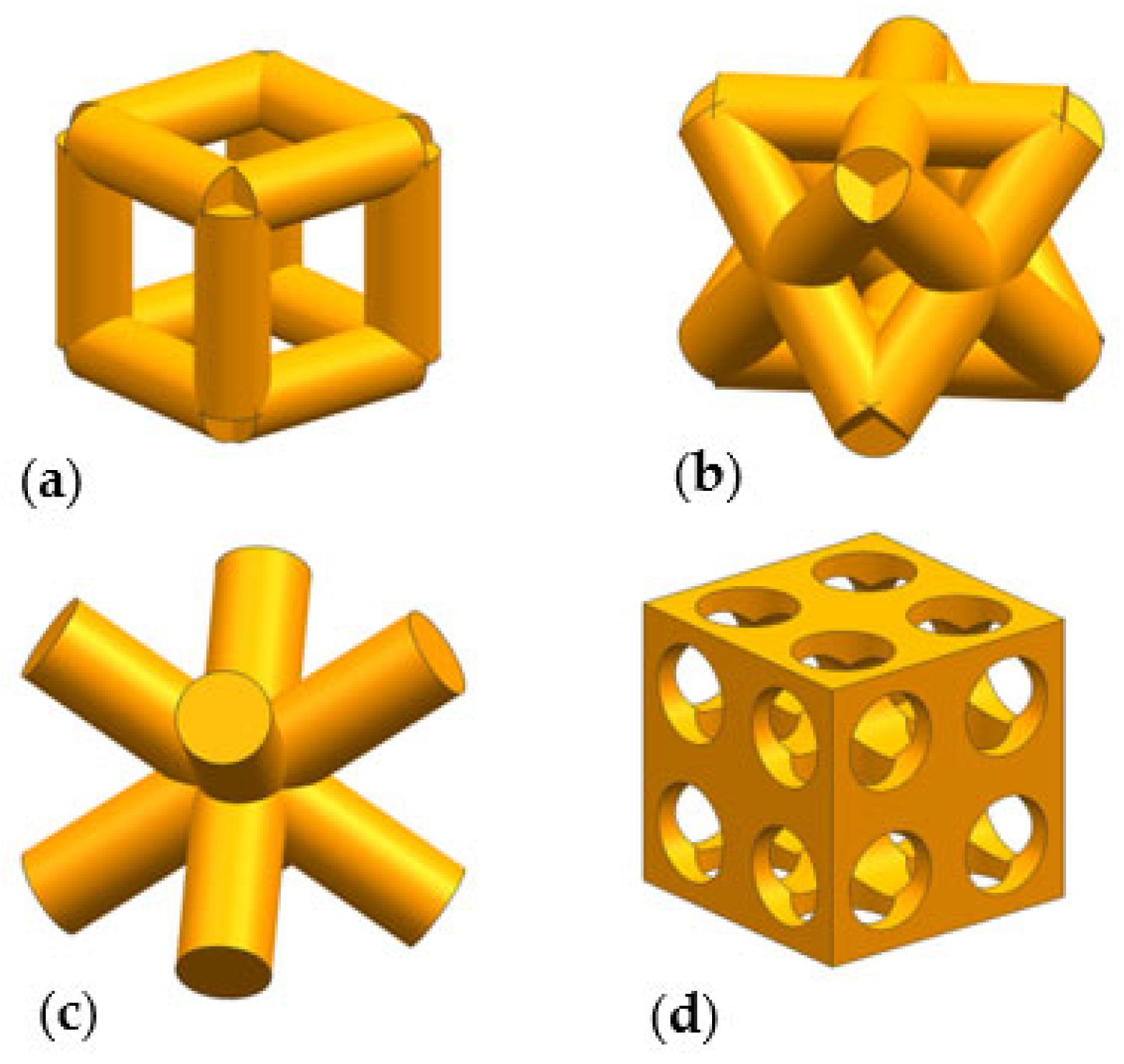
2.1. Design of Porous Structure
2.1.1. Design of Strut Diameter and Length
2.1.2. Porosity
2.1.3. Design Parameters
2.1.4. Material
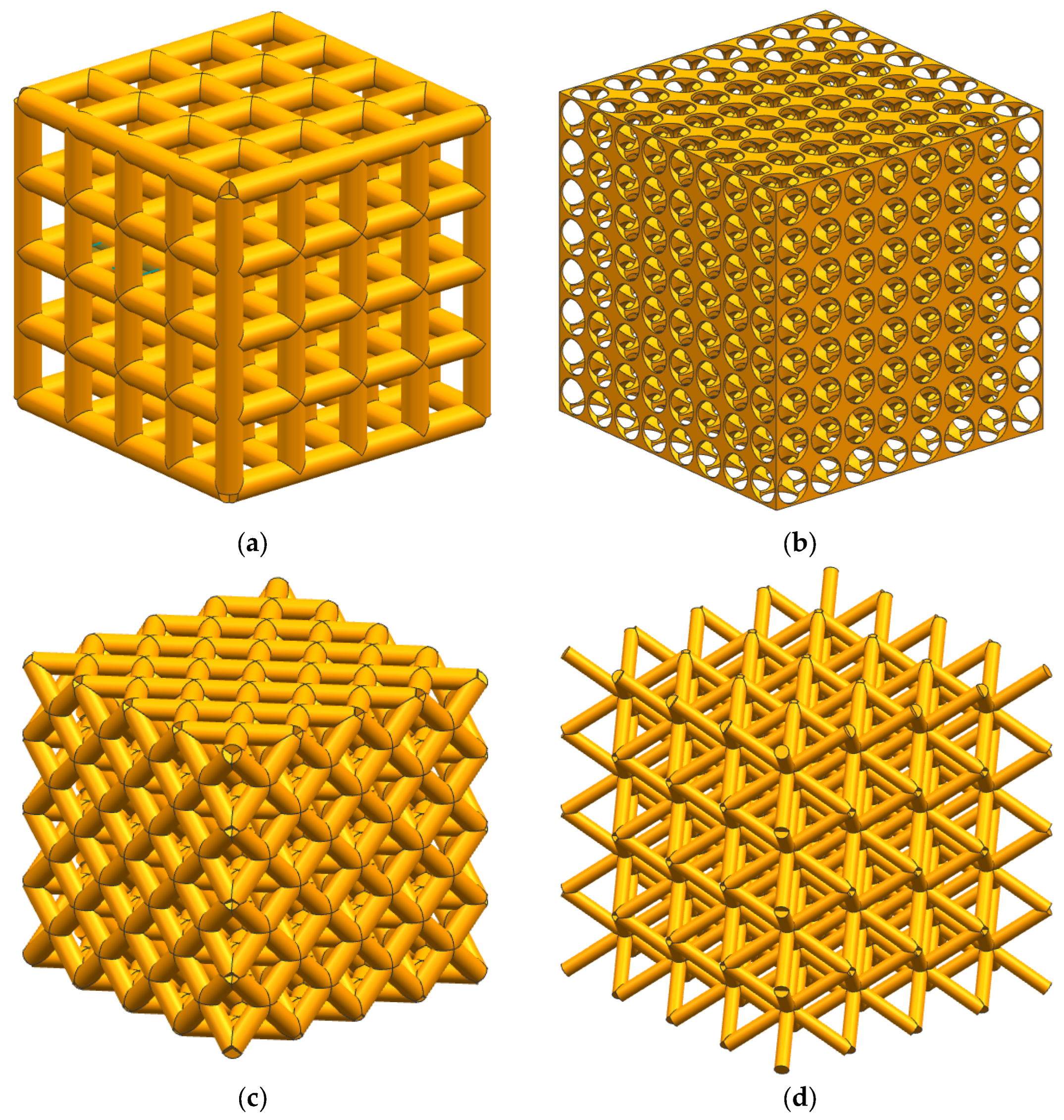
2.2. Porous Structure Models
3. Finite Element Simulation of the Porous Scaffold
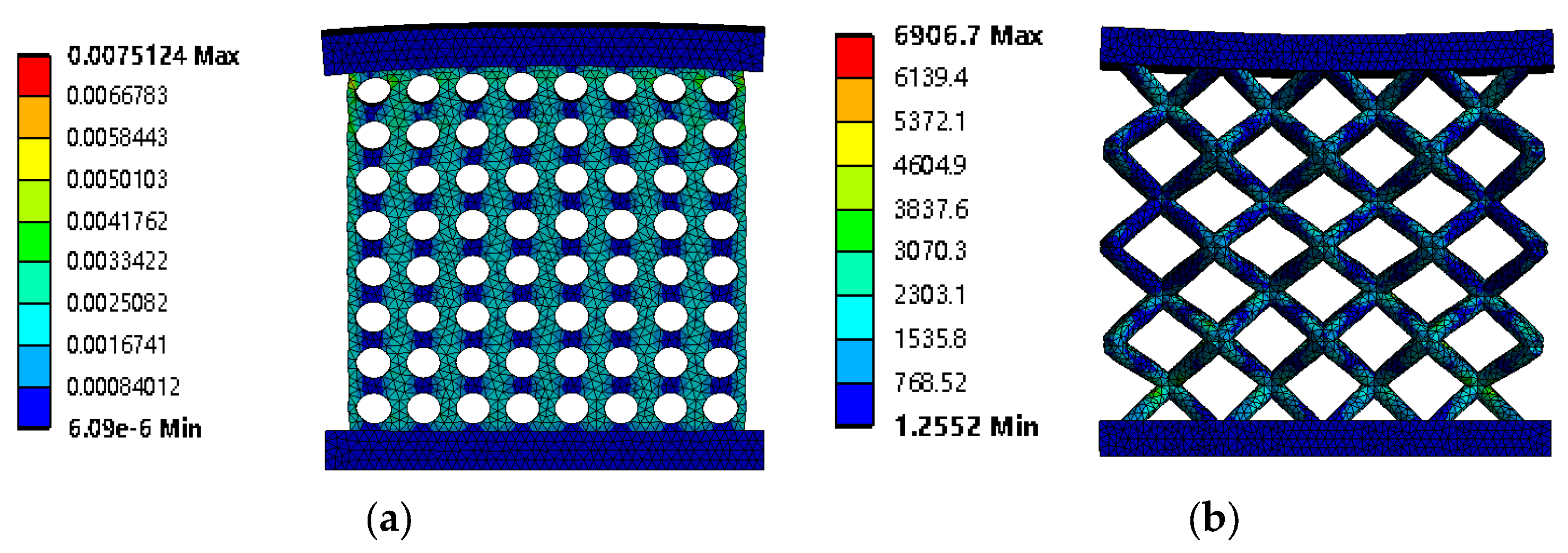
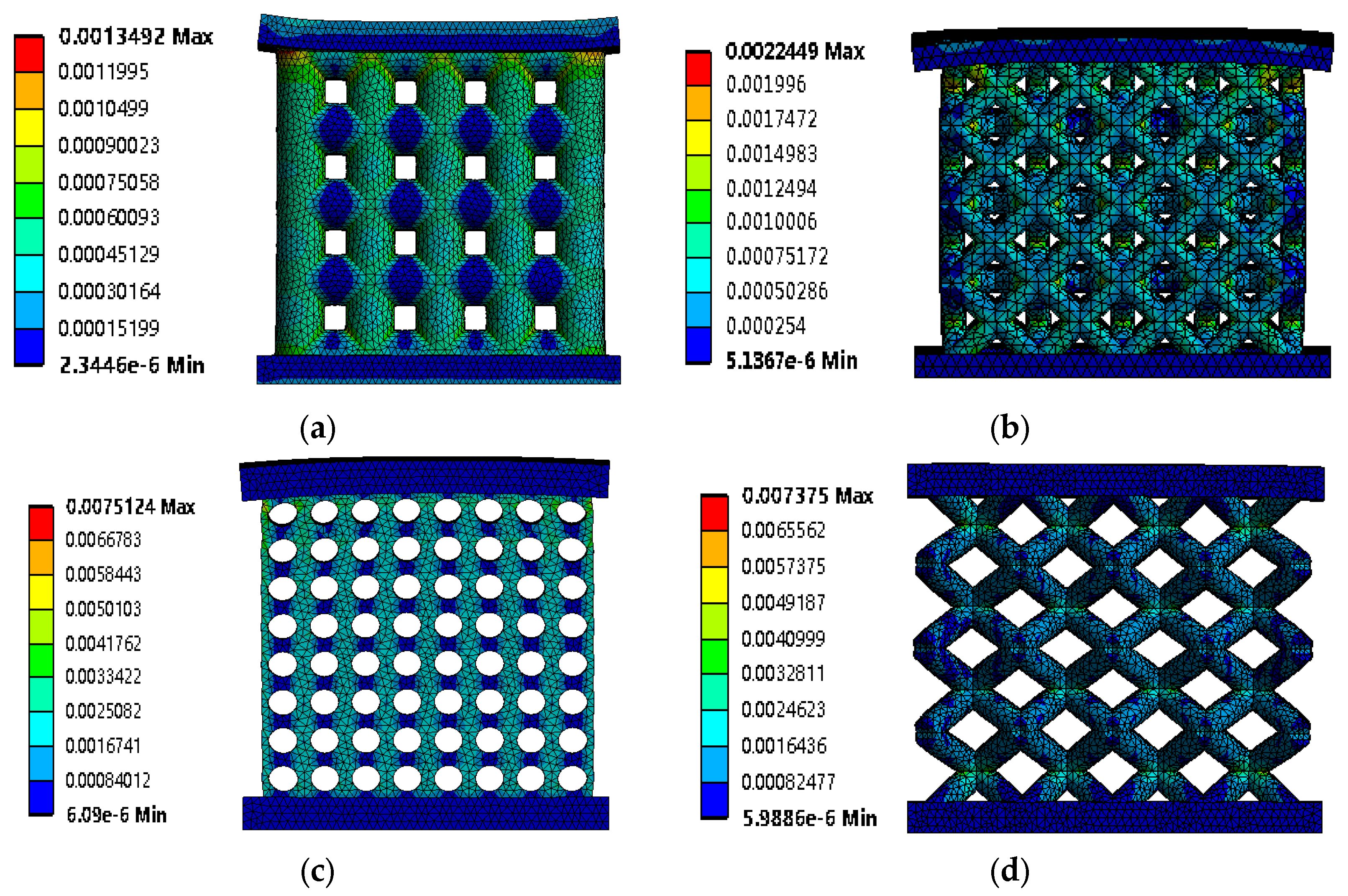
3.1. Compression Analysis
3.2. Compression Analysis of Low-Porosity Structures
3.3. Compression Analysis of High-Porosity Structures
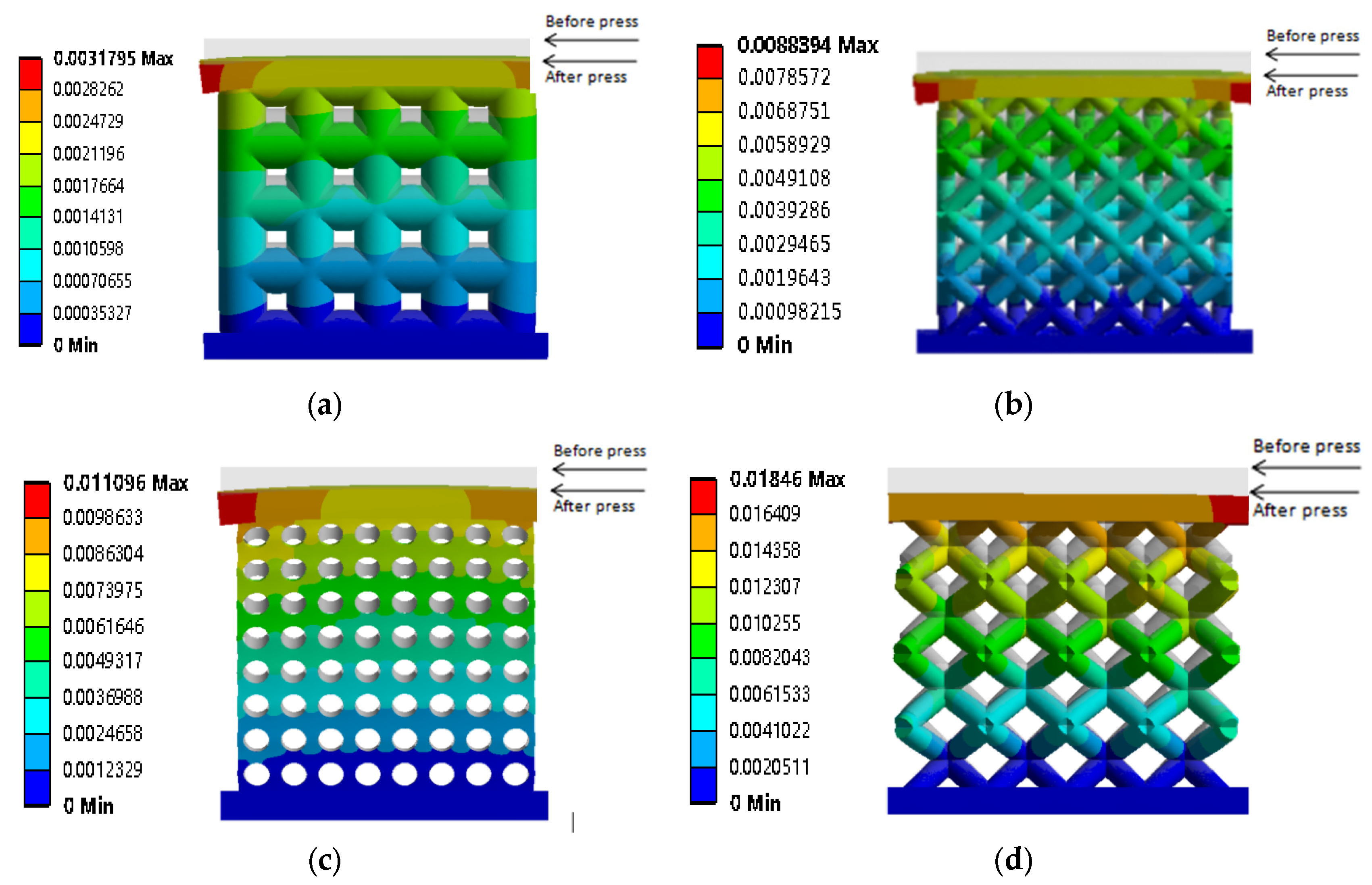
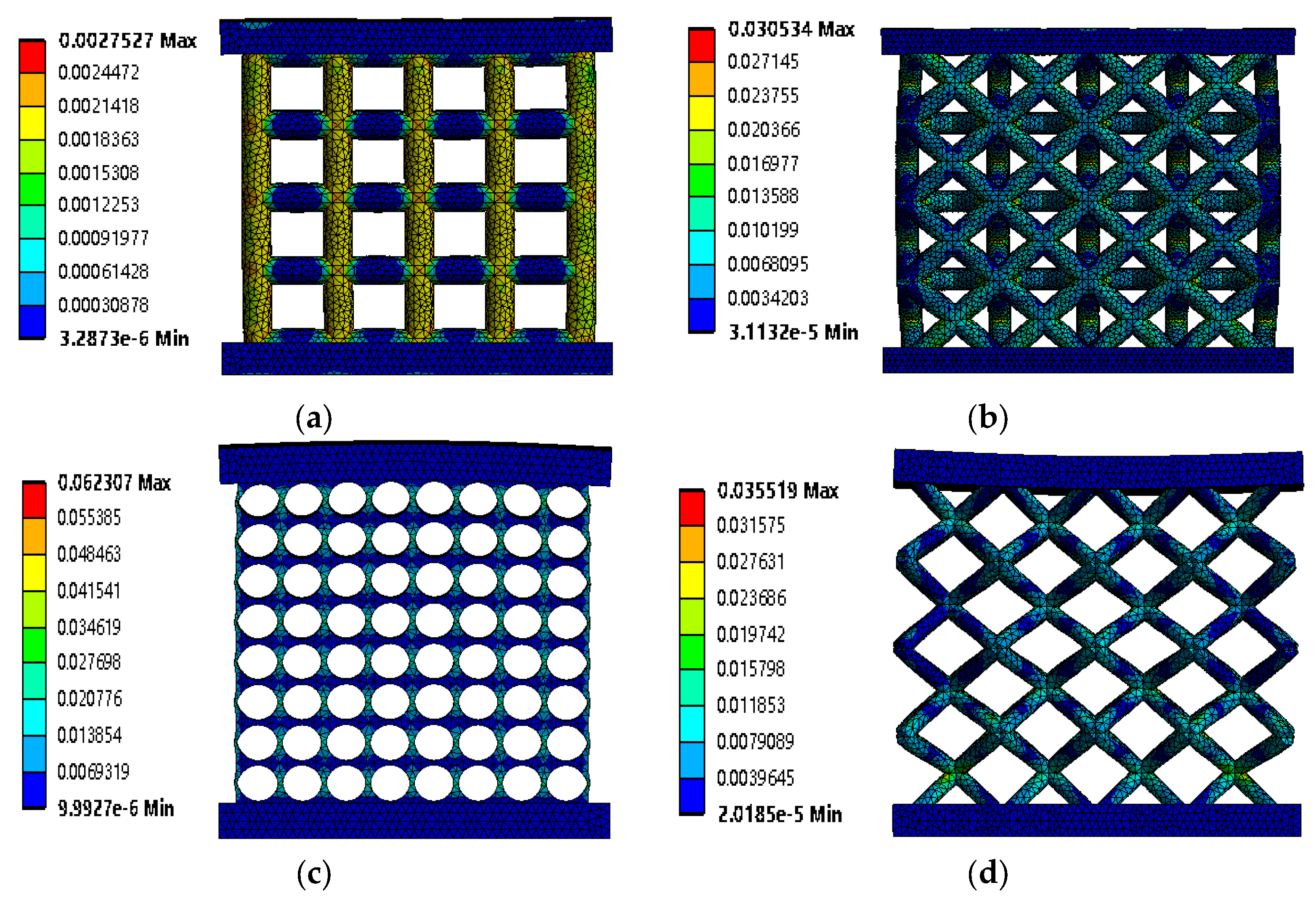
4. Porous Bracket Forming Simulation
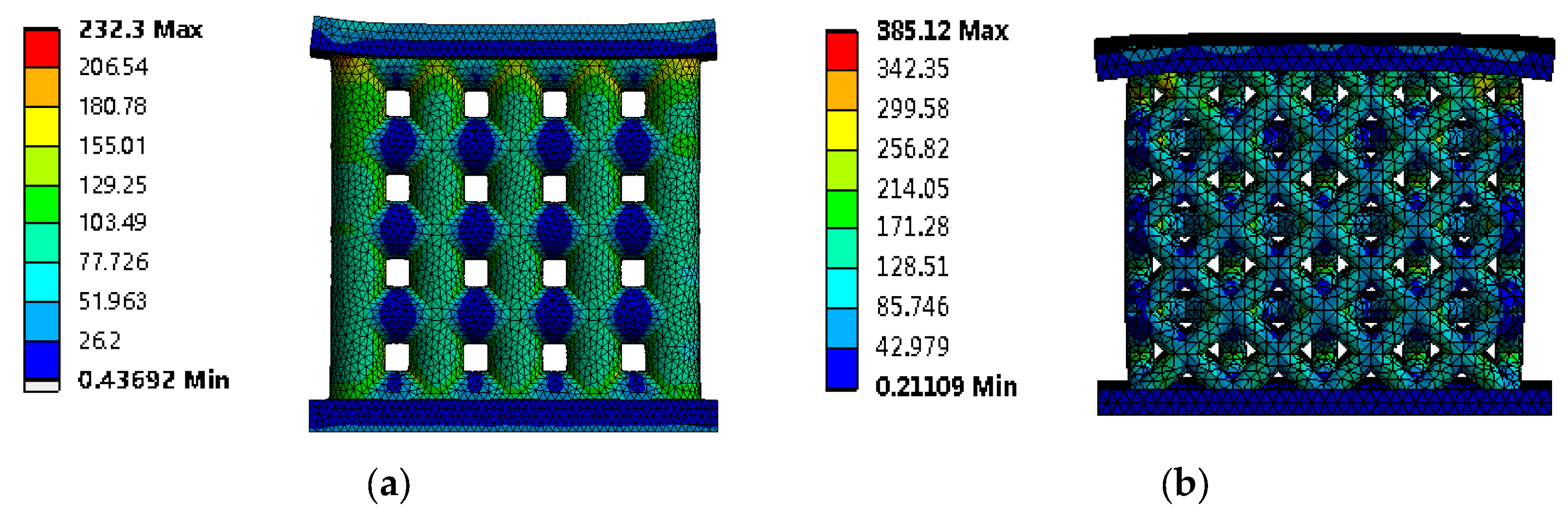
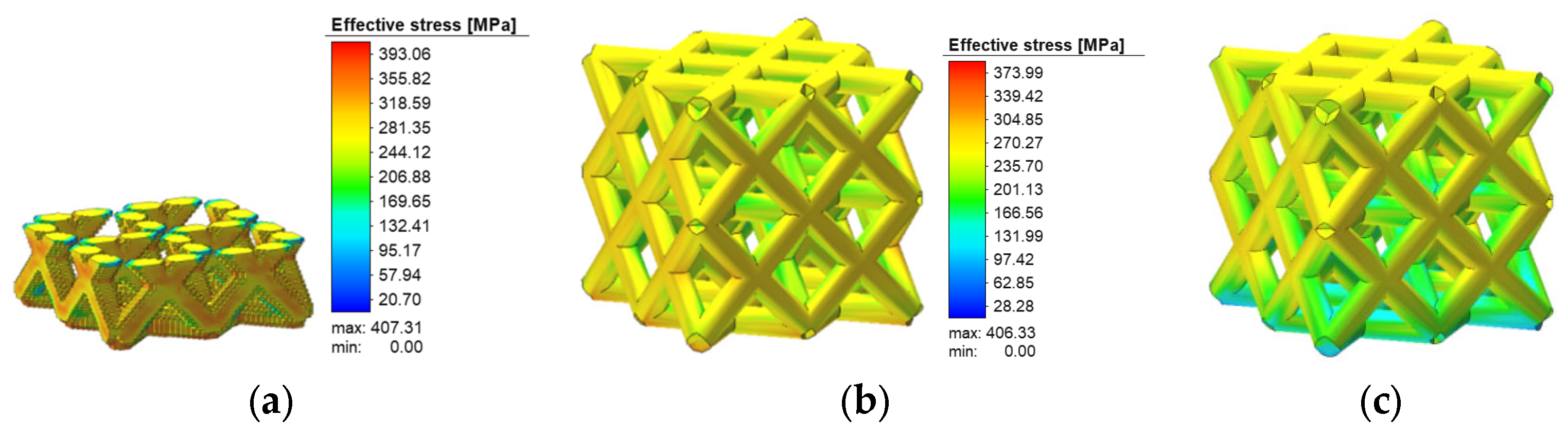
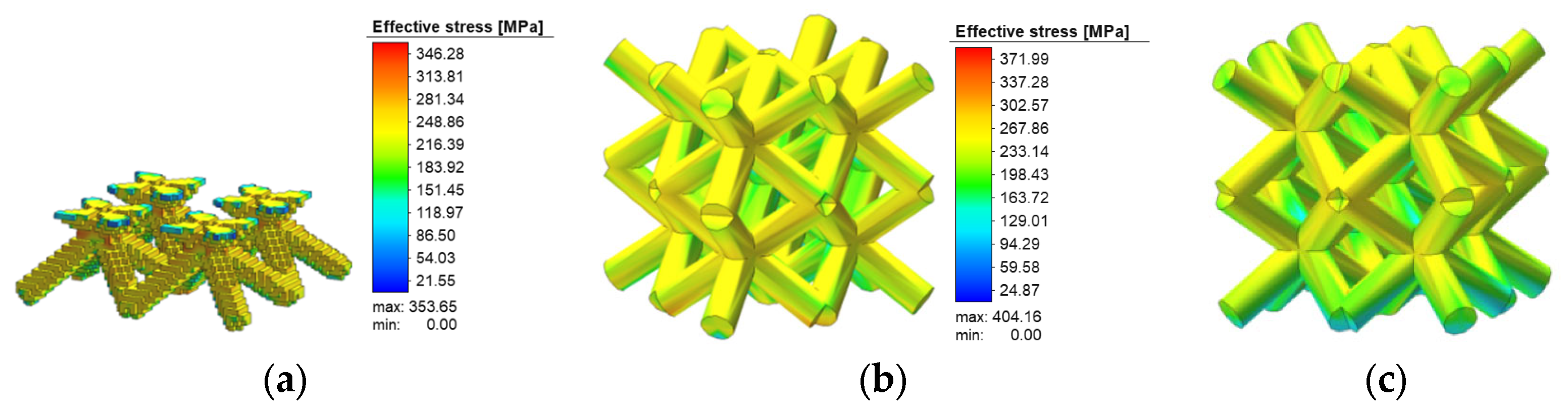
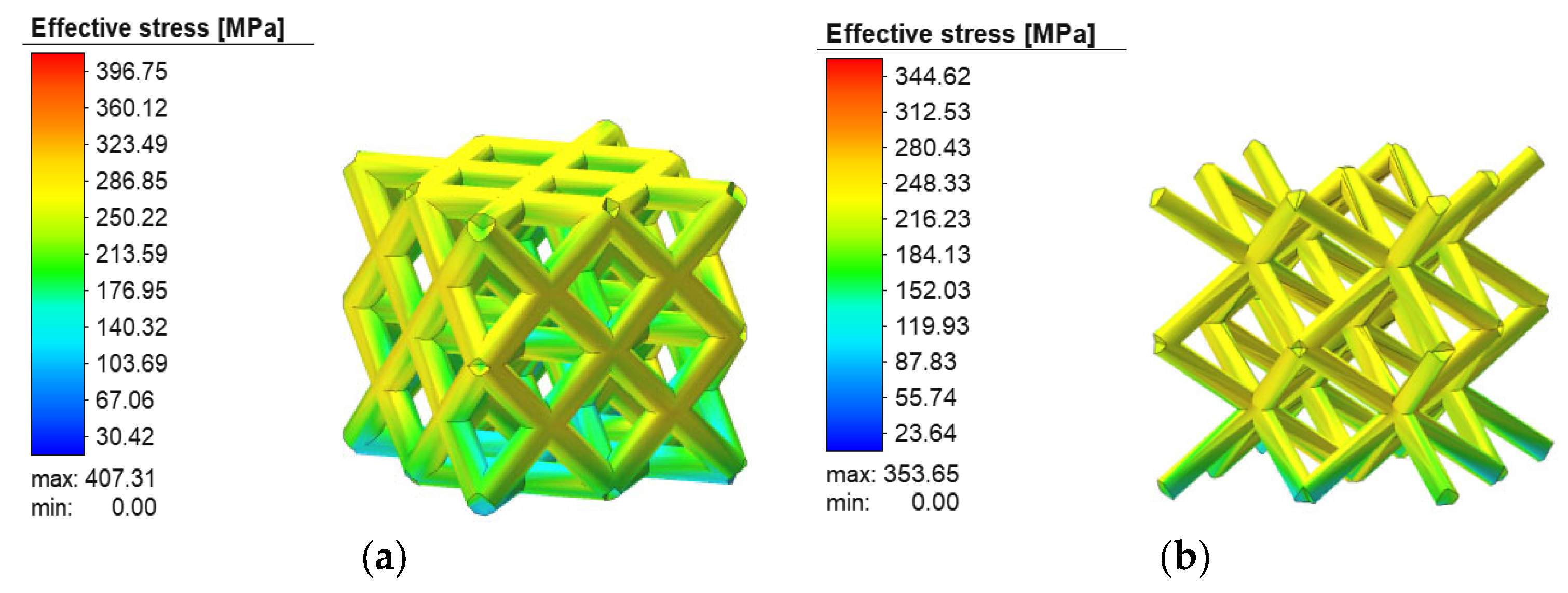
4.1. Stress Analysis of Low-Porosity Porous Structures in Additive Manufacturing
4.2. Analysis of Stress Results for Additively Manufactured High-Porosity Porous Structures
5. Conclusions
- A strut diameter that meets the manufacturing requirements of 3D printing technology was designed, followed by a pore size that can facilitate cellular transport of nutrients and metabolic waste. The porosity was also conducive to the growth of bone tissue into it, and four different types of unitary structures and finite element models of cuboid, diagonal, honeycomb, and body-centered cuboid were established;
- Combining the four different porous structures with different porosities, compression simulations were carried out, and the stresses were increased in the high-porosity more than in the low-porosity structures. The cubic structure was the best in low-porosity structures, and the face-centered cubic structure was the best in high-porosity structures; the cubic structure was the best from the point of view of strain combined with deformation volume. For the influence of mechanical properties, porosity is the main factor;
- Forming simulation analysis of porous structures shows that when fewer layers of suspended structures are constructed, the shrinkage force during the cooling phase is weakened by the limiting effect of the underlying powder, resulting in increased shrinkage. The energy density that can be absorbed by the metal material during construction easily induces a strong Marangoni effect, which can easily form cracks at the weld seam while adding to the risk of stress corrosion after implantation, as the human blood is weakly alkaline, which can accelerate stress corrosion near the weld seam;
- The greater the height, the lower the stress level of the base plate itself and the more uniform the stress level of the part before dismantling. The stress distribution before dismantling includes large tensile stress zones in the upper area of the part being built. The maximum stress (equal to the yield stress) is reached at the surface of the part. The removal of the part significantly reduces the residual stresses present in the part; the residual stresses are relaxed by uniform shrinkage and bending deformation. The stresses in the part after disassembly are much less than before disassembly.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, X. Structural Design of Artificial Bone Scaffolds Based on 3D Printing. Master’s Thesis, Guangxi University, Nanning, China, 2019. [Google Scholar]
- Shi, X.Q. Porous Structure Design and Performance Study of Ti6Al4V Femoral Supports Based on Additive Manufacturing. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar]
- Wieding, J.; Wolf, A.; Bader, R. Numerical optimization of open-porous bone scaffold structures to match the elastic properties of human cortical bone. J. Mech. Behav. Biomed. Mater. 2014, 37, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Cuadrado, A.; Yánez, A.; Martel, O.; Deviaene, S.; Monopoli, D. Influence of load orientation and of types of loads on the mechanical properties of porous Ti6Al4V biomaterials. Mater. Des. 2017, 135, 309–318. [Google Scholar] [CrossRef]
- Limmahakhun, S.; Oloyede, A.; Sitthiseripratip, K.; Xiao, Y.; Yan, C. Stiffness and strength tailoring of cobalt chromium graded cellular structures for stress-shielding reduction. Mater. Des. 2016, 114, 633–641. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Fang, G.; Zhou, J. Additively manufactured scaffolds for bone tissue engineering and the prediction of their mechanical behavior: A review. Materials 2017, 10, 50. [Google Scholar] [CrossRef]
- Surmeneva, M.; Surmenev, R.; Chudinova, E.; Koptioug, A.; Tkachev, M.S.; Gorodzha, S.N.; Rännar, L.-E. Fabrication of multiple-layered gradient cellularmetal scaffold via electron beam melting for segmental bone reconstruction. Mater. Des. 2017, 133, 195–204. [Google Scholar] [CrossRef]
- Dumas, M.; Terriault, P.; Brailovski, V. Modelling and characterization of a porosity graded latticestructure for additively manufactured biomaterials. Mater. Des. 2017, 121, 383–392. [Google Scholar] [CrossRef]
- Murr, L.E. Open-cellular metal implant design and fabrication for biomechanical compatibility withbone using electron beam melting. J. Mech. Behav. Biomed. Mater. 2017, 76, 164–177. [Google Scholar] [CrossRef]
- Zadpoor, A.; Hedayati, R. Analytical relationships for prediction of the mechanical propertie of additively manufactured porous biomaterials. J. Biomed. Mater. Res. Part A 2016, 104, 3164–3174. [Google Scholar] [CrossRef]
- Li, S.B. Numerical Simulation and Experimental Study on the Mechanical Properties of Porous Structure of 3D Printed Hip Prostheses. Master’s Thesis, Jilin University, Changchun, China, 2020. [Google Scholar] [CrossRef]
- Rodríguez-Montaño, Ó.L.; Cortés-Rodríguez, C.J.; Uva, A.E.; Fiorentino, M.; Gattullo, M.; Monno, G.; Boccaccio, A. Comparison of the mechanobiological performance of bone tissue scaffolds based on different unit cell geometries. J. Mech. Behav. Biomed. Mater. 2018, 83, 28–45. [Google Scholar] [CrossRef]
- Meng, X.N. Finite Element Analysis and Comparison of Biomechanical Properties of 2052–2102 and Plus Femoral Prostheses. Master’s Thesis, Shandong University, Jinan, China, 2016. [Google Scholar]
- Bragdon, C.R.; Jasty, M.; Greene, M.; Rubash, H.E.; Harris, W.H. Biologic fixation of total hip implants. Insights gained from a series of canine studies. J. Bone Jt. Surg. Am. Vol. 2004, 86 (Suppl. S2), 105–117. [Google Scholar] [CrossRef]
- Simoneau, C.; Terriault, P.; Jetté, B.; Dumas, M.; Brailovski, V. Development of a porous metallic femoral stem: Design, manufacturing, simulation and mechanical testing. Mater. Des. 2016, 114, 546–556. [Google Scholar] [CrossRef]
- Beaupré, G.S.; Orr, T.E.; Carter, D.R. An approach for time-dependent bone modeling and remodeling—Theoretical development. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 1990, 8, 651–661. [Google Scholar] [CrossRef] [PubMed]
- Marti, R.B. Porosity and specific surface of bone. Crit. Rev. Biomed. Eng. 1984, 10, 179–222. [Google Scholar]
- Coelho, P.; Fernandes, P.; Rodrigues, H.; Cardoso, J.; Guedes, J. Numerical modeling of bone tissue adaptation--a hierarchical approach for bone apparent density and trabecular structure. J. Biomech. 2009, 42, 830–837. [Google Scholar] [CrossRef] [PubMed]
- Tan, X.; Tan, Y.; Chow, C.; Tor, S.; Yeong, W. Metallic powder-bed based 3D printing of cellular scaffolds for orthopaedic implants: A state-of-the-art review on manufacturing, topological design, mechanical properties and biocompatibility. Mater. Sci. Eng. C 2017, 76, 1328–1343. [Google Scholar] [CrossRef] [PubMed]
- Limmahakhun, S.; Oloyede, A.; Chantarapanich, N.; Jiamwatthanachai, P.; Sitthiseripratip, K.; Xiao, Y.; Yan, C. Alternative designs of load–sharing cobalt chromium graded femoral stems. Mater. Today Commun. 2017, 12, 1–10. [Google Scholar] [CrossRef]
- Zhang, L.L.; Li, H.J.; Li, K.Z.; Wang, P.; Xu, X. Research progress on materials for artificial hip prostheses. Mater. Rev. 2008, 22, 113–116. [Google Scholar]
- Chuan, H. Study on Wear Behavior and Wear Particle Morphology of Artificial Hip Joints. Master’s Thesis, China University of Mining and Technology, Xuzhou, China, 2004. [Google Scholar]
- Ge, S.R.; Wang, C.T. Current status and prospects of research on human biological tribology. J. Tribol. 2005, 25, 186–191. [Google Scholar]
- Kannan, S.; Balamurugan, A.; Rajeswari, S. Hydroxyapatite coatings on sulfuric acid treated type 316L SS and its electrochemical behaviour in Ringer’s solution. Mater. Lett. 2003, 57, 2382. [Google Scholar] [CrossRef]
- Fan, X.; Chen, J.; Zou, J. Bone-like apatite formation on HA/316L stainless steel composite surface in simulated body fluid. Trans. Nonferrous Met. Soc. China 2009, 19, 347. [Google Scholar] [CrossRef]
- Ueda, Y.F.K.; Tanigawa, M. New measuring method of 3-dimensional residual stresses based on theory of inherent strain. J. Jpn. Soc. Nav. Archit. Ocean. Eng. 1979, 145, 203–211. [Google Scholar] [CrossRef]
- Wang, J.; Lu, H. Residual plastic strain finite element method for predicting welding deformation. J. Shanghai Jiaotong Univ. 1997, 31, 53–56. [Google Scholar]
- Wang, J.; Lu, H.; Wei, L. Theory and application of inherent strain finite element method in predicting welding deformation. J. Weld. 2002, 23, 36–40. [Google Scholar]
- Vossenberg, P.; Higuera, G.A.; van Straten, G.; van Blitterswijk, C.A.; van Boxtel, A.J. Darcian permeability constant as indicator for shear stresses in regular scaffold systems for tissue engineering. Biomech. Model Mechanobiol. 2009, 8, 499–507. [Google Scholar] [CrossRef] [PubMed]
- Gómez, S.; Vlad, M.; López, J.; Fernández, E. Design and properties of 3D scaffolds for bone tissue engineering. Acta Biomater. 2016, 42, 341–350. [Google Scholar] [CrossRef] [PubMed]
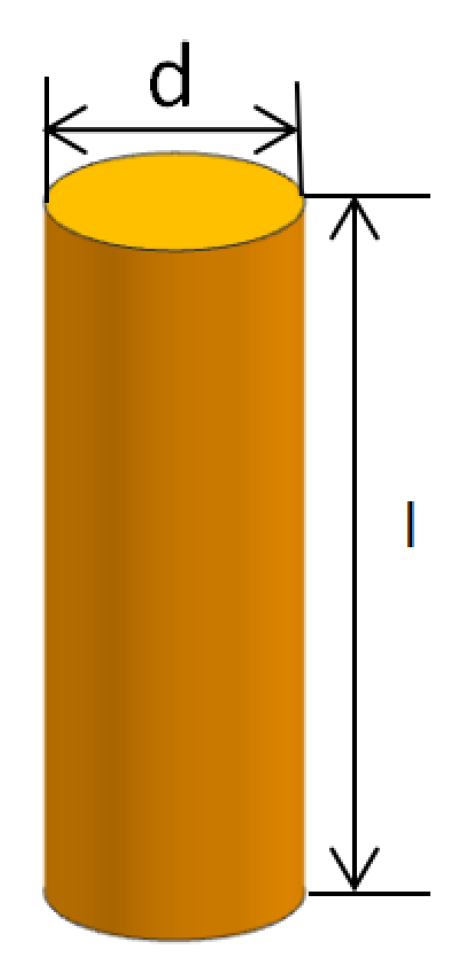






| Porous Structure | Strut Diameter (μm) | Pore Size (μm) | Porosity (%) | |
|---|---|---|---|---|
| High Porosity Level | Cubic | 350 | 650 | 85 |
| Face-centered cubic | 350 | 650 | 85 | |
| Honeycomb | 450 | 450 | 85 | |
| Body-centered cubic | 200 | 620 | 85 | |
| Low Porosity Level | Cubic | 700 | 300 | 65 |
| Face-centered cubic | 400 | 600 | 65 | |
| Honeycomb | 350 | 350 | 65 | |
| Body-centered cubic | 350 | 470 | 65 |
| Grade | C | Si | Mn | P | S | Ni | Cr | Mo |
|---|---|---|---|---|---|---|---|---|
| 00Cr17NiMo2 | ≤0.03 | ≤1.00 | ≤2.00 | ≤0.035 | ≤0.03 | ≤12.0–15.0 | ≤16.0–18.0 | ≤2.0–3.0 |
| Property | Yield Strength (MPa) | Tensile Strength (MPa) | Elongation (%) | Vickers Hardness (Hv) | Remarks |
|---|---|---|---|---|---|
| Standard | ≥205 | ≥520 | ≥40 | ≤200 | 2 B/1.5 t |
| Typical | 310 | 620 | 53 | 155 |
| Cubic | Body-Centered Cubic | Honeycomb | Face-Centered Cubic | |
|---|---|---|---|---|
| Strain (mm) | 0.000312 | 0.001013 | 0.000841 | 0.000438 |
| Deformation (mm) | 0.000968 | 0.008143 | 0.003922 | 0.002768 |
| Cubic | Body-Centered Cubic | Honeycomb | Face-Centered Cubic | |
|---|---|---|---|---|
| Strain (mm) | 0.000704 | 0.003176 | 0.002791 | 0.005581 |
| Deformation (mm) | 0.004098 | 0.072260 | 0.023360 | 0.041275 |
| Porous Structures | Cubic | Body-Centered Cubic | Honeycomb | Face-Centered Cubic | ||
|---|---|---|---|---|---|---|
| Porosity | ||||||
| Stress values (MPa) | high | 132.88 | 103.61 | 488.42 | 561.52 | |
| low | 59.52 | 75.422 | 152.58 | 178.75 | ||
| Strain values (mm) | high | 0.000704 | 0.002791 | 0.002791 | 0.003318 | |
| low | 0.000318 | 0.000841 | 0.000841 | 0.001013 | ||
| Porous Structures | Cubic | Face-Centered Cubic | Honeycomb | Body-Centered Cubic |
|---|---|---|---|---|
| Stress values (MPa) | 370.10 | 373.99 | 302.46 | 371.99 |
| Porous Structures | Cubic | Face-Centered Cubic | Honeycomb | Body-Centered Cubic |
|---|---|---|---|---|
| Stress values (MPa) | 388.02 | 396.75 | 325.68 | 344.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Xu, S.; Ju, X.; Tang, A.; Hu, X. Finite Element Analysis of Renewable Porous Bones and Optimization of Additive Manufacturing Processes. Coatings 2023, 13, 912. https://doi.org/10.3390/coatings13050912
Ma H, Xu S, Ju X, Tang A, Hu X. Finite Element Analysis of Renewable Porous Bones and Optimization of Additive Manufacturing Processes. Coatings. 2023; 13(5):912. https://doi.org/10.3390/coatings13050912
Chicago/Turabian StyleMa, Hailong, Shubo Xu, Xiaoyu Ju, Aijun Tang, and Xinzhi Hu. 2023. "Finite Element Analysis of Renewable Porous Bones and Optimization of Additive Manufacturing Processes" Coatings 13, no. 5: 912. https://doi.org/10.3390/coatings13050912
APA StyleMa, H., Xu, S., Ju, X., Tang, A., & Hu, X. (2023). Finite Element Analysis of Renewable Porous Bones and Optimization of Additive Manufacturing Processes. Coatings, 13(5), 912. https://doi.org/10.3390/coatings13050912





