The Influence of Niobium and Zirconium Addition on the Structural and Mechanical Properties of Yttrium Nitride: A First-Principles Study
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
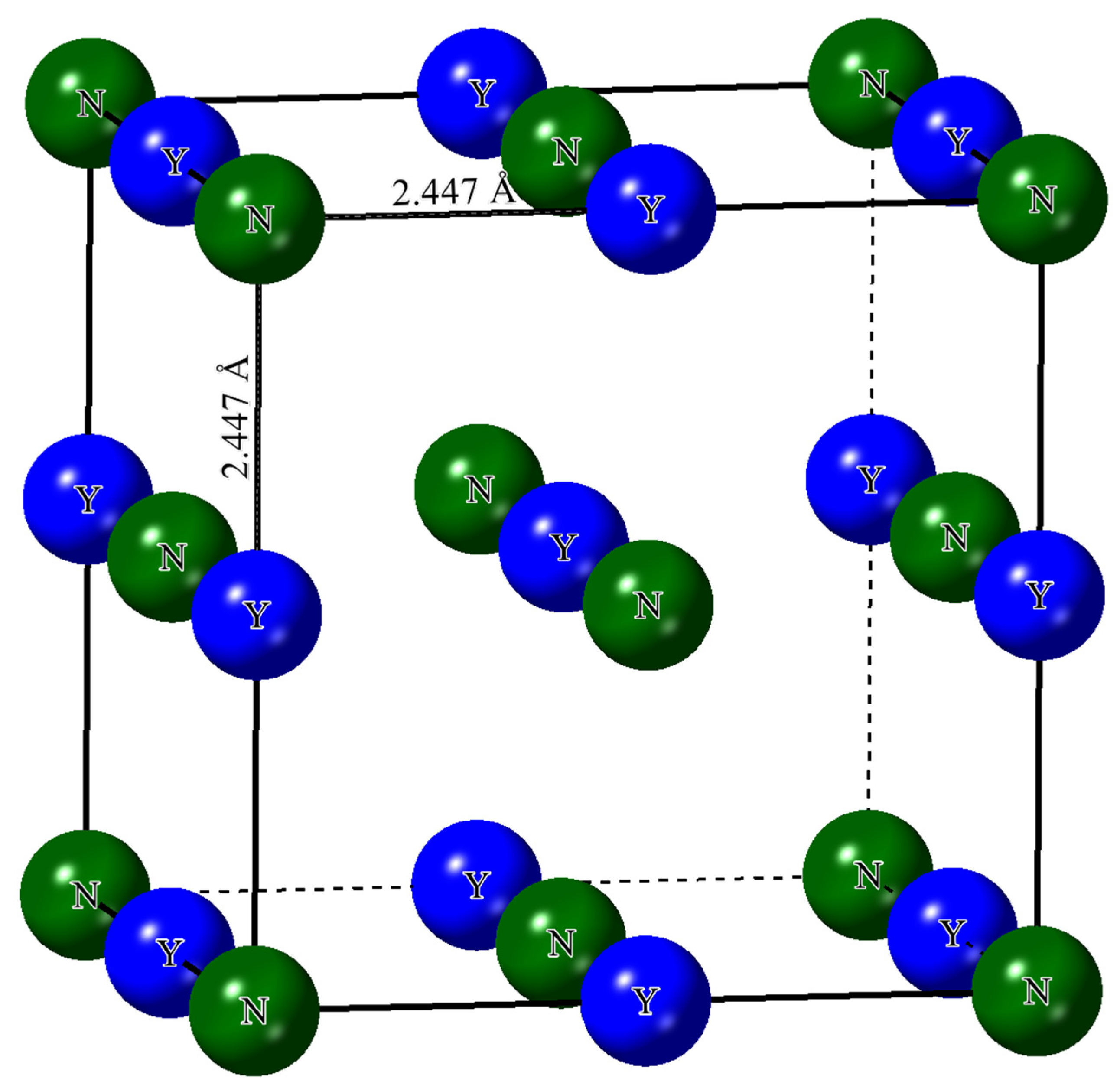
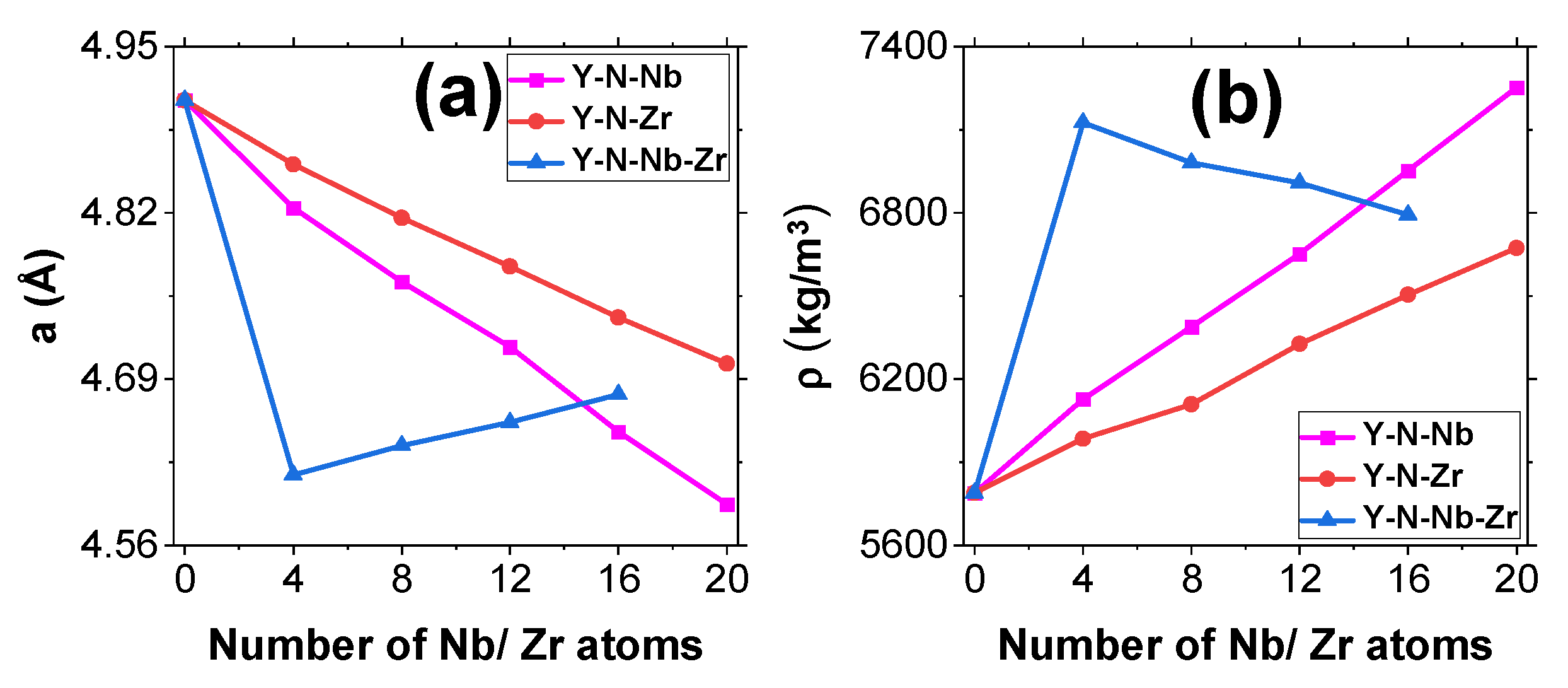
3.1. Structural Study
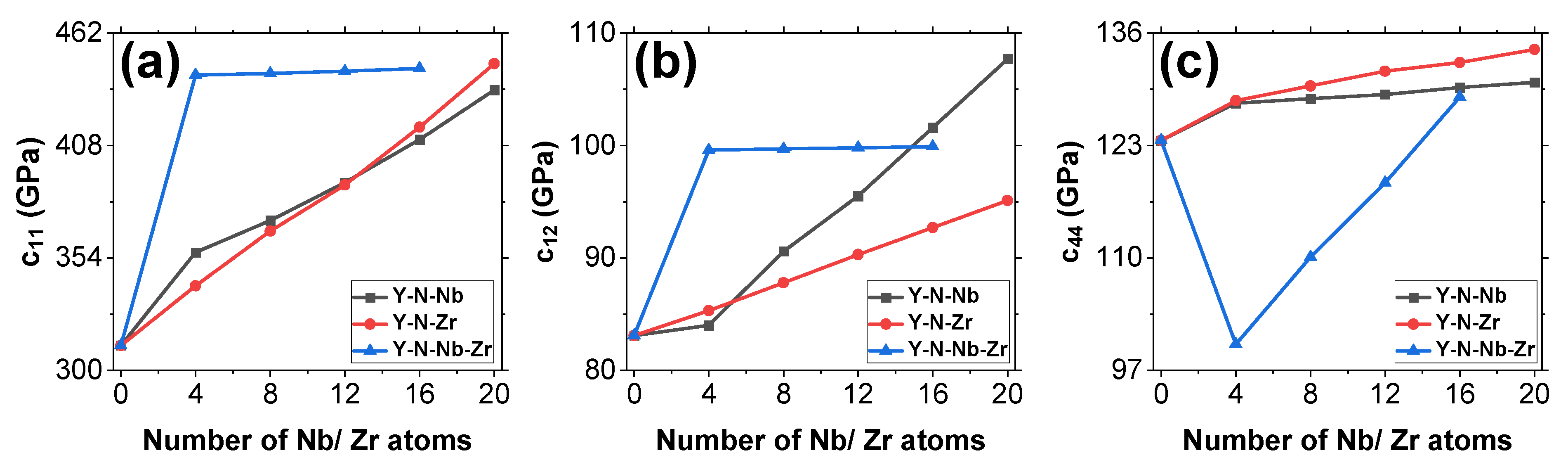
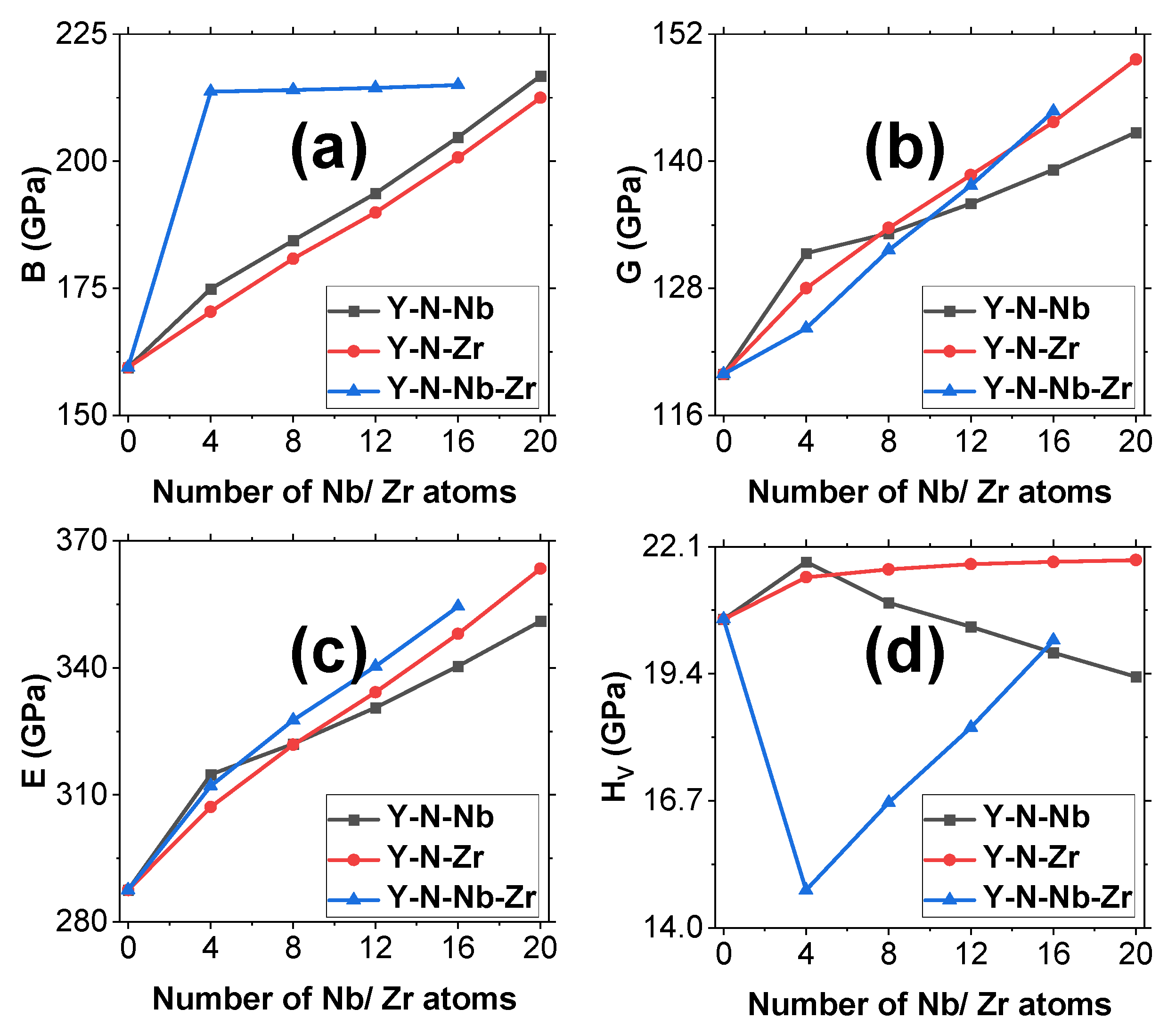
3.2. Mechanical Properties
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, L.; Edgar, J.H.; Peascoe-Meisner, R.A.; Gong, Y.; Bakalova, S.; Kuball, M. Sublimation crystal growth of yttrium nitride. J. Cryst. Growth 2010, 312, 2896–2903. [Google Scholar] [CrossRef]
- Garg, A.; Jonghe, L. Microencapsulation of silicon nitride particles with yttria and yttria-alumina precursors. J. Mater. 1990, 5, 136–142. [Google Scholar] [CrossRef]
- Saha, B.; Sands, T.; Waghmare, U. Electronic structure, vibrational spectrum, and thermal properties of yttrium nitride: A first-principles study. J. Appl. Phys. 2011, 109, 073720. [Google Scholar] [CrossRef]
- Cherchab, Y.; Mir, A.; González-Hernández, R.; Talbi, K.; Bennadji, A. The role of the scandium element concentration in the YN matrix: Ab initio study of structural, electronic, mechanical and thermal properties. Int. J. Quantum Chem. 2021, 121, e26791. [Google Scholar] [CrossRef]
- Cruz, W.; Díaz, J.; Mancera, L.; Takeuchi, N.; Soto, G. Yttrium nitride thin films grown by reactive laser ablation. J. Phys. Chem. Solids 2003, 64, 2273–2279. [Google Scholar] [CrossRef]
- Carlson, O.; Lichtenberg, R.; Warner, J. Solid solubilities of oxygen, carbon and nitrogen in yttrium. J. Less Common Met. 1974, 35, 275–284. [Google Scholar] [CrossRef]
- Beck, U.; Reiners, G.; Kopacz, U.; Jehn, H. Decorative hard coatings: Interdependence of optical, stoichiometric and structural properties. Surf. Coat. Technol. 1993, 60, 389–395. [Google Scholar] [CrossRef]
- Zheng, F.; Xiao, X.; Xie, J.; Zhou, L.; Li, Y.; Dong, H. Structures, properties and applications of two-dimensional metal nitrides: From nitride MXene to other metal nitrides. 2D Mater. 2022, 9, 022001. [Google Scholar] [CrossRef]
- Mehdinia, A.; Aziz-Zanjani, M. Recent advances in nanomaterials utilized in fiber coatings for solid-phase microextraction. Trends Anal. Chem. 2013, 42, 205–215. [Google Scholar] [CrossRef]
- Fischer-Cripps, A. Chapter 14—Mechanical characterizations of surfaces and coatings. In Materials Surface Processing by Directed Energy Techniques; European Materials Research Society Series; Pauleau, Y., Ed.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 475–499. [Google Scholar] [CrossRef]
- Wu, B.; Yuan, A.; Xiao, Y.; Wang, Y.; Lei, J. Study on a polyacrylate-based waterborne coating: Facile preparation, convenient self-healing behavior and photoluminescence properties. J. Mater. Chem. C 2020, 8, 12638–12647. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, K.; Huang, H.; Cui, X.; Shi, X.; Ma, X.; Li, B.; Zhang, Z.; Tang, X.; Chiang, M. Bioinspired wear-resistant and ultradurable functional gradient coatings. Small 2018, 14, 1802717. [Google Scholar] [CrossRef]
- Tolstov, A.; Pokhilenko, N.; Samsonov, N. New opportunities for producing rare earth elements one of the arctic raw material source. J. Sib. Fed. Univ. 2017, 10, 125–138. [Google Scholar] [CrossRef]
- Galletti, A.; Pampaloni, G. Niobium complexes as catalytic precursors for the polymerization of olefins. Coord. Chem. Rev. 2010, 254, 525–536. [Google Scholar] [CrossRef]
- Ghosh, S.; Sharma, A.; Talukder, G. Zirconium: An abnormal trace element in biology. Biol. Trace Elem. Res. 1992, 35, 247–271. [Google Scholar] [CrossRef] [PubMed]
- Bird, K.; Richardson, K. Zirconium for superior corrosion resistance. Adv. Mater. Process. 1997, 151, 19–20. [Google Scholar]
- Available online: http://crystallography.net/cod/result.php (accessed on 28 November 2023).
- Alruqi, A.B.; Ongwen, N.O. A comparative thermodynamic study of AlF3, ScF3, Al0.5Sc0.5F3, and In0.5Sc0.5F3 for optical coatings: A computational study. Coatings 2023, 13, 1840. [Google Scholar] [CrossRef]
- Ongwen, N.O.; Ogam, E.; Otunga, H.O. Ab initio study of elastic properties of orthorhombic cadmium stannate as a substrate for the manufacture of MEMS devices. Mater. Today Commun. 2021, 26, 101822. [Google Scholar] [CrossRef]
- Avery, P.; Wang, X.; Oses, C.; Gossett, E.; Proserpio, D.M.; Toher, C.; Curtarolo, S.; Zurek, E. Predicting superhard materials via a machine learning informed evolutionary structure search. Comput. Mater. 2019, 5, 89. [Google Scholar] [CrossRef]
- Wang, J.; Chen, S.; Yang, Y.; Yu, Y.; Dong, H.; Li, Y. Bulk structure of Si2BN predicted by computational approaches. Diam. Relat. Mater. 2022, 130, 109530. [Google Scholar] [CrossRef]
- Matar, S.F.; Solozhenko, V.L. New superhard tetragonal BCN from crystal chemistry and first principles. Materialia 2022, 26, 101581. [Google Scholar] [CrossRef]
- Rajasekaran, G.; Narayanan, P.; Parashar, A. Effect of point and line defects on mechanical and thermal properties of graphene: A review. Crit. Rev. Solid State 2016, 41, 47–71. [Google Scholar] [CrossRef]
- Miskin, M.; Khaira, G.; Pablo, J.; Jaeger, H. Turning statistical physics models into materials design engines. Proc. Natl. Acad. Sci. USA 2015, 113, 34–39. [Google Scholar] [CrossRef] [PubMed]
- Holec, D.; Friák, M.; Neugebauer, J.; Mayrhofer, P.H. Trends in the elastic response of binary early transition metal nitrides. Phys. Rev. B 2012, 85, 064101. [Google Scholar] [CrossRef]
- Miháliková, I.; Friák, M.; Jirásková, Y.; Holec, D.; Koutná, N.; Šob, M. Impact of nano-scale distribution of atoms on electronic and magnetic properties of phases in Fe-Al nanocomposites: An ab initio study. Nanomaterials 2018, 8, 1059. [Google Scholar] [CrossRef]
- Vo, T.; Reeder, B.; Damone, A.; Newell, P. Effect of domain size, boundary, and loading conditions on mechanical properties of amorphous silica: A reactive molecular dynamics study. Nanomaterials 2020, 10, 54. [Google Scholar] [CrossRef]
- Safont, G. Mechanical properties of materials. In Introduction to Contact Mechanics; Mechanical Engineering Series; Springer: Boston, MA, USA, 2007. [Google Scholar] [CrossRef]
- Pius, K.K.; Ongwen, N.O.; Mageto, M.; Odari, V.; Gaitho, F.M. Mechanical properties of Al–Mg–Si alloys (6xxx Series): A DFT-based study. Alloys 2023, 2, 213–226. [Google Scholar] [CrossRef]
- Smirnova, E.; Sotnikov, A.; Ktitorov, S.; Schmidt, H. Low temperature acoustic characterization of PMN single crystal. J. Appl. Phys. 2017, 122, 084103. [Google Scholar] [CrossRef]
- Nazir, M.; Mahmood, T.; Zafar, A.; Akhtar, N.; Hussain, T.; Saeed, M.; Aleem, F.; Saeed, A.; Raza, J.; Cao, C. Electronic, optical and elastic properties of cubic zirconia (c-ZrO2) under pressure: A DFT study. Phys. B Condens. 2021, 604, 412462. [Google Scholar] [CrossRef]
- Yang, J.W.; An, L. Ab initio calculation of the electronic, mechanical, and thermodynamic properties of yttrium nitride with the rock salt structure. Phys. Status Solidi B 2014, 251, 792–802. [Google Scholar] [CrossRef]
- Hao, A.; Yang, X.; Wang, X.; Yu, R.; Liu, R. First-principles investigations on electronic and elastic properties of YX (X = N, P, As and Sb) under high pressure. Comput. Mater. Sci. 2010, 48, 59–64. [Google Scholar] [CrossRef]
- Available online: https://www.lakeshore.com/docs/default-source/default-document-library/magnesium-fluoride-mgf2-transmission-curve-datasheet.pdf?sfvrsn=8be6c56a_2 (accessed on 28 November 2023).
- Suprapedi; Muljadi; Sardjono, P. The characterization of ceramic alumina prepared by using additive glass beads. IOP Conf. Ser. Mater. Sci. Eng. 2017, 299, 012043. [Google Scholar] [CrossRef]
- Maidanik, G.; Maga, L. Analytical evaluation in the design of a coating. J. Sound Vib. 2008, 309, 150–166. [Google Scholar] [CrossRef]
- Reddy, R.; Ahammed, Y.; Gopal, K.; Azeem, P.; Rao, T.; Reddy, P. Optical electronegativity, bulk modulus and electronic polarizability of materials. Opt. Mater. 2000, 14, 355–358. [Google Scholar] [CrossRef]
- Shiue, S. Design of the interfacial shear strength between the glass fiber and primary coating in double-coated optical fibers. J. Lightwave Technol. 1999, 17, 1657–1661. [Google Scholar] [CrossRef]
- Chen, S.; Shiue, S. Theoretical analysis of the interfacial-shear-stress induced delamination of polymeric coatings from the glass fibers in double-coated optical fibers during temperature cycling. Opt. Fiber Technol. 2006, 12, 268–275. [Google Scholar] [CrossRef]
- Shen, T.; Shiue, S. Long-term thermally interfacial-shear-stress-induced delamination of polymeric coatings from glass fibers in double-coated optical fibers. Opt. Eng. 2003, 42, 1456–1459. [Google Scholar] [CrossRef]
- Ali, M.; Islam, A.; Hossain, M.; Parvin, F. Phase stability, elastic, electronic, thermal and optical properties of Ti3Al1−xSixC2 (0 ≤ x ≤ 1): First principles study. Phys. B Condens. Matter 2012, 407, 4221–4228. [Google Scholar] [CrossRef]
- Guenther, K.; Bangert, H.; Kaminitschek, A.; Wagendristel, A. Ultra-microhardness testing of optical coatings. In Third Topical Meeting on Optical Interference Coatings; Technical Digest Series; Paper WA5; Optica Publishing Group: Monterey, CA, USA, 1984. [Google Scholar] [CrossRef]

| Sample | Yttrium | Nitrogen | Niobium | Zirconium | |
|---|---|---|---|---|---|
| CY | 32 | 32 | 0 | 0 | |
| Y-N-Nb | CYN_1 | 28 | 32 | 4 | 0 |
| CYN_2 | 24 | 32 | 8 | 0 | |
| CYN_3 | 20 | 32 | 12 | 0 | |
| CYN_4 | 16 | 32 | 16 | 0 | |
| CYN_5 | 12 | 32 | 20 | 0 | |
| Y-N-Zr | CYZ_1 | 28 | 32 | 0 | 4 |
| CYZ_2 | 24 | 32 | 0 | 8 | |
| CYZ_3 | 20 | 32 | 0 | 12 | |
| CYZ_4 | 16 | 32 | 0 | 16 | |
| CYZ_5 | 12 | 32 | 0 | 20 | |
| Y-N-Nb-Zr | CYNZ_1 | 12 | 32 | 4 | 16 |
| CYNZ_2 | 12 | 32 | 8 | 12 | |
| CYNZ_3 | 12 | 32 | 12 | 8 | |
| CYNZ_4 | 12 | 32 | 16 | 4 |
| Category | Sample | |||||
|---|---|---|---|---|---|---|
| CY | 4.908 (4.88 [1]) (4.917 [4]) | 5788 (5750 [25]) | 312.0 (314.34 [4]) | 83.1 (81 [26]) | 123.6 (124 [26]) | |
| Y-N-Nb | CYN_1 | 4.824 | 6127 | 356.6 | 84.0 | 127.9 |
| CYN_2 | 4.766 | 6388 | 372.0 | 90.6 | 128.4 | |
| CYN_3 | 4.715 | 6652 | 390.2 | 95.5 | 128.9 | |
| CYN_4 | 4.649 | 6953 | 410.9 | 101.6 | 129.7 | |
| CYN_5 | 4.592 | 7253 | 434.7 | 107.7 | 130.3 | |
| Y-N-Zr | CYZ_1 | 4.858 | 5985 | 340.6 | 85.3 | 128.2 |
| CYZ_2 | 4.816 | 6109 | 366.9 | 87.8 | 129.9 | |
| CYZ_3 | 4.778 | 6327 | 389.1 | 90.3 | 131.6 | |
| CYZ_4 | 4.738 | 6504 | 416.8 | 92.7 | 132.6 | |
| CYZ_5 | 4.702 | 6673 | 447.3 | 95.1 | 134.1 | |
| Y-N-Nb-Zr | CYNZ_1 | 4.615 | 7125 | 441.9 | 99.6 | 100.0 |
| CYNZ_2 | 4.638 | 6981 | 442.7 | 99.7 | 110.1 | |
| CYNZ_3 | 4.656 | 6908 | 443.7 | 99.8 | 118.7 | |
| CYNZ_4 | 4.678 | 6792 | 445.1 | 99.9 | 128.6 |
| Category | Sample | ||||
|---|---|---|---|---|---|
| CY | 159.4 (159.2 [32]) | 119.9 (120.5 [32]) | 287.5 (289.2 [33]) | 20.56 (21.01 [32]) | |
| Y-N-Nb | CYN_1 | 174.9 | 131.3 | 314.8 | 21.78 |
| CYN_2 | 184.4 | 133.2 | 322.0 | 20.91 | |
| CYN_3 | 193.7 | 136.0 | 330.6 | 20.40 | |
| CYN_4 | 204.7 | 139.2 | 340.4 | 19.85 | |
| CYN_5 | 216.8 | 142.7 | 351.0 | 19.34 | |
| Y-N-Zr | CYZ_1 | 170.4 | 128.0 | 307.1 | 21.45 |
| CYZ_2 | 180.8 | 133.7 | 321.8 | 21.62 | |
| CYZ_3 | 189.9 | 138.7 | 334.2 | 21.73 | |
| CYZ_4 | 200.7 | 143.7 | 348.0 | 21.78 | |
| CYZ_5 | 212.5 | 149.6 | 363.4 | 21.82 | |
| Y-N-Nb-Zr | CYNZ_1 | 213.7 | 124.2 | 312.1 | 14.80 |
| CYNZ_2 | 214.0 | 131.6 | 327.6 | 16.66 | |
| CYNZ_3 | 214.4 | 137.7 | 340.3 | 18.26 | |
| CYNZ_4 | 215.0 | 144.7 | 354.5 | 20.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alruqi, A.B. The Influence of Niobium and Zirconium Addition on the Structural and Mechanical Properties of Yttrium Nitride: A First-Principles Study. Coatings 2023, 13, 2078. https://doi.org/10.3390/coatings13122078
Alruqi AB. The Influence of Niobium and Zirconium Addition on the Structural and Mechanical Properties of Yttrium Nitride: A First-Principles Study. Coatings. 2023; 13(12):2078. https://doi.org/10.3390/coatings13122078
Chicago/Turabian StyleAlruqi, Adel Bandar. 2023. "The Influence of Niobium and Zirconium Addition on the Structural and Mechanical Properties of Yttrium Nitride: A First-Principles Study" Coatings 13, no. 12: 2078. https://doi.org/10.3390/coatings13122078
APA StyleAlruqi, A. B. (2023). The Influence of Niobium and Zirconium Addition on the Structural and Mechanical Properties of Yttrium Nitride: A First-Principles Study. Coatings, 13(12), 2078. https://doi.org/10.3390/coatings13122078






