Gradation Optimization Based on Micro-Analysis of Rutting Behavior of Asphalt Mixture
Abstract
:1. Introduction
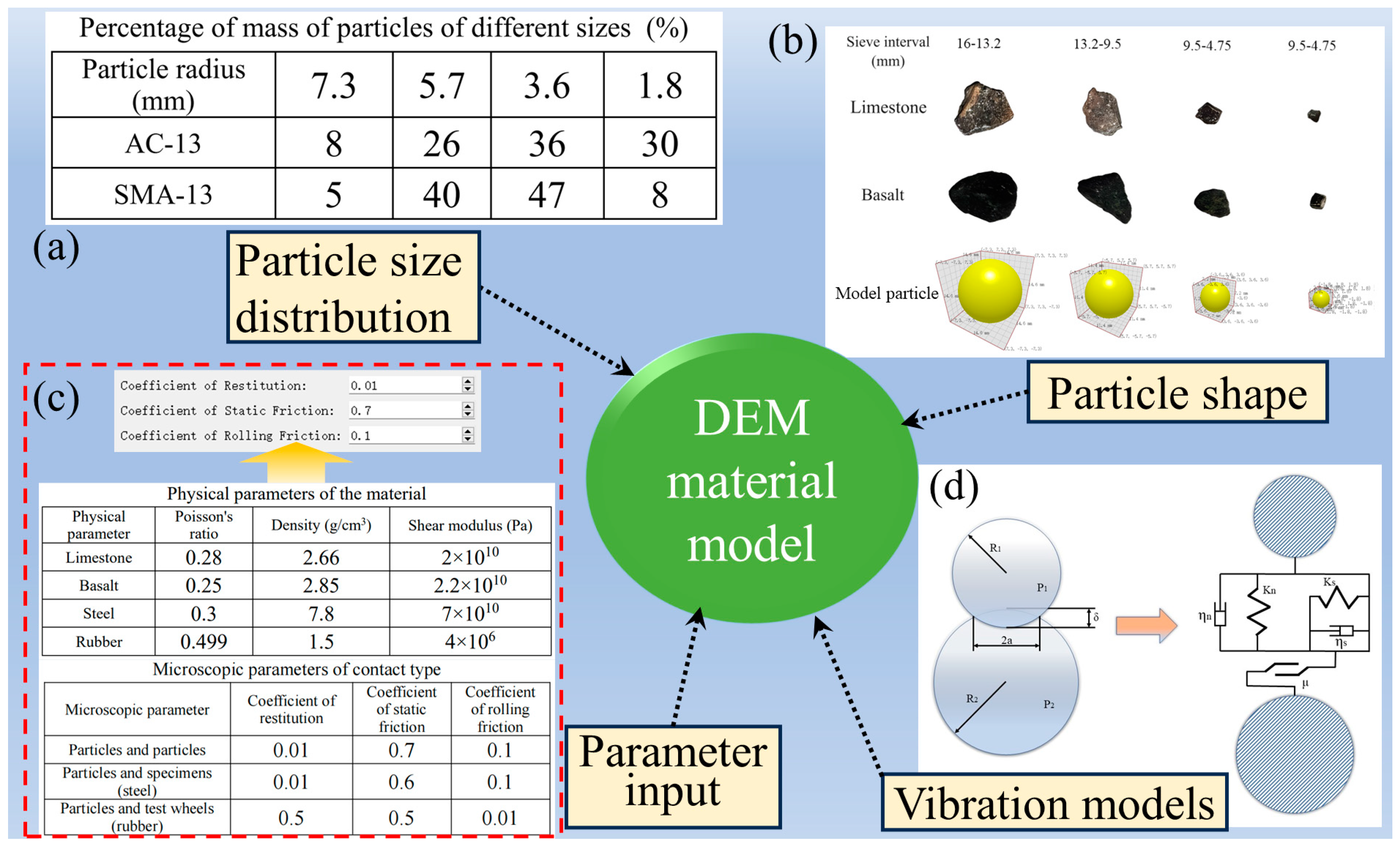
2. Discrete Element Simulation
2.1. Establishment of Material Model
2.2. Interparticle Contact Model
2.3. Material Parameter Calibration
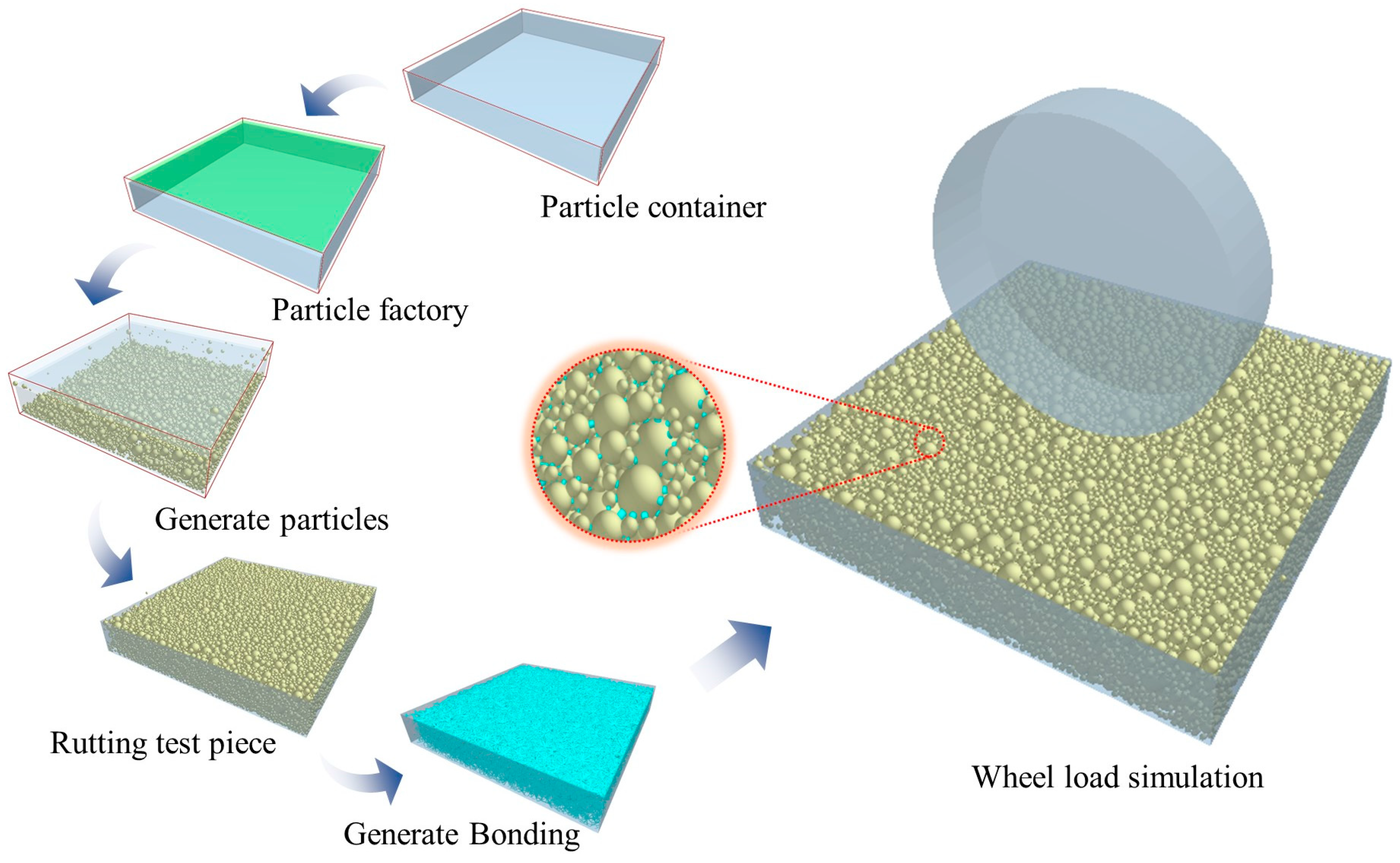
2.4. Establishment of Rutting Model
3. Simulation Results and Analysis
3.1. Interparticle Correlation State Analysis
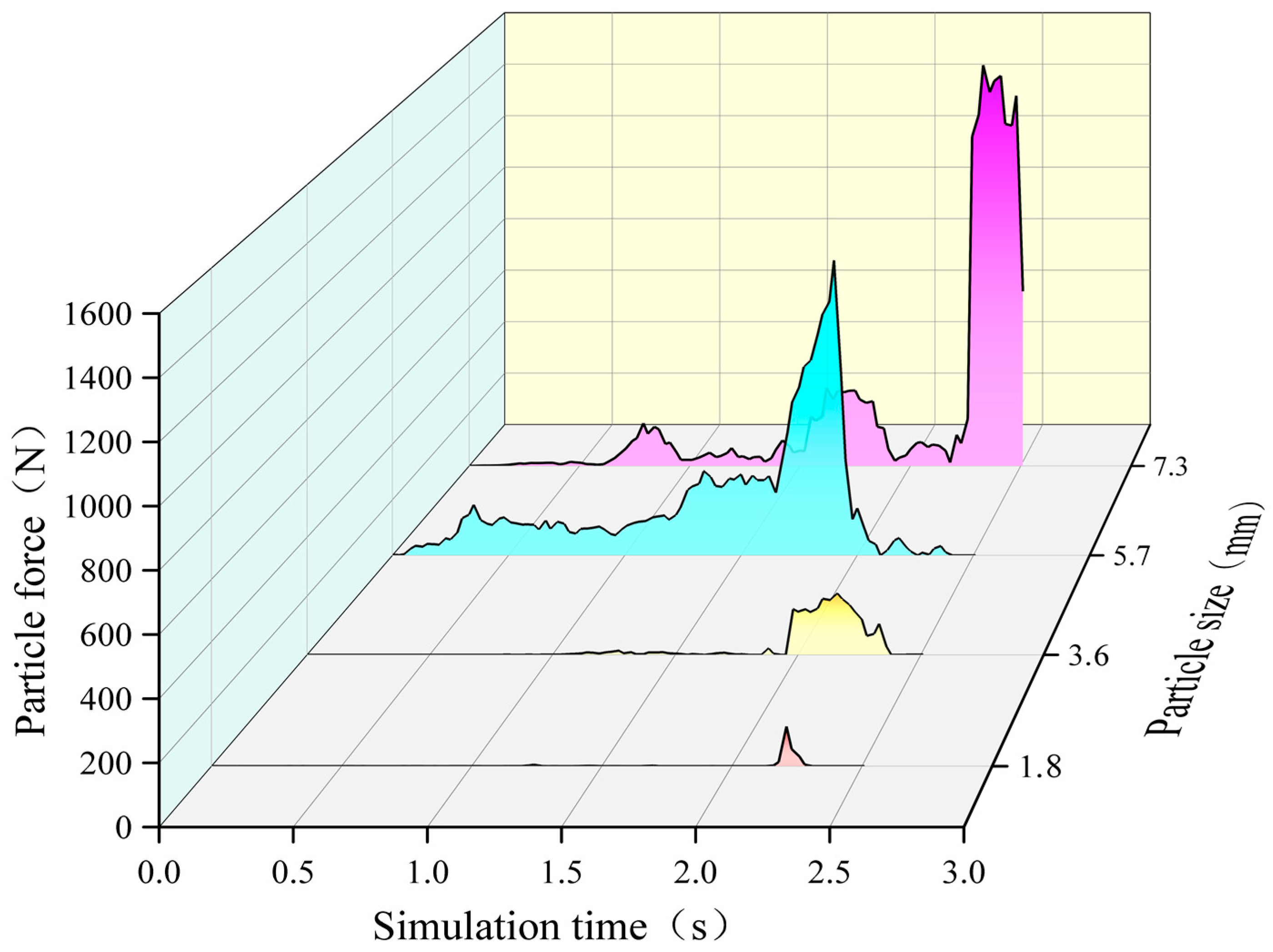
3.2. Force of Particles with Different Sizes in Rutting
3.3. The Force Curve of Particles in Asphalt Mixtures
3.3.1. Force Curve Analysis of Particles with Different Sizes
3.3.2. Comparative Analysis of Forces on Particles of the Same Size
4. Asphalt Mixture Gradation Optimization, Design, and Verification
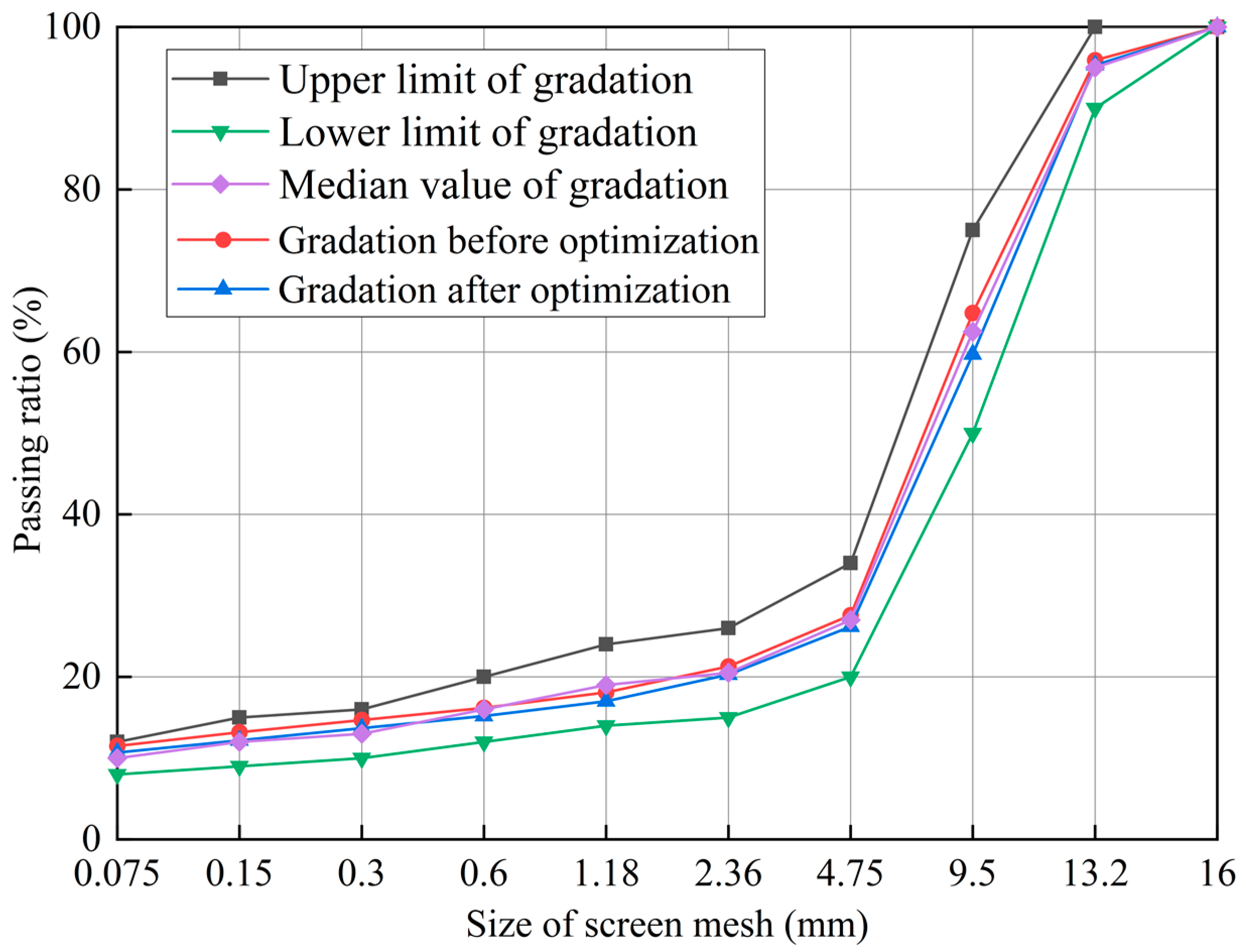
4.1. Gradation Optimization Design
4.2. Asphalt Mixture Performance Test
4.2.1. High-Temperature Rutting Test
4.2.2. Low-Temperature Bending Test
4.2.3. Water Stability Performance Test
5. Conclusions
- (1)
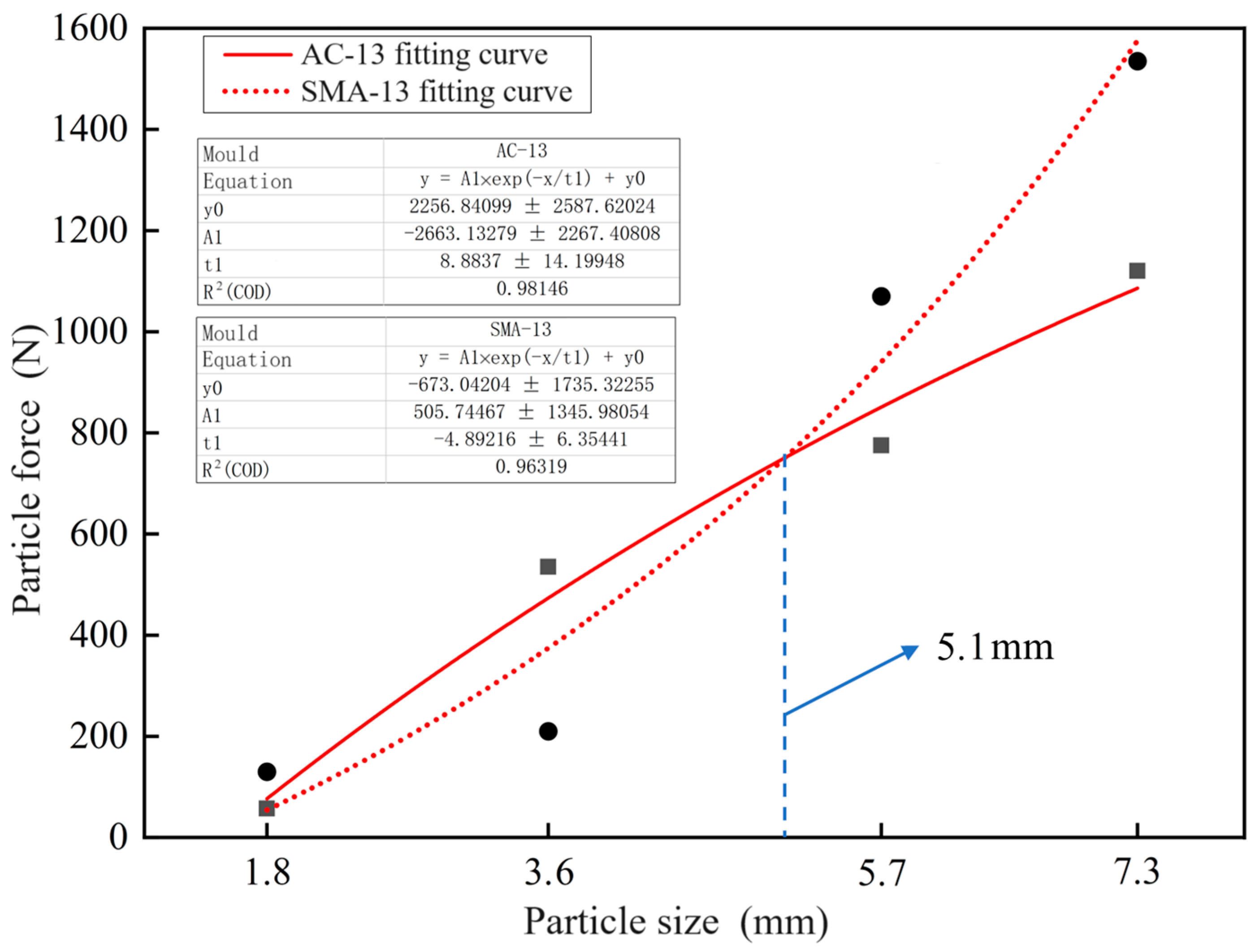
- In the AC-13 asphalt mixture, particles with a radius of more than 1.8 mm are the main bearing particles. In the SMA-13 asphalt mixture, the particles with a radius of more than 3.6 mm are the main bearing particles. Small particle-size particles play a filling role. The particle force limit value of the two types of asphalt mixture is proportional to the particle size.
- (2)
- When the particle radius is less than 5.1 mm, the particle force value of the AC-13 asphalt mixture is greater than that of SMA-13. When the particle radius is greater than 5.1 mm, the particle force value of the SMA-13 asphalt mixture is greater than that of AC-13. For particles with a radius of 5.7 mm and 7.3 mm, the force limit value of the SMA-13 asphalt mixture is increased by about 30% compared to that of the AC-13 asphalt mixture.
- (3)
- Through laboratory experimental research, the dynamic stability, flexural tensile strength, water immersion residual stability, and freeze-thaw splitting strength ratios of the AC-13 asphalt mixture after optimization are 8.5%, 9.2%, 1.6%, and 1.9% higher than those before optimization. The dynamic stability, flexural tensile strength, water immersion residual stability, and freeze-thaw splitting strength ratios of the SMA-13 asphalt mixture after optimization are 10.6%, 7.3%, 0.7%, and 2.1% higher than those before optimization. The road performance of the asphalt mixture after gradation optimization has improved, which shows that the gradation optimization method is feasible.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, D.D.; Wei, L.Y.; Zhang, J.X. Experimental study on performance of asphalt mixture designed by different method. Procedia Eng. 2016, 137, 407–414. [Google Scholar] [CrossRef]
- Wong, W.G.; Han, H.F.; He, G.P.; Wang, K.C.P.; Lu, W.M. Rutting response of hot-mix asphalt to generalized dynamic shear moduli of asphalt binder. Constr. Build. Mater. 2004, 18, 399–408. [Google Scholar] [CrossRef]
- Topal, A.; Sengoz, B. Determination of fine aggregate angularity in relation with the resistance to rutting of hot-mix asphalt. Constr. Build. Mater. 2005, 19, 155–163. [Google Scholar] [CrossRef]
- Morea, F.; Agnusdei, J.O.; Zerbino, R. The use of asphalt low shear viscosity to predict permanent deformation performance of asphalt concrete. Mater. Struct. 2011, 44, 1241–1248. [Google Scholar] [CrossRef]
- Guan, H.X.; Zhang, Q.S.; Liu, J. Rutting test improving methods of asphalt mixture. J. Traffic Transp. Eng. 2011, 11, 16–21. [Google Scholar]
- Li, Q.; Ni, F.J. Comparison of anti-rutting performance tests for asphalt mixture. J. Southeast Univ. Nat. Sci. Ed. 2014, 44, 1266–1270. [Google Scholar]
- Huang, W.D.; Mo, D.C.; Lyu, Q.; Zheng, M.; Zhou, L. High temperature performance evaluation of TB composite modified asphalt mixture based on Hamburg wheel tracking test. J. Chang. Univ. Nat. Sci. Ed. 2020, 40, 12–21. [Google Scholar]
- Wang, H.; Tan, H.Q.; Zhang, J.P. Effects of molding shape and air void of asphalt mixture specimen on APA rutting tests. J. Southeast Univ. Nat. Sci. Ed. 2016, 46, 589–593. [Google Scholar]
- Du, R.Y.; Lin, Y.G. Study on Application Range of Hamburg Rut and APA Rut Test. J. China Foreign Highw. 2019, 39, 237–242. [Google Scholar]
- Barksdale, R.D. Laboratory Evaluation of Rutting in Base Course Materials. In Proceedings of the Third International Conference on the Structural Design of Asphalt Pavements, London, UK, 7–11 January 1972. [Google Scholar]
- Romain, J.E. Rut Depth Manual-Asphalt Pavements and Overlays for Road Traffic; Shell International Petroleum Company: London, UK, 1978. [Google Scholar]
- Hills, J.F.; Brian, D.; Loo, P.P. The Correlation of Rutting and Creep Tests of Asphalt Mixes. In Flexible Pavements; Transport and Road Research Laboratory (TRRL): Wokingham, UK, 1974. [Google Scholar]
- Zhang, H.Q. The Application Study of the United Prediction Model of the Volumetric Parameters and Rutting Resistance Performance of Asphalt Mixture. Master’s Thesis, Shandong University, Jinan, China, 2009. [Google Scholar]
- Xie, L.B. Research of Asphalt Pavement Rutting Prediction Model Based on Temperature Filed and Dynamic Modulus. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2013. [Google Scholar]
- Rougier, E.; Knight, E.E.; Broome, S.T.; Sussman, A.J.; Munjiza, A. Validation of a three-dimensional finite-discrete element method using experimental results of the split Hopkinson pressure bar test. Int. J. Rock Mech. Min. Sci. 2014, 70, 101–108. [Google Scholar] [CrossRef]
- Feng, H.; Pettinari, M.; Hofko, B.; Stang, H. Study of the internal mechanical response of an asphalt mixture by 3-D discrete element modeling. Constr. Build. Mater. 2015, 77, 187–196. [Google Scholar] [CrossRef]
- Liu, Y.; You, Z.; Zhao, Y. Three-dimensional discrete element modeling of asphalt concrete: Size effects of elements. Constr. Build. Mater. 2012, 37, 775–782. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Qian, G.; Zheng, J.; Zhang, Y. Three-dimensional simulation of aggregate and asphalt mixture using parameterized shape and size gradation. J. Mater. Civ. Eng. 2019, 31, 4019004. [Google Scholar] [CrossRef]
- Mahmoud, E.; Masad, E.; Nazarian, S. Discrete element analysis of the influences of aggregate properties and internal structure on fracture in asphalt mixtures. J. Mater. Civ. Eng. 2010, 22, 10–20. [Google Scholar] [CrossRef]
- Chen, J.; Pan, T.; Huang, X. Discrete element modeling of asphalt concrete cracking using a user-defined three-dimensional micromechanical approach. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2011, 26, 1215–1221. [Google Scholar] [CrossRef]
- Meza-Lopez, J.; Noreña, N.; Meza, C.; Romanel, C. Modeling of asphalt concrete fracture tests with the discrete-element method. J. Mater. Civ. Eng. 2020, 32, 4020228. [Google Scholar] [CrossRef]
- Xue, B.; Xu, J.; Pei, J.Z.; Zhang, J.P.; Li, R. Investigation on the micromechanical response of asphalt mixture during permanent deformation based on 3D virtual wheel tracking test. Constr. Build. Mater. 2021, 267, 121031. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, E.L.; Li, N.P.; Wang, L.F.; Si, C.D.; Wang, C.Y. Micromechanical analysis of the rutting evolution of asphalt pavement under temperature–stress coupling based on the discrete element method. Constr. Build. Mater. 2022, 325, 126800. [Google Scholar] [CrossRef]
- Wang, H.N.; Bu, Y.; Wang, Y.Z.; Yang, X.; You, Z.P. The effect of morphological characteristic of coarse aggregates measured with fractal dimension on asphalt mixture’s high-temperature performance. Adv. Mater. Sci. Eng. 2016, 2016, 6264317. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, D.Y.; Zhang, Y.; Hong, J.X. Micromechanical response of aggregate skeleton within asphalt mixture based on virtual simulation of wheel tracking test. Constr. Build. Mater. 2016, 111, 153–163. [Google Scholar] [CrossRef]
- Yu, C.C. Meso-Structural Character Analysis on the Rutting of Asphalt Pavement Based on Discrete Element Simulation. Master’s Thesis, Shijiazhuang Tiedao University, Shijiazhuang, China, 2020. [Google Scholar]
- Ma, T.; Zhang, D.Y.; Zhang, Y.; Wang, S.Q.; Huang, X.M. Simulation of wheel tracking test for asphalt mixture using discrete element modelling. Road Mater. Pavement Des. 2018, 19, 367–384. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, D.Y.; Zhang, Y.; Zhao, Y.L.; Huang, X.M. Effect of air voids on the high-temperature creep behavior of asphalt mixture based on three-dimensional discrete element modeling. Mater. Des. 2016, 89, 304–313. [Google Scholar] [CrossRef]
- Yu, H.; Ma, T.; Wang, D.; Wang, Z.; Lye, S.; Zhu, X.Y. Review on China’s pavement engineering research 2020. China J. Highw. Transp. 2020, 33, 1–66. [Google Scholar]
- Zhang, D.M.; Zheng, Y.M.; Yuan, G.C.; Guo, H.; Zhou, Q.; Qian, G.P.; Liang, B. Comparative analysis of rheological and microscopic performance of SBS modified asphalt based on field aging and laboratory aging. Fuel 2023, 352, 128933. [Google Scholar] [CrossRef]
- Castillo-Camarena, E.A.; Williams, S. Application of percent within limits concepts on a balanced mix design of asphalt mixture. Int. J. Pavement Eng. 2022, 1–23. [Google Scholar] [CrossRef]
- Xu, S.F.; Peng, G.; Zhang, Y.X.; Guo, Y.T.; Suo, Z.; Xu, Y. Design Method of asphalt pavement mixture based on performance balance approach. J. Transp. Eng. Part B Pavements 2021, 147, 4021009. [Google Scholar] [CrossRef]
- Chen, J.; Li, H.; Wang, L.; Wu, J.; Huang, X. Micromechanical characteristics of aggregate particles in asphalt mixture. Constr. Build. Mater. 2015, 91, 80–85. [Google Scholar] [CrossRef]
- Jiang, W.; Sha, A.M.; Xiao, J.J. Comparison and selection of gradation for porous asphalt concrete based on discrete element method. J. Jilin Univ. 2011, 41, 68–72. [Google Scholar]
- Miao, Y.H.; Yu, W.X.; Hou, Y.; Guo, L.Y.; Wang, L.B. Investigating the functions of particles in packed aggregate blend using a discrete element method. Materials 2019, 12, 556. [Google Scholar] [CrossRef]
- Yu, H.; Shen, S. Impact of Aggregate Packing on Dynamic Modulus of Hot Mix Asphalt mixture Using Three-Dimensional Discrete Element Method. Constr. Build. Mater. 2012, 26, 302–309. [Google Scholar] [CrossRef]
- Leon, L.P.; Gay, D. Gene expression programming for evaluation of aggregate angularity effects on permanent deformation of asphalt mixture. Constr. Build. Mater. 2019, 211, 470–478. [Google Scholar] [CrossRef]
- Guo, Y.; Zhao, C.; Markine, V.; Jing, G.; Zhai, W. Calibration for discrete element modelling of railway ballast: A review. Transp. Geotech. 2020, 23, 100341. [Google Scholar] [CrossRef]
- Jaradat, K.A.; Abdelaziz, S.L. On the use of discrete element method for multi-scale assessment of clay behavior. Comput. Geotech. 2019, 112, 329–341. [Google Scholar] [CrossRef]
- Hu, G.M. Analysis and Simulation of Particle System by Discrete Element Method; Wuhan University of Technology Press: Wuhan, China, 2010. [Google Scholar]
- Pue, J.D.; Emidio, G.D.; Flores, R.D.V.; Bezuijen, A.; Cornelis, W.M. Calibration of dem material parameters to simulate stress-strain behaviour of unsaturated soils during uniaxial compression. Soil Tillage Res. 2019, 194, 104303. [Google Scholar] [CrossRef]
- JTG E20-2011 T0719-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Research Institute of Highway Ministry of Transport: Beijing, China, 2011.
- Cong, L.Y. Simulation Test of Asphalt Mixture Rutting Based on Discrete Element Method. Master’s Thesis, Harbin Engineering University, Harbin, China, 2019. [Google Scholar]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Research Institute of Highway Ministry of Transport: Beijing, China, 2011.
- JTG E20-2011 T0728-2000; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Research Institute of Highway Ministry of Transport: Beijing, China, 2011.
- JTG E20-2011 T0709-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Research Institute of Highway Ministry of Transport: Beijing, China, 2011.
- JTG E20-2011 T0729-2000; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Research Institute of Highway Ministry of Transport: Beijing, China, 2011.







| Type of Mixture | (N/m3) | (N/m3) | (Pa) | (Pa) | (mm) |
|---|---|---|---|---|---|
| AC-13 | 2.11 × 1010 | 1.01 × 1010 | 2.31 × 105 | 2.77 × 105 | 0.53 |
| SMA-13 | 2.32 × 109 | 1.11 × 109 | 1.58 × 107 | 2.83 × 107 | 0.86 |
| Type of Mixture | Gradation Type | Dynamic Stability (Times/mm) | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | Average | ||
| AC-13 | Gradation before optimization | 4227 | 4134 | 4192 | 4184 |
| Gradation after optimization | 4583 | 4502 | 4529 | 4538 | |
| SMA-13 | Gradation before optimization | 5574 | 5623 | 5649 | 5615 |
| Gradation after optimization | 5968 | 6276 | 6381 | 6208 | |
| Type of Mixture | Gradation Type | Flexural Tensile Strength (MPa) | Maximum Bending Strain (10−6) | Bending Stiffness Modulus (MPa) |
|---|---|---|---|---|
| AC-13 | Gradation before optimization | 10.32 | 2587.2 | 3989.85 |
| Gradation after optimization | 11.27 | 2896.3 | 3891.61 | |
| SMA-13 | Gradation before optimization | 12.08 | 2752.8 | 4388.87 |
| Gradation after optimization | 12.96 | 3021.6 | 4289.77 |
| Type of Mixture | Gradation Type | Water Immersion Residual Stability (%) | Freeze-Thaw Splitting Strength Ratio (%) |
|---|---|---|---|
| AC-13 | Gradation before optimization | 87.9 | 79.6 |
| Gradation after optimization | 89.3 | 81.1 | |
| SMA-13 | Gradation before optimization | 91.7 | 86.4 |
| Gradation after optimization | 92.3 | 88.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Xu, H.; Wang, J.; Hang, J.; Wang, K.; Hu, P.; Li, H. Gradation Optimization Based on Micro-Analysis of Rutting Behavior of Asphalt Mixture. Coatings 2023, 13, 1965. https://doi.org/10.3390/coatings13111965
Guo Q, Xu H, Wang J, Hang J, Wang K, Hu P, Li H. Gradation Optimization Based on Micro-Analysis of Rutting Behavior of Asphalt Mixture. Coatings. 2023; 13(11):1965. https://doi.org/10.3390/coatings13111965
Chicago/Turabian StyleGuo, Qingliang, Hao Xu, Junjie Wang, Jiezhou Hang, Kun Wang, Peng Hu, and Hongzhen Li. 2023. "Gradation Optimization Based on Micro-Analysis of Rutting Behavior of Asphalt Mixture" Coatings 13, no. 11: 1965. https://doi.org/10.3390/coatings13111965
APA StyleGuo, Q., Xu, H., Wang, J., Hang, J., Wang, K., Hu, P., & Li, H. (2023). Gradation Optimization Based on Micro-Analysis of Rutting Behavior of Asphalt Mixture. Coatings, 13(11), 1965. https://doi.org/10.3390/coatings13111965





