Graded Minimal Surface Structures with High Specific Strength for Broadband Sound Absorption Produced by Laser Powder Bed Fusion
Abstract
:1. Introduction
2. Materials and Methods
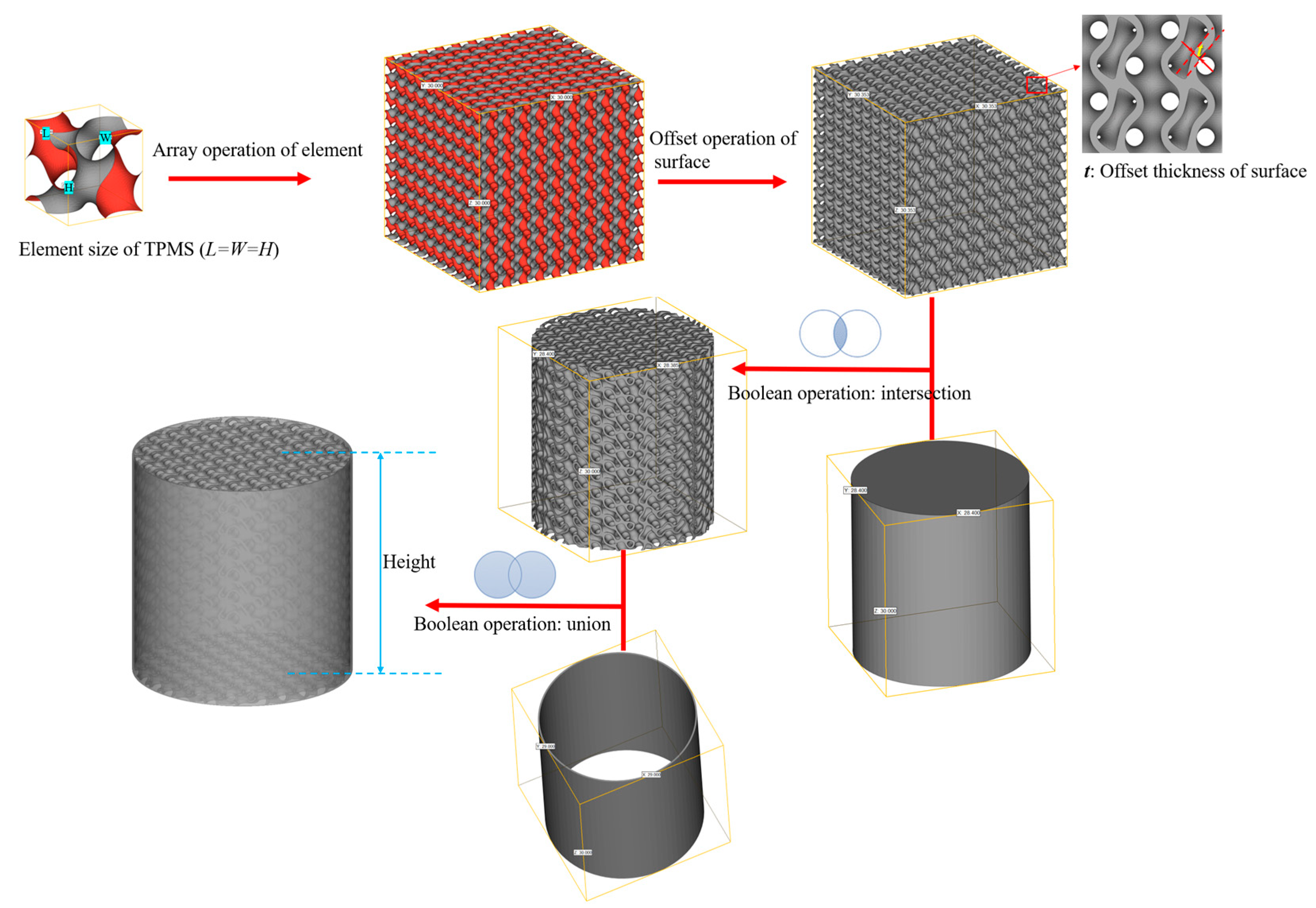
2.1. Modelling of TPMS
2.1.1. Design of Homogeneous TPMS
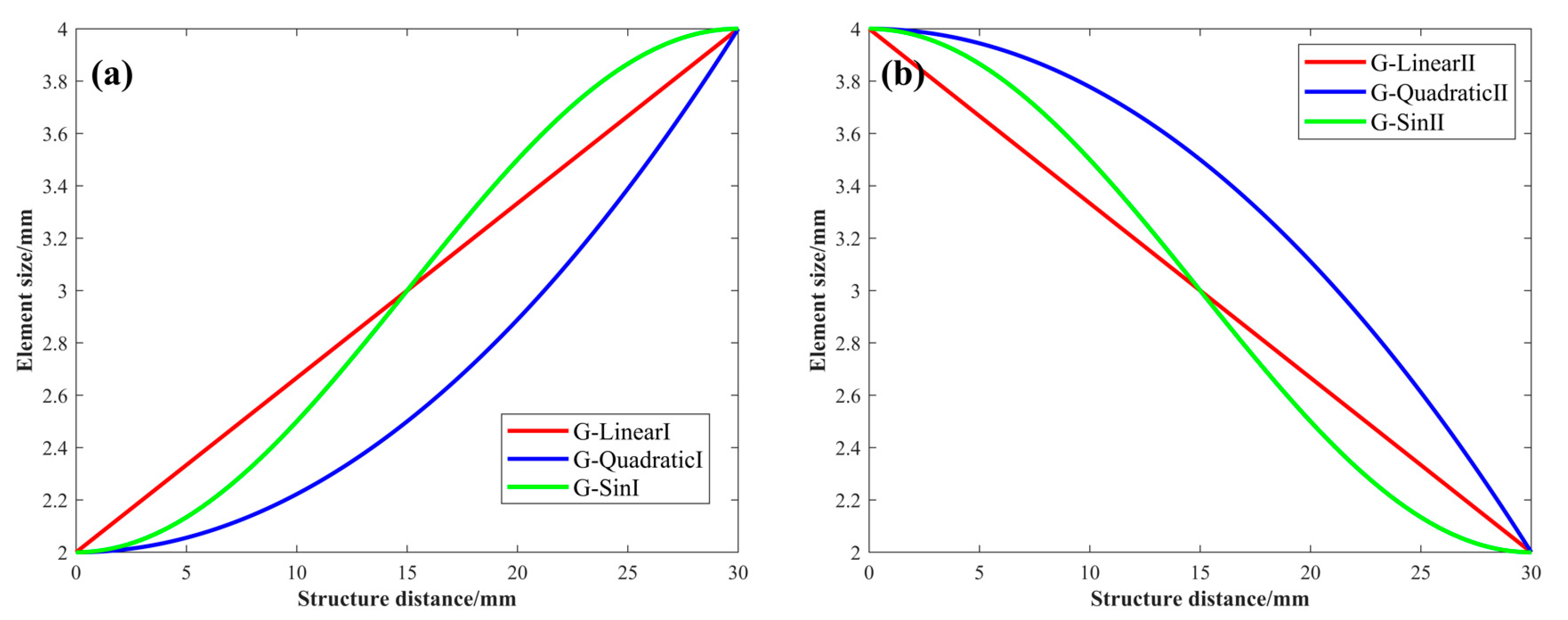
2.1.2. Design of Graded TPMS
2.2. Additive Manufacturing
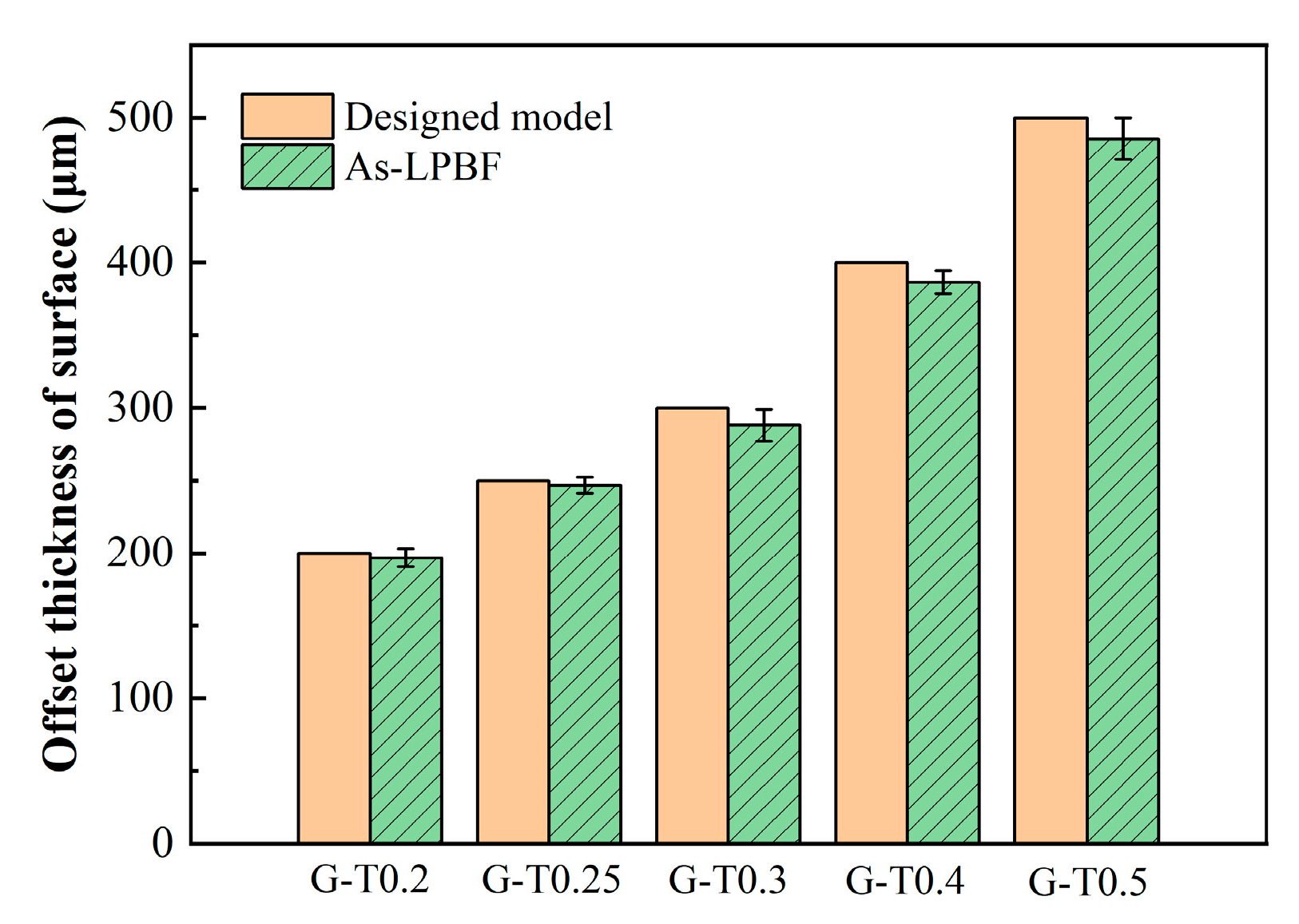
2.3. Dimensional Accuracy Measurement
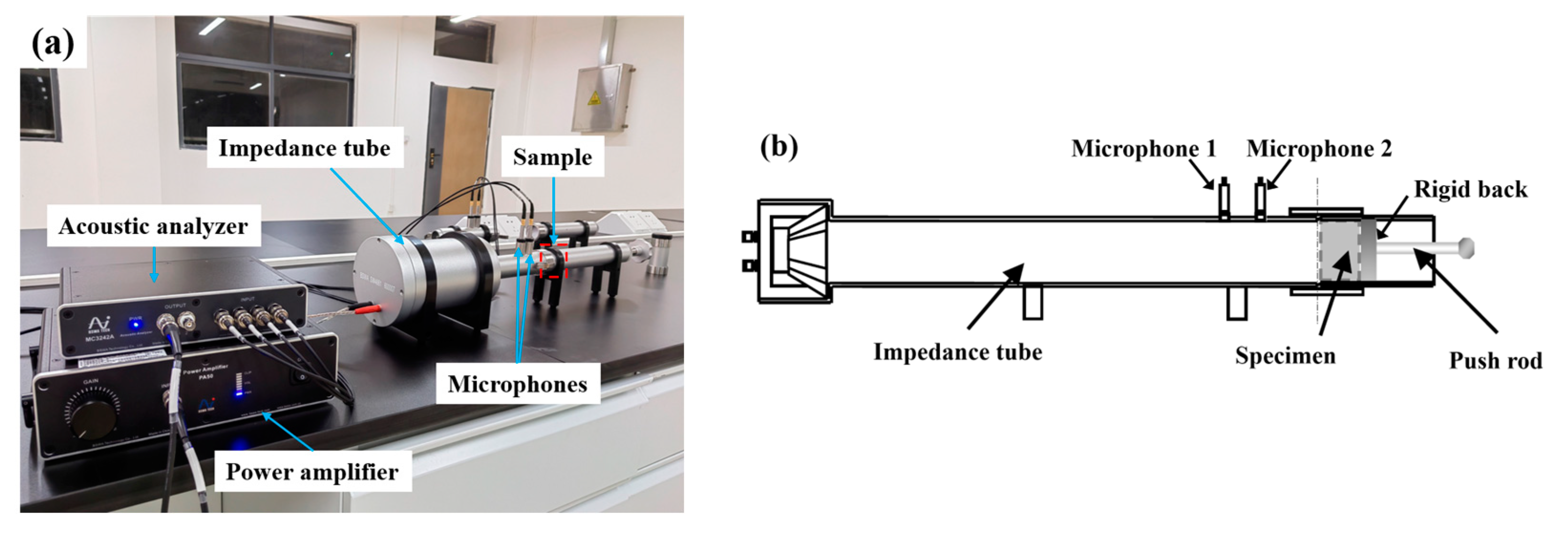
2.4. Sound Absorption Coefficient Test
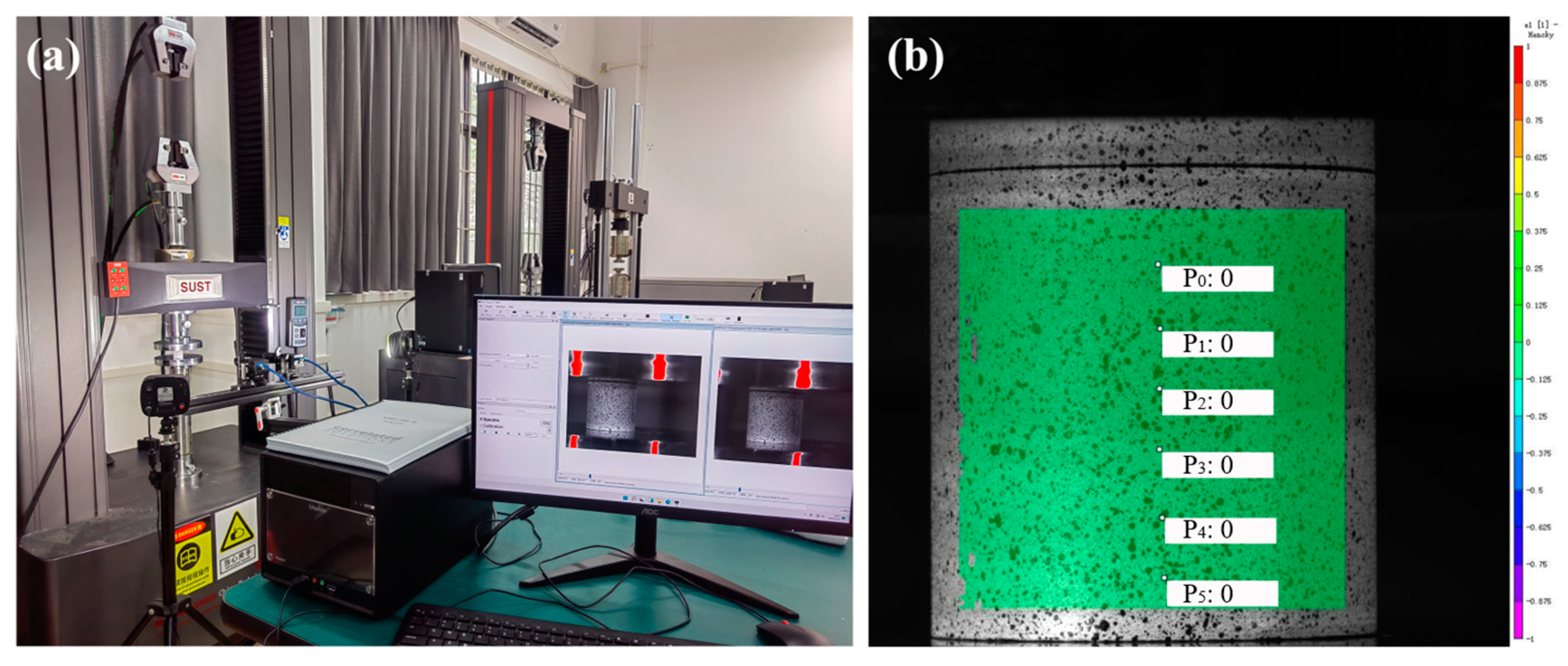
2.5. Mechanical and DIC Test
3. Results and Discussion
3.1. Forming Quality by LPBF
3.2. Sound Absorption Characteristics of Homogeneous TPMS
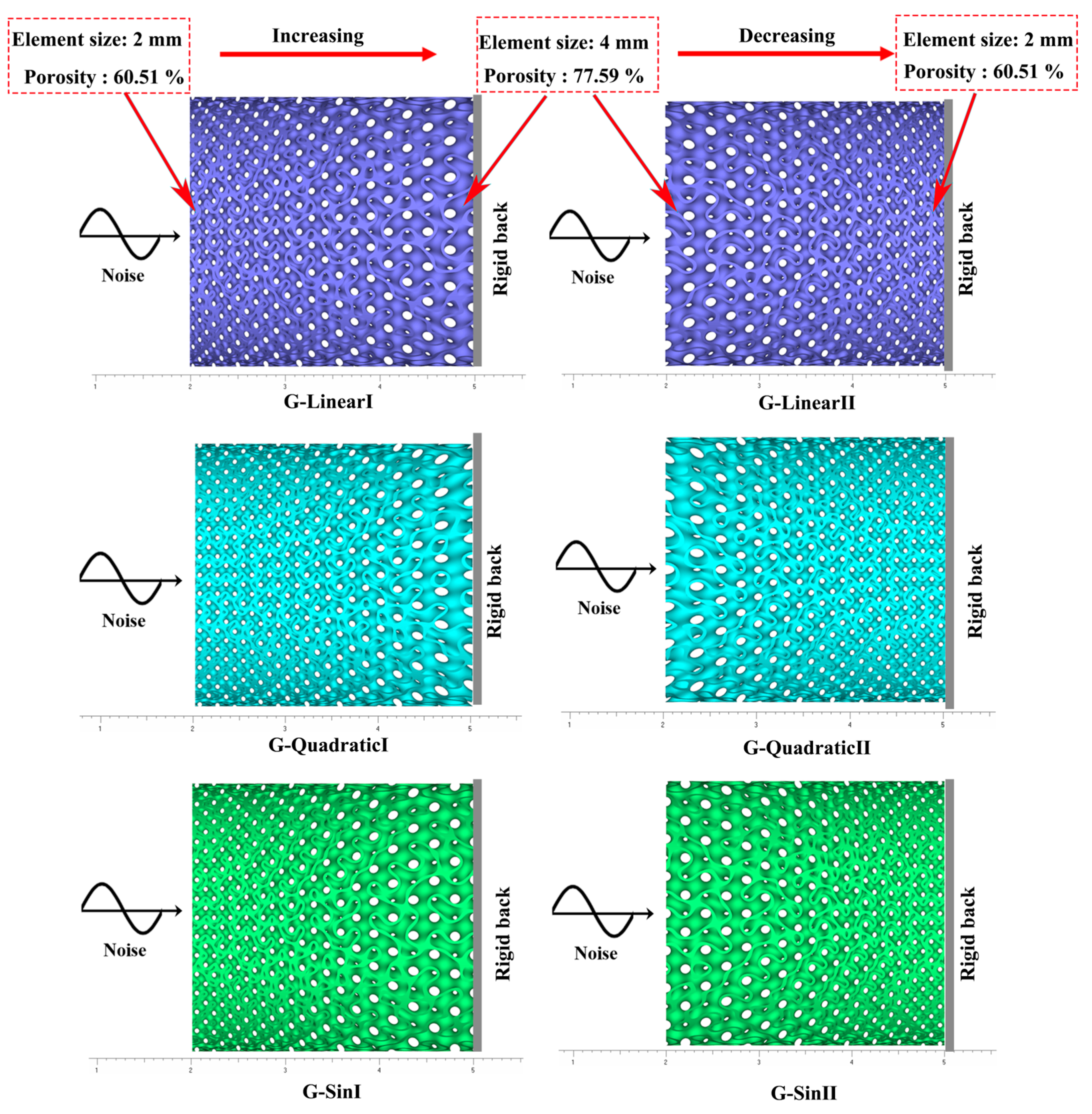
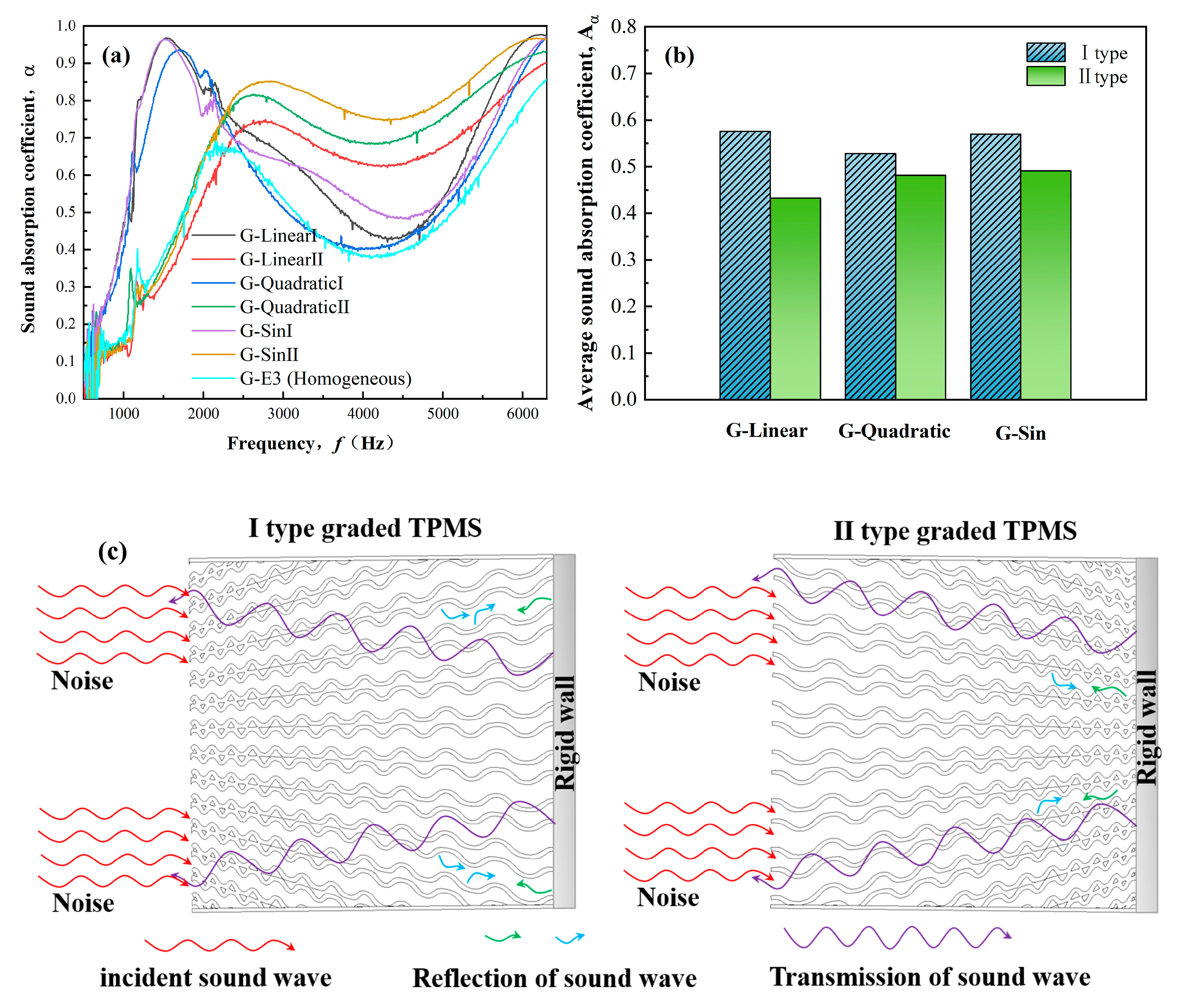
3.3. Sound Absorption Characteristics of Graded TPMS
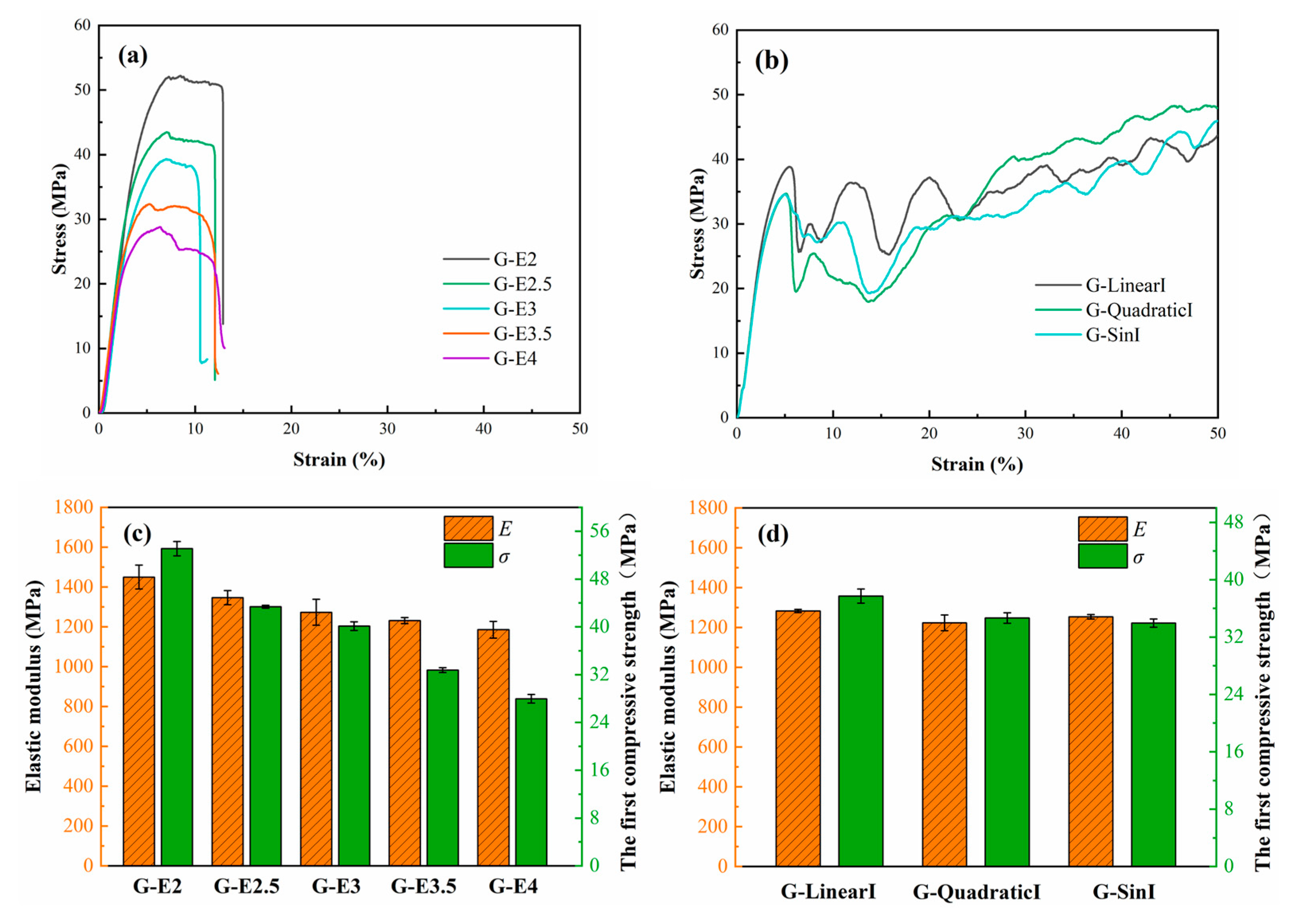
3.4. Mechanical Properties of TPMS
4. Conclusions
- (1)
- The frequency corresponding to the sound absorption peak shifts to low frequencies as the height of the material increases. The sound absorption coefficient of the gyroid increases as the height of the material increases from 3 to 30 mm, the offset thickness of the surface increases from 0.2 to 0.5 mm, and the element size decreases from 4 to 2 mm. Based on the contour of sound absorption, the optimized structural design interval parameters were obtained independently for each parameter, and all other parameters were kept constant.
- (2)
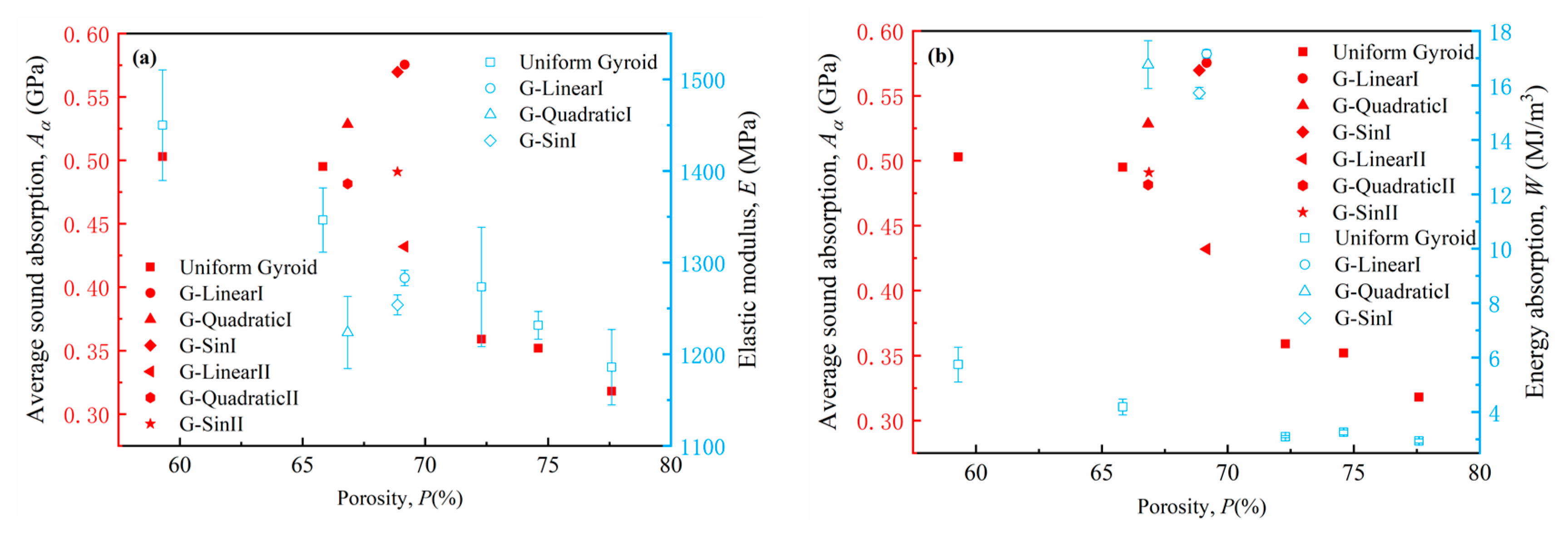
- The graded direction and function have an impact on the sound absorption characteristics. Owing to the multiple scattering and Helmholtz-resonator-like effect, the first resonance peak of the graded TPMS with porosity from 60.51 to 77.59% is higher than the graded TPMS with porosity from 77.59 to 60.51%, and the former achieves perfect absorption at 1528 Hz, and the latter has a broadband sound absorption coefficient.
- (3)
- The compressive yield plateau of homogeneous TPMS is short due to the 45° shearing band, and graded TPMS has a long yield plateau in a layer-wise failure pattern. The length of the yield plateau determines that the energy absorption value of graded TPMS is higher than that of homogeneous TPMS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rastegar, N.; Ershad-Langroudi, A.; Parsimehr, H.; Moradi, G. Sound-absorbing porous materials: A review on polyurethane-based foams. Iran. Polym. J. 2022, 31, 83–105. [Google Scholar] [CrossRef]
- Allard, J.; Atalla, N. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mamtaz, H.; Hosseini Fouladi, M.; Nuawi, M.Z.; Narayana Namasivayam, S.; Ghassem, M.; Al-Atabi, M. Acoustic absorption of fibro-granular composite with cylindrical grains. Appl. Acoust. 2017, 126, 58–67. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Chen, T.; Ying, Z. Research on the sound absorption characteristics of porous metal materials at high sound pressure levels. Adv. Mech. Eng. 2015, 7, 1–7. [Google Scholar] [CrossRef]
- Leclaire, P.; Umnova, O.; Dupont, T.; Panneton, R. Acoustical properties of air-saturated porous material with periodically distributed dead-end pores. J. Acoust. Soc. Am. 2015, 137, 1772–1782. [Google Scholar] [CrossRef]
- Palma, G.; Mao, H.; Burghignoli, L.; Göransson, P.; Iemma, U. Acoustic Metamaterials in Aeronautics. Appl. Sci. 2018, 8, 971. [Google Scholar] [CrossRef]
- Bheekhun, N.; Abu Talib, A.R.; Hassan, M.R. Aerogels in Aerospace: An Overview. Adv. Mater. Sci. Eng. 2013, 2013, 406065. [Google Scholar] [CrossRef]
- Cobo, P.; Simón, F. Multiple-Layer Microperforated Panels as Sound Absorbers in Buildings: A Review. Buildings 2019, 9, 53. [Google Scholar] [CrossRef]
- Choe, H.; Sung, G.; Kim, J.H. Chemical treatment of wood fibers to enhance the sound absorption coefficient of flexible polyurethane composite foams. Compos. Sci. Technol. 2018, 156, 19–27. [Google Scholar] [CrossRef]
- Guo, J.; Xiao, Y.; Ren, H.; Chen, H.; Yu, D.; Wen, J. Broadband low-frequency sound insulation of double-panel metastructures with a perforated lattice truss-core sandwich plate. Mech. Syst. Signal Process 2023, 200, 110634. [Google Scholar] [CrossRef]
- Xie, S.; Yang, S.; Yang, C.; Wang, D. Sound absorption performance of a filled honeycomb composite structure. Appl. Acoust. 2020, 162, 107202. [Google Scholar] [CrossRef]
- Kong, X.; Liu, B.; Li, Z.; Zhang, P.; Shi, C. Research on Sound Absorption Properties of Tri-Periodic Minimal Surface Sandwich Structure of Selective Laser Melting Titanium Alloy. Mater. Trans. 2023, 64, 861–868. [Google Scholar] [CrossRef]
- Gama, N.; Ferreira, A.; Barros-Timmons, A. Polyurethane Foams: Past, Present, and Future. Materials 2018, 11, 1841. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.-Y.; Alhammadi, A.; Giannini, V.; Al Teneiji, M.; Lee, D.-W. Elastic Vibration Bandgap of Architectured Materials based on Triply Periodic Minimal Surfaces. In Proceedings of the 2021 Fifteenth International Congress on Artificial Materials for Novel Wave Phenomena (Metamaterials), New York, NY, USA, 20–24 September 2021; pp. 11–14. [Google Scholar]
- Johnston, W.; Sharma, B. Additive manufacturing of fibrous sound absorbers. Addit. Manuf. 2021, 41, 101984. [Google Scholar] [CrossRef]
- Monkova, K.; Vasina, M.; Monka, P.P.; Kozak, D.; Vanca, J. Effect of the Pore Shape and Size of 3D-Printed Open-Porous ABS Materials on Sound Absorption Performance. Materials 2020, 13, 4474. [Google Scholar] [CrossRef]
- Zieliński, T.G.; Opiela, K.C.; Pawłowski, P.; Dauchez, N.; Boutin, T.; Kennedy, J.; Trimble, D.; Rice, H.; Van Damme, B.; Hannema, G.; et al. Reproducibility of sound-absorbing periodic porous materials using additive manufacturing technologies: Round robin study. Addit. Manuf. 2020, 36, 101564. [Google Scholar] [CrossRef]
- Cavalieri, T.; Boulvert, J.; Gabard, G.; Romero-García, V.; Escouflaire, M.; Regnard, J.; Groby, J.-P. Graded and Anisotropic Porous Materials for Broadband and Angular Maximal Acoustic Absorption. Materials 2020, 13, 4605. [Google Scholar] [CrossRef]
- Boulvert, J.; Humbert, T.; Romero-García, V.; Gabard, G.; Fotsing, E.R.; Ross, A.; Mardjono, J.; Groby, J.-P. Perfect, broadband, and sub-wavelength absorption with asymmetric absorbers: Realization for duct acoustics with 3D printed porous resonators. J. Sound Vib. 2022, 523, 116687. [Google Scholar] [CrossRef]
- Liu, Z.; Zhan, J.; Fard, M.; Davy, J.L. Acoustic properties of a porous polycarbonate material produced by additive manufacturing. Mater. Lett. 2016, 181, 296–299. [Google Scholar] [CrossRef]
- Opiela, K.C.; Zieliński, T.G.; Attenborough, K. Limitations on validating slitted sound absorber designs through budget additive manufacturing. Mater. Des. 2022, 218, 110703. [Google Scholar] [CrossRef]
- Yang, W.; An, J.; Chua, C.K.; Zhou, K. Acoustic absorptions of multifunctional polymeric cellular structures based on triply periodic minimal surfaces fabricated by stereolithography. Virtual Phys. Prototyp. 2020, 15, 242–249. [Google Scholar] [CrossRef]
- Gao, N.; Tang, L.; Deng, J.; Lu, K.; Hou, H.; Chen, K. Design, fabrication and sound absorption test of composite porous metamaterial with embedding I-plates into porous polyurethane sponge. Appl. Acoust. 2021, 175, 107845. [Google Scholar] [CrossRef]
- Prasetiyo, I.; Anwar, K.; Brahmana, F.; Sakagami, K. Development of stackable subwavelength sound absorber based on coiled-up system. Appl. Acoust. 2022, 195, 108842. [Google Scholar] [CrossRef]
- Feng, Y.; Zong, D.; Hou, Y.; Yin, X.; Zhang, S.; Duan, L.; Si, Y.; Jia, Y.; Ding, B. Gradient structured micro/nanofibrous sponges with superior compressibility and stretchability for broadband sound absorption. J. Colloid Interface Sci. 2021, 593, 59–66. [Google Scholar] [CrossRef]
- Yang, K.; Long, G.; Tang, Z.; Pan, X.; Su, W.; Xie, Y. Mechanical and acoustic properties of ceramsite sound absorbing boards with gradient structure. Acoust. Aust. 2022, 50, 393–403. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.; Ju, Z.; Zhao, J.; Hu, M.; Gao, M.; Luo, J.; Pu, H. Ultra-Broadband Sound Absorbing Materials Based on Periodic Gradient Impedance Matching. Front. Mater. 2022, 9, 909666. [Google Scholar] [CrossRef]
- Umnova, O.; Brooke, D.; Leclaire, P.; Dupont, T. Multiple resonances in lossy acoustic black holes—Theory and experiment. J. Sound Vib. 2023, 543, 117377. [Google Scholar] [CrossRef]
- Yang, X.; Shen, X.; Bai, P.; He, X.; Zhang, X.; Li, Z.; Chen, L.; Yin, Q. Preparation and Characterization of Gradient Compressed Porous Metal for High-Efficiency and Thin-Thickness Acoustic Absorber. Materials 2019, 12, 1413. [Google Scholar] [CrossRef]
- Boulvert, J.; Cavalieri, T.; Costa-Baptista, J.; Schwan, L.; Romero-Garcia, V.; Gabard, G.; Fotsing, E.R.; Ross, A.; Mardjono, J.; Groby, J.-P. Optimally graded porous material for broadband perfect absorption of sound. J. Appl. Phys. 2019, 126, 175101. [Google Scholar] [CrossRef]
- ASTM E1050-12; Standard Test Method for Impedance and Absorption of Acoustical Materials Using a Tube, Two Microphones and a Digital Frequency Analysis System. ASTM: West Conshohocken, PA, USA, 2012.
- ISO 13314:2011; Mechanical Testing of Metals Ductility Testing Compression test for Porous and Cellular Metals. ISO Publishing: Geneve, Switzerland, 2011.
- Guan, X.; Yang, J.; Deckers, E.; Hornikx, M. Computational Characterization of Functionally Graded Porous Ansorbers Based On Triply Periodic Minimal Surfaces (TPMS). In Proceedings of the 10th Convention of the European Acoustics Association, Turin, Italy, 11–15 September 2023. [Google Scholar]
- Zhang, X.H.; Qu, Z.G.; He, X.C.; Lu, D.L. Experimental study on the sound absorption characteristics of continuously graded phononic crystals. AIP Adv. 2016, 6, 105205. [Google Scholar] [CrossRef]
- Zhang, X.; Qu, Z.; Xu, Y. Enhanced sound absorption in two-dimensional continuously graded phononic crystals. Jpn. J. Appl. Phys. 2019, 58, 090904. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.; Aremu, A.; Tuck, C.; Ashcroft, I.; Wildman, R.D.; Hague, R. A mechanical property evaluation of graded density Al-Si10-Mg lattice structures manufactured by selective laser melting. Mater. Sci. Eng. A 2016, 670, 264–274. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, L.; Yan, X.; Wang, Z.; Li, X.; Fang, G. Revealing the apparent and local mechanical properties of heterogeneous lattice: A multi-scale study of functionally graded scaffold. Virtual Phys. Prototyp. 2022, 18, 1. [Google Scholar] [CrossRef]
- Yang, L.; Mertens, R.; Ferrucci, M.; Yan, C.; Shi, Y.; Yang, S. Continuous graded Gyroid cellular structures fabricated by selective laser melting: Design, manufacturing and mechanical properties. Mater. Des. 2019, 162, 394–404. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, Y.; Wang, D.; Song, C.; Chen, J. Microstructure and mechanical properties of CuSn/18Ni300 bimetallic porous structures manufactured by selective laser melting. Mater. Des. 2019, 165, 107583. [Google Scholar] [CrossRef]
- Liu, F.; Ran, Q.; Zhao, M.; Zhang, T.; Zhang, D.Z.; Su, Z. Additively manufactured continuous cell-size gradient porous scaffolds: Pore characteristics, mechanical properties and biological responses in vitro. Materials 2020, 13, 2589. [Google Scholar] [CrossRef]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.Y.; Wei, J.; Lu, W.F. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, F.; Zhang, X.; Zhang, K.; Wang, X.; Gan, D.; Yang, B. Cell-size graded sandwich enhances additive manufacturing fidelity and energy absorption. Int. J. Mech. Sci. 2021, 211, 106798. [Google Scholar] [CrossRef]
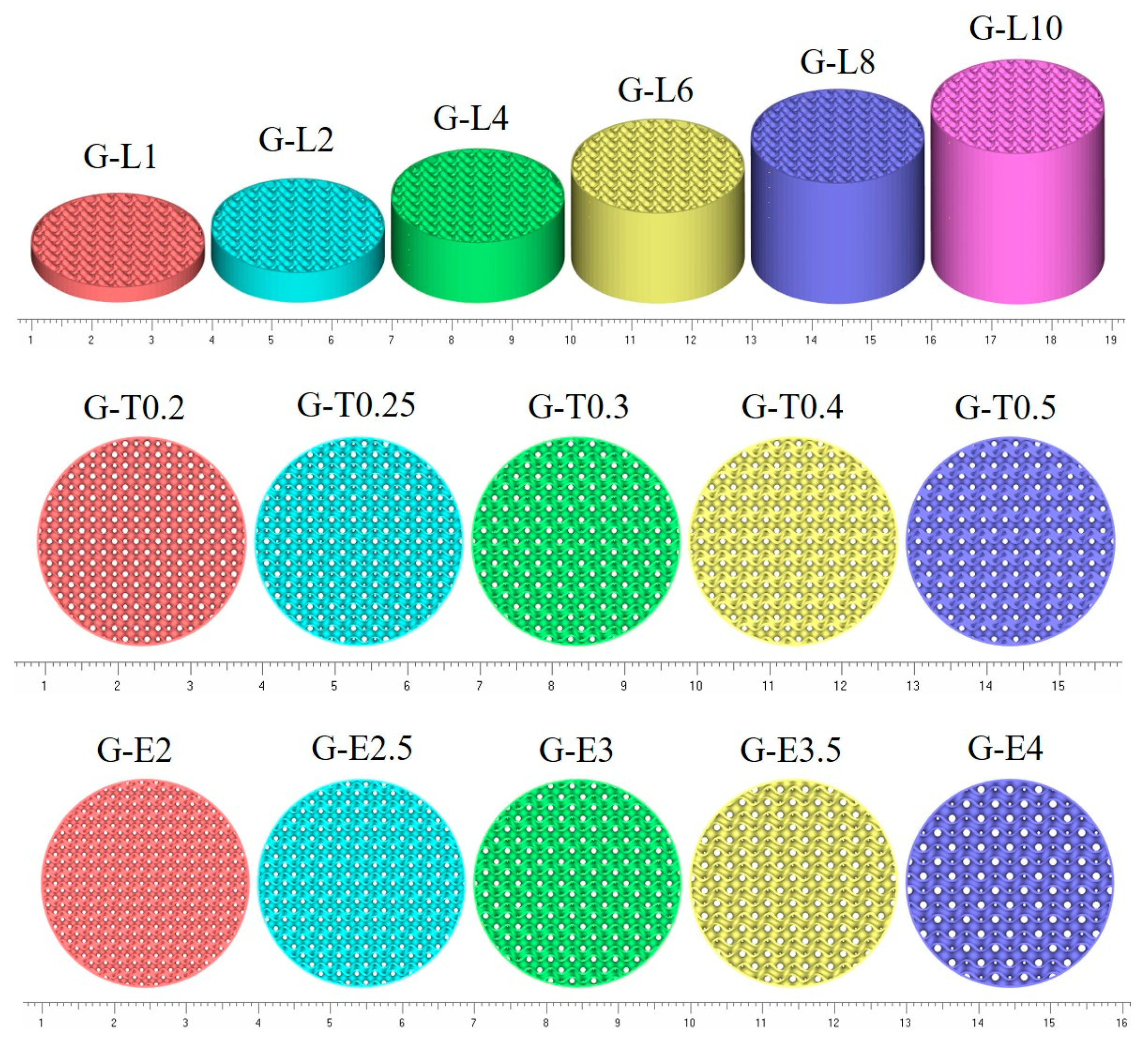





| Specimens | Number of Layers | Height/mm | Element Size/mm | Offset Thickness of Surface/mm | Porosity/% |
|---|---|---|---|---|---|
| G-L1 | 1 | 3 | 3 | 0.3 | 72.29 |
| G-L2 | 2 | 6 | 3 | 0.3 | 72.29 |
| G-L4 | 4 | 12 | 3 | 0.3 | 72.29 |
| G-L6 | 6 | 18 | 3 | 0.3 | 72.29 |
| G-L8 | 8 | 24 | 3 | 0.3 | 72.29 |
| G-L10 | 10 | 30 | 3 | 0.3 | 72.29 |
| G-T0.2 | 10 | 30 | 3 | 0.2 | 80.57 |
| G-T0.25 | 10 | 30 | 3 | 0.25 | 75.21 |
| G-T0.3 | 10 | 30 | 3 | 0.3 | 72.29 |
| G-T0.4 | 10 | 30 | 3 | 0.4 | 65.52 |
| G-T0.5 | 10 | 30 | 3 | 0.5 | 60.51 |
| G-E2 | 15 | 30 | 2 | 0.3 | 59.30 |
| G-E2.5 | 12 | 30 | 2.5 | 0.3 | 65.83 |
| G-E3 | 10 | 30 | 3 | 0.3 | 72.29 |
| G-E3.5 | 8.6 | 30 | 3.5 | 0.3 | 74.60 |
| G-E4 | 7.5 | 30 | 4 | 0.3 | 77.59 |
| Specimens | Number of Layers | Height (mm) | Element Size (mm) | Offset Thickness of Surface (mm) | Porosity (%) |
|---|---|---|---|---|---|
| G-LinearI | 10 | 30 | 2→4 | 0.3 | 69.16 |
| G-LinearII | 10 | 30 | 4→2 | 0.3 | 69.16 |
| G-QuadraticI | 10 | 30 | 2→4 | 0.3 | 66.84 |
| G-QuadraticII | 10 | 30 | 4→2 | 0.3 | 66.84 |
| G-SinI | 10 | 30 | 2→4 | 0.3 | 68.87 |
| G-SinII | 10 | 30 | 4→2 | 0.3 | 68.87 |
| Laser Power (W) | Scanning Speed (mm/s) | Layer Thickness (mm) | Scanning Space (mm) |
|---|---|---|---|
| 150 | 1300 | 0.03 | 0.09 |
| Element | Al | Si | Mg | Cu | Fe | Mn | Ni | O |
|---|---|---|---|---|---|---|---|---|
| Composition (wt. %) | Bal. | 6.730 | 0.678 | 0.045 | 0.281 | 0.198 | 0.012 | 0.070 |
| Specimen | Porosity (%) | f1 (Hz) | α1 | FWHM (Hz) | Aα | Flow Resistance (Pa·s/m2) |
|---|---|---|---|---|---|---|
| G-L1 | 72.29 | - | - | - | 0.038 | 4382 |
| G-L2 | 72.29 | - | - | - | 0.055 | 2561 |
| G-L4 | 72.29 | 5712 | 0.498 | 4379 | 0.152 | 3429 |
| G-L6 | 72.29 | 3866 | 0.605 | 3938 | 0.253 | 2454 |
| G-L8 | 72.29 | 2652 | 0.661 | 3929 | 0.313 | 1829 |
| G-L10 | 72.29 | 2234 | 0.685 | 1624 | 0.359 | 1800 |
| G-T0.2 | 80.57 | 2244 | 0.627 | 3224 | 0.374 | 1640 |
| G-T0.25 | 75.21 | 2144 | 0.630 | 2866 | 0.375 | 1734 |
| G-T0.3 | 72.29 | 2234 | 0.685 | 1624 | 0.359 | 1800 |
| G-T0.4 | 65.52 | 2146 | 0.739 | 2656 | 0.415 | 2234 |
| G-T0.5 | 60.51 | 2166 | 0.821 | 2323 | 0.430 | 2348 |
| G-E2 | 59.30 | 2096 | 0.868 | 2747 | 0.503 | 3917 |
| G-E2.5 | 65.83 | 2054 | 0.802 | 3081 | 0.495 | 3895 |
| G-E3 | 72.29 | 2234 | 0.685 | 1624 | 0.359 | 1800 |
| G-E3.5 | 74.60 | 2094 | 0.606 | 2890 | 0.352 | 1403 |
| G-E4 | 77.59 | 2094 | 0.546 | 2991 | 0.318 | 1076 |
| Specimen | Porosity (%) | f1 (Hz) | α1 | FWHM (Hz) | Aα | Flow Resistance (Pa·s/m2) |
|---|---|---|---|---|---|---|
| G-LinearI | 69.16 | 1534 | 0.968 | 2815 | 0.5755 | 5082 |
| G-LinearII | 69.16 | 2772 | 0.749 | 5436 | 0.4320 | 3032 |
| G-QuadraticI | 66.84 | 1680 | 0.936 | 2205 | 0.5284 | 3341 |
| G-QuadraticII | 66.84 | 2610 | 0.817 | 6009 | 0.4815 | 4026 |
| G-SinI | 68.87 | 1528 | 0.964 | 3425 | 0.5697 | 4666 |
| G-SinII | 68.87 | 2834 | 0.852 | 7411 | 0.4910 | 4545 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Liu, C.; Deng, M.; Li, Y.; Li, J.; Wang, D. Graded Minimal Surface Structures with High Specific Strength for Broadband Sound Absorption Produced by Laser Powder Bed Fusion. Coatings 2023, 13, 1950. https://doi.org/10.3390/coatings13111950
Zhang M, Liu C, Deng M, Li Y, Li J, Wang D. Graded Minimal Surface Structures with High Specific Strength for Broadband Sound Absorption Produced by Laser Powder Bed Fusion. Coatings. 2023; 13(11):1950. https://doi.org/10.3390/coatings13111950
Chicago/Turabian StyleZhang, Mingkang, Chang Liu, Mingjian Deng, Yuhao Li, Jinwei Li, and Di Wang. 2023. "Graded Minimal Surface Structures with High Specific Strength for Broadband Sound Absorption Produced by Laser Powder Bed Fusion" Coatings 13, no. 11: 1950. https://doi.org/10.3390/coatings13111950
APA StyleZhang, M., Liu, C., Deng, M., Li, Y., Li, J., & Wang, D. (2023). Graded Minimal Surface Structures with High Specific Strength for Broadband Sound Absorption Produced by Laser Powder Bed Fusion. Coatings, 13(11), 1950. https://doi.org/10.3390/coatings13111950








